Monocular 3D Head Reconstruction via Prediction and Integration of

Normal Vector Field

Oussema Bouaﬁf

1,2

, Bogdan Khomutenko

and Mohamed Daoudi

MCQ-Scan, Lille, France

IMT Lille Douai, Univ. Lille, CNRS UMR 9189 CRIStAL, Lille, France

Keywords:

3D Head Reconstruction, Face Reconstruction, Monocular Reconstruction, Facial Surface Normals, Deep

Learning, Synthetic Data.

Abstract:

Reconstructing the geometric structure of a face from a single input image is a challenging active research area

in computer vision. In this paper, we present a novel method for reconstructing 3D heads from an input image

using a hybrid approach based on learning and geometric techniques. We introduce a deep neural network

trained on synthetic data only, which predicts the map of normal vectors of the face surface from a single

photo. Afterward, using the network output we recover the 3D facial geometry by means of weighted least

squares. Through qualitative and quantitative evaluation tests, we show the accuracy and robustness of our

proposed method. Our method does not require accurate alignment due to the image-to-image translation

network and also successfully recovers 3D geometry for real images, despite the fact that the model was

trained only on synthetic data.

1 INTRODUCTION

In the last decades, 3D face models have been em-

ployed in several applications of Computer Vision.

Unlike 2D face images, the three-dimensional face

model reconstruction can encounter different prob-

lems, such as variations in poses and illumination

(Abate et al., 2007). A 3D face model has the po-

tential to achieve state-of-the-art performances on ap-

plications such as gender classiﬁcation (Han et al.,

2009), facial animation (Thies et al., 2016) and face

recognition (Blanz and Vetter, 2003).

Originally, the problem has been treated using the

following techniques. A large part of the proposed

solutions use facial landmarks, that is, a set of auto-

matically detected key points on the face, which can

be used as a guideline for the reconstruction process.

Many methods are based on optimization algorithms

and use the 3D Morphable Model (3DMM) pro-

posed by Blanz and Vetter (Blanz and Vetter, 1999),

which is a statistical model of texture and shape.

Some approaches are based on structure from mo-

tion, optical ﬂow or shape from shading procedures

(Kemelmacher-Shlizerman and Basri, 2010). Despite

the fact that the use of these elements allows us to per-

form the reconstruction, there are some difﬁcult cases

for such methods. They are sensitive to light condi-

tions, reﬂections, shadows, and image quality.

Another way to separate 3D face reconstruction

methods is to take into account the number of in-

put images. Monocular methods have a signiﬁcant

drawback which is the fact of being unable to re-

cover precise geometric measurements with a single

frontal view. In addition, the local details that char-

acterize the shape of the face between all surfaces

are complex to grasp, resulting in very similar re-

constructions from one subject to another. However,

with multiview-based methods, it is possible to have

a more faithful 3D reconstruction since we exploit the

geometric constraints of several images in different

views. However, these methods frequently produce

noisy results.

More recently, solutions to address this problem

have changed with Convolutional Neural Networks

(CNNs) and request only a single image as input

(Richardson et al., 2017; Dou et al., 2017). But one of

the most known difﬁculties to apply neural networks

is the lack of 3D faces data sets. To answer this need,

many approaches propose to use synthetic data or 3D

models ﬁtted by using one of the methods cited above.

In some cases, when the training set is limited, end-

to-end learning systems tend to perform worse than

geometric methods.

In this paper, we propose a hybrid method com-

Bouaﬁf, O., Khomutenko, B. and Daoudi, M.

Monocular 3D Head Reconstruction via Prediction and Integration of Normal Vector Field.

DOI: 10.5220/0008961703590369

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages

359-369

ISBN: 978-989-758-402-2; ISSN: 2184-4321

359

Figure 1: The pipeline of our proposed method. Given an input facial image, we estimate two different maps (magnitude

of depth gradient map W (a), normal surface map N (b)) through a network which was trained using a fully synthetic data

set. Using these generated maps, we reconstruct the 3D facial shape by a weighted least squares normal integration technique

where W acts as a weight map.

posed of a learning-based approach and a geomet-

ric one that is capable of reconstructing face surface

from an input facial image. In the ﬁrst stage, from the

learning approach, we show that a Generative Adver-

sarial Model (GAN) can translate a facial image into

two maps: normals of facial surface (N) and gradient

magnitude (W ). Using these maps in a weighted least

squares (WLS) technique, we retrieve the 3D facial

surface.

The main contributions of this paper are:

• We use a fully synthetic data set of 3D human

heads composed of different elements including

3D faces geometry from the LYHM (Dai et al.,

2017) model, hair models from (Hu et al., 2015)

database and different faces textures, eye colors

and eyeglass patterns (Section 3.1),

• A Generative Adversarial Model (GAN) from (Su

et al., 2018) adapted to predict different images

from the input face image that will be used during

the reconstruction step (Section 3.2),

• A more reliable head reconstruction using a novel

normal integration technique based on a weighted

least squares method (Section 3.3).

2 RELATED WORK

In this section, we review works on 3D face recon-

struction methods, prediction and integration of nor-

mals.

The different components of the human face may

be divided into two broad groups, one for the low-

detail geometry (e.g., nose, cheek, forehead) and the

other one for the high-detail geometry (e.g., wrinkles,

eyebrows, beards, and pores). Methods such as multi-

view geometry (Furukawa and Ponce, 2009) and

structure-from-motion (Gonzalez-Mora et al., 2010),

which are based on reconstruction from multiple im-

ages, can recover the low-detail geometry features.

However, to be able to capture the high-detail geo-

metric features, successful solutions rely on profes-

sional capture systems such as 3D laser scans or high-

precision multi-view light stage systems such as those

used in (Ghosh et al., 2011). In reality, these kinds

of methods require a signiﬁcant investment in space,

time and ﬁnances for the large setup, powerful light

sources, as well as extensive calibrations of the posi-

tion and direction of the light sources.

Monocular 3D Face Reconstruction Methods:

Generally, the best-known methods that use few im-

ages, or a single image, as the input to reconstruct a

3D face are based on the work of Blanz and Vetter

(Blanz and Vetter, 1999), who proposed the 3D Mor-

phable Model (3DMM). The model consists of a sep-

arate shape model and an albedo model, constructed

using Principal Component Analysis (PCA). The key

idea behind the 3DMM is that, given a sufﬁciently

large data set of 3D faces, one can accurately recon-

struct any new shape and texture as a linear combi-

nation of the shapes and textures of the 3D faces in

the data set. The use of 3DMM allows us to recon-

struct a new 3D face from one or more images by

ﬁnding the linear combination of the statistical model

bases that best ﬁts the given 2D image(s). For exam-

ple, (Amberg et al., 2008) ﬁt an expression-invariant

3DMM to noisy laser scans using an Iterative Closest-

Point (ICP) registration method. In (Zollh

ofer et al.,

2011), authors propose to ﬁt a 3DMM directly to the

aggregated data from a consumer depth camera. Their

idea was to deform the mean shape of a 3DMM to

the aggregated depth data using the non-rigid registra-

tion method from (Sumner et al., 2007). Most other

methods are based on landmarks (Booth et al., 2017),

edges (Bas et al., 2016) and local image features (Hu-

ber et al., 2015). Recently, Convolutional Neural Net-

works (CNNs) were used with 3DMMs to reconstruct

3D faces from a single input photo. (Tran et al., 2017)

ﬁt the 3DMM to the images in a data set and com-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

360

bined the shape and texture vectors that corresponded

to images of the same person. They proposed us-

ing regression methods to obtain the 3DMM shape

and texture parameters directly from an input photo.

(Dou et al., 2017) proposed UH-E2FAR, an end-to-

end 3D face reconstruction method based on deep

neural networks. They introduced two key compo-

nents - a fusion-CNN and a multi-task learning loss.

With both components, they divided 3D face recon-

struction into two sub tasks - predicting the neutral

3D facial shape and the expression parameters of a

3DMM - using a single frontal image from each per-

son. (Richardson et al., 2017) proposed an end-to-

end approach composed of two connected networks

(CoarseNet and FineNet) to produce coarse and ﬁne

details of facial shape. (Sela et al., 2017) presented an

algorithm which employs an Image-to-Image trans-

lation network that jointly maps the input image to

a depth image and a facial correspondence map. A

model-free approach was proposed by (Feng et al.,

2018a) which learns 3D face curves from horizontal

and vertical epipolar plane images of a light ﬁled im-

ages using a densely connected network (FaceLFnet).

Produced curves are combined together to obtain a

more accurate combined 3D point cloud. In (Feng

et al., 2018b), an encoder-decoder structure was used

to learn a transfer function between an input RGB im-

age and the UV position map, which was a 2D repre-

sentation designed to record the 3D shape of a com-

plete face in UV space.

Prediction of Normals: Normal maps are used in

various graphics applications like 3D shape recon-

struction or adding details to allow rendering of sur-

faces to be more realistic. But producing high-

quality normal maps for complex objects represents

a challenging task. To resolve this problem, sev-

eral learning-based works have been proposed. Part

of these applications were devoted to the generation

of normal maps based on sketches with deep neural

networks. In (Su et al., 2018) work, an interactive

method for normal map generation from sketch input

was proposed where the U-Net (Ronneberger et al.,

2015) architecture was adopted in a conditional GAN

framework. (Lun et al., 2017) used ConvNet network

to predict depth and normal maps from multi-view

sketches, and then combine outputs into a 3D point

cloud via energy minimization. Another sketch-based

work was proposed by (Hudon et al., 2018), were

they present a way of predicting high-resolution nor-

mal maps directly without any user annotation or in-

teraction. Using a multi-scale representation of their

input images, they ensure the efﬁciency and qual-

ity of produced data. Another category of methods

was proposed to predict the normal map from differ-

ent objects or (outdoor/indoor) scenes. Several ap-

proaches have been addressed by (Bansal et al., 2016)

with a skip-network model, (Qiu et al., 2019) with

a jointly predicted depth and surface normal from a

single image, (Wang et al., 2015) with a network to

estimate both local and global normal map estima-

tion. Similarly to our work, (Trigeorgis et al., 2017)

proposed a 3D face reconstruction method based on

integration normal method where facial normal map

is produced by a fully-convolutional network. Our

proposed pipeline is different from (Trigeorgis et al.,

2017) in three important aspects: ﬁrstly, we use a fully

synthetic data set of 3D heads, whereas the (Trige-

orgis et al., 2017) data set was composed of various

data sets mainly limited to the facial part of the head.

Secondly, (Trigeorgis et al., 2017) explored various

DCNN architectures whereas we use the symmetric

skipping network (U-Net) (Ronneberger et al., 2015)

with a discriminator (Su et al., 2018), a common fea-

ture of Generative Adversarial Networks. Thirdly,

(Trigeorgis et al., 2017) used the standard Frankot-

Chellappa method (Frankot and Chellappa, 1988a) to

recover 3D facial shape from predicted normals. We

use a weighted least square method along with mag-

nitude depth gradient maps as a way to improve the

reconstruction quality in the neighborhood of depth

discontinuities. Furthermore, we provide quantitative

evaluation of the reconstruction precision, performed

on the BU-3DFE (Yin et al., 2006) data set.

Integration of Normal: Various approaches have

suggested to estimate the depth maps from normals

for a long time and they are generally classiﬁed in

several groups. In (Frankot and Chellappa, 1988b)

and (Simchony et al., 1990), Discrete Fourier Trans-

form and Discrete Cosine transform-based methods

are proposed. Some other basis variants have been

proposed where they use shapelets (Kovesi, 2005),

wavelet (Hsieh et al., 1995) or Dirac delta functions

(Karac¸alı and Snyder, 2003). The reconstruction via

the Poisson equation (Simchony et al., 1990) is prob-

ably the most well-known technique. This approach

uses the `

norm since it is assumed that the residual

gradient follows a normal distribution. And so, the

problem is quadratic and therefore admits a unique

and simple solution. On the other hand, the `

norm

does not support the presence of outliers, which can

produce deformed surfaces. In this context, (Agrawal

et al., 2006) propose a general framework to extend

the Poisson equation. Other approaches known as

regularization methods (Terzopoulos, 1988; Harker

and Oleary, 2015) have been proposed and attempt

to smooth depth gradients under certain criteria. Fi-

Monocular 3D Head Reconstruction via Prediction and Integration of Normal Vector Field

361

nally, the latest approaches are weighted-based, and

they use the constraint partially by a weighting map

where weight values were planned to deal with local

discontinuity. Similarly to these works (Qu

eau and

Durou, 2015; Wang et al., 2012), we propose the use

of a weighting map generated from a deep neural net-

work model. Recently, (Xie et al., 2019) proposed

an approach based on a discrete framework for dis-

continuity preservation where two normal incompati-

bility features and an efﬁcient discontinuity detection

scheme were introduced. More normals integration

state-of-art methods were explained in (Qu

eau et al.,

2018).

3 PROPOSED METHOD

In this section, we describe the details of our proposed

framework as illustrated in Fig. 1. Our method takes

a facial image as input and the network produces two

outputs which are aligned with the input image: an es-

timated normal surface N and an image of estimated

magnitude of the depth gradient W. All of these out-

puts are used in a 3D reconstruction algorithm guided

by W to recover the 3D surface of the face. Firstly,

we introduce the synthetic data set generation method

used to produce data for the training stage in Section

3.1. In Section 3.2 we describe our network model

architecture which was used in (Su et al., 2018) and

illustrated in Fig. 3. Finally, the details of our recon-

struction stage are explained in Section 3.3.

3.1 Synthetic Data Generation

Compared to (Trigeorgis et al., 2017) work, which

was based on a mix of synthetic and real data to train

the network, our proposed model has been trained

only on synthetic data. To do that, we have set up

a synthetic data generator composed of several parts

that gives us a complete human head model. We used

for the 3D human head model a 3DMM craniofacial

model proposed by (Dai et al., 2017). The Liver-

pool York Head Model (LYHM) (Dai et al., 2017) has

been used to provide a parametric model to synthe-

size heads with a known ground truth geometry. Its

composed of two parametric models: the shape and

the texture. Changing the shape and the texture pa-

rameters can create different subjects.

In our work, we use only the shape part which was

described with a linear model that is used to generate

novel 3D head examples as follows :

X = X

+Wy

(1)

Where X is the 3D head, X

the mean face shape,

W is the principal components of the shape model,

Figure 2: Training data samples. From top to bottom: Syn-

thetic facial images. Normal surface maps N. Gradient

Magnitude maps W .

and y is the corresponding coefﬁcient vector shape.

Using this model, an inﬁnite number of synthetic

faces can be generated by choosing a pair of param-

eters from a normal distribution y ∼ N(0,1). For

the hair we use different models from the (Hu et al.,

2015) data set with different colors and the Kajiya-

kay model (Kajiya and Kay, 1989) for the hair light-

ing rendering. We also use different male and female

face textures directly mapped with the 3D head model

and we align the head with a 3D eyes model where we

randomly change the color of the iris for each head

model. Finally, we also simulate six different 3D

glasses models to create some occlusions. Once the

different 3D components were aligned, random heads

are generated under various illumination conditions,

shadows, poses, scales, coefﬁcients for physically-

based materials. Finally, to make the model insen-

sitive to the background, a random background image

taken from the COCO data set (Lin et al., 2014) is

added. Some examples of the training data set used

for this work are shown in Fig. 2.

Once the ﬁnal 3D head model has been gener-

ated as detailed above, we compute the normal sur-

face only for the head and eyes models by using the

angle weighted method from (Klasing et al., 2009) as

written in (2). Normal values n

are calculated for

each vertex location p

∈ Re

, given the set of vertices



i,1

i,2

,...,q

i,k



that are adjacent to p

∑

j=1

i, j

− p

] × [q

i, j+1

− p

]

|[q

i, j

− p

] × [q

i, j+1

− p

= arccos



i, j

− p

i, j+1

− p

i, j

− p

||q

i, j+1

− p



(2)

The choice fell on the use of normals for various

reasons. First, components of normal ﬁeld deﬁne lo-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

362

cal geometric properties and hence disentangled from

one another across certain distances in the sense that

we can predict them completely independently, in

contrast to the depth values which should be predicted

all together. That is, without knowing the depth value

of the tip of the nose, for example, one cannot predict

the value for the eyes. Second, normals are invariant

to translation and scaling. To improve the quality of

3D reconstruction, the generation of gradient magni-

tude map |∇ f (x, y)| from the pixel-wise depth image

is proposed (third row in Fig. 2). The effect of using

this information is analysed in Section 3.3

3.2 Network Structure

The proposed GAN architecture is based on (Su et al.,

2018) work, where a network has been trained to map

the normal surface map from a sketch and a binary

point mask inputs. Some changes have been made

to this network to adapt it to our problematic (more

details in Fig. 3).

Figure 3: Our neural network architecture aims to gener-

ate two maps given facial input image. The input training

data as is shown on the left is composed of a facial input

image and two ground-truth maps: N and W. The encoder-

decoder’s input is the image of the face, while at the output

it produces two different maps (shown on the right). Af-

ter that, we inject ground truth and generated maps together

with the facial image as the input of discriminator. In this

stage, we check if the generated maps are real or fake, so

we encourage the encoder-decoder to produce more realis-

tic maps according to face image input. The spatial size and

the number of layers are indicated in and above each block,

respectively.

The model is composed of a encoder-decoder net-

work and a discriminator, proposed in (Ronneberger

et al., 2015). All training images have 128 × 128 pix-

els size. As an input, we stack three images, the facial

image (RGB), N (three channels) and W (single chan-

nel), while we have only two generated maps.

The encoder has the same elements as the discrim-

inator (discussed below), the decoder is composed of

ReLU activation function, deconvolution, batch nor-

malization, and a dropout unit. To reduce the informa-

tion loss between successive layers, we use a symmet-

ric connection between the encoder and the decoder

(Ronneberger et al., 2015). Therefore, we concate-

nate each layer of the encoder with the corresponding

channel in the decoder. The encoder-decoder is com-

posed of 16 layers. In the output layer, tanh is used as

an activation function, since N lies in the range [-1, 1].

The discriminator is composed of 4 layers, and it is

inspired by the encoder. Each layer is composed of:

convolution, batch normalization, and ReLU activa-

tion function. We adopt the loss function used in (Su

et al., 2018) for our purposes. Our objective function

becomes:

F = E

x∼p

data

,y∼p

[D(y/x)] − E

˜y∼p

gen

[D( ˜y/x)]−

= E

y∼p

, ˜y∼p

gen

[||y − ˜y||

]

(3)

Where x represents the input face image, y is the

corresponding concatenated input maps, ˜y is the gen-

erated outputs. P

data

, P

, and P

gen

are the distributions

of real input data, input map and generated outputs

data, respectively. The encoder-decoder loss is mixed

with a pixel wised loss L

penalized by λ

to mea-

sure the difference between the generated maps and

the real input maps, and so to supervise the training

process.

3.3 3D Face Reconstruction

Our 3D reconstruction solution is based on the inte-

gration of normals guided by the magnitude of the

depth gradient, to improve the reconstruction preci-

sion in the presence of discontinuities. For this, we

retrieve the two output maps W and N from the gen-

erative model where:

• W : R

→ R is the magnitude of depth gradient,

• N : R

→ R

is the normal surface map.

Thenceforth, we compute depth gradient G based on

N as described in the following:

G : R

→ R

G(u,v) =



p(u,v)

q(u,v)







−

(u,v)

−

(u,v)





(4)

where N

, N

, and N

are the three components of N

and (u,v) represents the pixels of the discrete domain

Ω ⊂ R

. After that, we feed G(u, v) and W (u, v) into a

weighted least squares solver deﬁned in a continuous

setting as follows:

argmin

u,v∈Ω

w(u,v)||∇h(u,v) − G(u,v)||

dudv

(5)

Monocular 3D Head Reconstruction via Prediction and Integration of Normal Vector Field

363

w(u,v) =

1 + λW (u,v)

(6)

w(u,v) is the weight term used to enforce confor-

mity of the reconstructed surface with the gradient

term near the face discontinuities. In (6), λ is a crit-

ical parameter to tune (see details in section 4.2). In

this step, we estimate depth map values of a function

h : R

→ R within the reconstruction domain Ω where

G and W are deﬁned. In the discrete setting, our min-

imization problem is formulated as below:

argmin

∑

u,v∈Ω

u+0.5,v

u+1,v

− h

u,v

− p

u+0.5,v

)

u,v+0.5

u,v+1

− h

u,v

− q

u,v+0.5

)

(7)

Where (u + 0.5, v) and (u,v + 0.5) are the average

points between two successive pixels along the hor-

izontal and vertical axes respectively. For example,

gradient between pixels is deﬁned in this way:

u+0.5,v

u,v

+ p

u+1,v

)

u,v+0.5

u,v

+ q

u,v+1

)

(8)























  



  









Figure 4: Illustration of our discretization method.

An illustration of our discretization method on a

regular square 2D grid is shown in Fig. 4. This is a

classical linear least-square problem, we solve it us-

ing the Ceres solver (Agarwal et al., ). Evaluation of

the reconstruction quality is given in section 4.2.

4 EXPERIMENTAL RESULTS

This section presents three sets of experiments that

were conducted to evaluate the performance of our 3D

reconstruction method. Firstly, we discuss the quality

of our training model in Section 4.1. Then, we show

our contribution to the reconstruction method and the

advantage it brings compared to other normals inte-

grations method in Section 4.2. Finally, we verify

this by qualitative and quantitative experiments on a

known database in Section 4.3.

Test Data set: To evaluate the quality of predicted

maps from our trained model and also our 3D recon-

struction method, we generate a test data set from

our generator described in the Section 3.1. This

test data set is used in our experiments. It consists

of 200 images of people (equitably distributed be-

tween males and females) generated with their corre-

sponding ground truth maps that include face images,

normal surface maps, gradient magnitude maps, and

depth maps. Depth is measured in units equivalent to

the pixel size.

4.1 Training Evaluation

Table 1: Mask and Normals evaluations for test data set. We

show in the top table part our segmentation results using

precision and recall percentage. The second part contains

angular error results.

Mask Evaluation

precision 93.72 %

recall 98.40 %

Normals Evaluation

Mean 10.01°

Std 12.45°

< 10° 67.50 %

< 20° 92.65 %

< 30° 97.13 %

To train the model, we have used 40,000 facial images

(20,000 for males and also for females) and their cor-

responding maps. We train the model for about 1700

epochs with a learning rate of 1e − 4, 64 as a batch

size, 500 for λ

, and using RMSprop optimizer. We

also add random blur effect and gaussian noise as data

augmentation.

To evaluate our Image-to-Image translation

model, we show in Fig. 5 different examples with

ground truth and maps produced by our GAN model.

We can well notice that with the use of our synthetic

data which contain occlusions (hair, glasses, random

backgrounds), the network succeeds to separate

properly the whole head. In situations where there

are covered parts, the network tries predicting a more

approximate form of the precise shape hidden by

the hair in most cases. Using the test database, we

performed some experiments to evaluate the accuracy

of our network. Table 1 shows the results indicating

a signiﬁcant percentage of precision and recall,

which explains that most of the pixels produced by

the network correspond to the pixels of ground truth

maps. In a second time, we evaluated the precision

on the N maps and for this, we calculated the angular

error between the maps of the ground truth and those

produced by the network.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

364

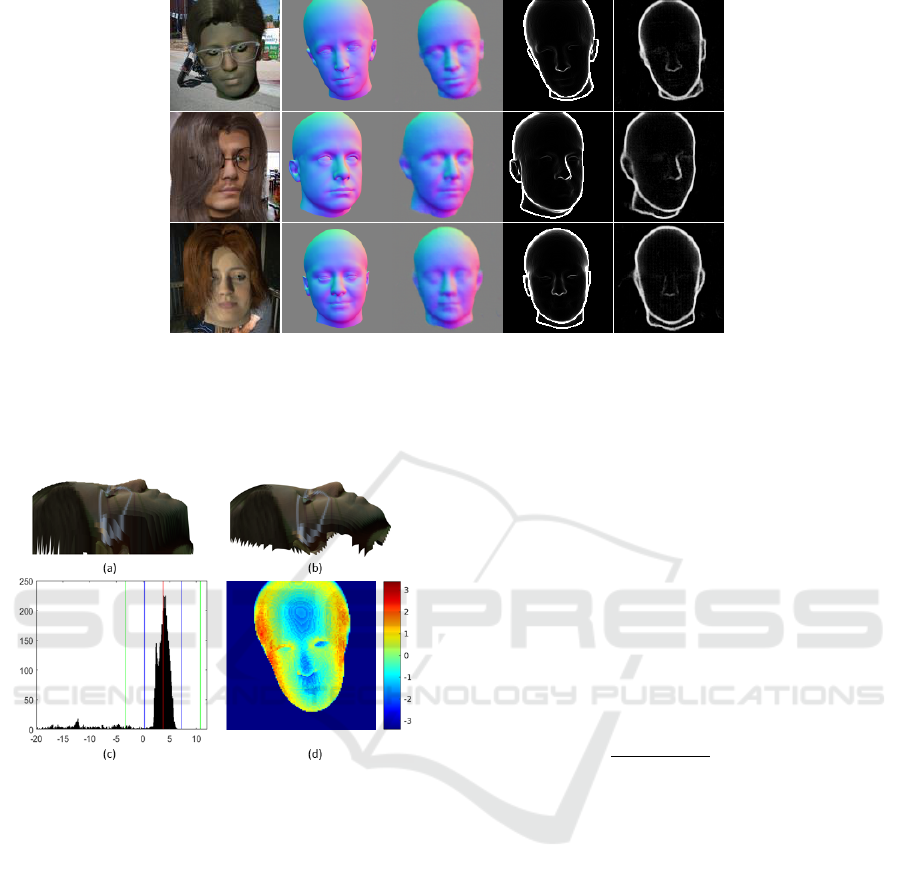
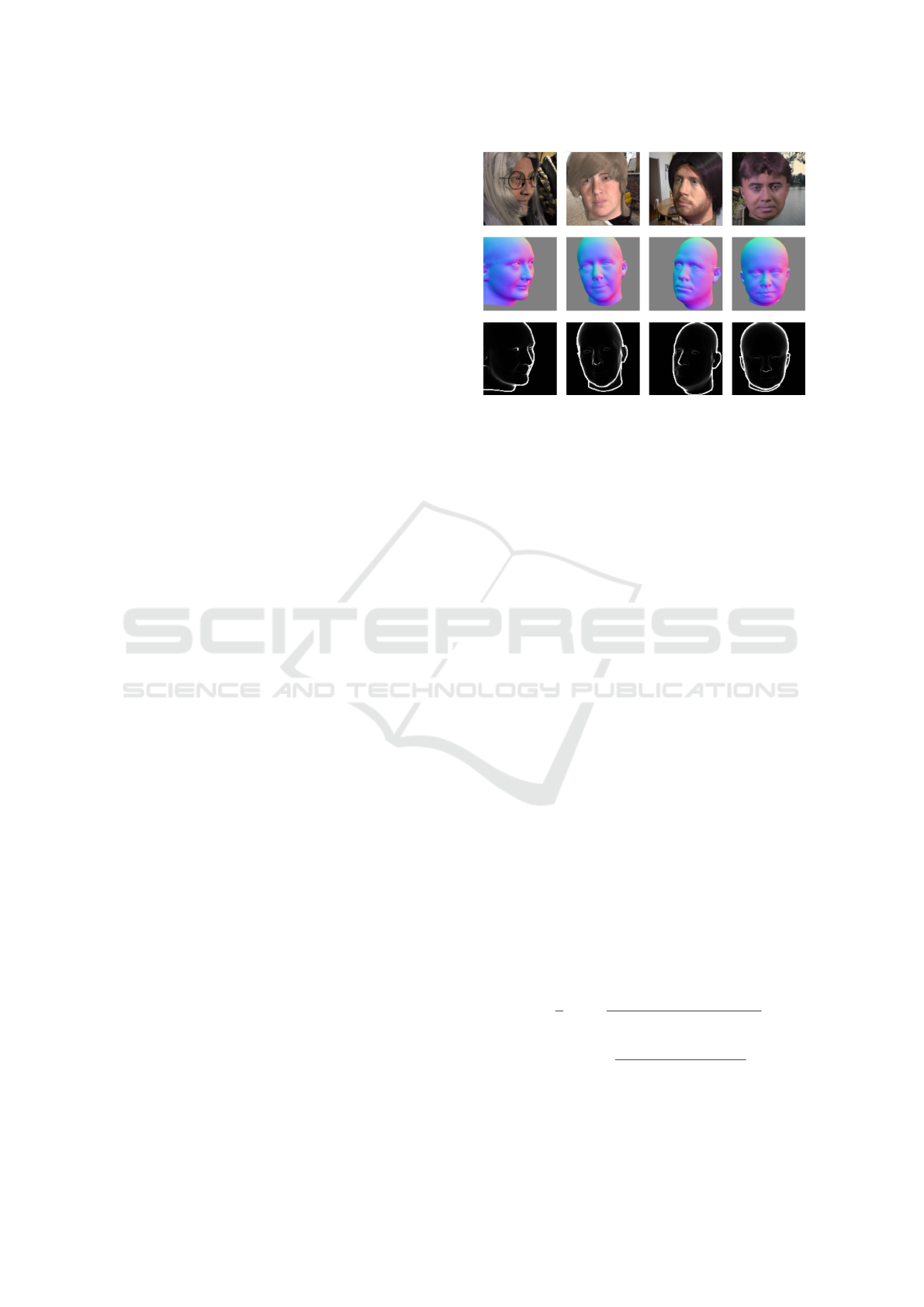
Figure 5: Comparison between ground-truth and estimates N and W maps. The ﬁrst column contains the facial input image,

second and fourth columns contain ground-truth maps, third and ﬁfth contain estimated maps.

4.2 Reconstruction Method Evaluation

Figure 6: Example of reconstruction result on synthetic data

from test data set

(a) Ground truth surface.

(b) Reconstructed surface.

cate M

val

, M

val

± θ and M

val

± 3σ

respectively.

(d) Heat map with pixels errors after eliminating the bias.

The depth error is measured in units equivalent to pixels.

The image resolution is 128 × 128.

Using the test data set, we evaluate in this step, the

efﬁciency of our proposed method in 3D face recon-

struction. To do this, ﬁrstly we describe the λ param-

eter tuning procedure to optimize our reconstruction

method. Secondly, we show a comparison between

the ground truth and the reconstructed depth map us-

ing the optimal λ value that minimizes the reconstruc-

tion error. Once the depth is reconstructed, we com-

pare it to the ground truth, available in the test set.

The evaluation procedure used to ﬁnd the optimal λ is

implemented as follows:

Step 1: compute the error map between the ground

truth and the reconstructed depth maps :

Err

= d

− d

where z

and z

are the ground truth and re-

constructed depths respectively; only the in-

tersection of domains Ω

and Ω

is used.

Step 2: compute median value M of Err

and given

a ﬁxed threshold θ = 7, we compute the stan-

dard deviation σ

of Err

for values which

lie in [M

val

− θ,M

val

+ θ].

Step 3: compute the variance V

of Err

in [M

val

−

3σ

val

+ 3σ

] range.

We perform these steps for all test examples and we

compute σ =

∑

i=1

Var

/N for different λ values

ranging from 0 to 0.3. The inﬂuence of the choice

of λ on the 3D reconstruction is show in Fig. 8. The

choice λ = 0 corresponds to the least squares solution

without weighting. We found that the optimal value

is λ = 0.1. This value is used in all experiments here-

inafter. In Fig. 6, we illustrate an example from the

comparison procedure described above.

4.3 Final Evaluation

In order to analyze the performance of the pipeline as

a whole, we performed a qualitative experiment on a

set of images of celebrities and a quantitative experi-

ment on a 3D facial data set to test its accuracy.

For qualitative analysis, we show in Fig. 7 our re-

sults on the image of certain celebrities. One can see

that our method produces high-quality results that bet-

ter ﬁt the overall structure. As we use a full 3DMM

head model that also includes the cranial part, our

method allows us to recover the 3D model of the head

Monocular 3D Head Reconstruction via Prediction and Integration of Normal Vector Field

365

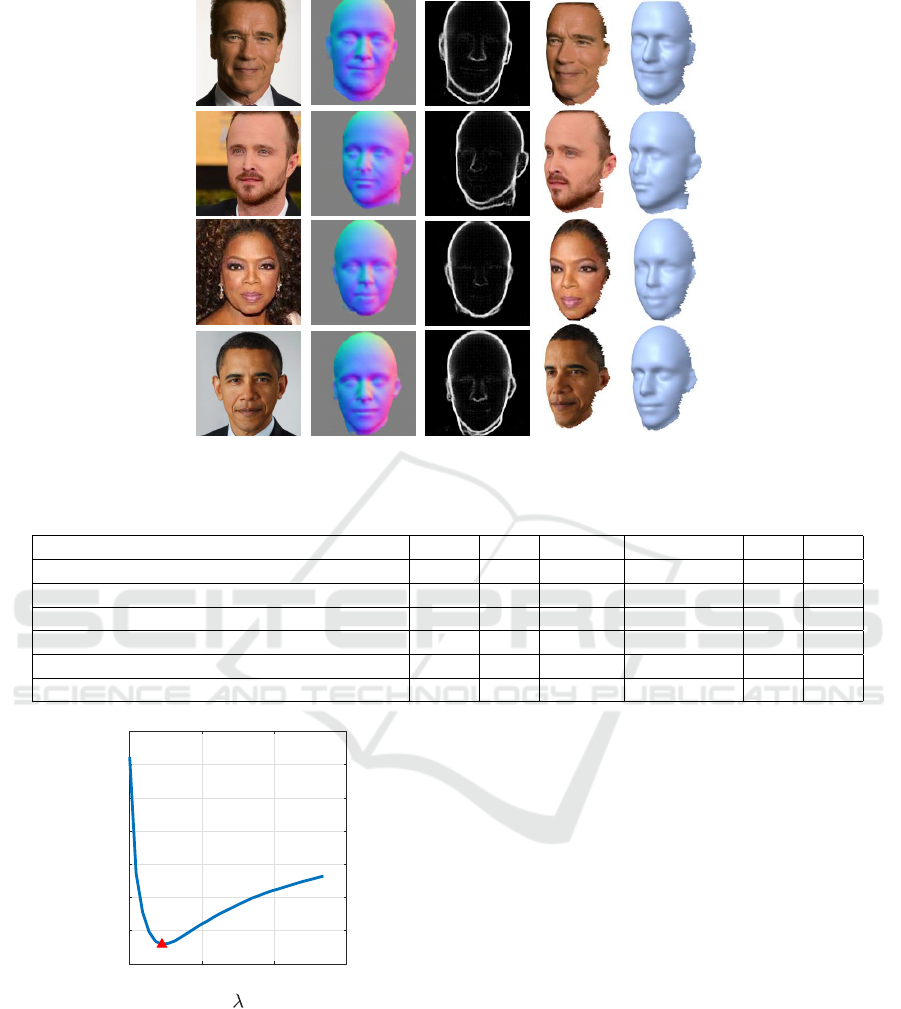
Figure 7: Visual surface reconstruction results from some celebrities facial images. Columns contain in order; input image,

estimated N map, estimated W map and the last two columns contain 3D shape reconstruction.

Table 2: Quantitative comparison on the BU-3DFE (Yin et al., 2006) data set. Lowers are better.

Method Mean Std Median 90% largest ¯e σ

(Kemelmacher-Shlizerman and Basri, 2010) 3.89 4.14 2.94 7.34 N/A N/A

(Zhu et al., 2015) 3.85 3.23 2.72 6.82 N/A N/A

(Richardson et al., 2017) 3.61 2.99 2.72 6.82 N/A N/A

(Sela et al., 2017) 3.51 2.69 2.65 6.59 N/A N/A

(Feng et al., 2018a) 2.78 2.04 1.73 5.30 N/A N/A

Ours 3.04 1.78 2.62 5.48 0.10 2.18

0 0.2 0.4 0.6

1.04

1.06

1.08

1.1

1.12

1.14

1.16

1.18

Std

Figure 8: The effect of λ on reconstruction accuracy in

terms of standard deviation on the test data set.

for any visible pixel on the image and it also predicts

any area hidden by the hair (third and fourth row in

Fig. 7). We also indicate the inferior quality of recon-

struction for surfaces containing the neck due to the

discontinuity between the face and neck parts (ﬁrst

and second rows in Fig. 7).

Quantitative results are reported in Table 2. For

evaluation, we use the BU-3DFE (Yin et al., 2006)

data set which contains 3D faces of 100 subjects with

seven different expressions and each 3D model has

corresponding 2D images. Using only neutral ex-

pressions subjects for our comparison process, we

crop each reconstructed model on the part represent-

ing the valid pixels to take into account in the compar-

ison. After alignment and registration process based

on iterative closest point (ICP) with the ground truth

model, we compute the absolute depth error. Note

that we eliminate examples when the alignment pro-

cess fails. Finally, we report depth errors evaluated

by mean, standard deviation, median, and the aver-

age ninety percent most signiﬁcant error. Note that

we report the results obtained on the same data set di-

rectly from (Feng et al., 2018a) paper. From Table 2,

we can see that our method produces results compa-

rable to the state of the art. The performance of (Feng

et al., 2018a) work is slightly better than ours, and

we believe that is due to the fact they use part of the

BU-3DFE (Yin et al., 2006) data set for training. This

data set is acquired using a special sensor, while our

model is trained only with generated synthetic data.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

366

Figure 9: Reconstruction results for three BU-3DFE examples from two different viewpoints. From left to right: input

image, normal map (N), front-view ground-truth model, front-view reconstructed model, slide-view ground-truth model and

side-view reconstructed model.

We also provide another way of estimating the er-

ror between the reconstruction and the ground truth.

The criterion is standard deviation σ of per-vertex er-

rors between the reconstruction and the ground truth

projected on the normals of the ground truth (mean of

this error being very close to zero after surface regis-

tration). By doing so we evaluate the error between

two surfaces in the normal direction instead of dis-

tances between points. Since the models do not have

the same meshes, we ﬁnd nearest neighbor for each

vertex of the reconstruction. The criteria are deﬁned

as follows:

¯e =

∑

k=1

− b

V =

M − 1

∑

k=1

((a

− b

− ¯e)

σ =

∑

k=1

(9)

where N is the total number of examples in the BU-

3DFE (Yin et al., 2006) data set, M is the total number

of vertices per model. a

and b

are the coordinates of

vertices from the estimated and ground truth models

respectively and n

is the normals coordinates from

the ground truth model. The values of this calculation

are reported in the sixth and seventh column of the

Table 2.

5 CONCLUSION

In this work, we have presented a hybrid 3D face re-

construction approach composed of both learning and

geometric based methods. The ﬁrst stage of our main

block is an image-to-image translation network that

produces normal surface map (N) and gradient mag-

nitude map (W ) from a facial input image. The sec-

ond stage is integration of normals based on weighted

least squares, which uses our network outputs to gen-

erate the depth facial map. Our deep learning model

has been trained on a fully synthetic facial data set.

We have performed three experiments to evalu-

ate our pipeline performance: ﬁrst, we show that the

neural network generates accurate maps of normals.

Next, experiments conﬁrm the effectiveness of using

the W map as a weight during the reconstruction step

to resolve discontinuous boundary artifacts. In the

ﬁnal experiment, we demonstrate that the proposed

framework achieves the state-of-the-art performance

in 3D face reconstruction. We also propose a new

error calculation method, which, we think, is more

representative for this type of evaluation. Using this

criterion with explicitly written equations avoids any

ambiguity on how exactly the evaluation is done and

what is the meaning of the obtained value.

Two loss functions L

and L

have been tested as

a pixel loss for network training. L

shows a bet-

ter performance in ﬁne detail reconstruction. And

yet some facial features of generated normal maps

are still slightly blurred. One possible improvement

would be to increase the network complexity and to

modify the output layers in order to get sharp details.

Despite the robust performance in many cases, our

method has a certain number of limitations. The head

generator does not include facial expressions and has

limited age range. But these limitations can be over-

come by using a better synthetic data generator, it is

not a fundamental limitation of the proposed method.

Furthermore this method is generic and can be ap-

plied to any kind of 3D object reconstruction if the

right data generator is available. Synthetic data sets

allow us to train complex models with virtually un-

limited data supply. It accelerates training process by

Monocular 3D Head Reconstruction via Prediction and Integration of Normal Vector Field

367

drastically reducing data markup step. On the other

hand synthetic data can introduce certain biases in the

learning process and therefore one should try to make

the generator as photo-realistic as possible. One way

of doing that is using GAN architectures in combina-

tion of classical 3D rendering.

REFERENCES

Abate, A. F., Nappi, M., Riccio, D., and Sabatino, G.

(2007). 2d and 3d face recognition: A survey. Pat-

tern Recognition Letters, 28(14):1885–1906.

Agarwal, S., Mierle, K., and Others. Ceres solver. http:

//ceres-solver.org.

Agrawal, A., Raskar, R., and Chellappa, R. (2006). What

is the range of surface reconstructions from a gradient

ﬁeld? In European conference on computer vision,

pages 578–591. Springer.

Amberg, B., Knothe, R., and Vetter, T. (2008). Expres-

sion invariant 3d face recognition with a morphable

model. In Automatic Face & Gesture Recognition,

2008. FG’08. 8th IEEE International Conference on,

pages 1–6. IEEE.

Bansal, A., Russell, B., and Gupta, A. (2016). Marr revis-

ited: 2d-3d alignment via surface normal prediction.

In Proceedings of the IEEE conference on computer

vision and pattern recognition, pages 5965–5974.

Bas, A., Smith, W. A., Bolkart, T., and Wuhrer, S. (2016).

Fitting a 3d morphable model to edges: A comparison

between hard and soft correspondences. In Asian Con-

ference on Computer Vision, pages 377–391. Springer.

Blanz, V. and Vetter, T. (1999). A morphable model for

the synthesis of 3d faces. In Proceedings of the 26th

annual conference on Computer graphics and interac-

tive techniques, pages 187–194. ACM Press/Addison-

Wesley Publishing Co.

Blanz, V. and Vetter, T. (2003). Face recognition based

on ﬁtting a 3d morphable model. IEEE Transac-

tions on pattern analysis and machine intelligence,

25(9):1063–1074.

Booth, J., Antonakos, E., Ploumpis, S., Trigeorgis, G.,

Panagakis, Y., Zafeiriou, S., et al. (2017). 3d face

morphable models in-the-wild. In Proceedings of

the IEEE Conference on ComputerVision and Pattern

Recognition.

Dai, H., Pears, N., Smith, W. A. P., and Duncan, C. (2017).

A 3d morphable model of craniofacial shape and tex-

ture variation. In The IEEE International Conference

on Computer Vision (ICCV).

Dou, P., Shah, S. K., and Kakadiaris, I. A. (2017). End-to-

end 3d face reconstruction with deep neural networks.

In Proc. IEEE Conference on Computer Vision and

Pattern Recognition, pages 21–26.

Feng, M., Zulqarnain Gilani, S., Wang, Y., and Mian, A.

(2018a). 3d face reconstruction from light ﬁeld im-

ages: A model-free approach. In Proceedings of the

European Conference on Computer Vision (ECCV),

pages 501–518.

Feng, Y., Wu, F., Shao, X., Wang, Y., and Zhou, X.

(2018b). Joint 3d face reconstruction and dense align-

ment with position map regression network. arXiv

preprint arXiv:1803.07835.

Frankot, R. T. and Chellappa, R. (1988a). A method

for enforcing integrability in shape from shading al-

gorithms. IEEE Trans. Pattern Anal. Mach. Intell.,

10(4):439–451.

Frankot, R. T. and Chellappa, R. (1988b). A method for

enforcing integrability in shape from shading algo-

rithms. IEEE Transactions on pattern analysis and

machine intelligence, 10(4):439–451.

Furukawa, Y. and Ponce, J. (2009). Accurate camera cali-

bration from multi-view stereo and bundle adjustment.

International Journal of Computer Vision, 84(3):257–

268.

Ghosh, A., Fyffe, G., Tunwattanapong, B., Busch, J., Yu,

X., and Debevec, P. (2011). Multiview face capture

using polarized spherical gradient illumination. In

ACM Transactions on Graphics (TOG), volume 30,

page 129. ACM.

Gonzalez-Mora, J., De la Torre, F., Guil, N., and Zapata,

E. L. (2010). Learning a generic 3d face model from

2d image databases using incremental structure-from-

motion. Image and Vision Computing, 28(7):1117–

1129.

Han, X., Ugail, H., and Palmer, I. (2009). Gender classiﬁca-

tion based on 3d face geometry features using svm. In

CyberWorlds, 2009. CW’09. International Conference

on, pages 114–118. IEEE.

Harker, M. and Oleary, P. (2015). Regularized recon-

struction of a surface from its measured gradient

ﬁeld. Journal of Mathematical Imaging and Vision,

51(1):46–70.

Hsieh, J.-W., Liao, H.-Y. M., Ko, M.-T., and Fan, K.-C.

(1995). Wavelet-based shape from shading. Graphical

Models and Image Processing, 57(4):343–362.

Hu, L., Ma, C., Luo, L., and Li, H. (2015). Single-view

hair modeling using a hairstyle database. ACM Trans-

actions on Graphics (Proceedings SIGGRAPH 2015),

34(4).

Huber, P., Feng, Z.-H., Christmas, W., Kittler, J., and

Ratsch, M. (2015). Fitting 3d morphable face mod-

els using local features. In Image Processing (ICIP),

2015 IEEE International Conference on, pages 1195–

1199. IEEE.

Hudon, M., Grogan, M., Pag

es, R., and Smoli

c, A. (2018).

Deep normal estimation for automatic shading of

hand-drawn characters. In European Conference on

Computer Vision, pages 246–262. Springer.

Kajiya, J. T. and Kay, T. L. (1989). Rendering fur with

three dimensional textures. In ACM Siggraph Com-

puter Graphics, volume 23, pages 271–280. ACM.

Karac¸alı, B. and Snyder, W. (2003). Reconstructing dis-

continuous surfaces from a given gradient ﬁeld using

partial integrability. Computer Vision and Image Un-

derstanding, 92(1):78–111.

Kemelmacher-Shlizerman, I. and Basri, R. (2010). 3d face

reconstruction from a single image using a single ref-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

368

erence face shape. IEEE transactions on pattern anal-

ysis and machine intelligence, 33(2):394–405.

Klasing, K., Althoff, D., Wollherr, D., and Buss, M. (2009).

Comparison of surface normal estimation methods for

range sensing applications. In 2009 IEEE Interna-

tional Conference on Robotics and Automation, pages

3206–3211. IEEE.

Kovesi, P. (2005). Shapelets correlated with surface nor-

mals produce surfaces. In Tenth IEEE International

Conference on Computer Vision (ICCV’05) Volume 1,

volume 2, pages 994–1001. IEEE.

Lin, T.-Y., Maire, M., Belongie, S., Hays, J., Perona, P.,

Ramanan, D., Doll

ar, P., and Zitnick, C. L. (2014).

Microsoft coco: Common objects in context. In Euro-

pean conference on computer vision, pages 740–755.

Springer.

Lun, Z., Gadelha, M., Kalogerakis, E., Maji, S., and Wang,

R. (2017). 3d shape reconstruction from sketches via

multi-view convolutional networks. In 2017 Interna-

tional Conference on 3D Vision (3DV), pages 67–77.

IEEE.

Qiu, J., Cui, Z., Zhang, Y., Zhang, X., Liu, S., Zeng, B., and

Pollefeys, M. (2019). Deeplidar: Deep surface normal

guided depth prediction for outdoor scene from sparse

lidar data and single color image. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition, pages 3313–3322.

eau, Y. and Durou, J.-D. (2015). Edge-preserving inte-

gration of a normal ﬁeld: Weighted least-squares, tv

and lˆ 1 approaches. In International Conference on

Scale Space and Variational Methods in Computer Vi-

sion, pages 576–588. Springer.

eau, Y., Durou, J.-D., and Aujol, J.-F. (2018). Normal in-

tegration: a survey. Journal of Mathematical Imaging

and Vision, 60(4):576–593.

Richardson, E., Sela, M., Or-El, R., and Kimmel, R.

(2017). Learning detailed face reconstruction from a

single image. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

1259–1268.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. In International Conference on Medical

image computing and computer-assisted intervention,

pages 234–241. Springer.

Sela, M., Richardson, E., and Kimmel, R. (2017). Unre-

stricted facial geometry reconstruction using image-

to-image translation. arxiv.

Simchony, T., Chellappa, R., and Shao, M. (1990). Di-

rect analytical methods for solving poisson equations

in computer vision problems. IEEE transactions on

pattern analysis and machine intelligence, 12(5):435–

446.

Su, W., Du, D., Yang, X., Zhou, S., and Fu, H. (2018). Inter-

active sketch-based normal map generation with deep

neural networks. Proceedings of the ACM on Com-

puter Graphics and Interactive Techniques, 1(1):22.

Sumner, R. W., Schmid, J., and Pauly, M. (2007). Em-

bedded deformation for shape manipulation. In ACM

Transactions on Graphics (TOG), volume 26, page 80.

ACM.

Terzopoulos, D. (1988). The computation of visible-surface

representations. IEEE Transactions on Pattern Analy-

sis & Machine Intelligence, (4):417–438.

Thies, J., Zollhofer, M., Stamminger, M., Theobalt, C., and

Nießner, M. (2016). Face2face: Real-time face cap-

ture and reenactment of rgb videos. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition, pages 2387–2395.

Tran, A. T., Hassner, T., Masi, I., and Medioni, G. (2017).

Regressing robust and discriminative 3d morphable

models with a very deep neural network. In Computer

Vision and Pattern Recognition (CVPR), 2017 IEEE

Conference on, pages 1493–1502. IEEE.

Trigeorgis, G., Snape, P., Zafeiriou, S., and Kokkinos, I.

(2017). Normal Estimation For ”in-the-wild” Faces

Using Fully Convolutional Networks. In Computer

Vision and Pattern Recognition (CVPR).

Wang, X., Fouhey, D., and Gupta, A. (2015). Designing

deep networks for surface normal estimation. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition, pages 539–547.

Wang, Y., Bu, J., Li, N., Song, M., and Tan, P. (2012). De-

tecting discontinuities for surface reconstruction. In

Proceedings of the 21st International Conference on

Pattern Recognition (ICPR2012), pages 2108–2111.

IEEE.

Xie, W., Wang, M., Wei, M., Jiang, J., and Qin, J. (2019).

Surface reconstruction from normals: A robust dgp-

based disconti-nuity preservation approach. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pat-tern Recognition, pages 5328–5336.

Yin, L., Wei, X., Sun, Y., Wang, J., and Rosato, M. J.

(2006). A 3d facial expression database for facial

behavior research. In 7th international conference

on automatic face and gesture recognition (FGR06),

pages 211–216. IEEE.

Zhu, X., Lei, Z., Yan, J., Yi, D., and Li, S. Z. (2015). High-

ﬁdelity pose and expression normalization for face

recognition in the wild. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion, pages 787–796.

Zollh

ofer, M., Martinek, M., Greiner, G., Stamminger, M.,

and S

ußmuth, J. (2011). Automatic reconstruction of

personalized avatars from 3d face scans. Computer

Animation and Virtual Worlds, 22(2-3):195–202.

Monocular 3D Head Reconstruction via Prediction and Integration of Normal Vector Field

369