
Fast Local LUT Upsampling
Hiroshi Tajima, Teppei Tsubokawa, Yoshihiro Maeda and Norishige Fukushima
∗
Nagoya Institute of Technology, Japan, Tokyo University of Science, Japan
∗
https://fukushima.web.nitech.ac.jp/en/
Keywords:
Edge-preserving Filtering, Local LUT Upsampling, Acceleration, Bilateral Filtering, L
0
Smoothing.
Abstract:
Edge-preserving filters have been used in various applications in image processing. As the number of pixels
of digital cameras has been increasing, the computational cost becomes higher, since the order of the filters
depends on the image size. There are several acceleration approaches for the edge-preserving filtering; how-
ever, most approaches reduce the dependency of filtering kernel size to the processing time. In this paper, we
propose a method to accelerate the edge-preserving filters for high-resolution images. The method subsam-
ples an input image and then performs the edge-preserving filtering on the subsampled image. Our method
then upsamples the subsampled image with the guidance, which is the high-resolution input images. For this
upsampling, we generate per-pixel LUTs for high-precision upsampling. Experimental results show that the
proposed method has higher performance than the conventional approaches.
1 INTRODUCTION
Edge-preserving filtering smooths images while
maintaining the outline in the images. There are vari-
ous edge-preserving filters for various purposes of im-
age processing, such as bilateral filtering (Tomasi and
Manduchi, 1998), non-local means filtering (Buades
et al., 2005), DCT filtering (Yu and Sapiro, 2011),
BM3D (Dabov et al., 2007), guided image fil-
tering (He et al., 2010), domain transform filter-
ing (Gastal and Oliveira, 2011), adaptive manifold fil-
tering (Gastal and Oliveira, 2012), local Laplacian fil-
tering (Paris et al., 2011), weighted least square fil-
tering (Levin et al., 2004), and L
0
smoothing (Xu
et al., 2011). The applications of the edge-preserving
filters include noise removal (Buades et al., 2005),
outline emphasis (Bae et al., 2006), high dynamic
range imaging (Durand and Dorsey, 2002), haze re-
moving (He et al., 2009), stereo matching (Hosni
et al., 2013; Matsuo et al., 2015), free viewpoint
imaging (Kodera et al., 2013), depth map enhance-
ment (Matsuo et al., 2013).
The computational cost is the main issue in the re-
search of edge-preserving filtering. There are several
acceleration approaches for each filter, such as bilat-
eral filtering (Durand and Dorsey, 2002; Yang et al.,
2009; Adams et al., 2010; Chaudhury et al., 2011;
Chaudhury, 2011; Chaudhury, 2013; Sugimoto and
Kamata, 2015; Sugimoto et al., 2016; Ghosh et al.,
2018; Maeda et al., 2018b; Maeda et al., 2018a; Sugi-
moto et al., 2019; Fukushima et al., 2019b), non-local
means filtering (Adams et al., 2010; Fukushima et al.,
2015), local Laplacian filtering (Aubry et al., 2014),
DCT filtering (Fujita et al., 2015; Fukushima et al.,
2019a), guided image filtering (Murooka et al., 2018;
Fukushima et al., 2018) and weighted least square fil-
tering (Min et al., 2014). The computational time of
each filter, however, depends on image resolution, and
it is rapidly increasing, e.g., a camera in cellphone
even have 12M pixels. For such a high-resolution im-
age, we require more acceleration techniques.
Processing with subsampling and then upsam-
pling is the most straightforward approach to ac-
celerate image processing. This approach dramat-
ically reduces processing time; however, the accu-
racy of the approximation is also significantly de-
creased. Subsampling loses high-frequency and large
edges in images; hence, the resulting images also
lose the information. Different from super-resolution
problems, subsampling/upsampling for acceleration
can utilize a high-resolution input image as a guid-
ance signal. Joint bilateral upsampling (Kopf et al.,
2007) and guided image upsampling (He and Sun,
2015) utilize the high-resolution image for high-
quality upsampling as extensions of joint bilateral fil-
tering (Petschnigg et al., 2004; Eisemann and Durand,
2004). However, both upsampling methods are spe-
cific for accelerating bilateral filtering and guided im-
age filtering. More application-specific upsampling,
e.g., depth map upsampling (Fukushima et al., 2016),
improves the upsampling quality.
To accelerate arbitrary edge-preserving filtering,
Tajima, H., Tsubokawa, T., Maeda, Y. and Fukushima, N.
Fast Local LUT Upsampling.
DOI: 10.5220/0008963200670075
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
67-75
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
67
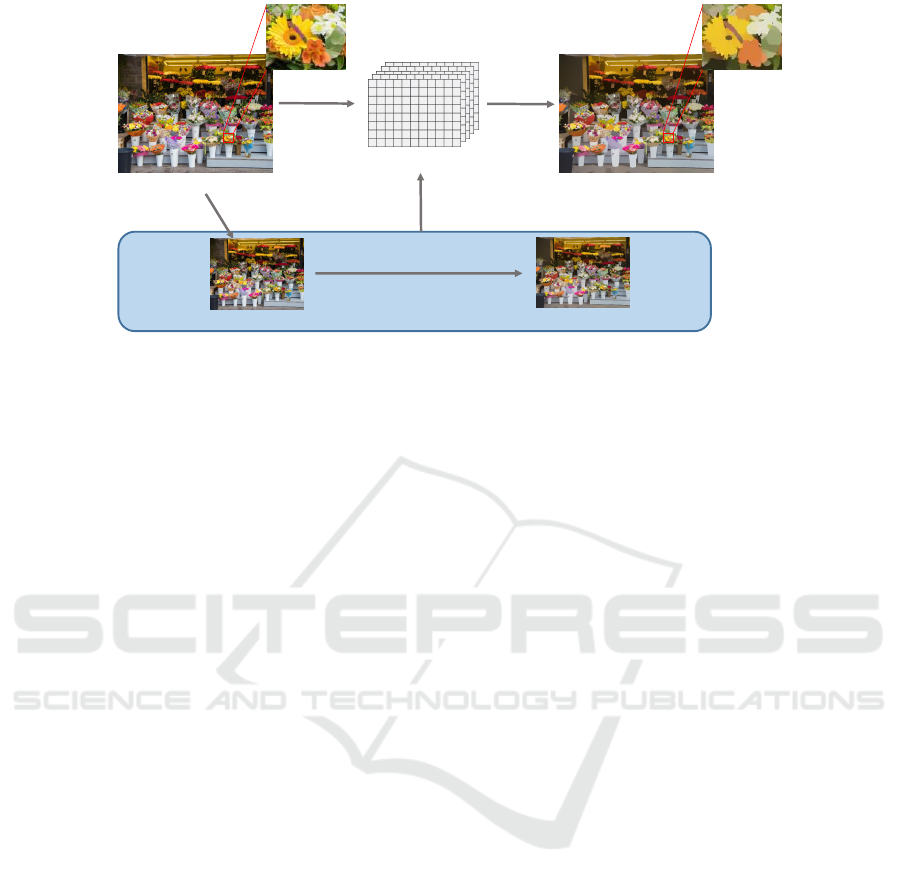
Input Image
Low-resolution Input Image Low-resolution Output Image
Output Image
Subsampling
Edge-preserving Filtering
Generating
Local LUT
Reference
Output
Local LUT
Figure 1: Local LUT upsampling: an input image is downsampled, and then the image is smoothed by arbitrary edge-
preserving filtering. Next, we create per-pixel LUTs by using the correspondence between subsampled input and output
images. Finally, we convert the input image into the approximated image by the LUT.
we proposed a new upsampling method named fast
local look-up table (LUT) upsampling, which has
higher accuracy with fast computational ability than
the conventional method (Tajima et al., 2019). Fig-
ure 1 indicates an overview of our method. In
the method, edge-preserving filtering, which has the
highest cost in the processing, is performed in the
downsampled domain for acceleration. Then our
method utilizes high-resolution information for accu-
rate upsampling.
This work is an extension of our previous
work (Tajima et al., 2019). The contribution of this
work is improving the computational method of per-
pixel LUT to achieve better accuracy with saving
computational time than conventional work. Also, the
proposed method is justified by state-of-the-arts up-
sampling methods (Chen et al., 2016).
2 LOCAL LUT
2.1 Concept of Local LUT
We review the concept of local LUT upsampling.
Usually, image intensity transformation by using
LUT, such as contrast enhancement, gamma correc-
tion, and tone mapping, we use a LUT for each
pixel. We call this method as global LUT. The global
LUT can represent any point-wise operations for each
pixel, but this approach cannot represent area-based
operations, such as image filtering.
By contrast, our approach of the local LUT gener-
ates per-pixel LUTs. The LUT maps pixel values of
the input image to that of an image processing result.
The local LUT T
T
T at a pixel p
p
p has following relation-
ship between an input image I
I
I and an output image
J
J
J.
J
J
J
p
p
p
= T
T
T
p
p
p
[I
I
I
p
p
p
], (1)
where T [·] represents LUT reference operation. If
we have the output of edge-preserving filtering, we
can easily transform the input image into the edge-
preserving result by referring the LUT. It is nonsense
that the output image is required for generating the
output image itself. Therefore, we generate the local
LUT in the subsampled image domain for accelera-
tion. The proposed method generates per-pixel LUTs
for the function from the correspondence between a
subsampled input image and its filtering result.
The local LUT for each pixel is created from
neighboring pairs of low-resolution input and out-
put image around a target pixel. Luminance values
around the neighboring region have high correlations.
Also, the correlation between the output of filtering
and the input image becomes high. Therefore we ag-
gregate the mapping relationship around neighboring
pixels.
Figure 2 shows the scatter plot of intensity pair
between a local patch of an input image and a fil-
tered image. The correspondence map almost repre-
sents the local LUT, but there are two issues; multiple
output candidates and gap issues. LUT requires one-
to-one mapping for each intensity of input and output,
but this scatter plot represents one-to-zero or one-to-
n matching. Our previous work (Tajima et al., 2019)
and this work solves the issues.
2.2 Conventional Approach
We shortly introduce the computing method of the lo-
cal LUT in (Tajima et al., 2019). Initially, an input
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
68

0
32
64
96
128
0 32 64 96 128
Output
Input
Gap
Multiple output candidates
I J
↓
↓
Figure 2: Issues in generating local LUT: We make a
scatter-plot for correspondence between input and output
subsampled images in a local window. The scatter-plot al-
most represents the LUT for mapping input to output. But
there are two problems; gap and multiple-output candidates.
image I
I
I is subsampled to generate a low-resolution
input image I
I
I
↓
:
I
I
I
↓
= S
s
(I
I
I), (2)
where S
s
is a subsampling operator. Then, edge-
preserving filtering is applied for I
I
I
↓
and the subsam-
pled output J
J
J
↓
is obtained as follows:
J
J
J
↓
= F(I
I
I
↓
), (3)
where F is an operator of arbitrary edge-preserving
filtering. Then, we create a local LUT on a pixel from
the correspondence between I
I
I
↓
and J
J
J
↓
. Let be p
p
p
↓
the
target pixel in the subsampled images of I
I
I
↓
and J
J
J
↓
.
The local LUT on p
p
p
↓
is defined as follows:
T
T
T
p
p
p↓
= Func{I
I
I
↓
,J
J
J
↓
, p
p
p
↓
,W
p
p
p↓
}, (4)
where W
p
p
p↓
is a set of neighboring pixels around p
p
p
↓
.
Func{·} indicates each approach for generating the
local LUT.
Here, we review two conventional approaches
to generating the local LUT, which is proposed
in (Tajima et al., 2019). The first one is the dynamic
programming approach (DP). This approach simul-
taneously solves the problems of gap and multiple-
candidates. This algorithm is shown in Algorithm 1.
In the approach, we count frequency of one-to-one
mapping of intensity between the images I
I
I
↓
and J
J
J
↓
in local window W
p
p
p↓
. Let introduce a frequency map
f
p
p
p↓
(s,t) on a pixel p
p
p
↓
, where s and t are an intensity
value on I
I
I
↓
and J
J
J
↓
, respectively. The frequency is
counted by gathering around a pixel W
p
p
p↓
.
Also, we consider quantization of the intensity for
acceleration. S
c
(x) is a quantization function and de-
fined by:
S
c
(x) = bx/lc (5)
where l is a quantization parameter. The output of the
local LUT has 256/l dimensions. We call the number
of intensity candidates as the number of bins.
Algorithm 1: DP approach.
Input: I
I
I
↓
, J
J
J
↓
, p
p
p
↓
, W
p
p
p↓
Initialization: N = (2r +1)
2
Initialization: L = the number of bins
Initialization: f
p
p
p↓
(s,t) = 0|
∀s,t
Let q
q
q
↓
be a neigboring pixel ({q
q
q
1↓
, ··· , q
q
q
N↓
} ∈ W
p
p
p↓
)
For (n = 1 to N)
f
p
p
p↓
(S
c
(I
I
I
q
q
q
n↓
),S
c
(J
J
J
q
q
q
n↓
)) + +
For (i = 1 to L − 1)
f
p
p
p↓
(i,0)+ = f
p
p
p↓
(i − 1, 0)
f
p
p
p↓
(0,i)+ = f
p
p
p↓
(0,i − 1)
For (s = 1 to L − 1)
For (t = 1 to L − 1)
C
1
= f
p
p
p↓
(s − 1,t −1) + O
C
2
= f
p
p
p↓
(s − 1,t)
C
3
= f
p
p
p↓
(s,t − 1)
f
p
p
p↓
(s,t) = max(C
1
,C
2
,C
3
) + f
p
p
p↓
(s,t)
index(s,t) = arg max
m
C
m
(m = 1, 2,3)
s = L − 1, t = L − 1
While (s ≥ 0 and t ≥ 0)
T
T
T
p
p
p↓
[s] = t
Switch(index(s,t))
1 : s − −, t −−
2 : s − −
3 : t − −
Algorithm 2: WTA approach.
Input: I
I
I
↓
, J
J
J
↓
, p
p
p
↓
, W
p
p
p↓
Initialization: N = (2r +1)
2
Initialization: L = the number of bins
Initialization: f
p
p
p↓
(s,t) = 0|
∀s,t
Let q
q
q
↓
be a neigboring pixel ({q
q
q
1↓
, ··· , q
q
q
N↓
} ∈ W
p
p
p↓
)
For (n = 1 to N)
f
p
p
p↓
(S
c
(I
I
I
q
q
q
n
↓
),S
c
(J
J
J
q
q
q
n
↓
)) + +
For (s = 0 to L − 1)
T
T
T
p
p
p↓
[s] = arg max
t
f
p
p
p↓
(s,t)
For (s = 0 to L − 1)
If (T
T
T
p
p
p↓
[s] = 0)
Inter polate(T
T
T
p
p
p↓
[s])
After constructing the frequency map, we opti-
mize the result by using DP. The parameter O in Algo-
rithm 1 represents an offset value to enforce diagonal
matching. The cost function of f can be recursively
updated. After filling the cost function, we trace back
the function to determine a solid pass. Note that DP
approach ensures the monotonicity in the local LUT.
The second approach is the winner-takes-all ap-
proach (WTA). The algorithm is shown in Algo-
rithm 2. In this approach, the output value of T
T
T
p
p
p↓
[s] is
determined as the most frequent intensity in the out-
Fast Local LUT Upsampling
69

put image for intensity s in the input image. How-
ever, this approach still has the gap problem in the
LUT; thus, we interpolate the gap. ”Interpolate(·)” in
the algorithm indicates linearly interpolating between
the nearest existing values in bins. For the bound-
ary condition of interpolation, we set T
T
T
p
p
p↓
[0] = 0 and
T
T
T
p
p
p↓
[255] = 255. The solution cannot keep mono-
tonicity for the local LUT. The fact sometimes gen-
erates negative edges.
After WTA and DP, the matrix indicates one-to-
one mapping. We call this per-pixel mapping function
T
T
T
p
p
p↓
as local LUT. These approaches require a fre-
quency map, i.e., 2D histogram. The number of ele-
ments in the map is L
2
. Usually, L = 256 for no-range
downsampling case, we initialize 65536 elements per
each pixel by setting 0. By contrast, the size of the
local window is r × r, and typically r = 2, 3, 4, or
5. Thus, the size of the frequency map is dominant.
Also, the cost of memory access for more massive ar-
ray has higher than arithmetic operations in current
computers (Hennessy and Patterson, 2017).
3 PROPOSED METHOD
3.1 Fast Local LUT
In this section, we propose an acceleration method of
local LUT computation. For acceleration, we remove
the computing process of the frequency map counting
from the algorithm. We call the new approach fast
local LUT (FLL).
In FLL, we solve the multiple-candidates problem
in the local LUT computation by giving priority to the
correspondence matching. The priority is the near-
ness of distance between a target pixel position and
reference pixel position of neighborhood pixels. If
we have multiple candidates, we adopt the intensity
of the pixel where locates the nearest position from
the center of the local window. With this priority, we
can directly compute a local LUT on a pixel without
counting the frequency map.
We implemented two methods to solve the local
LUT with the nearness priority. Note that both two
methods have the same result. The first implementa-
tion is raster scan order computation. This approach
determines the output values of the local LUT by
scanning the local window with the raster scan order.
The algorithm 3 shows this method. In this method,
we compare spatial distance of L
1
norm between p
p
p
↓
and q
q
q
n↓
, when T
T
T
p
p
p
↓
[S
c
(I
I
I
q
q
q
n↓
)] already has the output
value. Therefore, this method has two comparing op-
erations, i.e., NULL check and distance comparison.
Algorithm 3: FLL (Raster scan).
Input: I
I
I
↓
, J
J
J
↓
, p
p
p
↓
, W
p
p
p↓
Initialization: N = (2r +1)
2
Initialization: L = the number of bins
Let q
q
q
↓
be a neigboring pixel ({q
q
q
1↓
, ··· , q
q
q
N↓
} ∈ W
p
p
p↓
)
For (n = 1 to N)
distance[n] = |p
p
p
↓
−q
q
q
n↓
| //computable in advance
For (n = 1 to N)
If (T
T
T
p
p
p↓
[S
c
(I
I
I
q
q
q
n
↓
)]=NULL)
T
T
T
p
p
p↓
[S
c
(I
I
I
q
q
q
n
↓
)] = S
c
(J
J
J
q
q
q
n
↓
)
index[S
c
(I
I
I
q
q
q
n
↓
)] = distance[n]
Else
If (distance[n] ≤ index[S
c
(I
I
I
q
q
q
n
↓
)])
T
T
T
p
p
p↓
[S
c
(I
I
I
q
q
q
n
↓
)] = S
c
(J
J
J
q
q
q
n
↓
)
index[S
c
(I
I
I
q
q
q
n
↓
)] = distance[n]
For (s = 0 to L − 1)
If (T
T
T
p
p
p↓
[s] = 0)
Inter polate(T
T
T
p
p
p↓
[s])
Algorithm 4: FLL (Spiral).
Input: I
I
I
↓
, J
J
J
↓
, p
p
p
↓
, W
p
p
p↓
Initialization: k = 0, N = (2r +1)
2
Initialization: L = the number of bins
Let q
q
q
↓
be a neigboring pixel ({q
q
q
1↓
, ··· , q
q
q
N↓
} ∈ W
p
p
p↓
)
For (n = 1 to N)
distance[n] = |p
p
p
↓
−q
q
q
n↓
| //computable in advance
For (d = 2r to 0)
For (n = 1 to N)
If (distance[n] = d)
s index[k+ +] = n //computable in advance
For (i = 1 to N)
n = s index[i]
T
T
T
p↓
[S
c
(I
I
I
q
q
q
n↓
)] = S
c
(J
J
J
q
q
q
n↓
)
For (s = 0 to L − 1)
If (T
T
T
p
p
p↓
[s] = 0)
Inter polate(T
T
T
p
p
p↓
[s])
The second implementation is that determines out-
put values of local LUT in the spiral scanning or-
der. Generating this order, we sort the pair of input
and output intensity by the key of L
1
norm distance
between p
p
p
↓
and q
q
q
n↓
with descending order. Algo-
rithm 4 shows the algorithm of this method. In this
method, the value is overwritten by a new one, even
if T
T
T
p
p
p
↓
[S
c
(I
I
I
q
q
q
n↓
)] already has the output value, because
new one in the sorted order must have the nearer dis-
tance than the previous one. Therefore, there is no
comparing operation. Besides, the sorted order is
computable in advance and only computes at once;
thus, this method additionally reduces computational
time.
Figure 3 shows the generated local LUT of each
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
70

0
32
64
96
128
0
32
64
96
128
Output
Input
(a) Scatter plot
0
32
64
96
128
0
32
64
96
128
Output
Input
(b) DP
0
32
64
96
128
0
32
64
96
128
Output
Input
(c) WTA
0
32
64
96
128
0
32
64
96
128
Output
Input
(d) FLL
Figure 3: Scatter plot of input and output values and results
of each approach for generating local LUT on p
p
p. The num-
ber of bins is 128, i.e., quantization level is l = 2. The radius
of neiboring pixels is r = 5. The subsampling rate is 1/16.
approach, i.e., DP, WTA, and FLL.
3.2 Upsampling of Local LUT
The local LUT has three-dimensional information,
such as n, p
p
p = (x,y); however, all elements are sub-
sampled. It has not enough to map an input image into
an output image in a high-resolution image. There-
fore, we upsample the local LUT to intensity and spa-
tial dimention. The upsampling is defined as follows:
˜
T
T
T = S
−1
c
(S
−1
s
(T
T
T
↓
)), (6)
where
˜
T
T
T and T
T
T
↓
are tensors, which gathers each lo-
cal LUT for each pixels. S
−1
c
(·) and S
−1
s
(·) are tensor
upsampling operators for the intensity and spatial do-
main of the tensors, respectively. Finally, the output
image is generated by referring to the local LUT and
input intensity of I
I
I
p
p
p
. The output is defined by:
J
J
J
p
p
p
=
˜
T
T
T
p
p
p
[I
I
I
p
p
p
]. (7)
For intensity and spatial domain upsampling,
we used linear upsampling for intensity, and bilin-
ear or bicubic upsampling for spatial domain. We
call linear-bilinear pair as tri-linear upsampling, and
linear-bicubic pair as linear-bicubic upsampling.
4 EXPERIMENTAL RESULTS
We accelerated two edge-preserving filters, such as
iterative bilateral filtering and L
0
smoothing by sub-
sampling based acceleration methods. These filters
can mostly smooth images; however, the compu-
tational cost is high. We compared the proposed
method of the local LUT upsampling with the conven-
tional method of the cubic upsampling (CU), guided
image upsampling (GIU) (He and Sun, 2015) and bi-
lateral guided upsampling (BGU) (Chen et al., 2016)
by approximation accuracy and computational time.
Also, we compared the proposed method with na
¨
ıve
implementation, which does not subsample images,
in computational time. For the proposed method,
we also compared the fast local LUT upsampling
(FastLLU) with the conventional approach of local
LUT upsampling (LLU), which use WTA for local
LUT generation. Also, we evaluated tri-linear inter-
polation and linear-bicubic interpolation for interpo-
lating the local LUT. We utilized eight high-resolution
test images: artificial (3072 × 2048), bridge (2749 ×
4049), building (7216 × 5412), cathedral(2000 ×
3008), deer (4043 × 2641), fireworks (3136 × 2352),
flower (2268 × 1512), tree (6088 × 4550). We used
peak-signal noise ratio (PSNR) for accuracy evalua-
tion, and we regarded the results of the na
¨
ıve filtering
as ground truth results.
We implemented the proposed method by C++
with OpenMP parallelization. We also used Intel
IPP for the cubic upsampling, which is optimized by
AVX/AVX2. For guided image upsampling, we also
optimized by AVX/AVX2 with OpenCV functions.
For downsampling in the proposed method, we use
the nearest neighbor downsampling. For this down-
sampling, we used OpenCV and Intel IPP for the op-
eration with cv::INTER NN option. The used com-
puter was Intel Core i7 6700 (3.40 GHz) and com-
piled by Visual Studio 2017. We used r = 2 for local
LUT upsampling, iteration = 10, σ
s
= 10, σ
c
= 20,
r = 3σ
s
for iterative bilateral filtering, and λ = 0.01
and κ = 1.5 for L
0
smoothing. PSNR and computa-
tional time are averages of eight high-resolution im-
ages.
Figure 4 shows the PSNR accuracy of each ac-
celeration method for iterative bilateral filtering and
L
0
smoothing, respectively. The number of bins of
the proposed method is 128. The local LUT based
methods, which are LLU and the proposed method of
fastLLU, have higher PSNR than other acceleration
methods. Note that a subsampling rate of 1/16 indi-
cates that the height and the width of images are mul-
tiplied by 1/4. Table 1 shows detail information for
LLU and fastLLU. The proposed method of fastLLU
Fast Local LUT Upsampling
71
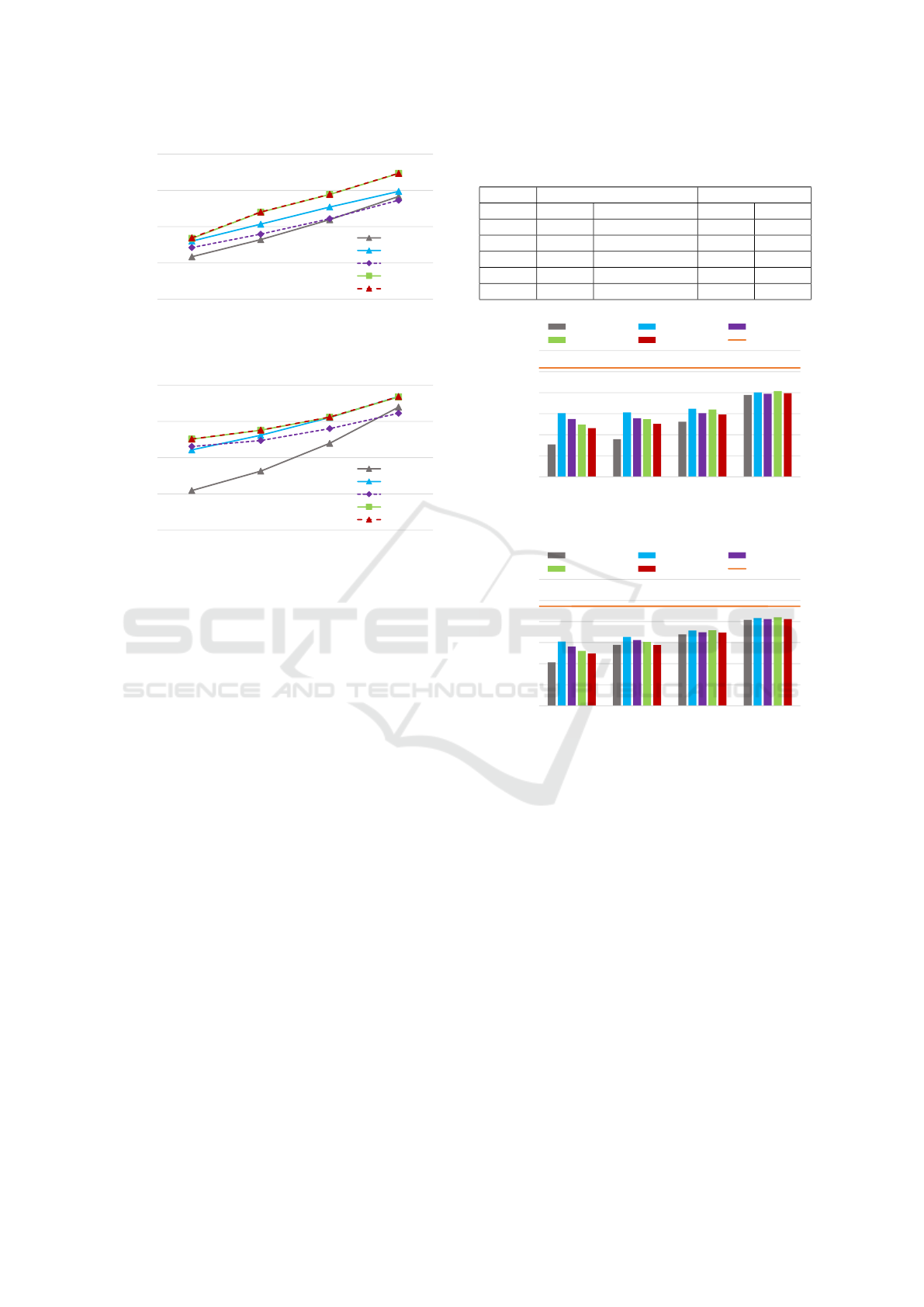
20
25
30
35
40
1/256
1/64
1/16
1/4
PSNR [dB]
Subsampling rate
CU
GIU
BGU
LLU
FastLLU
(a) Iterative bilateral filtering
20
25
30
35
40
1/256
1/64
1/16
1/4
PSNR [dB]
Subsampling rate
CU
GIU
BGU
LLU
FastLLU
(b) L
0
smoothing
Figure 4: Approximation accuracy of PSNR for each accel-
eration method with changing subsampling rate.
is slightly better than the conventional approach of
LLU.
Figure 5 shows the computational time of each
acceleration method for two edge-preserving filters.
The horizontal line of the graph shows the computa-
tional time of na
¨
ıve implementation. The computa-
tional time is an average of 10 trials. The fastLLU
is the second fastest of five methods, which is ×100
faster than the na
¨
ıve implementation when the sub-
sampling rate is 1/64. Cubic upsampling is simple
and fast, but the performance is not high.
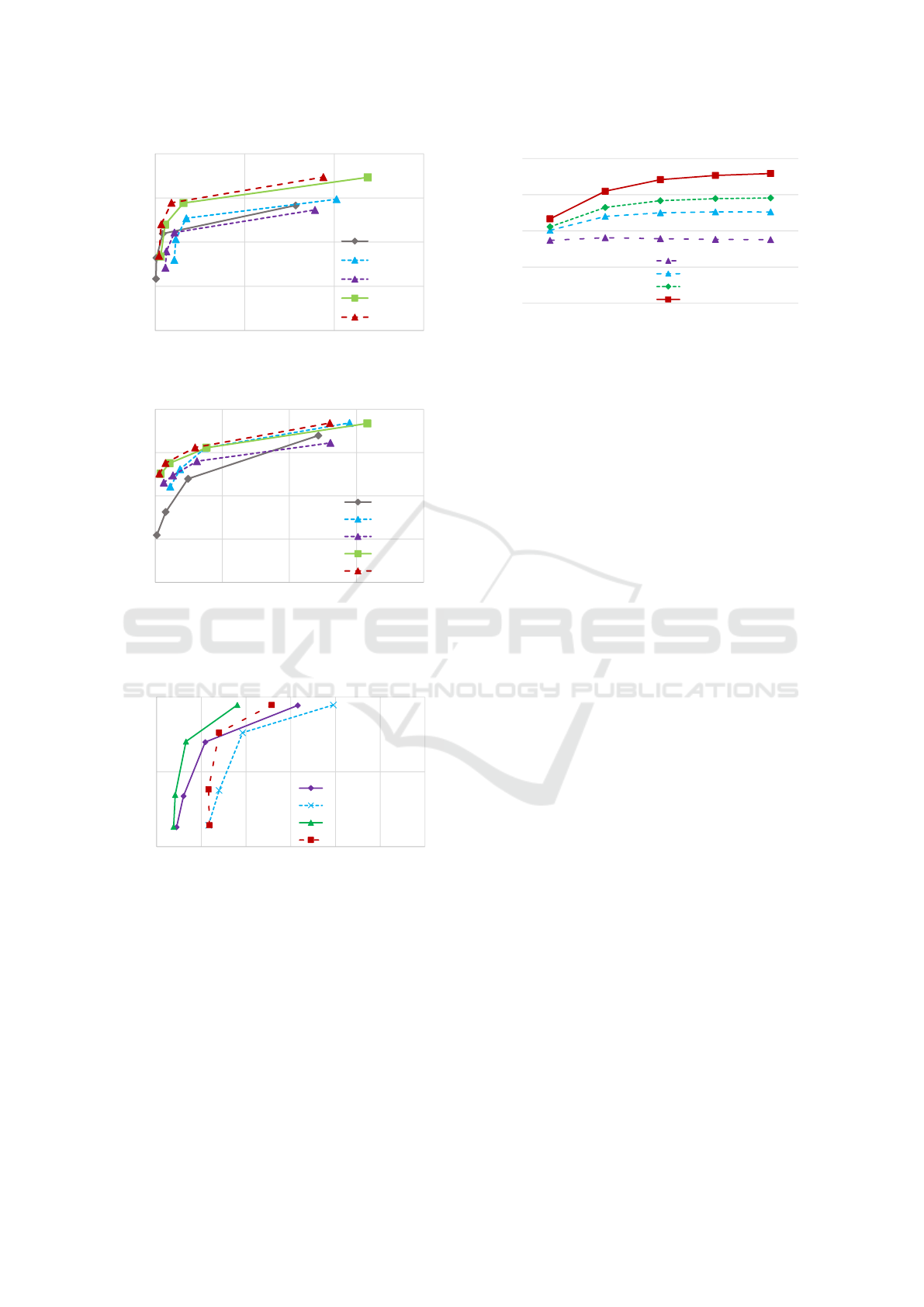
Figure 6 shows the trade-off between the PSNR
accuracy and the computational time by changing the
subsampling rate from 1/4 to 1/256. Results show that
the fastLLU has the best performance in this trade-off
among these acceleration methods.
Figure 7 also shows the trade-off between the
PSNR accuracy and the computational time of local
LUT based methods. The result shows that the FLL
based upsampling (fastLLU) is faster than the WTA
based local LUT upsampling (LLU), and also have a
little higher PSNR. The result also shows that using
bicubic interpolation for spatial domain obtains slight
higher PSNR, though it takes a longer time.
Figure 8 show the relationship between spa-
tial/intensity subsampling rate and PSNR for iterative
bilateral filtering. The spatial subsampling has a more
Table 1: Approximation accuracy of PSNR for LLU and
FastLLU (FLLU).
Iterative bilateral filtering L
0
smoothing
LLU FLLU LLU FLLU
1/1024 26.296 26.322 31.652 31.675
1/256 28.377 28.460 32.548 32.572
1/64 31.985 32.023 33.774 33.798
1/16 34.438 34.465 35.568 35.598
1/4 37.340 37.367 38.373 38.422
1
10
100
1000
10000
100000
1000000
1/256
1/64
1/16
1/4
Time [ms]
Subsampling rate
CU
GIU
BGU
LLU
FastLLU
naive
(a) Iterative bilateral filtering
1
10
100
1000
10000
100000
1000000
1/256
1/64
1/16
1/4
Time [ms]
Subsampling rate
CU
GIU
BGU
LLU
FastLLU
naive
(b) L
0
smoothing
Figure 5: Computational time for na
¨
ıve implementation and
each acceleration method with changing subsampling rate.
significant effect than the range subsampling.
Figures 9 and 10 depict input image and results
of each acceleration method for iterative bilateral fil-
tering and L
0
smoothing, respectively. We omit the
result of LLU because the result is similar to the
FastLLU.
Figure 11 depict results of each approach of the
proposed method for L
0
smoothing.
5 CONCLUSIONS
In this paper, we proposed an acceleration method
for edge-preserving filtering with image upsampling.
The local LUT upsampling has higher approximation
accuracy than conventional methods. Also, the lo-
cal LUT upsampling accelerates ×100 faster than the
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
72
20
25
30
35
40
0
5000
10000
15000
PSNR [dB]
Time [ms]
CU
GIU
BGU
LLU
FastLLU
(a) Iterative bilateral filtering
20
25
30
35
40
0
5000
10000
15000
20000
PSNR [dB]
Time [ms]
CU
GIU
BGU
LLU
FastLLU
(b) L
0
smoothing
Figure 6: Changing subsampling rate performance in PSNR
w.r.t. the computational time of each acceleration method.
25
30
35
0
500
1000
1500
2000
2500
3000
PSNR [dB]
Time [ms]
WTA-tri-linear
WTA-linear-bicubic
FLL-tri-linear
FLL-linear-bicubic
Figure 7: Changing subsampling rate performance in PSNR
w.r.t. the computational time of each approach for the pro-
posed (Iterative bilateral filtering).
na
¨
ıve implementation. We also described that fast
LUT upsampling could obtain a higher approximation
of accuracy and faster computational time than using
the WTA approach. Also, by using bicubic interpola-
tion, the proposed method can output more accurate
results.
20
25
30
35
40
16
32
64
128
256
PSNR [dB]
Number of bins
subsampling rate : 1/256
subsampling rate : 1/64
subsampling rate : 1/16
subsampling rate : 1/4
Figure 8: Accuracy of PSNR by changing the number of lut
bins for the proposed method (Iterative bilateral filtering).
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI
(JP17H01764, 18K18076, 19K24368).
REFERENCES
Adams, A., Baek, J., and Davis, M. A. (2010). Fast high-
dimensional filtering using the permutohedral lattice.
Computer Graphics Forum, 29(2):753–762.
Aubry, M., Paris, S., Hasinoff, S. W., Kautz, J., and Durand,
F. (2014). Fast local laplacian filters: Theory and ap-
plications. ACM Transactions on Graphics, 33(5).
Bae, S., Paris, S., and Durand, F. (2006). Two-scale tone
management for photographic look. ACM Transac-
tions on Graphics, pages 637–645.
Buades, A., Coll, B., and Morel, J. M. (2005). A non-local
algorithm for image denoising. In Proc. Computer Vi-
sion and Pattern Recognition (CVPR).
Chaudhury, K. N. (2011). Constant-time filtering using
shiftable kernels. IEEE Signal Processing Letters,
18(11):651–654.
Chaudhury, K. N. (2013). Acceleration of the shiftable o(1)
algorithm for bilateral filtering and nonlocal means.
IEEE Transactions on Image Processing, 22(4):1291–
1300.
Chaudhury, K. N., Sage, D., and Unser, M. (2011).
Fast o(1) bilateral filtering using trigonometric range
kernels. IEEE Transactions on Image Processing,
20(12):3376–3382.
Chen, J., Adams, A., Wadhwa, N., and Hasinoff, S. W.
(2016). Bilateral guided upsampling. ACM Trans.
Graph., 35(6):203:1–203:8.
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2007). Image denoising by sparse 3-d transform-
domain collaborative filtering. IEEE Transactions on
image processing, 16(8):2080–2095.
Durand, F. and Dorsey, J. (2002). Fast bilateral filtering
for the display of high-dynamic-range images. ACM
Transactions on Graphics, 21(3):257–266.
Fast Local LUT Upsampling
73

(a) input (b) na
¨
ıve (c) cubic
28.834 dB
(d) guided
28.936 dB
(e) BGU
27.189 dB
(f) Fast LLU
30.679 dB
Figure 9: Results of iterative bilateral filtering.
(a) input (b) na
¨
ıve (c) cubic
32.038 dB
(d) guided
34.451 dB
(e) BGU
33.796 dB
(f) fast LLU
35.143 dB
Figure 10: Results of L
0
smoothing.
(a) na
¨
ıve (b) DP
32.646 dB
(c) WTA
35.077 dB
(d) FLL
35.114 dB
Figure 11: Results of each approach for the proposed.
Eisemann, E. and Durand, F. (2004). Flash photography en-
hancement via intrinsic relighting. ACM Transactions
on Graphics, 23(3):673–678.
Fujita, S., Fukushima, N., Kimura, M., and Ishibashi, Y.
(2015). Randomized redundant dct: Efficient denois-
ing by using random subsampling of dct patches. In
Proc. ACM SIGGRAPH Asia 2015 Technical Briefs.
Fukushima, N., Fujita, S., and Ishibashi, Y. (2015). Switch-
ing dual kernels for separable edge-preserving fil-
tering. In Proc. IEEE International Conference on
Acoustics, Speech and Signal Processing (ICASSP).
Fukushima, N., Kawasaki, Y., and Maeda, Y. (2019a). Ac-
celerating redundant dct filtering for deblurring and
denoising. In IEEE International Conference on Im-
age Processing (ICIP).
Fukushima, N., Sugimoto, K., and Kamata, S. (2018).
Guided image filtering with arbitrary window func-
tion. In Proc. IEEE International Conference on
Acoustics, Speech and Signal Processing (ICASSP).
Fukushima, N., Takeuchi, K., and Kojima, A. (2016). Self-
similarity matching with predictive linear upsampling
for depth map. In Proc. 3DTV-Conference.
Fukushima, N., Tsubokawa, T., and Maeda, Y. (2019b).
Vector addressing for non-sequential sampling in fir
image filtering. In IEEE International Conference on
Image Processing (ICIP).
Gastal, E. S. L. and Oliveira, M. M. (2011). Domain
transform for edge-aware image and video processing.
ACM Transactions on Graphics, 30(4).
Gastal, E. S. L. and Oliveira, M. M. (2012). Adaptive man-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
74

ifolds for real-time high-dimensional filtering. ACM
Transactions on Graphics, 31(4).
Ghosh, S., Nair, P., and Chaudhury, K. N. (2018). Opti-
mized fourier bilateral filtering. IEEE Signal Process-
ing Letters, 25(10):1555–1559.
He, K. and Sun, J. (2015). Fast guided filter. CoRR,
abs/1505.00996.
He, K., Sun, J., and Tang, X. (2009). Single image haze
removal using dark channel prior. In Proc. Computer
Vision and Pattern Recognition (CVPR).
He, K., Sun, J., and Tang, X. (2010). Guided image fil-
tering. In Proc. European Conference on Computer
Vision (ECCV).
Hennessy, J. L. and Patterson, D. A. (2017). Computer Ar-
chitecture, Sixth Edition: A Quantitative Approach.
Morgan Kaufmann Publishers Inc., San Francisco,
CA, USA, 6th edition.
Hosni, A., Rhemann, C., Bleyer, M., Rother, C., and
Gelautz, M. (2013). Fast cost-volume filtering for
visual correspondence and beyond. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
35(2):504–511.
Kodera, N., Fukushima, N., and Ishibashi, Y. (2013). Fil-
ter based alpha matting for depth image based render-
ing. In Proc. IEEE Visual Communications and Image
Processing (VCIP).
Kopf, J., Cohen, M. F., Lischinski, D., and Uyttendaele, M.
(2007). Joint bilateral upsampling. ACM Transactions
on Graphics, 26(3).
Levin, A., Lischinski, D., and Weiss, Y. (2004). Coloriza-
tion using optimization. ACM Transactions on Graph-
ics, 23(3):689–694.
Maeda, Y., Fukushima, N., and Matsuo, H. (2018a). Ef-
fective implementation of edge-preserving filtering on
cpu microarchitectures. Applied Sciences, 8(10).
Maeda, Y., Fukushima, N., and Matsuo, H. (2018b). Taxon-
omy of vectorization patterns of programming for fir
image filters using kernel subsampling and new one.
Applied Sciences, 8(8).
Matsuo, T., Fujita, S., Fukushima, N., and Ishibashi, Y.
(2015). Efficient edge-awareness propagation via
single-map filtering for edge-preserving stereo match-
ing. In Proc. SPIE, volume 9393.
Matsuo, T., Fukushima, N., and Ishibashi, Y. (2013).
Weighted joint bilateral filter with slope depth com-
pensation filter for depth map refinement. In Proc.
International Conference on Computer Vision Theory
and Applications (VISAPP).
Min, D., Choi, S., Lu, J., Ham, B., Sohn, K., and Do,
M. N. (2014). Fast global image smoothing based on
weighted least squares. IEEE Transactions on Image
Processing, 23(12):5638–5653.
Murooka, Y., Maeda, Y., Nakamura, M., Sasaki, T., and
Fukushima, N. (2018). Principal component analysis
for acceleration of color guided image filtering. In
Proc. International Workshop on Frontiers of Com-
puter Vision (IW-FCV).
Paris, S., Hasinoff, S. W., and Kautz, J. (2011). Local
laplacian filters: Edge-aware image processing with
a laplacian pyramid. pages 68:1–68:12.
Petschnigg, G., Agrawala, M., Hoppe, H., Szeliski, R., Co-
hen, M., and Toyama, K. (2004). Digital photography
with flash and no-flash image pairs. ACM Transac-
tions on Graphics, 23(3):664–672.
Sugimoto, K., Fukushima, N., and Kamata, S. (2016).
Fast bilateral filter for multichannel images via soft-
assignment coding. In Proc. Asia-Pacific Signal and
Information Processing Association Annual Summit
and Conference (APSIPA).
Sugimoto, K., Fukushima, N., and Kamata, S. (2019). 200
fps constant-time bilateral filter using svd and tiling
strategy. In IEEE International Conference on Image
Processing (ICIP).
Sugimoto, K. and Kamata, S. (2015). Compressive bilat-
eral filtering. IEEE Transactions on Image Process-
ing, 24(11):3357–3369.
Tajima, H., Fukushima, N., Maeda, Y., and Tsubokawa, T.
(2019). Local lut upsampling for acceleration of edge-
preserving filtering.
Tomasi, C. and Manduchi, R. (1998). Bilateral filtering for
gray and color images. In Proc. International Confer-
ence on Computer Vision (ICCV), pages 839–846.
Xu, L., Lu, C., Xu, Y., and Jia, J. (2011). Image smoothing
via l0 gradient minimization. ACM Transactions on
Graphics.
Yang, Q., Tan, K. H., and Ahuja, N. (2009). Real-time o
(1) bilateral filtering. In Proc. Computer Vision and
Pattern Recognition (CVPR), pages 557–564.
Yu, G. and Sapiro, G. (2011). Dct image denoising: A sim-
ple and effective image denoising algorithm. Image
Processing On Line, 1:1.
Fast Local LUT Upsampling
75
