
EasyModel 1.1: User-friendly Stochastic and Deterministic Simulations
for Systems Biology Models
Jordi Bartolome
1 a
, Rui Alves
2 b
and Francesc Solsona
1 c
1
Dept. of Computer and Industrial Engineerings, Universitat de Lleida, C/Jaume II 69, Lleida, Spain
2
Dept. of Basic Medical Sciences, Universitat de Lleida, C/Montserrat Roig 2, Lleida, Spain
Keywords:
Systems, Biology, Model, Simulation, Stochastic, Deterministic, User-friendly, Web, Application,
Mathematica.
Abstract:
EasyModel is a user-friendly web application that uses Wolfram webMathematica for performing simulations
and analysis of systems biology models. EasyModel lets users create new models, load models from the
BioModels database, and import preexisting models from SBML files. EasyModel mainly targets the student
of bioinformatics or systems biology without the need of having Mathematica programming knowledge. In
addition, expert programmers may find it useful as a tool for quickly implementing new models in Mathe-
matica, which can then be downloaded as Mathematica notebooks to be tailored locally for more advanced
simulation and analysis. The version described in this manuscript introduces the stochastic simulation feature.
EasyModel is freely available at https://easymodel.udl.cat
1 INTRODUCTION
Molecular systems biology is a quantitative and inte-
grative discipline. This implies that using software for
mathematical modeling is a required skill for the sys-
tems biologist. Learning to create mathematical mod-
els for molecular systems biology is usually a task
with a slow learning curve, as it requires a significant
amount of technical skill.
Currently, there is a considerable array of tools
for modeling and simulating of biological systems
(SBML.org, 2019)(Alves et al., 2006). Most of these
tools are standalone and can be used in a normal
PC. There is a small number of general platforms for
mathematical computation (PMC) such as Mathemat-
ica or Maple that can be adapted for systems biol-
ogy modeling. These platforms offer a wide range of
mathematical solutions, with flexible graphical user
interfaces (GUI). Mathematica and Maple stand aside
from other PMC because they support symbolic anal-
ysis. A drawback of using these and other PMCs is
that the user must become an expert in coding for the
platform. This drawback can be partially overcome
by implementing a user-friendly application that uses
a
https://orcid.org/0000-0002-4348-9307
b
https://orcid.org/0000-0002-8112-5184
c
https://orcid.org/0000-0002-4830-9184
a PMC as the motor for calculations, as other mod-
eling tools have already demonstrated (Peters et al.,
2017)(Helikar et al., 2012)(Benque et al., 2012).
For this reason we designed EasyModel, a web
application for mathematical modeling in systems bi-
ology. It stands out for its user-friendly GUI that is
usable by both beginner and expert users (Bartolome
et al., 2019).
EasyModel 1.0 focused on the simulation of sys-
tems of ordinary differential equations using deter-
ministic algorithms (Ascher and Petzold, 1997). Nev-
ertheless, when the systems being modeled are com-
posed of a small number of molecules, stochas-
tic algorithms are more accurate (Maarleveld et al.,
2013), and linear noise analysis is a more appropri-
ate tool than sensitivity analysis to understand the
limitations and regulation of the system (Paulsson,
2004). While stochastic simulation and linear noise
analysis are available in several simulation applica-
tions (SBML.org, 2019)(Maarleveld et al., 2013)(Bal-
let et al., 2016), they lack the usability characteristics
EasyModel provides to new systems biologists. Be-
cause of the importance of stochasticity in molecular
systems biology, it is important that EasyModel also
provides this functionality to its users. Hence, this
manuscript describes the prototype for the next pro-
duction version of EasyModel. This prototype, which
we call EasyModel 1.1, enables a user-friendly sim-
Bartolome, J., Alves, R. and Solsona, F.
EasyModel 1.1: User-friendly Stochastic and Deterministic Simulations for Systems Biology Models.
DOI: 10.5220/0008966001450149
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 145-149
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
145

ulation and analysis of stochastic models in systems
biology.
2 EasyModel
2.1 Origin and Objectives
Wolfram Mathematica provides many ready-to-use
mathematical functions that are perfectly suited for
simulating and analyzing mathematical models of bi-
ological systems. Nevertheless, its use requires that
one knows how to create models for systems biology
and how to program in the Mathematica language.
This makes Mathematica less than ideal for use by be-
ginners and students of systems biology. EasyModel
is a web application that was created for facilitating
the use of Wolfram Mathematica for modeling by be-
ginner computational systems biologists, waiving the
need to know how to program in Mathematica or de-
velop mathematical models from scratch. Overall, our
application provides a user-friendly interface that al-
lows users to input the information for creating mod-
els in a simple way. Afterwards, it formats, wraps,
and processes the information to create a Mathemati-
cal notebook and configure the simulation and analy-
sis. This notebook is then sent to a webMathematica
engine that performs the calculations. webMathemat-
ica returns the output in graphical and text form and
our GUI picks up that information and provides it to
the user.
2.2 EasyModel Working Context
EasyModel uses a conceptual representation of
molecular biology networks and transforms that rep-
resentation into systems of autonomous ordinary dif-
ferential equations (ODE) that can be used to simulate
the dynamic behavior of the network. The networks
are represented in terms of individual processes or re-
actions that consume substrates, generate products,
and whose reaction rate can be modulated by modi-
fiers (activators or inhibitors). The rate of each reac-
tions is described by a kinetic function that depends
on some of the species in the networks and on reac-
tion specific parameters. The integration of all these
elements conforms a mathematical model of the bio-
logical network of interest (Figure1).
Users provide the program with the individual
processes using the following notation:
K
1
∗ S
1
+ ...− > C
1
∗ P
1
+ ...;M
1
;... (1)
In Equation 1 K
x
,C
x
represent the species coefficients,
S
x
represents the substrates (left-hand side of the ar-
row), P
x
represents the products (right-hand side of
the arrow), and M
x
represents modifier species that
influence the rate but are not substrates.
After the structure of the model is defined through
its processes, a kinetic rate law needs to be associated
to each of the reactions. These rate laws are standard
mathematical functions that depend on a subset of the
network species and on parameters whose values are
specific for each reaction. EasyModel allows users to
select rate laws with a predefined formalism (Power
Law, Mass Action, Saturating and cooperative (Sor-
ribas et al., 2007) or create custom made formulas.
2.3 Usage and Features
In the initial page of the web application, the visitor
can log in as a registered user or try the application as
a guest user. Guest users are provided with a brief tu-
torial on how to use EasyModel before accessing the
application itself. The tutorial can be skipped and it
is always available to consult in the Tools option. In
addition to the the tutorial, the application has Infor-
mation buttons all across the GUI so that users can
consult what to do next at each step.
The application is designed in 4 basic steps:
1. Select the model (or create a new one)
2. Modify or build the model
3. Configure the simulation/s
4. Get the simulation results
In step one, users must select a model repository:
public or private (see Figure 2). The public reposi-
tory includes built-in models. Many of these are ei-
ther from the BioModels Database (Le Nov
`
ere et al.,
2006) or developed and published by the other users
of the platform. The private repository permits users
to create new models or continue editing unfinished
models. Guest users can create new models to use but
they cannot be saved in the system. They can how-
ever download them in SBML form and re-upload
again at a later time by importing the SBML file. In
fact EasyModel complies with SBML (Hucka et al.,
2003) Level 3 Version 2 specification and it can up-
load models described with that specification. SBML
facilitates the interchange of biologic system models
between many available modeling tools.
Model building in step two requires defining the
individual reactions of the model (see Figure 3), as
well as the rate laws (see Figure 4). Users can either
select a predefined rate law or define a new one as
a standard mathematical function. Each reaction of
the system must have an assigned rate law, with its
set of parameter values. The parameters may have a
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
146
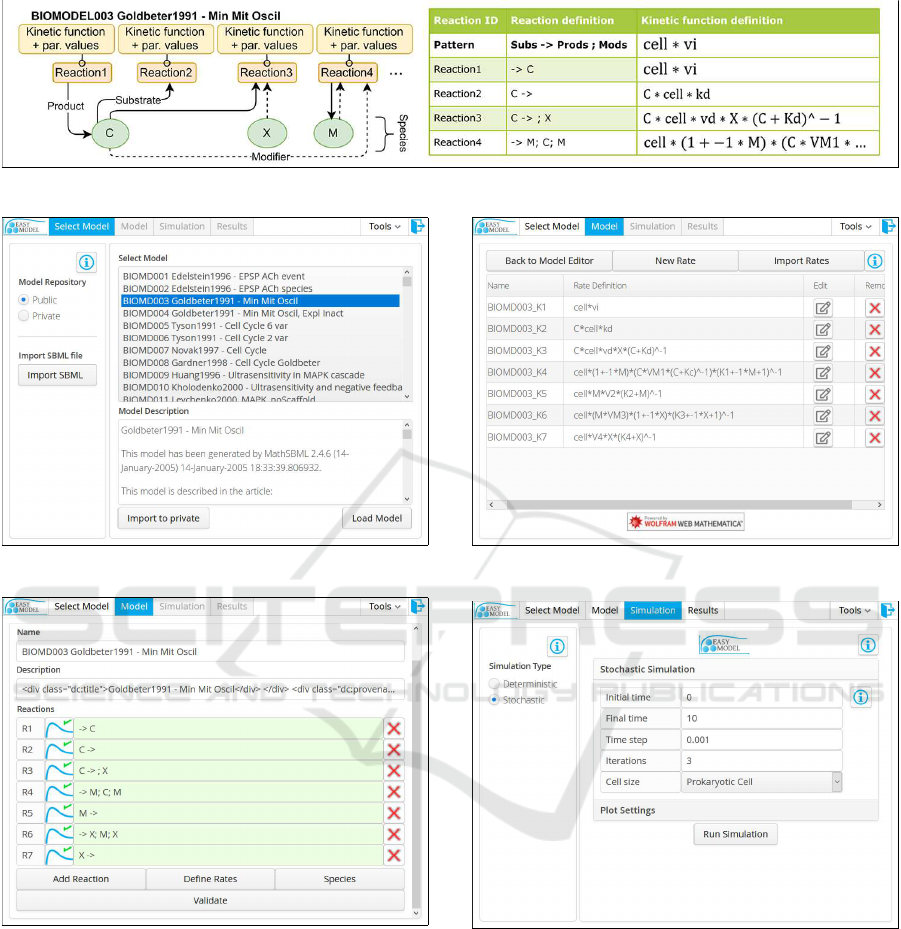
Figure 1: Biological system model BIOMODEL003 (Goldbeter, 1991).
Figure 2: Selecting model.
Figure 3: Modeling the reactions.
numerical value or be linked to a substrate or modifier
species of the network.
Initial concentrations of the system species must
be specified as well. If not, EasyModel automatically
sets them to 1.
To proceed to step three, EasyModel must validate
the model, warning the user if additional information
or modifications are required.
In step three, and after model validation, users
define what simulations and analyses are to be per-
formed in webMathematica (see Figure 5).
During the simulation configuration step, users
Figure 4: Defining the rate laws.
Figure 5: Stochastic simulation configuration.
can choose whether they will perform a determinis-
tic simulation (if the system has a large number of
molecules) or a stochastic simulation. This later type
of simulation is a new feature of the version being de-
scribed here.
For deterministic simulations, the user may per-
form time course and steady state simulations, as well
as sensitivity analysis with respect to model param-
eters and independent variables. Sensitivity analysis
can be requested for steady state and time-course sim-
ulations. A linear stability analysis of steady states
can also be performed.
EasyModel 1.1: User-friendly Stochastic and Deterministic Simulations for Systems Biology Models
147
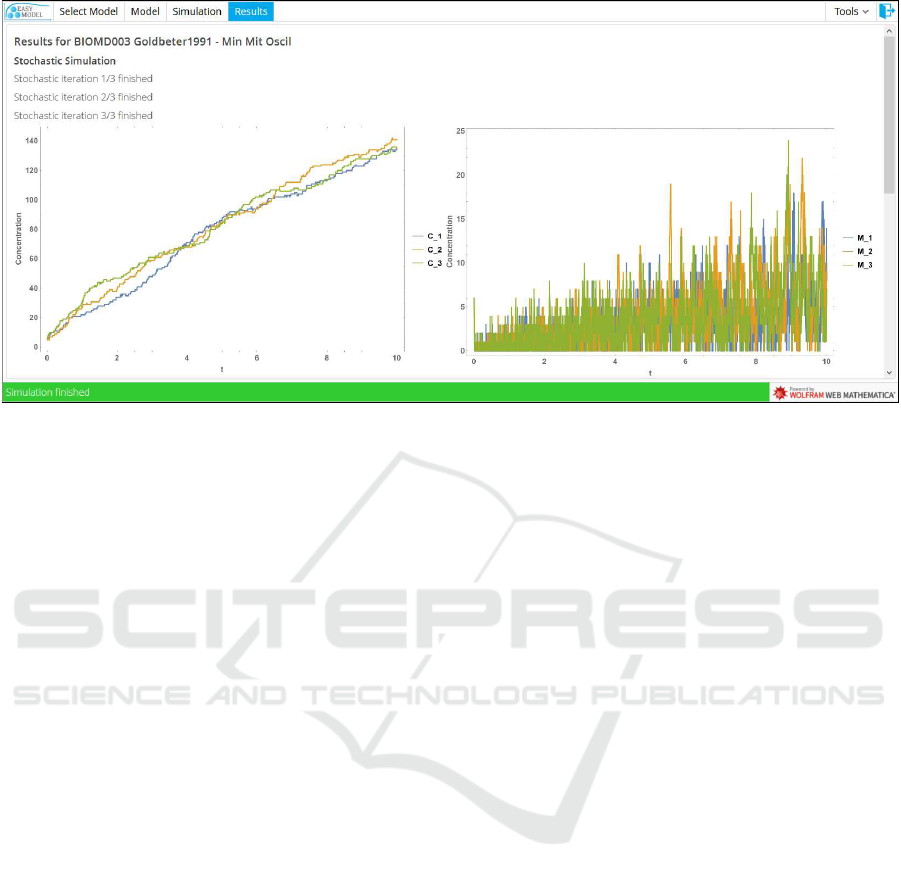
Figure 6: Stochastic simulation results.
For stochastic simulations, users define the phys-
ical size of the system, how many times they want to
repeat the simulation and how long the system is to
be simulated. EasyModel also provides the intrinsic
noise of the system for each dependent variable by
calculating the coefficient of variation and the quar-
tile coefficient of dispersion for each species. Default
cell size is considered by the program to be that of
Prokaryotic cell. Default number of repeat simula-
tion is set to 3. Default end time of the simulation is
set to 10 time units.
Once all actions are configured, the user presses
the simulation button and the program goes to step
four. In this step all the data is sent to the web-
Mathematica calculation engine (Mathematica ker-
nel), which performs the simulation and returns the
results to the user. Individual results are returned im-
mediately after being computed, in real-time (see Fig-
ure 6). Results are represented in plots and tables that
can be downloaded. The user can cancel the simu-
lation at any time and the system will stop after the
execution of the webMathematica command that was
being evaluated before pressing the button. In ad-
dition to the graphical representation of the results,
users may also download the generated Mathematica
notebook and the model in SBML format.
EasyModel stores user account information as
well as the the models and rate laws the users intro-
duce into the system. Simulation results are not stored
into the database.
2.4 Implementation
EasyModel is implemented by merging various tech-
nologies. The web application is written in Java EE,
using the open-source Vaadin 8 Framework for devel-
oping the web user interface (UI). The calculation en-
gine is the Wolfram webMathematica (Wolfram Re-
search Inc., 2108), which communicates with the Java
EE application. User data, such as user account, mod-
els and rate laws, is stored in a database using the
open-source MySQL 8 Community Server database
manager. Finally, the web application is deployed on
the Apache Tomcat 9 web application server.
To implement the SBML file format compatibility,
JSBML Java library (Dr
¨
ager et al., 2011) is used.
The source code is available at
https://github.com/jordibart/easymodel and licensed
under the GNU GPL. All the dependencies of Easy-
Model are open-source except for webMathematica,
which requires a commercial license.
3 CONCLUSIONS
EasyModel is a user-friendly tool for creating and
analyzing simple mathematical models of biological
networks in systems biology. While it is aimed at
novel systems biologists and students, the tool can
also be of profit for more advanced researchers, as
they can quickly implement their models and down-
load them for further local tailoring for more ad-
vanced analysis.
While the production version of EasyModel is
limited to deterministic simulation and analysis, here
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
148

we present an evolution of the tool that enables
stochastic simulations and biological noise analysis
in the context of those simulations. Stochastic simula-
tions are significantly more complex in computational
terms and require longer CPU times to conclude than
analogous deterministic simulations. Nevertheless,
this type of simulations accurately describes the dy-
namic behavior of systems with a small number of
molecules, something that deterministic simulations
can not always do.
This new prototype of EasyModel 1.1 is now be-
ing tested before it is rolled out to replace the cur-
rent 1.0 production version. Once this task is done
we will implement additional functionality to enable
user-friendly ways to merge individual models, to
scan parameter values and independent variables, and
to perform bifurcation analysis.
ACKNOWLEDGEMENTS
This work was partially supported by Minis-
terio de Economia, Industria y Competitividad
[TIN2017-84553-C2-2-R]; Ministerio de Educacion
[PRX18/00142]; and by Bridge Grants from Univer-
sitat de Lleida and INSPIRES.
REFERENCES
Alves, R., Antunes, F., and Salvador, A. (2006). Tools for
kinetic modeling of biochemical networks. Nature
Biotechnology, 24(6):667–672.
Ascher, U. M. and Petzold, L. R. (1997). Computer
Methods for Ordinary Differential Equations and
Differential-Algebraic Equations.
Ballet, P., Rivi
`
ere, J., Pothet, A., Theron, M., Pichavant,
K., Abautret, F., Fronville, A., and Rodin, V. (2016).
Modelling and simulating complex systems in biol-
ogy: Introducing NetBioDyn - a pedagogical and in-
tuitive agent-based software. In Multi-Agent-Based
Simulations Applied to Biological and Environmental
Systems, pages 128–158. IGI Global.
Bartolome, J., Alves, R., Solsona, F., and Teixido, I. (2019).
EasyModel: user-friendly tool for building and analy-
sis of simple mathematical models in systems biology.
Bioinformatics.
Benque, D., Bourton, S., Cockerton, C., Cook, B., Fisher, J.,
Ishtiaq, S., Piterman, N., Taylor, A., and Vardi, M. Y.
(2012). Bio Model Analyzer: Visual Tool for Mod-
eling and Analysis of Biological Networks. LNCS,
7358:686–692.
Dr
¨
ager, A., Rodriguez, N., Dumousseau, M., D
¨
orr, A., Wr-
zodek, C., Le Nov
`
ere, N., Zell, A., and Hucka, M.
(2011). JSBML: a flexible Java library for working
with SBML. Bioinformatics, 27(15):2167–2168.
Goldbeter, A. (1991). A minimal cascade model for the
mitotic oscillator involving cyclin and cdc2 kinase.
Proceedings of the National Academy of Sciences,
88(20):9107–9111.
Helikar, T., Kowal, B., McClenathan, S., Bruckner, M.,
Rowley, T., Madrahimov, A., Wicks, B., Shrestha, M.,
Limbu, K., and Rogers, J. A. (2012). The Cell Col-
lective: toward an open and collaborative approach to
systems biology. BMC systems biology, 6:96.
Hucka, M., Finney, A., Sauro, H. M., Bolouri, H., Doyle,
J. C., Kitano, H., and Forum, t. r. o. t. S. (2003). The
systems biology markup language (SBML): a medium
for representation and exchange of biochemical net-
work models. Bioinformatics, 19(4):524–531.
Le Nov
`
ere, N., Bornstein, B., Broicher, A., Courtot, M.,
Donizelli, M., Dharuri, H., Li, L., Sauro, H., Schilstra,
M., Shapiro, B., Snoep, J. L., and Hucka, M. (2006).
{BioModels Database}: a free, centralized database
of curated, published, quantitative kinetic models of
biochemical and cellular systems. Nucleic Acids Re-
search, 34(Database issue):D689—-D691.
Maarleveld, T. R., Olivier, B. G., and Bruggeman, F. J.
(2013). StochPy: A comprehensive, user-friendly tool
for simulating stochastic biological processes. PLoS
ONE, 8(11).
Paulsson, J. (2004). Summing up the noise in gene net-
works.
Peters, M., Eicher, J. J., van Niekerk, D. D., Waltemath, D.,
and Snoep, J. L. (2017). The JWS online simulation
database. Bioinformatics, 33(10):btw831.
SBML.org (2019). SBML Software Ma-
trix http://sbml.org/SBML
Software Guide/
SBML Software Matrix (12-12-2019).
Sorribas, A., Hern
´
andez-Bermejo, B., Vilaprinyo, E., and
Alves, R. (2007). Cooperativity and saturation in bio-
chemical networks: A saturable formalism using Tay-
lor series approximations. Biotechnology and Bio-
engineering, 97(5):1259–1277.
Wolfram Research Inc. (2108). WebMathematica
3.4.3. www.wolfram.com/products/webmathematica
(5/6/19).
EasyModel 1.1: User-friendly Stochastic and Deterministic Simulations for Systems Biology Models
149
