Skeleton-geodesic Distances for Shape Recognition: Efficient
Computation by Continuous Skeleton
Nikita Lomov
Lomonosov Moscow State University, GSP-1, Leninskie Gory, Moscow, 119991, Russian Federation
Keywords:
Shape Description, Skeleton-geodesic Distance, Shape Context, Polygonal Figure, Voronoi Diagram.
Abstract:
We consider the problem of determining the distance between points of a planar shape, which would be infor-
mative and resistant to shape transformations, including flexible articulations. The proposed distance is defined
as the length of the shortest path through the skeleton between the projections of the points on the skeleton
and called skeleton-geodesic distance. To calculate the values of interest, a continuous medial representation
of polygonal shape is used. The method of calculating the distance is based on the following principle: at
first, calculate all skeleton-geodesic distances between pairs of “reference” points, which are the vertices of
the skeleton, using the traditional graph algorithms; then refine them by adding the distances from the points
in question to the nearest reference points. This approach allows us to achieve computational efficiency and
to derive analytical formulas for direct calculation. An analogue of shape context using skeleton-geodesic
distances and angles between branches of the skeleton is proposed. Examples of using these descriptors in the
task of recognition of flexible objects are presented, showing that the distance proposed often provides greater
performance compared to Euclidean or geodesic distances.
1 INTRODUCTION
In computer vision tasks related to the shape recogni-
tion for objects in images, methods that use the dis-
tribution of distances between points of the shape in
a feature description are very popular. Perhaps the
most famous of these methods is the shape context
(Belongie et al., 2002), which builds joint histograms
of distances and angles for contour points. How-
ever, it was noted that the Euclidean distance used
in this method does not describe shapes very well in
the case of flexible articulations. Therefore, modifi-
cations of this algorithm were developed, using the
distance of path lying inside the figure (Ling and Ja-
cobs, 2007), otherwise — geodesic distances (Jain
and Zhang, 2005). Geodesic distances are well estab-
lished in the field of recognition of three-dimensional
shapes (Shamai and Kimmel, 2017), where they also
proved to be resistant to shape variations.
Existing algorithms of geodesic distances com-
putation involve numerical methods like fast march-
ing (Sethian, 1999) of another propagation techniques
(C
´
ardenes et al., 2010) that operate on pixel level.
This is time consuming, especially in cases when the
distances between multiple points are analyzed, since
it is necessary to run a geodesic distance transform for
each of them. At the same time, there are examples
of distances, which are also determined by the lengths
of the inner-paths of the figure, and therefore resistant
to flexible deformations, but these paths are defined
in a nontrivial way. Such an approach was proposed
in (Cuisenaire, 1999), where the paths that lie in-
side the figure, but are sufficiently far from its border,
were considered. In addition, in the paper (Boluk and
Demirci, 2015) the distances from the points of the
skeleton to the ends of its branches computed as the
lengths of skeleton lines were investigated. Develop-
ing these ideas, in this paper we suggest an alternative
of traditional geodesic distances — skeleton-geodesic
distances, which are determined by the shortest paths
lying on the medial axis. Skeleton-geodesic distances
share many useful features of classic geodesic dis-
tances, such as rotation invariance and resistance to
flexible articulations. At the same time their calcula-
tion uses a contour-skeleton representation, which is
much more compact than pixel-wise. Moreover, it is
sufficient to calculate the distances for a certain set of
“reference” points, and the distances at intermediate
points can be interpolated without loss of accuracy.
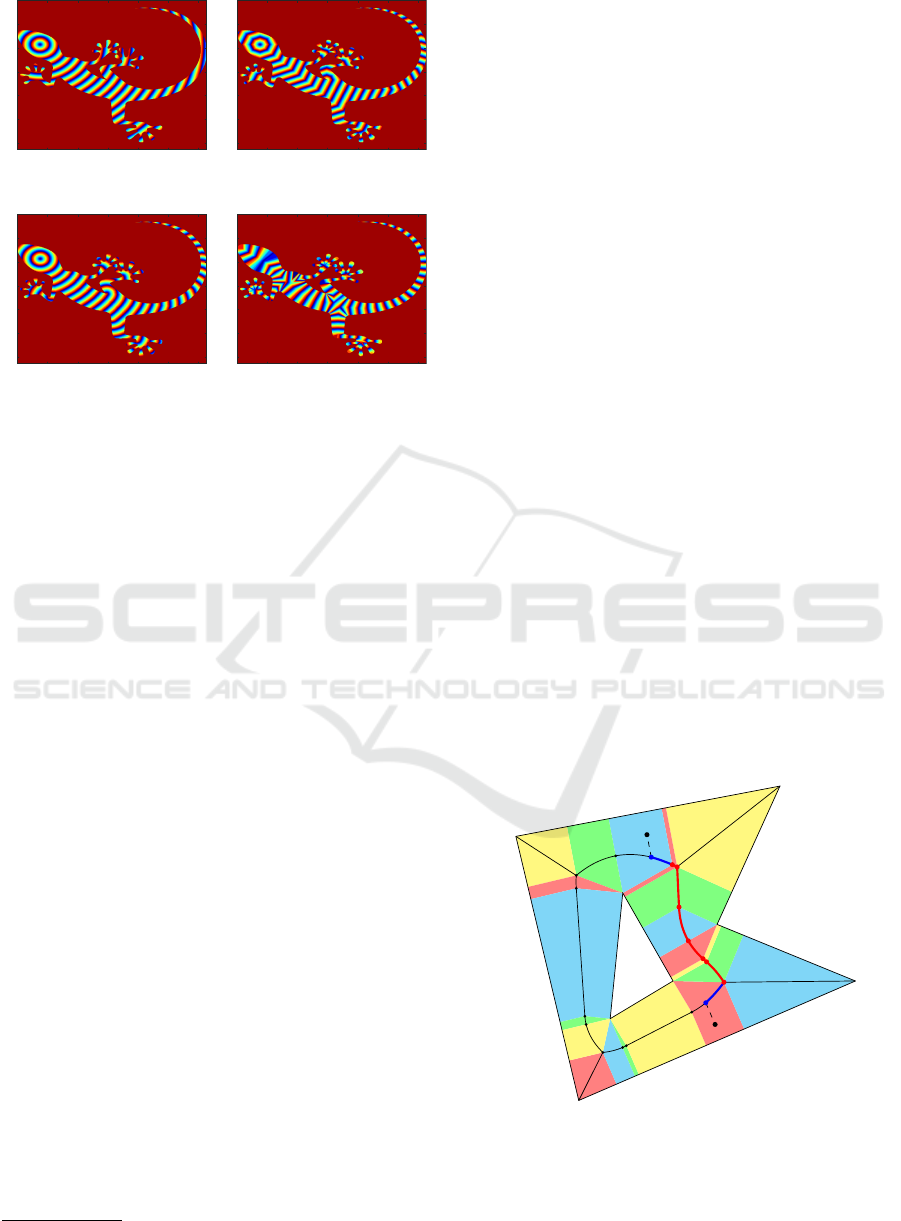
In Figure 1 you can see how much skeleton-
geodesic distances differ from the usual ways of
defining the distances between points of the shape.
Lomov, N.
Skeleton-geodesic Distances for Shape Recognition: Efficient Computation by Continuous Skeleton.
DOI: 10.5220/0008968003070314
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
307-314
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
307

100 200 300 400 500 600
100
200
300
400
500
600
100 200 300 400 500 600
100
200
300
400
500
600
(a) (b)
100 200 300 400 500 600
100
200
300
400
500
600
100 200 300 400 500 600
100
200
300
400
500
600
(c) (d)
Figure 1: Map of distances to the same point for different
types of distance: (a) Euclidean, (b) geodesic with quasi-
Euclidean metric (c) geodesic with Euclidean metric, (d)
skeleton-geodesic.
2 BASIC CONCEPTS
Definition 1. Skeleton is the set of centers of all
inscribed empty (maximal by inclusion) circles of a
shape.
Definition 2. Skeleton-geodesic distance between
points p and q of the skeleton of figure A (denoted
by d
Geod(Sk(A))
(p,q)) is the length of the shortest path
between these points passing through the skeleton
1
.
Definition 3. Spoke is a line segment from the skele-
ton point to any nearest boundary point.
Definition 4. Skeletal projection of the point p ∈ A
(denoted by p
Sk(A)
) is the origin of the spoke, which
the point p lies on.
Since a set of spokes covers the entire figure,
and for each of its points, the spoke is uniquely de-
fined (Mestetskiy, 2015) the skeletal projection is also
uniquely defined for each point of the shape. As a
result, we can extend the definition 2 and calculate
skeleton-based distances for all points of the figure.
Definition 5. Skeleton-geodesic distance between ar-
bitrary points p and q of A is considered to be the
skeleton-geodesic distance between their projections:
d
Geod(Sk(A))
(p,q) = d
Geod(Sk(A))
(p
Sk(A)
,q
Sk(A)
). (1)
Note that the skeletal geodesic distance is not a
distance in the strict sense, but is a factor-distance,
since the distance between all points lying on the
spokes with the same origin is equal to zero. Because
1
Further we use a simpler notation: d
skel
(p,q).
of this, we can talk about the distances between the
spokes, as well as about the distances between indi-
vidual points.
Methods for constructing continuous skeletons of
polygonal figures, as well as for approximating ob-
jects in a binary image by polygons, are known and
well developed (Mestetskiy and Semenov, 2008). The
boundary of the polygonal figure can be represented
as the set of point-sites (vertices of a figure) and
segment-sites (sides of boundary polygons). Voronoi
diagram (VD) of line segments is defined for these set
of sites. The skeleton is obtained from the subgraph of
VD lying inside the figure by cutting off the bisectors
between concave point-sites and adjacent segment-
sites. Each edge of the skeleton is associated with
a pair of sites for which this edge is a bisector — the
common boundary of their Voronoi cells. So, a skele-
ton of polygonal figure can be considered as a planar
graph S = (V,E) with edges in the form of linear and
parabolic segments.
Definition 6. Bicircle of the edge e ∈E is the union of
all inscribed circles centered on e. The edge is called
the axis of bicircle.
Definition 7. Proper region of the bicircle of edge e
is the closure of the union of all spokes incidental to
internal points of e.
Proper regions cover the entire figure and inter-
sect only along their boundary spokes. These con-
cepts will help us in the direct calculation of skeleton-
geodesic distances.
3 IDEA OF THE ALGORITHM
q
0
p
0
q
p
Figure 2: Example of skeleton-geodesic path between
points p and q lying on the spokes p
0
p
00
and q
0
q
00
respec-
tively. It consists of the main part located between the ver-
tices of the skeleton (red line) and additions — parts lying
inside proper regions of p and q (blue lines). Proper regions
are painted in different colors.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
308

The skeleton-geodesic distance between the points p
and q can be calculated once as follows:
1. Find the skeletal projections of p and q.
2. For projections that do not coincide with the ver-
tices of the skeleton, split the edges to which they
belong into two parts.
3. Use the standard shortest-path search algorithm in
the graph for a modified (with edges split) skele-
ton — Dijkstra’s algorithm or one of the algo-
rithms for determining the least common ancestor
if there are no cycles in the skeleton and it can be
represented by a tree.
This approach is illustrated in Figure 2. Neverthe-
less, it can be ineffective in a mass query, as it will re-
quire constant modification of the original graph and
repeated launch of the shortest path algorithm for very
similar graphs.
Notice that to determine the skeletal projection of
an arbitrary point of a figure, we can first determine
its proper region. The desired region can be found
as a result of solving the geometric search problem,
or, which is a more realistic option, — in the case of
uniform generation of points inside the figure or on
the contour, the necessary points can be generated for
each proper region separately.
Suppose the skeleton is structured so that for any
adjacent vertices, the shortest path along the skeleton
is the edge connecting them. Consider the point p
1
belonging to the proper region of the edge (a
1
,b
1
) of
length l
1
, and the point p
2
belonging to the proper
region of the edge (a
2
,b
2
) of length l
2
. Let also
d
skel
(p
1
,a
1
) = d
1
and d
skel
(p
2
,a
2
) = a
2
. Then
d
skel
(p
1
,b
1
) = l
1
−d
1
,
d
skel
(p
2
,b
2
) = l
2
−d
2
.
(2)
In this case, two different options can be distin-
guished:
1. The edges (a
1
,b
1
) and (a
2
,b
2
) are the same. Then
d
skel
(p
1
, p
2
) = |d
1
−d
2
|.
(3)
2. The edges (a
1
,b
1
) and (a
2
,b
2
) are different. Then
d
skel
(p
1
, p
2
) = min(d
skel
(a
1
,b
1
) + d
1
+ d
2
),
d
skel
(a
1
,b
2
) + d
1
+ l
2
−d
2
,
d
skel
(a
2
,b
1
) + l
1
−d
1
+ d
2
,
d
skel
(a
2
,b
2
) + l
1
−d
1
+ l
2
−d
2
).
(4)
Bicircle is called monotonic, if the radial function
(the radius of inscribed circle) decreases or increases
monotonically along its axis. It can be shown that the
path between the points of the same edge does not go
beyond it if all bicircles of the skeleton are monotonic.
Thus, it is more convenient to consider only mono-
tonic bicircles. As shown in (Lomov and Mestetskiy,
2017), a nonmonotonic bicircle can always be split
into a pair of monotonic ones with the disjointness
property of proper regions preserved.
In this case, in turn, two new questions arise:
how to determine d
skel
(u,v) for the ends of the edges
u,v ∈V and how to determine d
i
, i = 1, 2 . The first
problem is solved by running the Johnson algorithm
(Johnson, 1977) to search for all shortest paths in a
skeleton graph. The progress of the second one de-
pends on the type of proper region, the coordinates
of its points and the coordinates of the point p itself.
Consider the regions of each type in more detail.
4 SEARCH FOR THE INCIDENT
SPOKE
Three types of bicircles are distinguished depend-
ing on the pair of generating sites of its edge: lin-
ear (two segment-sites), parabolic (segment-site and
point-site) and hyperbolic (two points-sites). Such
terminology is motivated by the nature of the depen-
dence of inscribed circle radius on the position of the
point on the axis of the bicircle. The axis of the
parabolic bicircle is a segment of the parabola, and
axes of other two types are linear segments. Further
we denote the ends of the edge of the bicircle as A
and B, an arbitrary point of the proper region as P, the
length of the edge as l and d
skel
(P,A) = λ.
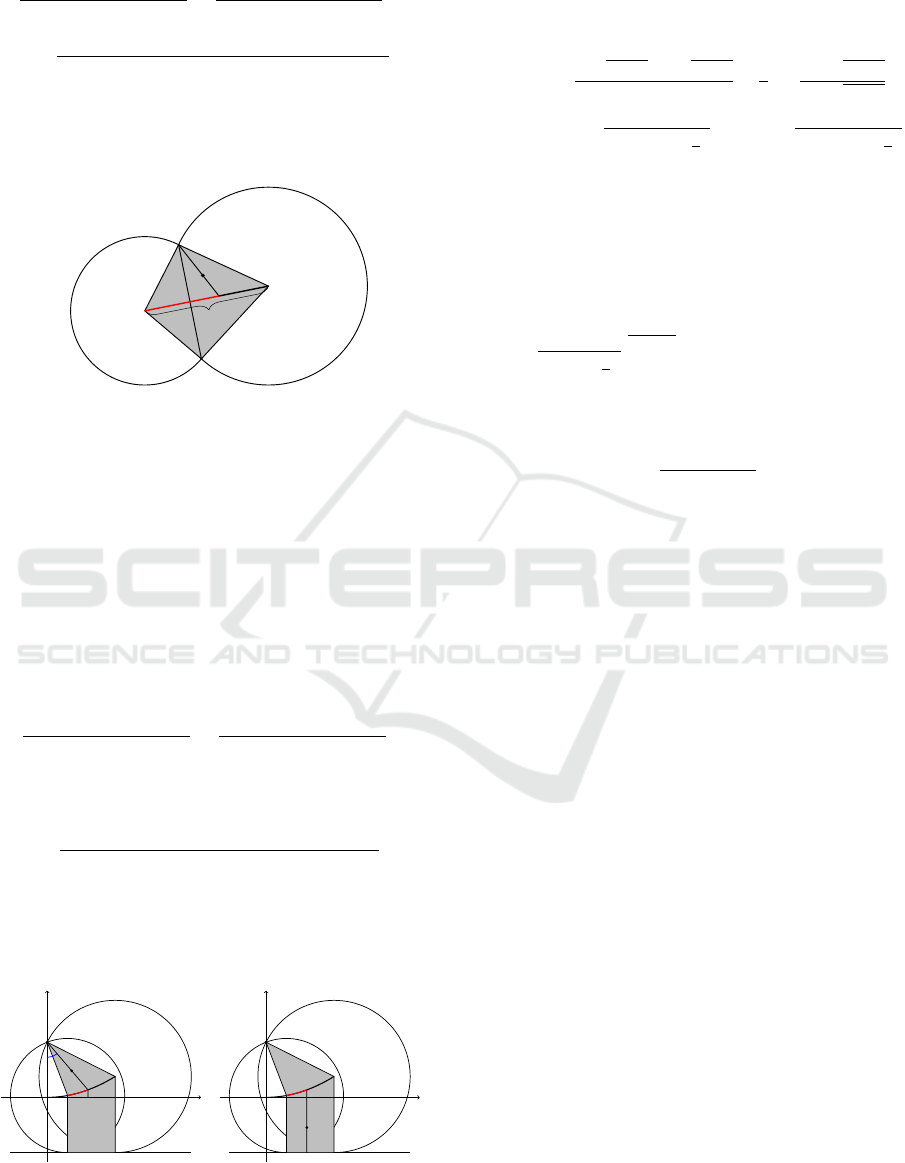
4.1 Linear Bicircle
l
λ
A
B
A
1
B
1
A
2
B
2
P
1
P
P
0
Figure 3: Linear bicircle.
Let the projections of A and B onto the first site are
A
1
and B
1
and onto the second site are A
2
and B
2
re-
spectively (Figure 3). Without loss of generality, we
assume that P is closer to the site A
1
B
1
, i.e. belongs to
the polygon AA
1
B
1
B. Let P belong to the spoke P
0
P
1
,
P
0
∈ AB, P
1
∈ A
1
B
1
. Then P
0
P||AA
1
, which means
(x
P
0
,y
P
0
) = (x
A
+ α(x
B
−x
A
),y
A
+ α(y
B
−y
A
)),
Skeleton-geodesic Distances for Shape Recognition: Efficient Computation by Continuous Skeleton
309

x
P
−x
A
−α(x
B
−x
A
)
x
A
1
−x
A
=
y
P
−y
A
−α(y
B
−y
A
)
y
A
1
−y
A
,
α =
(x
P
−x
A
)(y
A
1
−y
A
) −(y
P
−y
A
)(x
A
1
−x
A
)
(y
B
−y
A
)(x
A
1
−x
A
) −(x
B
−x
A
)(y
A
1
−y
A
)
,
(5)
and λ = αl.
4.2 Hyperbolic Bicircle
l
λ
A
B
C
D
P
0
P
Figure 4: Hyperbolic bicircle.
Denote the point-sites C and D and suppose that P is
closer to the site C, that is, it is located inside triangle
ACB (Figure 4). If P coincides with C, then a con-
tinuum of spokes passes through this point. Although
the set of such “singular” points has measure zero, in
this case the required spoke by definition is the one
with the minimum length (since a site-point can lie
on the border of several proper regions, the desired
spoke can be located in another region).
If P 6= C, a unique spoke passes through P, starting
from the point P
0
(x
A
+ α(x
B
−x
A
),y
A
+ α(y
B
−y
A
)).
Find α. According to the equation of the line,
x
P
−x
C
x
A
+ α(x
B
−x
A
) −x
C
=
y
P
−y
C
y
A
+ α(y
B
−y
A
) −y
C
,
(x
P
−x
C
)(y
A
+ α(y
B
−y
A
) −y
C
) =
= (y
P
−y
C
)(x
A
+ α(x
B
−x
A
) −x
C
),
α =
(y
P
−y
C
)(x
A
−x
C
) −(x
P
−x
C
)(y
A
−y
C
)
(x
P
−x
C
)(y
B
−y
A
) −(y
P
−y
C
)(x
B
−x
A
)
,
(6)
and λ = αl.
4.3 Parabolic Bicircle
x
y
x
1
x
0
x
2
A
B
C
C
1
P
0
P
θ
x
y
x
1
x
0
x
2
A
B
1
P
1
B
C
C
1
P
0
P
(a) (b)
Figure 5: Parabolic bicircle.
The case of a parabolic bicircle is the most compli-
cated. Firstly, the length of the parabolic edge is not
equal to the Euclidean distance between its ends, but
is calculated by the formula
L(x
1
,x
2
) =
x
2
√
x
2
2
+p
2
−x
1
√
x
2
1
+p
2
2p
+
p
2
ln




x
2
+
√
x
2
2
+p
2
x
1
+
√
x
2
1
+p
2




,
(7)
where x
1
=
q
2p(|AC|−
p
2
), x
2
=
q
2p(|BC|−
p
2
)
and p is the focal parameter of the parabola. First,
consider the case in which the nearest site is a point-
site (Figure 5a). Denote C
1
the projection of the point-
site on the segment-site, then p = |CC
1
|. Let the an-
gle C
1
CP be equal to θ, then, according to the equa-
tion of the parabola in the polar coordinate system,
the radial function in the origin of the desired spoke
P
0
is equal to ρ =
p
1+cosθ
, and its abscissa is equal to
x
0
=
q
2p(ρ −
p
2
).
If the closest site is a segment-site, we determine
the value x
0
as |C
1
P
1
| (Figure 5b):
x
0
=
h
−−→
C
1
P,
−−→
C
1
B
1
i
x
2
. (8)
Then, regardless of which site is the closest, λ is
calculated by the formula
λ = L(x
1
,x
0
). (9)
5 SKELETON-GEODESIC SHAPE
CONTEXT
The classic shape context introduced in (Belongie
et al., 2002) analyzes the relative position of the con-
tour points {p
j
} relative to the selected point p
i
using
the Euclidean distance r and polar angle φ:
h
i
(k,t) = #{p
j
: j 6= i, r(p
j
−p
i
) ∈ bin
r
(k),
φ(p
j
−p
i
) ∈ bin
a
(t)}
(10)
In that case, if the shape is subjected to flexi-
ble articulations, say, the rotation of individual shape
parts around their junctions, such distances are un-
stable. In (Ling and Jacobs, 2007) an alternative ap-
proach to determining distances and angles in cal-
culating the shape context was proposed. The dis-
tance is the length of the shortest path between the
points lying entirely inside the figure, i.e. geodesic
distance (the term inner-distance is used in the arti-
cle). Since the contour representation is used in the
form of closed polylines, the shortest path from P to
Q is also a polygonal chain. We denote its vertices
by C
1
C
2
...C
N
, C
1
= P, C
N
= Q. The inner-angle
when calculating the descriptor for P is the angle be-
tween the tangent to the contour in P and the vector
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
310

−−→
C
1
C
2
. Such an angle is not only insensitive to rota-
tion, but also to articulations of individual parts of the
shape, since they lead to bendings in the middle sec-
tions of the shortest path, and the direction of its be-
ginning in the local coordinate system associated with
the boundary tangent changes slightly.
p
q
θ
2 4 6 8 10 12
1
2
3
4
5
6
7
8
p
q
θ
2 4 6 8 10 12
1
2
3
4
5
6
7
8
p
q
θ
2 4 6 8 10 12
1
2
3
4
5
6
7
8
Figure 6: Shape context of different types calculated for p:
Euclidean (top row), geodesic (middle), skeleton-geodesic
(bottom). The shortest path from p to q is shown in blue.
Developing these ideas, we suggest a new varia-
tion of shape context, skeleton-geodesic shape con-
text. The distance is considered to be skeleton-
geodesic distance, and the angle is the angle be-
tween the tangent to the skeleton edge at the start
of the shortest path and the tangent to the boundary.
The skeleton-geodesic shape context shares necessary
insensitivity properties to rotations and articulations
with the inner-distance shape context.
The types of defining the shape context are shown
in Figure 6. In contrast to the Euclidean distance
shape context, inner-distance and skeleton-geodesic
distance contexts lead to a much more concentrated
distribution of characteristics in the feature space.
For shape matching and comparison we will
use the dynamic programming approach proposed in
(Ling and Jacobs, 2007). Given two shapes A and B
described by point sequences on their contour, e.g.,
p
1
, p
2
,..., p
n
for A with n points, and q
1
,q
2
,...,q
m
for B with m points. The matching from A to B is
a mapping from 1, 2, . . . , n to 0, 1, 2, . . . , m, where p
i
is matched to q
π(i)
if π(i) 6= 0 and otherwise left un-
matched. π should minimize the match cost C(π) de-
fined as
C(π) =
∑
1≤i≤n
c(i,π(i)) (11)
where c(i,0) = τ is the penalty for leaving p
i
un-
matched, and for 1 ≤ j ≤ m, c(i, j) is the cost of
matching p
i
to q
j
. For example, the distance between
two K-bin shape context histograms h
A,i
and h
B, j
of
points p
i
∈ A and q
j
∈ B respectively is defined using
the χ
2
statistic:
c(i, j) ≡
1
2
∑
1≤k≤K
[h
A,i
(k) −h
B, j
(k)]
2
h
A,i
(k) + h
B, j
(k)
. (12)
The skeleton-geodesic shape context of p
i
can be
calculated directly, assuming that the points of inter-
est are distributed uniformly along the contour C, by
analyzing the distribution function
F
R,Φ
(a,b) = P(R ≤a, Φ ≤ b) =
= P(r(p − p
i
) ≤ a, φ(p − p
i
) ≤ b | p ∼U(C)),
(13)
h
i
(k,t)
n −1
≈ F
R,Φ
(a
k
,b
t
) −F
R,Φ
(a
k−1
,b
t−1
), (14)
where [a
k−1
,a
k
] and [b
t−i
,b
t
] are the bounds of the
k-th and t-th histogram bins for distance and angle.
Breaking the contour into disjoint sections coin-
ciding with the boundaries of the bicircles, we can
consider each edge individually and reconstruct the
result using the Bayes’ formula.
6 EXPERIMENTS
6.1 Runtime Analysis
Proposed algorithm for calculating skeleton-geodesic
distances (SGD) implemented in C++ was com-
pared in terms of time-consumption with algorithm
of geodesic distance transform (GDT) computation
from (C
´
ardenes et al., 2003), because its source code
is available for free. To compare a similar output
format, distance transforms — maps of the distances
from the selected point to points with integer coordi-
nates — were calculated. Time was averaged over
10000 launches of DT. The experiments were con-
ducted on a laptop with Intel
R
Core
TM
i5-4210U and
6GB RAM.
Skeleton-geodesic Distances for Shape Recognition: Efficient Computation by Continuous Skeleton
311

Results (Table 1) show that the proposed algo-
rithm requires appreciable time for preprocessing, but
after it works significantly faster than its counterpart.
It is also confirmed that the preprocessing time de-
pends on the complexity of the skeleton representa-
tion, whereas the time of distance map computation is
linear in the number of pixels. Analytical calculation
of the shape context context (SC) pays off if the num-
ber of edges of the skeleton is much lower than n, the
number of points sampled at the contour. Since n usu-
ally does not exceed several hundred, this approach is
justified only for fairly simple shapes.
Table 1: Computational costs for the construction of
geodesic distance descriptors.
Image
Size 626 ×562 322 ×512 2000 ×1053
Object pixels 73214 53531 297438
Skeleton edges 910 2672 8729
GDT time, ms 22.412 13.353 91.712
SGDT time, ms 2.279 1.815 10.547
SGD preproc. time, ms 76 958 9935
SC time (1 point), ms 0.310 0.624 1.975
6.2 Recognition by Histograms
Figure 7: Images from Tools dataset.
Tools dataset (Bronstein et al., 2008) shown in Figure
7 consists of 35 images of articulated shapes (silhou-
ettes): 5 images for 7 types of tools (scissors, pliers,
pincers, knives). Each shape differs by an articula-
tion. For every image cumulative skeleton-geodesic
histogram, reflecting the proportion of pairs of points,
the distance between which does not exceed a spec-
ified value, was computed. These histograms were
normalized by the square of the area of the figure
along the y-axis, and by the maximum distance in the
figure along the x-axis. Thus, all histograms are lo-
cated in a unit square. For greater visibility, the func-
tion of the basic profile, describing the distances be-
tween points from unit distribution on a line:
f (x) = 2x −x
2
, (15)
was subtracted. Thus, the increase of the resulting
functions (Fig. 8) indicates the total concentration of
points at a given distance level, and the decrease indi-
cates the total rarefaction.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
Figure 8: Skeleton-geodesic distance distributions for ob-
jects in Tools dataset. Each plot corresponds to one of seven
classes.
After that, the L
1
-distances between the his-
tograms were calculated, they are visualized in Figure
9a. For all 35 objects, the nearest 3 objects belong to
the same class, and for only one object out of 35 the
fourth nearest object belongs to the wrong class. At
the same time, for geodesic distances, only 80% of
the objects of the four nearest neighbors belong to the
correct class (Fig. 9b). The experiment shows that the
skeleton-geodesic distances are more resistant to the
“hinge-type” articulations than usual geodesic ones.
This can be explained by the fact that the skeleton,
being equidistant from two contour sections, halves
the deviation of one of them, if the second remains
unchanged.
5 10 15 20 25 30 35
5
10
15
20
25
30
35
0
20
40
60
80
100
120
5 10 15 20 25 30 35
5
10
15
20
25
30
35
0
10
20
30
40
50
60
70
80
90
100
(a) (b)
Figure 9: Dissimilarities between histograms of (a)
skeleton-geodesic distances and (b) traditional geodesic dis-
tances for Tools dataset.
6.3 Recognition by Shape Context
Following experiments compare three types of shape
context descriptors based on Euclidean distance,
inner-distance and skeleton-geodesic distance. In
all of them, the measure of difference between
shapes will be calculated based on dynamic pro-
gramming approach described above. Parameters
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
312

of the methods are n (number of contour points),
n
d
(number of distance bins in shape context his-
togram), n
θ
(number of angle bins), k (number of
points in primary alignment in DP method) and
h (maximum Hausdorff distance between initial
figure and figure after skeleton pruning). When
conducting experiments, we used the code of Eu-
clidean and inner-distance shape context available at
http://www.dabi.temple.edu/
∼
hbling/code data.htm
(“Shape Matching” section).
6.3.1 Kimia 216 Dataset
Figure 10: Half of the images from Kimia 216 dataset.
The Kimia 216 database
2
provided by Brown Univer-
sity contains 216 images from 12 categories (Fig. 10).
We use parameters n = 100, n
d
= 5, n
θ
= 12, k = 4
and h = 1. The retrieval result is summarized as the
number of 1st, 2nd and 3rd closest matches that fall
into the correct category. The results are listed in Ta-
ble 2. It shows that skeleton-geodesic shape context
determines the total population of images of the same
class slightly better than its counterparts.
Table 2: Evaluation performance on Kimia 216 dataset.
Distance 1st 2nd 3rd 4th 5th 6th
Euclidean 216 216 215 215 213 213
Inner 216 216 215 214 213 211
Skeleton 216 216 215 214 214 212
Distance 7th 8th 9th 10th 11th Total
Euclidean 211 204 201 193 184 96.00%
Inner 211 204 204 203 183 96.38%
Skeleton 211 208 208 206 189 97.18%
6.3.2 Swedish Leaf Dataset
Figure 11: Class instances from Swedish Leaf dataset.
The Swedish Leaf
3
dataset provided by Link
¨
oping
University contains isolated leaves from 15 differ-
ent Swedish tree species, with 75 leaves per species
2
http://vision.lems.brown.edu/sites/default/files/216db.
tar.gz
3
https://www.cvl.isy.liu.se/en/research/datasets/
swedish-leaf/
(Fig. 11). We tested our descriptors with parameters
n = 128, n
d
= 8, n
θ
= 12, k = 1 (images are normal-
ized by orientation, so we can assume that the top-left
points should coincide) and h = 2. To evaluate the
effect of choosing the type of distance, experiments
with distance only (n
θ
= 1) were also conducted. We
used a binarized version of this dataset and chose for
each species 25 images for training and 50 for testing.
Classification was done by nearest neighbor method,
the recognition results are summarized in Table 3. It
is noteworthy that adding information about the an-
gles does not have a significant impact on the result,
perhaps because of the convexity of most shapes. The
good results of the Euclidean distance, apparently, are
due to the fact that the shapes can be considered rigid,
and not subject to significant articulations.
Table 3: Classification performance on Swedish Leaf
dataset.
Distance type Distance + angle Distance only
Euclidean 94.80 94.00
Inner 94.13 92.80
Skeleton 94.67 93.20
6.3.3 MPEG7 Dataset
Figure 12: Class instances from MPEG7 dataset.
The widely tested MPEG7 CE-Shape-1
4
database
consists of 1400 silhouette images from 70 classes.
Each class has 20 different shapes, first of them are
shown in Fig. 12. The recognition rate is measured
by the so-called Bullseye test: for every image in the
database, the top 40 most similar candidates are deter-
mined and the percentage of hits in the top-40 of the
desired class from the maximum possible (20×1400)
is calculated. The parameters in our experiment are:
n = 100, n
d
= 8, n
θ
= 12, k = 8 and h = 3. When
aligning the contours, the points were considered both
in the forward and in the reverse order, to provide
the resistance to reflection. Table 4 lists obtained re-
sults for different types of shape context taking into
account angle information and without it.
Although our method is superior to its competitors
with full information used, its advantage when work-
4
http://www.dabi.temple.edu/
∼
shape/MPEG7/dataset.
html
Skeleton-geodesic Distances for Shape Recognition: Efficient Computation by Continuous Skeleton
313

Table 4: Classification performance on MPEG7 dataset.
Distance type Distance + angle Distance only
Euclidean 86.14 73.13
Inner 85.52 72.61
Skeleton 87.35 77.25
ing only with distances is much more impressive.
This leaves open the question of a better determina-
tion of the angles between the points of the shape. In
addition, histogram comparisons based on the χ
2
cri-
terion are also not well suited for fairly concentrated
distribution, such as skeleton-geodesic shape context,
that leaves the task of designing a better way to com-
pare such histograms for future research. We also
note that, as in the previous experiment, the inner-
distances did not demonstrate their advantage over the
Euclidean ones, being used in completely the same
manipulations.
7 CONCLUSION
In this article we proposed a method for describing
the shape using the distribution of distances between
its points, which are calculated using a skeleton. It
is shown that using a continuous skeletal representa-
tion, the basis of calculations can be reduced to clas-
sical algorithms on graphs. Proposed distance can be
used in many 2D shape recognition algorithms as a re-
placement for the Euclidean or geodesic distance, for
example, we designed an analogue of very popular
shape context descriptor. Remarkable that such de-
scriptor can be considered from the point of view of
probability theory, it can be calculated with high accu-
racy based on the continuous model, and all the nec-
essary formulas are derived analytically. Estimates
of temporal costs show that the method takes some
time to preprocess the image, but after that it does
distant transformations much faster than this is done
for commonly used inner-distances, so with a mass
query, the gain in time consumption is powerful. A
computational experiments demonstrate that the pro-
posed method of specifying distances is more resis-
tant to a fairly wide class of flexible articulations than
the usual geodesic distance and, especially, Euclidean
one. The way to develop our approach is to design a
more efficient procedure for comparing descriptors.
ACKNOWLEDGEMENTS
The work was funded by Russian Foundation of Basic
Research grant No. 20-01-00664.
REFERENCES
Belongie, S. J., Malik, J., and Puzicha, J. (2002). Shape
matching and object recognition using shape contexts.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 24(4):509–522.
Boluk, S. A. and Demirci, M. F. (2015). Shape classification
based on skeleton-branch distances. In Proceedings of
the International conference on computer vision the-
ory and applications (VISAPP 2015), pages 353–359.
SCITEPRESS, Portugal.
Bronstein, A. M., Bronstein, M. M., Bruckstein, A. M., and
Kimmel, R. (2008). Analysis of two-dimensional non-
rigid shapes. International Journal of Computer Vi-
sion, 78(1):67–88.
C
´
ardenes, R., Alberola-L
´
opez, C., and Ruiz-Alzola, J.
(2010). Fast and accurate geodesic distance transform
by ordered propagation. Image and Vision Computing,
28(3):307–316.
C
´
ardenes, R., Warfield, S. K., Mac
´
ıas, E. M., and Ruiz-
Alzola, J. (2003). Occlusion points propagation
geodesic distance transformation. In Proceedings of
the International Conference on Image Processing,
ICIP 2003, pages 361–364. IEEE.
Cuisenaire, O. (1999). Distance transformations: fast al-
gorithms and applications to medical image process-
ing. PhD thesis, Universite Catholique de Louvian,
Louvain-la-Neuve, Belgium.
Jain, V. and Zhang, H. (2005). Robust 2D shape correspon-
dence using geodesic shape context. In Proceedings
of Pacific Graphics, pages 121–124.
Johnson, D. B. (1977). Efficient algorithms for shortest
paths in sparse networks. J. ACM, 24(1):1–13.
Ling, H. and Jacobs, D. W. (2007). Shape classification us-
ing the inner-distance. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 29(2):286–299.
Lomov, N. and Mestetskiy, L. (2017). Pattern width de-
scription through disk cover – application to digital
font recognition. In Proceedings of the 12th Inter-
national Joint Conference on Computer Vision, Imag-
ing and Computer Graphics Theory and Applications
(VISIGRAPP 2017), Volume 4: VISAPP, pages 484–
492. SCITEPRESS, Portugal.
Mestetskiy, L. (2015). Medial width of polygonal and cir-
cular figures — approach via line segment voronoi di-
agram. In Proceedings of the International conference
on computer vision theory and applications (VISAPP
2015), pages 379–386. SCITEPRESS, Portugal.
Mestetskiy, L. and Semenov, A. (2008). Binary im-
age skeleton — continuous approach. In VISAPP
2008 — 3rd International Conference on Computer
Vision Theory and Applications, Proceedings, vol-
ume 1, pages 251–258. SCITEPRESS — Science and
Technology Publications, Portugal.
Sethian, J. A. (1999). Fast marching methods. SIAM Re-
view, 41(2):199–235.
Shamai, G. and Kimmel, R. (2017). Geodesic distance de-
scriptors. In Proceedings of the Conference on Com-
puter Vision and Pattern Recognition (CVPR 2017),
pages 3624–3632. IEEE Computer Society.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
314