
Matching-aware Shape Simplification
Enrico S. Miranda
1 a
, Rog
´
erio Lu
´
ıs C. Costa
1 b
, Paulo Dias
2 c
and Jos
´
e Moreira
2 d
1
IEETA, University of Aveiro, Portugal
2
DETI - IEETA, University of Aveiro, Portugal
Keywords:
Polygon Simplification, Spatio-temporal Data, Shape Matching.
Abstract:
Current research has shown significant interest in spatio-temporal data. The acquisition of spatio-temporal
data usually begins with the segmentation of the objects of interest from raw data, which are then simplified
and represented as polygons (contours). However, the simplification is usually performed individually, i.e.,
one polygon at a time, without considering additional information that can be inferred by looking at the
correspondences between the polygons obtained from consecutive snapshots. This can reduce the quality
of polygon matching, as the simplification algorithm may choose to remove vertices that would be relevant
for the matching and maintain other less relevant ones. This causes undesired situations like unmatched
vertices and multiple matched vertices. This paper presents a new methodology for polygon simplification that
operates on pairs of shapes. The aim is to reduce the occurrence of unmatched and multiple matched vertices,
while maintaining relevant vertices for image representation. We evaluated our method on synthetic and real
world data and performed an extensive comparative study with two well-known simplification algorithms.
The results show that our method outperforms current simplification algorithms, as it reduces the amount of
unmatched vertexes and of vertexes with multiple matches.
1 INTRODUCTION
Over the last few decades, the amount of geograph-
ical data being generated is increasing greatly. De-
velopments in sensor technology have expanded the
availability of geographical data being used for sev-
eral purposes. With the growing body of spatial data,
there is also an increasing demand for tools to deal
with spatio-temporal data. The applications can be as
diverse as monitoring Glacier-Ocean boundaries, for-
est cover and iceberg tracking.
Spatio-temporal data is often acquired at discrete
times and represented as an ordered sequence of snap-
shots. Each snapshot consists of a timestamp and a
geometry. The acquisition of each snapshot can be
summarized in the following steps: 1) obtain the raw
data, 2) use image segmentation to extract the con-
tour of the objects of interest and 3) apply simplifica-
tion of the contour to obtain the polygon to be stored
in a database. These steps are depicted in Figure 1.
The extracted polygons are then interpolated as slices
a
https://orcid.org/0000-0003-1483-8448
b
https://orcid.org/0000-0003-2306-7585
c
https://orcid.org/0000-0002-3754-2749
d
https://orcid.org/0000-0003-4633-6944
between two shapes (McKenney and Webb, 2010).
Thus, spatio-temporal data can be represented by a
geometry and a function used to represent its evolu-
tion over time (Forlizzi et al., 2000). Such high-level
abstraction model treats real world entities as moving
points, moving lines or moving regions. One key as-
pect of such representation is the selection of the func-
tion used to represent the data evolution, which is of-
ten called in the context of moving regions as Region
Interpolation Problem (Tøssebro and G
¨
uting, 2001;
Heinz and G
¨
uting, 2016). The interpolation methods
derive the function of transition for a pair of shapes,
and build the whole evolution by interpolating each
pair of shapes sequentially. Any simplification algo-
rithm that can be applied to a pair shapes can be used
on the snapshots being interpolated. It can then be ap-
plied to a whole time series, two snapshots at a time,
on the same way that interpolation methods are exe-
cuted.
Region interpolation methods often require the
definition of a matching between the vertices of two
shapes representing an object of interest in two con-
secutive observations. Shape Matching or Vertex Cor-
respondence Problem is the process of finding good
matches (Liu et al., 2004; Van Kaick et al., 2011).
Miranda, E., Costa, R., Dias, P. and Moreira, J.
Matching-aware Shape Simplification.
DOI: 10.5220/0008969402790286
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages
279-286
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
279

(a) Raw data (b) Segmented
data
(c) Contour Ex-
traction
(d) Simplified
Polygon
Figure 1: Data acquisition process.
There are two main issues that can arise during
shape matching. First, some vertices in a shape may
have no corresponding vertices in the other shape.
Second, two or more vertices in a shape may cor-
respond to a single vertex in the other shape. Such
problems may be influenced by the simplification al-
gorithm. Since some interpolation methods require
an one-to-one correspondence between the vertices
of the two shapes (Moreira et al., 2016), a post-
processing step is usually need to fix these issues.
This paper presents a novel technique for simpli-
fication with a focus on matching that we call Match-
ing Aware Simplification (MAS). Our technique is
meant to be applied to two shapes of the same ob-
ject at different times or in shapes to be matched.
The focus is on preserving vertices that are impor-
tant to define a correspondence with vertices of the
other shape, which would be discarded by other
simplifications algorithms (e.g. Ramer-Douglar-
Peucker algorithms (Douglas and Peucker, 1973)
and Visvalingam-Whyatt algorithm (Visvalingam and
Whyatt, 1993)). Our technique is able to deliver poly-
gons that lead to better automatic vertex matching.
We evaluate the results on real world and artificial
data, and we perform a wide numeric evaluation over
a publicly available dataset.
This paper is organized as follows. The next sec-
tion presents an overview on related work. Section 3
details the proposed method. Section 4 presents the
experimental results. Finally, Section 5 presents the
conclusion and guidelines for future work.
2 BACKGROUND AND RELATED
WORK
2.1 Polygon Simplification
Image segmentation algorithms return all pixels (ver-
tices) defining the boundaries of an object of inter-
est. That means the representation of the objects’ ge-
ometry is noisy and may have hundreds or thousands
of vertices. However, a large number of vertices can
be detrimental to the performance of algorithms, e.g.,
to find a correspondence between the vertices of two
shapes (Shape Matching), or to estimate the transfor-
mation of an object between two snapshots (Region
Interpolation). In addition, noisy boundaries can cre-
ate unwanted behavior during the interpolations.
Boundaries and shapes can be simplified using
different families of algorithms. The first algorithm
for simplification was the Ramer-Douglas-Peucker
(RDP) algorithm, published in 1972 (Ramer, 1972)
and 1973 (Douglas and Peucker, 1973). In the RDP
algorithm, a line segment is defined between the first
and last vertexes of a polyline to be simplified. Then,
the most distant vertex from this line segment is in-
cluded in the simplified line (a polyline) - as long as
the vertex distance is over an accepted threshold value
(ξ). This process is now applied recursively on all sub
lines on the polyline until there are no vertices over ξ
distance from the line. In order to apply this process
to a polygon, we need to pick two vertices as refer-
ence vertices for the polylines.
Another common approach to polygon simplifi-
cation is using Visvalingam-Whyatt (VW) algorithm
(Visvalingam and Whyatt, 1993). In the VW algo-
rithm, for every vertex in a line or polygon, we build
a triangle between this vertex and the previous and
next vertices. Then, the area of each triangle is calcu-
lated, and all vertices of triangles with an area below
a threshold ξ are removed. This process is applied
iteratively until no triagle has an area below ξ.
Accounting that the morphing or interpolation
happens between two different shapes, one can use
this additional information to create different simplifi-
cations. Baxter et al. (Baxter III et al., 2009) proposed
a method for compatible embedding of two shapes,
and later generalized the approach for multiple shapes
(Baxter et al., 2009). This method reduces the num-
ber of vertices on a polygon, however to keep the
textures inside the polygon during the morphing pro-
cess, the reduction of vertices aims at embedding and
not at simplification of the geometry. While suited
for morphing animations, embedding creates defor-
mations on the polygon when used on real world data.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
280

Take iceberg tracking for instance, where one would
rather be close to the original shape and area than en-
sure embedding on a bigger polygon that loses infor-
mation.
These techniques are characteristic in that they are
suited for simplification of a single polygon or poly-
line, with minimal information loss (RDP and VW),
or they are suited for animation (embedding). But
they have no regard to the temporal behaviors of the
shape. Our method, on the other hand, uses the infor-
mation of two consecutive representations of the same
shape in order to simplify each object. We maintain
vertices that are more relevant to represent the tempo-
ral evolution of the object.
2.2 Shape Matching
In order to use the region interpolation functions on
the continuous spatio-temporal data representation,
simplified polygons generated for consecutive snap-
shots need to be matched. The matching can be based
on segments or concavities (Tøssebro and G
¨
uting,
2001) (McKenney and Webb, 2010) or based on ver-
tices (Moreira et al., 2016) (Baxter III et al., 2009).
The Shape Matching algorithms must provide a cor-
respondence between the vertices of two shapes, as
depicted in Figure 2. It can also be seen that some
vertices might have no match, or match more than one
vertex. There are surveys on Shape Matching or Ver-
tex Correspondence Problem (Van Kaick et al., 2011).
Figure 2: Vertex matching (Van Kaick et al., 2007).
One algorithm with good results for fully auto-
matic 2D vertex matching is presented on (Van Kaick
et al., 2007). This algorithm performs vertex match-
ing so that the vertices matched are both in simi-
lar places in space, while also aiming at keeping the
geodesic distance (distances within the contour) be-
tween every pair of vertices similar. The additional
requirement that a pair of vertices in one shape main-
tain similar distances to the matched pair of vertices
on the other shape leads to a matching that is rela-
tively robust.
Since the existing simplification algorithms are fo-
cused exclusively on the simplification of shapes one-
by-one, two implications arise: 1) the simplification
may select vertices in a shape that are distant from the
(a) Raw data from
ice01
(b) Raw data
from ice02
(c) Polygon from
ice01
(d) Polygon from
ice02
(e) Vertex matching for B-15a
Figure 3: B-15a extraction and matching.
possible corresponding vertices in the other shape; or
2) the corresponding parts of two shapes may have
a different number of vertices. These cases are de-
picted in Figure 3, where the two polygons represent
the shape of iceberg B-15a at different times (from
now on called ice01 and ice02). The shapes were sim-
plified using RDP and the correspondences between
the vertices were performed using (Van Kaick et al.,
2007).
3 MULTIPLE-SHAPE AWARE
SIMPLIFICATION
The workflow to prepare spatio-temporal data
for interpolation can be summarized in 3 main
steps (Duarte et al., 2018). First, we extract the
region-of-interest from each raster image (Segmenta-
tion). Then, the amount of vertices on the shape is
reduced (Simplification). Finally, a one-to-one corre-
spondence between the vertices must be found. In this
workflow, only the third step takes into account more
than one shape. We aim to improve this process by ex-
Matching-aware Shape Simplification
281

tending the use of information from a pair of shapes
into the simplification step, reducing matching errors.
3.1 Compatible Simplification
Our method relies on implicit information, as we
know that we are simplifying a pair of related shapes
instead of an individual shape. We call this simpli-
fication of two shapes simultaneously as compatible
simplification. The aim is to be able to consider the
importance of the vertices to represent a shape at a
given time and also their importance to establish cor-
respondence with vertices in the other shape. For in-
stance, we want to keep vertices that represent dis-
tinct features in a shape. We also want vertices that
should represent that distinct feature in the matched
shape. Our method operates before the vertex corre-
spondence problem, avoiding the need of optimiza-
tion and user interaction. This method can also be
paired with any correspondence algorithm.
Our method has two main objectives and one mi-
nor objective. The first is to simplify a polygon in a
way that will reduce the need for adjustments during
the matching step, like adding extra vertices to solve
the vertex correspondence problem. Notice that the
added vertices were part of the full set of vertices be-
fore simplification. Re-adding a vertex into a contour
that was removed during simplification means that lo-
cal information was lost. Since our method deals with
simplification using knowledge that is relevant to per-
form vertex correspondences in a later step, we are
call it Matching Aware Simplification (MAS). Our
proposed method strives to keep vertices that will be
representative on future or past shapes by design.
The second main objective is to allow sim-
pler matching by providing matching algorithms
with locally-aware vertices in order to reduce ver-
tex matching complexity. Since algorithms can work
with locality of data in order to help finding the ver-
tex correspondences (Van Kaick et al., 2011), provid-
ing the algorithms with better locality should help the
matching process.
In order to keep vertices that allow better match-
ing, similar sub regions should be represented with
similar resolution or density of vertices. This minor
objective follows from the two main objectives.
3.2 The MAS Algorithm
In the following, we consider the raw contours to be
simplified as P, the source polygon, and the matched
polygon as Q, the target polygon. We assume that P
and Q were previously aligned to account for both ro-
tation and translation. We also define p ∈ P and q ∈ Q
(a) Source (P) (b) Target (Q)
Figure 4: Artificial Polygons for illustration.
(a) Source (P) (b) Target (Q)
Figure 5: Local cost for vertices (triangle area).
as vertices. Figure 4 presents two artificial polygons
that will be used to illustrate cost calculations.
We start by defining a cost function for each ver-
tex, which represents the loss of information for re-
moving this vertex (Equation 1). It introduces a pa-
rameter, t factor, representing the preference between
keeping temporal information or single shape infor-
mation.
cost
p
= max(cost single
p
, cost matched
p
∗t f actor)
(1)
In order to consider the loss of information on of
P and Q, we assume the cost to remove the vertex
p as the maximum of the cost to remove that vertex
considering a single shape (P) and of the cost for loss
of feature representation on the matched shape (Q).
We define the cost to remove a vertex for a single
shape as the area of the triangle given by p, p − 1 and
p + 1, similar to VW algorithm (Equation 2). It is
also possible to use other measures, like the distance
between p and the line connecting p − 1 and p + 1,
which would lead to a MAS simplification based on
the RDP algorithm. Any future cost metric for single-
shape simplification could also be applied at this step.
Figure 5 shows a calculation for some vertices.
cost single
p
= area triangle(p, p + 1, p −1) (2)
We represent the loss of matching information on
two different steps. A significant vertex represents ei-
ther a feature present in Q and not in P, or a vertex
on P needed to morph into the feature of Q. The first
case where P has a distinct and unique feature (like a
curvature or a distinctive deformation), the vertex has
a cost unique f eature as seen on Equation 3. This
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
282

cost measures how distant the vertex is from the other
shape - a vertex far from the other shape represents a
distinct feature. Figure 6a shows this metric for three
different vertices of Q.
cost unique f eature
p
= min(d
pq
)∀q ∈ Q)
(3)
(a) Distinct fea-
tures cost on Q (P
on background)
(b) Matching ver-
tices on P (Q on
background)
Figure 6: Matching costs.
We also define a cost for a matched feature, which
is complementary to the distinct feature. This cost is
defined in Equation 4. This cost prioritizes vertices of
P that are the closest vertices for a distinct feature of
Q, and could be good candidates for future matching.
In the example in Figure 6b, the vertex at the top (with
c = 1) is important to morph into the topmost vertex
of Q.
cost matched f eature
i
= max(d
pq
)∀q ∈ Q|
d
pq
= min(d
kq
)∀k ∈ P
(4)
Finally, we define the loss of information of vertex
p in the matching with Q as the maximum of the two
complementary costs, as seen on Equation 5.
cost time
i
= max(cost unique f eature
p
,
cost matched f eature
i
)
(5)
Given this definition of cost, our SIMPLIFY func-
tion starts by removing the vertex in P with lowest
cost, then removing the vertex in Q with lowest cost,
and iterating as many times as necessary to achieve
the desired number or vertices in the simplified poly-
gon.
function SIMPLIFY(P, Q, size)
while kPk > size ∨ kQk > size do
if kPk > size then
r ← p ∈ P|cost(p) = min(cost(k)∀k ∈
P)
P ← P − r
end if
if kQk > size then
r ← q ∈ Q|cost(q) = min(cost(k)∀k ∈
Q)
Q ← Q − r
end if
end while
end function
4 EXPERIMENTAL RESULTS
In order to evaluate our proposals, we made several
experiments on publicly available datasets of artificial
and real world data, and compared the use of state-of-
the art simplification algorithms. In all experiments,
the tolerance for each algorithm until 95% of the ver-
tices of the original contour were removed. This way,
the algorithms can be compared because they all keep
the same amount of information.
In Sections 4.1 and 4.2, we discuss the simplifi-
cation quality presenting a visual analysis of selected
pairs of images. Then, in Section 4.3, we present a de-
tailed numeric comparison of MAS matching quality
(using several metrics) for every pair of image in the
216 Binary Shape Database from Brown University
(Sebastian et al., 2004).
4.1 Visual Qualitative Analysis -
Artificial Data
For the artificial data, we used two shapes from the
Brown University Binary Image dataset (Sebastian
et al., 2004), named arb01 and arb02. We can see
that for both arb01 and arb02 (Figure 7) the simpli-
fied shapes cannot be visually distinguished from the
original image, leading to similar results of the con-
tour features.
Considering arb01, the feature highlighted in Fig-
ure 8 can be represented using few vertices, since its
shape is triangular. However, in arb02, more vertices
are needed to represent the same feature, because the
shape is a round curve. It is important to keep a simi-
lar number of vertices in arb01 and arb02 for the ver-
tex matching. This is depicted in Figure 8, where the
simplification algorithms are compared side-by-side,
showing how MAS keeps more points on the details
than both RDP and VW.
Our method chooses the vertices to be kept con-
sidering the context of the target shape. We can see
on Figure 7 that RDP and VW keep vertices on lines
that could be considered not-important (because they
do not play an important role on the definition of the
source and target shapes or on the definition of the
correspondences between them), like the lower in-
clined line in RDP or the left upper line in VW.
4.2 Visual Qualitative Analysis -
Real-world Data
For the real world data, we used two images of
Iceberg B-15a taken at different times (Figure 3)
(RossSea subsets, 2016). Each simplification method
produces a slightly different shape, as we can see in
Matching-aware Shape Simplification
283

(a) arb01 (b) arb02
(c) MAS on
arb01
(d) MAS on
arb02
(e) DP on arb01 (f) DP on arb02
(g) VW on arb01 (h) VW on arb02
Figure 7: Comparison of arb01 and arb02.
(a) VW on
arb01
(b) DP on
arb01
(c) MAS on
arb01
(d) VW on
arb02
(e) DP on
arb02
(f) MAS on
arb02
Figure 8: Highlight on the feature-area representation to all
simplification algorithms.
Figure 9. However, the results of the methods are vi-
sually very similar.
It is visually perceptible in the highlighted area of
Figure 9 that the distribution of the vertices in the sim-
plified shapes is more similar in our method (consid-
ering the number of vertices and the spacing between
them). This better distribution of number of vertices
and spacing can also be seen on the left side of the
shape. Thus, our method performed as expected, pro-
viding more similar distributions of vertices on both
shapes with noisy borders.
(a) ice01 (b) ice02
(c) MAS on ice01 (d) MAS on ice02
(e) DP on ice01 (f) DP on ice02
(g) VW on ice01 (h) VW on ice02
Figure 9: Comparison of ice01 and ice02.
When dealing with real world data the borders are
noisy, and the noise can influence RDP or VW on se-
lecting the vertices to keep. Our goal was to remove
these influences by using information from the other
polygon and we can see in Figure 9 that our method
provides a more similar density of vertices along the
boundaries.
4.3 Simplification and Matching
Analysis - Binary Shape Database
In order to provide a complete evaluation, we applied
our method on the 216 Binary Shape Brown dataset
(Sebastian et al., 2004). It is composed of 216 images
divided in 18 classes. This dataset is widely used in
polygon matching and image retrieval benchmarks.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
284
For the testing, we first aligned the shapes using
the Iterative Closest Point method (Tihonkih et al.,
2016). For the hammer class the ICP method failed
to provide several correct rotations of the objects, and
so, they were removed from the test dataset.
We evaluated the performance of the simplifica-
tion in the Vertex Correspondence Problem. For
this test, we used the VCP algorithm developed by
(Van Kaick et al., 2007) and recorded the number of
vertices without a correspondence and the number of
vertices with multiple matches, and considered both
cases as anomalous vertices.
Since the VCP algorithm is an heuristic, it can
generate distinct results on consecutive executions.
To account for this, we ran 35 replications for each
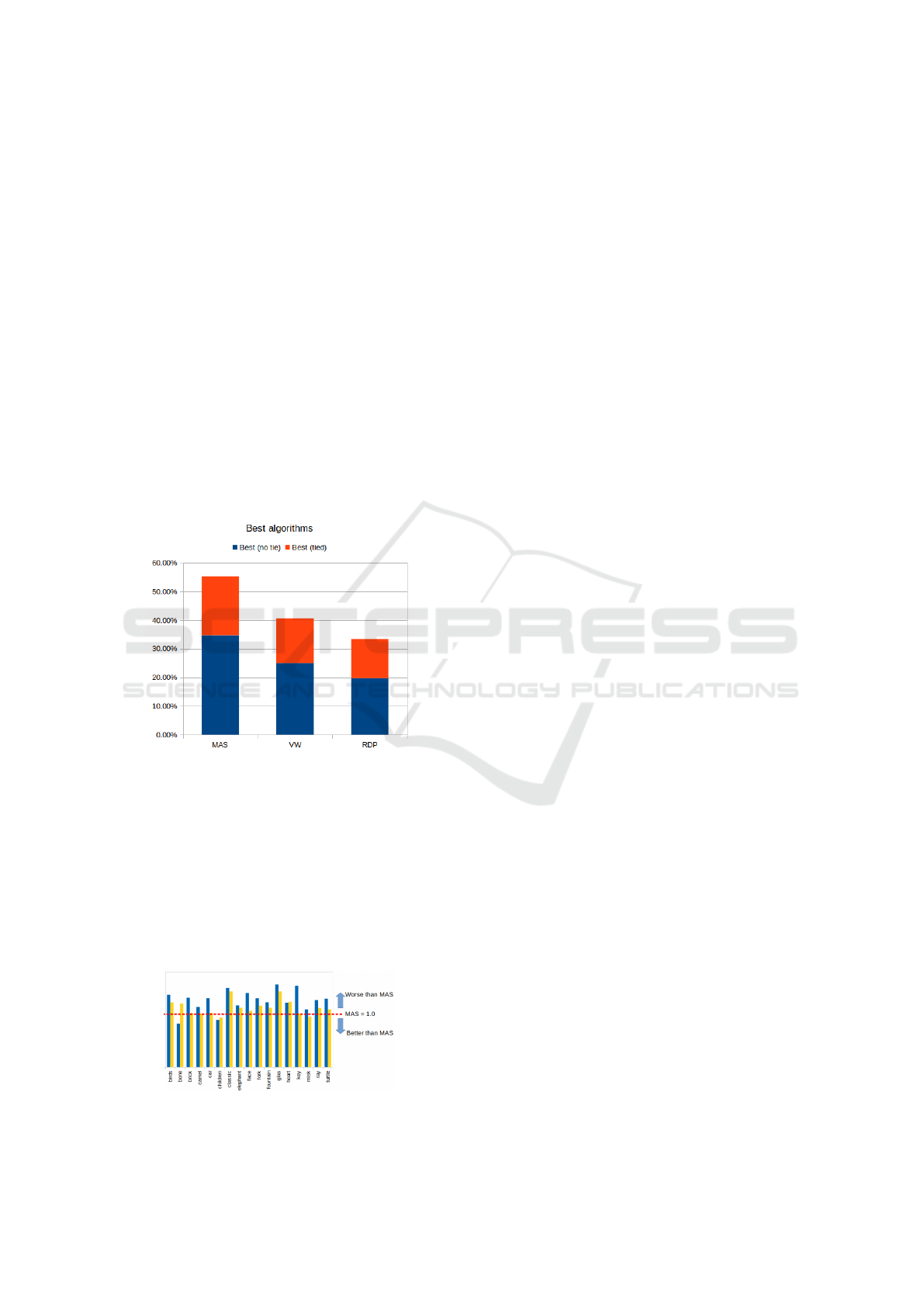
pair of images. Our method was able to be the better
than RDP and VW on 35% of the images, and being
the best tied with either RDP or VW on 21%. Thus,
our method was the best choice on more than half of
the images. The results can be seen on Figure 10.
Figure 10: Performance comparison between algorithms.
It is also important to evaluate the gap of perfor-
mance instead of just which algorithm is best. For
this analysis, we compared the number of anomalous
points generated by each method. Figure 11 presents
these results. Our method is able to improve by a
wide margin on some categories. However, when our
method is not the best the gap is much smaller. Over-
all, our method can perform significantly better on the
majority of the cases, or slightly worse on a few cases.
Figure 11: Anomalous vertices generated.
Finally, we selected a pair of shapes for visual as-
sessing of our method (Figure 12). It can be seen
that MAS represents all fork prongs with 2 points in
both shapes. Both VW and RDP chose to simplify
matching prongs with a different number of points
on each shape. Also, on the fork handle,the number
of pointed obtained using VW and RDP greatly dif-
fers, and MAS performs with closer density on both
shapes. These findings are highlighted in the images.
5 CONCLUSION
Current technology has enabled us to gather a rich set
of spatial data, leading to a growing body of historical
data. This has led to an increased interest in spatio-
temporal data processing and analysis.
Using the continuous spatio-temporal model to
represent real world data involves several steps, in-
cluding image acquisition and segmentation, object
simplification and shape matching. Although data ac-
quisition can have a significant impact on the quality
of the data, few works exist on transforming raw data
into spatio-temporal data representations. Also, after
image acquisition and segmentation the set of points
of the contour has to be simplified in order to obtain
a polygon. Current simplification algorithms account
only for a single shape at a time. This can lead to a
loss of information about the evolution of the shapes
over time.
In this work, we deal with shape simplification
for polygon matching. We presented an algorithm
for simplification of 2D polygons. Our method
makes use of implicit information that arises from
the knowledge that we have more than one shape
to be matched. Our Matching Aware Simplifica-
tion method improves simplification quality, leading
to less anomalous points during matching than other
simplification methods. Our method can also be com-
bined with any matching algorithm on the next stage
leading to improved matching results. The proposed
simplification technique should allow for easier auto-
matic correspondence of vertices on real world phe-
nomena shapes.
In the future, we are interested in expanding re-
search on the next step of the spatio-temporal acqui-
sition workflow: the vertex correspondence problem.
Since it is expected that avoiding to remove vertices
from a shape (source) that may have a correspondence
with vertices of another shape (target) in a sequence of
observations will lead to more natural interpolations,
we also aim at developing workflows to evaluate the
impact of each step of the process on the quality of the
Matching-aware Shape Simplification
285
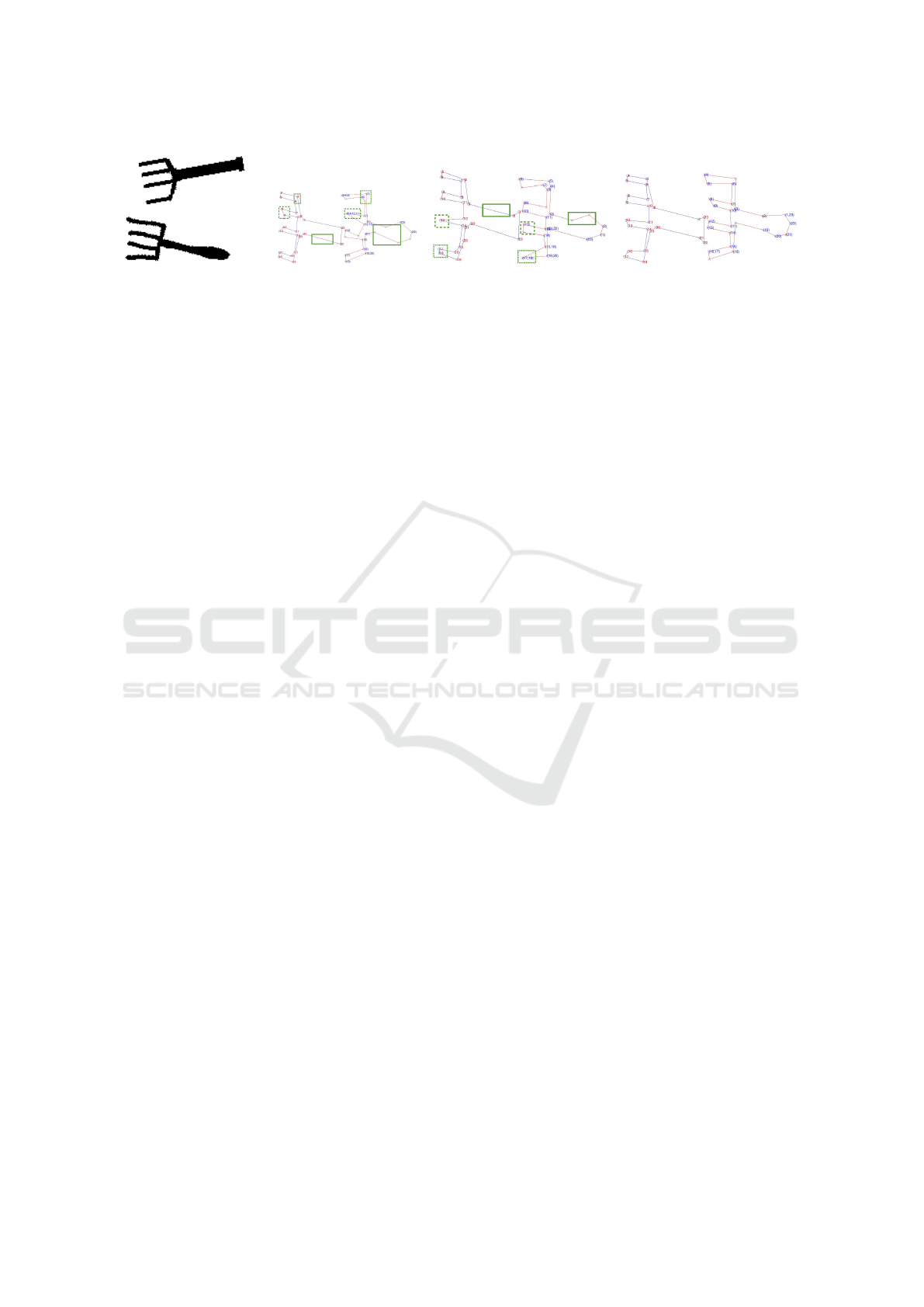
(a) Fork19.pgm and
Fork03.pgm
(b) VW matching (c) RDP matching (d) MAS matching
Figure 12: Matchings between Fork03 and Fork19.
interpolations. Finally, we would also want to work
on all steps of the interpolation process of multiple
snapshots, instead of two - including simplification,
matching and interpolation functions.
ACKNOWLEDGEMENTS
This work is partially funded by National Funds
through the FCT in the context of the projects
UID/CEC/00127/2013 and POCI-01-0145-FEDER-
032636.
REFERENCES
Baxter, W., Barla, P., and Anjyo, K. (2009). N-way morph-
ing for 2d animation. Computer Animation and Vir-
tual Worlds, 20(2-3):79–87.
Baxter III, W. V., Barla, P., and Anjyo, K.-i. (2009). Com-
patible embedding for 2d shape animation. IEEE
Transactions on Visualization and Computer Graph-
ics, 15(5):867–879.
Douglas, D. H. and Peucker, T. K. (1973). Algorithms for
the reduction of the number of points required to rep-
resent a digitized line or its caricature. Cartographica:
the international journal for geographic information
and geovisualization, 10(2):112–122.
Duarte, J., Dias, P., and Moreira, J. (2018). An evaluation
of smoothing and remeshing techniques to represent
the evolution of real-world phenomena. In Interna-
tional Symposium on Visual Computing, pages 57–67.
Springer.
Forlizzi, L., G
¨
uting, R. H., Nardelli, E., and Schneider, M.
(2000). A data model and data structures for moving
objects databases. In Proceedings of the 2000 ACM
SIGMOD International Conference on Management
of Data, SIGMOD ’00, pages 319–330, New York,
NY, USA. ACM.
Heinz, F. and G
¨
uting, R. H. (2016). Robust high-quality
interpolation of regions to moving regions. GeoInfor-
matica, 20(3):385–413.
Liu, L., Wang, G., Zhang, B., Guo, B., and Shum, H.-Y.
(2004). Perceptually based approach for planar shape
morphing. In Proceedings of the Computer Graphics
and Applications, 12th Pacific Conference, PG ’04,
pages 111–120, Washington, DC, USA. IEEE Com-
puter Society.
McKenney, M. and Webb, J. (2010). Extracting moving
regions from spatial data. In Proceedings of the 18th
SIGSPATIAL International Conference on Advances
in Geographic Information Systems, GIS ’10, pages
438–441, New York, NY, USA. ACM.
Moreira, J., Dias, P., and Amaral, P. (2016). Represen-
tation of continuously changing data over time and
space: Modeling the shape of spatiotemporal phenom-
ena. In 2016 IEEE 12th International Conference on
e-Science (e-Science), pages 111–119. IEEE.
Ramer, U. (1972). An iterative procedure for the polygonal
approximation of plane curves. Computer graphics
and image processing, 1(3):244–256.
RossSea subsets (2016). Rosssea subsets.
http://rapidfire.sci.gsfc.nasa.gov/imagery/ sub-
sets/?project=antarctica&subset=RossSea&
date=11/15/20. Accessed: 2016-09-20.
Sebastian, T. B., Klein, P. N., and Kimia, B. B. (2004).
Recognition of shapes by editing their shock graphs.
IEEE Transactions on Pattern Analysis & Machine In-
telligence, (5):550–571.
Tihonkih, D., Makovetskii, A., and Kuznetsov, V. (2016).
A modified iterative closest point algorithm for shape
registration. In Applications of Digital Image Process-
ing XXXIX, volume 9971, page 99712D. International
Society for Optics and Photonics.
Tøssebro, E. and G
¨
uting, R. H. (2001). Creating represen-
tations for continuously moving regions from obser-
vations. In International Symposium on Spatial and
Temporal Databases, pages 321–344. Springer.
Van Kaick, O., Hamarneh, G., Zhang, H., and Wighton, P.
(2007). Contour correspondence via ant colony op-
timization. In 15th Pacific Conference on Computer
Graphics and Applications (PG’07), pages 271–280.
IEEE.
Van Kaick, O., Zhang, H., Hamarneh, G., and Cohen-Or,
D. (2011). A survey on shape correspondence. In
Computer Graphics Forum, volume 30, pages 1681–
1707. Wiley Online Library.
Visvalingam, M. and Whyatt, J. D. (1993). Line general-
isation by repeated elimination of points. The carto-
graphic journal, 30(1):46–51.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
286
