Developing a Machine Learning Model for Predicting Postnatal Growth
in Very Low Birth Weight Infants
Andrea Seveso
1 a
, Valentina Bozzetti
2
, Paolo Tagliabue
2
, Maria Luisa Ventura
2
and Federico Cabitza
1 b
1
Department of Computer Sciences, Systems and Communications, University of Milano-Bicocca, Milan, Italy
2
Neonatal Intensive Care Unit, MBBM Foundation, San Gerardo Hospital, Monza, Italy
Keywords:
Machine Learning, Neonatal, Clinical Decision Support Systems, Data Science.
Abstract:
Objective of the work is the development of prognostic machine learning models that predict qualitative and
quantitative measures of postnatal growth in very low birth weight preterm infants. Observational retrospective
data about 964 infants at risk are retrieved from “Fondazione Monza e Brianza per il bambino e la mamma“’s
electronic medical record. Both prenatal (gestational, socioeconomic, etc.) and perinatal (nutritional, respi-
ratory assistance, drug prescription and daily growth) data up to a week after birth are the features included.
Model’s performances are compared to previous literature and human performance, showing a substantial
improvement (in e.g., best regression MAE=0.49, best classification AUC=0.94).
1 MOTIVATIONS AND
BACKGROUND
With increasing survival of preterm neonates, opti-
mizing postnatal growth is an essential component in
the medical management of this population.
Postnatal growth in premature infants is a strong
predictor of outcomes, both as a reflection of concur-
rent morbidities as well as long-term neurodevelop-
ment. In extremely low birth weight (BW) infants
(ELBW; BW<1000g), poor growth during neonatal
intensive care unit (NICU) stay is associated with
adverse short-term outcomes, as well as it exerts a
significant, and independent effect, on neurodevelop-
ment outcome in infancy.
Despite the increasing knowledge about neonatal
nutrition and growth, the NICHD Neonatal Research
Network found the overall incidence of extrauterine
growth restriction (EUGR) to be 79% among ex-
tremely preterm infants (Clark et al., 2003, Miller
et al., 2014, Ehrenkranz et al., 2006). Therefore,
maintaining adequate nutrition and growth in this
high-risk population is an important, and difficult
to achieve, goal in the NICU. (Lucas et al., 1998,
Hayakawa et al., 2003,Stoll et al., 2010)
a
https://orcid.org/0000-0001-7132-7703
b
https://orcid.org/0000-0002-4065-3415
The prevention of growth impairment and se-
vere nutrient deficits during hospital stay may be
achieved through the implementation of the knowl-
edge of macro nutrients/micro nutrients needs, the
optimization of nutritional policies and the individ-
ualization of the nutritional intervention. Optimizing
postnatal growth is in fact an integral component of
the management strategies for preterm infants, and
an important outcome measure in the NICU. EUGR
therefore may be used as one of the objective mea-
sures of quality of nutritional care in premature in-
fants - lower EUGR incidence meaning better quality
of care.
Objective of the analyses will be to develop and
validate a model that correlates prenatal and perinatal
features, such as nutritional intakes (both parenteral,
e.g. intravenously and enteral, e.g. orally) on postna-
tal growth and is able to make a prediction on the in-
fant’s growth at discharge. In other words, we would
like to investigate: can we predict accurately the
postnatal growth, and does the prediction’s inter-
pretation make clinical sense?
The paper is organized as follows: section 2
presents the methods used to collect data and the de-
velopment of the models; section. 3 presents the main
results. Finally, section. 4 discusses the findings of
this work and its limitations.
490
Seveso, A., Bozzetti, V., Tagliabue, P., Ventura, M. and Cabitza, F.
Developing a Machine Learning Model for Predicting Postnatal Growth in Very Low Birth Weight Infants.
DOI: 10.5220/0008972804900497
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 5: HEALTHINF, pages 490-497
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 MATERIALS AND METHODS
2.1 Data Available
The observational data has been retrieved from “Fon-
dazione Monza e Brianza per il bambino e la sua
mamma“s (FMBBM) Neonatal Intensive Care Unit
(NICU), one of the largest and most advanced NICUs
in Italy. FMBBM’s electronic registry, Metavision, is
property of ‘iMDsoft‘.
Infants at risk were included (gestational age<32
weeks OR birth weight<1500g), born from January
2006 to July 2019. The patients come from tertiary
care. It is a monocentric study: all the infants were
inborn in the San Gerardo hospital, were admitted to
the NICU up to 1 day from their birth and had a stay
time over 7 days (mean, sd 45±29).
2.2 Outcome
The definitions of EUGR are not consistent in the lit-
erature. Several methods have been proposed to quan-
tify the degree of EUGR.
Weight alone shouldn’t be used as an indica-
tor of wellness; a score that considers the infant’s
age, sex and weight needs to be used. In 2014,
the Intergrowth-21st Consortium published interna-
tional standards for newborn baby size and postnatal
growth (Villar et al., 2014), based on neonates with no
major complications or ultrasound evidence of fetal
growth restriction (FGR), who were born to healthy
mothers without risk factors for FGR.
The Weight Z score was calculated at discharge
using the postnatal growth for preterm infants calcu-
lator (The International Fetal and Newborn Growth
Consortium for the 21st Century, 2019). The Z score
at discharge was selected as the quantitative measure
of EUGR for each patient, and it is the target of the
predictive regression model. For the binary classi-
fication model, we defined the EUGR positive class
as <10th percentile at discharge (Radmacher et al.,
2003).
2.3 Related Work
It is possible to compare our regression model with
an existing work from Lin et al (Lin et al., 2015). The
inclusion criteria are similar. Lin et al. also use 32
weeks as a threshold for gestational age; however they
don’t consider birth weight. They also exclude deaths,
unlike in this work. Overall, they include 1,714 in-
fants, compared to our 964. Their outcome was se-
lected as the difference of Weight Z scores from birth
to discharge; in this work Z score at discharge alone
is considered as the quantitative outcome. Also, the Z
scores were calculated using a different method (Fen-
ton, 2003). The model used for prediction is a stan-
dard multivariate linear regression. Only two risk fac-
tors were considered by the authors: birth weight Z
score and completed weeks of gestation. As reported
by Lin et al., many important variables are missing
from their model, and many of these are implemented
in this work as suggested in their discussion, such as
Apgar score, gender and ethnicity.
Other works include the one of (Radmacher et al.,
2003), who use a logistic regression to predict a bi-
nary EUGR class. We will compare our performance
to their reported AUC score. (Lee et al., 2018) is also
related, however it does not report any performance
metric for comparison.
2.4 Features and Preprocessing
We decided to include in the model both prenatal and
perinatal features.
• With prenatal features we mean parameters or
events occurred before the birth.
• With perinatal features we mean parameters or
events occurred after birth (within the first week).
It is thought that most of the main events that influ-
ence the outcome results and therefore condition the
infant growth happen up to this period.
Neonatal characteristics are recorded: gestational
age, being appropriate or small for gestational age,
birth weight, length, head circumference, Apgar score
at 1 and 5 minutes. Additional neonatal features are:
twin or simple childbirth, fetal position at birth, am-
niotic fluid and placenta appearance, fetal distress,
PROM duration, GBS screening risk factors and out-
come. Centiles and Z scores at birth weight are calcu-
lated using the Lancet 21st Intergrowth newborn size
for very preterm infants calculator (The International
Fetal and Newborn Growth Consortium for the 21st
Century, 2019). Infants with birth weight above 10th
or below 10th percentile for gestational age, accord-
ing to the Lancet 21st Intergrowth chart, are classi-
fied as appropriate for gestational age (AGA) or small
for gestational age (SGA), respectively. Corrected
age is calculated from the chronological age adjust-
ing for gestational age. Nutritional intakes, both en-
teral and parenteral, are retrieved. Cumulative nutri-
tional intakes are calculated as the sum of the daily
intakes. Family features are included, such as: alco-
hol or smoke abuse during pregnancy, pathologies and
social problems, whether the course of pregnancy was
pathological or physiological, eventual consanguinity
of the parents and their profession, level of schooling,
ethnicity, age at child’s birth and anamnesis.
Developing a Machine Learning Model for Predicting Postnatal Growth in Very Low Birth Weight Infants
491

Figure 1: Descriptive statistics with violin plots, showing the probability density of numerical data.
Perinatal features were also recorded, up to a week
from birth. Average daily hours of mother’s and fa-
ther’s presence in the NICU are included. For en-
coding morbidity, therapy was used as a reliable in-
dicator, as database input is always required from an
operator before prescribing any medication. 64 differ-
ent drugs usage were recorded, each one encoded as
number of prescription days during the first 7 days af-
ter birth. Another 44 additional drugs were present in
the database, however, they were not included in this
work, as they were never prescribed to any of the in-
fants. For infants with respiratory assistance the most
common respiratory assistance mode during day 0 to
6 was included. Weight percentiles after birth were
calculated daily using the 21st Intergrowth postna-
tal growth for preterm infants calculator (The Inter-
national Fetal and Newborn Growth Consortium for
the 21st Century, 2019).
Missing values were imputed using K Nearest
Neighbors (KNN) for numeric values (k=3). For cate-
gorical values, depending on the nature of the feature,
they were imputed as ‘Unknown’ (when such values
were already present in the data) or using KNN impu-
tation otherwise.
HEALTHINF 2020 - 13th International Conference on Health Informatics
492

Table 1: Descriptive statistics of categorical features. Most common % calculated over non-null values.
Feature Unique values Most common (MC) MC % Miss %
Sex 2 Male 51.5 0.0
GA Aspect 3 AGA 68.7 19.5
Social Problems 3 No 57.8 0.0
Pregnancy Alcohol 3 No 93.0 0.0
Pregnancy Pathology 26 MPP < 34 GA weeks 26.7 0.0
Pregnancy Smoke 4 No 83.9 0.0
Fetal Position 8 Vertex 65.4 0.0
Birth Mode 6 C-sec, no labor 53.5 0.0
Birth Twins 2 Simple 75.2 0.0
Pregnancy Course 3 Pathological 82.0 0.0
Amniotic Fluid 8 Normal 71.4 0.0
PROM 4 No 62.6 0.0
Fetal Distress 5 No 66.9 0.0
Placenta 10 Normal 46.5 0.0
Group B Streptococcus (GBS) Screening 5 Not carried out 57.6 0.0
GBS Risk Factors 6 GA < 37 not induced 35.2 0.0
GBS Intrapartum 4 Adequate 49.3 0.0
Parents Consanguinity 5 No 60.3 0.0
Profession Father 7 Employee: blue collar 35.6 0.0
Schooling Father 6 Secondary school 37.6 0.0
Anamnesis Mother 18 Nothing to report 73.2 0.0
Profession Mother 7 Employee: white collar 35.4 0.0
Schooling Mother 6 Secondary school 42.2 0.0
Ethnicity Mother 10 Mediterranean Europe 68.9 0.0
2.5 Predicting Postnatal Growth with
Machine Learning
The features described in the previous section com-
prise of 245 features before encoding the categorical
features. After creating dummies with one-hot encod-
ing from the categorical features there are 411 fea-
tures available. The large number of predictors calls
for a feature selection, that is automated in the se-
lected machine learning models.
Two specific machine learning models were
taken into consideration: Random Forest (RF) and
Least Absolute Shrinkage and Selection Operator
(LASSO). A baseline model will also be provided, us-
ing a basic decision tree regressor. The intent is to
show the performance of a basic model, and to com-
pare the improvements of RF and LASSO over it.
Hyper parameter selection was automated with a
grid search. For each model, the best performing pa-
rameters were selected, and performances were tested
with 5-fold nested cross validation. The following
hyper parameters were attempted for each model: (i)
Random Forest: max depth ∈ {5, 10, 20} × number
of estimators {50, 100}, (ii) LASSO: Alpha ∈ {0.5,
1.0, 2.0}, (iii) Decision Tree: max depth ∈ {5, 10, 20,
unlimited}.
Models’ regression performances are reported
with the Mean Absolute Error (MAE) and coefficient
of determination (R
2
) metrics.
The performance of the model is also compared
with the performance on 30 test cases of a human be-
ing, an experienced doctor (and co-author of this ar-
ticle). As the doctor performance is based only on
few numerical features made available in a CSV file,
she is expected to have prognostic performance lower
than the machine. She is also asked to report her con-
fidence in the prediction in a 4-value scale, from 1
meaning ‘not confident at all’ to 4 ‘almost certain’.
We are aware that the better predictive perfor-
mance of the model would not be enough to assert
the usefulness of the proposed model, let alone gen-
eral over-performance (as a human interpreter would
never ground on tabular values only for their progno-
sis). That notwithstanding, demonstrating the model
supremacy represents a necessary (but not sufficient)
condition to consider the model reliable.
2.6 Dichotomized Classification
We also show the results of a classification model.
The target variable was dichotomized as follows: pos-
itive (EUGR) in the weight Intergrowth percentile at
Developing a Machine Learning Model for Predicting Postnatal Growth in Very Low Birth Weight Infants
493

Table 2: Best performing regression models for each estimator. Performance assessed with R
2
and MAE score. Mean and
95% CI calculated over 5 fold nested cross validation. Table sorted by mean R
2
.
Estimator Hyperparameters R2 (mean, CI) MAE (mean, CI)
Random Forest Max Depth: 10,
N Estimators: 50
0.74 [0.71, 0.77] 0.49 [0.47, 0.52]
LASSO Alpha: 0.5 0.62 [0.58, 0.67] 0.60 [0.54, 0.65]
Human Doctor None 0.32 [-0.11, 0.75] 0.59 [0.57, 0.62]
Decision Tree Max Depth: 5 0.54 [0.47, 0.61] 0.64 [0.61, 0.67]
Table 3: Best performing classification models for each estimator. Performance assessed with Accuracy, ROC AUC and
Matthews Correlation Coefficient (MCC) score. Mean and 95% CI calculated over 5 fold nested cross validation. Table
sorted by mean AUC.
Estimator Hyperparameters Accuracy (mean, CI) AUC (mean, CI) MCC (mean, CI)
Random Forest Max Depth: 10,
N Estimators: 50
0.84 [0.83, 0.86] 0.94 [0.92, 0.95] 0.71 [0.69, 0.72]
SVC Degree: 3,
Kernel: poly
0.83 [0.82, 0.85] 0.92 [0.90, 0.93] 0.66 [0.63, 0.69]
Logistic Penalty: l1 0.80 [0.79, 0.80] 0.86 [0.85, 0.87] 0.60 [0.53, 0.67]
NB None 0.73 [0.71, 0.74] 0.77 [0.75, 0.78] 0.44 [0.36, 0.51]
discharge was under or equal to the 10th percentile,
negative (not EUGR) otherwhise. Other features were
not changed from the regression model.
The following hyper parameters were attempted
for each model: (i) Logistic Regression: model
penalty ∈ {L1, L2}, (ii) Random Forest: max depth
∈ {5, 10, 20} × number of estimators {50, 100}, (iii)
SVC: model degree ∈ {2, 3, 4} × Kernel: Poly, (iv)
Naive Bayes: no hyperparameters.
Models’ classification performances are reported
with accuracy, ROC AUC and Matthews Correlation
Coefficient (MCC) metrics.
3 RESULTS
3.1 Patients’ Descriptive Statistics
Figure 1 and table 1 describe the predictors for 964
eligible infants. Nutritional intakes and 64 drugs nu-
merical features are not included for brevity.
3.2 Regression Performance
Performances are calculated on the test set over 5
folds. The train set for each fold comprises 771 in-
fants, while the test set 193. A baseline is provided
by the means of a simple decision tree.
Regression performances are shown in table 2.
Only the best hyperparameters combination is shown
for each model. The overall best performing model
is Random Forest with a max depth of 10 and 50
estimators.
The model performs better than the clinician, as it
was expected for this particular experiment. However,
the average error is not significantly different. The
human performance (MAE 0.52 [0.41, 0.64], R2 0.32
[-0.11, 0.75]) and the model’s MAE 95% confidence
interval (mean 0.49, CI 95% [0.47, 0.52]) overlap.
However, the clinician’s confidence in her predic-
tions was quite low: a median of 2 (on a scale from 1
to 4, where 1 means “not confident at all” and 4 “al-
most certain”). Out of 30 manual test cases, the “not
confident at all” option was selected 5 times (17%),
“not very confident” 19 times (63%), “confident” 6
times (20%) and “almost certain” was never selected.
3.3 Classification Performance
After dichotomization, 527 (55%) infants are in the
’EUGR’ class, 437 (45%) in the ’not EUGR’ class.
The class distribution was balanced, so accuracy is a
reliable estimate of the model performance. Classifi-
cation performances are shown in table 3. Only the
best hyperparameters combination is shown for each
model. The overall best performing model is Ran-
dom Forest with a max depth of 10 and 50 estima-
tors, and its ROC curve is shown in figure 3.
3.4 Model Explanation
The most important features for the regressor model
are shown in figure 4.
The birth weight Z score and centile reveal the fe-
tus health status. These growth parameters measured
at birth highly reflect the intrauterine growth. Accord-
HEALTHINF 2020 - 13th International Conference on Health Informatics
494

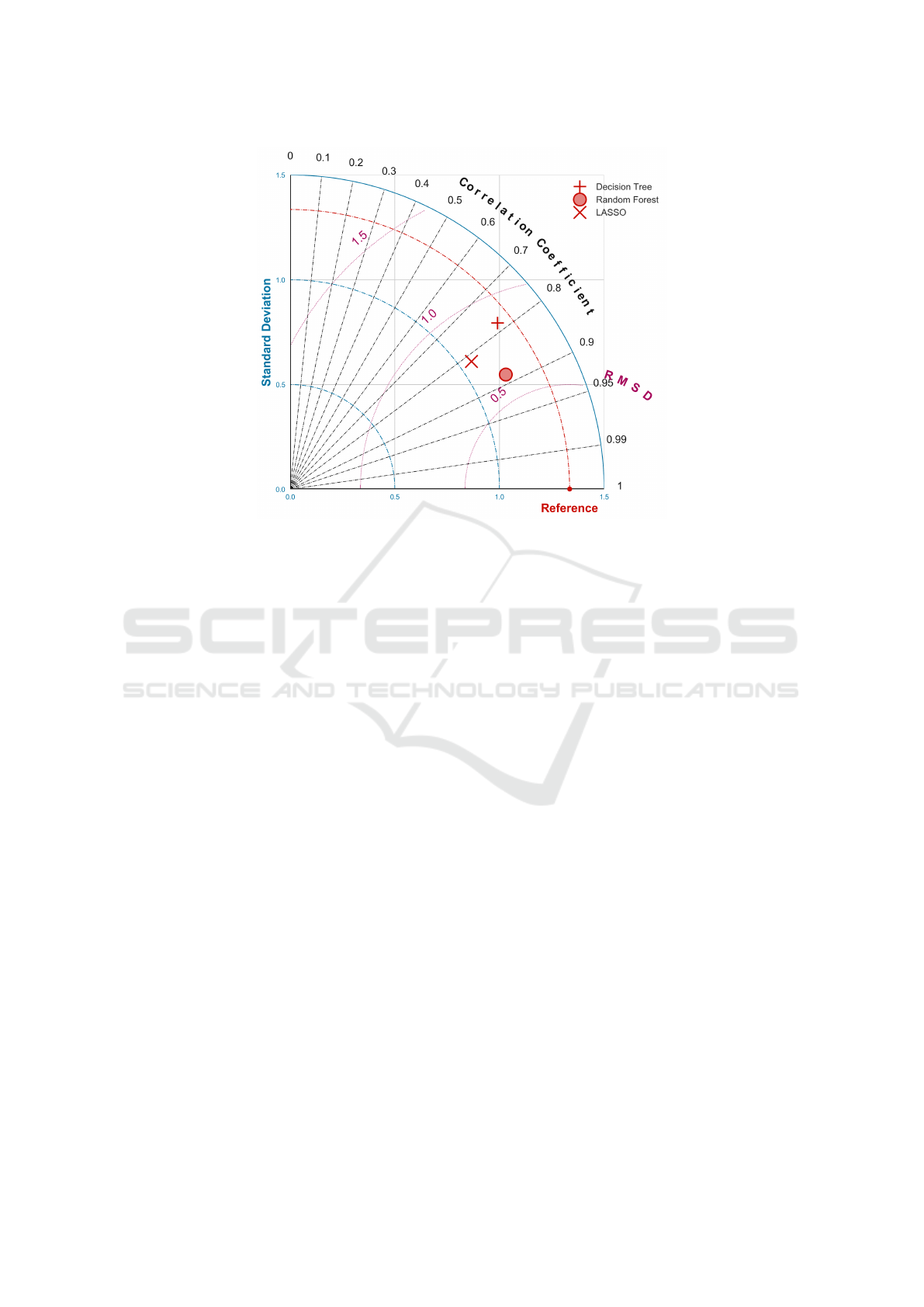
Figure 2: Taylor diagram showing the performance of each machine learning regression model.
ing to the model, the prenatal conditions deeply im-
pact on growth outcome stressing the importance of a
careful obstetrical management of pregnant women.
Among the features that impact on outcomes, the
growth parameters are the most important. The cen-
tile at day 6, that is the expression of the weight in-
crease after the physiological weight loss of the first
3-5 days of life, seems to be determinant to ensure a
proper growth also later on in life. There is a strict
correlation between growth parameters and fluid (ex-
pressed as water) intake. It is very difficult to admin-
ister the proper amount of fluid to preterm infants. If
on one hand an adequate fluid supply may reduce the
entity of weight loss and therefore the entity of ex-
trauterine growth restriction, on the other hand it has
been demonstrated a correlation among high fluid in-
takes and morbidities (respiratory distress syndrome,
arterial ductus patency. . . ).
The electrolytes (as potassium and sodium) play
a major role too. This is strictly related to the fluid
balance. Administration of sodium and potassium in
the first 3 days of life is a highly debated topic in
the scientific literature. It’s quite impossible to avoid
sodium administration after birth as sodium is con-
tained in many parenteral nutrients (as phosphorus
and amino acids compounds). Quite often the neona-
tologist has to decide if allowing to give sodium to
infant to respect his phosphorus requirements or to
allow the physiologic extracellular liquid reduction
thus avoiding sodium (and therefore phosphorus) in-
take. Thanks to this model it’s now extremely clear
that early sodium administration highly impacts on
growth.
The model moreover considers all the therapies
administered to the patients. The infants at more risk
of growth restriction are those who receive antibiotic
therapy (ceftazidime and gentamycin) expression of
occurrence of severe sepsis. Surprisingly those fac-
tors impact on growth more than caloric and proteic
supply.
Gestational age is a determinant factor; it is well
known that the lower the GA, is the higher the risk of
growth impairment is.
4 DISCUSSION AND
CONCLUSIONS
The Machine Learning models predict the patient’s
postnatal growth at discharge. The prediction can be
made at one week after birth by providing the required
features. We have also shown which parameters (fea-
tures) are the most predictive, globally.
We compared our regression performance with
those reported in the specialist literature (see sec-
tion 2.3): notably, Lin et al. (Lin et al., 2015) report a
simple multivariate linear regression model with a R
2
score of 0.23; conversely, ours achieved an R
2
0.74
[0.72, 0.75]. To justify this impressive improvement,
we could notice that our model encompasses features
of postnatal care in the NICU, which their model did
not consider.
Developing a Machine Learning Model for Predicting Postnatal Growth in Very Low Birth Weight Infants
495

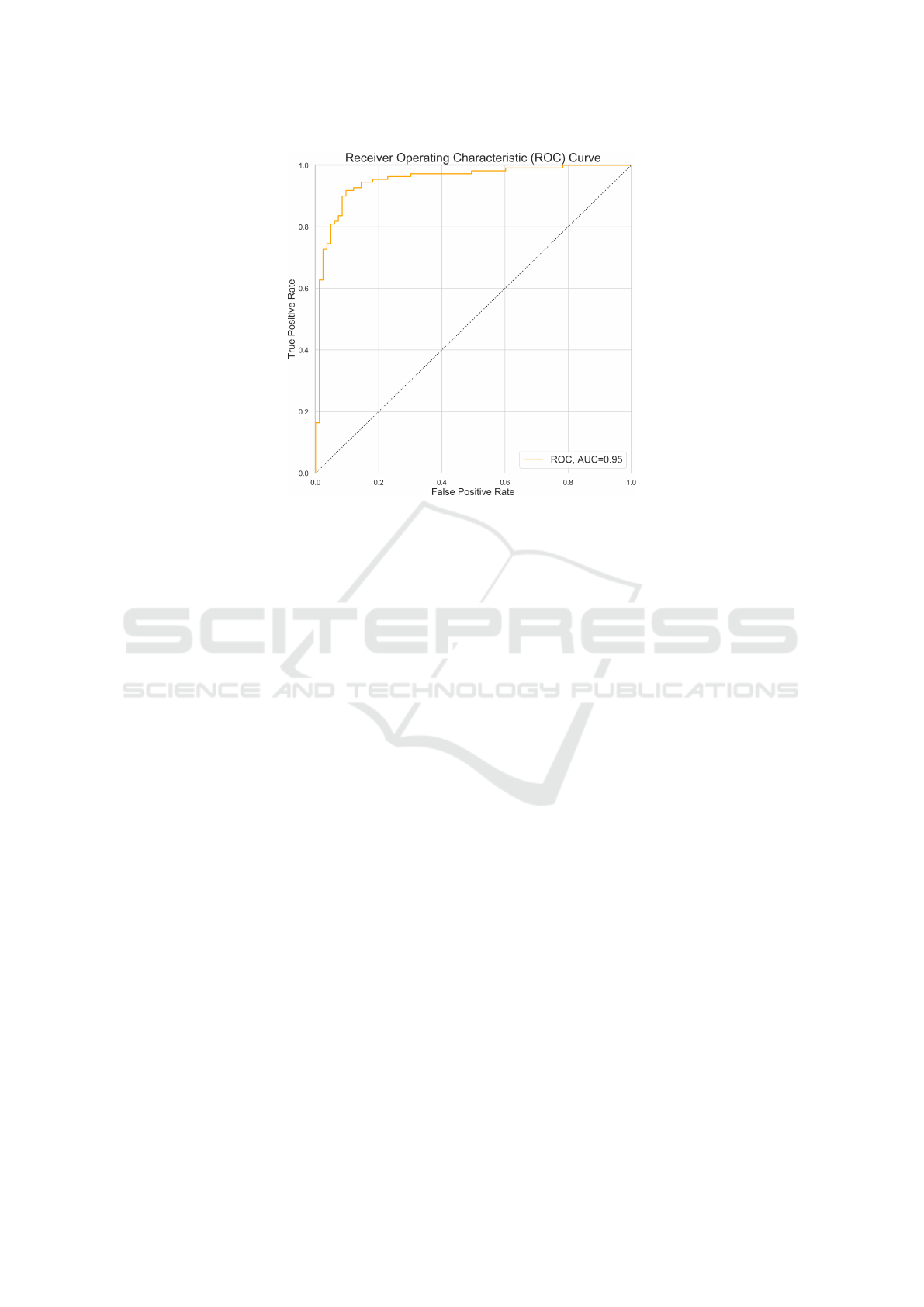
Figure 3: Receiver Operating Characteristic (ROC) Curve for Random Forest classifier, AUC=0.95.
In fact, the Random Forest model that achieved
the best performance in our user study, encompassed
hundreds of features. As discussed by Lin et al.,
adding too many factors introduces complexity from
the data collection side, with relatively small returns
on performance improvement. Thus, a limitation of
our work is that many of the features considered are
not easy to collect reliably, especially in less digi-
talized NICUs; this might have negative effects on
the real-world applicability of the model. Moreover,
comparing our classification performance to (Rad-
macher et al., 2003), the authors report an AUC
of 0.85; ours achieved a significantly higher perfor-
mance: 0.94 [0.92, 0.95].
Comparing our regression performance to the
clinician’s performance, we found that the average er-
ror is not significantly different, as seen in section 3.2.
The confidence reported by the clinician was low; this
might be because the prediction was made on the ba-
sis of tabular data instead of a live examination of
the patient (i.e., the ordinary way to make a clinical
and prognostic assessment for a doctor). However,
the closeness of the two performances indicate that
the proposed model has a potential for being useful
in supporting a more objective clinician assessments.
Future work could be aimed at comparing our model
with the prediction of a clinician who knows and can
visit the patient personally. In that case, we expect
that the clinician will have higher accuracy.
The doctor was also asked to express what is in
her opinion the maximum acceptable error (or equiv-
alently minimum acceptable accuracy) on the part of a
predictive model to consider this still useful for prog-
nostic or therapeutic purposes. The error had to be
expressed in terms of Z score, in a scale from zero (=
only a perfect model that does not make any error is
useful) to 3 (= a model that committed an error equal
to practically half the tabulated weight). The doctor
proposed a threshold at approximately two third of
a standard deviation, an higher error than the mean
MAE of our best performing model (Random For-
est, MAE=0.49). This indicates that the predictive
model’s error might be useful for clinicians, although
more doctors’ opinions must be collected before mak-
ing any definitive claim. We plan to spread this poll
to other NICU practitioners and neonatologists to get
an estimate of this minimum acceptable accuracy.
As for other future work, we would like to im-
prove on the following aspects:
• To produce a more parsimonious model that uses
less features with similar performances, in partic-
ular, to include only features that are easy to col-
lect in order to make the model as accessible as
possible;
• To test the performance of the above, less complex
model on other NICUs, even in those that do not
have access to electronic data recording;
• To evaluate the real-world use of the model (both
usefulness and utility);
• To investigate the complex relationship between
doctors and AI explanations, in both agreements
and disagreements (Ribeiro et al., 2016).
In conclusion, the model provides solid perfor-
mance and a substantial improvement over the litera-
ture (Lin et al., 2015,Radmacher et al., 2003), but still
HEALTHINF 2020 - 13th International Conference on Health Informatics
496

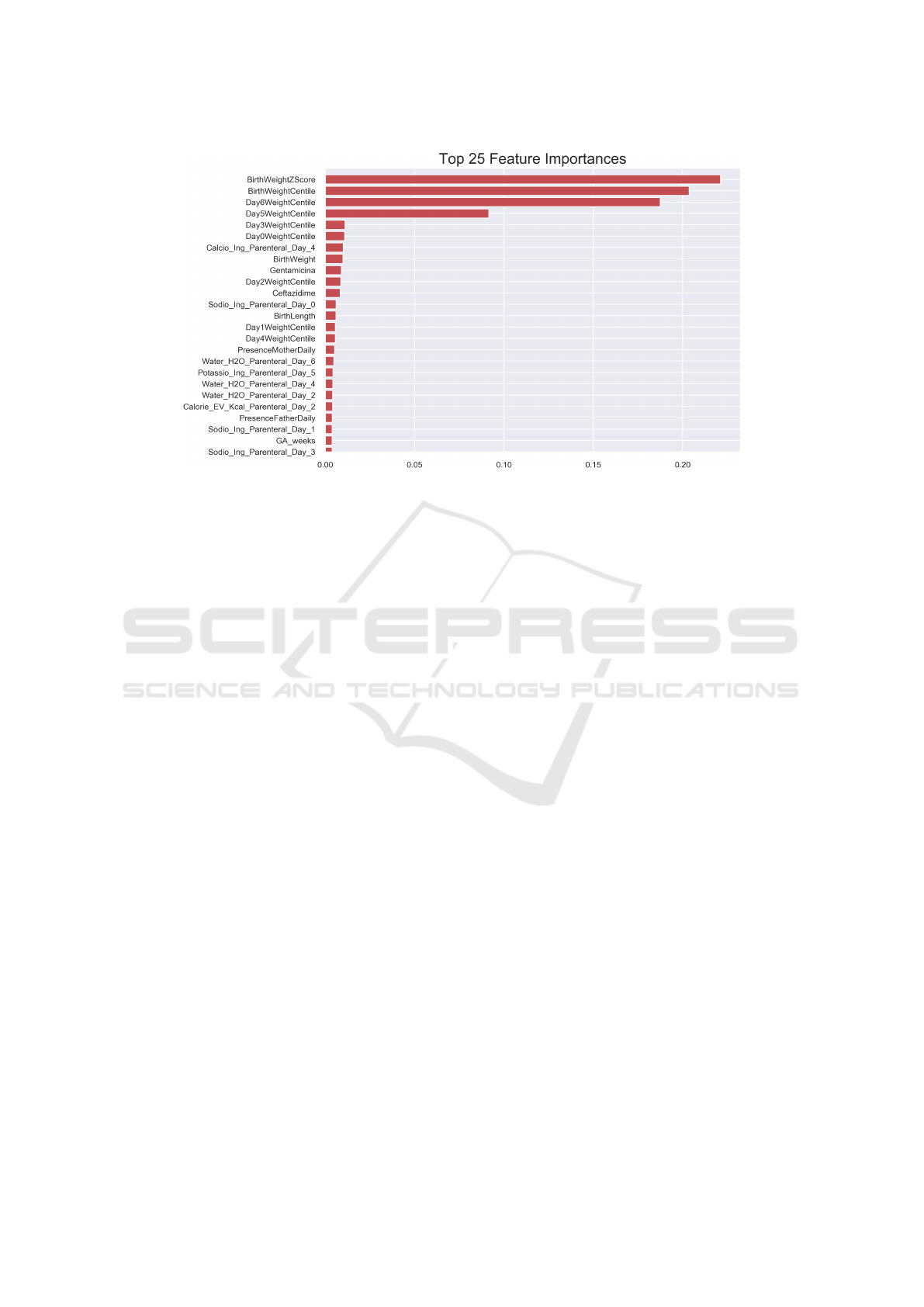
Figure 4: Feature importance. The x axis marks the average decrease in variance over all the estimators (trees).
lacks a pragmatic validation in the field of work (Cab-
itza and Zeitoun, 2019).
REFERENCES
Cabitza, F. and Zeitoun, J.-D. (2019). The proof of the pud-
ding: in praise of a culture of real-world validation for
medical artificial intelligence. Annals of translational
medicine, 7(8).
Clark, R. H., Thomas, P., and Peabody, J. (2003). Extrauter-
ine growth restriction remains a serious problem in
prematurely born neonates. Pediatrics, 111(5):986–
990.
Ehrenkranz, R. A., Dusick, A. M., Vohr, B. R., Wright,
L. L., Wrage, L. A., Poole, W. K., et al. (2006).
Growth in the neonatal intensive care unit influ-
ences neurodevelopmental and growth outcomes of
extremely low birth weight infants. Pediatrics,
117(4):1253–1261.
Fenton, T. R. (2003). A new growth chart for preterm ba-
bies: Babson and benda’s chart updated with recent
data and a new format. BMC pediatrics, 3(1):13.
Hayakawa, M., Okumura, A., Hayakawa, F., Kato, Y.,
Ohshiro, M., Tauchi, N., and Watanabe, K. (2003).
Nutritional state and growth and functional maturation
of the brain in extremely low birth weight infants. Pe-
diatrics, 111(5):991–995.
Lee, S. M., Kim, N., Namgung, R., Park, M., Park, K., and
Jeon, J. (2018). Prediction of postnatal growth fail-
ure among very low birth weight infants. Scientific
reports, 8(1):3729.
Lin, Z., Green, R. S., Chen, S., Wu, H., Liu, T., Li, J., Wei,
J., and Lin, J. (2015). Quantification of eugr as a mea-
sure of the quality of nutritional care of premature in-
fants. PloS one, 10(7):e0132584.
Lucas, A., Morley, R., and Cole, T. J. (1998). Randomised
trial of early diet in preterm babies and later intelli-
gence quotient. Bmj, 317(7171):1481–1487.
Miller, M., Vaidya, R., Rastogi, D., Bhutada, A., and Ras-
togi, S. (2014). From parenteral to enteral nutri-
tion: a nutrition-based approach for evaluating post-
natal growth failure in preterm infants. Journal of Par-
enteral and Enteral Nutrition, 38(4):489–497.
Radmacher, P. G., Looney, S. W., Rafail, S. T., and
Adamkin, D. H. (2003). Prediction of extrauterine
growth retardation (eugr) in vvlbw infants. Journal
of Perinatology, 23(5):392.
Ribeiro, M. T., Singh, S., and Guestrin, C. (2016). Why
should i trust you?: Explaining the predictions of any
classifier. In Proceedings of the 22nd ACM SIGKDD
international conference on knowledge discovery and
data mining, pages 1135–1144. ACM.
Stoll, B. J., Hansen, N. I., Bell, E. F., Shankaran, S., Lap-
took, A. R., Walsh, M. C., Hale, E. C., Newman, N. S.,
Schibler, K., Carlo, W. A., et al. (2010). Neonatal
outcomes of extremely preterm infants from the nichd
neonatal research network. Pediatrics, 126(3):443–
456.
The International Fetal and Newborn Growth Consor-
tium for the 21st Century (2019). Intergrowth-21
standards and tools. https://intergrowth21.tghn.org/
standards-tools/. Accessed: 2019-10-10.
Villar, J., Ismail, L. C., Victora, C. G., Ohuma, E. O.,
Bertino, E., Altman, D. G., Lambert, A., Papa-
georghiou, A. T., Carvalho, M., Jaffer, Y. A., et al.
(2014). International standards for newborn weight,
length, and head circumference by gestational age
and sex: the newborn cross-sectional study of the
intergrowth-21st project. The Lancet, 384(9946):857–
868.
Developing a Machine Learning Model for Predicting Postnatal Growth in Very Low Birth Weight Infants
497