Manifold Learning-based Clustering Approach Applied to
Anomaly Detection in Surveillance Videos
Leonardo Tadeu Lopes
1
, Lucas Pascotti Valem
1
, Daniel Carlos Guimar
˜
aes Pedronette
1
,
Ivan Rizzo Guilherme
1
, Jo
˜
ao Paulo Papa
2
, Marcos Cleison Silva Santana
2
and Danilo Colombo
3
1
Department of Statistics, Applied Math. and Computing, UNESP - S
˜
ao Paulo State University, Rio Claro, SP, Brazil
2
School of Sciences, UNESP - S
˜
ao Paulo State University, Bauru, SP, Brazil
3
Cenpes, Petr
´
oleo Brasileiro S.A. - Petrobras, Rio de Janeiro, RJ, Brazil
Keywords:
Clustering, Unsupervised Manifold Learning, Anomaly Detection, Video Surveillance.
Abstract:
The huge increase in the amount of multimedia data available and the pressing need for organizing them in dif-
ferent categories, especially in scenarios where there are no labels available, makes data clustering an essential
task in different scenarios. In this work, we present a novel clustering method based on an unsupervised man-
ifold learning algorithm, in which a more effective similarity measure is computed by the manifold learning
and used for clustering purposes. The proposed approach is applied to anomaly detection in videos and used in
combination with different background segmentation methods to improve their effectiveness. An experimental
evaluation is conducted on three different image datasets and one video dataset. The obtained results indicate
superior accuracy in most clustering tasks when compared to the baselines. Results also demonstrate that the
clustering step can improve the results of background subtraction approaches in the majority of cases.
1 INTRODUCTION
Due to the continuous advances in the acquisition,
storage and sharing technologies for visual content,
the volume of image and video data have growing ver-
tiginously. Similar to many other applications, the in-
crease in both volume and variety of data requires ad-
vances in methodology to automatically understand,
process, and summarize the data. One of the most
promising ways consists in organizing objects into
sensible groupings (Jain, 2010).
In this scenario, clustering can be seen as an es-
sential component of various data analysis or machine
learning based applications. Different from super-
vised classification, where we are given labeled sam-
ples, there is no label attached to the patterns. In
this challenging scenario, the natural grouping of data
based on some inherent similarity is to be discov-
ered (Saxena et al., 2017). More formally, clusters
can be defined as high-density regions in the feature
space separated by low-density regions (Jain, 2010).
However, similar to many other data mining
and machine learning methods, clustering approaches
critically depend on a good metric in the input space.
In fact, this problem is particularly acute in unsuper-
vised settings such as clustering, and is related to the
perennial problem of there often being no right an-
swer for clustering (Xing et al., 2002). For images
represented in high dimensional spaces, their compar-
ison is often based on the use of the Euclidean dis-
tance applied on their corresponding feature vectors.
However, the pairwise distance analysis provides only
locally restrict comparisons and ignores more global
relationships and the dataset structure itself. In fact,
collection of images are often encoded in a much
lower-dimensional intrinsic space, and therefore cap-
turing and exploiting the intrinsic manifold structure
becomes a central problem for different vision, learn-
ing, and retrieval tasks. In this scenario, unsupervised
manifold methods have been proposed with the aim
of replacing pairwise measures by more global affin-
ity measures capable of considering the dataset mani-
fold (Pedronette et al., 2018).
In this paper, a novel clustering method is pro-
posed based on an unsupervised manifold learning al-
gorithm. A more effective similarity measure is com-
puted by the manifold learning and used for cluster-
ing purposes. The manifold learning algorithm (Pe-
dronette et al., 2018) models the dataset similarity
structure in a graph based on the k-reciprocal refer-
404
Lopes, L., Valem, L., Pedronette, D., Guilherme, I., Papa, J., Santana, M. and Colombo, D.
Manifold Learning-based Clustering Approach Applied to Anomaly Detection in Surveillance Videos.
DOI: 10.5220/0008974604040412
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
404-412
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ences encoded in the ranking information. The graph
considers crescent neighborhood depths, providing a
multi-level analysis. While the edges of the Recipro-
cal k-nearest neighbors Graph (kNN Graph) provide
a strong indication of similarity, the Connected Com-
ponents are exploited for capturing the intrinsic ge-
ometry of the dataset. Further, the strongly connected
components are used to define the clusters. Addi-
tionally, we exploit the proposed clustering approach
for deriving a novel method for anomaly detection
in video sequences. The proposed method uses the
cluster information and a semi-supervised strategy for
identifying the normal and abnormal frames. Next,
the frames detected as normal are provided as input
for the background subtraction approaches. An exper-
imental evaluation was conducted on various datasets
for assessing the effectiveness of the proposed cluster-
ing approach, including applications for anomaly de-
tection on video surveillance. The obtained results in-
dicate superior accuracy in most clustering tasks com-
pared to the baselines. Results also demonstrate that
the clustering step can improve the results of back-
ground subtraction approaches.
The remaining of the paper is organized as fol-
lows: Section 2 discusses the related work and prob-
lem formulation. Section 3 presents the proposed
clustering method. Section 4 presents our approach
based on clustering information for semi-supervised
anomaly detection. Section 5 presents the experimen-
tal evaluation and, finally, Section 6 draws conclu-
sions and discusses future works.
2 RELATED WORK
Clustering is an important unsupervised learning
technique that has been extensively studied in the past
decades. It consists on separating data into subsets
based on items, features or attributes with the main
objective of maximizing the inner similarity between
subset items and minimize the similarity between sub-
sets.
Clustering techniques are usually divided into four
categories: (i) partional-based methods, that consist
on the computation of a pre-determined number of
centroids and in the clustering of elements around
them; (ii) hierarchical-based methods, that work with
pairwise similarity to divide or to agglomerate the
items of the dataset into clusters; (iii) graph-based
methods, that interpret the data and their relationship
in a graph to determine the best combination of items
and clusters; and (iv) the density-based methods, that
separate the dataset items based on the density regions
and the boundaries of their distributions.
Each category introduces different approaches to
separate the items into clusters. Although there are
various known clustering methods, there is not a
definitive algorithm capable of separate all kinds of
data correctly, efficiently and free of parameters in
multiple scenarios. The parameter dependency of
most clustering methods represents one of the major
difficulties of the area and heavily affects the data sep-
aration quality. K-means, for example, is known for
its highly sensibility to the number of clusters and the
selection of the initial centroids (Jain, 2010). Those
parameters are generally related to the dataset distri-
bution and are not easy to set.
One of the many strategies being applied to clus-
tering is the neighborhood relationship, which can
be exploited to discover natural separations of the
dataset. From the recent methods that employ the
neighborhood relationship to clusterize items, we can
cite: (i) FINCH (Sarfraz et al., 2019) exploits the first
neighbor relationship between items and clusters in
order to unite them until only two clusters remain; (ii)
Munec (Ros and Guillaume, 2019) utilizes the mutual
neighborhood relationship between the dataset items
to define heuristics, which are used as the stop crite-
ria for the merging process. Besides, both retrieve
hierarchical agglomerative clusters. Different from
most previously proposed methods, our approach em-
ploys a reciprocal kNN Graph-based manifold learn-
ing strategy (Pedronette et al., 2018) with the objec-
tive of retrieving an improved distance measure and a
set of high-reliable initial clusters.
In one of many applications, clustering is applied
to videos as a separate stage with the objective of
improving the general effectiveness of a surveillance
system (Li et al., 2012; Lawson et al., 2016). They
are often jointly used with other traditional subtrac-
tor approaches, once the pixel-by-pixel classification
generally presents performance constraints, specially
in scenarios of high dimensionality.
The volume of data generated by surveillance sys-
tems has increased considerably in the recent years
specially due to the decreasing cost of technologies
to capture, store, and share images (Sodemann et al.,
2012). However, since the amount of data has in-
creased much faster than the availability of human ob-
servers and there is a pressing need for assuring secu-
rity in diverse scenarios, a required solution is the de-
velopment of automated video surveillance systems.
Despite the recent advances, there are multiple
challenges to be addressed (Bouwmans and Garcia-
Garcia, 2019), such as: (i) the process of acquiring
groundtruth labels for long video sequences is a com-
plicated and time demanding task; (ii) it is possible to
have multiple anomaly scenarios which are not cov-
Manifold Learning-based Clustering Approach Applied to Anomaly Detection in Surveillance Videos
405

ered by the training or known samples; (iii) anomaly
frames are usually rare, which makes the training data
highly imbalanced; and (iv) some methods are very
sensible to illumination variations.
The traditional background subtractors often per-
form statistical operations for detecting outlier data,
which is usually applied pixel-by-pixel. In the Mix-
ture of Gaussians - MOG (KaewTraKulPong and
Bowden, 2002), each pixel is modelled according to
a Gaussian distribution, and the ouliers are classified
as anomalies. The MOG has different variations, e.g.,
MOG2 (Zivkovic, 2004), which implements some op-
timizations, including automatic setup for the number
of clusters.
More recently, deep learning approaches have
gained a lot of attention due to their high effective
results. There are different types of networks that
can be employed for anomaly detection (Chalapathy
and Chawla, 2019), where the most popular ones are
the auto-encoders (Gong et al., 2019). Auto-encoders
are unsupervised neural networks which aim at recon-
structing a learned image. After being trained, they
use the reconstruction error to determine if there is an
anomaly or not.
Different from what has been done in the majority
of the works, we exploit the idea of using clustering
as a pre-processing step for improving the data pro-
vided to train the subtractors. The strategy is evalu-
ated in several traditional background subtractors and
positive gains were obtained in most of the cases.
3 PROPOSED METHOD
In this section, we present the proposed clustering
method. Along the text, some notations will be pre-
sented to give context or describe situations occur-
ring on the method. Table 1 details those notations
for a better understanding of the paper. This work is
based on three main hypotheses, which are: (i) a dis-
tance measure based on manifold learning can be used
as a pre-processing step for improving the formation
of output clusters; (ii) the connected components ob-
tained from the kNN Graph, enhanced by the man-
ifold learning procedure, can provide high-reliable
small clusters; (iii) an agglomerative step based on the
distance measure generated by the manifold learning
can retrieve clusters with better final formation.
The proposed approach is illustrated on Figure 1,
where each number represents a step described on the
following subsections. Section 3.1 presents the rank
definition, Section 3.2 describes the manifold learning
step and Section 3.3 presents the initial clusters for-
mulation. Finally, Section 3.4 defines the final clus-
ters formulation.
Table 1: Method notations description.
Notation Description
k
Parameter that defines the size of neighborhood
explored by the manifold learning process and the
minimum number of images contained on each of
the final clusters.
L
Defines the size of each ranked list that will be
considered for normalization and sort through the
method stages.
t
k
The actual iteration of k.
c
k
Size of the reciprocal neighborhood utilized to
compute the initial clusters of our method.
3.1 Rank Model
In this work, we consider the retrieval problem for-
mulation as defined in (Pedronette et al., 2018). A
set of ranked lists T = {τ
1
, τ
2
, . . . , τ
n
} is obtained
by computing a ranked list for every object present
in the collection, using the Euclidean distance as the
distance function ρ. In this scenario, τ
q
represents the
ranked list of o
q
and τ
q
( j) represents the position of
o
j
in o
q
ranked list. This set represents a rich dis-
tance/similarity information source about the collec-
tion C , which is employed in through the next stages
of the proposed clustering approach.
3.2 Manifold Learning Approach
The Reciprocal kNN Graph and Connected Compo-
nents algorithm is a proposed method (Pedronette
et al., 2018) that exploits a set of ranked lists T
to compute a manifold learning-based improved dis-
tance measure to the dataset.
Our proposed approach utilizes this algorithm by
exploiting the reciprocal relationship edges in order
to discover a set of initial clusters formed by low-size
high-reliable clusters and by using the computed dis-
tance on the agglomerative stage of the final clusters
formulation process. By using definitions and inter-
pretations developed in this manifold learning algo-
rithm (Pedronette et al., 2018), its steps are described
throughout this subsection.
First, based on the ranked lists described in Sec-
tion 3.1, the algorithm performs a rank normalization,
due to the information presented on those ranks not
being symmetric. The new dataset rank is obtained
by the normalized distance function ρ
n
:
ρ
n
(i, j) = τ
i
( j) + τ
j
(i) + max(τ
i
( j), τ
j
(i)), (1)
where τ
i
( j) ≤ L and ρ
n
(i, j) ≤ 3 × L. Based on the
new distance values obtained by ρ
n
, the set of ranked
lists T is updated and sorted, until the top-L positions.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
406

Dataset
Ranked lists
Manifold learning through
connected components
Enhanced
ranked lists
Initial clusters
through kNN
items
Final clusters
Figure 1: Workflow of our proposed clustering approach.
On a second stage, the algorithm computes a
reciprocal kNN Graph, G
r
= (V, E), where the
dataset objects are represented as the graph nodes
and the edges are computed based on an incremen-
tal k-reciprocal neighborhood, considering different
thresholds of k. For this, the reciprocal neighborhood
N
r
is defined as
N
r
(q, k) = {S ⊆ C , |S | = k ∧∀o
i
∈ S :
τ
q
(i) ≤ k ∧ τ
i
(q) ≤ k}, (2)
representing a set of objects contained in the k-top po-
sitions of τ
q
, where ∀o
i
∈ N
r
(q, k), τ
i
(q) ≤ k.
For each iteration of k, represented by t
k
, the edges
of the reciprocal kNN Graph can be obtained as:
E = {(o
q
, o
j
) | o
j
∈ N
r
(q, t
k
)}, (3)
in this way, an edge will be created from o
i
to o
j
if the
objects are reciprocal neighbors until the top-t
k
rank
positions of each other.
For computing the improved distance measure to
the dataset, the manifold learning algorithm retrieves
information from both the edges and the Connected
Components (CCs), formulated by them, on every it-
eration of t
k
. The CCs computation retrieves a set S =
{P
1
, P
2
, . . . , P
m
}, such that {P
1
∪ P
2
∪ · · · ∪ P
m
} = S
and {P
1
∩ P
2
∩ ··· ∩ P
m
} =
/
0. Notice that the thresh-
old t
k
is directly related to the number of connected
components m: the higher the value of t
k
, the more
connected the graph becomes, thus decreasing m (Pe-
dronette et al., 2018).
On the final stage, the algorithm updates G
r
for
different depths of reciprocal neighborhood and, for
each depth t
k
6 k, the similarity scores are increased
such that higher weights are assigned to neighbors at
top positions.
First, a score based on the graph edges is com-
puted. Each pair of images (o
i
, o
j
) contained in E(q)
represents an increase in similarity between them,
since both have edges to o
q
. Therefore, w
e
(i, j) is de-
fined as follow:
w
e
(i, j) =
k
∑
t
k
=1
∑
q∈C ∧i, j∈E(q)
(k − t
k
+ 1). (4)
Analogously, the information provided by con-
nected components define a similarity score w
c
(i, j).
This score represents a similarity increase between
objects o
i
and o
j
, when they are in the same CC,
which is also defined considering different t
k
values:
w
c
(i, j) =
k
∑
tk
∑
i, j∈C
l
(k − t
k
+ 1). (5)
Both w
e
(i, j) and w
c
(i, j) will assume higher val-
ues as early the connection between o
i
and o
j
on G
r
is
computed, highlighting the manifold structure present
on the dataset. The combination them defines w(i, j)
as: w(i, j) = w
e
(i, j) + w
c
(i, j).
Finally, a Reciprocal kNN Graph CCs Distance
(Pedronette et al., 2018), ρ
r
is inversely proportional
to the similarity score, and it is computed as follows:
ρ
r
(i, j) =
1
1 + w(i, j)
. (6)
Based on this new distance ρ
r
, a more effective set of
ranked lists T
r
is obtained. Both ρ
r
and T
r
are used to
retrieve the clusters present on the dataset.
3.3 Initial Clusters
As described on Section 3.2, the CCs retrieved by the
manifold learning algorithm can represent the natu-
ral clusters of the dataset, matching with the cluster
definition on Section 2. Therefore, the simple output
Manifold Learning-based Clustering Approach Applied to Anomaly Detection in Surveillance Videos
407

Video
Frames
Cluster Method
(e.g., ReckNN)
...
Abnormality Cluster
Normality Cluster
Mean Image
for Normality
Mean Image
for Abnormality
Background Subtractor
(e.g., MOG)
Apply to
...
...
...
Provide to
Figure 2: Our proposed video anomaly detection workflow.
based on the CC retrieved on a t
k
iteration of the man-
ifold learning algorithm represents a clusterization of
the dataset structure.
However, the manifold learning algorithm (Pe-
dronette et al., 2018) does not provide an heuristic
to determine whether an edge between two objects o
i
and o
j
should be created or if two connected com-
ponents linked by few or even one edge should be
united. Therefore, for datasets with ineffective ranked
lists, the algorithm tends to unite non-similar CCs,
leading to an ineffective clustering process.
To avoid incorrect unions, we exploit the con-
nected components retrieved with low reciprocal
neighborhood size. Based on a parameter c
k
, de-
scribed on Table 1, we define a new graph G
c
and
create edges for the reciprocal neighborhoods of size
c
k
, N
r
(q, c
k
). The set of edges for G
c
, E
c
, can be de-
fined as: E
c
= {(o
q
, o
j
) | o
j
∈ N
r
(q, c
k
)}.
By the computation of the CCs contained in G
r
,
we retrieve a set of clusters S
c
= {C
1
, C
2
, . . . , C
m
},
where m represents the initial number of clusters ob-
tained from the dataset. The S
c
is composed of uni-
tary clusters, which are the set majority, and some
non-unitary clusters that represent reliable connec-
tions that will affect the final agglomeration.
3.4 Final Clusters
Finally, our method iterates over S
c
, described in Sec-
tion 3.3. On each iteration, the smallest cluster, rep-
resented by C
A
, is united to the closest cluster in the
set. To compute the distance between clusters C
A
and
C
B
we apply the average-linkage connection (Saxena
et al., 2017) based on the distance function ρ
r
re-
trieved by the manifold learning algorithm. This dis-
tance is represented by d(C
A
, C
B
).
This approach was chosen for taking advantage of
the initial cluster formats, as described on Section 3.3.
Based on d(C
A
, C
B
), we retrieve the closest cluster to
C
A
, represented by f (C
A
):
f (C
A
) = argmin
C
B
∈S\{C
A
}
d(C
A
, C
B
). (7)
From this formulation, we update the cluster C
A
=
C
A
∪ f (C
A
) and remove f (C
A
) from the set, updating
S
c
= S
c
\ f (C
A
).
Such process is repeated until a condition is
achieved, which is based on parameter k: ∀C
i
∈ S
c
:
|C
i
| ≤ k.
After the clusters fusion, the proposed clustering
through manifold learning algorithm retrieves a hier-
archical agglomerative average-linkage cluster (Sax-
ena et al., 2017) taking advantage of the enhanced
ranked lists, obtained by the manifold learning algo-
rithm described on Section 3.2, to deliver a more ef-
fective clustering of the dataset.
4 ANOMALY DETECTION
In this work, we propose an anomaly detection frame-
work which employs a clustering technique as a pre-
processing step in order to improve the results of
background segmentators. This is accomplished by
clustering a set of frames that correspond to normality
and should be provided for training of the background
segmentator strategies.
The proposed clustering approach is applied for
detecting anomalies in videos considering the work-
flow presented in Figure 2. First, we take all the video
frames and provide them as input for a convolutional
neural network pre-trained on the ImageNet and ex-
tract features for every frame (in this work, we used
the AlexNet (Krizhevsky et al., 2012) model). These
features are clustered by our approach in two different
clusters.
The following task is to decide which cluster
refers to normality. Since the largest cluster does not
necessarily refer to the normality, we use some la-
beled frames (around 10) to decide about its class,
which makes our approach semi-supervised when ap-
plied to anomaly detection. The cluster that has most
of the frames that are labeled as normal is adopted as
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
408

the normality cluster and the other one as the abnor-
mality cluster. The mean image of the frames in both
clusters highlights the difference between them.
Finally, the frames classified as normal are pro-
vided as input for a background subtraction approach
(e.g., MOG, MOG2, kNN). With the normality infor-
mation provided by the cluster we can make the sub-
tractor even more effective when applied to the video
frame as shown in the next section.
5 EXPERIMENTAL EVALUATION
The experimental analysis considered three differ-
ent image datasets: (i) MPEG-7, 1400 images, 70
classes (Latecki et al., 2000); (ii) Flowers, 1360 im-
ages, 17 classes (Nilsback and Zisserman, 2006); and
(iii) Corel5k, 5000 images, 50 classes (Liu and Yang,
2013).
In order to evaluate our approach for anomaly de-
tection in videos, we used the ChangeDetection 2014
(CD2014) (Wang et al., 2014) dataset, which is com-
posed of 11 video categories with 4 to 6 video se-
quences in each category, given a total of 53 videos.
All the videos consist in the task of foreground seg-
mentation given a background frame (that can be
static, dynamic or even present shadow or luminance
variations, for example).
For all the experiments, we considered c
k
= 3 and
k = 50, except for MPEG-7, where k = 15 was used
based on the lower class size presented by the dataset.
For the compared clustering methods, the number of
cluster was defined to the exact number of classes in
the dataset and the Euclidean distance was used.
For evaluating the accuracy and robustness of
the proposed approach, we used different exter-
nal measures: Precision, Recall, F-Measure (Sax-
ena et al., 2017), Adjusted Rand Index (ARI) (Hu-
bert and Arabie, 1985), Normalized Mutual Infor-
mation (NMI) (Strehl and Ghosh, 2002; Kuncheva
and Vetrov, 2006), and V-Measure (Rosenberg and
Hirschberg, 2007). In this work, the true positives,
false positives, true negatives, and false negatives
were computed considering all the possible pairs of
the available dataset elements. The true positives, for
example, were computed as the number of all the pos-
sible pairs where two elements belong to the same
class.
Our approach was employed on traditional clus-
tering tasks and video anomaly detection. We also
provided some visualization results.
5.1 Clustering Evaluation
The proposed clustering approach was evaluated in
comparison to different clustering approaches (k-
Means, Agglomerative, FINCH, AffinityPropagation)
considering different effectiveness measures. Table 2
presents the results for image datasets. It can be seen
that our results are better or comparable to the base-
lines in most cases.
Table 2: Results for external measures on image datasets
considering predefined parameters.
Dataset Desc. Method F-Meas. ARI NMI V-Meas.
MPEG-7
CFD
Agglom. 0.5131 0.5042 0.9043 0.8676
FINCH 0.4745 0.4650 0.8707 0.8372
Aff. Prop. 0.0353 0.0089 0.6632 0.1924
ReckNN 0.9104 0.9091 0.9699 0.9676
ASC
Agglom. 0.6060 0.5994 0.9143 0.8881
FINCH 0.6347 0.6286 0.9152 0.8752
Aff. Prop. 0.0622 0.0374 0.6103 0.3582
ReckNN 0.8269 0.8243 0.9660 0.9530
Flowers
ACC
K-Means 0.1780 0.1250 0.2844 0.2822
Agglom. 0.1458 0.0744 0.2519 0.2320
FINCH 0.1095 0.0031 0.3366 0.2040
Aff. Prop. 0.0817 0.0628 0.5008 0.3876
ReckNN 0.1890 0.1355 0.2912 0.2863
ResNet
K-Means 0.6205 0.5967 0.7375 0.7356
Agglom. 0.4380 0.3941 0.6661 0.6235
FINCH 0.2166 0.1306 0.6530 0.5145
Aff. Prop. 0.2973 0.2808 0.8335 0.6590
ReckNN 0.6582 0.6363 0.7727 0.7684
Corel5k
ACC
K-Means 0.2206 0.2041 0.4739 0.4708
Agglom. 0.1462 0.1215 0.4237 0.3895
FINCH 0.0831 0.0490 0.4856 0.3625
Aff. Prop. 0.1335 0.1268 0.6382 0.5359
ReckNN 0.2469 0.2320 0.4987 0.4931
ResNet
K-Means 0.7735 0.7687 0.8956 0.8903
Agglom. 0.4765 0.4625 0.8309 0.7859
FINCH 0.4098 0.3916 0.9006 0.8131
Aff. Prop. 0.3269 0.3217 0.9304 0.7753
ReckNN 0.8300 0.8266 0.9136 0.9073
For a better understanding of how our approach
performs compared to the methods already proposed,
we provide a visual analysis for the different cluster-
ing methods considered in this work. In this analysis,
we considered three different toy datasets that contain
samples which can be represented in a 2D space: from
(Fr
¨
anti and Sieranoja, 2018), we considered the two
datasets “Spirals” and “Jain” from the “Shape Sets”
category. We also considered a synthetically gen-
erated “Two Circles” pattern, which consists in two
concentric circles.
In the first experiment, we applied an agglomera-
tive average-linkage clustering method on the gener-
ated “Two Circles” dataset points. In order to show
the impact of the manifold learning, we used the dis-
tance measures calculated by the manifold learning
step of our approach as input to the same agglomer-
ative clustering method. The results are presented in
Figure 4. The agglomerative average-linkage cluster-
ing method was not able to separate the classes cor-
Manifold Learning-based Clustering Approach Applied to Anomaly Detection in Surveillance Videos
409

Spiral Jain Two-Circles
K-Means
Spectral
Birch
ReckNN
Figure 3: Visual clustering results for different methods (rows) and datasets (columns).
(a) Original (b) Manifold learning
Figure 4: Manifold learning application on Two Circles
dataset for agglomerative average-linkage clustering.
rectly with the original points. However, when apply-
ing the clustering pre-processing, the agglomerative
method performs the clusterization correctly.
For the second experiment, Figure 3 presents the
results for four different methods and the three toy
datasets considered. Each data sample is represented
by a dot in the graph, the colors correspond to the
assigned cluster and each line on the figure represents
a different clustering method. Notice that the colors
can change based on the cluster where the points were
assigned, but the separation can be the same.
The results show that our approach (ReckNN) was
capable of separating the three datasets correctly and
is equal to the expected groundtruth. K-means was
not able to separate any of the datasets correctly be-
cause it relies on the election of cluster centroids and
the partition of the data around them, not being capa-
ble of work with those types of clusters. Spectral is
a graph based clustering method that was able to sep-
arate the “Spirals” and “Jain” datasets, but was not
able to separate the “Two Circles” dataset. Birch is a
hierarchical agglomerative method, which could only
separate correctly the “Jain” dataset with the average-
linkage measure.
5.2 Anomaly Detection
The proposed approach was applied to classify the
video frames into two different groups: normality and
abnormality. For the groundtruth, we consider that a
frame contains abnormality if it has at least one abnor-
mal pixel. Table 4 presents the results for our method
considering this scenario. The results are reported for
each category and for all the videos. Notice that our
approach is very effective in scenarios of dynamic
background (F-Measure of 90.45%) and less effec-
tive for the categories thermal and turbulence. Be-
sides that, we still achieved an average F-Measure of
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
410

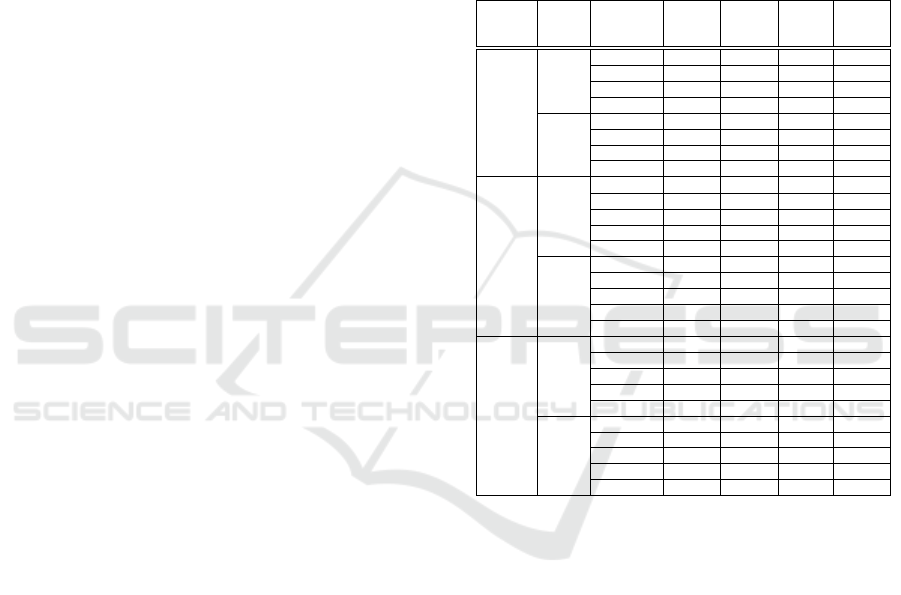
Table 3: F-Measure (%) considering a pixel classification on the CD2014 dataset.
Video Category
MOG MOG2 kNN
Original + ReckNN Gain Original + ReckNN Gain Original + ReckNN Gain
PTZ 03.04 07.43 +144.41% 08.27 08.15 -1.45% 40.54 40.74 +0.49%
badWeather 15.57 43.26 +177.84% 46.58 48.76 +4.68% 41.93 42.14 +0.50%
baseline 55.24 75.67 +36.98% 57.29 57.80 +0.89% 61.37 61.58 +0.34%
cameraJitter 19.86 34.01 +71.25% 35.04 35.89 +2.43% 40.77 41.51 +1.82%
dynamicBackground 29.11 38.41 +31.95% 32.11 32.35 +0.75% 29.49 30.27 +2.65%
intermittentObjectMotion 09.50 09.16 -3.58% 08.85 08.23 -7.01% 24.43 24.45 +0.08%
lowFramerate 03.93 20.80 +429.26% 19.52 19.52 +0.00% 53.85 54.52 +1.24%
nightVideos 03.49 05.44 +55.87% 05.76 05.77 +0.17% 39.08 39.19 +0.28%
shadow 43.10 47.63 +10.51% 56.80 50.55 -11.01% 52.84 53.00 +0.30%
thermal 31.56 63.13 +100.03% 59.33 56.96 -4.00% 25.09 25.26 +0.68%
turbulence 23.94 46.05 +92.36% 17.61 20.12 +14.25% 21.88 22.26 +1.74%
Video Mean 25.38 34.50 +35.93% 31.22 30.70 -1.69% 38.53 38.85 +0.83%
Table 4: Frame classification on the CD2014 dataset.
Video Category Effectiveness Results (%)
Prec. Recall F-Measure
PTZ 49.5470 84.4237 59.8211
badWeather 88.2413 83.4106 85.7288
baseline 87.9231 49.7181 61.2019
cameraJitter 83.9073 66.9326 73.6511
dynamicBackground 97.1419 84.9615 90.4595
intermittentObjectMotion 90.1273 55.2816 63.3464
lowFramerate 70.4134 89.4819 73.4952
nightVideos 78.5681 70.9663 74.1175
shadow 97.6668 54.1271 67.2922
thermal 100.00 39.1372 52.8663
turbulence 55.3361 68.0135 53.7700
Video Mean 83.4433 67.0873 69.1754
69.18% considering all the dataset videos.
The results for foreground segmentation consider-
ing the evaluation pixel-by-pixel (F-Measure) is pre-
sented in Table 3. It compares the original back-
ground subtractors with and without the use of our
approach as a pre-processing step. The results evince
that our method can be used to increase the original
results by a significant margin, but it depends on the
subtractor being used. Gains up to +35.93% were
achieved considering the average of all the videos for
the MOG subtractor. However, the clustering pre-
processing achieved a loss of -1.69% for MOG2 due
to the results obtained in the shadow category. These
values indicate that the clustering pre-processing have
not worked for shadow videos when combined with
MOG2. In most cases, our approach provided signifi-
cant gains in relation to the original results.
6 CONCLUSION
In this work, we have presented an approach for unsu-
pervised data clustering evaluated in different appli-
cations. We achieved results that are better or com-
parable to the other classic clustering methods for
different external measures on image datasets. Be-
sides that, the method was also applied for cluster-
ing of video frames aiming at building a more robust
normality (background) model improving the orig-
inal background subtraction approaches. As a fu-
ture work, we intend to improve the parameter esti-
mations, apply the pre-clustering step to other fore-
ground segmentation approaches, as well to deter-
mine a heuristic approach to analyse the cluster cre-
ation process in order to remove arbitrary parameters
from the algorithm.
ACKNOWLEDGEMENTS
The authors are grateful to the S
˜
ao Paulo Re-
search Foundation - FAPESP (#2013/07375-0,
#2014/12236-1, #2017/25908-6, #2018/15597-6,
#2018/21934-5, #2019/07825-1, and #2019/02205-
5), the Brazilian National Council for Scientific and
Technological Development - CNPq (#308194/2017-
9, #307066/2017-7, and #427968/2018-6), and
Petrobras (#2017/00285-6).
REFERENCES
Bouwmans, T. and Garcia-Garcia, B. (2019). Background
subtraction in real applications: Challenges, current
models and future directions. CoRR, abs/1901.03577.
Chalapathy, R. and Chawla, S. (2019). Deep learning for
anomaly detection: A survey. CoRR, abs/1901.03407.
Fr
¨
anti, P. and Sieranoja, S. (2018). K-means properties
on six clustering benchmark datasets. Applied Intel-
ligence, 48(12):4743–4759.
Gong, D., Liu, L., Le, V., Saha, B., Mansour,
M. R., Venkatesh, S., and van den Hengel, A.
(2019). Memorizing normality to detect anomaly:
Memory-augmented deep autoencoder for unsuper-
vised anomaly detection. CoRR, abs/1904.02639.
Hubert, L. and Arabie, P. (1985). Comparing partitions.
Journal of Classification, 2(1):193–218.
Jain, A. K. (2010). Data clustering: 50 years beyond k-
means. Pattern Recognition Letters, 31(8):651 – 666.
Manifold Learning-based Clustering Approach Applied to Anomaly Detection in Surveillance Videos
411

KaewTraKulPong, P. and Bowden, R. (2002). An Im-
proved Adaptive Background Mixture Model for Real-
time Tracking with Shadow Detection, pages 135–144.
Springer US, Boston, MA.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).
Imagenet classification with deep convolutional neu-
ral networks. In Proceedings of the 25th Interna-
tional Conference on Neural Information Processing
Systems - Volume 1, NIPS’12, pages 1097–1105.
Kuncheva, L. I. and Vetrov, D. P. (2006). Evaluation of
stability of k-means cluster ensembles with respect
to random initialization. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 28(11):1798–
1808.
Latecki, L. J., Lakamper, R., and Eckhardt, U. (2000).
Shape descriptors for non-rigid shapes with a single
closed contour. In CVPR, pages 424–429.
Lawson, W., Hiatt, L., and Sullivan, K. (2016). Detecting
anomalous objects on mobile platforms. In 2016 IEEE
Conference on Computer Vision and Pattern Recogni-
tion Workshops (CVPRW), pages 1426–1433.
Li, H., Achim, A., and Bull, D. (2012). Unsupervised video
anomaly detection using feature clustering. Signal
Processing, IET, 6:521–533.
Liu, G.-H. and Yang, J.-Y. (2013). Content-based image
retrieval using color difference histogram. Pattern
Recognition, 46(1):188 – 198.
Nilsback, M.-E. and Zisserman, A. (2006). A visual vo-
cabulary for flower classification. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition, volume 2, pages 1447–1454.
Pedronette, D. C. G., Gonc¸alves, F. M. F., and Guilherme,
I. R. (2018). Unsupervised manifold learning through
reciprocal knn graph and connected components for
image retrieval tasks. Pattern Recognition, 75:161 –
174. Distance Metric Learning for Pattern Recogni-
tion.
Ros, F. and Guillaume, S. (2019). Munec: a mutual
neighbor-based clustering algorithm. Information Sci-
ences, 486:148–170.
Rosenberg, A. and Hirschberg, J. (2007). V-measure: A
conditional entropy-based external cluster evaluation
measure. In Proceedings of the 2007 Joint Confer-
ence on Empirical Methods in Natural Language Pro-
cessing and Computational Natural Language Learn-
ing (EMNLP-CoNLL), pages 410–420, Prague, Czech
Republic. Association for Computational Linguistics.
Sarfraz, S., Sharma, V., and Stiefelhagen, R. (2019). Effi-
cient parameter-free clustering using first neighbor re-
lations. In The IEEE Conference on Computer Vision
and Pattern Recognition (CVPR).
Saxena, A., Prasad, M., Gupta, A., Bharill, N., Patel, O. P.,
Tiwari, A., Er, M. J., Ding, W., and Lin, C.-T. (2017).
A review of clustering techniques and developments.
Neurocomputing, 267:664 – 681.
Sodemann, A. A., Ross, M. P., and Borghetti, B. J.
(2012). A review of anomaly detection in automated
surveillance. IEEE Transactions on Systems, Man,
and Cybernetics, Part C (Applications and Reviews),
42(6):1257–1272.
Strehl, A. and Ghosh, J. (2002). Cluster ensembles - a
knowledge reuse framework for combining partition-
ings. Journal of Machine Learning Research, 3:583–
617.
Wang, Y., Jodoin, P., Porikli, F., Konrad, J., Benezeth, Y.,
and Ishwar, P. (2014). Cdnet 2014: An expanded
change detection benchmark dataset. In 2014 IEEE
Conference on Computer Vision and Pattern Recogni-
tion Workshops, pages 393–400.
Xing, E. P., Ng, A. Y., Jordan, M. I., and Russell, S. (2002).
Distance metric learning, with application to cluster-
ing with side-information. In Proceedings of the 15th
International Conference on Neural Information Pro-
cessing Systems, NIPS’02, pages 521–528.
Zivkovic, Z. (2004). Improved adaptive gaussian mixture
model for background subtraction. In Proceedings -
International Conference on Pattern Recognition, vol-
ume 2, pages 28 – 31 Vol.2.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
412