Coarse to Fine Vertebrae Localization and Segmentation

with SpatialConﬁguration-Net and U-Net

Christian Payer

1,2 a

, Darko

Stern

1,2 b

, Horst Bischof

2 c

and Martin Urschler

1,3 d

Ludwig Boltzmann Institute for Clinical Forensic Imaging, Graz, Austria

Institute of Computer Graphics and Vision, Graz University of Technology, Graz, Austria

School of Computer Science, The University of Auckland, Auckland, New Zealand

Keywords:

Vertebrae Localization, Vertebrae Segmentation, SpatialConﬁguration-Net, U-Net, VerSe 2019 Challenge.

Abstract:

Localization and segmentation of vertebral bodies from spine CT volumes are crucial for pathological diagno-

sis, surgical planning, and postoperative assessment. However, fully automatic analysis of spine CT volumes

is difﬁcult due to the anatomical variation of pathologies, noise caused by screws and implants, and the large

range of different ﬁeld-of-views. We propose a fully automatic coarse to ﬁne approach for vertebrae localiza-

tion and segmentation based on fully convolutional CNNs. In a three-step approach, at ﬁrst, a U-Net localizes

the rough position of the spine. Then, the SpatialConﬁguration-Net performs vertebrae localization and identi-

ﬁcation using heatmap regression. Finally, a U-Net performs binary segmentation of each identiﬁed vertebrae

in a high resolution, before merging the individual predictions into the resulting multi-label vertebrae segmen-

tation. The evaluation shows top performance of our approach, ranking ﬁrst place and winning the MICCAI

2019 Large Scale Vertebrae Segmentation Challenge (VerSe 2019).

1 INTRODUCTION

Localization and segmentation of vertebral bodies

from spinal CT volumes is a crucial step for many

clinical applications involving the spine, e.g., patho-

logical diagnosis (Forsberg et al., 2013), surgical

planning (Knez et al., 2016), and postoperative as-

sessment (Amato et al., 2010). Due to the highly

repetitive structure of vertebrae, large variation in the

appearance of different pathologies including frac-

tures and implants, as well as different ﬁeld-of-views,

most methods for localizing and segmenting vertebral

bodies are based on machine learning. As both local-

ization and segmentation are difﬁcult tasks on their

own, the majority of proposed methods focus on only

one task.

For the task vertebrae localization, or more gen-

erally anatomical landmark localization, a widely

used way of incorporating global shape informa-

tion is to use statistical shape models (Cootes et al.,

1995). (Lindner et al., 2015) extend upon this strat-

https://orcid.org/0000-0002-5558-9495

https://orcid.org/0000-0003-3449-5497

https://orcid.org/0000-0002-9096-6671

https://orcid.org/0000-0001-5792-3971

egy by using a constrained local model that itera-

tively reﬁnes global landmark conﬁguration on top

of local feature responses generated from random

forests. (Glocker et al., 2012) have combined ran-

dom forests with graphical models based on Markov

random ﬁeld restricting the responses to only feasi-

ble locations. In addition to extending their method,

(Glocker et al., 2013) have introduced the MICCAI

CSI 2014 Vertebrae Localization and Identiﬁcation

Challenge dataset, which has been used as a bench-

mark for localizing and identifying vertebrae in spinal

CT volumes. Although a lot of research has focused

on improving landmark localization methods incor-

porating random forests (Ebner et al., 2014; Lindner

et al., 2015; Bromiley et al., 2016; Urschler et al.,

2018), due to the advances of deep learning (Le-

Cun et al., 2015), most recent best-performing meth-

ods for anatomical landmark localization are based

on convolutional neural networks (CNNs). (Chen

et al., 2015) proposed a framework that combines

random forest used for coarse landmark localiza-

tion, a shape model incorporating the information of

neighboring landmarks for reﬁning their positions,

and CNNs for identiﬁcation of landmarks. How-

ever, their proposed method does not use the full

potential of CNNs, as they are only used for iden-

124

Payer, C., Štern, D., Bischof, H. and Urschler, M.

Coarse to Fine Vertebrae Localization and Segmentation with SpatialConﬁguration-Net and U-Net.

DOI: 10.5220/0008975201240133

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages

124-133

ISBN: 978-989-758-402-2; ISSN: 2184-4321

tiﬁcation, not for localization. In the related com-

puter vision task human pose estimation, (Toshev and

Szegedy, 2014) introduced CNNs to regress coor-

dinates of landmarks. However, regressing the co-

ordinates directly involves a highly nonlinear map-

ping from input images to point coordinates (Pﬁs-

ter et al., 2015). Instead of regressing coordinates,

(Tompson et al., 2014) proposed a simpler, image-

to-image mapping based on regressing heatmap im-

ages, which encode the pseudo-probability of a land-

mark being located at a certain pixel position. Us-

ing the heatmap regression framework for anatomical

landmark localization, (Payer et al., 2016) proposed

the SpatialConﬁguration-Net (SC-Net) that integrates

spatial information of landmarks directly into an end-

to-end trained, fully-convolutional network. Building

upon (Payer et al., 2016), (Yang et al., 2017) gen-

erate predictions for vertebral landmarks with miss-

ing responses, by incorporating a pre-trained model

of neighboring landmarks into their CNN. Recently,

(Mader et al., 2019) adapted the heatmap regression

networks for predicting more than a hundred land-

marks on a dataset of spinal CT volumes. (Liao

et al., 2018) proposed a three stage method for verte-

brae identiﬁcation and localization. They pre-train a

network to classify and localize vertebrae simultane-

ously, use the learned weights to generate responses

with a fully convolutional network, and ﬁnally re-

move false-positive responses with a bidirectional re-

current neural network. To reduce the amount of in-

formation that needs to be processed, (Sekuboyina

et al., 2018) proposed to project the 3D information

of spine anatomy into 2D sagittal and coronal views,

and solely use these views as input for their 2D CNN

for vertebrae identiﬁcation and localization. How-

ever, due to this projection, beneﬁcial volumetric in-

formation may be lost. Very recently, (Payer et al.,

2019) improved their volumetric fully convolutional

SC-Net, outperforming other methods on the dataset

of the MICCAI CSI 2014 Vertebrae Localization and

Identiﬁcation Challenge (Glocker et al., 2013).

For the task vertebrae segmentation, due to the

speciﬁc shape of vertebrae, many methods incorpo-

rate models of their shape. Using statistical shape

models, (Klinder et al., 2009) introduce a multi-

stage approach for identifying and segmenting ver-

tebral bodies. (Hammernik et al., 2015) use the

mean shape of a vertebra as initialization for their

convex variational framework. Other methods mod-

eling the vertebra shape include superquadric mod-

els (

Stern et al., 2011), models based on game the-

ory (Ibragimov et al., 2014), as well as atlas-based

models (Wang et al., 2016). Similar to vertebrae lo-

calization, recently, machine learning approaches are

Vertebrae

Localization

Spine

Localization

Vertebrae

Segmentation

F A, C  F

Figure 1: Overview of our proposed coarse to ﬁne fully au-

tomatic vertebrae localization, identiﬁcation, and segmenta-

tion. The three-step approach works for spine CT volumes

having a large range of different ﬁeld-of-views, as well as

pathologies.

predominantly used for vertebrae segmentation, due

to the large variation of the appearance and patholo-

gies in clinical CT volumes of the spine. (Chu et al.,

2015) proposed to use random forests for identify-

ing the centroids of vertebral bodies. These centroids

are then used to restrict another random forest that

performs voxelwise labeling and segmentation of the

vertebral body. Coupling shape models with CNNs,

(Korez et al., 2016) use the outputs of a CNN as prob-

ability maps for a deformable surface model to seg-

ment vertebral bodies. Evaluated on the challenging

MICCAI 2016 xVertSeg dataset identifying and seg-

menting lumbar vertebrae, (Sekuboyina et al., 2017)

and (Janssens et al., 2018) use similar two stage ap-

proaches to ﬁrst localize a bounding box around the

lumbar region, and then to perform a multi-label seg-

mentation of the vertebrae within this region. How-

ever, as the xVertSeg dataset is only used for seg-

menting the ﬁve lumbar vertebrae, these methods are

not designed for spinal CT images that have a vary-

ing number of visible vertebrae. A different approach

was introduced by (Lessmann et al., 2019), who use a

single network to use instance segmentation of all ver-

tebrae. By traversing the spinal column with a sliding

window, they propose to segment each vertebra at a

time, while the network incorporates information of

Coarse to Fine Vertebrae Localization and Segmentation with SpatialConﬁguration-Net and U-Net

125

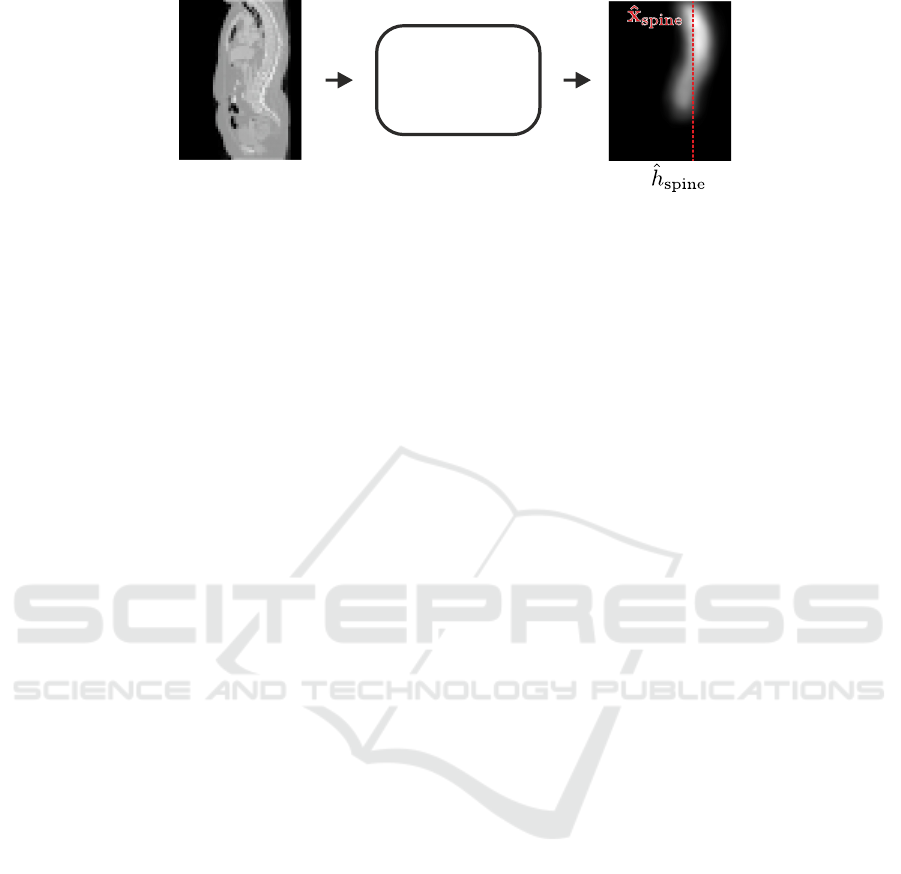
Spine

Localization

U-Net

Network Input

Figure 2: Input volume and the predicted spine heatmap

spine

of the spine localization network. The predicted coordi-

nate

spine

is the x and y coordinate of the center of mass of

spine

already segmented vertebrae.

Our main contributions presented in this paper are:

• We developed a coarse to ﬁne fully automatic

method for localization, identiﬁcation, and seg-

mentation of vertebrae in spine CT volumes. We

ﬁrst roughly localize the spine, then localize and

identify individual vertebrae, and ﬁnally segment

each vertebra in high resolution.

• We tackle the challenging problem of simultane-

ously segmenting and labeling vertebrae in the

presence of highly repetitive structures by doing

the localization and identiﬁcation step ﬁrst, and

then doing a binary segmentation of individually

identiﬁed vertebrae.

• We perform evaluation and comparison to state-

of-the-art methods on the MICCAI 2019 Large

Scale Vertebrae Segmentation Challenge (VerSe

2019), involving real-world conditions concern-

ing image composition and pathologies. Our pro-

posed method achieves top performance, ranking

ﬁrst place and winning the VerSe 2019 challenge.

2 METHOD

We perform vertebrae localization and segmentation

in a three-step approach (see Fig. 1). Firstly, due to

the large variation of the ﬁeld-of-view of the input CT

volumes, a CNN with a coarse input resolution pre-

dicts the approximate location of the spine. Secondly,

another CNN in higher resolution performs multiple

landmark localization and identiﬁcation of the indi-

vidual vertebra centroids. Lastly, the segmentation

CNN in the highest resolution performs a binary seg-

mentation of each localized vertebra. The results of

the individually segmented vertebrae are then merged

into the ﬁnal multi-label segmentation.

2.1 Spine Localization

Due to the varying ﬁeld-of-view, spine CT volumes

often contain lots of background that does not con-

tain useful information, while the spine may not be in

the center of the volume. To ensure that the spine is

centered at the input for the subsequent vertebrae lo-

calization step, as a ﬁrst step, we predict the approxi-

mate x and y coordinates

spine

∈ R

of the spine. For

localizing

spine

, we use a variant of the U-Net (Ron-

neberger et al., 2015) to perform heatmap regres-

sion (Tompson et al., 2014; Payer et al., 2016) of

the spinal centerline, i.e., the line passing through

all vertebral centroids. The target heatmap vol-

ume

∗

spine

(x;σ

spine

) : R

→ R of the spinal center-

line is generated by merging Gaussian heatmaps with

size σ

spine

of all individual vertebrae target coordi-

nates

∗

into a single volume (see Fig. 2). We use the

L2-loss to minimize the difference between the tar-

get heatmap volume

∗

spine

and the predicted heatmap

volume

spine

(x) : R

→ R. The ﬁnal predicted spine

coordinate

spine

is the x and y coordinate of the center

of mass of

spine

Our variant of the U-Net is adapted such that it

performs average instead of max pooling and linear

upsampling instead of transposed convolutions. It

uses ﬁve levels where each convolution layer has a

kernel size of [3×3×3] and 64 ﬁlter outputs. Further-

more, the convolution layers use zero padding such

that the network input and output sizes stay the same.

Before processing a spine CT volume, it is resam-

pled to a uniform voxel spacing of 8 mm and centered

at the network input. The network input resolution is

[64 × 64×128], which allows spine CT volumes with

an extent of up to [512 × 512 × 1024] mm to ﬁt into

the network input. This extent was sufﬁcient for the

network to predict x

spine

for all spine CT volumes of

the evaluated dataset.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

126

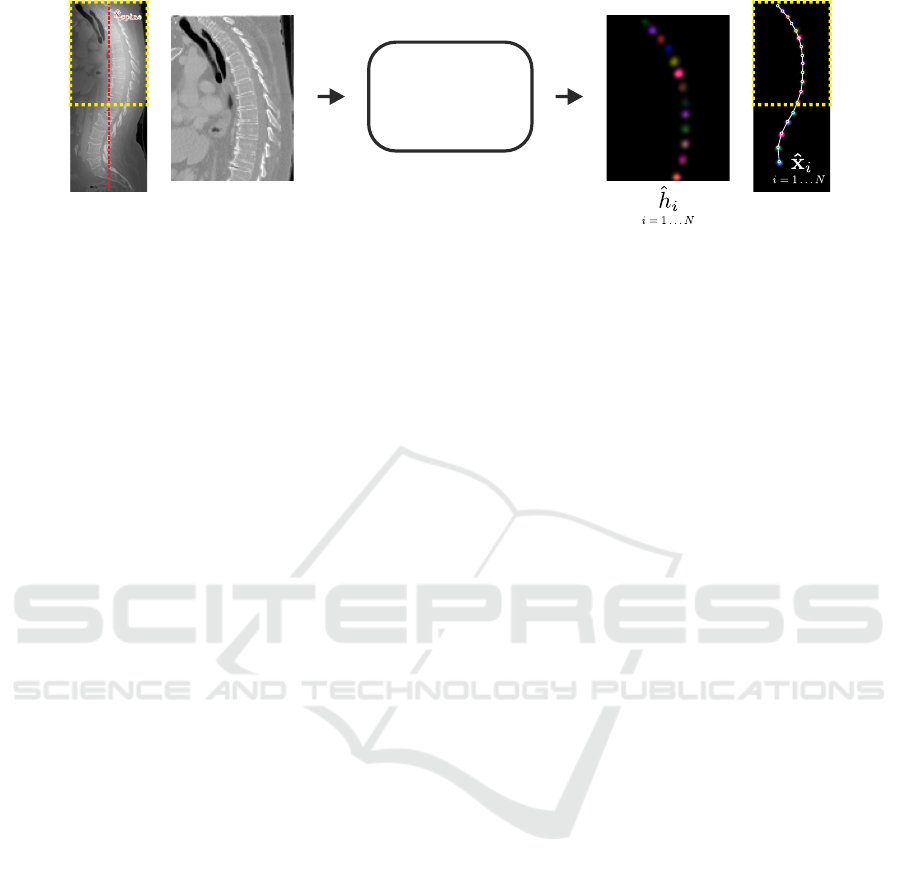
Vertebrae

Localization

SC-Net

Network Input

Figure 3: Input volume and individual heatmap predictions of the vertebrae localization network. The yellow rectangle

indicates that not the whole input volume is processed at once, but overlapping cropped sub-volumes that are centered at

spine

The network predicts simultaneously N heatmaps, i.e., a single heatmap

for each individual vertebrae v

. For visualization,

the predicted heatmaps are colored individually and combined into a single image. The ﬁnal landmark coordinates

are

identiﬁed as the longest sequence of local maxima of

that does not violate anatomical constraints.

2.2 Vertebrae Localization

To localize centers of the vertebral bodies, we

use the SpatialConﬁguration-Net (SC-Net) proposed

in (Payer et al., 2019). The network effectively com-

bines the local appearance of landmarks with their

spatial conﬁguration. The local appearance part of

the network uses ﬁve levels consisting of two convo-

lution layers before downsampling to the lower level,

and two convolution layers after concatenating with

the upsampled lower level. Each convolution layer

uses a leaky ReLU activation function and has a ker-

nel size of [3 ×3×3] and 64 ﬁlter outputs. The spatial

conﬁguration part consists of four convolutions with

[7 × 7 × 7] kernels in a row and is processed in one

fourth of the resolution of the local appearance part.

The SC-Net performs heatmap regression of the N

target vertebrae v

with i = 1 . . . N, i.e., each target

coordinate

∗

is represented as a Gaussian heatmap

volume

∗

(x;σ

) : R

→ R centered at

∗

. For N tar-

get vertebrae v

, the network predicts simultaneously

all N output heatmap volumes

(x) : R

→ R. As loss

function, we use a modiﬁed L2-loss function, which

also allows learning of the individual σ

values for the

target Gaussian heatmap volumes

∗

L =

∑

i=1

∑

(x) −

∗

(x;σ

+ αkσ

. (1)

For more details of the network architecture and loss

function, we refer to (Payer et al., 2019).

A schematic representation of how the input vol-

umes are processed to predict all heatmaps

is shown

in Fig. 3. Each network input volume is resampled

to have a uniform voxel spacing of 2 mm, while the

network is set up for inputs of size [96 × 96 × 128],

which allows volumes with an extent of [192× 192 ×

256] mm to ﬁt into the network. With this extent,

many images of the dataset do not ﬁt into the net-

work and cannot be processed at once. To narrow the

processed volume to the approximate location of the

spine, we center the network input at the predicted

spine coordinate

spine

(see Sec. 2.1). Furthermore,

as some spine CT volumes have a larger extent in the

z-axis (i.e., the axis perpendicular to the axial plane)

that would not ﬁt into the network, we process such

volumes the same way as proposed by (Payer et al.,

2019). During training, we crop a subvolume at a ran-

dom position at the z-axis. During inference, we split

the volumes at the z-axis into multiple subvolumes

that overlap for 96 pixels, and process them one after

another. Then, we merge the network predictions of

the overlapping subvolumes by taking the maximum

response over all predictions.

We predict the ﬁnal landmark coordinates

x as fol-

lows: For each predicted heatmap volume, we detect

multiple local heatmap maxima that are above a cer-

tain threshold. Then, we determine the ﬁrst and last

vertebrae that are visible on the volume by taking the

heatmap with the largest value that is closest to the

volume top or bottom, respectively. We identify the

ﬁnal predicted landmark sequence by taking the se-

quence that does not violate the following conditions:

consecutive vertebrae may not be closer than 12.5 mm

and farther away than 50 mm, as well as the following

landmark may not be above a previous one.

2.3 Vertebrae Segmentation

For creating the ﬁnal vertebrae segmentation, we use

a U-Net (Ronneberger et al., 2015) set up for binary

segmentation to separate a vertebra from the back-

ground (see Fig. 4). The ﬁnal semantic label of a

vertebra is identiﬁed through the localization label as

predicted by the vertebrae localization network (see

Sec. 2.2). Hence, we use a single network for all

Coarse to Fine Vertebrae Localization and Segmentation with SpatialConﬁguration-Net and U-Net

127

Vertebrae

Segmentation

U-Net

Network Input

Figure 4: Input volume and segmented vertebrae of the spine segmentation network. The yellow rectangle shows the cropped

region around a single vertebrae v

and indicates that each localized vertebra

is processed individually. Each individual

vertebra sigmoid prediction

is then transformed and resampled back to the original position. The ﬁnal multi-label segmen-

tation

ﬁnal

is obtained by setting the label at each voxel to the label of

that has the largest response.

vertebrae v

, as the network does not need to iden-

tify, which vertebra it is segmenting, but it only needs

to separate each vertebra individually from the back-

ground.

Since each vertebra is segmented independently,

the network needs to know, which vertebra it should

segment in the input volume. Thus, from the whole

spine CT image, we crop the region around the lo-

calized vertebra, such that the vertebra is in the

center of the cropped image. During training, we

use the ground-truth vertebra location

∗

, while dur-

ing inference, we use the predicted vertebra coordi-

nate

. Additionally, we create an image of a Gaus-

sian heatmap centered at the vertebra coordinate

Both the cropped and the heatmap image are used

as an input for the segmentation U-Net. The U-Net

is modiﬁed as described in Sec. 2.1. It is set up to

predict a single output volume

(x) : R

→ (0, 1),

while the sigmoid cross-entropy loss is minimized

to generate predictions close to the target binary la-

bel volume

∗

(x) : R

→ {0, 1}. The input volumes

are resampled to have a uniform voxel spacing of

1 mm, while the network is set up for inputs of size

[128 × 128 × 96], which allows volumes with an ex-

tent of [128 ×128 × 96] mm.

To create the ﬁnal multi-label segmentation result,

the individual predictions of the cropped vertebra in-

puts need to be merged. Therefore, the sigmoid out-

put volumes

of each cropped vertebrae i are trans-

formed and resampled back to their position in the

original input volume. Then, for each voxel in the ﬁ-

nal label image

ﬁnal

(x) : R

→ {0 . . . N}, the predicted

label is set to the label i of the vertebra that has the

largest sigmoid response. If for a pixel no vertebra

prediction

has a response > 0.5, the pixel is set to

be the background.

3 EVALUATION

We evaluate our proposed framework for multi-label

spine localization and segmentation on the dataset of

the VerSe 2019 challenge

. The dataset consists of

spine CT volumes of subjects with various patholo-

gies, where every fully visible vertebra from C1 to

L5 is annotated. As some subjects contain the addi-

tional vertebra L6, at maximum N = 25 vertebrae are

annotated. The training set consists of 80 spine CT

volumes with corresponding ground-truth centroids

∗

and segmentations

∗

for each vertebra v

The VerSe 2019 challenge contains two test sets.

The ﬁrst test set consists of 40 publicly available spine

CT volumes with hidden annotations. The partici-

pants of the challenge had to submit the predictions

on the ﬁrst test set to the evaluation servers, which

did in turn evaluate and rank the submitted results on

a public leaderboard. The second test set consists of

an additional 40 hidden spine CT volumes. To ob-

tain evaluation results on the second test set, the chal-

lenge participants had to submit a Docker image of

the proposed method that creates the predictions. The

organizers of the challenge then performed an inter-

nal evaluation on the hidden second test set. The ﬁnal

rank of each participant of the VerSe 2019 challenge

is deﬁned by the performance on the 80 CT volumes

of both test sets and was announced at the workshop

of MICCAI 2019 (Sekuboyina, 2019).

3.1 Implementation Details

Training and testing of the network were done in Ten-

sorﬂow

, while we perform on-the-ﬂy data prepro-

https://verse2019.grand-challenge.org/

https://www.tensorﬂow.org/

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

128

Table 1: Results of a three-fold cross-validation on the VerSe 2019 challenge training set consisting of 80 volumes. The table

shows results grouped by cervical, thoracic, and lumbar vertebrae, as well as results for all vertebrae combined.

Vertebrae v

(in mm)

mean ± SD

% (#identiﬁed of #total)

Dice

mean ± SD

(in mm)

mean ± SD

Cervical (i = C1 . . . C7) 7.45 ± 8.70 91.07% (102 of 112) 0.91 ± 0.10 5.88 ± 9.50

Thoracic (i = T1 . . . T12) 5.56 ± 6.31 88.99% (388 of 436) 0.93 ± 0.14 6.78 ± 16.67

Lumbar (i = L1 . . . L6) 4.48 ± 2.08 90.45% (284 of 314) 0.96 ± 0.02 6.41 ± 9.05

All (i = C1 . . . L6) 5.71 ± 6.28 89.79% (774 of 862) 0.94 ± 0.11 6.53 ± 13.49

cessing and augmentation using SimpleITK

. We per-

formed network and data augmentation hyperparam-

eter evaluation on initial cross-validation experiments

using the training set of the VerSe 2019 challenge.

All networks are trained with a mini-batch size of 1,

while the spine localization network is trained for

20,000 iterations, the vertebrae localization network

for 100,000 iterations, and the vertebrae segmenta-

tion network for 50,000 iterations. For the U-Net we

use the Adam optimizer (Kingma and Ba, 2015) with

a learning rate of 10

−4

, for the SC-Net we use the

Nesterov (Nesterov, 1983) optimizer with a learning

rate of 10

−8

. The spine and vertebrae localization net-

works use L2 weight regularization factor of 5

−4

, the

vertebrae segmentation network uses a factor of 10

−7

We set σ

spine

= 3 pixel for the spine localization net-

work; Same as in (Payer et al., 2019), we set α = 100

in (1) for learning the size σ

of the target heatmaps

∗

in the vertebrae localization network.

Due to the different orientations, each CT vol-

ume is transformed into a common orientation for

further processing. Furthermore, to reduce noise on

the input volumes, they are smoothed with a Gaus-

sian kernel with σ = 0.75 mm. To obtain an appro-

priate range of intensity values for neural networks,

each intensity value of the CT volumes is divided

by 2048 and clamped between −1 and 1. For data

augmentation during training, the intensity values are

multiplied randomly with [0.75, 1.25] and shifted by

[−0.25, 0.25]. The images are randomly translated by

[−30, 30] voxels, rotated by [−15

◦

, 15

◦

], and scaled

by [−0.85, 1.15]. We additionally employ elastic de-

formations by randomly moving points on a regular

6×6 pixel grid by 15 pixels and interpolating with 3rd

order B-splines. All augmentation operations sample

randomly from a uniform distribution within the spec-

iﬁed intervals.

Training took ≈ 3:30 h for the spine localization

network, ≈ 28:00 h for the vertebrae localization net-

work, and ≈ 12:00 h for the vertebrae segmentation

network, on an Intel Core i7-4820K workstation with

an NVIDIA Titan V running Arch Linux. The in-

ference time is dependent on the ﬁeld-of-view and

http://www.simpleitk.org/

the number of visible vertebrae on the input CT vol-

ume. On the 40 volumes of the test 1 set of the VerSe

2019 challenge, inference per volume takes on aver-

age ≈ 4:20 m, divided into ≈ 5 s for spine localiza-

tion, ≈ 45 s for vertebrae localization, and ≈ 3:30 m

for vertebrae segmentation.

3.2 Metrics

The localization performance is evaluated with two

commonly used metrics from the literature, describ-

ing localization error in terms of both local accuracy

and robustness towards landmark misidentiﬁcation.

The ﬁrst measure, the point-to-point error PE

( j)

for

each vertebra i in image j, is deﬁned as the Euclidean

distance between the target coordinate

∗

( j)

and the

predicted coordinate

( j)

. This allows calculation of

the mean and standard deviation (SD) of the point-to-

point error for all images overall or only a subset of

landmarks. The second measure, the landmark iden-

tiﬁcation rate ID

, is deﬁned as the percentage of cor-

rectly identiﬁed landmarks over all landmarks i. As

deﬁned by (Glocker et al., 2013), a predicted land-

mark is correctly identiﬁed, if the closest ground-truth

landmark is the correct one, and the distance from

predicted to ground-truth position is less than 20 mm.

The segmentation performance is also evaluated

with two commonly used metrics from the literature.

The ﬁrst measure is the Dice score Dice

( j)

for each

label i in image j, which is deﬁned as twice the car-

dinality of the intersection of ground-truth label

∗

( j)

and predicted label

( j)

divided by the sum of the car-

dinality of both ground-truth and prediction. The sec-

ond measure is the Hausdorff distance H

( j)

between

ground-truth label

∗

( j)

and predicted label

( j)

for each

label i in image j, which is deﬁned as the greatest of

all the distances from a point in one set to the closest

point in the other set. For both measures, the mean

and standard deviation for all images over all or only

a subset of labels are calculated.

Coarse to Fine Vertebrae Localization and Segmentation with SpatialConﬁguration-Net and U-Net

129

Table 2: Results on the overall VerSe 2019 challenge test set, which is comprised of 40 volumes in test 1 set and 40 volumes

in test 2 set. The table lists all methods that submitted valid localizations or segmentations, which allowed the organizers to

calculate the evaluated metrics. The predictions for vertebrae localization and segmentation of test 1 set were generated and

submitted by the participants, while the predictions of test 2 set were generated by the organizers with the submitted Docker

images. The methods are ranked as described in the VerSe 2019 challenge evaluation report (Sekuboyina, 2019). The metrics

show the mean values for all vertebrae of test 1 and test 2 set, respectively. Entries with a ”–” indicate failure of metric

calculation, because of erroneous or missing predictions, or missing Docker images.

Rank Team Score

test 1 set test 2 set

all

DSC

all

DSC

all

christian payer 0.691 95.65 4.27 0.909 6.35 94.25 4.80 0.898 7.34

iFLYTEK 0.597 96.94 4.43 0.930 6.39 86.73 7.13 0.837 11.67

nlessmann 0.496 89.86 14.12 0.851 8.58 90.42 7.04 0.858 9.01

huyujin 0.279 – – 0.847 12.79 – – 0.818 29.44

yangd05 0.216 62.56 18.52 0.767 14.09 67.21 15.82 0.671 28.76

ZIB 0.215 71.63 11.09 0.670 17.35 73.32 13.61 0.690 19.25

AlibabaDAMO 0.140 89.82 7.39 0.827 11.22 – – – –

christoph 0.107 55.80 44.92 0.431 44.27 54.85 19.83 0.464 42.85

INIT 0.084 84.02 12.40 0.719 24.59 – – – –

brown 0.022 – – 0.627 35.90 – – – –

LRDE 0.007 0.01 205.41 0.140 77.48 0.00 1000.00 0.356 64.52

3.3 Results

We evaluated our proposed framework on the

MICCAI VerSe 2019 Grand Challenge. We per-

formed a three-fold cross-validation on the publicly

available training set consisting of 80 annotated vol-

umes to evaluate the individual steps of our proposed

approach, i.e., spine localization, vertebrae localiza-

tion, and vertebrae segmentation. As the purpose of

this cross-validation is to show the performance of the

individual steps, instead of using the predictions of

the previous steps as inputs (i.e.,

spine

for vertebrae

localization, and

for vertebrae segmentation), the

networks use the ground-truth annotations as inputs

(i.e.,

∗

spine

for vertebrae localization, and

∗

for verte-

brae segmentation).

The results for the three-fold cross-validation of

the individual steps of our approach are as follows:

For spine localization, the PE

spine

mean ± SD is

4.13 ± 8.97 mm. For vertebrae localization and seg-

mentation, Table 1 shows quantitative results for the

cervical, thoracic, and lumbar vertebrae, as well as for

all vertebrae combined.

We participated in the VerSe 2019 challenge at

MICCAI 2019 to evaluate our whole fully automatic

approach and compare the performance to other meth-

ods. For this, we trained the three individual net-

works for spine localization, vertebrae localization,

and vertebrae segmentation on all 80 training images.

We performed inference on the test volumes by us-

ing the predictions from the previous step as inputs

for the next step. We submitted our predictions on

the test 1 set, as well as a Docker image for the or-

ganizers to generate predictions on the hidden test 2

set. Table 2 shows the quantitative results on the test 1

and test 2 sets of methods that submitted valid predic-

tions before the deadlines of the VerSe 2019 challenge

as announced at the challenge workshop at MICCAI

2019 (Sekuboyina, 2019). Our fully automatic ap-

proach ranked ﬁrst on the combined localization and

segmentation metrics on the overall 80 volumes of

both test sets.

4 DISCUSSION

As announced at the VerSe 2019 workshop at

MICCAI 2019, our method won the VerSe 2019

challenge. Our fully automatic vertebrae localiza-

tion and segmentation ranked ﬁrst on the 80 volumes

of both test 1 and test 2 set combined, supporting

the proposed three-step approach that combines the

SpatialConﬁguration-Net (Payer et al., 2019) and the

U-Net (Ronneberger et al., 2015) in a coarse to ﬁne

manner.

The cross-validation experiments on the 80 anno-

tated training volumes conﬁrm the good performance

of the individual steps of our proposed three-step ap-

proach (see Sec. 3.3 and Table 1). The ﬁrst stage,

the spine localization, performs well in approximat-

ing the center position of the spine, achieving a point

error PE

spine

of 4.13 mm. Visual inspection showed

only one failure case for a CT volume that is com-

pletely out of the training data distribution. This vol-

ume does not show the spine, but the whole legs. Only

in the top of the volume, a small part of the spine is

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

130

visible, speciﬁcally the two vertebrae L4 and L5.

The second stage, the vertebrae localization,

achieves a mean point error PE

all

of 5.71 mm and an

identiﬁcation rate ID

all

of 89.79% for all vertebrae.

By analyzing the individual predictions for cervical,

thoracic, and lumbar vertebrae, we see differences

among the vertebrae types. As the thoracic vertebrae

are in the middle, being far away from the visible top

or bottom of the spine, it is harder for the network

to distinguish between these vertebrae. This can be

seen in the smaller ID

thoracic

of 88.99%, as compared

to ID

cervical

= 91.07% and ID

lumbar

= 90.45%. How-

ever, having more training data of individual verte-

brae helps the networks for predicting the vertebral

centroids more accurately, which can be seen at the

smaller PE

lumbar

of 4.48 mm (on average ≈ 62 anno-

tations) as compared to PE

thoracic

= 5.56 mm (≈ 36

annotations) and PE

lumbar

= 7.45 mm (≈ 16 annota-

tions per vertebrae).

Having more annotations per vertebrae is also

beneﬁcial for the ﬁnal third stage, the vertebrae seg-

mentation. Here we can observe that again the lum-

bar vertebrae have the best performance in terms of

Dice score Dice

lumbar

= 0.96, while the Dice score de-

creases with less training data per vertebrae type, i.e.,

Dice

thoracic

= 0.93 and Dice

cervical

= 0.91. However,

for the Hausdorff metric H , we do not see notewor-

thy differences among the vertebrae types. Moreover,

the standard deviations of H are large, which indi-

cates outliers. We think that this is due to noise in the

ground-truth annotation, sometimes containing spu-

riously annotated voxels far off the actual vertebrae

region. Such misannotated isolated pixels are negli-

gible in the Dice score, but lead to large errors and

standard deviations in the Hausdorff metric.

The values on the test sets consisting of 80 vol-

umes in Table 2 demonstrate the overall performance

of our fully automatic, coarse to ﬁne approach. When

compared with the results of the cross-validation, the

localization results improved on both test sets, as can

be seen in both PE

all

= 4.27 mm and PE

all

= 4.80 mm,

as well as ID

all

= 95.65% and ID

all

= 94.25%. This

indicates that the localization network beneﬁts from

more training data (80 CT volumes in the test sets as

compared to ≈ 54 in the cross-validation), especially

due to the large variation and different pathologies in

the dataset.

For the segmentation metrics, the results on the

test sets are slightly worse as compared to the cross-

validation, i.e., Dice

all

= 0.909 and Dice

all

= 0.898, as

well as H

all

= 6.35 mm and H

all

= 7.34 mm. The rea-

son for this performance drop is that the vertebrae seg-

mentation is dependent on the vertebrae localization.

In contrast to the cross-validation, which uses the

ground-truth vertebral centroids

∗

as input to show

the performance of the segmentation network alone,

the segmentation network that generated results on

the test sets takes the predicted vertebral centroids

as input to show the performance of the whole fully

automatic approach.

When compared to other methods on both test

sets, our method achieves the overall best perfor-

mance. There exists a large gap between our method

and the next best ranking methods in both localiza-

tion and segmentation performance. However, when

looking at the individual test sets, we can see that in

test 1 set the second-best method has a better ID

all

and

Dice

all

as compared to our method, while our method

has a better PE

all

and H

all

. Nevertheless, in test 2 set

the second-best method has a performance drop in all

evaluation metrics, while the results from our method

are stable. The better performance on the hidden test 2

set shows the good generalization capabilities of our

method, enabling it to surpass all other methods and

to win the VerSe 2019 challenge.

5 CONCLUSION

In this paper, we have presented a three-step fully au-

tomatic approach that performs vertebrae localization

and segmentation in a coarse to ﬁne manner. By com-

bining the SpatialConﬁguration-Net (SC-Net) for ver-

tebrae localization and identiﬁcation with the U-Net

for vertebrae segmentation, our method has achieved

top performance in the dataset of the VerSe 2019 chal-

lenge. The good generalization of our method to the

hidden test 2 set of the challenge has enabled our

method to rank ﬁrst and to win the challenge overall.

The competing methods await more detailed analysis

and comparison in the paper summarizing the VerSe

2019 challenge. In future work, we plan to investi-

gate how to combine the individual networks of our

three-step approach into a single end-to-end trainable

model.

ACKNOWLEDGEMENTS

Stern and M. Urschler gratefully acknowledge the

support of NVIDIA Corporation with the donation of

the Titan Xp and Titan V GPUs used in this research.

REFERENCES

Amato, V., Giannachi, L., Irace, C., and Corona, C. (2010).

Accuracy of Pedicle Screw Placement in the Lum-

Coarse to Fine Vertebrae Localization and Segmentation with SpatialConﬁguration-Net and U-Net

131

bosacral Spine Using Conventional Technique: Com-

puted Tomography Postoperative Assessment in 102

Consecutive Patients. J. Neurosurg. Spine, 12(3):306–

313.

Bromiley, P. A., Kariki, E. P., Adams, J. E., and Cootes, T. F.

(2016). Fully Automatic Localisation of Vertebrae in

CT Images Using Random Forest Regression Voting.

In Comput. Methods Clin. Appl. Spine Imaging, pages

51–63.

Chen, H., Shen, C., Qin, J., Ni, D., Shi, L., Cheng, J.

C. Y., and Heng, P.-A. (2015). Automatic Localiza-

tion and Identiﬁcation of Vertebrae in Spine CT via

a Joint Learning Model with Deep Neural Networks.

In Proc. Med. Image Comput. Comput. Interv., pages

515–522.

Chu, C., Belav

y, D. L., Armbrecht, G., Bansmann, M.,

Felsenberg, D., and Zheng, G. (2015). Fully Auto-

matic Localization and Segmentation of 3D Vertebral

Bodies from CT/MR Images via a Learning-Based

Method. PLoS One, 10(11):e0143327.

Cootes, T. F., Taylor, C. J., Cooper, D. H., and Graham,

J. (1995). Active Shape Models-Their Training and

Application. Comput. Vis. Image Underst., 61(1):38–

59.

Ebner, T.,

Stern, D., Donner, R., Bischof, H., and Urschler,

M. (2014). Towards Automatic Bone Age Estima-

tion from MRI: Localization of 3D Anatomical Land-

marks. In Proc. Med. Image Comput. Comput. Interv.,

pages 421–428.

Forsberg, D., Lundstr

om, C., Andersson, M., Vavruch, L.,

Tropp, H., and Knutsson, H. (2013). Fully Auto-

matic Measurements of Axial Vertebral Rotation for

Assessment of Spinal Deformity in Idiopathic Scolio-

sis. Phys. Med. Biol., 58(6):1775–1787.

Glocker, B., Feulner, J., Criminisi, A., Haynor, D. R., and

Konukoglu, E. (2012). Automatic Localization and

Identiﬁcation of Vertebrae in Arbitrary Field-of-View

CT Scans. In Proc. Med. Image Comput. Comput. In-

terv., pages 590–598.

Glocker, B., Zikic, D., Konukoglu, E., Haynor, D. R., and

Criminisi, A. (2013). Vertebrae Localization in Patho-

logical Spine CT via Dense Classiﬁcation from Sparse

Annotations. In Proc. Med. Image Comput. Comput.

Interv., pages 262–270.

Hammernik, K., Ebner, T., Stern, D., Urschler, M., and

Pock, T. (2015). Vertebrae Segmentation in 3D CT

Images Based on a Variational Framework. In Com-

put. Methods Clin. Appl. Spine Imaging, pages 227–

233.

Ibragimov, B., Likar, B., Pernu

s, F., and Vrtovec, T. (2014).

Shape Representation for Efﬁcient Landmark-Based

Segmentation in 3-D. IEEE Trans. Med. Imaging,

33(4):861–874.

Janssens, R., Zeng, G., and Zheng, G. (2018). Fully Au-

tomatic Segmentation of Lumbar Vertebrae from CT

Images Using Cascaded 3D Fully Convolutional Net-

works. In Proc. Int. Symp. Biomed. Imaging, pages

893–897. IEEE.

Kingma, D. P. and Ba, J. (2015). Adam: A Method for

Stochastic Optimization. Int. Conf. Learn. Represent.

arXiv1412.6980.

Klinder, T., Ostermann, J., Ehm, M., Franz, A., Kneser, R.,

and Lorenz, C. (2009). Automated Model-Based Ver-

tebra Detection, Identiﬁcation, and Segmentation in

CT images. Med. Image Anal., 13(3):471–482.

Knez, D., Likar, B., Pernus, F., and Vrtovec, T. (2016).

Computer-Assisted Screw Size and Insertion Trajec-

tory Planning for Pedicle Screw Placement Surgery.

IEEE Trans. Med. Imaging, 35(6):1420–1430.

Korez, R., Likar, B., Pernu

s, F., and Vrtovec, T. (2016).

Model-Based Segmentation of Vertebral Bodies from

MR Images with 3D CNNs. In Proc. Med. Image

Comput. Comput. Interv., pages 433–441.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learn-

ing. Nature, 521(7553):436–444.

Lessmann, N., van Ginneken, B., de Jong, P. A., and I

sgum,

I. (2019). Iterative Fully Convolutional Neural Net-

works for Automatic Vertebra Segmentation and Iden-

tiﬁcation. Med. Image Anal., 53:142–155.

Liao, H., Mesﬁn, A., and Luo, J. (2018). Joint Vertebrae

Identiﬁcation and Localization in Spinal CT Images

by Combining Short- and Long-Range Contextual In-

formation. IEEE Trans. Med. Imaging, 37(5):1266–

1275.

Lindner, C., Bromiley, P. A., Ionita, M. C., and Cootes, T. F.

(2015). Robust and Accurate Shape Model Match-

ing Using Random Forest Regression-Voting. IEEE

Trans. Pattern Anal. Mach. Intell., 37(9):1862–1874.

Mader, A. O., Lorenz, C., von Berg, J., and Meyer, C.

(2019). Automatically Localizing a Large Set of Spa-

tially Correlated Key Points: A Case Study in Spine

Imaging. In Proc. Med. Image Comput. Comput. In-

terv., pages 384–392.

Nesterov, Y. (1983). A Method of Solving A Convex Pro-

gramming Problem With Convergence rate O(1/kˆ2).

In Sov. Math. Dokl., volume 27, pages 372–376.

Payer, C.,

Stern, D., Bischof, H., and Urschler, M. (2016).

Regressing Heatmaps for Multiple Landmark Local-

ization Using CNNs. In Proc. Med. Image Comput.

Comput. Interv., pages 230–238.

Payer, C.,

Stern, D., Bischof, H., and Urschler, M. (2019).

Integrating Spatial Conﬁguration into Heatmap Re-

gression Based CNNs for Landmark Localization.

Med. Image Anal., 54:207–219.

Pﬁster, T., Charles, J., and Zisserman, A. (2015). Flowing

ConvNets for Human Pose Estimation in Videos. In

Proc. Int. Conf. Comput. Vis., pages 1913–1921.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-Net:

Convolutional Networks for Biomedical Image Seg-

mentation. In Proc. Med. Image Comput. Comput. In-

terv., pages 234–241.

Sekuboyina, A. (2019). VerSe 19: Evaluation Re-

port. https://deep-spine.de/verse/verse19 evaluation

report.pdf. Accessed: 2019-11-14.

Sekuboyina, A., Rempﬂer, M., Kuka

cka, J., Tetteh, G.,

Valentinitsch, A., Kirschke, J. S., and Menze, B. H.

(2018). Btrﬂy Net: Vertebrae Labelling with Energy-

Based Adversarial Learning of Local Spine Prior.

Proc. Med. Image Comput. Comput. Interv., pages

649–657.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

132

Sekuboyina, A., Valentinitsch, A., Kirschke, J. S., and

Menze, B. H. (2017). A Localisation-Segmentation

Approach for Multi-label Annotation of Lumbar Ver-

tebrae using Deep Nets. arXiv:1703.04347.

Stern, D., Likar, B., Pernu

s, F., and Vrtovec, T. (2011).

Parametric Modelling and Segmentation of Vertebral

Bodies in 3D CT and MR Spine Images. Phys. Med.

Biol., 56(23):7505–7522.

Tompson, J., Jain, A., LeCun, Y., and Bregler, C. (2014).

Joint Training of a Convolutional Network and a

Graphical Model for Human Pose Estimation. In Adv.

Neural Inf. Process. Syst., pages 1799–1807.

Toshev, A. and Szegedy, C. (2014). DeepPose: Human Pose

Estimation via Deep Neural Networks. In Proc. Com-

put. Vis. Pattern Recognit., pages 1653–1660.

Urschler, M., Ebner, T., and

Stern, D. (2018). Integrating

Geometric Conﬁguration and Appearance Informa-

tion into a Uniﬁed Framework for Anatomical Land-

mark Localization. Med. Image Anal., 43:23–36.

Wang, Y., Yao, J., Roth, H. R., Burns, J. E., and Summers,

R. M. (2016). Multi-atlas Segmentation with Joint

Label Fusion of Osteoporotic Vertebral Compression

Fractures on CT. In Comput. Methods Clin. Appl.

Spine Imaging, pages 74–84.

Yang, D., Xiong, T., Xu, D., Huang, Q., Liu, D., Zhou,

S. K., Xu, Z., Park, J. H., Chen, M., Tran, T. D., Chin,

S. P., Metaxas, D., and Comaniciu, D. (2017). Auto-

matic Vertebra Labeling in Large-Scale 3D CT Using

Deep Image-to-Image Network with Message Passing

and Sparsity Regularization. In Proc. Inf. Process.

Med. Imaging, pages 633–644.

Coarse to Fine Vertebrae Localization and Segmentation with SpatialConﬁguration-Net and U-Net

133