Fully Automated Volumetric Measurement of Malignant Pleural

Mesothelioma from Computed Tomography Images by Deep Learning:

Preliminary Results of an Internal Validation

Owen Anderson

1,3

, Andrew C. Kidd

, Keith A. Goatman

, Alexander J. Weir

, Jeremy Voisey

Vismantas Dilys

, Jan P. Siebert

and Kevin G. Blyth

2,4

School of Computing Science, University of Glasgow, 18 Lilybank Gardens, Glasgow, U.K.

Pleural Disease Unit, Queen Elizabeth University Hospital, 1345 Govan Road, Glasgow, U.K.

Canon Medical Research Europe, 2 Anderson Place, Edinburgh, U.K.

Institute of Infection, Immunity and Inﬂammation, University of Glasgow, 120 University Place, Glasgow, U.K.

Keywords:

Malignant Pleural Mesothelioma (MPM), Deep Learning (DL), Convolutional Neural Network (CNN),

Computed Tomography (CT), Image Segmentation.

Abstract:

Malignant Pleural Mesothelioma (MPM) is a cancer associated with prior exposure to asbestos ﬁbres. Unlike

most tumours, which are roughly spherical, MPM grows like a rind surrounding the lung. This irregular shape

poses signiﬁcant clinical and technical challenges. Accurate tumour measurements are necessary to determine

treatment efﬁcacy, but manual segmentation is tedious, time-consuming and associated with high intra- and

inter-observer variation. In addition, uncertainty is compounded by poor differentiation in the computed

tomography (CT) image between MPM and other common features. We describe herein an internal validation

of a fully automatic tool to generate volumetric segmentations of MPM tumours using a convolutional neural

network (CNN). The system was trained using the ﬁrst 123 CT volumetric datasets from a planned total of 403

scans. Each scan was manually segmented to provide the expert ground truth. Evaluation was by seven-fold

cross validation on a subset of 80/123 datasets that have full volumetric segmentations. The mean volume

of MPM tumour in these datasets is 405.1 cm

(standard deviation 271.5 cm

). Following three-dimensional

binary closing of the manual annotations to improve inter-slice consistency, the mean volume difference

between the manual and automatic measurements is 27.2 cm

, which is not signiﬁcantly different from zero

difference (

p = 0.225

). The 95% limits of agreement between the manual and automated measurements

are between -417 and +363 cm

. The mean Dice overlap coefﬁcient was 0.64, which is comparable with

inter-observer measurements reported elsewhere. To our knowledge, this is the ﬁrst algorithm of its kind that

fully automates and evaluates measurement of the MPM tumour volume. The next step will be to evaluate the

method on the remaining unseen multi-centre evaluation set. Such an algorithm has possible future application

to pharmaceutical trials (where it offers a repeatable study end point) and to routine care (where it allows

tumour progression to be assessed rapidly to enhance therapeutic clinical decision making).

1 INTRODUCTION

Mesothelioma is a cancer associated with asbestos

exposure. Mesothelioma can occur in the abdomen

and testes, but the vast majority of cases (more than

90%) develop in the pleural space surrounding the

lungs (Attanoos and Gibbs, 1997) — this is known as

Malignant Pleural Mesothelioma (MPM).

The gold-standard measurement for any tumour

is volume, however surrogate metrics are often em-

ployed to reduce measurement time. For many tu-

mours, for example lung nodules, volume measure-

ment is straightforward because such tumours can be

assumed to be approximately spherical — an assump-

tion which is valid because, unimpeded, they tend to

grow isotropically. The assumption of sphericity un-

derpins the RECIST (Response Evaluation Criteria in

Solid Tumours) score (Schwartz et al., 2016), where

measurements of tumour diameter is sufﬁcient to track

tumour development in response to treatment.

In contrast, however, MPM tumours develop like

a rind around the lungs, following the bounds of the

pleural cavity and adopting an irregular shape with a

high surface-to-volume ratio. To measure MPM, the

Anderson, O., Kidd, A., Goatman, K., Weir, A., Voisey, J., Dilys, V., Siebert, J. and Blyth, K.

Fully Automated Volumetric Measurement of Malignant Pleural Mesothelioma from Computed Tomography Images by Deep Learning: Preliminary Results of an Internal Validation.

DOI: 10.5220/0008976100640073

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 2: BIOIMAGING, pages 64-73

ISBN: 978-989-758-398-8; ISSN: 2184-4305

modiﬁed RECIST (or mRECIST) score is employed

(Byrne and Nowak, 2004). Rather than diameter, the

thickness of the tumour is measured at multiple loca-

tions perpendicular to the lung wall. The sum of these

thickness measurements at two time points are used

to generate an mRECIST report, that categorises the

tumour as either (Eisenhauer et al., 2009):

•

Complete Response (CR), indicating a disappear-

ance of all known disease;

•

Partial Response (PR), indicating a

30%

or more

decrease in the mRECIST score;

•

Stable disease/No change, indicating that no new

lesions have appeared, and the mRECIST score

has not signiﬁcantly changed;

•

Progressive Disease (PD), indicating a

20%

more increase in the mRECIST score, or the ap-

pearance of new lesions.

The mRECIST score is known to exhibit poor intra-

and inter-annotator agreement (Yoon et al., 2016). One

component of this variability arises from ambiguities

in interpretation of the CT images, and another com-

ponent is from the highly heuristic nature of the mRE-

CIST scoring system.

Image Interpretation:

Labby et al. (Labby et al.,

2013) demonstrate that there is signiﬁcant lack of con-

sistency among observers in area delineation of tu-

mours in single CT slices, a method of measurement

independent of the mRECIST score. They report a

95%

conﬁdence interval between ﬁve observers span-

ning

311%

and

111%

for single time-point measure-

ments of baseline and response images respectively.

The research suggests that CT images of MPM are

inherently ambiguous and any measurements based on

such images are highly subjective.

Measurement Interpretation:

The heuristic and

sparse basis of the mRECIST score leads to noise

inherent to the measurement. A major component of

the variability between experts is the choice of sample

location, although Armato et al. (Armato et al., 2014)

demonstrate that even when experts are provided

with the coordinate locations at which to measure

tumour thickness, signiﬁcant variation remains due to

choice of angle at which to make the one-dimensional

measurement.

The mRECIST measurement remains the clinical stan-

dard due to its feasibility — full volumetric tumour de-

lineations by multiple experts would result in the most

representative measurement of change (Frauenfelder

et al., 2011), but full three-dimensional delineation is

extremely time consuming.

1.1 Prior Work

The widely recognised inadequacy of current mesothe-

lioma measurements has resulted in development of a

number of algorithms, to automate or semi-automate

interpretation of CT images.

Chaisaowong et al. (Chaisaowong et al., 2013) de-

tect and delineate pleural thickening by modelling the

healthy pleura and differencing this with the CT im-

ages, followed by prediction reﬁnement using a 3-D

Gibbs-Markov random ﬁeld. Pleural thickening can

develop into MPM, and they report that this algorithm

could be used for early detection of the cancer. They

evaluate on 27 sites of pleural thickening, meaning it

is unclear whether the algorithm has the performance

required for the technically demanding application.

Sensakovic et al. (Sensakovic et al., 2011) aim to

segment a plural volume. They ﬁrst segment the lung

parenchyma, then the hemi-thoracic cavity (with some

user input to inform the liver boundary delineation),

and based on this derive the pleural volume. They

report a median Jaccard index of 0.484 over 31 pa-

tients (which equates a Dice coefﬁcient of 0.65), at

one time-point, providing analysis at the level of area

in randomly selected sub-sections of the 31 CT im-

ages, rather than across the totality of the CT images.

The median Jaccard index across the same subsections

when comparing three observers was 0.517 (equat-

ing a Dice coefﬁcient of 0.68), a value similar to that

achieved by the semi-automated method.

Gudmundsson et al. (Gudmundsson et al., 2018)

describe their approach to segment plural thickening

from CT images in a fully automated fashion using

deep CNNs. First, the images are preprocessed to re-

move the patient couch and air from the CT image.

Following this, a U-Net is applied to delineate healthy

thoracic tissue from areas of pleural thickening, which

can include MPM tumour, plural effusion and pleural

plaques. The U-Net which is applied is a choice of

two, dependant on the laterality (left or right) of the

disease, which must be known in order to deploy the al-

gorithm. They report median Dice coefﬁcients ranging

from 0.662 to 0.800 across two test sets (totalling 131

slices from 43 patients) and reference segmentations

of MPM tumour from three and ﬁve observers for the

two test sets. Across the same images, inter-observer

comparisons yielded median Dice coefﬁcients ranging

from 0.648 to 0.814, similar to those achieved by the

automated method. Because the automated method

does not aim to differentiate MPM tumour from pleu-

ral ﬂuid, the authors describe that 7 out of 15 outlier

slices where the algorithm over-predicts tumour area

contain pleural effusion.

Chen et al. (Chen et al., 2017) describe their

Fully Automated Volumetric Measurement of Malignant Pleural Mesothelioma from Computed Tomography Images by Deep Learning:

Preliminary Results of an Internal Validation

semi-automated approach for volumetric assessment

of mesothelioma from CT. The process depends on

20-30 seed points per slice, placed by an expert within

the area of MPM tumours, that are used to initialise a

random walk segmentation. The mean Dice coefﬁcient

across 15 patients was reported to be 0.825.

Brahim et al. (Brahim et al., 2018) propose a semi-

automated volumetric method for MPM segmentation

based on identiﬁcation of the thoracic cavity and sub-

sequent texture analysis to locate the tumoral regions.

Across 10 CT images, a Dice coefﬁcient of 0.88 is

achieved.

The methods described by Chaisaowong et al.

(Chaisaowong et al., 2013) and Gudmundsson et al.

(Gudmundsson et al., 2018) aim to derive pleural thick-

ening, and Sensakovic et al. (Sensakovic et al., 2011)

semi-automate the delineation of a pleural volume.

A confounding factor in MPM development is pleu-

ral effusion. Differentiating MPM tumour from ﬂuid

poses a technical challenge because the structures can

have overlapping values of Hounsﬁed Units in CT

images (Ng et al., 1999), however for quantitative

measurements of patient progression, e.g. tumour vol-

ume change, it becomes necessary for any automated

method to differentiate tumour from pleural effusion,

because the volume of ﬂuid and tumour are unrelated.

This is explored in a later conference abstract (Gud-

mundsson et al., 2019).

The purpose of the current manuscript is to re-

port the preliminary ﬁndings of an ongoing effort to

develop a fully-automated method for volumetric seg-

mentation by deep learning. The data reported here are

the result of an internal validation in 108 patients (123

CT scans). To our knowledge there are, at present,

no other volumetric evaluations of a fully automated

system for the measurement of mesothelioma tumour

volume.

2 METHODOLOGY

A convolutional neural network was trained to segment

MPM tumour in CT datasets as part of a multi-centre,

retrospective cohort study funded by the Cancer Inno-

vation Challenge (Scottish Health Council). The study

will conclude in 2020 after analysis of 403 patients

with MPM previously recruited to two mesothelioma

research studies.

2.1 Data Selection

The automated system was trained and cross-validated

on 123 volumetric CT datasets from 108/403 subjects

recruited to the DIAPHRAGM and PRISM research

studies. All subjects had a conﬁrmed histological

diagnosis of MPM.

DIAPHRAGM.

(Diagnostic and Prognostic Biomark-

ers in the Rational Assessment of Mesothelioma)

(Tsim et al., 2016) was a prospective, multi-centre,

observational study that recruited 747 patients over

3 years from 23 UK sites at ﬁrst presentation of

MPM. A sub-group of 23/747 patients (who had

contemporaneous CT and MRI scans) were selected

for this study. All the images used from this study

were acquired pre-treatment. The MR images are

helpful in disambiguating confounding features in the

CT images.

PRISM.

(Prediction of ResIstance to chemotherapy

using Somatic copy number variation in Mesothe-

lioma) (Blyth et al., 2018) is an ongoing retrospective

cohort study, in which the primary objective is

to determine a genomic classiﬁer that predicts

chemo-resistance in MPM. It involves retrieval of

tumour blocks and CT images before and after

chemotherapy in 380 patients with MPM from ﬁve

UK centres. 123 CT images from 85/380 PRISM

subjects are included in this study (43 images acquired

pre-treatment, and 80 images acquired post-treatment).

All of the CT volumes utilised in this project are

from centres across Glasgow. Images from the DI-

APHRAGM study were typically acquired earlier in

the patient care pathway than those from the PRISM

study. Consequently the tumour volumes tend to

be smaller and thinner in the DIAPHRAGM study

volumes. This difference is illustrated in ﬁgure 1,

that shows slices from a DIAPHRAGM and PRISM

dataset.

2.2 Seven-fold Cross-validation

The internal validation is in the form of

-fold cross

validation, where the value

k = 7

was chosen to max-

imise the amount of training data available for each

model, whilst providing robust group statistics for each

test set. The data splits during the seven-fold cross val-

idation were complicated by the sparse ground truth

segmentations, which although they were suitable for

training could not be used to measure volume accuracy.

The sparse datasets were included in the training sets

for all seven folds.

The training data was divided as follows. Of

the 123 annotated datasets, 80 were fully annotated

(pre-treatment) and 43 were sparsely annotated (post-

treatment). The 80 fully annotated datasets were ran-

domly assigned to seven folds, consisting of 11 or 12

BIOIMAGING 2020 - 7th International Conference on Bioimaging

Figure 1: Two axial CT slices from two subjects in the

cohort, with manually derived MPM tumour segmentation

shown in red. Top: A slice from a CT image taken in the

DIAPHRAGM study. Bottom: A slice from a CT image

taken in the PRISM study. The unsegmented areas (in grey)

represent adjacent pleural ﬂuid.

datasets per fold. During evaluation of each fold the re-

maining six folds were divided by a 30:70 split respec-

tively between a set used to select the best performing

model and determine the optimal model threshold, and

the training set (to which the 43 sparsely annotated

volumes were also added).

Since neighbouring slices in the CT images are

highly correlated, including all the slices in training

can lead to over-ﬁtting to the datasets with more slices.

To counter this the fully segmented volumes are also

sparsely sampled during training, using 100 slices per

volume.

2.3 Ground Truth

2.3.1 Ground Truth Generation

In total 123 CT volumes were manually segmented by

a respiratory clinician with training in mesothelioma

identiﬁcation and image analysis. The volumes were

annotated using Myrian software (Intrasense, Paris).

For 80 of the CT datasets every slice containing MPM

was annotated to provide a full segmentation of the

tumour. Since an interim analysis suggested that ad-

jacent slices are highly correlated a more sparse an-

notation was performed for 43 datasets, where only

every ﬁfth slice was annotated. The sparse annotation

enabled more subjects to be included in the training

set, increasing the diversity of the training population

for considerably less effort. Since adjacent slices are

highly correlated, there is little disbeneﬁt to training

with sparser slices. However, the sparse annotations

in these datasets mean these datasets were not suitable

to evaluate volume accuracy, and were not included in

the accuracy metrics.

2.3.2 Ground Truth Inter-slice Consistency

Processing

The manual annotation of the tumour was performed

in the axial plane. Interim results suggested this could

lead to inconsistencies between slices, where the dis-

continuous nature of the annotations when viewed in

the orthogonal sagittal and coronal planes contrasts

with the contiguous nature of the tumour when viewed

in the plane of annotation (ﬁgure 1). This between-

slice inconsistency can have a signiﬁcant effect on

volumetric measurements.

For this reason inter-slice inconsistencies were re-

duced using a three-dimensional binary closing opera-

tion having an

11 × 11 × 11

voxel structuring element.

In addition to reducing inter-slice inconsistency, holes

in the MPM tumour smaller than ﬁve voxels in diame-

ter will be closed. The downside to this processing is

that genuine holes in the tumour drawn by the annota-

tor will be removed.

2.4 Convolutional Neural Network

Architecture

A Convolutional Neural Network (CNN) with a U-Net

architecture (Ronneberger et al., 2015) was trained for

mesothelioma segmentation — similar to the method

proposed by Gudmundsson et al. (Gudmundsson et al.,

2018). Speciﬁcally, our network arcutechture is a mod-

iﬁed 2-D U-Net which consumes three consecutive

axial slices at a time, and returns the segmentation of

the central slice. The encoder portion of the U-Net

employs a VGG classiﬁer, which has been pre-trained

on the ImageNet challenge data (Jia Deng et al., 2009)

— the three consecutive axial slices are fed into what

were the red, blue and green colour channels of the

pre-trained network. CT image intensities input to

the network are clipped to [-1050, +1100] Hounsﬁeld

Units, and normalised to range [-1, +1]. All network

activations are rectiﬁed linear units, aside from the

Fully Automated Volumetric Measurement of Malignant Pleural Mesothelioma from Computed Tomography Images by Deep Learning:

Preliminary Results of an Internal Validation

ultimate layer of the network, for which a softmax

activation is used. The algorithm is shown schemati-

cally in ﬁgure 2, and was implemented using the Keras

framework (Chollet, 2015).

The raw output of the model is a predicted prob-

ability of MPM tumour for every voxel in the input

CT volume. To evaluate total volume measurements,

this output is binarised by applying a threshold. The

threshold which results in the best performance varies

slightly between models — different training datasets

have varying levels of complexity, leading to models

which predict in varying probability ranges, speciﬁc

to each model. After the model has converged, the

images in the internal validation set are used to deter-

mine the optimal algorithm threshold. Across these

subjects, the threshold was optimised to provide the

highest mean Dice coefﬁcient between the binarised

prediction and ground truth annotation.

The Adam optimiser is used, with a cyclic learn-

ing rate (Smith, 2017), where the learning rate (

)

has been set to oscillate between

lr = 0.0001

and

lr = 0.003

, with a full cycle duration of one epoch.

The algorithm consumes three axial slices, at their

original resolution (which is typically within the range

0.71 mm to 1.34 mm). Dropout (with a rate of 0.2)

(Srivastava et al., 2014) and batch normalisation (Ioffe

and Szegedy, 2015) are used at the locations illustrated

in ﬁgure 2. For our experiments, the batch size was set

to 8 slices (with context) per batch, allowing the model

with 10,019,874 parameters to train on the available

GPU.

Categorical cross-entropy was selected for the ob-

jective function, despite being a binary classiﬁcation

task. The output of the network is therefore two chan-

nels: one representing tumour, and the other represent-

ing background. This objective function was selected

to improve convergence over that achieved using bi-

nary cross-entropy. Due to the random ordering of

the slices during training, the ﬁrst few batches may be

predominantly tumour negative. In this case binary

cross-entropy tends to result in weights at the decoder

rapidly tending towards zero, at which point conver-

gence halts as gradients no longer propagate through

the network. In contrast, by using categorical cross-

entropy, a non-zero signal is always required in one of

the two output channels, regardless of the class balance

of that example slice. This decreases the likelihood

that weights will tend to zero in the early stages of

training, increasing the repeatability of experiments

between runs and folds of analysis.

The network is trained for 30 epochs, after which

the best model is selected based on the average voxel-

level accuracy for the internal validation set.

Figure 2: A schematic of the U-Net model architecture. The

blue boxes represent a stack of convolutional ﬁlters, with

the number of ﬁlters per stack shown to the left of each box.

All ﬁlters have a dimensionality of

3 × 3

. Green and orange

boxes represent dropout and batch normalisation layers re-

spectively. The blue arrows represent skip connections by

feature concatenation.

2.4.1 Tumour Volume

At the validation stage, the algorithm is used to predict

MPM tumour presence for every slice of the CT vol-

umes in the validation set, to generate a full volumetric

segmentation of the tumour. The tumour volume is

calculated as follows:

M(x, y, z) =

(

1 if P(x, y, z) > t

0 else,

(1)

where

describes a mask image of same dimension-

ality as the input CT image, with each voxel assigned

a binary value of one to indicate MPM tumour and

zero elsewhere.

is calculated by evaluating the

probability map (

P(x, y, z)

) with respect to the optimal

threshold,

. These binary maps are then converted

into measurements of tumour volume (

) by summing

BIOIMAGING 2020 - 7th International Conference on Bioimaging

across the CT image, and multiplying by the voxel

volume of the CT image,

V = S

∑

x=0

∑

y=0

∑

z=0

M(x, y, z), (2)

where

and

denote the voxel sizes in x,y and z

respectively.

2.5 Validation Metrics

Since only images from a single time point are avail-

able for each study subject in this preliminary eval-

uation we are unable to evaluate the volume change

accuracy. Instead, segmentation accuracy and absolute

volume correspondence between the algorithm and the

manual observer are evaluated here.

2.5.1 Agreement (Bland-Altman)

Volumetric agreement between the manual and auto-

mated volumetric segmentations was determined us-

ing Bland-Altman analysis (Martin Bland and Altman,

1986). This plots the difference between the two mea-

surements versus the mean of the two measurements.

The following statistics were derived from this analy-

sis:

The mean difference (or bias) between the two

measurement methods

A test whether the mean difference between the

two measurement methods is signiﬁcantly different

from zero. This was determined using a two-sided

paired

-test (MATLAB statistics toolbox, Math-

works, Natick).

The 95% limits of agreement (Martin Bland and

Altman, 1986).

A test whether the difference between the mea-

surement methods increases (or decreases) as the

tumour volume increases. This was determined

from the slope of a least squares regression ﬁt to

the points in the Bland-Altman plot. Speciﬁcally

it tests whether the slope is statistically different

from a zero gradient, based on a

-statistics (MAT-

LAB statistics toolbox, Mathworks, Natick).

2.5.2 Region Overlap (Dice)

Whilst volumetric agreement is important, as it is the

physical property of interest, alone it does not guaran-

tee that given identical volumes the same two regions

have been delineated, indeed it does not prove they

even intersect. To determine the overlap between the

manual and automated regions the Dice score was cal-

culated (the Dice coefﬁcient is equivalent to the F1

score).

3 RESULTS

The prediction time using the algorithm on the full

resolution CT datasets was approximately one minute

per volume, using an Nvidia 1080Ti graphics process-

ing unit (GPU), 32 GB of RAM and a 12-core Intel

Xeon CPU (3.40 GHz). Manual annotation time varied

between subjects, taking approximately 2.5 hours per

volume.

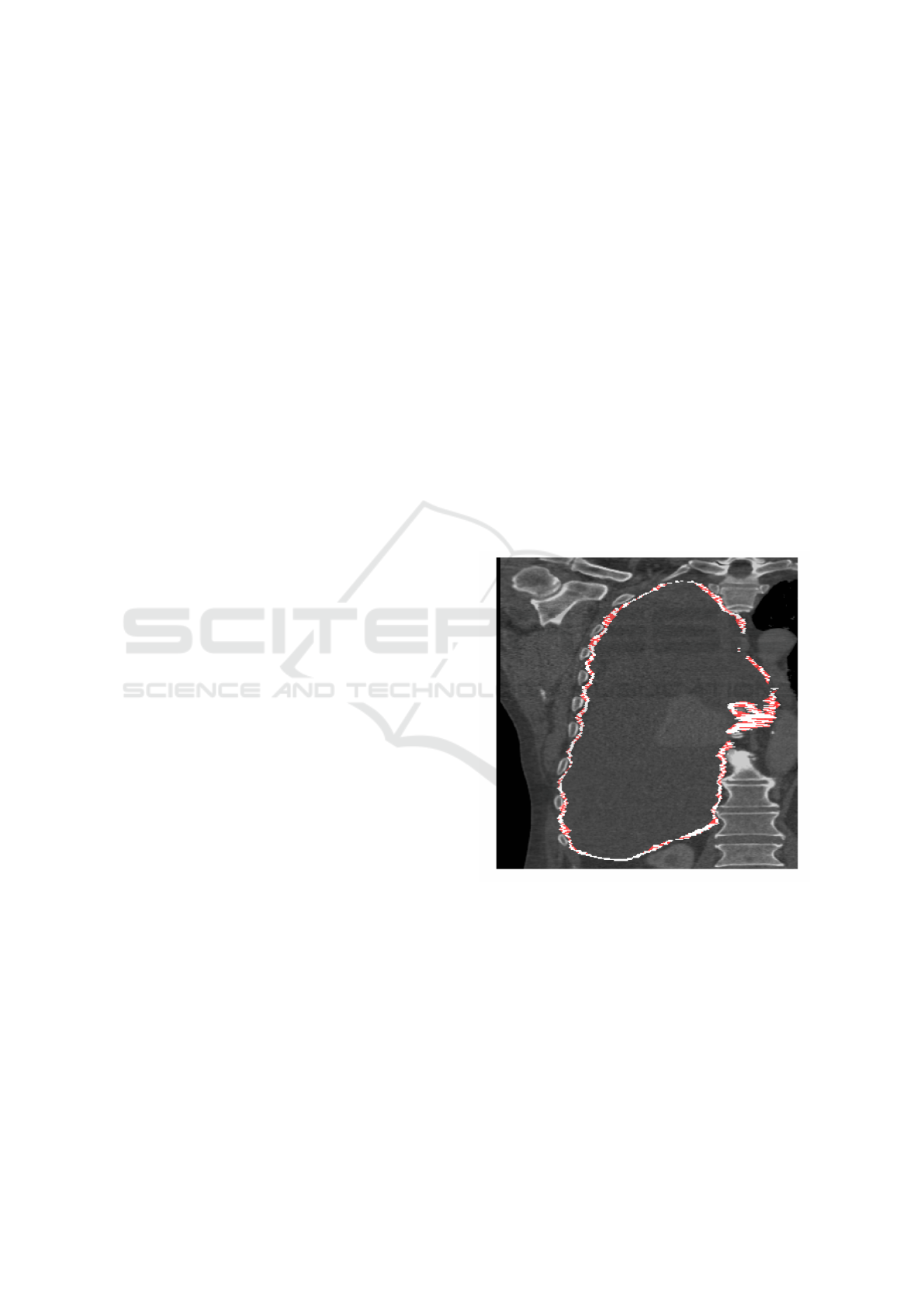
3.1 Inter-slice Consistency Processing

As described in section 2.3.2, three-dimensional binary

closing was proposed to improve inter-slice manual

segmentation consistency. Figure 3 shows a typical

binary closing result, highlighting the additional vox-

els added by the closing operation. Note how, at least

visually, the closed version appears more contiguous

and physically more plausible. Following closing the

detected plural volume in the cohort increases from

301.1 cm

(standard deviation 263.9 cm

) to 514.7 cm

(standard deviation 336.1 cm

Figure 3: A CT coronal view of a subject with MPM, show-

ing the right lung. The white annotation indicates the loca-

tion of tumour, as drawn by an expert annotator in the axial

plane, which follows the bounds of the pleural cavity, sur-

rounding a region of pleural effusion. Red shows the regions

which are closed by a binary closing operation.

3.2 Volumetric Agreement

The mean predicted volume for the cohort over the

seven-fold analysis was 547.2 cm

(standard deviation

290.9 cm

Fully Automated Volumetric Measurement of Malignant Pleural Mesothelioma from Computed Tomography Images by Deep Learning:

Preliminary Results of an Internal Validation

3.2.1 Raw Manual Annotations

The mean tumour volume in the raw manual segmen-

tations is 405.1 cm

(standard deviation 271.5 cm

which is signiﬁcantly lower than the automatically de-

tected volume. Figure 4 shows a Bland-Altman plot

representing how the volume error varies with tumour

volume. Here the manual measurement is the raw

ground truth annotation (i.e. without the binary clos-

ing operation to increase consistency between slices).

A minor, though statistically signiﬁcant, trend is ob-

served where the volume error increases slightly with

tumour volume (

p < 0.001

). This indicates that the

algorithm, on average, tends to over-segments the tu-

mour compared with the raw ground truth.

3.2.2 Closed Manual Annotations

Following binary closing the mean tumour volume of

the manual segmentations increased to 574.4 cm

(stan-

dard deviation 327.1 cm

). Figure 5 shows the Bland-

Altman plot using the closed annotations, indicating

a mean difference of -27.2 cm

, which is not signiﬁ-

cantly different from zero mean difference (

p = 0.225

The upper and lower 95% limits of agreement are [-

414.2, +360.5] cm

, respectively. For ease of compari-

son to other methods, the results are equivalent to 95%

limits of agreement which span 129.2% of the total

tumour volume.

In ﬁgure 5 four of the measurement differences are

outliers, i.e. outside of the 95% limits of agreement:

one represents under-segmentation compared with the

ground truth, while the other three represent over-

segmentations. Inspection of the under-segmentation

case found that the MPM tumour in this image is un-

usually thick compared with the other images in the

training cohort. It is likely the algorithm fails to gen-

eralise to this degree of thickening, previously un-

seen during training. For the remaining three outliers,

where the algorithm over-segments with respect to the

ground truth, inspection ﬁnds extremely narrow tu-

mour in these images. The algorithm often identiﬁes

the bulk of the tumour mass (where it is thicker and

more visible), but does not propagate the tumour into

the rind-like surface which, although narrow, encloses

a signiﬁcant proportion of the lung surface area. This

is potentially where the slice-based nature of the ap-

proach limits performance. A fully 3D CNN approach

may offer higher accuracy in such cases.

3.3 Region Overlap (Dice Score)

Analysis of the Dice coefﬁcient shows signiﬁcant vari-

ation between subjects (presumably reﬂecting the fact

that some datasets are simply more difﬁcult to segment

0 250 500 750 1000 1250 1500

Mean of both measurements

-800

-600

-400

-200

200

400

600

800

1000

Difference between measurements

Figure 4: Bland-Altman analysis of the algorithm-annotator

agreement for tumour volume measurements, across

sub-

jects. The central dashed line indicates a mean difference

142.2

over-segmentation by the algorithm. Outer

dashed lines indicate upper and lower 95% limits of agree-

ment of [−224.1, +508.5] cm

respectively.

0 200 400 600 800 1000 1200 1400 1600 1800

Mean of both measurements

-1200

-1000

-800

-600

-400

-200

200

400

600

800

Difference between measurements

Figure 5: Bland-Altman analysis of the algorithm-annotator

agreement for tumour volume measurements across

sub-

jects, using cleaned ground truth. The central dashed line in-

dicates a mean difference of

−27.2

under-segmentation

by the algorithm. Outer dashed lines indicate upper and

lower 95% limits of agreement of [

−414.2

+360.5

] cm

respectively.

than others) and between analysis folds (i.e. some mod-

els work better than others, depending on the combina-

tion of datasets used to train them). The mean overall

Dice coefﬁcient is 0.64 (standard deviation 0.12) us-

ing the binary closed ground truth. In comparison,

the Dice score is 0.55 (standard deviation also 0.12)

versus the raw ground truth, conﬁrming higher voxel-

wise correspondence following binary closing to im-

prove inter-slice consistency. The standard deviation

reﬂects the wide range of tumour shapes and volumes

in this dataset (c.f. section 2.1). Figure 6 shows the

ground truth and predicted tumour for a subject from

the PRISM sub-cohort.

BIOIMAGING 2020 - 7th International Conference on Bioimaging

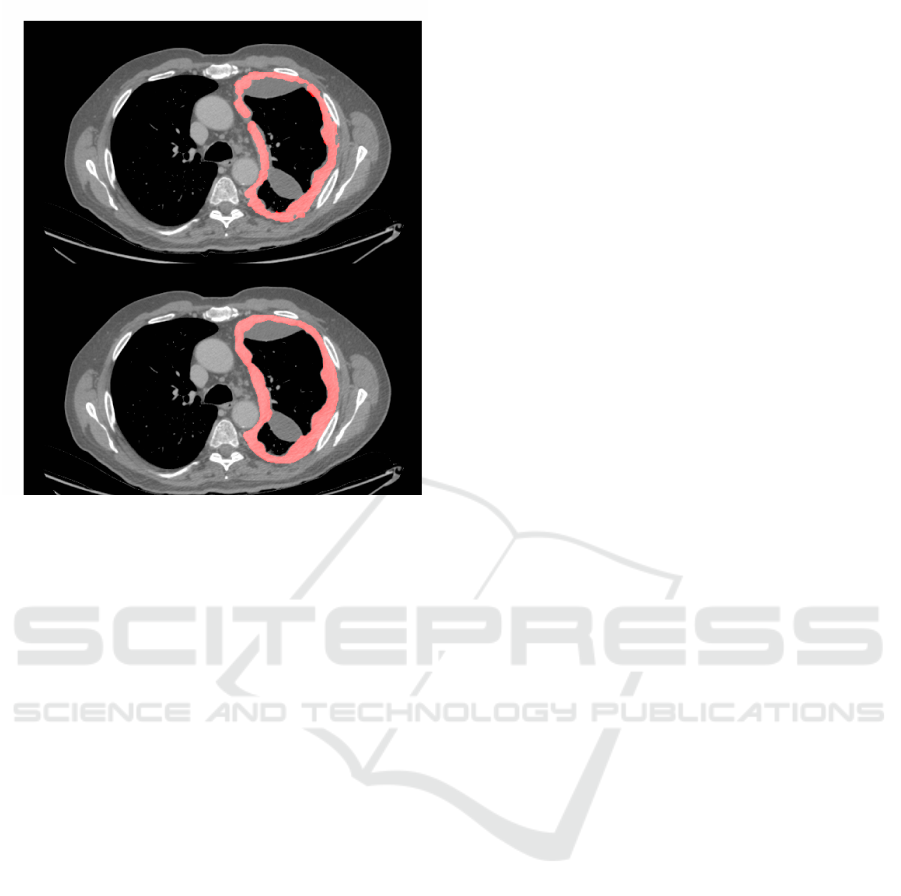
Figure 6: A CT slice from a subject positive for MPM. Top:

Image overlaid with the ground truth segmentation (in red).

Bottom: The corresponding predicted segmentation from

one of the seven-fold models.

4 DISCUSSION

Accurate measurements of MPM tumour volume could

beneﬁt both routine care and clinical trials. Although

there is currently no curative treatment, accurate mea-

surements could support clinicians in ﬁnding the most

effective therapy for each patient. Used as a robust

treatment response metric, volumetric measurements

could also enable smaller and/or more powerful clini-

cal trials.

However, manual measurements suffer from poor

repeatability and/or are time consuming and tedious to

perform. Even volumetric measurements suffer both

aleatoric and epistemic uncertainty. Aleatoric uncer-

tainty arises from the intrinsic uncertainty inherent

in the task. For mesothelioma segmentation a major

source of uncertainty stems from the unusually high

surface-to-volume ratio of the tumour. Placement of

edge points is inherently uncertain, and long, narrow

regions have a large proportion of edge voxels. For

example, an uncertainty of only half a voxel in the

edge delineation of the tumour can result in a total

tumour volume error as high as 60% (based on an

analysis of the tumour shapes in this cohort). Uncer-

tainty also arises from ambiguous structures within the

CT images, that appear very similar to mesothelioma.

However, this feature ambiguity is also a source of

epistemic uncertainty, since with more knowledge and

experience it may be possible to disambiguate the con-

founding features based on knowledge, for example,

by inference based on the known likelihood of a certain

feature occurring in a particular location. It is clear

that a substantial amount of the annotation process is

based on the annotator’s experience and knowledge of

how the tumour manifests. This could be expressed

as a complex set of prior probabilities, given the in-

formation contained in the image, the knowledge that

the image contains a mesothelioma tumour, and the

characteristics of such tumours.

It is perhaps remarkable that, given such a chal-

lenging task, such promising algorithm performance

can be achieved. This is exactly the kind of application

where deep learning algorithms can demonstrate their

strengths.

4.1 Principal Findings

The principal ﬁndings of this study are:

Following three-dimensional binary closing of the

manual annotations to improve inter-slice consis-

tency, there is no signiﬁcant mean volume differ-

ence between the manual and automatic measure-

ments.

The 95% limits of agreement between the manual

and automated measurements are between -417

and +363 cm

3. The mean Dice overlap coefﬁcient was 0.64.

4.2 Critical Analysis

Chen et al. achieve a Dice coefﬁcient of 0.825, using

a semi-automated approach requiring human placed

candidate points. This is higher than our mean Dice

coefﬁcient of 0.64. Some of this difference may arise

from the fully-automated nature of our approach, but

we also note that on some of our image datasets we

achieve similarly high Dice scores. Some images

are intrinsically more difﬁcult to annotate than others,

whether manually or automatically, and agreement will

depend on the disease characteristics in the cohort. For

example, Sensakovic et al. (Sensakovic et al., 2011)

found a median Dice coefﬁcient of 0.68 between three

manual observers, when annotating random slices of

CT images from 31 subjects. Generally, it is easier

to annotate images containing larger MPM tumour

volumes, where a higher Dice coefﬁcient is more eas-

ily achieved due to the lower surface-to-volume ratio.

Although these provide interesting comparisons, we

can draw only limited conclusions without a truly like-

for-like comparison of the two methods, tested on the

same cohort.

Fully Automated Volumetric Measurement of Malignant Pleural Mesothelioma from Computed Tomography Images by Deep Learning:

Preliminary Results of an Internal Validation

Labby et al. (Labby et al., 2013) report relative

95% limits of agreement between ﬁve observers span-

ning 311% for area measurement of MPM tumours,

across 31 subjects. Although we report volumetric

measurement, the 95% limits of agreement in this

evaluation span just 129.2%. However, we note that

this is only comparing against a single observer; the

same observer used to train the model. Labby et al.

also includes ﬁgures showing how different observers

consistently annotate differently, i.e. some observers

consistently segment less tumour than others.

For the task of MPM segmentation, where the dis-

ease characteristics can vary dramatically between sub-

jects, time-points and observers, performance of an

algorithm depends heavily on the training and testing

cohort. An increased variance between subjects means

that a large and diverse test set is required to truly es-

tablish whether any automated method can generalise

to unseen cases. A potential limitation of this work

is that we have demonstrated the performance of the

algorithm on 80 subjects which have not undergone

treatment for the disease, all from imaging centres

based in Glasgow, annotated by a single observer. Al-

though this is an unusually large cohort for which to

have full volume annotation of MPM tumour, we ex-

pect that a large, independent and varied test set by

multiple observers is still necessary to truly determine

the performance of this algorithm.

4.3 Future Work

The automated algorithm will shortly be evaluated on

the remaining unseen evaluation datasets, acquired

from multiple institutions (only 123/403 datasets were

used in the internal validation). This evaluation will

determine whether the algorithm performance exceeds

that of the current clinical standard mRECIST scor-

ing system. Cross-validation can only tell us so much

about the performance of an algorithm. The future

external validation will also provide a more realis-

tic and unbiased assessment of its performance using

data from multiple independent centres not involved

in training the algorithm. In addition, inter- and intra-

observer repeatability measurements for these subjects

will provide further context for the performance of this

algorithm.

5 CONCLUSIONS

We have performed an internal validation to explore

the utility of a deep learning approach for fully auto-

mated measurements of MPM in CT images. Binary

closing was found to improve the inter-slice consis-

tency of manual annotations. Following binary closing

there was no signiﬁcant mean difference between the

manual and automated measurements. To our knowl-

edge, this is the ﬁrst volumetric evaluation of a fully

automated system to segment pleural volume. The

next step will be to evaluate the method on the re-

maining unseen multi-centre evaluation set. Such an

algorithm has possible future application to pharma-

ceutical trials (where it offers a repeatable study end

point) and to routine care (where it allows tumour pro-

gression to be assessed rapidly to enhance therapeutic

clinical decision making).

REFERENCES

Armato, S. G., Nowak, A. K., Francis, R. J., Kocherginsky,

M., and Byrne, M. J. (2014). Observer variability in

mesothelioma tumor thickness measurements: Deﬁn-

ing minimally measurable lesions. Journal of Thoracic

Oncology.

Attanoos, R. L. and Gibbs, A. R. (1997). Pathology of

malignant mesothelioma. Histopathology, 30(5):403–

418.

Blyth, K., Kidd, A., Winter, A., Baird, W., Dick, C., Hair, J.,

Bylesjo, M., Lynagh, S., Sloan, W., Cowell, G., Noble,

C., Smith, A., Westwood, P., Hopkins, T., Williams, N.,

Walter, H., King, A., and Fennell, D. (2018). An update

regarding the Prediction of ResIstance to chemotherapy

using Somatic copy number variation in Mesothelioma

(PRISM) study. Lung Cancer.

Brahim, W., Mestiri, M., Betrouni, N., and Hamrouni, K.

(2018). Malignant pleural mesothelioma segmentation

for photodynamic therapy planning. Computerized

Medical Imaging and Graphics.

Byrne, M. J. and Nowak, A. K. (2004). Modiﬁed RECIST

criteria for assessment of response in malignant pleural

mesothelioma. Annals of Oncology.

Chaisaowong, K., Akkawutvanich, C., Wilkmann, C., and

Kraus, T. (2013). A fully automatic probabilistic 3D

approach for the detection and assessment of pleural

thickenings from CT data. In Computational Intelli-

gence in Medical Imaging.

Chen, M., Helm, E., Joshi, N., Gleeson, F., and Brady, M.

(2017). Computer-aided volumetric assessment of ma-

lignant pleural mesothelioma on CT using a random

walk-based method. International Journal of Computer

Assisted Radiology and Surgery.

Chollet, F. (2015). Keras.

Eisenhauer, E. A., Therasse, P., Bogaerts, J., Schwartz, L. H.,

Sargent, D., Ford, R., Dancey, J., Arbuck, S., Gwyther,

S., Mooney, M., Rubinstein, L., Shankar, L., Dodd, L.,

Kaplan, R., Lacombe, D., and Verweij, J. (2009). New

response evaluation criteria in solid tumours: Revised

RECIST guideline (version 1.1). European Journal of

Cancer.

Frauenfelder, T., Tutic, M., Weder, W., G

otti, R. P., Stahel,

R. A., Seifert, B., and Opitz, I. (2011). Volumetry: An

BIOIMAGING 2020 - 7th International Conference on Bioimaging

alternative to assess therapy response for malignant

pleural mesothelioma? European Respiratory Journal.

Gudmundsson, E., Straus, C., Li, F., Kindler, H., and Armato,

S. (2019). P1.06-04 Deep Learning-Based Segmen-

tation of Mesothelioma on CT Scans: Application to

Patient Scans Exhibiting Pleural Effusion. Journal of

Thoracic Oncology.

Gudmundsson, E., Straus, C. M., and Armato, S. G. (2018).

Deep convolutional neural networks for the automated

segmentation of malignant pleural mesothelioma on

computed tomography scans. Journal of Medical Imag-

ing.

Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-

celerating deep network training by reducing internal

covariate shift. In Proc. Int. Conf on Machine Learn-

ing (ICML), volume 37 of Proceedings of Machine

Learning Research, pages 448–456.

Jia Deng, Wei Dong, Socher, R., Li-Jia Li, Kai Li, and Li

Fei-Fei (2009). ImageNet: A large-scale hierarchical

image database. In 2009 IEEE Conference on Com-

puter Vision and Pattern Recognition.

Labby, Z. E., Straus, C., Caligiuri, P., Macmahon, H., Li, P.,

Funaki, A., Kindler, H. L., and Armato, S. G. (2013).

Variability of tumor area measurements for response as-

sessment in malignant pleural mesothelioma. Medical

Physics.

Martin Bland, J. and Altman, D. G. (1986). Statistical Meth-

ods for Assessing Agreement Between Two Methods

of Clinical Measurement. The Lancet.

Ng, C. S., Munden, R. F., and Libshitz, H. I. (1999). Malig-

nant pleural mesothelioma: The spectrum of manifes-

tations on CT in 70 cases. Clinical Radiology.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-Net:

Convolutional Networks for Biomedical Image Seg-

mentation. Medical Image Computing and Computer-

Assisted Intervention.

Schwartz, L. H., Liti

ere, S., De Vries, E., Ford, R., Gwyther,

S., Mandrekar, S., Shankar, L., Bogaerts, J., Chen, A.,

Dancey, J., Hayes, W., Hodi, F. S., Hoekstra, O. S.,

Huang, E. P., Lin, N., Liu, Y., Therasse, P., Wolchok,

J. D., and Seymour, L. (2016). RECIST 1.1 - Update

and clariﬁcation: From the RECIST committee. Euro-

pean Journal of Cancer.

Sensakovic, W. F., Armato, S. G., Straus, C., Roberts, R. Y.,

Caligiuri, P., Starkey, A., and Kindler, H. L. (2011).

Computerized segmentation and measurement of ma-

lignant pleural mesothelioma. Medical Physics.

Smith, L. N. (2017). Cyclical learning rates for training

neural networks. In IEEE Winter Conference on Appli-

cations of Computer Vision.

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and

Salakhutdinov, R. (2014). Dropout: A Simple Way to

Prevent Neural Networks from Overﬁtting. Journal of

Machine Learning Research, 15:1929–1958.

Tsim, S., Kelly, C., Alexander, L., McCormick, C., Thomson,

F., Woodward, R., Foster, J. E., Stobo, D. B., Paul, J.,

Maskell, N. A., Chalmers, A., and Blyth, K. G. (2016).

Diagnostic and Prognostic Biomarkers in the Rational

Assessment of Mesothelioma (DIAPHRAGM) study:

Protocol of a prospective, multicentre, observational

study. BMJ Open.

Yoon, S. H., Kim, K. W., Goo, J. M., Kim, D. W., and Hahn,

S. (2016). Observer variability in RECIST-based tu-

mour burden measurements: A meta-analysis. Euro-

pean Journal of Cancer, 53:5–15.

Fully Automated Volumetric Measurement of Malignant Pleural Mesothelioma from Computed Tomography Images by Deep Learning:

Preliminary Results of an Internal Validation