
A Genetic Algorithm Optimising Control Point Placement for Edge
Bundling
Ryosuke Saga
1 a
, Tomoki Yoshikawa
1
, Ken Wakita
2 b
, Ken Sakamoto
2
, Gerald Schaefer
3
and Tomoharu Nakashima
1 c
1
Graduate School of Humanities and Sustainable System Sciences, Osaka Prefecture University,
1-1 Gakuen-cho, Naka-ku, Sakai, Osaka, Japan
2
School of Computing, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo, Japan
3
Department of Computer Science, Loughborough University, Epinal Way, Loughborough, U.K.
{saga@cs., sza01319@edu., tomoharu.nakashima@kis.}osakafu-u.ac.jp, {wakita@is.,sakamoto.k.ap@m.}titech.ac.jp,
Keywords: Edge Bundling, Optimisation, Genetic Algorithm, Control Point.
Abstract: This paper describes a novel approach of edge bundling that employs a genetic algorithm (GA) to optimise
the placement of control points. Edge bundling is a useful technique to reduce visual clutter and a number of
model-based edge bundling approaches have been introduced in the literature. However, these do not attempt
to optimise aesthetic rules directly. Differently from them, our approach assumes that edge bundling is
regarded as an optimisation problem for aesthetic rules. To solve this problem, we present an GA-based
algorithm where gene representation defines control points of edges in order to allow flexibility and the fitness
function is defined based on quantitative criteria for edge bundling. Experimental results using a visualisation
of a Japanese airline map demonstrates the feasibility of our proposed method and its usability.
1 INTRODUCTION
Edge bundling is a method to decrease visual clutter
and thus improve understanding the layout of edges
by bundling edges based on certain rules.
Edge bundling is a well researched research topic.
Most works in this area define a model to express
edge bundling with one of the best known methods
being Holten’s work where they proposed
Hierarchical Edge Bundling for a graph based on a
tree structure (Holten, 2006).
Geometry-Based Edge Bundling (GBEB)
proposed by Cui et al. (2008) realises edge bundling
so as to bend edges based on meshes generated
through a Delaunay triangulation, although this
approach sometimes leads to some extreme bends. On
the other hand, Holten et al. (2009) proposed Force-
Directed Edge Bundling (FDEB) which performs
bundling based on Hooke's law. Also, Selassie et al.
(2011) introduced Divided Edge Bundling by
improving FDEB to apply to directed graph, while
a
https://orcid.org/0000-0003-1528-6534
b
https://orcid.org/0000-0003-2489-9017
c
https://orcid.org/0000-0002-1443-0816
Hurter et al. (2012) proposed Kernel Density
Estimation Edge Bundling based on image-based
visualisation. Yamashita et al. (2017) presented a
Line-Graph Based Edge Bundling that is based on the
idea that clustered edges should be bundled with the
clusters being detected by a line-graph.
In this paper, we propose an approach that differs
from the above-mentioned ones. In particular, we
propose a genetic algorithm (GA)-based approach for
edge bundling. GA (Goldberg, 1989) is a well-known
optimisation technique that is rooted in a model of
evolution and the principle of survival of the fittest. A
characteristic feature of our approach is that it allows
for a flexible implementation and to easily modify
parameters and fitness function.
Some recent related approaches also regard edge
bundling as an optimisation problem. In particular,
the work by Ferreira et al. (2018) formulates an
optimisation problem where the number of edges
including bundled edges is minimised based on the
assumption that only edges sharing the same vertex
Saga, R., Yoshikawa, T., Wakita, K., Sakamoto, K., Schaefer, G. and Nakashima, T.
A Genetic Algorithm Optimising Control Point Placement for Edge Bundling.
DOI: 10.5220/0008983202170222
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 3: IVAPP, pages
217-222
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
217
should be bundled. They also use constraints on the
bundled edges, in particular an angle threshold and
compatibility constraints.
In this paper, we take quantitative criteria based
on aesthetic rules into consideration and solve the
optimisation problem using a genetic algorithm. For
this, we adopt the control points approach used in
FDEB and the criteria from (Sakamoto et al., 2019;
Saga, 2016; Saga, 2018). As a result, we are able to
overcome the overcome the shortcomings of
Ferreira’s model.
The main contributions of this paper are the
following:
▪ It is the first approach of a genetic algorithm-
based edge bundling algorithm optimising control
points with regards to an aesthetic evaluation
index.
▪ We show that edge bundling using a
computational intelligence approach to
optimisation yields a feasible method.
▪ We discuss the extensibility of our proposed
method and its application in future work
2 GA-BASED EDGE BUNDLING
2.1 Genetic Algorithm
Genetic algorithms, which belong to the family of
evolutionary algorithms, simulate Darwin's theory of
evolution (Goldberg, 1989). GAs are employed to
solve difficult, often NP-hard, optimisation problems.
The genetic representation and fitness function
depend on the problem and domain to solve. After
these are defined, a GA proceeds iteratively through
stages of selection, crossover, and mutation to
improve a population of individuals that expresses
candidate solutions to the problem.
2.2 Genetic Representation
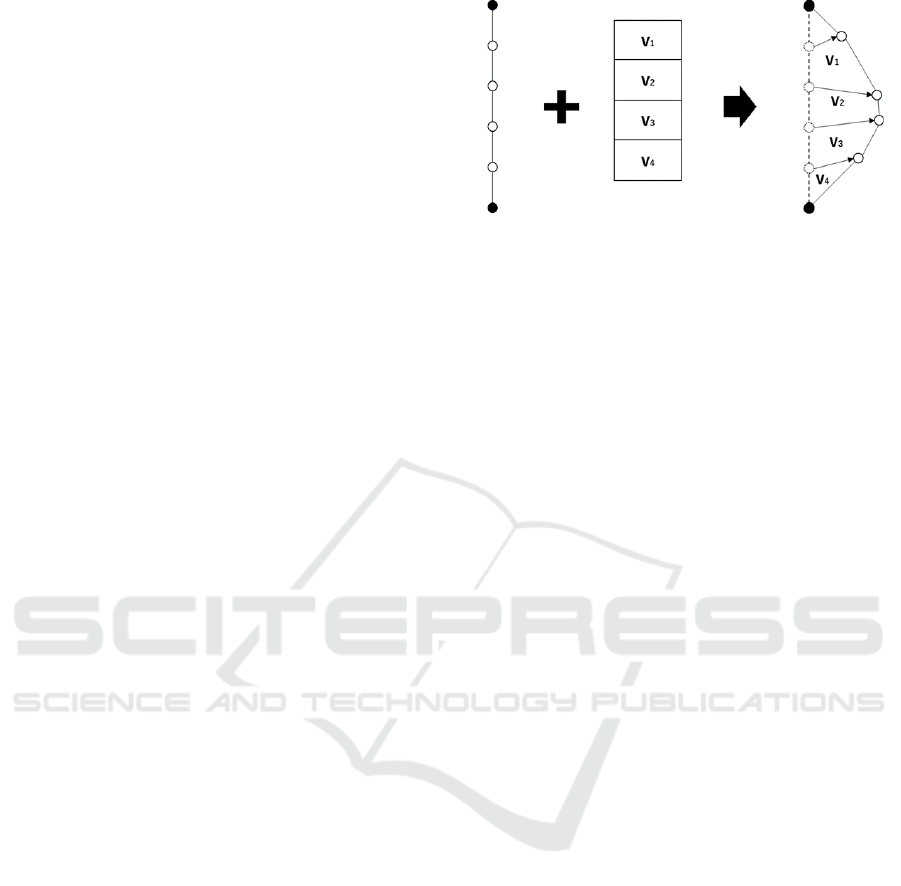
In our approach, the genetic representation we choose
is based on control-based approaches differently from
Ferreira’s. The approach employed in FDEB divides
an edge uniformly by c control points. By moving
these control points the edges can be controlled for
edge bundling. In our algorithm, edges in the input
graph are also divided based on c uniformly spaced
points as shown in Figure 1. For each control point,
we then store a displacement vector v (as (x,y)-co-
ordinates) whose distance we limit. Thus, for n edges
and using c control points per edge, we encode 2*n*c
parameters.
Figure 1: Genetic representation.
2.3 Fitness Function
An appropriate fitness function is key to a successful
GA. Some investigations of graph layout using GA
for visualisation design the fitness function based on
aesthetics rules (Eloranta et al. 2001, Wang et al.
2005,). In graph drawing, the following rules are
generally accepted:
(1) Uniform spatial distribution of vertices;
(2) Minimise the total edge length on the pre-
condition that the distance between any two
vertices is no less than the given minimum value;
(3) Uniform edge length;
(4) Maximise the smallest angle between edges
incident on the same vertex;
(5) The angles between edges incident on the same
vertex should be as uniform as possible;
(6) Minimise the number of edge crossings;
(7) Exhibit any existing symmetric feature.
For our problem at hand, it is necessary to
quantify such aesthetics rules for edge bundling.
Here, there are also some general accepted aesthetic
rules like for the general graph drawing problem
which have been introduced in the literature
(Sakamoto et al., 2019). The data-ink ratio (Tufte
2001) is one of the most widely used ones to evaluate
visualisation results quantitatively in all of
visualization problems. It is based on the ink amount
required for drawing a visualised figure. The path
quality, proposed by Cui in GBEB, is also useful to
evaluate the degree of zig-zag in edge bundling.
Furthermore, Saga (2016, 2018) proposed three
quantitative criteria to evaluate edge bundling which
are formulated from the difference of edge length,
area illustrated by edges (which is similar to data-ink
ratio), and density of edges.
In our approach, we adopt these three criteria
together with the path quality by Cui.
2.3.1 Mean Edge Length Difference
Mean Edge Length Difference (MELD) is a criterion
to express the difference from the original edges after
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
218

edge bundling. A smaller change of edge lengths
indicates superior edge bundling because of over-
bundling, whereas a large change often leads to a loss
of the meaning of the original network. MELD is
calculated as
(1)
where n is the number of edges, E is the edge set, and
L(e) and L’(e) are the lengths of edge e before and
after edge bundling, respectively. Employing this
criterion, we can prevent edges from over-bending
and over-bundling. MELD can be normalised to [0;1]
by
In our approach, we aim to minimise the MELD.
2.3.2 Mean of Occupation Area
Mean of Occupation Area (MOA) indicates the
degree among the compressed areas before and after
edge bundling. Based on the idea that better bundling
can compress the area occupied by the edges, MOA
is calculated as
(2)
where N is the number of total areas, O(e) is the set of
areas occupied by edge e based on an occupation
degree (we use 5% of unit area), and | | indicates the
number of elements contained by a set. Minimising
the MOA is one of our optimisation goals.
2.3.3 Edge Density Distribution
Edge Density Distribution (EDD) is rooted in the idea
that a better edge bundling method can gather edges
within a unit area and that the density per unit is high.
EDD is calculated from an image by
(3)
where A is a set of unit areas, p(a) is the rate of the
number of pixels, in which the edges pass in Area a,
and p is a mean of p(a). A variance-based measure,
the EDD is higher when the values are concentrated
on some ranges.
However, this calculation does not work well as it
is calculated from an image and it is difficult to
express the density correctly from an image. Also,
EDD does not work well when edge spread in an area
due to zig-zag although path quality mentioned later
can address this.
Therefore, we redefine EDD to express the
density more clearly by counting not the area but the
number of edges per pixel and calculating the
variance of edges as
(4)
where P is a set of pixels, H(p) is the number of edges
pathing pixel p, and H is the average of H(p). We aim
to maximise the EDD.
2.3.4 Path Quality
Path Quality (PQ) expresses the degree of zig-zag.
The lower the PQ, the better the edge bundling. PQ is
calculated by the summation of angle differences
between neighbours as
(5)
with
(6)
and
(7)
, where m is the number of segments divided by
control points+1, and A
i
is the angle between the
original edge and the segment edge. In our GA, we
try to maximise PQ.
We use the above four criteria separately and
perform multi-objective optimisation.
2.4 Genetic Operations
We employ a standard genetic algorithm. We perform
random initialisation, use uniform crossover and
uniform mutation, while we update the population
based on an elitist strategy. Note that, this problem is
solved as a multi-objective optimisation problem, so
that in our elitist strategy, pareto solutions are
regarded as elite and inherited to the next generation
while the remaining individuals are selected
randomly from parents and offsprings.
3 EXPERIMENTS
3.1 Goal, Dataset, and Parameters
To confirm the usability of our proposed method, we
perform a set of experiments using a Japanese airline
map with 79 nodes and 233 edges. Figure 2 shows the
map as well as the result obtained by FDEB.
A Genetic Algorithm Optimising Control Point Placement for Edge Bundling
219

Figure 2: The original Japanese flight map and FDEB result
Figure 3: The results of our proposed method (First row: population:200 max: 300, Second row: population: 500, max:750).
For our algorithm, we used the following
parameter settings: number of generations: 750,
population: (initial 200, maximum 300) and (initial
500, maximum 700); mutation probability: 0.01,
crossover probability: 0.7, s of MOA: 5; c (the
number of control points): 4; v: 20, 30, and 50.
3.2 Results
Figure 3 shows one of the pareto solutions for each of
the tested values for v and population sizes.
From these, we see that all results have areas
where edges are successfully bundled. For v=20 and
v=30, mainly, edges in the area where the edge
density is low in the original graph (for example,
around Sado Island) were separated without being
bundled well. This is probably due to the fact that the
edges cannot be deformed to an appropriate bundle
position due to the number of control points and their
limits of displacement distance.
Overall, edges tend to be less smooth as the
displacement distance is increased. This is likely
caused by control point moving more than necessary
given the wider range of flexibility.
We can also compare the difference of the results
between population configurations. From Figure 3,
we can see that a larger population leads to an
improved visualisation.
Interestingly, our proposed method is able to
separate the route from Tokyo to Okinawa (in the
bottom-left area of the graph) clearly for v=30 and 50,
whereas FDEB is unable to do so.
We notice that in our results the edges still show
some zig-zag appearance, this is not unexpected since
the path quality is only one of the four criteria we
employ.
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
220

Figure 4: Fitness Function (x: generation, y: criteria).
Figure 4 plots the four criteria of the fitness
function as the GA progresses through the
generations. From there figure, we can be seen that
the values converge and the evolution has stopped.
Therefore, it is speculated that this result has fallen
into local optimization, and it is speculated that this
will be an issue. In other words, there is room to
improve the quality when we can prevent the
algorithm from falling into local optimization.
4 CONCLUSIONS
In this paper, we have proposed a genetic algorithm-
based edge bundling methods for visualisation
applications. We employ control point information
that is encoded in the GA together with a fitness
function that optimises several aesthetic rules. The
obtained results on a Japanese air route map confirm
the applicability and usability of our proposed
algorithm. We conclude with some issues that we
plan to investigate in future work.
4.1 Fitness Function
The employed fitness function and be modified or
extended to consider also the possibility of
faithfulness (Nguyen et al., 2013; Nguyen and Eades,
2017) and other indicators such as the ink-ratio.
4.2 Extensibility
In this approach presented here, the genetic
representation is based on control points. Adding
information on nodes and aesthetic rules of nodes
would allow also edge bundling in consideration of
the arrangement of nodes. Also, in this work, we have
employed only a simple standard GA whereas a large
number of other, more advanced GA algorithm can be
utilised.
4.3 Limitations
In this study, our aim is to highlight the potential of
generating an acceptable edge map visualisation
employing computational intelligence for edge
bundling. There are of course still limitations. One is
the computational complexity, which is a general
drawback of black-box optimisation techniques such
as GAs, in particular for large graphs. There is also a
problem with visual encoding. Although we do not
discuss visual encoding here, this extension can also
be applied if information on Visual Encoding is added
to a single locus.
ACKNOWLEDGEMENTS
This work is supported by 16K01250 and also
supported by NVIDIA Corporation with the donation
of the Titan Xp GPU used for this research.
REFERENCES
Holten, D., 2006. Hierarchical edge bundles: visualization
of adjacency relations in hierarchical data. In IEEE
Transactions on Visualization and Computer Graphics,
volume 12, number 5, pages 741–748.
Cui, W., Zhou, H., Qu, H., Wong, P. C., Li, X., 2008.
Geometry-based edge clustering for graph
visualization. In IEEE Transactions on Visualization
and Computer Graphics, volume 14, number 6, pages
1277–1284.
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
1 100 199 298 397 496 595 694 793 892 991
MOA
0
50
100
150
200
250
300
1 100 199 298 397 496 595 694 793 892 991
PQ
0
0.05
0.1
0.15
0.2
0.25
1 100 199 298 397 496 595 694 793 892 991
EDD
0
20
40
60
80
100
1 100 199 298 397 496 595 694 793 892 991
MELD
A Genetic Algorithm Optimising Control Point Placement for Edge Bundling
221

Holten, D., Wijk, J. J. Van., 2009. Force-directed edge
bundling for graph visualization. In Computer Graphics
Forum, volume 28, issue 3, pages 983–990.
Selassie, D., Heller, B., Heer, J., 2011. Divided edge
bundling for directional network data. In IEEE
Transaction Visualization & Computer Graphics,
volume 17, number 12, pages 2354–2363.
Hurter, C., Ersoy, O., Telea, A., 2012. Graph bundling by
kernel density estimation. In Computer Graphics
Forum, volume 31, number 3, pages 865–874.
Yamashita, T., Saga, R., 2017. Cluster-based edge bundling
based on a Line Graph, In Proceedings of the 12th
International Joint Conference on Computer Vision,
Imaging and Computer Graphics Theory and
Applications, pages 311-316.
Goldberg, D. E., 1989. Genetic Algorithms in Search,
Optimization and Machine Learning, Addison-Wesley
Longman Publishing Co., Inc..
Ferreira, J., Nascimento, H., Foulds, L., 2018. An
evolutionary algorithm for an optimization model of
edge bundling. In Information, volume 9, number 7.
Eloranta, T., Makinen, E, TimGA: A Genetic Algorithm for
Drawing Undirected Graphs, Divulgaciones
Matematicas, volume 9, number. 2, pages 155–171,
2001
Zhang, Q., Liu, H., Zhang,W., and Guo, Y. Drawing
Undirected graphs with genetic algorithms, Proceeding
of ICNC 2005, LNCS 3612, pages. 28-36, 2005.
Sakamoto, K., Saga, R., Wakita, K., 2019. A review on
quality assessment metrics for edge bundling
techniques. In 2019 Pacific Visualization Symposium
(PacificVis), pages 327–329.
Tufte, E. The Visual Display of Quantitative Information,
Graphics Press USA, 2001.
Saga, R., 2016. Quantitative evaluation for edge bundling
based on structural aesthetics. In EuroVis’ 16, pages
17–19.
Saga, R., 2018. Validation of quantitative measures for
edge bundling by comparing with human feeling. In
EuroVis’ 18, pages 25–27.
Nguyen, Q., Eades, P., Hong, S., 2013. On the faithfulness
of graph visualizations. In 2013 IEEE Pacific
Visualization Symposium (PacifficVis), pages 209–216.
Nguyen, Q. H., Eades, P., 2017. Towards faithful graph
visualizations. arXiv preprint arXiv: 1701.00921.
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
222
