
Efficient Visualization and Set-theoretic Difference Operations for
Accurate Geometric Modeling in Real-time Simulations
Alexander Leutgeb
a
, Michael Florian Hava
b
and Alexander Hans Leitner
c
Unit Industrial Software Applications, RISC Software GmbH, Softwarepark 35, Hagenberg, Austria
Keywords:
Implicit Representation, Point Cloud Fitting, Set-theoretic Modeling, Ray Casting, Real-time Simulation.
Abstract:
We present a novel approach, which supports efficient visualization and set-theoretic difference operations for
accurate geometric modelling in real-time simulations. The geometric operands can be in any representation
as long as they are watertight and are convertible to an oriented point cloud. A novel region growing based
fitting routine converts the oriented point clouds into a watertight piecewise quadratic implicit representation.
During set-theoretic modeling these implicit representations are mapped to the fixed depth hierarchical grid
of the resulting geometric model. Thereby a surface elimination algorithm removes parts not contributing
to the final surface. This guarantees that the number of already performed modeling operations have only a
minor performance impact on the algorithms processing the model. For visualization a novel ray casting based
approach was developed, enabling interactive frame rates at Full-HD screen resolutions. The evaluation of the
developed method proves its modeling performance and high geometric accuracy by means of the simulation
of subtractive manufacturing examples.
1 INTRODUCTION
There is a strong need for an efficient visualization
and set-theoretic difference operations in the context
of accurate geometric modeling in real-time simu-
lations. For example, the simulation of subtractive
manufacturing - material removal processes, such as
milling, turning or drilling - have become complex
tasks, requiring efficient systems for their geometric
model computation and visualization. The complex
multi-axis milling processes result in workpieces with
a high-quality surface finish requiring manufacturing
tolerances up to 0.001 mm generated by thousands of
removal steps.
Conventional solid modeling systems build the
foundation for computer-assisted geometric design
of “Virtual Products” via Computer Aided Design
(CAD) software. These systems are implemented
with respect to modeling capabilities, geometric mod-
eling precision, exchangeability of geometric for-
mats between different CAD systems, a geometric
representation, which is adequate for further anal-
ysis in the fields of Computer-Aided Engineering
a
https://orcid.org/0000-0001-8934-4501
b
https://orcid.org/0000-0002-5085-1490
c
https://orcid.org/0000-0002-4081-2586
(Finite-Element-Analysis and Computational-Fluid-
Dynamics). Their modeling operations do not offer
the necessary performance to support the application
in real-time simulations.
Our approach is a geometric modeling sys-
tem, which supports efficient visualization and set-
theoretic difference operations for accurate geomet-
ric modelling in real-time simulations. Thereby the
number of already performed set-theoretic difference
operations has only a minor performance impact
on the algorithms processing the geometric model.
The obtainable precision of the resulting geometric
model matches the requirements of industrial applica-
tions. The algorithms of the system utilize the paral-
lelization potential of modern hardware architectures.
Summarizing, the novelties introduced in this work
are mainly:
• A region growing based fitting routine for ori-
ented points clouds with an implicit representa-
tion using piecewise quadratic functions. The re-
sulting representation is watertight.
• A fixed depth hierarchical grid with an efficient
elimination strategy during set-theoretic modeling
operations.
• An efficient ray casting based visualization sup-
porting interactive frame rates.
Leutgeb, A., Hava, M. and Leitner, A.
Efficient Visualization and Set-theoretic Difference Operations for Accurate Geometric Modeling in Real-time Simulations.
DOI: 10.5220/0008983802990306
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages
299-306
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
299

2 RELATED WORK
Implicit surfaces are mostly defined by polynomials,
of which Quadrics are the most prominent represen-
tatives (Menon, 1996). These are polynomials of de-
gree two, which in contrast to polynomials of higher
degree, have closed and efficient solutions for certain
geometric problems like intersection computations.
Distance functions d(p) are special functions from R
3
to R, these compute the distance to the nearest point
on the implicit surface defined via d(p) = 0 for each
point p ∈ R
3
(Diener, 2012). Signed distance func-
tions (SDF) compute the signed distance, in which
negative distances usual represent the inside of an ob-
ject. In contrast to general implicit functions, dis-
tance functions offer several advantages considering
the simplicity of several computations, like surface
normals (normalized gradient d(p)) and set-theoretic
operations.
2.1 Discrete Signed Distance Fields
Adaptively sampled distance fields (ADF) use an Oc-
tree for hierarchical space decomposition and each
cell stores at its eight corner positions the discretized
values of a signed distance function (Frisken et al.,
2000). The hierarchical subdivision follows the shape
of the object according to a defined approximation er-
ror. Because of this adaptivity, complex geometric
objects can be represented in a memory efficient way.
This approach enables an efficient computation of the
set-theoretic operations union, intersection, and dif-
ference. One prominent method for the visualization
of adaptively sampled distance fields is Sphere Trac-
ing. The work of (Bastos and Celes, 2008) represents
an efficient implementation on Graphics Processing
Units (GPUs).
OpenVDB (Museth, 2013) supports a hierarchi-
cal data structure for the efficient representation of
sparse, time-varying volumetric data discretized on
a 3D grid. These values can be of scalar (signed
distance field) or vector (velocity vector field) type.
In contrast to an Octree, where the branching fac-
tor per dimension is two and its depth determines
the precision, OpenVDB uses a tree structure with a
fixed depth, and the precision depends on the branch-
ing factor per dimension at each hierarchical level.
An Octree based approach has a higher memory ef-
ficiency because of better adaptivity to the geometric
shape, but has higher run-times for searching specific
cells and set-theoretic modeling operations. Besides
the simulation of time-varying changes of volumes,
OpenVDB also supports efficient set-theoretic mod-
eling.
The approaches in this section have the following
limitation: In order to reach a high modeling accuracy
the size of the leaf cells has to be very fine. This fine
granularity has a negative performance impact on set-
theoretic modeling operations.
2.2 Continuous Signed Distance
Functions
Multi-level partition of unity (MPU) implicits sup-
port an adaptive error-driven approximation of a sur-
face via signed distance functions in a precise and fast
way (Ohtake et al., 2003). In order to create the im-
plicit representation, the geometric object (in the con-
crete case defined via an oriented point cloud) is spa-
tial subdivided according to an Octree structure. In
each Octree cell a piecewise quadratic function (lo-
cale shape function) is created, which approximates
the geometry assigned to the according cell. These
shape functions behave like signed distance functions
and yield a value close to zero in the proximity of
the surface of the approximated geometric shape, a
positive value inside and a negative value outside.
In the case, the local shape function exceeds a de-
fined approximation error for the cell assigned geo-
metric object, the fitting routine subdivides the cell
further and performs the approximation on the new
child cells. The algorithm repeats this process until
the approximation error falls below a defined thresh-
old. Locale shape functions are generic Quadrics, bi-
variate Quadrics and their set-theoretic combination.
By this distinction, it is possible to approximate flat
surfaces as well as surfaces with geometric features
like corners and edges at a high precision. The usage
of signed distance functions enables shape blending,
offsetting, and set-theoretic operations like union, in-
tersection, and difference. Visualization methods for
MPU implicits are direct rendering in polygonised
form or Sphere Tracing (Hart, 1996). Because the
MPU approach offers set-theoretic modeling by com-
bining two distinct geometric objects at the time of
visualization, it does not scale with increasing num-
ber of set-theoretic operations.
Sparse low-degree implicits (SLIM) is a method
approximating the surface of a geometric object with
surface elements (Surfel) (Ohtake et al., 2005). The
geometric object is in form of a point cloud. The
definition of a Surfel consists of a sphere (specified
via center and radius), and a function approximating
the surface inside the sphere. Functions can be linear,
quadratic or cubic polynomials. The global surface
results from overlapping Surfels and is not continu-
ous. Surface continuity is guaranteed during visual-
ization via ray casting. The construction of the Surfel
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
300

representation happens in a hierarchical way, by start-
ing with Surfels with a big radius. Depending on a
cost function, which considers the approximation er-
ror and memory efficiency the fitting routine further
subdivides these Surfels into finer ones. The SLIM
approach has the problem, in order to represent ge-
ometric features like edges or corners with high ge-
ometric accuracy the subdivision of the Surfels must
be very fine.
3 GEOMETRIC
REPRESENTATION
Our implicit representation is based on the work of
(Ohtake et al., 2003) and supports the following kinds
of local fitted functions inside a support sphere:
• A bivariate quadratic polynomial in local coordi-
nates.
• A piecewise quadratic surface that fits an edge or
a corner.
3.1 Point Cloud Generation
The newly developed geometric modeling method re-
quires a watertight implicit representation of the geo-
metric objects involved in set-theoretic modeling op-
erations. In order to obtain the implicit representation
for a given triangle mesh, it is first converted into an
oriented point cloud with a specified uniform point
density ρ. For each triangle of the input mesh points
are generated:
• Triangle vertices: For each triangle vertex a point
is generated.
• Triangle edges: If a triangle edge width length l
is longer than ρ, then the edge is split into dl/ρe
parts and points are generated between neighbour-
ing parts.
• Triangle area: The longest edge of a triangle
forms the base vector. The height vector is or-
thogonal to the base vector and its magnitude rep-
resents the triangle height. The base and height
vector form a Cartesian coordinate system, in
which an algorithm generates at regular ρ posi-
tions points in both dimensions, but only if the
point is enclosed by the triangle.
For each generated point the surface normal at its
position is computed. Points shared by multiple tri-
angles with different face normals are replicated with
the respective normal.
3.2 Overall Fitting Procedure
For the region growing based approximation of the
oriented point cloud P the metric ρ(P) is introduced.
As the radius of the support sphere during fitting is at
least 2ρ, it is guaranteed that the number of points is
sufficient for fitting the local shape function.
ρ(P) = max
a∈P
( min
b∈P∧a6=b
(ka − bk)) (1)
The region growing approach starts with a seed-
ing phase. Thereby the algorithm chooses a random
not already approximated point from the overall point
cloud as center for an initial support sphere with ra-
dius 4ρ. In the case of a successful fit with a lo-
cal function, the algorithm shrinks the support sphere
with radius r by ρ. The space between the initial and
the shrunken sphere is the boundary region (see Fig-
ure 1). All points inside the shrunken support sphere
are considered as approximated. Now the growing
phase begins and the algorithm adds points not al-
ready approximated from this boundary region to the
set of growing points. Now a new center for a new
initial support sphere with radius 4ρ is chosen from
this set of growing points. After a successful fit in-
side the newly created support sphere, the not ap-
proximated points from the new bounding region ex-
tend the set of the growing points. Points considered
as approximated are removed from the set of grow-
ing points. Region growing continues until there are
no more growing points left. If there are any non-
approximated points left, the two stage fitting process
starts again.
Figure 1: Feeding and growing stages.
For each cluster the fitting with local functions
is performed yielding individual bivariate quadratic
polynomials. If the approximation error exceeds the
defined error threshold, the algorithm shrinks the sup-
port sphere by a factor of 0.85 and local function fit-
ting starts again. If the radius gets smaller than 2ρ
fitting is not possible at all.
The overall region growing algorithm works in
parallel in the following way. First the oriented point
Efficient Visualization and Set-theoretic Difference Operations for Accurate Geometric Modeling in Real-time Simulations
301

cloud is placed into a regular grid with cell size 4ρ per
dimension. The grid is partitioned into n work slices
along the dimension with the highest spatial extent,
where n is two times the number of logical processors.
The minimum slice thickness of two times the cell
size prevents race conditions during parallel code ex-
ecution. The parallel region growing algorithm works
in two phases:
• Phase 1: Each logical processor executes the re-
gion growing algorithm inside work slices with an
even sequence number.
• Phase 2: Each logical process executes the region
growing algorithm inside work slices with an odd
sequence number.
The result of the algorithm is a watertight approx-
imation of the oriented point cloud with overlapping
support spheres and local functions.
4 GEOMETRIC MODELING
4.1 Hierarchical Space Decomposition
(a) (b)
Figure 2: (a) Grid occupancy of first set-theoretic differ-
ence operand (support spheres are red and local functions
are blue). (b) Modeling grid after set-theoretic difference
operation.
During set-theoretic modeling the geometric operand
represented by support spheres with their local
functions is mapped to a hierarchical grid with a
fixed depth (see Figure 2). The developed space-
partitioning scheme is similar to OpenVDB (Museth,
2013) and shares the same advantages (see section
2.1). The cells of the grid can have the classifica-
tions inside, outside or surface. By convention the
initial geometric object is considered as the first set-
theoretic difference operand and therefore its surface
orientation is inverted (see Figure 2 (a)) and the initial
modeling grid is completely inside. Surface classifi-
cation can only occur on cell level 2, whereas the clas-
sifications inside and outside can also occur on higher
cell levels. The mapping of the surface represented
via the support spheres with their local functions to
cells works as following. The algorithm checks each
support sphere if it overlaps with cells at cell level 0.
If this is the case, it checks the overlap for each child
cell at the next cell level. It repeats this procedure un-
til cell level 2 is reached. Section 4.2 explains check-
ing for actual surface contribution of a support sphere
with its local function on cell level 2. The finest cell
level 3 stores a per geometric object grid occupancy
bit mask and an accumulated deletion bit mask. The
mapping logic for cell level 3 is the same as for cell
level 2. Section 4.3 explains the usage of cell level 3
in the context of surface elimination.
4.2 Cell Classification
Surface Cells. A support sphere and its local function
are only assigned to a cell on level 2, if there actually
is a surface contribution inside the cell. The surface
contribution is computed in the following way. At
first the algorithm computes the axis aligned bound-
ing box (overlap box) resulting from the overlap be-
tween the support sphere and the cell. If the function
has a surface contribution inside the cell it must cross
at least one of the six faces of the overlap box. In
Figure 3 you see one face of the overlap box colored
green. The red circle marks the intersection between
the support sphere and a face plane. The blue curve
marks the intersection between the local function and
the face plane. The green filled circles mark the posi-
tions, where the signed distance function is evaluated,
and contain the sign of the value. In the case this po-
sition is outside the support sphere, the green filled
circles are empty. In Figure 3 (a) to (c) you see the
recursive subdivision scheme of the algorithm, which
stops depending on the following cases:
• There are sign changes between neighboring eval-
uation points so the function crosses the space
between these two points and we have a surface
contribution inside the cell. The reference point
(filled red circle) is the intersection between a line
ranging between these two points and the local
function.
• The size in both dimensions of the subdivided
rectangular areas falls under a certain threshold so
no surface contribution was detected.
The reference point is needed for inside/outside calcu-
lation during visualization via ray casting (see section
5.2).
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
302
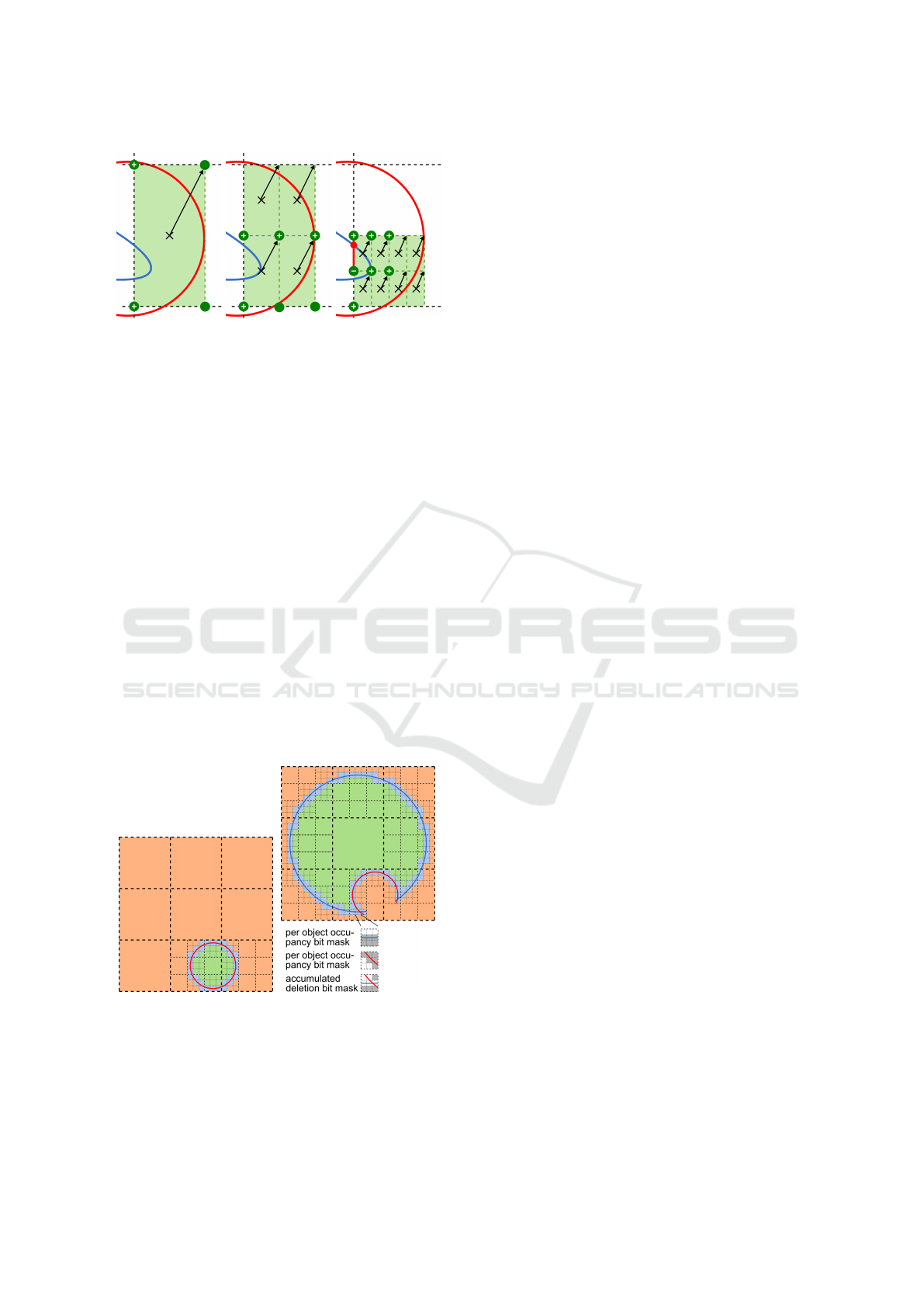
(a) (b) (c)
Figure 3: Determination of surface contribution for local
function. (a) Initial area. (b) Areas after first subdivision.
(c) Areas after second subdivision.
Inside/Outside Cells. The classification algorithm
categorizes the non-surface cells into inside or outside
cells in the following three ways, sorted by increasing
computational costs:
1. Adopt the classification of direct neighboring cell.
2. If cell center is inside a support sphere evaluate
the according signed distance function for the po-
sition and derive classification from sign of result.
3. If cell center is outside of any support sphere, cre-
ate a line ranging from the cell center to the cen-
ter of the closest support sphere. Compute the in-
tersection point between the line and the support
sphere. Evaluate signed distance function for in-
tersection position and derive classification from
sign of result.
4.3 Surface Elimination
(a) (b)
Figure 4: (a) Grid occupancy of second set-theoretic differ-
ence operand. (b) Modeling grid after set-theoretic differ-
ence operation showing surface elimination.
Figure 4 illustrates the process of surface elimina-
tion. (a) shows the grid occupancy of the second set-
theoretic difference operand. In (b) you see the mod-
eling grid after the set-theoretic difference operation,
where all the surface cells of the initial geometric ob-
ject inside the surface cells of the set-theoretic differ-
ence operand were cleared. Clearing in this context
means removing all surfaces from surface cells and
changing the cell classification from surface to out-
side. If all child cells of a parent cell have the same
cell classification outside, then the subdivision of the
parent cell into child cells is withdrawn and the algo-
rithm transfers the child cell classification to the par-
ent cell. Additional surface elimination can occur by
using the information from cell level 3. Thereby we
have to differentiate between two different cases:
• If all the bits in the accumulated deletion bit mask
are set, then all surfaces from the surface cell are
removed and the cell classification is changed to
outside.
• If for all the set bits of the per object occupancy bit
mask the according bits in the accumulated dele-
tion bit mask are set, then the surface of the geo-
metric object can be removed.
5 VISUALIZATION
5.1 Ray Casting of Watertight Surfaces
For the visualization of surfaces resulting from set-
theoretic modeling ray casting was first mentioned in
the work of (Roth, 1982). Thereby the operands in-
volved during modeling must be in watertight form.
The basic idea is to calculate the surface intersec-
tions of all involved geometrics objects with the ray.
Then the algorithm sorts the intersections according
to an increasing distance between ray origin and in-
tersections. Now the algorithm calculates the result-
ing surface point in the following way. It starts with a
counter initialized with a predefined value. By going
through the list of intersections it decrements or in-
crements this counter depending on the fact if a ray
enters respectively leaves a geometric object at the
current intersection. The method detects entering or
leaving by using the surface normal at the intersection
point and the normalized ray direction. If the normal-
ized ray direction points into the same half-space as
the surface normal the ray leaves the geometric ob-
ject, otherwise the ray enters it. If during counting the
counter reaches a defined value the resulting surface
point is hit. This visualization principle is also appli-
cable to the developed surface representation, because
overlapping support spheres with local functions de-
scribe a watertight surface of a geometric operand.
Efficient Visualization and Set-theoretic Difference Operations for Accurate Geometric Modeling in Real-time Simulations
303
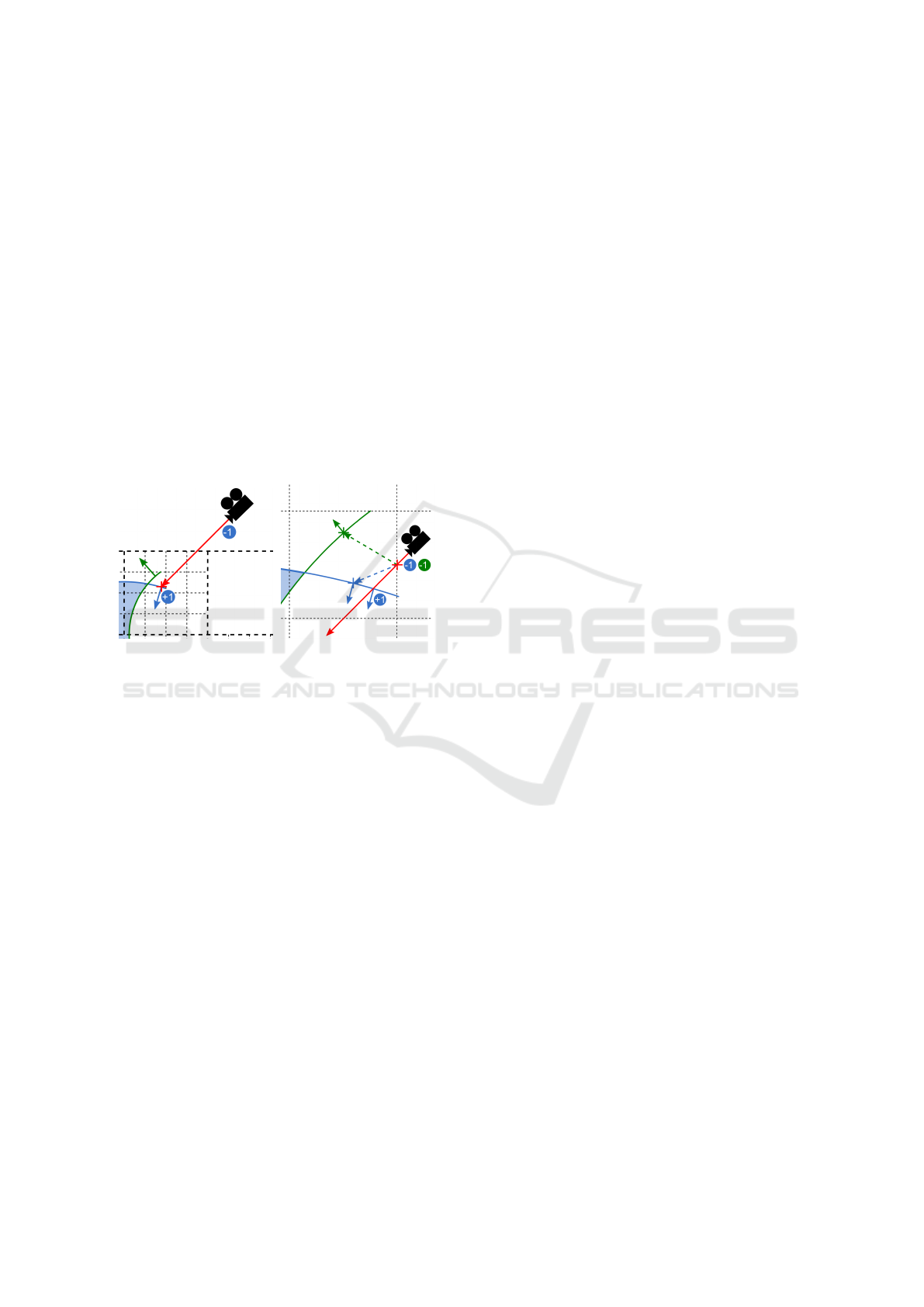
5.2 Ray Casting of Non-watertight
Surfaces
Because of the surface elimination during set-
theoretic modeling we lose the watertightness of the
geometric operands. In Figure 5 (a) you see the grid
occupancy in the case of a set-theoretic difference op-
eration where the initial geometry is colored blue and
the subtractive geometry is colored green. By conven-
tion, we define the initial geometric object as first sub-
tractive geometric object. Therefore the counter at the
ray origin is initialized with -1 (ray origin inside ini-
tial geometric object). During counting, the algorithm
reaches the resulting surface point, if the counter gets
the value 0. If we execute the usual counting proce-
dure, the resulting surface point will be wrong, be-
cause of the missing ray intersections between the ray
and the geometric objects.
(a) (b)
Figure 5: (a) Wrong resulting surface point (red cross ) dur-
ing counting. (b) Calculating the number of geometric ob-
jects containing the entry point (red cross) and surface point
evaluation via counting.
The solution to this problem is to perform the
counting procedure not globally but locally on surface
cell level. Therefor we must first reconstruct the miss-
ing ray entries for all geometric objects inside a sur-
face cell (see Figure 5 (b)). That means the algorithm
calculates the point, where the ray enters the surface
cell (entry point). Then it calculates the number of ge-
ometric objects containing the entry point. Therefor it
builds for each geometric object a secondary ray rang-
ing from the entry point to the reference point on the
surface of the geometric object. It computes all inter-
sections between the secondary ray and the piecewise
surfaces of the geometric object and determines the
closest intersection to the entry point. For the closest
intersection, the procedure computes the surface nor-
mal via the gradient of the according local function.
If this surface normal and the secondary ray direction
point into the same half-space, the entry point is in-
side the geometric object. After the computation of
the number of geometric objects containing the en-
try point, the algorithm initializes the counter with its
negative value. Then it computes the intersections be-
tween the ray and the surfaces of the geometrics ob-
jects. These intersections are again sorted according
to an increasing distance between ray origin and inter-
section. By going through the list of intersections the
procedure decrements or increments this counter as
usual. If the counter gets to 0, the algorithm reached
the resulting surface point.
5.3 Acceleration Structure and
Coherent Ray Traversal
For ray casting a two level hierarchical grid is used
with matching positions between level 2 cells of the
modeling grid and leaf cells of the ray casting grid.
Usually in ray-casting spatial decomposition tech-
niques follow the shape of the geometric objects (e.g.
Bounding Volume Hierarchies and kd-Trees). The de-
veloped approach subdivides space at fixed boundary
positions, because of the surface elimination strategy.
The work of (Wald et al., 2009) gives an overview of
the different spatial decomposition techniques in the
context of ray casting.
This two level grid approach offers a good com-
promise between traversal time, actual surface evalua-
tion time inside cells, and sparsity. Based on the work
of (Kalojanov et al., 2011) we expect this design to
be adequate for a future implementation for Graphics
Processing Units (GPUs). During ray casting the rays
for the whole screen resolution are organized in co-
herent ray packets traversing the two level grid slice
by slice. Neighboring rays inside a ray packet mostly
traverse the same cells so the algorithm benefits from
the induced memory coherence. A packet size of 4x4
rays turned out to be the most performant for the over-
all ray-casting procedure. The work of (Wald et al.,
2006) gives an introduction into ray casting of scenes
with coherent grid traversal, comparing the visualiza-
tion times for different ray packet sizes.
During ray-casting we intersect each cell of the
traversed slices with the rays of the ray packet. The
algorithm marks the rays, which have already inter-
sected the resulting surface, as inactive. The remain-
ing active rays are compacted for vectorized process-
ing. Depending on the number of active rays inter-
secting a cell the algorithm branches in a vectorized or
scalar processing intersection routine. In the current
implementation, the threshold for vectorized process-
ing is at least 4 rays intersecting a cell. By using Cen-
tral Processing Units (CPUs) at least with Streaming
SIMD Extension 4 (SSE4) support, we can perform 4
single precision floating point calculations in parallel
at CPU core level.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
304

6 EVALUATION
The experimental results presented in this section are
based on the following hardware configuration: Intel
Xeon E5-1660 v4 (eight cores @ 3.4 GHz [Turbo],
theoretical peak performance 435.2 GFlops in single
precision) and 32 GB DDR4 2400 RAM. For evalu-
ation, we are using a static grid configuration of 20
cells per dimension at level 0, 5 at level 1, 5 at level 2
and 3 at level 3. All renderings were performed with
a resolution of 1920 x 1080. The point clouds of the
geometric operands were fitted with a geometric ap-
proximation error of 0.01 % of the maximal spatial
model extent.
Comparing to Related Work. To compare our
method with the approaches (MPU, 2003) and (SLIM,
2005) we use two different geometric modeling ex-
amples based on subtractive manufacturing processes,
see Figure 6 and Table 1. Note that only our approach
is parallelized, therefore a speedup of up to factor 8 is
to be expected.
(a) Impeller (b) Gear
Figure 6: Resulting geometric objects.
Table 1: Point cloud size of initial and subtractive objects.
Example Initial Subtractive
Impeller 536959 19896
Gear 263854 44120
Table 2 and Table 3 summarize the measured
times in milliseconds for fitting and rendering of one
frame. As the MPU and SLIM implementations do
not make use of parallel code exeuction, we pro-
vide single-threaded measurements (Our
ser
) in addi-
tion to multi-threaded ones (Our
par
). Given the non-
embarrassingly parallel nature of overall fitting we
cannot achieve the theoretical maximum speedup, yet
still outperform the single threaded alternatives in all
but one test. Even if we switch to serial execution
our approach to rendering outperforms the alterna-
tives due to conceptual differences.
Table 2: Comparison of fitting times in milliseconds.
Example MPU SLIM Our
ser
Our
par
Imp.
init
6300 107711 13684 1369
Imp.
sub
870 1720 2541 751
Gear
init
4339 51423 6870 1061
Gear
sub
2671 2158 9130 2925
Table 3: Comparison of rendering times in milliseconds.
Example MPU SLIM Our
ser
Our
par
Imp.
init
15930 1750 778 125
Imp.
sub
6548 510 394 112
Gear
init
16923 870 406 90
Gear
sub
26311 1570 1308 270
Benchmarking of Geometric Modeling Examples.
In both of these examples the simulation starts with
an initial geometry and consecutively applies set-
theoretic difference operations. The measured model-
ing times vary considerably depending on the amount
of cells affected by the respective operation. The
number of already completed modeling steps has only
negligible impact (see Figure 7).
(a) Impeller
(b) Gear
Figure 7: Measured times for modeling and visualization of
one frame.
Analyzing the rendering performance, one can see
that the number of already completed modeling oper-
ations only marginally impacts our visualization ap-
proach. Figure 6 presents the resulting geometric ob-
jects after the completion of all modeling operations
from the perspective used for the visualization bench-
marking. Even though modeling in example Impeller
affects large parts in image space and rendering times
are bound to rise, there is only moderate growth in
rendering time. In example Gear the rendering times
Efficient Visualization and Set-theoretic Difference Operations for Accurate Geometric Modeling in Real-time Simulations
305

stay almost constant, because only very small parts in
image space are affected by the overall modeling.
7 CONCLUSIONS
The experimental results have proven that our ap-
proach is proper for precise geometric modeling in
real-time simulations. The number of already com-
pleted modeling operations has only a minor perfor-
mance impact on the algorithms processing the geo-
metric model, provided the surface elimination works
in an efficient way. Currently the surface elimination
algorithm uses as smallest elimination granularity the
cells of the hierarchical modeling grid at the finest
level. A cell is marked for deletion, if it is completely
covered by a geometric modeling operand. A future
extension to the elimination strategy is the detection
of complete containment of one geometric operand in
another one on surface cell level, which is not limited
by fixed spatial boundaries. Some additional points
for future improvements are:
• The visualization routine would benefit from an
implementation for Graphics Processing Units
(GPUs), due to the embarrassingly parallel prob-
lem formulation of ray casting.
• Introduction of set theoretic union operation re-
quiring an extension to the surface elimination
and visualization strategy.
ACKNOWLEDGEMENTS
This project is co-financed by the European Fund for
Regional Development (EFRE) and the state of Upper
Austria as part of the program “Investing in Growth
and Jobs” (IWB). Further information can be found
on https://www.iwb2020.at.
REFERENCES
Bastos, T. and Celes, W. (2008). Gpu-accelerated adap-
tively sampled distance fields. In 2008 IEEE Inter-
national Conference on Shape Modeling and Applica-
tions, pages 171–178.
Diener, C. L. (2012). Procedural modeling with signed dis-
tance functions. Unpublished bachelor’s thesis, Karl-
sruher Institute of Technology, Karlsruhe, Germany.
Frisken, S. F., Perry, R. N., Rockwood, A. P., and Jones,
T. R. (2000). Adaptively sampled distance fields: A
general representation of shape for computer graph-
ics. In Proceedings of the 27th Annual Conference on
Computer Graphics and Interactive Techniques, SIG-
GRAPH ’00, pages 249–254, New York, NY, USA.
ACM Press/Addison-Wesley Publishing Co.
Hart, J. C. (1996). Sphere tracing: a geometric method for
the antialiased ray tracing of implicit surfaces. The
Visual Computer, 12(10):527–545.
Kalojanov, J., Billeter, M., and Slusallek, P. (2011). Two-
level grids for ray tracing on gpus. Computer Graph-
ics Forum, 30(2):307–314.
Menon, J. (1996). An introduction to implicit techniques.
In Course Notes of the 23rd Annual Conference on
Computer Graphics and Interactive Techniques - Im-
plicit Surfaces for Geometric Modeling and Computer
Graphics, pages 13–26, New Orleans, LA, USA.
MPU (2003). Mpu software. http://home.eps.hw.ac.uk/
∼
ab226/software/mpu implicits/mpu/mpu oct 03.zip.
Retrieved July 7, 2016, from Heriot Watt University.
Museth, K. (2013). Vdb: High-resolution sparse vol-
umes with dynamic topology. ACM Trans. Graph.,
32(3):27:1–27:22.
Ohtake, Y., Belyaev, A., and Alexa, M. (2005). Sparse
low-degree implicit surfaces with applications to high
quality rendering, feature extraction, and smoothing.
In Proceedings of the Third Eurographics Sympo-
sium on Geometry Processing, SGP ’05, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
Ohtake, Y., Belyaev, A., Alexa, M., Alexa, M., Turk, G.,
and Seidel, H.-P. (2003). Multi-level partition of unity
implicits. ACM Trans. Graph., 22(3):463–470.
Roth, S. D. (1982). Ray casting for modeling solids. Com-
puter Graphics and Image Processing, 18(2):109 –
144.
SLIM (2005). Slim software. http://www.riken.go.jp/
lab-www/VCAD/VCAD-Team/members/ohtake/
slim/. Retrieved July 7, 2016, from RIKEN.
Wald, I., Ize, T., Kensler, A., Knoll, A., and Parker, S. G.
(2006). Ray tracing animated scenes using coherent
grid traversal. ACM Trans. Graph., 25(3):485–493.
Wald, I., Mark, W. R., G
¨
unther, J., Boulos, S., Ize, T., Hunt,
W., Parker, S. G., and Shirley, P. (2009). State of the
art in ray tracing animated scenes. Computer Graphics
Forum, 28(6):1691–1722.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
306
