
Modelling Brain Lesion Volume in Patches with CNN-based Poisson
Regression
Kevin Raina
a
Department of Mathematics and Statistics, University of Ottawa, Ontario, Canada
Keywords:
Stroke, Brain Lesions, MRI, Poisson Regression (PR), Convolutional Neural Network.
Abstract:
Monitoring the progression of lesions is important for clinical response. Summary statistics such as lesion
volume are objective and easy to interpret, which can help clinicians assess lesion growth or decay. CNNs are
commonly used in medical image segmentation for their ability to produce useful features within large con-
texts and their associated efficient iterative patch-based training. Many CNN architectures require hundreds
of thousands parameters to yield a good segmentation. In this work, an efficient, computationally inexpensive
CNN is implemented to estimate the number of lesion voxels in a predefined patch size from magnetic reso-
nance (MR) images. The output of the CNN is interpreted as the conditional Poisson parameter over the patch,
allowing standard mini-batch gradient descent to be employed. The ISLES2015 (SISS) data is used to train
and evaluate the model, which by estimating lesion volume from raw features, accurately identified the lesion
image with the larger lesion volume for 86% of paired sample patches. An argument for the development and
use of estimating lesion volumes to also aid in model selection for segmentation is made.
1 INTRODUCTION
Many segmentation challenges have been undertaken
recently, showing the need for automated models in
clinical settings (Maier et al., 2017; Winzeck et al.,
2018; Bakas et al., 2018). Along with strong predic-
tive power, these challenges stress the importance of
fast inference, as lesions can quickly spread. For in-
stance, ischemic stroke lesions cause increasing tis-
sue death within hours of onset, requiring reperfu-
sion therapies around this time. The stroke progresses
through acute, sub-acute and chronic stages within
days. Gliomas, the most common type of malignant
brain tumour, grows at a rate of increasing severity
depending on the grade. As the tumour gets larger,
symptoms often worsen, reinforcing the need to mon-
itor lesion growth.
A simple, yet powerful, summary statistic is the
lesion volume, or when the brain is represented as
labelled voxels, the lesion label count. In a clini-
cal study, (Alexander et al., 2010) showed that le-
sion volume is a significant covariate for understand-
ing ischemic stroke deficits after the initial onset. In
application, lesion volume has generally been a de-
pendable factor in the prognosis of ischemic stroke
a
https://orcid.org/0000-0002-6240-9675
(Merino et al., 2007; Rivers et al., 2006) and multi-
ple sclerosis (Zivadinov et al., 2012; Bagnato et al.,
2011). The objectivity of counts enables straightfor-
ward inference: a higher lesion label count means the
lesion has grown.
In comparison to segmenting entire 3D medical
images, directly estimating the number of lesion vox-
els in the brain from raw features should be expected
to require less computational resources since it is
no longer necessary to provide detailed information
about the lesion’s appearance. Nonetheless, in a study
by (Erskine et al., 2005) comparing the effects on vol-
ume estimation by using different magnetic resonance
imaging scanners, lesion volume was estimated from
a computer-assisted segmentation tool. Other meth-
ods for estimating lesion volume favored a geometric
approach, wherein the lesion’s surface area per slice is
calculated and the estimate is derived by summing ac-
cross slices (Park et al., 2013; Filippi et al., 1995). In
contrast, the output of our proposed statistical direct
lesion counting model is a single non-negative integer
that doesn’t require sophisticated viewing software or
significant memory usage.
CNNs have shown promising results in lesion seg-
mentation, as in the works of (Kamnitsas et al., 2017),
(Havaei et al., 2017) and (Ronneberger et al., 2015),
due to their ability to produce useful features from
172
Raina, K.
Modelling Brain Lesion Volume in Patches with CNN-based Poisson Regression.
DOI: 10.5220/0009102701720176
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 2: BIOIMAGING, pages 172-176
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
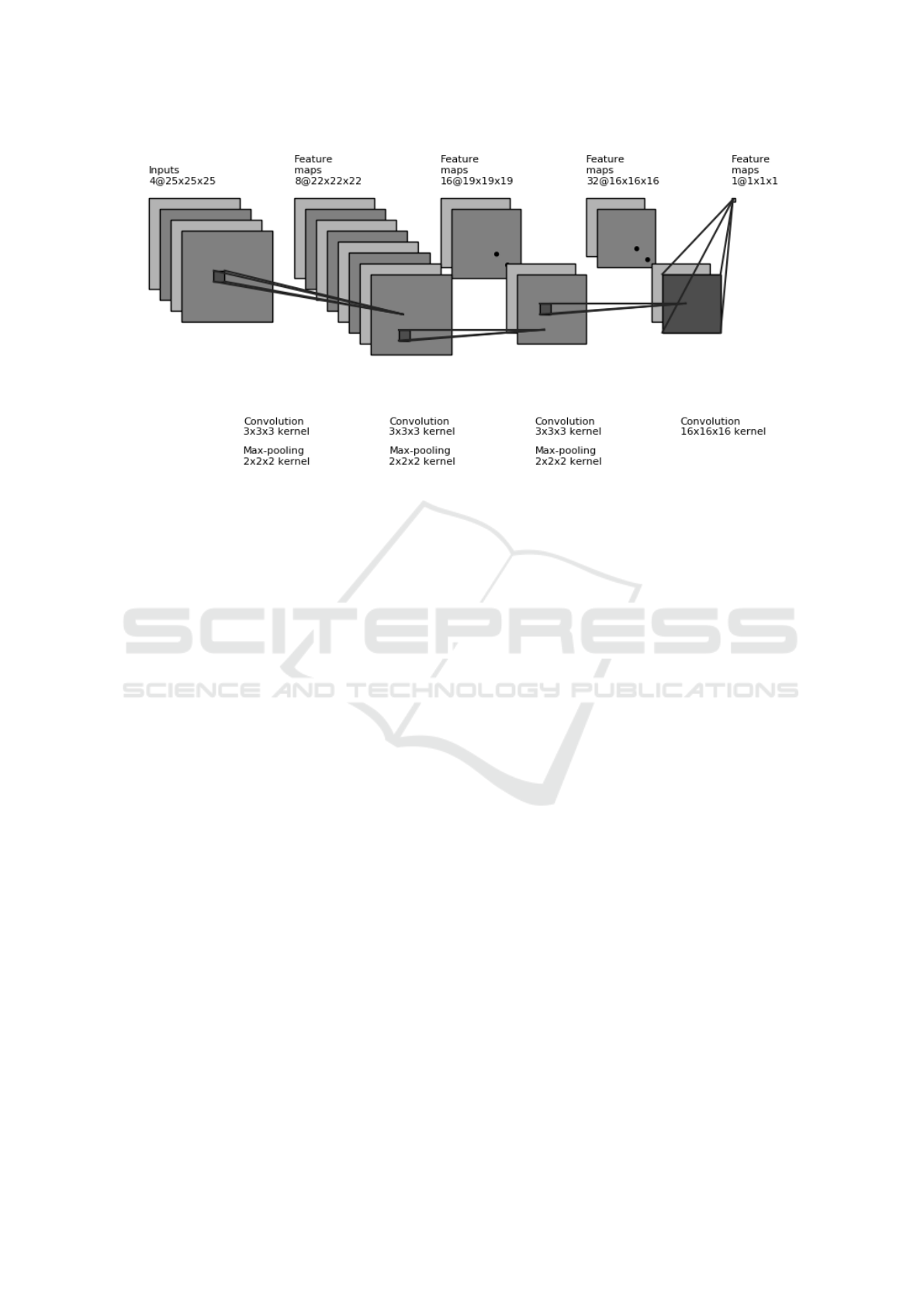
Figure 1: 3D architecture employed for counting lesions. The input tensor is obtained by stacking patches from the patient’s
brain MRI over 4 different modalities. After applying convolution and pooling operations, the final output is a real number.
large visual spatial contexts combined with efficient
iterative patch-based training and dense inference.
The output of the CNN is often interpeted as the pa-
rameter of a conditional distribution. For instance, in
(Kamnitsas et al., 2017; Havaei et al., 2017), the out-
put at each voxel is the parameter of a Bernoulli con-
ditional distribution. The Poisson distribution is gen-
erally well known for modelling counts over time and
space, and particularly has been applied to modelling
the count of multiple sclerosis lesions over time (Alt-
man and Petkau, 2005; Albert et al., 1994). For this
reason, we propose the lesion label counts, or equiv-
alently lesion volume, in a predefined patch size is
assumed to follow a Poisson distribution conditional
on the patch features. The CNNs of (Kamnitsas et al.,
2017) and (Havaei et al., 2017) use hundreds of thou-
sands of parameters for segmentation. Using CNNs,
coupled with good distributional assumptions, should
allow for smaller architectures and faster convergence
on the counting task.
One prior related work by (Dubost et al., 2017)
used a 3D CNN, similar to U-Net (Ronneberger et al.,
2015) to predict global lesion label count, but pro-
duces a segmentation when testing by using a remov-
able global pooling layer. A drawback of estimating
global lesion label counts is the need for more pa-
tient brain images, since an entire brain serves as a
single sample. In their study, training was performed
on 1,289 3D PD-weighted MRI scans, whereas some
challenges provide limited training instances (Maier
et al., 2017). Another challenge with global lesion
counts is being able to efficiently produce scalar out-
puts from larger 3D information, which would require
additional preprocessing and transformations. Esti-
mation of counts in patches can help in these situa-
tions.
This paper is organized as follows: Section 2 de-
scribes the methods, Section 3 presents the results,
and a discussion follows in Section 4.
2 METHODS
2.1 Architecture
The proposed network is shown in Figure 1. As in-
put it stacks 25 × 25 × 25 patches from each MR se-
quence, runs 3 layers of convolution and max pooling
which have sizes 3 × 3 × 3 and 2 × 2 × 2 respectively,
followed by a final convolution of size 16 ×16 ×16 to
output one real number. In addition to the convolution
and max pooling operations, Leaky ReLU nonlinear-
ity was used. It is important to note the number of
output activations at each layer are considerably small
to reduce the total number of parameters. The patch is
not only a parameter of the training features, but is in-
tertwined with the task as well, since it delineates the
region over which the lesion label count is estimated.
Training: A block diagram of the methodology is
shown in Figure 2. In accordance with the notation
of Figure 2, the architecture associates one real num-
ber N to each input tensor. Then, the model can be
formulated as: c|X ∼ Pois(e
N(X ,Θ)
), where c is the
lesion label count over the patch, X are the input fea-
Modelling Brain Lesion Volume in Patches with CNN-based Poisson Regression
173

Figure 2: Block diagram representation of the CNN-based Poisson Regression model. The predicted count is obtained by
flooring the estimated conditional Poisson parameter (λ).
tures used in the architecture, and Θ are the param-
eters of the architecture. In order to train the pa-
rameters from observed counts c
i
(assumed to Pois-
son distributed with rate λ
i
), mini-batch gradient de-
scent with a batch size b is used to minimize the
average negative log-likelihood, −
1
b
∑
b
i=1
log(
λ
c
i
i
e
−λ
i
c
i
!
),
plus additional L1 and L2 regularization terms to pre-
vent overfitting. The samples used in the mini-batch
were taken so as to ensure the lesion count was non-
zero by insisting the central voxel be lesion. Since
training only samples non-zero counts, it will not be
efficient at predicting counts for completely randomly
sampled patches, for which zero counts are more fre-
quent. A possible workaround for this task is using
a zero-inflated Poisson model (ZIP) (Lambert, 1992),
which is suggested for a future study.
2.2 Implementation Details
The open-source software Tensorflow was used to
implement the model (Abadi et al., 2016). Non-
zero counts were sampled in mini-batches of size 10.
Weights were initialized under a Gaussian with mean
0 and standard deviation of 0.001, while biases are
initialized to 0. Moreover, the Adam Optimizer was
used with initial learning rate of 10
−4
, and training
was stopped when the average cost over 1, 000 itera-
tions increased. This always happened within 15,000
iterations. In comparison, the segmentation CNN of
(Kamnitsas et al., 2017) has default training configu-
rations set to 70,000 iterations, demonstrating a quick
ability to learn for direct counting models. L1 regu-
larization and L2 regularization were used and set to
10
−8
and 10
−6
respectively. In addition to regulariza-
tion, dropout on all hidden layers was employed at a
rate ot 0.5. At prediction time, the mean Poisson rate
was floored to provide an integer estimate. Table 1
summarizes the implementation details.
3 EXPERIMENTS AND RESULTS
3.1 Dataset
The architecture and model were trained and evalu-
ated on the ISLES2015 (SISS) training data, which
Table 1: Numerical summary of implementation details.
Implementation Detail Value
Batch size (b) 10
Kernel initialization mean(std.) 0(0.001)
Learning rate 10
−4
L1, L2 coefficients 10
−8
,10
−6
Dropout 0.5
consists of 28 patients with sub-acute ischemic stroke.
All data come from the same clinical center, which
provided 4 MR sequences for each patient: FLAIR,
DWI, T1 and T1-contrast. Images are of size 230 ×
230 × 153/154, are processed to not contain the skull
and have isotropic 1mm
3
voxel resolution. Sub-acute
ischemic stroke lesions have large variation in size.
For instance, in the dataset, the smallest lesion con-
sists of 106 voxels, and the largest consists of 233,547
voxels. From the 28 brains, 20 were randomly se-
lected to form the training set, and the remaining 8
formed the validation set. This selection was carried
out once, and the same split was used across all ex-
periments. It should be acknowledged that the choice
of the training and validation split will have an effect
on performance due to the aformentioned variability
in lesion count.
3.2 Model Performance
To evaluate the performance of the architecture, sev-
eral metrics are calculated on 10,000 patches sampled
to have a non-zero lesion label count from the valida-
tion set. Sampling was done by first selecting the vali-
dation brain and then selecting a patch from the brain.
Estimated counts that surpassed the possible count in
the predefined patch size were adjusted to predict the
maximum possible count. In the experiment applied
to the ISLES2015 (SISS) data, the mean absolute er-
ror (MAE) rounded up to the nearest integer was com-
puted to be 1,458. In addition, over the same samples
the average estimated count to true count ratio was
computed to be 1.15. Finally, the mean relative error
(MRE) was 0.42 for the ischemic stroke lesions. True
patch lesion label counts vary from a few hundred to
15,000, indicating a promising initial result. Figure 3
plots the estimated and true counts for 200 samples.
BIOIMAGING 2020 - 7th International Conference on Bioimaging
174
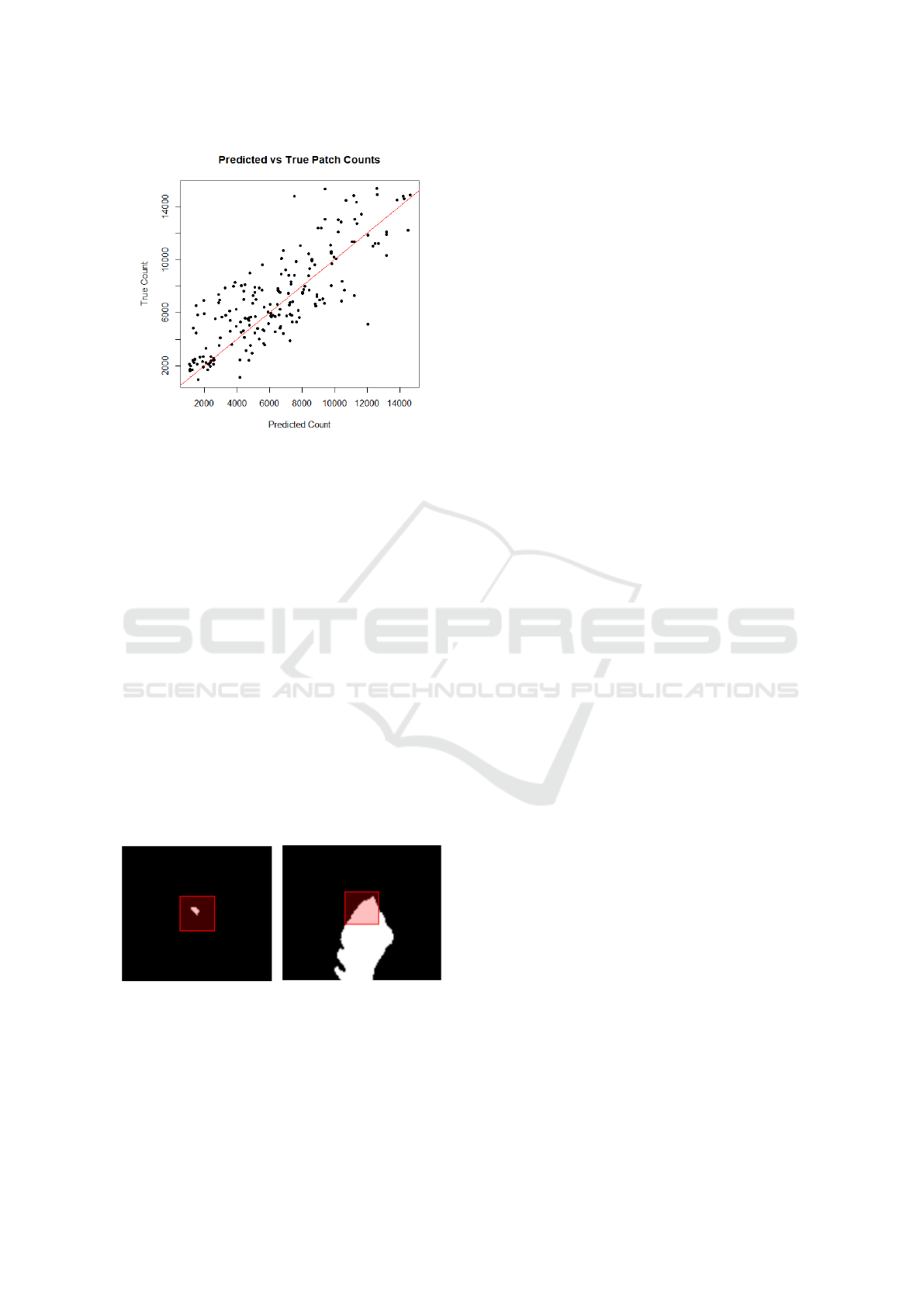
Figure 3: Plot of true count and estimated count for 200
lesion patch samples. Coefficient of multiple correlation
(Pearson’s correlation coefficient between predicted and ac-
tual values) of R = 0.81.
3.3 Predicting Count Order
The second experiment was to order pairs of patches
by lesion label count, which can be applied in a clin-
ical setting to compare lesion images over time and
assess growth or decay. Given any two image patches
containing lesions, the goal is to evaluate the model’s
ability to identify the image with the larger (equiva-
lently smaller) lesion volume using the proposed esti-
mation. In the experiment, 10,000 pairs of non-zero
count patches are sampled from the validation fold. A
sample is counted as correct if the predicted counts
preserve the same order as the true counts. Running
the experiment on the ISLES2015 (SISS) data gives a
correct order prediction for 86 % of samples, demon-
strating good ordering capabilities. Figure 4 shows an
accurately predicted sample.
Figure 4: Example of predicting count order, where the red
square outline represents the middle slice of the 25
3
patch.
The true counts from left to right are: 356 and 5297. The
predicted counts from left to right are: 501 and 5640. In
this case, the model accurately identifies the left image as
having the smaller lesion volume.
4 FUTURE WORK
4.1 Extension to Arbitrary Patches
The analysis and modelling undertaken in the previ-
ous sections were done on patches that contain lesion
voxels. That is, the patches were sampled to contain
lesion voxels. Although it was shown that this has the
potential for modelling lesion growth or decay by first
estimating lesion volume, relaxing this restriction al-
lows for the prediction of counts in arbitrary patches,
which are more frequently zero counts. Due to the un-
balanced nature of the data, one proposition for a fu-
ture study is to combine a zero-inflated Poisson model
which is known to account for excess zero counts in
data, with CNNs.
4.2 Location Detection
Being able to predict counts in arbitrary patches can
form the basis for lesion location detection. A pos-
sible algorithm could be to randomly sample patches
from one brain, predict their counts, and record the
central voxel position for the patch with the maxi-
mum predicted count. The voxel position returned
by the algorithm should identify an area of signifi-
cant lesion presence in the brain, assuming the model
is well-tuned. Though simple, the algorithm is theo-
retically stable when applied on a single lesion, since
applying true counts in place of predictions will al-
ways return the location of a lesion provided a lesion
is present.
Rather than recording just the maximum predicted
count from the given sample, another option would be
to order the predicted counts for samples drawn from
one brain. From a pre-defined quantile, larger counts
a long with their central voxel positions will delineate
the lesion.
4.3 Model Selection for Segmentation
The size of a lesion is one of the factors that can
allow some configurations of a segmentation algo-
rithm to perform better than others (Kamnitsas et al.,
2017). Smaller lesions, often found in sub-acute is-
chemic stroke, are usually tougher to segment and
produce lower dice coefficients (Havaei et al., 2017)
than larger lesions due to a relatively higher num-
ber of false positives compared to true positives. For
CNNs, configurations mainly pertain to the architec-
ture employed. Given that some architectures may
segment smaller lesions better, one option is to regress
the architecture employed for a brain, on an estimate
of the global lesion label count in the brain.
Modelling Brain Lesion Volume in Patches with CNN-based Poisson Regression
175

5 DISCUSSION
Direct counting models might be useful in clinical
settings. Some potential examples are but not lim-
ited to: monitoring and locating lesions. They can
also aid segmentation by selecting configurations of
segmentation algorithms based on global lesion size,
from raw data, and reducing the required segmenta-
tion area through lesion detection. Further develop-
ments need to be made to predict patch counts, includ-
ing: improving accuracy in the predictions of non-
zero counts, accounting for highly imbalanced zero
counts, developing sampling-based algorithms for le-
sion location detection, and providing aggregate patch
measures to predict global lesion count. This will in-
crease the effectiveness and broaden the applications
of direct counting models.
REFERENCES
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean,
J., Devin, M., Ghemawat, S., Irving, G., Isard, M.,
et al. (2016). Tensorflow: a system for large-scale
machine learning. In OSDI, volume 16, pages 265–
283.
Albert, P. S., McFarland, H. F., Smith, M. E., and Frank,
J. A. (1994). Time series for modelling counts from a
relapsing-remitting disease: application to modelling
disease activity in multiple sclerosis. Statistics in
Medicine, 13(5-7):453–466.
Alexander, L. D., Black, S. E., Gao, F., Szilagyi, G.,
Danells, C. J., and McIlroy, W. E. (2010). Correlat-
ing lesion size and location to deficits after ischemic
stroke: the influence of accounting for altered peri-
necrotic tissue and incidental silent infarcts. Behav-
ioral and brain functions, 6(1):6.
Altman, R. M. and Petkau, A. J. (2005). Application of hid-
den markov models to multiple sclerosis lesion count
data. Statistics in Medicine, 24(15):2335–2344.
Bagnato, F., Ikonomidou, V. N., van Gelderen, P., Auh,
S., Hanafy, J., Cantor, F. K., Ohayon, J., Richert,
N., and Duyn, J. (2011). Lesions by tissue specific
imaging characterize multiple sclerosis patients with
more advanced disease. Multiple Sclerosis Journal,
17(12):1424–1431.
Bakas, S., Reyes, M., Jakab, A., Bauer, S., Rempfler, M.,
Crimi, A., Shinohara, R. T., Berger, C., Ha, S. M.,
Rozycki, M., et al. (2018). Identifying the best ma-
chine learning algorithms for brain tumor segmen-
tation, progression assessment, and overall survival
prediction in the brats challenge. arXiv preprint
arXiv:1811.02629.
Dubost, F., Bortsova, G., Adams, H., Ikram, A., Niessen,
W. J., Vernooij, M., and De Bruijne, M. (2017). Gp-
unet: Lesion detection from weak labels with a 3d
regression network. In International Conference on
Medical Image Computing and Computer-Assisted In-
tervention, pages 214–221. Springer.
Erskine, M., Cook, L., Riddle, K., Mitchell, J. R., and Kar-
lik, S. J. (2005). Resolution-dependent estimates of
multiple sclerosis lesion loads. Canadian journal of
neurological sciences, 32(2):205–212.
Filippi, M., Horsfield, M., Campi, A., Mammi, S., Pereira,
C., and Comi, G. (1995). Resolution-dependent esti-
mates of lesion volumes in magnetic resonance imag-
ing studies of the brain in multiple sclerosis. Annals
of Neurology: Official Journal of the American Neuro-
logical Association and the Child Neurology Society,
38(5):749–754.
Havaei, M., Davy, A., Warde-Farley, D., Biard, A.,
Courville, A., Bengio, Y., Pal, C., Jodoin, P.-M., and
Larochelle, H. (2017). Brain tumor segmentation
with deep neural networks. Medical image analysis,
35:18–31.
Kamnitsas, K., Ledig, C., Newcombe, V. F., Simpson,
J. P., Kane, A. D., Menon, D. K., Rueckert, D., and
Glocker, B. (2017). Efficient multi-scale 3D CNN
with fully connected CRF for accurate brain lesion
segmentation. Medical image analysis, 36:61–78.
Lambert, D. (1992). Zero-inflated poisson regression, with
an application to defects in manufacturing. Techno-
metrics, 34(1):1–14.
Maier, O., Menze, B. H., von der Gablentz, J., H
¨
ani, L.,
Heinrich, M. P., Liebrand, M., Winzeck, S., Basit, A.,
Bentley, P., Chen, L., et al. (2017). ISLES 2015 - a
public evaluation benchmark for ischemic stroke le-
sion segmentation from multispectral MRI. Medical
image analysis, 35:250–269.
Merino, J. G., Latour, L. L., Todd, J. W., Luby, M.,
Schellinger, P. D., Kang, D.-W., and Warach, S.
(2007). Lesion volume change after treatment with
tissue plasminogen activator can discriminate clinical
responders from nonresponders. Stroke, 38(11):2919–
2923.
Park, H.-J., Machado, A. G., Cooperrider, J., Truong-
Furmaga, H., Johnson, M., Krishna, V., Chen, Z., and
Gale, J. T. (2013). Semi-automated method for esti-
mating lesion volumes. Journal of neuroscience meth-
ods, 213(1):76–83.
Rivers, C., Wardlaw, J., Armitage, P., Bastin, M., Carpen-
ter, T., Cvoro, V., Hand, P., and Dennis, M. (2006).
Do acute diffusion-and perfusion-weighted mri le-
sions identify final infarct volume in ischemic stroke?
Stroke, 37(1):98–104.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:
Convolutional networks for biomedical image seg-
mentation. In International Conference on Medical
image computing and computer-assisted intervention,
pages 234–241. Springer.
Winzeck, S., Hakim, A., McKinley, R., Pinto, J. A., Alves,
V., Silva, C., Pisov, M., Krivov, E., Belyaev, M.,
Monteiro, M., et al. (2018). ISLES 2016 and 2017-
benchmarking ischemic stroke lesion outcome predic-
tion based on multispectral MRI. Frontiers in neurol-
ogy, 9.
Zivadinov, R., Heininen-Brown, M., Schirda, C. V., Poloni,
G. U., Bergsland, N., Magnano, C. R., Durfee, J.,
Kennedy, C., Carl, E., Hagemeier, J., et al. (2012).
Abnormal subcortical deep-gray matter susceptibility-
weighted imaging filtered phase measurements in pa-
tients with multiple sclerosis: a case-control study.
Neuroimage, 59(1):331–339.
BIOIMAGING 2020 - 7th International Conference on Bioimaging
176
