Quantitative Analysis of Facial Paralysis using GMM and Dynamic

Kernels

Nazil Perveen

1 a

, Chalavadi Krishna Mohan

1 b

and Yen Wei Chen

2 c

Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad, India

College of Information Science and Engineering, Ritsumeikan University, Kusatsu, Shiga, Japan

Keywords:

Facial Paralysis, Spatial and Temporal Features, Gaussian Mixture Model, Dynamic Kernels, Expression

Modeling, Yanagihara Grading Scales.

Abstract:

In this paper, the quantitative assessment for facial paralysis is proposed to detect and measure the different

degrees of facial paralysis. Generally, difﬁculty in facial muscle movements determines the degree with which

patients are affected by facial paralysis. In the proposed work, the movements of facial muscles are captured

using spatio-temporal features and facial dynamics are learned using large Gaussian mixture model (GMM).

Also, to handle multiple disparities occurred during facial muscle movements, dynamic kernels are used,

which effectively preserve the local structure information while handling the variation across the different de-

gree of facial paralysis. Dynamic kernels are known for handling variable-length data patterns efﬁciently by

mapping it onto a ﬁxed length pattern or by the selection of a set of discriminative virtual features using mul-

tiple GMM statistics. These kernel representations are then classiﬁed using a support vector machine (SVM)

for the ﬁnal assessment. To show the efﬁcacy of the proposed approach, we collected the video database of

39 facially paralyzed patients of different ages group, gender, and from multiple angles (views) for robust

assessment of the different degrees of facial paralysis. We employ and compare the trade-off between accu-

racy and computational loads for three different categories of the dynamic kernels, namely, explicit mapping

based, probability-based, and matching based dynamic kernel. We have shown that the matching based kernel,

which is very low in computational loads achieves better classiﬁcation performance of 81.5% than the existing

methods. Also, with the higher-order statistics, the probability kernel involves more communication overhead

but gives signiﬁcantly high classiﬁcation performance of 92.46% than state-of-the-art methods.

1 INTRODUCTION

Facial paralysis is the facial nerve paralysis, which

occurs due to temporary or permanent damage to the

facial nerve. There are multiple reasons like surgi-

cal, neurological, viral infections, injuries, etc., which

causes damage to the facial nerve. Due to the damage

in the facial nerve, there is loss in the movement of the

facial muscles, which restrain the patients to pose nor-

mal facial actions like smiling, closing of eyes, clos-

ing of the mouth, etc. Facial paralysis affect the pa-

tient face either on half or both sides.

To detect the level and intensity of the effect

caused by the facial paralysis to the patients face, mul-

tiple diagnoses are required by the clinicians. Most

https://orcid.org/0000-0001-8522-7068

https://orcid.org/0000-0002-7316-0836

https://orcid.org/0000-0002-5952-0188

of them involve subjective assessments like assign-

ing of grading score to the patient face based on cer-

tain facial expressions. The Yanagihara grading scale

by Hato et al. (2014) and House-Brackmann (HB)

grading scales by House and Brackmann (1985) are

the two mostly used subjective grading scores for

evaluating the facial paralysis and its effects. Due

to the easier interpretation of the grading levels and

the formation of the facial simple expression Satoh

et al. (2000), Yanagihara is the widely used tech-

niques in detecting different levels of facial paraly-

sis. There are 10 expressions in Yanagihara grad-

ing scale like rest videos (EP0), raising of eyebrows

(EP1), closure of eye gently (EP2), closure of eye

tightly (EP3), closure of paralyzed eye (EP4), wrin-

kle nose (EP5), puff out cheeks (EP6), toothy move-

ment (EP7), whistling movement (EP8), and under lip

turn down (EP9). Also, there are two different levels

of the grading scales using Yanagihara grading rules,

Perveen, N., Mohan, C. and Chen, Y.

Quantitative Analysis of Facial Paralysis using GMM and Dynamic Kernels.

DOI: 10.5220/0009104801730184

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages

173-184

ISBN: 978-989-758-402-2; ISSN: 2184-4321

173

i.e, 5-scores, and 3-scores grading scales. In 5-scores

grading scales, the listed expression posed by the pa-

tient is graded from score-0 to score-4, where score-0

denotes high-level of facial paralysis, score-1 denotes

almost facial paralysis, score-2 represents moderate,

score-3 represents slight facial paralysis and score-

4 denotes no facial paralysis. Similarly, in 3-scores

grading scales, the listed expression posed by the pa-

tient is graded from score-0 to score-2, where score-0

denotes high-level of facial paralysis and score-2 de-

notes low-level of facial paralysis (or no paralysis),

respectively.

Although subjective assessments are widely used

techniques but it highly depends on the expert’s opin-

ion of assigning grades while examining the patients

during facial expressions formation. This motivates

our research to develop a generalized model for the

quantitative assessments of the facial paralysis using

different dynamic kernels. Kernels effectively pre-

served the local structure and also able to handle large

variation globally. Thus, in the proposed approach

once the local attributes are captured implicitly by

the components of universal GMM, the kernels are

learned for the better representation of the video both,

locally and globally. Also, the video data mostly con-

tains a variable length sequence of the local feature

vector, therefore to handle the variability in the se-

quence of local features extracted from the videos,

dynamic kernels are used Dileep and Sekhar (2014).

The paper is organized as follows. In Section 2,

we discuss the previous work done for the quantitative

assessment of facial paralysis. Section 3 describes

the proposed quantitative assessment method in de-

tail. Experimental results are discussed in Section 4

to show the efﬁcacy of the proposed approach. Sec-

tion 5 concludes the work with future directions.

2 RELATED WORK

NGO et al. (2016) proposed the quantitative assess-

ment of the facial paralysis using 2D features. These

2D features were novel and robust spatio-temporal

features, which were computed frame-wise. Initially,

face was detected in the given frame using the Ad-

aBoost algorithm and then landmarks points were de-

tected. The facial landmark points were detected by

computing region of interest (ROI) using the perpen-

dicularity of inter-pupil distance with vertical face

mid line. Once the ROI area was selected the land-

mark points were placed and tracked throughout the

frames. The spatio-temporal features were extracted

using the tracked landmark points, which were then

classiﬁed using support vector machine (SVM) for

ﬁnding a different level of facial paralysis. The av-

erage accuracy achieved by this method is approxi-

mately 70% for only three categories of expressions

for 5-scoring levels.

He et al. (2009), proposes the novel block process-

ing techniques to capture the appearance information

at different resolutions. They use local binary pat-

tern (LBP) to extract appearance features from the

apex frame (i.e the frame in which facial expression is

highly active) at multiple block levels and at different

resolutions, which is known as multi-resolution LBP

(MLBP). These blocks were centered over the facial

regions like eyebrows, eyes, nose, and mouth. They

also, extracted motion information by tracking the fa-

cial muscle movement in the horizontal (x-axis) and

vertical (y-axis) direction. Once the feature from dif-

ferent regions is extracted they compare the symme-

try between normal facial regions with the paralyzed

facial region using resistor-average distance (RAD).

Finally, they use a support vector machine for the ﬁ-

nal assessment and score prediction based on RAD.

They evaluate their model with the House-Brackmann

(HB) grading scale on the self-collected and anno-

tated database. They use four expressions with a 5-

score grading scale to achieve average classiﬁcation

rate of 86.6%.

Liu et al. (2015) propose the thermal imaging

model for learning the facial paralysis effect. The

proposed approach demonstrate the change in facial

nerve functions, when the facial temperature changes.

The medical infrared thermal imager made of liquid

nitrogen was used for facial temperature distribution

acquisition. For collecting the infrared thermal im-

age dataset, patients should not drink and must sit for

20 minutes prior to adapt the room temperature be-

fore experiments start. Using the features like tem-

perature distribution, area ratio, and temperature dif-

ference over the region of interest of normal and para-

lyzed facial area, they classify the different level of fa-

cial paralysis. For classiﬁcation, K-nearest neighbor

classiﬁer (K-NN), support vector machines (SVM),

and radial basis function neural network (RBFNN)

was used. They evaluate their model for four expres-

sions with an average accuracy of 94% with RBFNN

classiﬁer.

Banks et al. (2015) developed the ofﬂine applica-

tion named eFace for detection of the unilateral facial

paralysis. The video of the patient with posing list of

facial expressions was recorded and fed into the eFace

for comparing the normal and affected side. Differ-

ent score to capture disﬁgurement severity was calcu-

lated like static scores, dynamic scores, and synkine-

sis score. Based on the computed scores the grading

from 1 to 100 is provided where 1 denotes high dis-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

174

Figure 1: Block diagram of the proposed approach, which comprises of the following steps.

ﬁgurement severity and 100 denotes least or no dis-

ﬁgurement severity. The evaluation was done on a

self-collected database of 25 subjects under expert su-

pervisions.

Ngo et al. (2016) proposed the objective evalua-

tion of the facial paralysis using 3D features. The

facial landmark points were evaluated from the ﬁrst

frame, which was tracked throughout the frames for

the given video. These landmarks points were then

used to calculate asymmetrically and movement fea-

tures in the 3-D space for capturing and comparing

the facial muscle movement between normal and par-

alyzed side of the face. This objective evaluation of

facial paralysis achieves an average recognition rate

of 66.475% for the four prominent expressions, i.e for

EP1, EP3, EP5, and EP7, respectively, for 5-scoring

levels.

Recently, Guo et al. (2017) proposed the deep neu-

ral network model for classifying the severity of the

facial paralysis. They use Google LeNet model for

the self-collected private database from 104 subjects.

They achieved the performance of 91.25% for four

expressions with a 5-score House-Brackmann (HB)

grading scale.

Thus, the related works mentioned above is highly

subjective and most of the approaches are based on

asymmetric features. Faces considered in the above

approaches are mostly frontal with patient posing

very few active expressions like opening and clos-

ing of eyes, mouth, etc. This motivates us to develop

the generalized model for predicting and classifying

different levels of facial paralysis by considering all

listed expressions in the literature. The following are

the major contribution of the paper:

1. The proposed approach train a large GMM with

seven views and multiple subjects to learn view

and subject invariant attributes from the videos for

the better assessments.

2. The proposed approach introduces dynamic ker-

nels, which handles the variation across various

facial muscle movements and effectively preserve

the local dynamic structure to distinguish the dif-

ferent degree level of facial paralysis.

3. The proposed approach, model all the 10 expres-

sions mentioned in the Yanagihara grading system

with all available scores i.e. 5-scores and 3-score

grading scales for effective assessment.

Thus, the propose approach address the limita-

tions of the existing work for better quantitative as-

sessment of facial paralysis. The next section de-

scribes the proposed approach in details.

3 PROPOSED APPROACH

The block diagram of the proposed approach is shown

in Figure 1. Initially, face in the collected input videos

is aligned using facial landmark points to remove un-

wanted background information. The aligned faces

Quantitative Analysis of Facial Paralysis using GMM and Dynamic Kernels

175

are then tracked for spatial and temporal feature ex-

traction. These features are then used for training

large Gaussian mixture model (GMM), which is then

used to compute the statistics of GMM for design-

ing of the dynamic kernel for quantitative assessment

of the facial paralysis. The details of the proposed

methodology are given as follows.

3.1 Data Pre-processing and Feature

Extraction

From the aligned face video, two descriptors, namely,

the histogram of optical ﬂow (HOF) and motion

boundary histogram (MBH) features are evaluated us-

ing dense trajectories Wang et al. (2015) as shown in

Figure 1-part (ii). Initially, the dense trajectory fea-

ture points are computed at 8 different spatial scales.

In each scale, the feature points are densely sampled

on a grid spaced by W = 5 pixels. Further, each fea-

ture points are tracked till the next frame by using me-

dian ﬁltering in the dense optical ﬂow ﬁeld. The tra-

jectories computed are tended to drift from their ini-

tial location if tracked for the longer period, thus, to

avoid the drifting issue the frame length for tracking

is ﬁxed to t = 15 frames.

Further, the local descriptors are computed around

the interest points in 3D video volume, as it is always

the effective way of capturing the motion information.

The size of the video volume considered is P ×P pix-

els, where P = 32. To ensure the dynamic structure of

the video the volume is further subdivided into spatio-

temporal grid of g

×g

, where g

= 2, g

= 2,

and g

= 3 are height, width, and temporal segment

lengths. Once, the HOF and MBH descriptors are

computed from each spatio-temporal grid, it is quan-

tized into 9 and 8 bins, respectively, and normalized

using RootSIFT method as mentioned in Wang et al.

(2015).

The size of the HOF descriptors obtained is of

108 dimensions (i.e., 2 ×2 ×3 ×9). Also, the size of

MBH descriptors obtained by computing the descrip-

tors from horizontal and vertical components of the

optical ﬂow, i.e MBH in x and y direction are of 192

dimensions (i.e. 96 dimensions for each direction).

The reason for using the above mention dense tra-

jectory, i.e., HOF and MBH descriptors are, all the

trajectories in the given video does not contain useful

information like trajectories cause due to large, sud-

den, and constant camera motions. Therefore these

trajectories are required to remove so to retain only

the essential foreground trajectories caused by the fa-

cial movements. The removal of such trajectories is

efﬁciently done by the improved dense trajectories,

which are far efﬁcient than commonly used features

like HOG3D, 3DSIFT, and LBP-TOP, etc, that are

usually computed in a 3D video volume around in-

terest points, which usually ignores the fundamental

dynamic structures in the video Wang et al. (2015).

3.2 Training of a Gaussian Mixture

Model (GMM)

The features obtained from different views and sub-

jects from the videos are extracted to train the

large Gaussian mixture model (GMM). The GMM is

trained for multiple components q = 1, 2, ··· , Q in or-

der to capture different facial movement attribute in

various Q components. Given a video V, the set of

local features are represented as v

, v

, ··· , v

, where

N is the total number of local features for the given V .

The likelihood of the particular feature v

generated

from the GMM model is given by

p(v

) =

∑

q=1

N (v

|µ

, σ

), (1)

where µ

, σ

represents mean and covariance for

each GMM component q, respectively. Further, w

represents GMM mixture weights, which should sat-

isfy the constraint

∑

q=1

= 1. Once the GMM is

trained, the probabilistic alignment of each feature

vector v

with respect to the qth component of the

GMM model is evaluated using as follows

p(q|v

) =

p(v

|q)

∑

q=1

p(v

|q)

, (2)

where p(v

|q) is the likelihood of a feature v

gen-

erated from a component q. Using the different pa-

rameters of the GMM, multiple dynamic kernel-based

representations are generated, which will efﬁciently

represent the given video. The next subsections de-

tailed the formulation of the dynamic kernels.

3.3 Dynamic Kernels

The selection of kernel function plays important role

in the performance of kernel methods. For static pat-

terns, several kernel functions are designed in past

decades The kernels designed for the varying length

patterns are known as dynamic kernels. Dynamic ker-

nels are either formed by converting variable length

patterns to static patterns or by designing new ker-

nel functions. In this sub-section, we present different

dynamic kernels, which effectively preserve local and

global information, respectively, for better represen-

tation of the given sample.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

176

3.3.1 Explicit Mapping based Dynamic Kernel

In the explicit mapping dynamic kernel, the set

of variable length local feature representations are

mapped onto ﬁxed dimensional feature representation

in the kernel space by GMM based likelihood. The

Fisher kernel (FK) used for the proposed approach

maps the set of variable length local features onto

the ﬁxed dimensional Fisher score. The Fisher score

is computed by evaluating the ﬁrst derivative of log-

likelihood for mean, covariance, and weight vector

using Equation 2 given by

(µ)

(V) =

∑

n=1

p(q|v

, (3)

(σ)

(V) =

∑

n=1

p(q|v

)[−u

+ h

]

, (4)

(w)

(V) =

∑

n=1

p(q|v

)



−

p(q

)

p(q|v

)



. (5)

where m

∑

−1

−µ

), u

= Σ

−1

and h



n1q

, m

n2q

, ··· , m

ndq



. For any d × d

matrix A with a

i j

, i, j = 1, 2, ··· , d as its elements,

vec(A) = [a

, a

, ··· , a

]

The ﬁrst-order derivative or the gradient of the

log-likelihood computed above represent the direc-

tions in which the parameters, namely, µ, Σ, and w

should be updated for the best ﬁt of the model. We in-

fer that the deviations that occurred, during the facial

movements of particular expressions are captured by

these gradients. The ﬁxed dimensional feature vector

known as the Fisher score vector is then computed by

stacking all the gradients from Equation 3, 4, and 5

given by

(V) =

(µ)

(V)

, ψ

(σ)

(V)

, ψ

(w)

(V)

. (6)

The Fisher score vector for all the Q components

of the GMM is given by

(V) =



(V)



. (7)

The Fisher score vector captures the similarities

across two samples, thus the kernel function for com-

paring two samples V

and V

, with given local fea-

tures is computed by

K(V

, V

) = Φ

)

−1

), (8)

Where I is knows as Fisher information matrix

given by

I =

∑

d=1

)Φ

)

. (9)

The Fisher information matrix captures the variabil-

ity’s in the facial movement across the two samples.

Thus both local and global information is captured

using Fisher score and Fisher information matrix in

Fisher kernel computation. However, the computation

complexity for the Fisher kernel is highly intensive.

The computation of gradient for mean, covariance,

and weight matrix involves Q×(N

), each. Then

the computation of the Fisher information matrix in-

volves D ×d

+ D computations, where D is the total

number of training examples. Similarly, the Fisher

score vector requires d

+ d

computations, where d

is the dimension of the Fisher score vector. Thus, the

total computation complexity of the Fisher kernel is

given as O(QN +Dd

+D +d

) as shown in Ta-

ble 1.

3.3.2 Probability based Dynamic Kernel

In probability-based dynamic kernels, the set of vari-

able length local feature representations are mapped

onto ﬁxed dimensional feature representation in the

kernel space by comparing the probability distribu-

tions of the local feature vectors. Initially, the maxi-

mum aposteriori (MAP) adaptation of means and co-

variances of GMM for each clip is given by

(V) = αF

(V) + (1 −α)µ

. (10a)

and

(V) = αS

(V) + (1 −α)σ

. (10b)

where F

(V) is the ﬁrst-order and S

(V) is the

second-order Baum-Welch statistics for a clip V, re-

spectively, which is calculated as

(V) =

(V)

∑

n=1

p(q|v

(11a)

and

(V) = diag

∑

n=1

p(q|v

, (11b)

respectively.

The adapted mean and covariance from each

GMM component depend on the posterior probabili-

ties of the GMM given for each sample. Therefore,

if the posterior probability is high then higher will

be the correlations among the facial movements cap-

tured in the GMM components. This shows that the

adapted mean and covariance for each GMM mixture

will have a higher impact than the full GMM model

means and covariances. Thus, the adapted means

from Equation 10a, for sample V is given by

(V) =



√

−

(V)



. (12)

Quantitative Analysis of Facial Paralysis using GMM and Dynamic Kernels

177

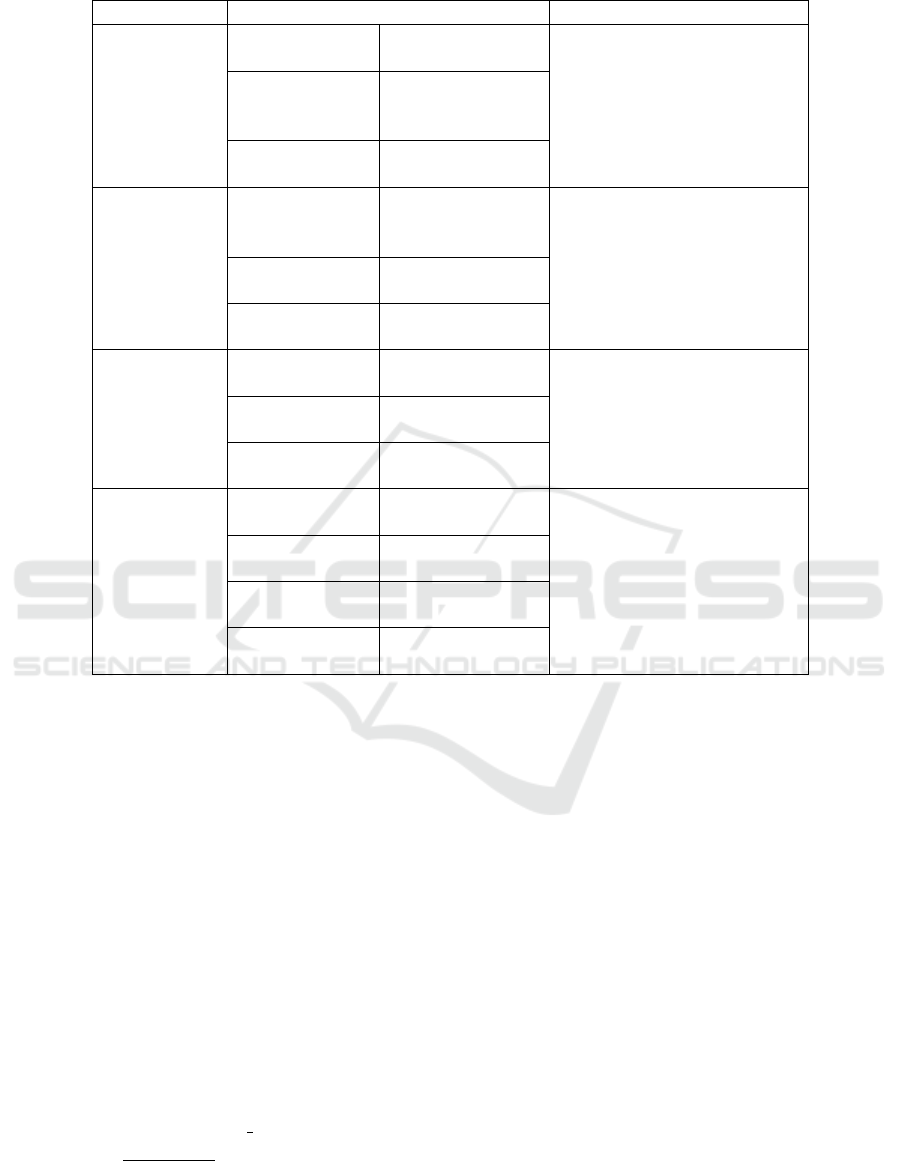
Table 1: Statistics of the collected database score-wise in 3-score grading scales.

Kernels Number of computations Computational Complexity

Fisher Kernel

(FK)

Gradient vector

computation

3 ×Q ×(N

+ N

)

O(QN + Dd

+ D + d

+ d

)

Fisher

information

matrix

D ×d

+ D

Kernel

computation

+ d

Intermediate

matching

kernel

(IMK)

Posterior

probability

computation

Q ×(N

+ N

)

O(QN)

Comparisons to

select features

Q ×(N

+ N

)

Base kernel

Computation

GMM

supervector

kernel

(GMM-SVK)

Mean

adaptation

Q ×(N

+ N

)

O(QN + Qd

+ d

)

Supervector

computation

Q ×(d

+ 1)

Kernel

computation

GMM

mean

interval

kernel

(GMM-MIK)

Mean

adaptation

Q ×(N

+ N

)

O(QN + Qd

+ Qd

+ Q

)

Covariance

adaptation

Q ×(N

+ N

)

Supervector

computation

Q ×(d

+ d

)

Kernel

computation

By stacking the GMM vector for each

component, a Qd × 1 dimensional super-

vector is obtained, which is known as

GMM supervector (GMM-SV) represented as

svk

(V) = [ψ

(V)

, ψ

(V)

, ··· , ψ

(V)

]

The GMM-SV used for comparing the similarity

across two samples, namely, V

and V

by construct-

ing GMM supervector kernel (GMM-SVK), which is

given by

svk

, V

) = S

svk

)

svk

). (13)

The GMM-SVK kernel formed above only uti-

lizes the ﬁrst-order adaptations of the samples for

each GMM components. Thus, the second-order

statistics, i.e., covariance adaptations is also in-

volved in constructing ﬁxed-length representation

from variable-length patterns is given by

(V) =

(V) −σ

−



(V) −µ



. (14)

Combining the GMM mean interval supervector

(GMM-GMI) for each component is computed as

mik

(V) = [ψ

(V)

, ψ

(V)

, ··· , ψ

(V)

]

Thus, to compare the similarity across the two

samples V

and V

, the kernel formation is performed

using GMM-GMI kernel also known as GMM mean

interval kernel (GMM-MIK) given by

mik

, V

) = S

mik

)

mik

). (15)

The ﬁxed-length representation formed by using

the posterior probabilities in the kernel space is a

high dimensional vector, which involves Q ×(N

) computations for mean adaptation and 2 ×Q ×

+ N

) for mean and covariance adaptations, re-

spectively. And the kernel computation required

Q ×(d

+ 1) and d

, where d

is the dimension of

local feature vector. The total computational com-

plexities of GMM-SVK and GMM-MIK kernels are

O(QN +Qd

) and O(QN +Qd

+Qd

respectively as shown in Table 1.

3.3.3 Matching based Dynamic Kernel

The kernels mentioned above are mentioned based

on the mapping of variable-length feature representa-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

178

Figure 2: Illustration of the facial paralysis patients posing 10 different expressions under expert supervision. Black patches

are imposed to hid the identity of the patient (best viewed in color).

tions to ﬁxed-length feature representations. This sec-

tion introduces the alternative approach for designing

of the new kernel for handling variable-length data,

known as matching based dynamic kernels. Various

matching based dynamic kernels are proposed in the

literature like summation kernel (SK), matching ker-

nel (MK), etc. However, these kernels are either com-

putationally intensive or not proved to be the Mercer’s

kernel. So, an intermediate matching kernel (IMK) is

formulated by matching a set of local feature vectors

by closest virtual feature vectors obtained using the

training data of all classes. Let Z = {z

, z

, ··· , z

}

be the virtual feature vectors. Then, the feature vec-

tors v

∗

and v

∗

in V

and V

, respectively, that are

nearest to q

virtual feature vector z

is determined

∗

= argmin

v∈V

D(v, z

) and v

∗

= argmin

v∈V

D(v, z

(16)

where D(., .) is a distance function, which mea-

sures the distance of a feature vector V

or V

to the

closest feature vector in Z. We hypothesize that the

distance function aid in ﬁnding the closest facial mus-

cle movement learned from the clip to one, which is

captured by GMM components. Once the closest fea-

ture vector is selected, the base kernel will be given

imk

, V

) =

∑

q=1

k(v

, v

). (17)

In the proposed approach, the GMM parameters

like mean, covariance, and weight are used as a set of

virtual feature vectors. And, the distance or closeness

measure is computed by using the posterior probabil-

ity of the GMM component generating the feature de-

scribed in Equation 2. Thus, the local feature vectors

close to the virtual feature vector for the given q is

v∗

and v∗

for clips V

and V

, respectively, which

is computed as

∗

= argmax

v∈V

p(q|v) and v

∗

= argmax

v∈V

p(q|v). (18)

The computational complexity of IMK is very low

compared to other mentioned dynamic kernels de-

ﬁned as (i) Q×(N

+ N

) comparisons for selection of

closest feature vector, (ii) Q ×(N

+ N

) required for

posterior probability computations, and (iii) Q base

kernel computations. Thus the total computational

complexity of IMK is given by O(QN) where N is

the set of local feature vector as shown in Table 1.

For classiﬁcation, support vector machine (SVM)

is built for each dynamic kernel. The SVM is a two-

class classiﬁer, For D training samples can be repre-

sented as (V

, y

)

d=1

, where y

represents the label

information of the particular class, then discriminant

function for SVM is given by,

f (V ) =

∑

d=1

∗

(V, V

) + b

∗

(19)

where D

be the number of support vectors, α

∗

the optimal values of the Lagrangian coefﬁcient and

∗

is the optimal bias. The sign value of the function

f decides the class of V . We use a one-against rest

approach with 10 fold cross-validation to discriminate

the sample of the particular class with all the other

classes.

4 EXPERIMENTAL RESULTS

In this section, we describes about the facial paralysis

dataset in detail. Also, we analyse different types of

dynamic kernels representations for better quantita-

tive assessments. We compare the proposed approach

with existing state of the art approaches and in last

we discuss the efﬁcacy of the proposed approach with

some ablations study.

4.1 Dataset Collection and Annotation

Protocol

To show the efﬁcacy of the proposed approach we

collected the video dataset of the facially paralyzed

Quantitative Analysis of Facial Paralysis using GMM and Dynamic Kernels

179

Figure 3: Camera position during the video recording of the

facially paralyzed patients, black patches are added to hide

the identity of the patient (best viewed in color).

patients under 3 expert supervision. The patients

concerned are taken in advance for the collection of

videos. Multiple subjects of various age group, gen-

der, races, etc, are collected. Also, the video recorded

is captured from seven different angle views by plac-

ing multiple cameras at different angle setting of +/-

◦

as shown in Figure 3. The main objective of col-

lecting subject and view-invariant videos of the pa-

tients is to develop an accurate and generalized model

for the quantitative assessment of facial paralysis.

The total number of video samples collected for the

experiments is 2717 from 39 subjects. These 39 sub-

jects are of different age starting from 17 years to 70

years, the detailed statistics of the dataset age-wise

and gender-wise is shown in Figure 4. During captur-

ing the patient videos, patients are asked to perform

the 10 expressions given on Figure 2 and also subjec-

tive assessments using Yanagihara grading scale un-

der 3 experts supervision are computed for ground

truth evaluation. The experts also grade the expres-

sions posed by the patients from score-0 to score-5.

As already mention, the grading provided by the ex-

perts are highly subjective, thus, for the ground truth

of the proposed model, we took 2 best subjective ex-

pert opinions out of 3 experts. Based on the subjective

assessments we divided the whole dataset into 2166

training videos and 551 testing videos for score-0 to

score-5 as shown in Table 2 and for score-0 to score-2

as shown in Table 3. Also, the testing video subjects

are not at all present in the training set in any condi-

tions during experimentation.

Table 2: Statistics of the collected database score-wise in

5-score grading scales.

Grading scores # of training videos # of testing videos # of total videos

Score 0 166 62 228

Score 1 322 104 426

Score 2 600 147 747

Score 3 539 140 679

Score 4 539 98 637

Total videos 2166 551 2717

Figure 4: Statistics of the data collected age-wise and

gender-wise (best viewed in color).

Table 3: Statistics of the collected database score-wise in

3-score grading scales.

Grading scores # of training videos # of testing videos # of total videos

Score 0 488 166 655

Score 1 1139 287 1426

Score 2 539 98 637

Total videos 2166 551 2717

4.2 Analysis of the Dynamic Kernels for

Quantitative Assessment of Facial

Paralysis

The classiﬁcation performance of various dynamic

kernel like Fisher kernel (FK), intermediate matching

kernel (IMK), supervector kernel (SVK), and mean

interval kernel (MIK) using different GMM compo-

nents, namely 32, 64, 128, 256, and 512 is shown

in Table 4 for 5-class grading score. The spatio-

temporal facial features, namely, histogram of optical

ﬂow (HOF) and motion boundary histogram (MBH)

are trained using GMM and classiﬁed using kernel-

based support vector machine (SVM) Cortes and Vap-

nik (1995). It can be observed that the best perfor-

Table 4: Classiﬁcation performance (%) of FK, IMK, SVK,

and MIK on different GMM components for 5-class grading

score.

# of

components

FK IMK SVK MIK

HOF MBH HOF MBH HOF MBH HOF MBH

32 37.3 40.1 67.1 70.5 68.8 74.1 70.5 75.2

64 43.6 44.5 72.3 73 69.7 76.2 72 75.8

128 45.5 45.5 74.1 75.8 71.4 77.3 73 78.6

256 47.9 48.6 76.6 77.9 78.4 82.2 86.5 90.7

512 46.8 47.9 76.2 76.2 72.3 78.4 81.5 87.1

mance kernels are probability-based kernels, namely,

support vector kernel (SVK) and mean interval kernel

(MIK) as it captures the ﬁrst-order and second-order

statistics of the learned GMM model. Also, it can

be observed that increasing the number of mixtures

in GMM increases the better generalization capability

of the model, however, it cannot be increased beyond

256 due to increase in demand of the local feature in-

formation, which cannot be addresses due to the lim-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

180

(a) 5-class grading score (b) 3-class grading score

Figure 5: Confusion matrix of MBH feature vector using GMM-MIK dynamic kernel with SVM for 256 components (best

viewed in color).

ited size of the dataset.

The confusion matrix for 5-class grading score is

given in Figure 5 (a), it can be observed that the mis-

classiﬁed samples are mostly present in the neighbor-

ing class, due to which we combined the score-0 class

examples with score-1 class examples and the score-2

class examples with score-3 class examples. Follow-

ing the previous work Ngo et al. (2016), NGO et al.

(2016), and Wachtman et al. (2002), we reduce the

number of classes from 5-class grading score to 3-

class grading to facilitate the comparison of the pro-

posed work with the state of the art approaches. The

classiﬁcation performance of the above fusion i.e. for

3-class grading scores are shown in Table 5 and con-

fusion matrices for the best performances are shown

in Figure 6.

Table 5: Classiﬁcation performance (%) of FK, IMK, SVK,

and MIK on different GMM components for 3-class grading

score.

# of

components

FK IMK SVK MIK

HOFMBHHOFMBHHOFMBHHOFMBH

32 52.6 53.8 68.8 71.4 71.4 72.3 85.9 87.2

64 53.7 55.2 70.5 75.8 76.8 79.2 86.9 89

128 55.2 58.2 73.2 76.2 78.8 79.9 88.9 90.8

256 62.3 63.2 78.4 81.5 82.4 84.1 90.2 92.5

512 55.4 59.9 75.8 78.6 80.2 81.7 89.6 91.5

4.3 Expression-wise Classiﬁcation

Performance and Comparison with

the State of Art Approaches

The performance comparison with the state of the art

methods is given in Table 6. Also, to show the efﬁcacy

of the proposed approach we evaluate the proposed

approach with most most popular, 3DCNN features

Tran et al. (2014) and classiﬁed the same using SVM.

Table 6: Comparison with state of the art methods.

Methods Accuracy (%)

PI Wachtman et al. (2002) 46.55

LBP He et al. (2009) 47.27

Gabor Ngo et al. (2014) 55.12

Tracking 2D NGO et al. (2016) 64.85

Tracking 3D Ngo et al. (2016) 66.47

C3d (from fc-8 layer and

on 5-class grading scores) Tran et al. (2014)

+ SVM

71.5

C3d features(from fc-8 layer and

on 3-class grading scores) Tran et al. (2014)

+ SVM

81.3

Proposed approach

(on 5-class grading scores)

90.7

Proposed approach

(on 3-class grading scores)

92.46

Table 7: Expression wise classiﬁcation performance (%) of

the proposed approach for the best model (MBH features

using MIK kernel for 512 components.

EP0 EP1 EP2 EP3 EP4 EP5 EP6 EP7 EP8 EP9

Proposed

5-score

grading score

75.4595.2386.4 91.9494.1395.9791.5793.7789.0193.04

Proposed

3-score

grading score

81.6894.8793.0497.4392.3 95.6 91.9495.2387.5495.23

It can be observed that the proposed approach has

better representative features than 3DCNN features.

Also, the expression wise classiﬁcation performance

of the best model i.e. MBH features with MIK ker-

nel for 256 components is given in Table 8. It can be

observed that the expression with fewer facial move-

ments like at rest expression (EP0) has lower perfor-

mance as compared to the expression with prominent

facial movements like the closure of eye tightly (EP3),

wrinkle nose (EP5), etc. We also compare the previ-

ous works and the proposed approach expression wise

in Table 9. However, it can be noticed that only a few

Quantitative Analysis of Facial Paralysis using GMM and Dynamic Kernels

181

(a) HOF (b) MBH

Figure 6: Confusion matrix of HOF and MBH feature vector using GMM-IMK dynamic kernel with SVM for 256 components

for 3-class grading scores (best viewed in color).

expressions from the previous works are compared,

this is due to the previous works only focus on the ex-

pressions which have notable (eminent/distinguished)

facial movements like wrinkle forehead (EP1), clo-

sure of eye tightly (EP3), wrinkle nose (EP5), and grin

(EP7). This is evaluated to facilitate the comparison

with the previous work.

Table 8: Expression wise classiﬁcation performance (%) of

the proposed approach for the best model (MBH features

using MIK kernel for 256 components.

Expression

Denotations

Proposed

5-score

grading score

Proposed

3-score

grading score

EP0 75.45 81.68

EP1 95.23 94.87

EP2 86.44 93.04

EP3 91.94 97.43

EP4 94.13 92.3

EP5 95.97 95.6

EP6 91.57 91.94

EP7 93.77 95.23

EP8 89.01 87.54

EP9 93.04 95.23

Table 9: Comparison of the classiﬁcation performance (%)

for the few prominent facial paralysis expressions with the

existing works.

PI LBPGabor

Tracking

Proposed

5-class

grading scores

Proposed

3-class

grading scores

EP150.7 58.3 62.4 69.4 70.9 95.23 94.87

EP348.2 48.9 53.1 62.1 63.3 91.94 97.43

EP548.1 41.8 50.5 57.3 58.2 95.97 95.6

EP739.2 40.1 54.5 70.6 73.5 93.77 95.23

4.4 Efﬁcacy of the Proposed Approach

Figure 7 shows the visualization of the kernel matrix

of the best performing MBH features with a mean in-

terval kernel (MIK) for 256 components and 3-class

grading score. The lighter shade of the diagonal ele-

ments show the higher values, which represents the

correctly classiﬁed elements while the off-diagonal

elements in darker shade represent the lower values.

Also, it can be inferred that using MIK as a distance

metric there is better separability among the different

levels of the facial paralysis.

Further, it can be observed from Table 8, expres-

sions like at rest (EP0) and closure of eye lightly

(EP2), where there are few or no facial movements

results in low performance of the proposed approach.

Also, from ﬁgures 8 (a) and 8 (b), it can be observed

that expressions having common facial movements

like blowing out cheeks (EP6) and whistling (EP8)

are confused with each other. And expression hav-

ing distinguished (uncommon) facial movements like

wrinkle forehead (EP1) and wrinkle nose (EP5) are

less confused with each other.

Figure 7: Mean interval kernel representation for motion

boundary histogram (MBH) features and uGMM 256 com-

ponents and 3-class grading score (best viewed in color).

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

182

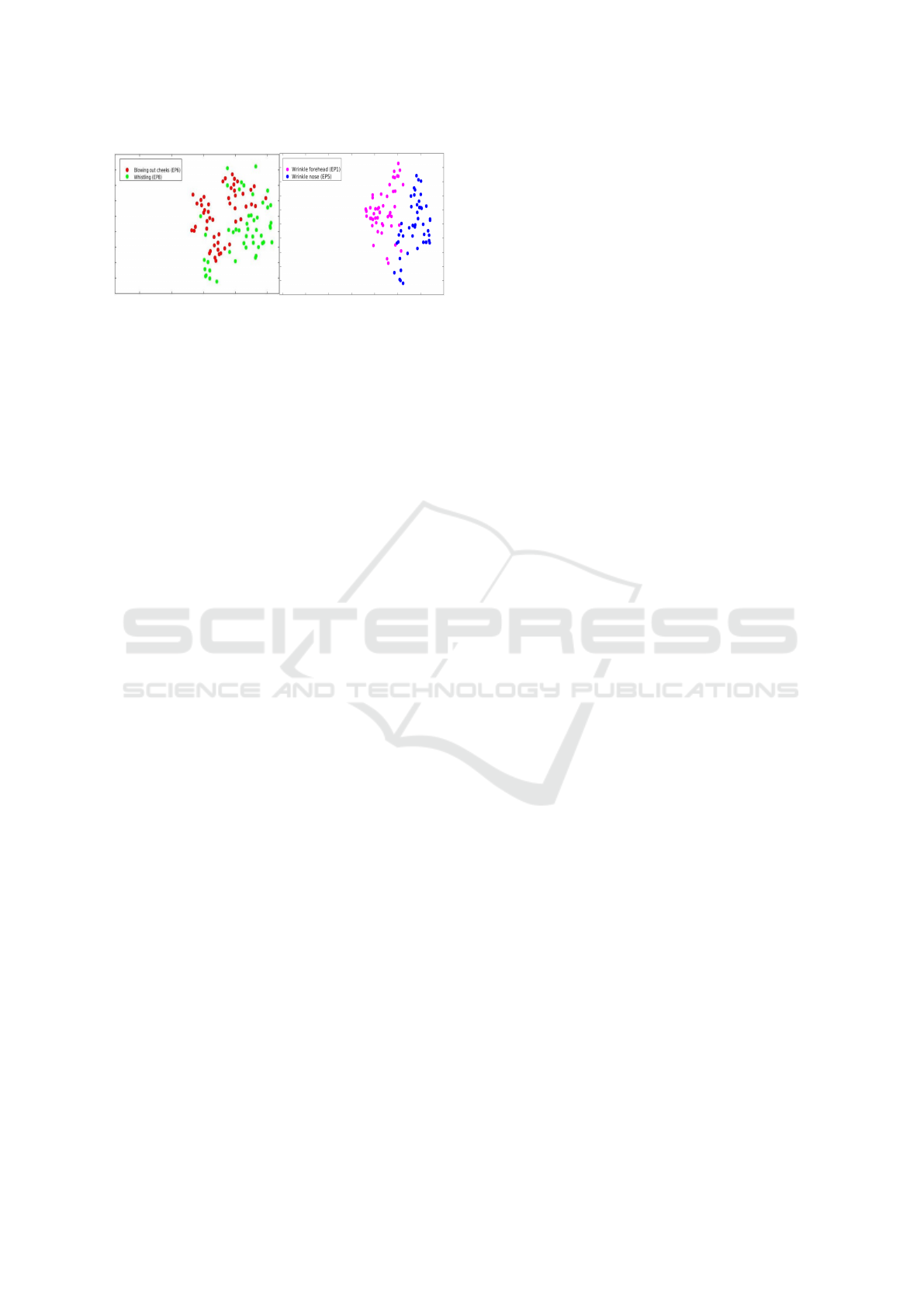
(a) (b)

Figure 8: t-sne plot for the expressions of facial paralysis

using MBH and GMM-MIK dynamic kernel based SVM

for 256 components for 3-class grading score (best viewed

in color). In (a) t-sne plot for expression blowing out cheeks

(EP6) and whistling (EP8) and in (b) for expression wrinkle

forehead (EP1) and wrinkle nose (EP5).

5 CONCLUSION

In this paper, we introduce a novel representation

of the facial features for variable length pattern us-

ing dynamic kernel-based classiﬁcation, which pro-

vide the quantitative assessment to the patients suffer-

ing from facial paralysis. Dynamic kernels are used

for representing the varying length videos efﬁciently

by capturing both local facial dynamics and preserv-

ing the global context. A universal Gaussian mixture

model (GMM) is trained on spatio-temporal features

to compute the posteriors, ﬁrst-order, and second-

order statistics for computing dynamic kernel-based

representations. We have shown that the efﬁcacy of

the proposed approach using different dynamic ker-

nels on the collected video dataset of facially par-

alyzed patients. Also, we have shown the compu-

tation complexity and classiﬁcation performance of

each dynamic kernels, where the matching based in-

termediate matching kernel (IMK) is computationally

efﬁcient as compared to other dynamic kernels. How-

ever, probability-based mean interval kernel (MIK) is

more discriminative but computationally complex. In

the future, the classiﬁcation performance has to be im-

proved further by improving the modeling of expres-

sions for better quantitative assessment of the facial

paralysis. Also, various quantitative assessment using

Perveen et al. (2012); Perveen et al. (2018); Perveen

et al. (2016) are need to be explore and compare for

better classiﬁcation performance.

REFERENCES

Banks, C. A., Bhama, P. K., Park, J., Hadlock, C. R., and

Hadlock, T. A. (2015). Clinician-Graded Electronic

Facial Paralysis Assessment: The eFACE. Plast. Re-

constr. Surg., 136(2):223e–230e.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine Learning, 20(3):273–297.

Dileep, A. D. and Sekhar, C. C. (2014). Gmm-based inter-

mediate matching kernel for classiﬁcation of varying

length patterns of long duration speech using support

vector machines. IEEE Transactions on Neural Net-

works and Learning Systems, 25(8):1421–1432.

Guo, Z., Shen, M., Duan, L., Zhou, Y., Xiang, J., Ding, H.,

Chen, S., Deussen, O., and Dan, G. (2017). Deep as-

sessment process: Objective assessment process for

unilateral peripheral facial paralysis via deep con-

volutional neural network. In 2017 IEEE 14th In-

ternational Symposium on Biomedical Imaging (ISBI

2017), pages 135–138.

Hato, N., Fujiwara, T., Gyo, K., and Yanagihara, N. (2014).

Yanagihara facial nerve grading system as a prognos-

tic tool in Bell’s palsy. Otol. Neurotol., 35(9):1669–

1672.

He, S., Soraghan, J. J., O’Reilly, B. F., and Xing, D. (2009).

Quantitative analysis of facial paralysis using local bi-

nary patterns in biomedical videos. IEEE Transac-

tions on Biomedical Engineering, 56(7):1864–1870.

House, J. W. and Brackmann, D. E. (1985). Facial nerve

grading system. Otolaryngology-Head and Neck

Surgery, 93(2):146–147. PMID: 3921901.

Liu, X., Dong, S., An, M., Bai, L., and Luan, J. (2015).

Quantitative assessment of facial paralysis using in-

frared thermal imaging. In 2015 8th International

Conference on Biomedical Engineering and Informat-

ics (BMEI), pages 106–110.

NGO, T. H., CHEN, Y.-W., MATSUSHIRO, N., and SEO,

M. (2016). Quantitative assessment of facial paralysis

based on spatiotemporal features. IEICE Transactions

on Information and Systems, E99.D(1):187–196.

Ngo, T. H., Chen, Y. W., Seo, M., Matsushiro, N., and

Xiong, W. (2016). Quantitative analysis of facial

paralysis based on three-dimensional features. In 2016

IEEE International Conference on Image Processing

(ICIP), pages 1319–1323.

Ngo, T. H., Seo, M., Chen, Y.-W., and Matsushiro, N.

(2014). Quantitative assessment of facial paralysis us-

ing local binary patterns and gabor ﬁlters. In Proceed-

ings of the Fifth Symposium on Information and Com-

munication Technology, SoICT ’14, pages 155–161,

New York, NY, USA. ACM.

Perveen, N., Gupta, S., and Verma, K. (2012). Facial ex-

pression recognition using facial characteristic points

and gini index. In 2012 Students Conference on Engi-

neering and Systems, pages 1–6.

Perveen, N., Roy, D., and Mohan, C. K. (2018). Sponta-

neous expression recognition using universal attribute

model. IEEE Transactions on Image Processing,

27(11):5575–5584.

Perveen, N., Singh, D., and Mohan, C. K. (2016). Sponta-

neous facial expression recognition: A part based ap-

proach. In 2016 15th IEEE International Conference

on Machine Learning and Applications (ICMLA),

pages 819–824.

Satoh, Y., Kanzaki, J., and Yoshihara, S. (2000). A com-

parison and conversion table of ’the house-brackmann

Quantitative Analysis of Facial Paralysis using GMM and Dynamic Kernels

183

facial nerve grading system’ and ’the yanagihara grad-

ing system’. Auris Nasus Larynx, 27(3):207 – 212.

Tran, D., Bourdev, L. D., Fergus, R., Torresani, L., and

Paluri, M. (2014). C3D: generic features for video

analysis. CoRR, abs/1412.0767.

Wachtman, G., Liu, Y., Zhao, T., Cohn, J., Schmidt, K.,

Henkelmann, T., VanSwearingen, J., and Manders, E.

(2002). Measurement of asymmetry in persons with

facial paralysis. In Combined Annual Conference of

the Robert H. Ivy and Ohio Valley societies of Plastic

and Reconstructive Surgeons.

Wang, H., Oneata, D., Verbeek, J., and Schmid, C. (2015).

A robust and efﬁcient video representation for action

recognition. International Journal of Computer Vi-

sion, 119(3):219–238.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

184