Multi-state Models for the Analysis of Survival Studies in Biomedical

Research: An Alternative to Composite Endpoints

Alicia Quir

1 a

, Armando P

erez de Prado

2 b

, Natalia Montoya

and Jos

e M. De la Torre Hern

andez

3 c

Departmento de Matem

aticas, Universidad de Le

on, Campus de Vegazana, Le

on, Spain

Unidad de Cardiolog

ıa Intervencionista, Complejo Asistencial Universitario de Le

on, Le

on, Spain

Unidad de Cardiolog

ıa Intervencionista, Hospital Universitario Marqu

es de Valdecilla, Santander, Spain

Keywords:

Adverse Events, Competing Risks, Composite Endpoints, Disability Model, Interventional Cardiology,

Multi-state Model, Survival Studies.

Abstract:

Primary endpoints of survival studies in biomedical research are usually composite endpoints, which indicate

whether any of a list of events is observed. They are practical to empower studies and in the presence of

competing risks, although constrained. In this work, we propose a more sophisticated modelization of the evo-

lution of the disease for a patient with multi-state models, which allow to deﬁne relationships between adverse

events by a state structure. Each transition between states may depend on different covariates, which pro-

vides a personalized prediction for patients, considering their characteristics, treatment and observed disease

evolution. In order to illustrate their performance, we analyze a study in interventional cardiology including

1008 patients with acute coronary syndrome who underwent percutaneous revascularization between 2013 and

2019. The results show the great potential of multi-states models for analyzing survival studies in biomedical

research.

1 INTRODUCTION

In biomedical research, prognostic studies are usually

conducted, in which patients are followed up for sev-

eral months after undergoing an intervention or being

prescribed a treatment. The objective of these studies

is either to evaluate the performance of the treatment /

intervention or to discover risks factors that inﬂuence

the patient’s outcome. A typical primary objective for

these studies is a composite endpoint, i.e. a variable

that indicates whether any of a list of events is ob-

served or not. The corresponding time is usually the

time of the ﬁrst observed event, for those patients pre-

senting one or more events, and the maximum time

for the rest of patients. The scheme of a composite

endpoint setting is depicted in Figure 1 (a).

Composite endpoints are mostly used for analyz-

ing survival studies in which events are rare, in order

to empower the studies (Irony, 2017; McCoy, 2018;

Ferreira-Gonzalez et al., 2008). This kind of vari-

https://orcid.org/0000-0001-5259-4793

https://orcid.org/0000-0003-3283-0597

https://orcid.org/0000-0003-4570-8902

ables also serve to avoid the assessment of the ef-

fect in presence of competing risks (McCoy, 2018;

Ferreira-Gonzalez et al., 2008).

Of course, this is a simple model which allows

for a easy implementation, commonly analyzed with

a Cox regression model and described by a Kaplan-

Meier curve. This composite endpoint framework al-

lows the researchers to answer questions like: Are pa-

tients with certain risk factors more likely to show ad-

verse events than patients without them? What is the

expected time to an adverse event of low risk patients?

The use of composite endpoints presents several

limitations. On one hand, interpretation of compos-

ite endpoints is a challenge (McCoy, 2018), specially

when the events included in the composite endpoint

show different clinical relevance or when the compo-

nents occur with heterogeneous frequency (Ferreira-

Gonzalez et al., 2008). On the other hand, according

to (Kip et al., 2008), the deﬁnition of a composite end-

point can vary between studies, making the research

results comparison difﬁcult.

In order to overcome these drawbacks, additional

individual analyses of the events are usually recom-

mended under a competing risks framework (N

nez

194

Quirós, A., Pérez de Prado, A., Montoya, N. and Hernández, J.

Multi-state Models for the Analysis of Survival Studies in Biomedical Research: An Alternative to Composite Endpoints.

DOI: 10.5220/0009105701940199

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 194-199

ISBN: 978-989-758-398-8; ISSN: 2184-4305

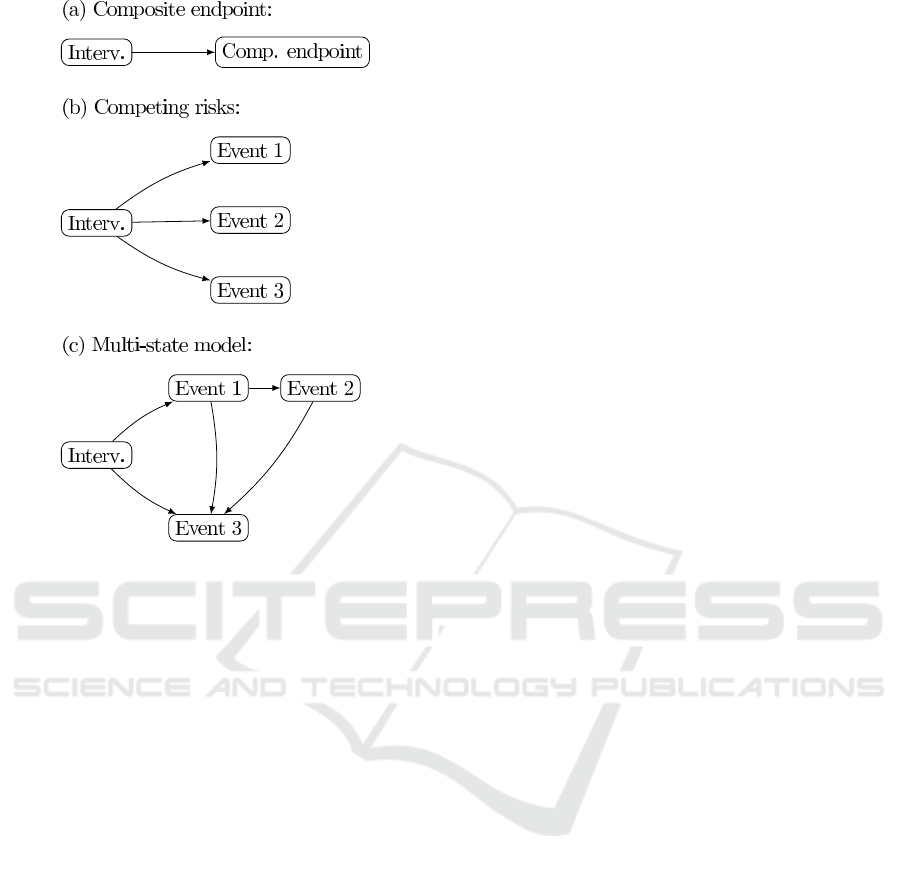
Figure 1: (a) Composite endpoint scheme. Composite end-

point includes events 1, 2 and 3; (b) Competing risks sce-

nario; (c) Multi-state model, with more structure.

et al., 2011; Austin et al., 2016). Formally, this de-

scribes an scenario as the one represented in diagram

(b) of Figure 1. This implies missing the occurrence

of events after the ﬁrst, for those patients who suffered

more than one event during the follow up.

With the advent of new technologies and of mul-

tidisciplinary groups, databases are larger and re-

searchers are now in the position of stating more com-

plex models that adapt better to the real evolution of

the disease. For instance, it is reasonable to consider

a model as the one described in diagram (c) of Figure

1. In this setting, more structure is given to the model,

for example, including the information that Event 2 is

preceded by Event 1. Fitting this model, researchers

will be able to answer questions like: Are high risk

patients more likely of suffer Event 3 after showing

an Event 1 post-treatment? What is the estimated so-

journ time after the occurrence of Event 2?

A multi-state model is the natural approach in

this setting, as it allows to consider survival models

with a complex structure of the states which patients

may visit along the follow up. Multi-state models

are closely connected with survival analysis, as tran-

sition intensities between states correspond to hazard

rate functions for times between transitions in survival

analysis (Meira-Machado et al., 2009). Furthermore,

multi-state models provide information about the ex-

pected time and the probability of moving from one

state to another, depending on certain risks factors or

treatment characteristics. Formally, multi-state mod-

els are a class of stochastic processes which model the

probability of visiting a certain set of discrete states in

continuous time (Andersen et al., 1993; Putter et al.,

2007).

This kind of models take into account all available

follow up data, i.e. all the events observed for each

patient. Additionally, multi-state models are able to

accommodate different sets of factors affecting each

transition, allowing personalized estimations. There-

fore, a prediction for a patient can be made consid-

ering his or her basal characteristics, treatment and

observed disease evolution.

In this work, we propose to examine survival

times and time to the ocurrence of adverse events in

conjunction with risks factors using multi-state mod-

els in survival study in biomedical research, as an al-

ternative to composite endpoints. For this purpose,

we analyze data from a longitudinal study in Cardio-

vascular research and compare the results obtained by

considering a composite endpoint scheme, a compet-

ing risks scenario, and a multi-state model.

2 MATERIALS AND METHODS

2.1 Data

We illustrate the implementation of multi-state mod-

els in survival studies in biomedical research, with

the data of a study in interventional cardiology. The

SYNERGY ACS registry (De la Torre Hernandez

et al., 2018) was a multi-center retrospective registry

carried out in 10 Spanish hospitals, including 1008

patients with acute coronary syndrome (ACS) who

underwent percutaneous revascularization with the

implantation of a SYNERGY stent and whose date

of procedure was between January 2013 and March

2019. After the treatment, several adverse events and

the corresponding times were recorded during the fol-

low up, including death, myocardial infarction (MI),

target lesion revascularization (TLR), stent thrombo-

sis, etc. For further information on the dataset see (De

la Torre Hernandez et al., 2018).

Time on study is assumed as the maximum time

and the date of intervention is ﬁxed as the start-

ing time for each patient. We have initially consid-

ered 15 prognostic factors or covariates: age, sex,

smoker, hypertension, diabetes, hyperlipidemia, prior

MI, prior PCI, peripheral vascular disease, type of

ACS, left ventricular ejection fraction (LVEF), dual

Multi-state Models for the Analysis of Survival Studies in Biomedical Research: An Alternative to Composite Endpoints

195

anti-platelet therapy (DAPT) period in months, num-

ber of diseased vessels, incomplete revascularization,

and stent thrombosis.

2.2 The Models

2.2.1 Composite Endpoint Scheme

We deﬁne a variable of Major Adverse Cardiac Events

(MACE) indicating whether a patient has suffered a

MI of has died during the follow up. MACE is there-

fore a composite endpoint.

As commonly done in cardiovascular research, a

Kaplan-Meier curve is used in order to describe data

and MACE is analyzed by a Cox multiple regression

model, selecting the variables according to Akaike’s

Information Criterion and clinical considerations.

2.2.2 Competing Risks Scenario

As can be observed in Figure 1, the competing risks

scenario is a particular example of multi-state model.

Here, the competing risks scenario is included as a

part of the multi-state model, as will be described be-

low.

2.2.3 The Disability Model

As commented above, multi-state models are very

useful for describing event-history data, providing a

better understanding of the disease process, and lead-

ing to a better knowledge of the evolution of the dis-

ease over time. Multi-state models are ﬂexible, allow-

ing for different structures to accommodate the rela-

tionship between the states of the processes. In this

particular example, we propose a multi-state model

known as the disability model, which is relevant in ir-

reversible diseases where the occurrence of a speciﬁc

adverse event increases the risk of death. The scheme

of the disability model used is depicted in Figure 2.

Figure 2: The disability model.

Formally, let Z(t) be the stochastic process de-

scribing the state of a ACS patient at time t, where t is

time since intervention. All living patients that have

not yet experienced a MI post-treatment are consid-

ered to be in state 1, patients move to state 2 when

they suffer a MI after treatment, and state 3 stands

for the death of the patient. The state space is thus

{1, 2,3} and state 3 is the absorbing state, meanwhile

states 1 and 2 are said to be transient. Transition prob-

abilities between states depend on a set of covariates,

, and can be determined from the hazard rate func-

tions for times between transitions. Let q

(t, x

) be

the instantaneous risk of moving from state r to s 6= r,

i.e.

(t, x

) = lim

δt→0

P(Z(t + δt) = s|Z(t) = r)

δt

, (1)

then

(t, x

) = q

(0)

exp(β

). (2)

Following this, times between transitions are assumed

to be exponential and a different model is ﬁtted to

each transition, in which the covariates are used to ex-

plain differences in the course of the disease among

the population (Jackson, 2011). Therefore, a joint

variable selection for the three models corresponding

to the different transitions between states is done. The

expressions to estimate the transition probabilities for

the disability model can be found in (Jackson, 2011)

and references therein. These estimations are based

on the likelihood maximization. The computation of

conﬁdence intervals for predicted values of the tran-

sitions probabilities are done using a normal approxi-

mation.

Note that the competing risks scenario is included

in the disability model, for this particular example.

In fact, the competing risk scenario is the disability

model without the transition from MI to Death.

For illustration of the model, two types of patients

are deﬁned -low and high risk- setting their character-

istics according to the selected covariates.

2.2.4 Software

We use the R statistical software (R Core Team,

2019), version 3.6.1, for data analysis. In particular,

the survival package (Therneau, 2015) is used for the

composite endpoint scheme analysis described above.

Regarding the multi-state model, it is ﬁtted with the

msm package (Jackson, 2011) for R. Figures are cre-

ated with ggplot2 (Wickham, 2016) and survminer

(Kassambara et al., 2019) packages.

3 RESULTS

The average follow-up was of 805.3 days (2 years, 2

months and 25.3 days), being of 5 days the shortest

BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms

196

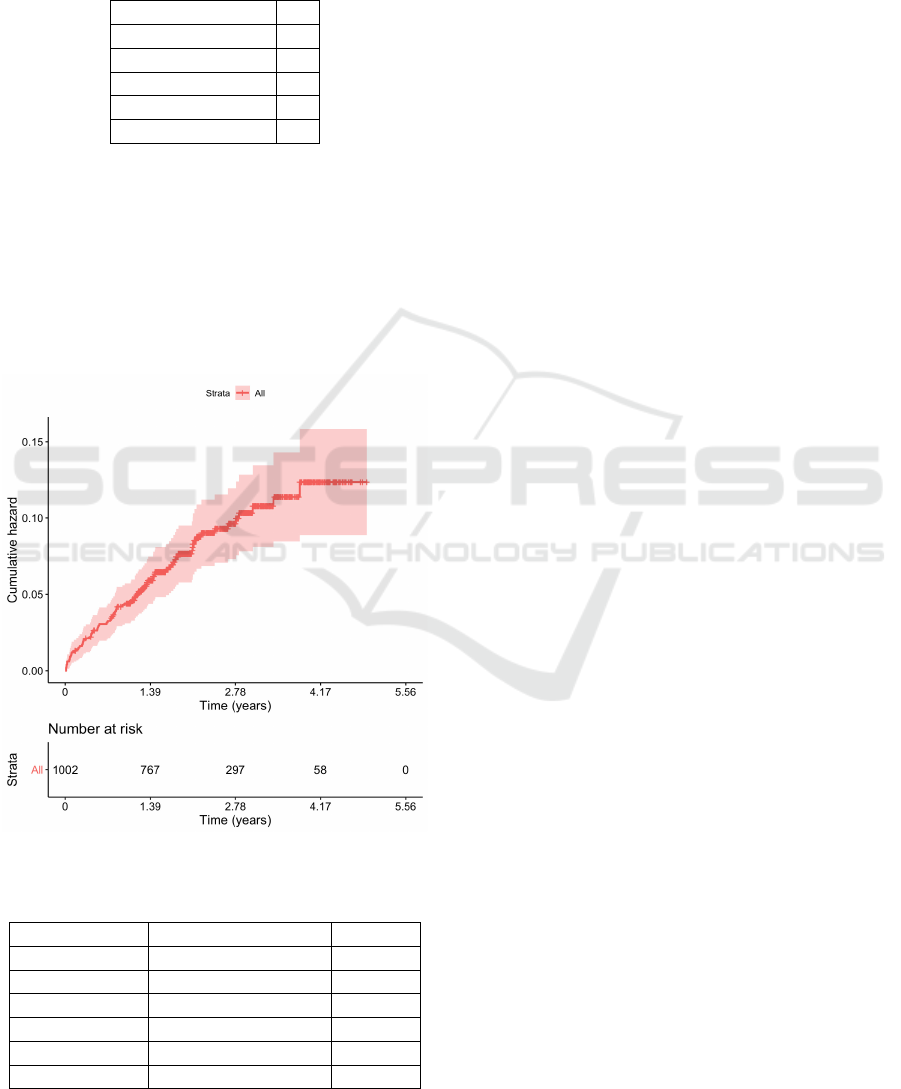
and 1771 days the longest follow up time. The ad-

verse events observed during the follow up are given

in the Table 1, in which MACE stands for the com-

posite endpoint of MI and all-cause Death.

Table 1: Adverse events.

Death 63

MI 31

Revascularization 48

TLR 14

Stent thrombosis 11

MACE 86

Death is the more frequent adverse event observed

in the sample, being of 6.25%, followed by revascu-

larization (4.76%, form which 29.17% were TLR),

MI (3.08%), and stent thrombosis (1.09%).

A Kaplan-Meier graphic of the variable MACE is

represented in Figure 3 and the result of the Cox mul-

tiple regression model for MACE -in terms of hazard

rate (HR)- is shown in Table 2.

Figure 3: Kaplan-Meier curve for MACE.

Table 2: Cox multiple regression model.

Covariate HR (95%CI) p-val

Age 1.04 (1.01 - 1.06) 0.005

LVEF 0.96 (0.94 - 0.98) < 0.001

N. dis. vessels 1.45 (1.03 - 2.02) 0.032

Prior PCI 2.97 (1.67 - 5.29) < 0.001

DAPT months 0.94 (0.88 - 1.01) 0.053

Stent thromb. 14.99 (5.10 - 44.03) < 0.001

Cox regression analysis revealed that age, LVEF,

number diseased vessels, prior PCI, DAPT time and

stent thrombosis were signiﬁcant factors of MACE,

from which LVEF and DAPT time were protective

(see Table 2). Note that this model provides the prog-

nostic factors for the composite endpoint MACE, in

which the two adverse events are jointly considered.

As explained before, we adjusted a disability

model considering three states:

• State 1:Treatment (908 alive patients and without

MI at the end of the follow up).

• State 2: MI (31 patients with MI after treatment).

• State 3: Death (63 patients died, 8 of them after a

post-treatment MI).

After adjusting the model, we can observe that pa-

tients that suffer a MI after the treatment have a higher

probability to die and that the expected time is 40 days

(19 - 77) after the MI. Additionally, after the treat-

ment, a patient has 1.5 more probability of dying than

to have an MI. This probability is multiplied by 424

for those patients who suffer post-treatment MI.

Transitions between states are determined by cer-

tain factors. In particular, the transition from treat-

ment to MI, 1 → 2, depends on diabetes -2.64 (1.18

- 5.90)-, the number of diseased vessels -1.86 (1.12

- 3.10)-, and stent thrombosis -44.84 (15.24 - 132)-.

Transition from treatment to Death, 1 → 3, is inﬂu-

enced by age -1.06 (1.03 - 1.09)-, LVEF -0.95 (0.92 -

0.97)-, and prior PCI -3.16 (1.65 - 6.07)-. The transi-

tion from MI to Death, 2 → 3, is determined by dia-

betes -8.54 (1.43 - 51.09)- and prior PCI -13.00 (1.35

- 124.94)-. These results are very similar to the ob-

tained in the Cox model for MACE, as expected, al-

though the algorithm was unable to converge when

incorporating DAPT months as a covariate. When

included alone, DAPT months resulted protective for

the transition from treatment to death. Note that the

uncertainty of the estimations for the transition 2 → 3

are larger due to the lower number of observations

available. It is worth to emphasize that, in this model,

it is possible to extract how the different characteris-

tics of the patient, the treatment or the evolution of the

disease affects patient prognosis, distinguishing MI

from Death and from Death after a post-treatment MI.

For example, Cox regression model above showed

that age was a signiﬁcant factor for MACE, mean-

while the disability model clariﬁes that this effect is

due to the fact that elder people are more prone to die.

This model allows for predictions of the transition

probabilities for any patient with speciﬁc values for

the covariates. In order to simplify and to facilitate

the interpretation of the results, two types of model

patients were described according to the ﬁtted disabil-

Multi-state Models for the Analysis of Survival Studies in Biomedical Research: An Alternative to Composite Endpoints

197

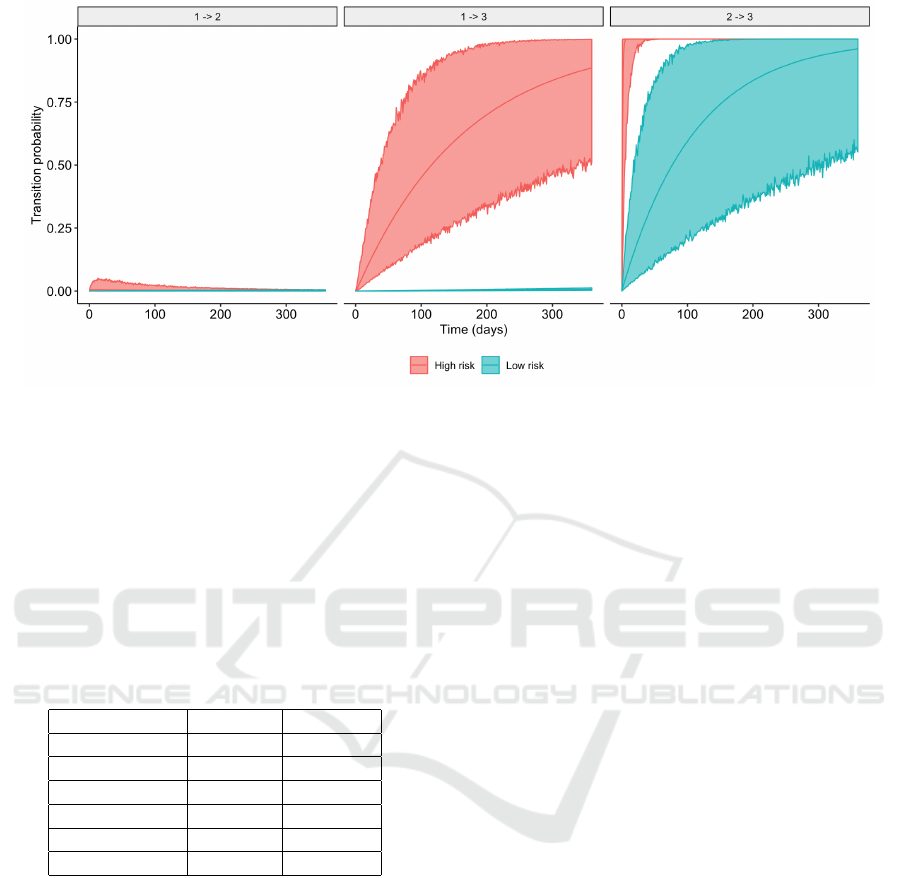
Figure 4: Probability and simulated 95% CI of 1 → 2 (left); 1 → 3 (middle); and 2 → 3 (right); for low and high risk patients.

ity model (see Table 3). A high risk patient is deﬁned

to be 79 years old (sample mean age plus a standard

deviation), diabetic, with a LVEF of 45 (sample mean

LVEF minus a standard deviation, as the factor is pro-

tective), presenting 3 diseased vessels and a prior PCI,

who suffer a stent thrombosis. Covariates values for

the low risk patient are opposite to the ones for the

high risk patient.

Table 3: High and low risk patients characteristics.

Low risk High risk

Age 54 79

Diabetes no yes

LVEF 65 45

N. dis. vessels 1 3

Prev. PCI no yes

Stent thromb. no yes

For high and low risk patients, Figure 4 shows

the ﬁrst year evolution after the treatment (transitions

1 → 2 and 1 → 3) and from post-treatment MI (tran-

sition 2 → 3), respectively. We can observe that, in

general, the high risk patient has a higher probabil-

ity of dying than the low risk patient, from both states

(treatment or MI). Regarding the transition from treat-

ment to MI, the probability is different during the ﬁrst

three months, approximately, becoming similar after

that. The width of the simulated conﬁdence intervals

reﬂects the uncertainty about the estimations, due to

the relatively low incidence of the adverse events.

4 CONCLUSIONS

In this work, we propose multi-state models as an al-

ternative to composite endpoint schemes for survival

studies in biomedical research. A practical example

has been used to illustrate and compare the perfor-

mance of an analysis based on a composite endpoint

with multi-states model.

Biomedical survival studies pursue to understand

the role and signiﬁcance of prognostic factors in sev-

eral features of the disease such as survival times, ad-

verse events incidence, response to treatment, compli-

cations, etc. Multi-state models are the natural mod-

els for describing the evolution of a disease over time.

Moreover, their ﬂexibility to accommodate different

situations via the state structure, provides them with

a great potential in the analysis of survival data in

biomedical research. Multi-states models provide in-

formation about the expected time and the probabil-

ity of moving from one state to another, depending

on risks factors, treatment characteristics and the past

evolution of the disease.

In contrast to other alternatives to composite end-

points, as the competing risks model, these models

take into account all available data regarding follow

up, without forcing the withdrawal from the study of a

patient for whom an adverse event has been observed.

By presenting a toy example, we have shown how

different covariates may affect the incidence of ad-

verse events, via a multi-state modelization. There-

fore, multi-states models have been proved to pro-

vide a more valuable information than composite end-

points, for clinicians and patients decision making. In

particular, predictions could be done to certain risk

BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms

198

groups, as shown, by deﬁning different characteris-

tics.

The implementation of multi-state models is not

straightforward, especially when considering more

complex states structures than the disability model.

Several issues must be taken into account, which were

out of the scope of this work. First, a Markov dis-

ability model has been considered, hence discarding

a semi-Markov model, i.e. a model in which sur-

vival time for a patient who has experienced a post-

treatment MI depends on the time from treatment

to MI. Therefore, the Markov assumption must be

checked during the analysis. Second, the choice of

the survival models to be use for transition times is

of great importance, and only some options can be

found already implemented in commercial software.

Estimation of the transition intensities will be inac-

curate when a low number of events are observed for

a transition, as can be observed in the results of this

work. Third, model assessment and variable selection

in this setting are still open questions.

Future versions of this work will consider

Bayesian inference in order to be able to work with

more sophisticated states structures and different sur-

vival models, as in (Armero et al., 2016). In that

work, although a relatively simple parametric model

for the hazard function (of each transition) was con-

sidered, posterior distributions of parameters had to

be approximated as software was unavailable, even

for a disability model. Our future research will surely

be a challenge in this sense, especially if a more com-

plex state structure is to be considered. That said,

Bayesian inference also has the advantage of stating

results in terms of probabilities, which are directly in-

terpretable. Such approach would allow us to give

personalized predictions, for example, the probabil-

ity of suffering a MI in the next three months taking

into account the patient’s history. Additionally, the

Bayesian approach provides an ideal framework for

the assessment of the model and for variable selection

in multi-state models, via the Bayes factor and model

simulation.

ACKNOWLEDGEMENTS

The authors want to thank the Epic foundation for

providing the data and useful insights about the re-

sults.

REFERENCES

Andersen, P., Borgan, P., Gill, R., and et al. (1993). Statis-

tical models based on counting processes. Springer,

New York.

Armero, C., Cabras, S., Castellanos, M., Perra, S., Quir

os,

A., Oruezabal, M., and Sanchez-Rubio, J. (2016).

Bayesian analysis of a disability model for lung can-

cer survival. Statistical Methods in Medical Research,

25(1):336–351.

Austin, P., Lee, D., and Fine, J. (2016). Introduction to the

analysis of survival data in the presence of competing

risks. Circulation, 133:601–609.

De la Torre Hernandez, J., Moreno, R., Gonzalo, N.,

Rivera, R., Linares, J., Veiga Fernandez, G., Gomez

Menchero, A., Garcia del Blanco, B., Hernandez,

F., Benito Gonzalez, T., Subinas, A., and Escaned,

J. (2018). The pt-cr everolimus stent with bioab-

sorbable polymer in the treatment of patients with

acute cononary syndromes. results from the syn-

ergy acs registry. Cardiovascular Revascularization

Medicine.

Ferreira-Gonzalez, I., Alonso-Coello, P., Sola, I., Pacheco-

Huergo, V., Domingo-Salvany, A., Alonso, J., Mon-

tori, V., and Permanyer-Miralda, G. (2008). Compos-

ite endpoints in clinical trials. Revista Espa

nola de

Cardiolog

ıa, 61(3):283–290.

Irony, T. (2017). The “utility” in composite out-

come measures. measuring what is important to pa-

tients. Journal of the American Medical Association,

318(18):1820.

Jackson, C. (2011). Multi-state models for panel data: The

msm package for R. Journal of Statistical Software,

38(8):1–29.

Kassambara, A., Kosinski, M., and Biecek, P. (2019).

survminer: Drawing Survival Curves using ’ggplot2’.

Kip, K., Hollabaugh, K., Marroquin, O., and Williams, D.

(2008). The problem with composite end points in

cardiovascular studies: The story of major adverse

cardiac events and percutaneous coronary interven-

tion. Journal of the American College of Cardiology,

51(7):701–707.

McCoy, C. (2018). Understanding the use of composite

endpoints in clinical trials. Western Journal of Emer-

gency Medicine, 19(4):631–634.

Meira-Machado, L., de U

na-

Alvarez, J., Cadarso-Su

arez,

C., and Andersen, P. (2009). Multi-state models for

the analysis of time-to-event data. Statistical Methods

in Medical Research, 18:195–222.

nez, E., Steyerberg, E., and N

nez, J. (2011). Estrate-

gias para la elaboraci

on de modelos estad

ısticos de re-

gresi

on. Revista Espa

nola de Cardiolog

ıa, 64:501–

507.

Putter, H., Fiocco, M., and Geskus, R. (2007). Tutorial in

biostatistics: competing risks and multi-state models.

Statistics in Medicine, 26:142–161.

R Core Team (2019). R: A Language and Environment for

Statistical Computing. R Foundation for Statistical

Computing, Vienna, Austria.

Therneau, T. M. (2015). A Package for Survival Analysis in

Wickham, H. (2016). ggplot2: Elegant Graphics for Data

Analysis. Springer-Verlag New York.

Multi-state Models for the Analysis of Survival Studies in Biomedical Research: An Alternative to Composite Endpoints

199