360-Degree Autostereoscopic Display using Conical Mirror and
Integral Photography Technology
Nobuyuki Ikeya and Kazuhisa Yanaka
Kanagawa Institute of Technology, Atsugi, Japan
Keywords: 360 Degrees, Autostereoscopic, Conical Mirror, Integral Photography.
Abstract: We propose a new 360° autostereoscopic display that combines a conical mirror and integral photography
technology. Our system is similar to the conventional holographic pyramid in that a 3D object appears to float
near the center. However, the pyramid consists of four planes with visible borders, whereas the conical mirror
only has a seamless curved surface. Therefore, a stereoscopic image can be observed from any angle. The
object displayed in the cone is a CG character. It is pre-rendered every 0.5° to obtain 720 still images. One IP
image is synthesized based on those still images. This system has the advantage of being manufactured at a
relatively low cost. Moreover, high reliability can be expected because this display has no mechanical moving
parts.
1 INTRODUCTION
A 3D display that resembles a real object from any
360° direction is an ideal display, and it has been
actively studied by researchers.
Jones et al. (2012) proposed a display that consists
of a high-speed video projector, a spinning mirror
covered by a holographic diffuser, and FPGA
circuitry. Takaki et al. (2012) proposed a 360° 3D
display with a table screen, which consists of a small
number of high-speed projectors and a rotating
screen. Xia et al. (2013) proposed a system using a
high frame-rate projector and a flat light-field
scanning screen and a revolving mechanism. In these
studies, mechanical moving parts are used. Yoshida
(2016) proposed a glasses-free tabletop 3D display in
which virtual objects appear to be floating on a flat
tabletop surface without using mechanical moving
parts; instead, a large number of projectors are used.
As another approach, a holographic pyramid can
be used to obtain a 360° field of view. In this method,
a pyramid made of a translucent material is placed
upside down on a flat display, and the image of the
flat display is reflected on the surface of the pyramid
for observation. In this case, if the image on the flat
display is 2D, then the image in the pyramid is its
mirror image. Therefore, the image is also 2D.
However, using integral photography (IP) instead
of a flat panel display, the image that appears to be
floating inside the pyramid can be turned into 3D.
Figure 1: Conventional system using a pyramid.
Figure 2: Our proposal using a conical mirror.
An autostereoscopic display that looks as if the
object is floating inside a square pyramid can be
created by combining a pyramid made of a material
that reflects light with IP (Yamanouchi et al. 2016)
(Anraku et al. 2018) However, as shown in Fig. 1,
the quadrangular pyramid consists of four surfaces:
front, back, left, and right. Therefore, the boundaries
814
Ikeya, N. and Yanaka, K.
360-Degree Autostereoscopic Display using Conical Mirror and Integral Photography Technology.
DOI: 10.5220/0009106208140818
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
814-818
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

between any two surfaces may be visible. We have
developed a new system (Fig. 2) that uses only curved
surfaces. The displayed object can be displayed in a
360° autostereoscopic view by using a cone instead
of a square pyramid.
2 METHOD
The proposed system consists of two parts. One is an
IP-type display in which a fly’s eye lens is
superimposed on a liquid crystal display (LCD) or an
organic light-emitting diode display, and each pixel
emits a light beam in a specific direction. The other is
a conical mirror that reflects light coming from an IP
display and directs the light in a 360° direction. The
IP image synthesis method is important here. In
conventional holographic pyramids, only four IP
images corresponding to the front, rear, left, and right
are synthesized. However, when using a conical
mirror, this method becomes inapplicable because the
surface is not a plane but is curved instead. Therefore,
a new method that is similar to ray tracing described
below is applied.
In general, light rays passing through the center of
a transparent sphere travel straight without being
refracted at the surface of the sphere.
Similarly, in a spherical lens, a ray passing
through the center of curvature goes straight without
being refracted.
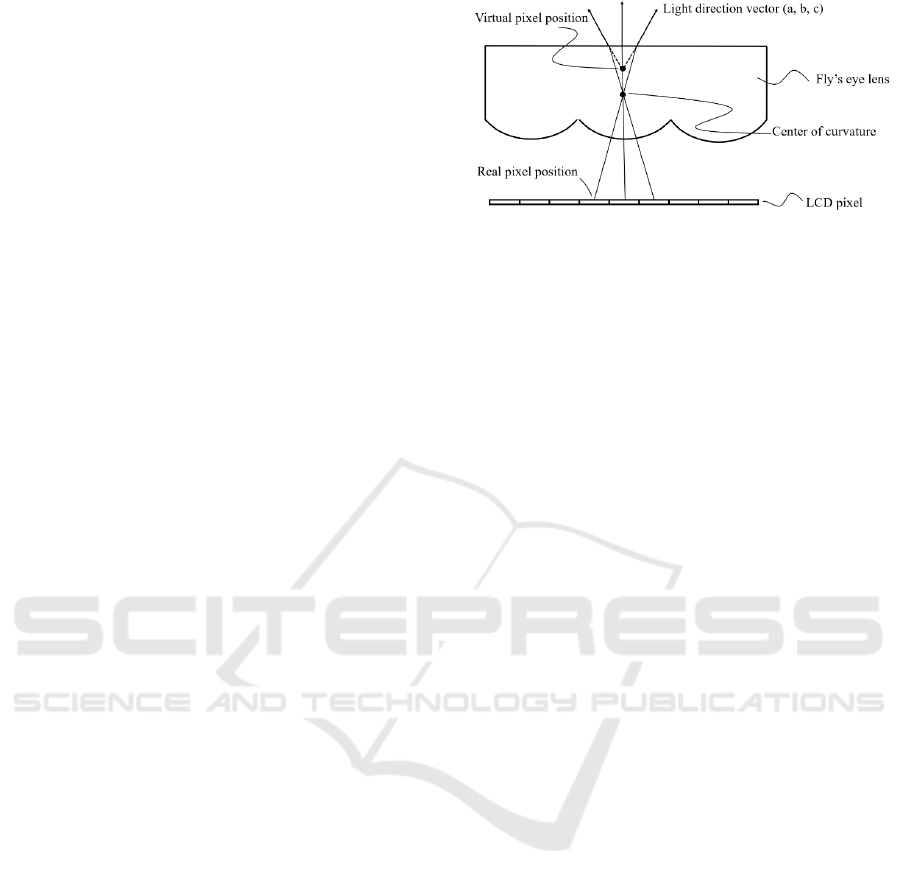
As shown in Fig. 3, the light emitted from each
pixel of the LCD is emitted to the space through a
minute convex lens, which is part of a fly’s eye lens.
Moreover, the path of the light can be accurately
calculated if the pixel pitch of the LCD and the lens
pitch of the fly’s eye lens are known.
In Fig. 3, assuming that the distance between the
LCD and the fly’s eye lens is the same as the focal
length of each convex lens, the convex lens changes
the light emitted from an LCD pixel into parallel rays.
The direction of the light beam can be calculated
using the property that a light beam passing through
the center of curvature goes straight. Considering that
light rays are refracted on the surface when exiting
the fly’s eye lens, the virtual pixel position is point P
= (p
x
, p
y
, p
z
), and the direction vector of the ray is u =
(u
x
, u
y
, u
z
). Here, the coordinate system is a
rectangular one with the origin at the vertex below the
cone.
Figure 3: Path of light emitted from LCD pixels.
In Fig. 4, light emitted from point P on the fly’s
eye lens in the direction vector u is assumed to be
reflected at point Q on the conical mirror and directed
to the direction vector v.
The equation light emitted from point P is as
follows, using t as a parameter.
x = u
x
× t + p
x
y = u
y
× t + p
y
z = u
z
× t + p
z
Meanwhile, the equation of the cone is as follows:
x
2
+ z
2
= y
2
.
By making these equations simultaneous, the
point Q = (q
x
, q
y
, q
z
) can be calculated, where the light
meets the conical mirror and the direction of the
reflected light.
Given that the normal of the conical surface at this
intersection is n = (n
x
, n
y
, n
z
) = (q
x
, q
y
, -q
z
), the
direction vector v = (v
x
, v
y
, v
z
) of the reflected light
can be obtained by Snell’s law. Furthermore, the
equation of the reflected light is as follows, where t is
a parameter.
x = v
x
× t + v
x
y = v
y
× t + v
y
z = v
z
× t + v
z
A square is selected among 720 squares passing
through the central axis of the conical mirror. The
projection of the square onto the XY plane must be
orthogonal to v. An image obtained by rendering an
object from this direction is assumed texture-mapped
in advance in this square. An image rendered from the
direction closest to v is selected among 720 still
images obtained by rendering an object from 720
directions. Proceeding from point Q in the direction
of −v, point R intersects the square. Thus, the pixel
value at such point is acquired and set as the value of
pixel P on the LCD.
When this process is performed for all pixels on
the LCD, one IP image is completed and displayed on
the LCD.
360-Degree Autostereoscopic Display using Conical Mirror and Integral Photography Technology
815

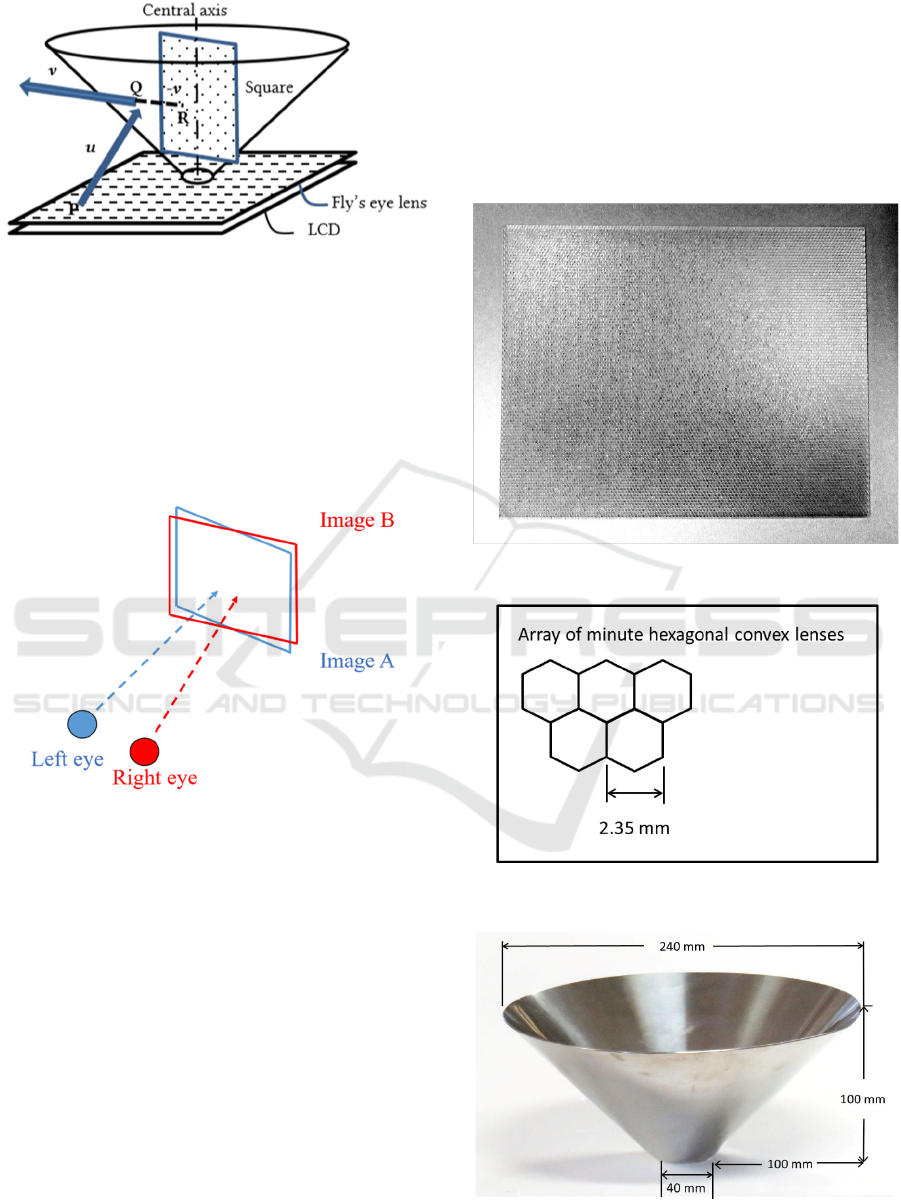
Figure 4: Principle of IP image synthesis.
The reason why stereoscopic display is possible with
this system is as follows. In Fig. 5, the left eye looks
at image A. The right eye sees image B. Here, images
A and B are two of the 720 images obtained from 720
directions.
Accordingly, stereoscopic images can be obtained
because the same subject seen from different
viewpoints enters the left eye and the right eye.
Figure 5: Reasons for stereoscopic viewing.
3 EXPERIMENTS
The experimental system consists of an IP-type
display consisting of a laptop PC, fly’s eye lens, and
a conical mirror.
Microsoft Surface Book 2 is used as a laptop PC.
Given that its LCD resolution is 2000 × 3000 and that
the screen size is 13.5 inches diagonally, the pixel
diagonal is 3065.5. Therefore, the resolution is 3065.5
/ 13.5 = 227.1 dpi (dots per inch).
Fig. 6 shows the appearance of the used fly’s eye
lens. The shape is shown in Fig. 7. The distance
between adjacent lenses, or lens pitch, is 2.35 mm, or
10.81 dpi. The number of LCD pixels per lens pitch
is 271.8 / 10.81 = 25.14. Given that this value is not
an integer, the extended partial view method (Yanaka
2008) is used to produce an IP image.
The LCD is combined with a coarse fly’s eye lens,
so the final resolution obtained is determined by the
fly’s eye lens. In this system, the final resolution is
10.81 dpi.
The conical mirror shown in Fig. 8 is made of
stainless steel and has an exterior mirror finish.
Figure 6: Fly’s eye lens.
Figure 7: Shape of the fly’s eye lens used.
Figure 8: Conical mirror.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
816

Unity-chan, a CG character provided by Unity
Technologies Japan, is used as a 3D object to be
displayed in a conical mirror. As shown in Fig. 9,
Unity-chan has been pre-rendered in 360° increments
every 0.5°, and 720 still images are obtained.
Figure 9: Pre-rendered images (© UTJ/UCL).
Figure 10: Finished IP image to be displayed on the LCD
of Microsoft Surface Book 2 with a resolution of 2000 ×
2000 pixels (Only the central part of the 2000 × 3000 pixel
LCD is used.).
Subsequently, an IP image (Fig. 10) is
synthesized using the method described in the
previous chapter. Unlike a normal IP image, the
synthesized image has an annular pattern because it
corresponds to 360°.
Fig. 11 shows an example of an autostereoscopic
image displayed by a system on a turntable. Our
system does not include mechanically moving parts.
The turntable is used only for shooting videos.
When this system is placed and observed on an
electric turntable, the autostereoscopic image can be
seen in any direction from any angle. However, the
current 3D image that appears inside the cone is
unclear. This problem will be improved in the future
by using high-resolution LCDs and fine fly’s eye
lenses.
Figure 11: Autostereoscopic image displayed with our
system on an electric turntable (© UTJ/UCL).
4 CONCLUSIONS
A new 360° autostereoscopic display is proposed.
The hardware of this system is simple, with a conical
mirror added to a conventional IP display. Therefore,
this system has the advantage of being manufactured
at a relatively low cost. Moreover, high reliability can
be expected because this display has no mechanical
moving parts.
At present, the displayed 3D objects are not very
clear. If high-resolution LCDs and fine, wide-angle
fly’s eye lenses are available in the future, then
improvements are expected. Another issue is that the
stereoscopic image is not animating but still.
However, when each frame of the animation is
created as an IP image, and the IP images are
connected together, an autostereoscopic animation
can be created. In addition, the parallax is only in the
horizontal direction, but it can be extended to add the
vertical parallax in principle. We will examine these
extensions in the future.
360-Degree Autostereoscopic Display using Conical Mirror and Integral Photography Technology
817

REFERENCES
Anraku, S., Yamanouchi, T., Yanaka, K., (2018). Real-time
Integral Photography Holographic Pyramid using a
Game Engine.In VISIGRAPP 2018 - Volume 4:
VISAPP, pp. 603 - 607.
Jones, A., McDowall, I., Yamada, H., Bolas, M., Debevec,
P., (2007). Rendering for an interactive 360° light field
display. In SIGGRAPH 2007 Papers Proceedings.
Takaki, Y., Uchida, S., (2012). Table screen 360-degree
three-dimensional display using a small array of high-
speed projectors. In Optics Express Vol. 20, Issue 8, pp.
8848-8861.
Xia, X., Liu, X., Li, H., Zheng, Z., Wang, H., Peng, Y.,
Shen, W., (2013). A 360-degree floating 3D display
based on light field regeneration. In Optics Express Vol.
21, Issue 9, pp. 11237-11247.
Yamanouchi, T., Maki, N., Yanaka, K., (2016).
Holographic Pyramid Using Integral Photography. In
The 2nd World Congress on Electrical Engineering and
Computer Systems and Science.
Yanaka, K. (2008). Integral photography using hexagonal
fly's eye lens and fractional view. In Proceedings
Volume 6803, Stereoscopic Displays and Applications
XIX; 68031K, 8 pages.
Yoshida, S., (2016). fVisiOn: 360-degree viewable glasses-
free tabletop 3D display composed of conical screen
and modular projector arrays. In Optics Express Vol.
24, Issue 12, pp. 13194-13203.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
818