Assessing the Adequability of FFT-based Methods on Registration of
UAV-Multispectral Images
Jocival Dantas Dias Junior
1
, Andr
´
e Ricardo Backes, Maur
´
ıcio Cunha Escarpinati,
Leandro Henrique Furtado Pinto Silva, Breno Corr
ˆ
ea Silva Costa and Marcelo Henrique Freitas Avelar
School of Computer Science, Federal University of Uberl
ˆ
andia, Uberl
ˆ
andia/MG, Brazil
{jocival.dias, backes, mauricio, leandro.furtado, breno.costa, avelar}@ufu.br
Keywords:
Multispectral Registration, Unmanned Aerial Vehicles, Precision Agriculture.
Abstract:
Precision farming has greatly benefited from new technologies over the years. The use of multispectral and
hyperspectral sensors coupled to Unmanned Aerial Vehicles (UAV) has enabled farms to monitor crops, im-
prove the use of resources and reduce costs. Despite widely being used, multispectral images present a natural
misalignment among the various spectra due to the use of different sensors, and the registration of these images
is a complex process. In this paper, we address the problem of multispectral image registration and present
a modification of the framework proposed by (Yasir et al., 2018). Our modification generalizes this frame-
work, originally proposed to work with keypoints based methods, so that spectral domain methods (e.g. Phase
Correlation) can be used in the registration process with great accuracy and smaller execution time.
1 INTRODUCTION
By 2050, the world’s population is expected to be
close to 10 billion people and according to (Hunter
et al., 2017), the world food production will have to
grow somewhere between 60% and 100% to be able
to feed this population. To meet this challenge, (Kim
et al., 2019) describe that agriculture will increasingly
need automation, robotics, artificial intelligence, big
data, the internet of things among others. In this sce-
nario, the purpose of Precision Agriculture (PA) is to
optimize planting costs, increase productivity, reduce
the environmental impact of agricultural activity and
reduce crop damage by pests.
Unmanned aerial vehicles (UAVs) have been
widely used in PA to monitor crops, plant growth esti-
mation, pesticide application and soil analysis. In ad-
dition, UAVs are also used in the development of new
methods for precision farming, thus helping to reduce
costs and hours of work, which results in higher pro-
ductivity (Mogili and Deepak, 2018).
In addition to UAVs, sensors are also an essen-
tial part of the capture process. The first UAVs
used cameras that captured only red, green and blue
(RGB) spectra (Hunt et al., 2010). New sensors allow
UAVs to capture multispectral and hyperspectral im-
ages (Berni et al., 2009), these have been used for a
variety of applications, such as verifying growth rate,
biomass rate and disease identification.
The development of new multispectral imaging
sensors and the ease brought by UAVs to capture
low and medium altitude images (100 to 400m), has
driven the development of computer vision and ma-
chine learning applications by the scientific com-
munity. Its main goal, is to optimize the results
obtained with precision farming (Diaz-Varela et al.,
2014; Gevaert et al., 2015; Gago et al., 2015; Mesas-
Carrascosa et al., 2017; Soares et al., 2018).
However, despite being easily obtainable, the reg-
istration of multispectral images obtained by UAVs
is a complex process as most multispectral cameras
use different sensors to obtain each spectrum, caus-
ing a natural misalignment among the various spec-
tra. Moreover, the process of image capturing is ex-
tremely dependent on the trajectory and stability of
UAVs, as well as others parameters (such as wind
speed or direction), which can lead to further mis-
alignment among the spectra.
The quality of the spectrum alignment is ex-
tremely important for many precision agriculture ap-
plications, for example semantic segmentation, weed
identification, vegetation indices and more. Usually,
the process of registration of agricultural images ob-
tained by UAVs is mainly performed by using ground
control points (GCP), i.e., objects or targets that will
appear across all spectra. These objects are used to
establish a relationship between the coordinates of
the various spectra and the coordinates of the ter-
rain. However, this method is difficult to implement
on large farms and too expensive for smaller ones.
In this work, we propose a modification of the
framework proposed by (Yasir et al., 2018) for the
process of registration of multispectral images ob-
tained by UAVs without using any kind of ground
control points (GCP). This modification aims to gen-
eralize the framework to methods that take into ac-
count the spectral domain (e.g. Phase Correlation)
while maintaining performance in spatial methods
(e.g. KAZE and SURF) and reducing the computa-
tional time of the framework.
To evaluate our modified framework we per-
formed a comparison with FFT-based Phase Corre-
lation (FFT-PC) (Reddy and Chatterji, 1996), Kaze
Features (KAZE) (Alcantarilla et al., 2012), and
Speeded-Up Robust Features (SURF) (Bay et al.,
2006) methods. We chose these methods because they
obtained good results in multispectral registration of
images obtained by UAVs in recent works. We tested
each method on two different crop datasets (Soybean
and Cotton). We chose these crops as they both lack
elements that ease the process of image alignment
(e.g. trees, fences or roads).
The remainder of this paper is organized as fol-
lows. In section 2, the authors present the related
works on registration of multispectral images ob-
tained by UAVs. Section 3 presents the image regis-
tration methods and frameworks utilized in the exper-
iments section. Section 4 demonstrate the proposed
modification to the framework. In section 5 are pre-
sented the datasets utilized in this work and the eval-
uation metric used to conduct the tests. The results
obtained by this work are presented in Section 6. Fi-
nally, Section 7 presents the conclusions.
2 RELATED WORK
In (Banerjee et al., 2018) the authors developed a
framework for multispectral registration of images
taken in a spectrally complex environment. The meth-
ods evaluated were Harris-Stephens Features (HSF),
Min Eigen Features (MEF), Scale Invariant Feature
Transformation (SIFT), Speeded-Up Robust Features
(SURF), Binary Robust Invariant Scalable Keypoints
(BRISK) and Features from Accelerated Segment
Test (FAST). It was also evaluated whether the tem-
poral order of image acquisition was higher than the
spectral order. The authors concluded that spectral or-
dering yielded higher results than temporal order and
that SURF was the best method for multispectral reg-
istration.
In (Yasir et al., 2018), the authors have developed
a data-driven framework that defines the target chan-
nel for multispectral registration based on the assump-
tion that a greater number of control points imply bet-
ter image alignment performance. Generally speak-
ing, this work attempts to verify all spectra taken two
by two to identify an order of spectra that, on aver-
age, maximizes the number of control points during
all steps of the alignment process.
The work in (Dias Junior et al., 2019) investigated
the application of the multispectral UAV image reg-
istration framework proposed by (Yasir et al., 2018)
in traditional methods present in the image registra-
tion literature. The evaluated methods were Binary
Robust Invariant Scalable Keypoints (BRISK), Min
Eigen Features (MEF), Kaze Features (KAZE). It was
also evaluated whether the union of features between
the methods produced a superior result. The au-
thors concluded that the best method for multispectral
recording of agricultural images obtained by UAVs
was KAZE.
3 IMAGE REGISTRATION
METHODS
According to (Oliveira and Tavares, 2014), image reg-
istration can be defined as the process of aligning two
or more images. The main goal of image registration
is to find a transformation that best aligns the elements
of interest in the images. In this section, we present
the image registration methods used in this work.
3.1 FFT-based Phase Correlation
This method was proposed as an extension of the
phase correlation technique to cover affine transfor-
mations in the images (i.e., rotation, translation, and
scaling). The authors used Fourier rotational and
scaling properties to find out the scale and rotational
movement so that the phase correlation method deter-
mines the translation movement.
This method consists of applying a 2D Fast
Fourier transform (FFT) method in both moving and
the target images. In the sequence, a high-pass em-
phasis filter is applied in the Fourier log-magnitude
spectra of the two images, which are then mapped to a
log-polar plane. For this conversion, only the two up-
per quadrants of the Fourier log-magnitude are used.
Then, the phase correlation technique is used to deter-
mine the scale and rotation of the images. The mov-
ing image is transformed using bilinear interpolation.
After that, the moving image and the target image are
different only by the translation, so the phase corre-
lation technique is applied to obtain and correct the
translation.
3.2 Kaze Features
Kaze Features (Alcantarilla et al., 2012) is a 2D fea-
ture detection and description method which works in
nonlinear scale space. The main advantage of oper-
ating in a nonlinear scale-space instead of a Gaussian
scale-space is the fact that the Gaussian scale-space
does not respect the natural edges of objects present
in the image. As a consequence, it smoothes equally
noise and details of the image, thus reducing the dis-
tinctiveness and location accuracy.
Given an image, the Kaze Features method builds
a nonlinear scale-space up to a maximum evolution
time using variable conductance diffusion and an Ad-
ditive Operator Splitting (AOS) technique. In this
scale-space, the blurring is locally adaptative to the
image data, which reduces the noise but maintaining
the boundaries of the objects. After the construction
of the nonlinear scale-space, we select the 2D features
that return a maximum of the scale-normalized deter-
minant of the Hessian response through the nonlinear
scale-space. Posteriorly, we compute the orientation
of keypoint and use the first-order image derivative
to obtain an orientation and scale-invariant descriptor
(Alcantarilla et al., 2012).
3.3 Speeded-UP Robust Features
Speeded-UP Robust Features (SURF) (Bay et al.,
2006) is a scale and rotation invariant keypoints de-
tector and descriptor. In comparison with traditional
methods, the SURF algorithm approximates or, in
some cases, outperforms these methods in robust-
ness, distinctiveness, and repeatability. Moreover, the
SURF can be computed and compared faster than
other methods (Bay et al., 2006).
To obtain this performance, SURF detects points
of interest with the aid of pre-computed integral im-
ages to approximate the determinant of the Hessian
matrix. Its descriptor describes a distribution of Haar-
wavelet responses within the neighborhood of the
point of interest. Integral images are also used to ob-
tain speed performance on the construction of SURF’s
descriptor (Bay et al., 2006). Besides, SURF’s de-
scriptor has only 64 dimensions, which results in a
reduction of time for feature computation and match-
ing.
3.4 Multispectral Registration
Framework
In (Yasir et al., 2018), the authors proposed a data-
driven multispectral registration framework to obtain
the best registration order based on the number of key-
points detected in each spectrum by each technique.
This framework consists of the construction of a com-
plete undirected weighted graph where the nodes are
the spectrum bands and the weights are the number of
keypoints detected by a single technique. Each edge
is labeled with its respective technique. Next, the au-
thors use Kruskal’s algorithm (Kruskal, 1956) to com-
pute the maximum spanning tree (MST) of the graph.
The MST removes the extras edges, i.e., techniques
which have fewer keypoints detected. All weights of
the MST are replaced by 1 and the all-pars-shortest-
path algorithm is used to determine the best alignment
order (Floyd, 1962), thus obtaining the best spectrum
order considering the number of keypoints.
4 PROPOSED APPROACH
The main limitation of the framework proposed by
(Yasir et al., 2018) is the fact that it supports only
image registration methods based on keypoints. Sev-
eral other methods that use the frequency domain, i.e.,
Fast Fourier transform-based (FFT-based) cannot be
used with this approach. Another problem is the fact
that it requires a high time for execution, which is de-
pendent on the method used to extract the keypoints.
To address this issue, in this work we propose
a modification of the framework proposed by (Yasir
et al., 2018). We replaced the amount of keypoints
metric used in the original approach by the 2D Pear-
son’s correlation coefficient (see Equation 1) (Kirch,
2008). This modification aims to generalize the
framework to methods that take into account the spec-
tral domain (e.g. Phase Correlation) and reducing the
computational time of the framework.
The modified framework consists of building a
complete undirected weighted graph where the nodes
of the graph are the channels to be aligned and the
weight is the 2D Pearson’s correlation coefficient
value obtained between the channels. Subsequently,
the Kruskal (Kruskal, 1956) algorithm is used to con-
struct a Maximum Spanning Tree. To find the chan-
nel to target for alignments, the weights between the
nodes are replaced by 1 and the Floyd-Warshall all-
pairs-shortest-path (Floyd, 1962) algorithm is used.
The node with the smallest sum of distances from
itself to all the other nodes is selected as the target
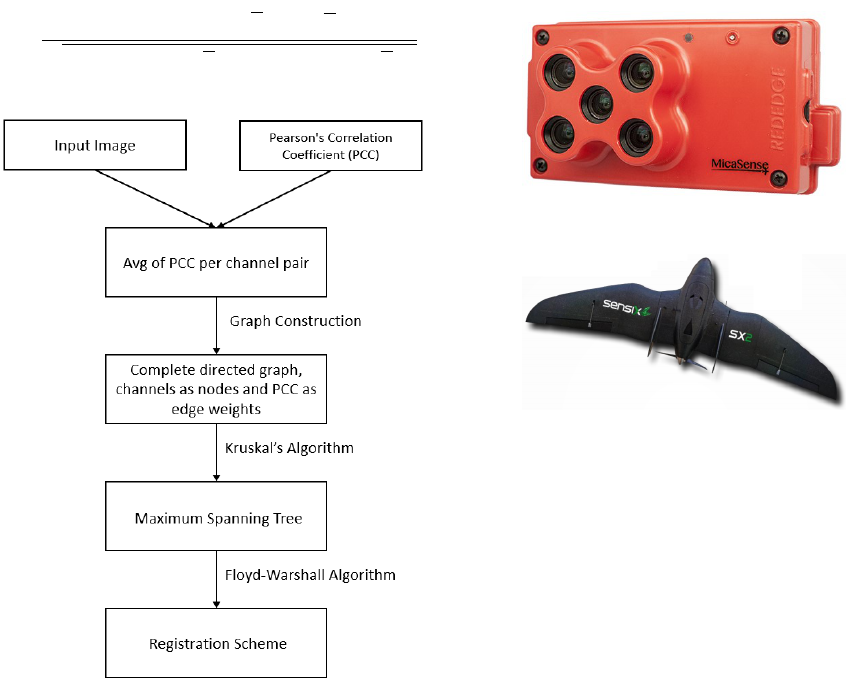
channel for the registration scheme. Figure 1 shows
the overview of the modified approach.
r =
∑
n
i=1
∑
m
j=1
(A
i j
− A)(B
i j
− B)
q
(
∑
n
i=1
∑
m
j=1
(A
i j
− A)
2
)(
∑
n
i=1
∑
m
j=1
(B
i j
− B)
2
)
(1)
Figure 1: Overview of the modified approach, modified
from (Yasir et al., 2018).
5 EXPERIMENTS
In this section we present a brief description of the
datasets and the evaluation metric used in the experi-
ments.
5.1 DATASET
In our experiments we used two datasets to evaluate
proposal performance, both containing images with
1280 × 960 pixels size with 96 dpi resolution and an
average of 70% overlap between images. The spectra
present in the images are, respectively, blue, green,
red, near-IR (NIR) and red-edge (REDEG). Images
were obtained on a single flight without any kind
of pre-processing and using a MicaSense Red-Edge
camera (MicaSense Inc. Seattle, WA, USA) (see Fig-
ure 2) coupled to a Micro UAV SX2 (Sensix Inno-
vations in Drone Ltda, Uberl
ˆ
andia, MG, Brazil) (see
Figure 3) at an average height of 100 meters.
Figure 2: MicaSense Red-Edge camera by MicaSense Inc.
Figure 3: Micro UAV SX2 by Sensix Innovations.
The first dataset was obtained from a soy-
bean plantation located respectively at the fol-
lowing decimal coordinate (−17.877308292165985,
−51.08216452139867). This dataset contains
1080 images (216 scenes and 5 channels), as
shown in Figure 4. The second dataset was
obtained from a cotton plantation at the fol-
lowing decimal coordinate (−17.820275501545474,
−50.32411830846922) and it contains 830 images
(166 scenes and 5 channels), as shown in Figure 5.
For both datasets, an expert targeted a spectrum and
noted the same 12 control points on each spectrum
of each image to construct ground truth for alignment
testing.
5.2 Evaluation Metric
In this work, we used back projection error (BP) (Ran
et al., 2016) to evaluate the methods compared. Given
X
i
and X
j
as the same control points defined by the
specialist on the, respectively, target image (i) and
moving image ( j) and T the similarity transforma-
tion matrix estimated by a method and d the euclidean
distance function, the back projection error can be de-
fined as shown in Equation 2. Smaller BP error indi-
cates better image registration performance.
BP(I, J) =
∑
x
i
,x
j
d
2
(X
i
, T X
j
) (2)
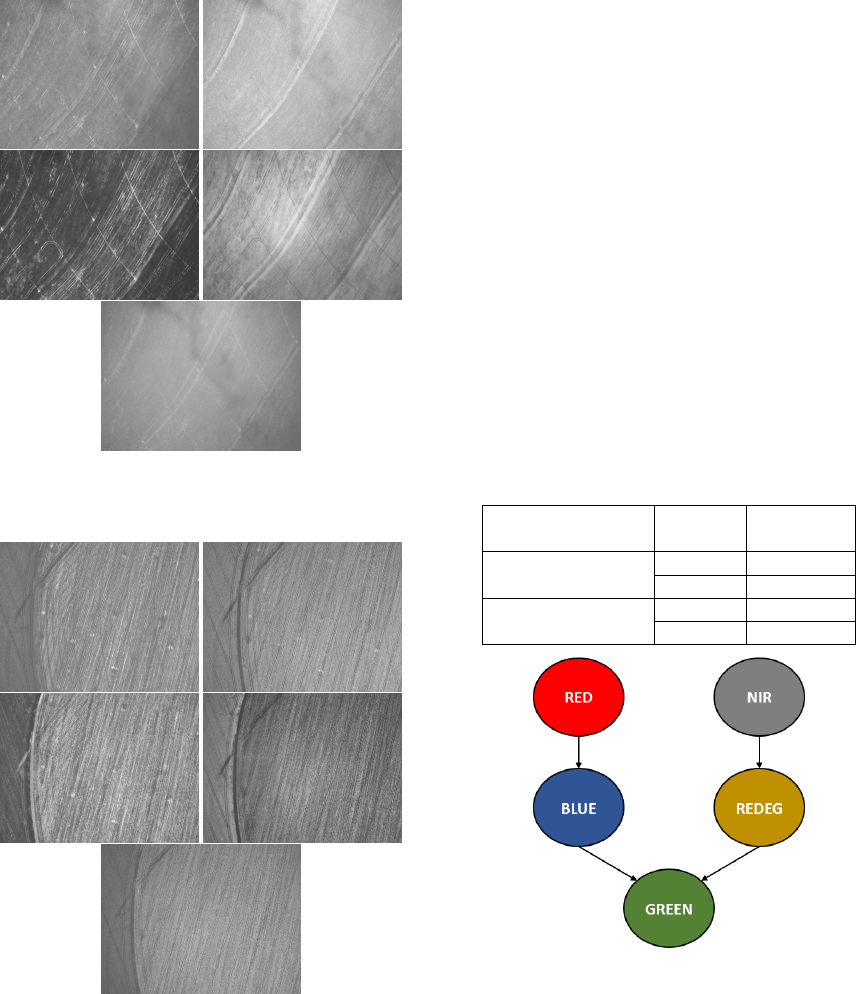
Figure 4: Example of an image scene containing all chan-
nels (Blue, Green, Red, near-IR, red-edge respectively) of
the soybean plantation dataset.
Figure 5: Example of an image scene containing all chan-
nels (Blue, Green, Red, near-IR, red-edge respectively) of
the cotton plantation dataset.
6 RESULTS
In this section, we present the results obtained by the
experiments conducted on this work.
6.1 Execution Time of the Framework
First, we evaluated if the modifications performed on
the framework reduces its execution time. To accom-
plish that we estimated the execution time of the orig-
inal framework proposed by (Yasir et al., 2018) with
KAZE Features and SURF techniques. As previous
stated, this framework computes the best multispec-
tral registration schema for each dataset. Then, we
estimated the execution time of the modified frame-
work, which uses Pearson correlation as metric. Ta-
ble 1 presents the average running time for both orig-
inal and modified frameworks in both Soybean and
Cotton datasets. It is possible to notice that the mod-
ified framework presented a reduction of 95.915% of
execution time compared to the original framework.
Despite the change in metric for construction of mul-
tispectral registration scheme, both original and mod-
ified framework result in the same scheme for image
registration (see Figure 6).
Table 1: Average of execution time by approach.
Approach Dataset
Execution
time (s)
(Yasir et al., 2018)
Soybean 1148
Cotton 4682
Our approach
Soybean 75
Cotton 76
Figure 6: Multispectral registration schema.
6.2 Registration Methods Comparison
In order to evaluate the performance of the registra-
tion method, we used two spectral orders: (i) the orig-
inal spectral order (Blue, Green, Red, RedEdge, and
Near-IR) and (ii) the spectral order obtained from the
registration framework. We applied both spectral or-
ders in each scene to determine the best alignment or-
der. The metric used to measure the resulting align-
ment was the Back Projection (BP) error, as described
in Section 5.2.
Considering that the images were taken at an av-
erage height of 100 meters and considering that the
MicaSense RedEdge sensor’s ground sample distance
(GSD) for this height is 6.8 centimeters per pixel, we
consider that the method failed to align the image if
its BP value is greater than 6 pixels, which represents
an error of approximately 40.8 centimeters. Table
2 shows the percentage of rejected images for each
method and dataset used.
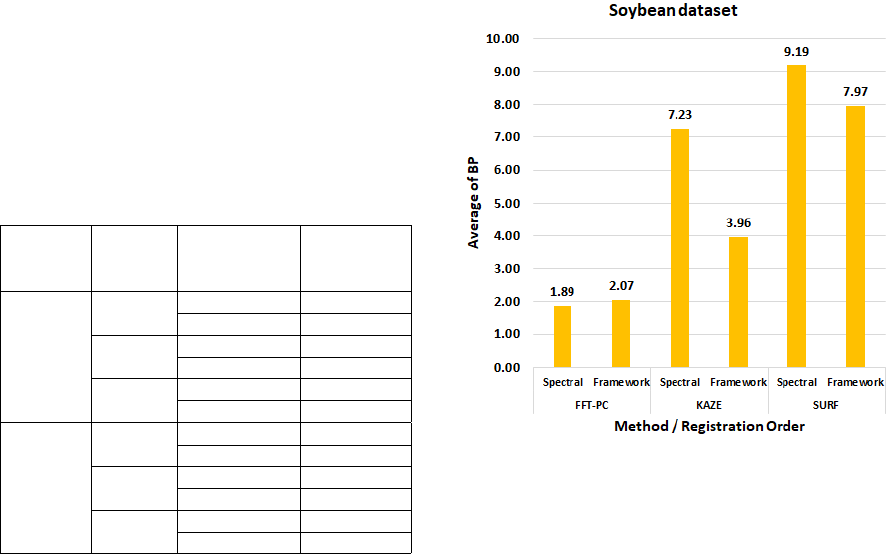
Notice that spatial methods (SURF and KAZE)
obtained a high percentage of failure in both datasets
when compared to the FFT-PC method. Both SURF
and KAZE presented more than 50% of failure in both
datasets. It is important to notice that the application
of the framework reduced the number of failures of
the spatial methods. The FFT-PC method obtained
superior results when compared to the spatial meth-
ods, presenting less than 1% of failure in the soybean
dataset and, on average, 20% of failure in the cotton
dataset. It is noteworthy here that the application of
the framework in the FFT-PC method caused a simple
increase in the number of failures.
The lower performance presented by spatial meth-
ods is a result of the peculiar characteristics that agri-
cultural images present. These images usually have
few structures that can be used during the alignment
process (e.g. streets, artificial objects, etc). In con-
junction with the small number of objects to aid align-
ment, agricultural images typically have similar char-
acteristics throughout the image, which results in sev-
eral outliers during the feature matching process, thus
impairing the quality of the alignment.
Table 2: Percentage of failed alignments for each combina-
tion of method and dataset used.
Dataset Method
Registration
Order
Percentage
of
Failure
Soybean
KAZE
Spectral 66.63%
Framework 28.14%
SURF
Spectral 89.77%
Framework 75.58%
FFT-PC
Spectral 0.93%
Framework 0.58%
Cotton
KAZE
Spectral 62.12%
Framework 38.94%
SURF
Spectral 75.30%
Framework 52.88%
FFT-PC
Spectral 19.24%
Framework 20.30%
In the sequence, we calculate the average BP error
for each dataset in the spectral orders (Blue, Green,
Red, RedEdge, and Near-IR) and the order gener-
ated by the modified framework. As can be seen
from Figures 7 and 8, the FFT-PC method outper-
formed all compared methods, regardless of the spec-
tral order applied for alignment. It is also important
to notice that in the spatial methods, the application
of the framework reduced the average alignment er-
ror, demonstrating that its application is feasible for
these methods. Interestingly, in the FFT-PC method,
the framework application generated a slight increase
in alignment error. Since the FFT-PC method does
not use features for the image alignment process, the
Pearson correlation between the two spectra was not
an adequate metric for the use of the framework in
spectral methods. The FFT-PC method is based on
the Fourier transform and its properties (e.g., scaling
and rotation), so that FFT similarity metrics between
Fourier spectra should be used as an attempt to im-
prove the comparison between spectra.
We also analyzed the main reason for the failures
obtained in each dataset. In the soybean dataset, most
of the failures were caused by a high amount of cloud
shadows present during the image capture process.
An example of these shadows can be seen in Figure
9. In this case, it would be suitable to use a shadow
detection and removal technique to optimize the qual-
ity of the alignment obtained.
Figure 7: Average of BP error for the soybean dataset.
7 CONCLUSION
In this work we explored the problem of multispectral
image registration and presented a modification of the
framework proposed by (Yasir et al., 2018). Our mod-
ification generalizes this framework, originally pro-
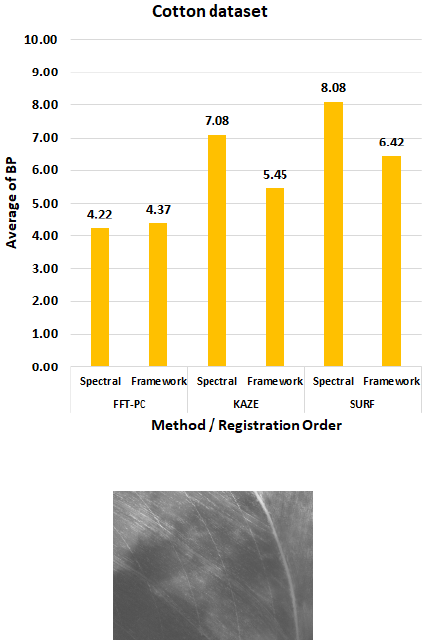
Figure 8: Average of BP error for the cotton dataset.
Figure 9: Example of shadow present in soybean dataset.
posed to work with keypoints based methods, so that
spectral domain methods (e.g. Phase Correlation) can
be used in the registration process.
Our modification generated, for both datasets
evaluated, the same registration order as obtained by
the original framewrok. However, our approach has
considerably reduced its execution time, thus making
it feasible to apply to large datasets. Moreover, our
modification reduced the back projection error of the
alignment when compared with the spectral order.
Although several methods in the literature use spa-
tial methods for multispectral image alignment ob-
tained by UAVs, the quality obtained by the spectral
method (FFT-PC) was considerably superior, which
corroborates this approach as an alternative for multi-
spectral registration of images obtained by UAVs.
ACKNOWLEDGEMENTS
The authors gratefully acknowledges CAPES (Co-
ordination for the Improvement of Higher Edu-
cation Personnel) (Finance Code 001) and CNPq
(National Council for Scientific and Technologi-
cal Development, Brazil) (Grant #301715/2018-1)
for the financial support and the company Sensix
(http://sensix.com.br) for providing the images used
in the tests.
REFERENCES
Alcantarilla, P. F., Bartoli, A., and Davison, A. J. (2012).
Kaze features. In Fitzgibbon, A., Lazebnik, S., Per-
ona, P., Sato, Y., and Schmid, C., editors, Computer
Vision – ECCV 2012, pages 214–227, Berlin, Heidel-
berg. Springer Berlin Heidelberg.
Banerjee, B. P., Raval, S. A., and Cullen, P. J. (2018). Align-
ment of uav-hyperspectral bands using keypoint de-
scriptors in a spectrally complex environment. Remote
Sensing Letters, 9(6):524–533.
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. In Leonardis, A., Bischof,
H., and Pinz, A., editors, Computer Vision – ECCV
2006, pages 404–417, Berlin, Heidelberg. Springer
Berlin Heidelberg.
Berni, J. A. J., Zarco-Tejada, P. J., Suarez, L., and Fereres,
E. (2009). Thermal and narrowband multispectral re-
mote sensing for vegetation monitoring from an un-
manned aerial vehicle. IEEE Transactions on Geo-
science and Remote Sensing, 47(3):722–738.
Dias Junior, J. D., Backes, A., and Escarpinati, M. (2019).
Detection of control points for uav-multispectral
sensed data registration through the combining of fea-
ture descriptors. In Proceedings of the 14th Interna-
tional Joint Conference on Computer Vision, Imag-
ing and Computer Graphics Theory and Applications,
pages 444–451.
Diaz-Varela, R., Zarco-Tejada, P., Angileri, V., and Loud-
jani, P. (2014). Automatic identification of agricul-
tural terraces through object-oriented analysis of very
high resolution dsms and multispectral imagery ob-
tained from an unmanned aerial vehicle. Journal of
Environmental Management, 134:117 – 126.
Floyd, R. W. (1962). Algorithm 97: Shortest path. Com-
mun. ACM, 5(6):345–.
Gago, J., Douthe, C., Coopman, R., Gallego, P., Ribas-
Carbo, M., Flexas, J., Escalona, J., and Medrano, H.
(2015). Uavs challenge to assess water stress for sus-
tainable agriculture. Agricultural Water Management,
153:9 – 19.
Gevaert, C. M., Suomalainen, J., Tang, J., and Kooistra, L.
(2015). Generation of spectraltemporal response sur-
faces by combining multispectral satellite and hyper-
spectral uav imagery for precision agriculture appli-
cations. IEEE Journal of Selected Topics in Applied
Earth Observations and Remote Sensing, 8(6):3140–
3146.
Hunt, E. R., Hively, W. D., Fujikawa, S. J., Linden, D. S.,
Daughtry, C. S. T., and McCarty, G. W. (2010). Acqui-
sition of nir-green-blue digital photographs from un-
manned aircraft for crop monitoring. Remote Sensing,
2:290–305.
Hunter, M. C., Smith, R. G., Schipanski, M. E., Atwood,
L. W., and Mortensen, D. A. (2017). Agriculture in
2050: Recalibrating Targets for Sustainable Intensifi-
cation. BioScience, 67(4):386–391.
Kim, J., Kim, S., Ju, C., and Son, H. I. (2019). Unmanned
aerial vehicles in agriculture: A review of perspective
of platform, control, and applications. IEEE Access,
7:105100–105115.
Kirch, W., editor (2008). Pearson’s Correlation Coefficient,
pages 1090–1091. Springer Netherlands, Dordrecht.
Kruskal, J. (1956). On the shortest spanning subtree of
a graph and the traveling salesman problem. In
Proceedings of the American Mathematical Society,
pages 48–50.
Mesas-Carrascosa, F. J., Rumbao, I. C., Torres-Snchez, J.,
Garca-Ferrer, A., Pea, J. M., and Granados, F. L.
(2017). Accurate ortho-mosaicked six-band multi-
spectral uav images as affected by mission planning
for precision agriculture proposes. International Jour-
nal of Remote Sensing, 38(8-10):2161–2176.
Mogili, U. R. and Deepak, B. B. V. L. (2018). Review on
application of drone systems in precision agriculture.
Procedia Computer Science, 133:502 – 509. Interna-
tional Conference on Robotics and Smart Manufactur-
ing (RoSMa2018).
Oliveira, F. and Tavares, J. (2014). Medical image registra-
tion: A review. Computer methods in biomechanics
and biomedical engineering, 17:73–93.
Ran, L., Liu, Z., Zhang, L., Xie, R., and 0009, T. L. (2016).
Multiple local autofocus back-projection algorithm
for space-variant phase-error correction in synthetic
aperture radar. IEEE Geosci. Remote Sensing Lett,
13(9):1241–1245.
Reddy, B. S. and Chatterji, B. N. (1996). An fft-based tech-
nique for translation, rotation, and scale-invariant im-
age registration. IEEE Transactions on Image Pro-
cessing, 5(8):1266–1271.
Soares, G., Abdala, D., and Escarpinati, M. (2018). Planta-
tion rows identification by means of image tiling and
hough transform. pages 453–459.
Yasir, R., Eramian, M., Stavness, I., Shirtliffe, S., and
Duddu, H. (2018). Data-driven multispectral image
registration. In 2018 15th Conference on Computer
and Robot Vision (CRV), pages 230–237.
