Fast and Realistic Approach to Virtual Muscle Deformation

∗

Martin Cervenka

1 a

and Josef Kohout

2 b

University of West Bohemia, Faculty of Applied Sciences,

Department of Computer Science and Engineering, Czech Republic

University of West Bohemia, Faculty of Applied Sciences,

NTIS - New Technologies for the Information Society, Czech Republic

Keywords:

Muscle Modelling, Muscle Deformation, Muscle Fibres, Position based Dynamics.

Abstract:

This paper describes a real-time simulation of muscle movement that is based on inverse kinematics where

bone placement is known apriori and muscle shape is calculated by a modiﬁed position-based dynamics (PBD)

method. The method is comparable and competitive with the others, moreover, it is enhanced with some novel

features like approach for respecting muscle anisotropy, really fast simplistic collision detection, etc. This

real-time simulation presents visual plausibility of resulting muscle deformation in most cases.

1 INTRODUCTION

One of the diseases with high prevalence is osteoporo-

sis (Wade et al., 2014). This disease causes weaken-

ing of bone tissue, which results in weak bones prone

to break. This is a valid reason to be concerned about

forces employed to softened bones. Bergmann et. al.

(Bergmann et al., 2001) show that twice as much force

is exerted during walking than during standing. In se-

vere cases, there is a chance that a weak bone is not

able to absorb surrounding forces and fractures.

Osteoarthritis is another musculoskeletal disease

to consider. In advanced stages, a form of treatment

is needed, which is usually done by replacing the

bone joint with an artiﬁcial one. Knowledge of forces

impacting the bone joint is essential for surgeons to

choose suitable artiﬁcial joint (Oatis, 2013). An inac-

curate choice of artiﬁcial joint may be painful for the

patient or even cause further harm.

A well-built model can be useful to predict the dis-

cussed forces. Such a model should be physically cor-

rect and should be also patient-speciﬁc because body

constitution varies in patients.

Modern technologies allow us to use computers to

simulate the musculoskeletal system (or its model, re-

spectively) and get some form of approximate values

https://orcid.org/0000-0001-9625-1872

https://orcid.org/0000-0002-3231-2573

∗

This work was supported by the Ministry of Educa-

tion, Youth and Sports of the Czech Republic, project SGS-

2019-016 and project PUNTIS (LO1506).

from this process. There are some models (e.g. (Delp

et al., 1990), (Arnold et al., 2009)) measured on single

patient; unfortunately, we need patient-speciﬁc mod-

els. Even though it may seem like a good idea to use

model measured on single patient for every other pa-

tient (for the sake of simplicity etc.), it neglects sig-

niﬁcant features of the individual patient. There are

statistical models as well (e.g., PCA based statisti-

cal model using data from 26 patients by Zhang et.

al. (Zhang et al., 2016)), which can achieve better re-

sults in general, despite these statistical models can-

not be as good as patient-speciﬁc models. However,

getting complete patient-speciﬁc data is nearly impos-

sible due to inaccurate measuring, complexity of data

processing, time consumption etc.

To give a real-life example where the simulation

is needed, calculation of the stresses to which bones

are subjected when performing a speciﬁc action can

provide fracture prediction for people suffering from

osteoporosis. This information enables better progno-

sis and more precise treatment, and a dynamical anal-

ysis and visualisation of muscle activity may help to

identify issues in the action of a professional athlete

that can lead to more effective training procedures and

the identiﬁcation of ways in which performance can

be improved. For such applications, a patient-speciﬁc

or subject-speciﬁc musculoskeletal model is essential

for the simulation and its visualisation.

We present a novel, real-time approach for mus-

cle modelling, derived from position-based dynam-

ics (well known in modern computer graphics ﬁeld).

Cervenka, M. and Kohout, J.

Fast and Realistic Approach to Virtual Muscle Deformation.

DOI: 10.5220/0009129302170227

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 5: HEALTHINF, pages 217-227

ISBN: 978-989-758-398-8; ISSN: 2184-4305

217

PBD was originally proposed by M

uller (M

uller et al.,

2007) and is currently still in development (e.g. cloth

and ﬂuid simulation (Shao et al., 2017)). Main contri-

butions are:

• Using computer graphics related PBD (position

based dynamic) method for muscle deformation,

• Extending PBD by concerning anisotropy of mus-

cles,

• Fast minimalistic implementation of muscle mod-

elling approach.

2 APPROACH

2.1 Static Model

Construction of a patient-speciﬁc model requires hav-

ing data on the anatomy of the individual patient.

Muscle parameters such as geometrical shape, attach-

ment sites, ﬁbre orientation, etc. are essential to

get accurate results of simulations. The geometrical

shape of a muscle can be extracted from MRI images

and this can be done automatically, though with some

issues. However, most parameters regarding the mus-

cle architecture cannot be extracted from these images

and generally, they are very difﬁcult, if not impossi-

ble, to get in vivo. Nevertheless, this information can

be obtained from cadaver measurements (not patient-

speciﬁc). It is possible then to combine this general

information with speciﬁc patient data.

In this paper, a subset of a comprehensive female

cadaver anatomical dataset (81 y/o, 167 cm, 63kg) is

used. Speciﬁcally, pelvic and femur bones together

with several muscles from the pelvic region have been

selected.

The complete data are publicly available in LHDL

dataset (Viceconti et al., 2008) and has been selected

because it includes high-quality surface meshes of

bones and muscles. Furthermore, the dataset was

improved by removing non-manifold edges, dupli-

cated vertices and degenerate triangles followed by

surface smoothing in both muscle and bone models

using MeshLab (Cignoni et al., 2008). The dataset

also contains muscle attachment areas and geometri-

cal paths of superﬁcial ﬁbres obtained from dissection

(Van Sint Jan, 2005).

2.2 Dynamic Model

Having a static model, a dynamic one can be ob-

tained quite simply providing that the motion data

for that model are available. If bones are assumed

as completely rigid, motion can be simulated via in-

verse kinematics. Inverse kinematics means that the

location and movement of all bones are known, and

muscle actual shape has to be determined according to

these situations. We note this is exactly the opposite

to what can be seen in real situation, where muscles

control bone movement.

In this paper, position-based dynamics (PBD),

which was introduced in (M

uller et al., 2007) as a fast,

stable, and controllable solution to various problems

in computer graphics, e.g., simulations of cloth or ﬂu-

ids, is used to reposition the vertices of the surface

mesh of muscle with the modelling constraints to pre-

serve the shape and volume of the muscle and prevent

mutual penetration of the muscle with the bones. De-

tails will be described in Section 3.

The muscle is then decomposed into a set of ﬁbres

using either Kukacka (Kohout and Kukacka, 2014) or

CHMD (Kohout and Cholt, 2017) method, depending

on which one is more appropriate in the concrete case.

Note that this set represents the dynamics of muscle

architecture. Details regarding muscle decomposition

will be described in Section 5.5.

3 PBD

uller (M

uller et al., 2007) in his paper described

PBD with four requirements:

1. Preserve local distances,

2. Maintain local shape,

3. Keep the original volume,

4. Not collide with other models.

In the context of muscle modelling, another re-

quirement, which considers muscle anisotropy, must

be introduced to model muscle motion accurately.

This will be described later.

PBD method is based on solving equation 1 for

discretized muscle model over and over again. It de-

scribes a movement of a single point (vertex) dur-

ing simulation (∆p

denote the difference in position

of ith point of the model), maintaining various fea-

tures. Mentioned features can be for example volume

or shape preservation, but it can be anything giving

meaning. Some of the preserved features are men-

tioned and further described later in the text.

∆p

= −

C (p

, . . . , p

)

∑



C (p

, . . . , p

)



·C (p

, . . . , p

) (1)

In above equation, C is a constraint function (more

details below), n is the number of points in the muscle

model and j is the number of constraint functions.

HEALTHINF 2020 - 13th International Conference on Health Informatics

218

Mathematically speaking, constraint function and

its gradients must be known to solve the deformation

problem.

3.1 Distance Constraint

A rather basic constraint, which we can imagine, is

restricting each model point to change the distance

from the others in its neighbourhood. This constraint

can be formulated as is in (2), where d is the original

distance between points p

and p

C (p

, p

) =

− p

− d (2)

3.2 Volume Constraint

Next, we can restrict the muscle model to change its

volume during the simulation process. To calculate

this constraint, we need to know how to measure the

volume of the model. Assuming triangular mesh, the

volume can be computed tetrahedron by tetrahedron,

which in summation eventually leads to constraint

function:

C (p

, . . . , p

) =

∑

i=1



× p



−V

(3)

In this function, m describes number of triangles

forming the muscle model, V

is muscle original vol-

ume and p

denotes jth point of the ith triangle.

3.3 Local Shape Constraint

Above described constraints are not enough to pre-

vent the surface from becoming noisy, full of unreal-

istic spikes. One possible solution to this problem is

to use the distance constraint not only to keep the dis-

tances between adjacent points but also between the

pairs of points lying on the opposite sides of the mus-

cle. This would, however, need to create a 3D mesh

ﬁrst, which would be quite complex to do. Another

option is to ensure that the local shape is maintained.

To achieve this, the angles between neighbouring tri-

angles should stay the same during deformation. Cal-

culating the angle of two triangles is integrated into

equation (4), where two triangles are described by

four points, sharing points with index 1 and 2.

C (p

, p

) = arccos (n

· n

) − ϕ

= arccos



− p

) × (p

− p

)

− p

) × (p

− p

)

− p

) × (p

− p

)

− p

) × (p

− p

)



− ϕ

(4)

3.4 Anisotropy

The PBD algorithm has been originally proposed in

the computer graphics ﬁeld to model isotropic mate-

rials (e.g., cloths). However, muscles are anisotropic

(may behave differently in two distinct directions), so

it is appropriate to take anisotropy into account. The

main idea is that muscle surface is stiffer in the direc-

tion perpendicular to the muscle ﬁbres and more ﬂexi-

ble in the direction parallel to these ﬁbres. Mathemat-

ically speaking, we multiply the distance constraint in

(2) with the result of equation (5).

= 1 − u

· v

(5)

The direction of ith edge is described by normal-

ized vector u

, v

denotes tangential direction normal

vector of nearest ﬁbre on the surface. If both vectors

are collinear, the result k

will be zero, meaning no

distance is preserved. If these two vectors are per-

pendicular, then k

is equal to one and edge length

will be well preserved. This behaviour is assured be-

cause value k

multiplies the result of distance con-

straint function in (2).

4 COLLISION HANDLING

In the simulation, moving muscles and bones should

not intersect each other. There are some methods with

different advantages and disadvantages, some of them

are described below.

4.1 Brute Force

The most simple way to detect a collision is to test

each primitive of a surface mesh with all primitives

of the other mesh for an intersection. Time complex-

ity in big-O notation is O(n

), where n is the number

of primitives (triangles in our case), which makes the

brute force approach suitable only for small models,

for which the overhead associated with more sophis-

ticated approaches is not amortized. For bigger (real)

models, we need a sort of space division algorithm.

4.2 Bounding Volume Hierarchies

One of the data structure suitable for space division is

a bounding volume hierarchy. The basic idea behind

the structure is that space is recursively subdivided

employing some volumetric (in 3D, planar in 2D) ge-

ometrical primitives (box, sphere, etc.). In big-O no-

tation, we achieve O



logn



or even O



log



, as-

suming the number of vertices of both tested meshes

Fast and Realistic Approach to Virtual Muscle Deformation

219

depends linearly on each other. The main disadvan-

tage is that the structure has to be built before the sim-

ulation or even updated every time the muscle shape

changes.

4.2.1 octree

A special case of bounding volume hierarchies is an

octree. The octree divides the three-dimensional box

into eight (therefore octree) smaller boxes (box is di-

vided in half in each axis). The division is done recur-

sively and stops when the box contains a sufﬁciently

small number of elements, i.e., vertices or triangles.

4.3 Voxelization

In this approach, the given three-dimensional box is

divided into n

(n division in each axis) equally sized

boxes. If n is selected carefully, every box contains

a (sufﬁciently small) constant number of element, so

testing can be theoretically done in O (1) time using

big-O notation, however, memory complexity will be





as far as every cube content has to be stored in

memory.

Our goal is to do a fast deformation, so we decided

memory is not an issue, therefore voxelization is used

in the proposed approach.

4.4 Collision Response

In our case, two main scenarios have to be distin-

guished. In the ﬁrst one, a muscle moves (e.g. be-

cause of surrounding forces) and hits a bone. When

vertices of the muscle collide, they are pushed back

in the direction they enter the bone so they will not

penetrate the bone anymore.

In the second scenario, a bone moves into a mus-

cle. In this case, the colliding muscle vertices did not

”enter” the bone, so we do not know the entering di-

rection. We propose a solution where the same trans-

formation used on colliding bone is applied to collid-

ing muscle vertices as well.

5 EXPERIMENTAL RESULTS

The real data described in Section 2.1 is used along

with an artiﬁcial dataset (described below) to test the

proposed approach. The results of the experiments

are described in detail below.

5.1 Artiﬁcial Data

To test collision detection and behaviour in extreme

cases, we prepared an artiﬁcial dataset, where a box

of 5292 triangles on its surface is squished between

two plates (12 triangles each). The initial setup is vi-

sualized in Fig.1.

Figure 1: Input artiﬁcial data.

At ﬁrst, in one hundred iterations, the top plate

moves to decrease the space between both places.

The distance between plates in 100

iteration is 10%

of the original distance in the ﬁrst iteration. Inverse

movement is then performed between 100

and 200

iteration, returning the plates to their initial position.

Additional one hundred iterations are used for box

stabilization.

As it can be seen in Fig.2, the box is squished quite

a lot. Despite the fact, it returns to its original shape

in 300

iteration (only with slight rotation caused by

asymmetrical triangulation). Even in 200

iteration

the results is acceptable, except one corner of the box.

0 50 100

150 200 300

Figure 2: Results in different simulation frames (artiﬁcial

data).

5.2 Iliacus

We also tested iliacus muscle, which connects the fe-

mur and pelvic bones from the front side. The bones

and the muscle are visualized in Fig.3. The muscle

HEALTHINF 2020 - 13th International Conference on Health Informatics

220

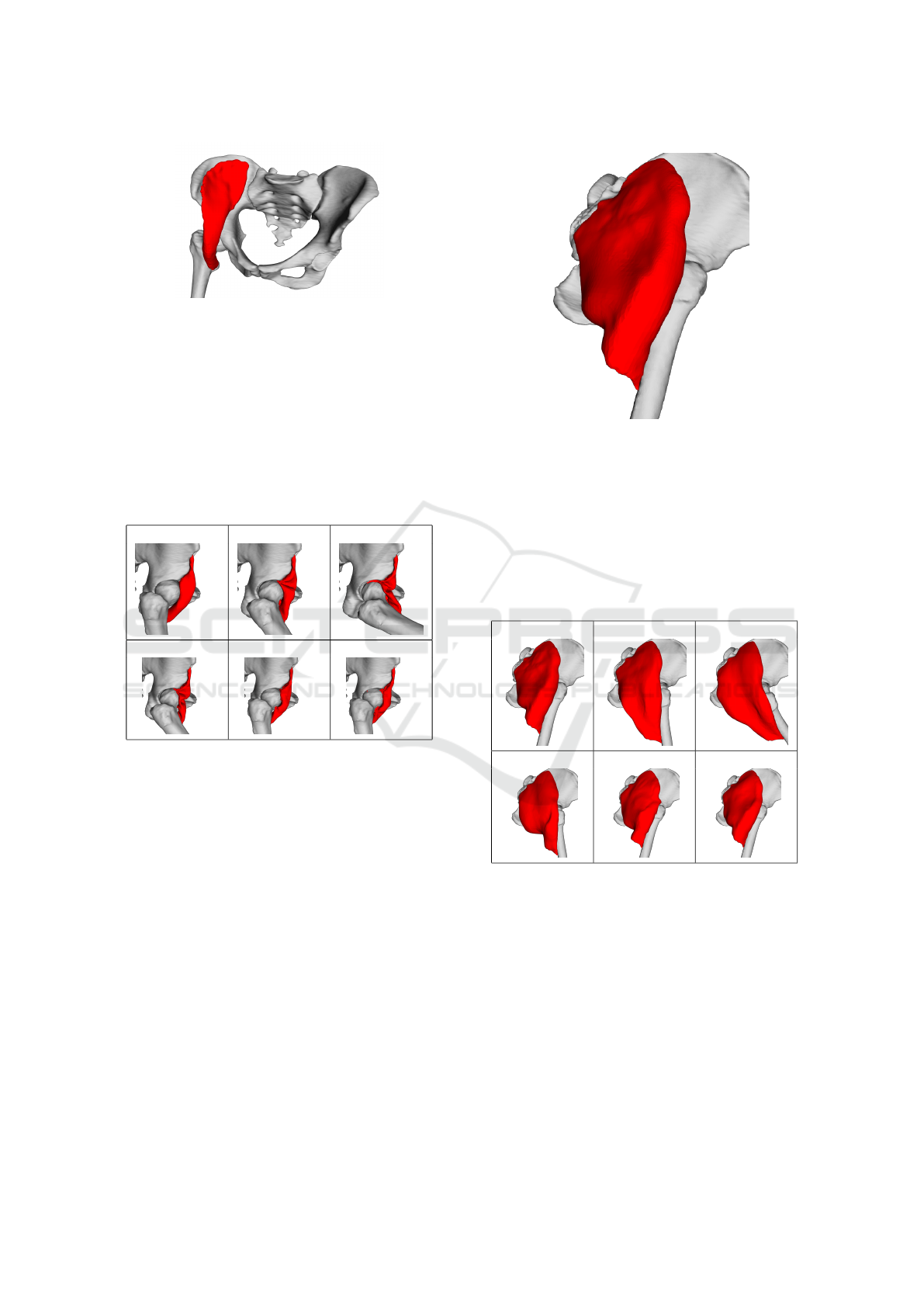
Figure 3: Input iliacus muscle and adjacent bones.

and bones are closed triangular meshes with 13858

and 254442 (42456 for femur) triangles, respectively.

A very similar simulation scenario like in the ar-

tiﬁcial data case has been applied to iliacus dataset.

The ﬁrst hundred iterations are used for hip ﬂexion.

The femur bone rotates one radian during this move-

ment. The second hundred iteration is allocated for

the inverse movement. The last hundred (200

-300

)

iterations are present to stabilize the muscle.

0 50 100

150 200 300

Figure 4: Results in different simulation frames (Iliacus

muscle data).

The posterior part of the iliacus muscle is pushed

into the joint during the ﬂexion, as it can be seen in

Fig.4. The explanation for this behaviour is as fol-

lows. This part of the mesh is unrealistically arched

towards the joint and, therefore, distance and local

shape constraints tend to move the points of this part

closer to the joint. As the femur and pelvic bones do

not touch, there is a narrow space into which this part

of the mesh can squeeze, and from which it is difﬁcult

to get out. Even though the result is not visually plau-

sible, the quantitative tests (described later) show that

all key factors of the muscle are preserved as much as

possible.

5.3 Gluteus Maximus

Gluteus maximus muscle is attached to the same

bones as iliacus muscle but from the other side. Tri-

Figure 5: Input gluteus maximus muscle and adjacent

bones.

angular mesh of the consits of 19752 triangles. Fig.5

shows how the model looks like.

The muscle undergoes the same movement sce-

nario as iliacus mentioned above. Visualization in 6

important iterations is shown in Fig.6. As we can see,

the result in iteration 300 is nearly the same as in the

ﬁrst iteration (the original muscle pose).

0 50 100

150 200 300

Figure 6: Results in different simulation frames (gluteus

maximus muscle data).

5.4 Other Muscles

Within this testing procedure, we have tested gluteus

medius and adductor brevis muscles. Both muscles

deform quite realistically, as it can be see in Fig.7 and

Fig.8, where the situation in the maximal hip ﬂexion

(same scenario like in gluteus maximus and iliacus

case) is shown.

Fast and Realistic Approach to Virtual Muscle Deformation

221

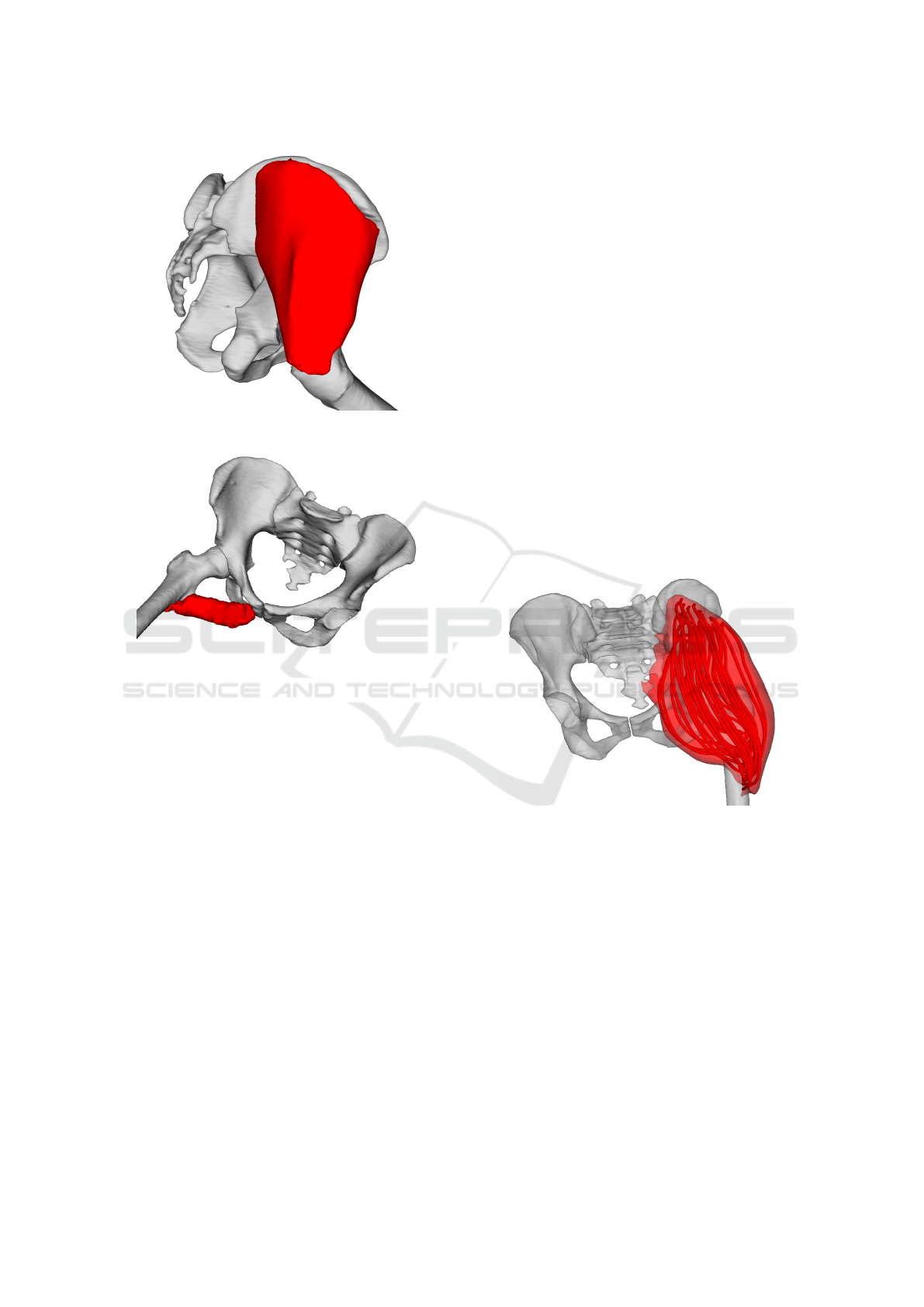
Figure 7: Gluteus medius in maximum ﬂexion position.

Figure 8: Adductor brevis in maximum ﬂexion position.

5.5 Muscle Decomposition

The approach described so far works primarily with

the surface model of a muscle. To calculate the forces

(and other physical properties of the muscle), the

muscle needs to be decomposed into individual ﬁbres.

This can be done using, for example, Kukacka or

CHMD muscle decomposition methods, which were

proposed in (Kohout and Kukacka, 2014) and (Ko-

hout and Cholt, 2017), respectively. In the following

subsections, we brieﬂy describes these methods.

5.5.1 Kukacka Decomposition

The inputs of the Kukacka decomposition method

(Kohout and Kukacka, 2014) are:

• Triangular (and manifold) surface model of the

muscle to decompose,

• Fibre template, giving information about internal

ﬁbre arrangement,

• Attachment areas to adjacent bones (origin and in-

sertion), deﬁned by a set of points lying on the

adjacent bone surface models

Decomposition is then done as follows. Attach-

ment areas are projected from the bone surface onto

the muscle surface to deﬁne the parts of the mus-

cle that are subsequently removed. Isocontours are

then computed on the modiﬁed muscle model, using

a piece-wise linear scalar ﬁeld. The scalar ﬁeld has its

maximum on the insertion boundary vertices, whereas

it has its minimum on the origin boundary vertices.

User can specify how many isocontours are generated

in this process.

Similarly to (Delp, 2005), muscle ﬁbre architec-

ture (template) is represented by a unit 3D space

with arbitrary (user-deﬁned) number of ﬁbres inside

the space. The ﬁbres are represented analytically by

Bezier spline curves. From multiple templates, one is

selected according to the muscle being modelled (de-

pends on if it has parallel or pennate ﬁbres, optionally

on a pennate angle, etc.) and it is mapped one-to-one

on isocontours calculated in the previous step, form-

ing the ﬁbres going through the muscle model. Fi-

nally, noise is eliminated using quadratic smoothing

to make the result more realistic and visually plausi-

ble.

Figure 9: Gluteus maximus decomposed to individual ﬁbres

by Kukacka’s (Kohout and Kukacka, 2014) algorithm.

5.5.2 CHMD Decomposition

A technique by Kohout & Cholt (Kohout and Cholt,

2017) performs a centripetal Catmull-Rom interpo-

lation of the input ﬁbres lying on the surface model

of the muscle, or nearby, to get the ﬁbres inside the

muscle. Their approach can even work with multiple

headed muscles, distributing the ﬁbres automatically

among the heads.

In comparison with Kukacka’s proposed method,

this method needs speciﬁcation of ﬁbres on the sur-

face, which typically requires some manual effort

because these are not available for the patient but

must be adopted from a cadaveric dataset. On the

HEALTHINF 2020 - 13th International Conference on Health Informatics

222

Figure 10: Gluteus maximus decomposed to ﬁbres by

Cholt’s (Kohout and Cholt, 2017) algorithm.

other hand, it can work with multiple headed muscles,

whereas Kukacka’s approach can not.

5.6 Quantitative Tests

To make some exact result, we use quantitative tests.

These tell us how well are constraints satisﬁed during

simulation.

Volume preservation constraint is tested by deter-

mining ratio between both original and actual vol-

umes. Fig.11 for artiﬁcial data, Fig.12 and Fig.13 for

real data respectively, show us the volume preserva-

tion results.

0 50 100 150 200 250 300

0.2

0.4

0.6

0.8

1.2

Iteration

Actual/original volume ratio

Volume preservation - Artificial

Volume ratio

Figure 11: Volume preservation of artiﬁcial data.

0 50 100 150 200 250 300

0.99

0.992

0.994

0.996

0.998

1.002

Iteration

Actual/original volume ratio

Volume preservation - Iliacus

Volume ratio

Figure 12: Volume preservation of iliacus muscle data.

0 50 100 150 200 250 300

0.99

0.992

0.994

0.996

0.998

1.002

Iteration

Actual/original volume ratio

Volume preservation - Glut. max.

Volume ratio

Figure 13: Volume preservation of gluteus maximus muscle

data.

As we can see from the results, the volume is well

preserved in both real data (the error is less than 1% in

both cases), on artiﬁcial data, there is a nice curve de-

scribing squishing (reducing) box volume during the

simulation and then restoring.

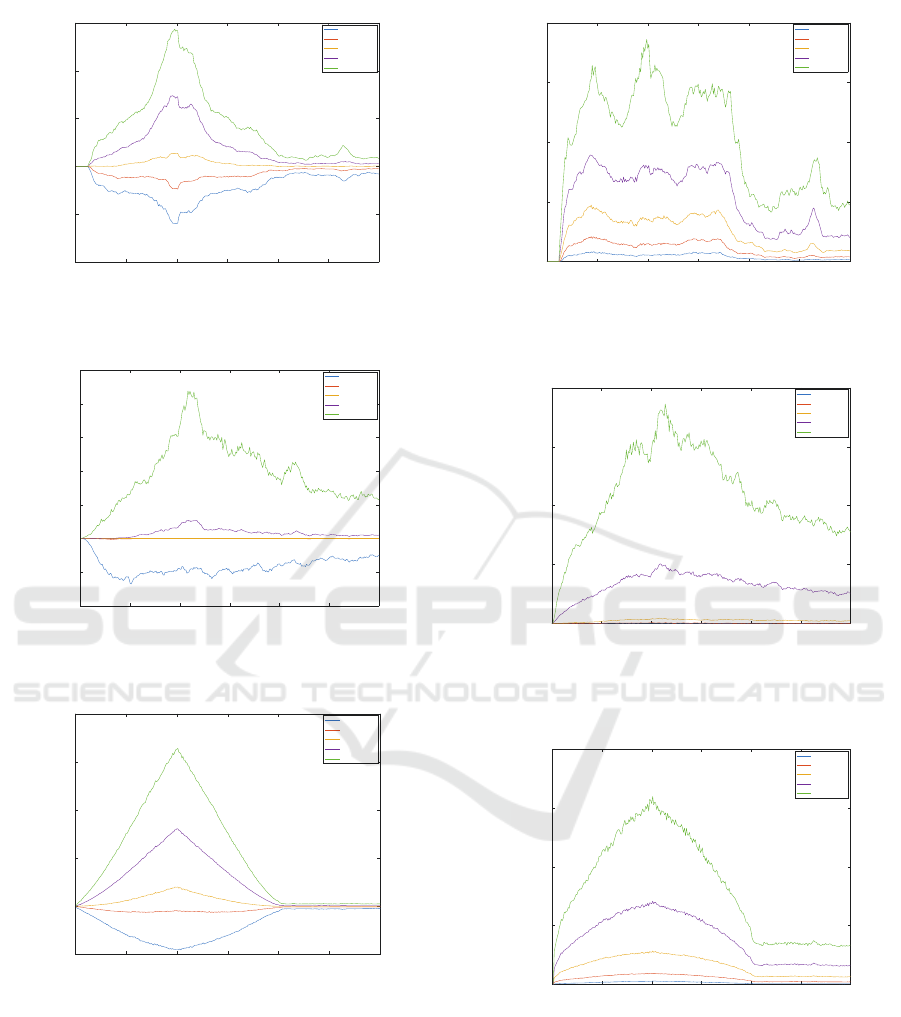
Next measurable property is average edge exten-

sion. At ﬁrst, we cannot say much about artiﬁcial data

(squished box) from the plot on Fig.14. As for the il-

iacus muscle, some edges remain longer than normal

(see Fig.15) because they are stuck in the hip joint. In

the case of gluteus maximus dataset (Fig.16), the ﬁrst

100 iterations show edge extension during hip ﬂexion

(it is correct behaviour because muscle extends in this

phase) and the second hundred iterations return the

average length extension to almost 1 (i.e., the mus-

cle returns to its original pose correctly). We can also

see that the last 100 iterations are not crucial in this

scenario.

We also tested how well the dihedral angles are

preserved during the simulation. In this paper, the di-

hedral angle is the angle between two adjacent trian-

gles in the muscle triangle mesh. According to plots

in Fig.17, Fig.18 and Fig.19, we can conclude that

there are some pairs of triangles which do not pre-

Fast and Realistic Approach to Virtual Muscle Deformation

223

0 50 100 150 200 250 300

0.6

0.8

1.2

1.4

1.6

Iteration

Actual/original edge length

Edge length extension - Artificial

10% quartile

25% quartile

50% quartile

75% quartile

90% quartile

Figure 14: Average edge extension of artiﬁcial data.

0 50 100 150 200 250 300

0.96

0.98

1.02

1.04

1.06

1.08

1.1

Iteration

Actual/original edge length

Edge length extension - Iliacus

10% quartile

25% quartile

50% quartile

75% quartile

90% quartile

Figure 15: Average edge extension of iliacus muscle data.

0 50 100 150 200 250 300

0.9

1.1

1.2

1.3

1.4

Iteration

Actual/original edge length

Edge length extension - Glut. max.

10% quartile

25% quartile

50% quartile

75% quartile

90% quartile

Figure 16: Average edge extension of gluteus maximus

muscle data.

serve its original angle, but most of them do.

5.7 Fibre Length

Last but not least, the lengths of ﬁbres were analyzed.

In the iliacus muscle case, as we can see in Fig.20,

many length curves exhibit two big bumps shortly af-

ter 100

iteration. This is caused by the fact that a

0 50 100 150 200 250 300

0.2

0.4

0.6

0.8

Iteration

Absolute dihedral angle change [degrees]

Dihedral angle preservation - Artificial

10% quartile

25% quartile

50% quartile

75% quartile

90% quartile

Figure 17: Average absolute dihedral angle change of arti-

ﬁcial data.

0 50 100 150 200 250 300

0.05

0.1

0.15

0.2

Iteration

Absolute dihedral angle change [degrees]

Dihedral angle preservation - Iliacus

10% quartile

25% quartile

50% quartile

75% quartile

90% quartile

Figure 18: Average absolute dihedral angle change of ilia-

cus muscle data.

0 50 100 150 200 250 300

0.05

0.1

0.15

0.2

Iteration

Absolute dihedral angle change [degrees]

Dihedral angle preservation - Glut. max.

10% quartile

25% quartile

50% quartile

75% quartile

90% quartile

Figure 19: Average absolute dihedral angle change of glu-

teus maximus muscle data.

part of the muscle is stuck in the hip joint (as dis-

cussed previously). Nevertheless, when the bones re-

turn to their initial rest-pose (i.e., after 200 iterations),

the vast majority of ﬁbres restore their original lengths

quite well. Gluteus maximus muscle behaves as ex-

pected – see Fig.21. During the ﬂexion, all lengths

increase; during the extension, they decrease.

HEALTHINF 2020 - 13th International Conference on Health Informatics

224

0 50 100 150 200 250 300

140

160

180

200

220

240

Iteration number

Fibre length [mm]

Fibre lengths - Iliacus

Figure 20: Total length of each individual ﬁbre during sim-

ulation in iliacus muscle.

0 50 100 150 200 250 300

150

200

250

300

350

400

Iteration number

Fibre length [mm]

Fibre lengths - Gluteus maximus

Figure 21: Total length of each individual ﬁbre during sim-

ulation in gluteus maximus muscle.

5.8 Speed

The proposed method was designed to be not only

precise, but mainly, fast. It was implemented in

C++ using VTK toolkit. Its current version is

publicly available at https://github.com/cervenkam/

muscle-deformation-PBD.

All testing scenarios above were measured how

fast each one is. FPS (Frames Per Second) is used

as speed metric in this case.

All tests were performed on Intel



Core

i7-

4930K 3.40GHz CPU, Radeon HD 8740 GPU and

WDC WD40EURX-64WRWY0 4TB HDD. Results

are listed on Tab.1.

As it can be seen from the results, FPS strictly de-

pends on number of triangles (Spearman’s ρ = −1).

The more triangles is used, the slower the method is.

Even though the program is mostly unoptimized

and runs sequentially at the moment, the FPS is sufﬁ-

cient for considered purposes in general.

Table 1: FPS of each simulation.

Deforming object Triangle count FPS

Gluteus maximus 19752 33.85

Abductor brevis 17124 35.89

Iliacus 13858 47.21

Gluteus medius 10622 57.12

Artiﬁcial box 5292 153.61

6 DISCUSSION

The most simple approach to muscle deformation

problem is probably to use line segments to approxi-

mate both muscles and tendons. An example is shown

in Fig.22. The coordinates of each end-point of the

corresponding line segments are updated when bone

moves, causing shortening or extending of the line

segments. Various values (e.g., moment arms) can be

consequently calculated from the length of each line.

These models are popular in practice (they are used,

e.g., in AnyBody

or OpenSim

) because of their sim-

plicity and speed. However, the accuracy of calcula-

tions based on these models is, especially, for com-

plex muscles, e.g., gluteus medius, low (Delp, 2005).

A model can be more precise if we assume more lines

(Valente et al., 2012) per a muscle or if we use more

complex lines wrapping around some kind of para-

metric surfaces (e.g. spheres, cylinders (Audenaert

and Audenaert, 2008), etc.), nonetheless, all of these

are difﬁcult to set up. This may be the reason why

most studies use gait2392 model shipped with Open-

Sim software even though there are no more than

three lines per muscle and these lines penetrate the

bones in some poses. Using our approach, described

in this paper, the user can easily generate hundreds of

lines (i.e., ﬁbres) automatically and impenetrability of

muscles and bones is guaranteed.

Figure 22: Muscle approximation using line segments – yel-

low lines (taken from (Kohout et al., 2013)).

Position-based dynamics (PBD), which is the core

part of our approach, was ﬁrstly introduced in (M

uller

et al., 2007) as a computer graphics algorithm. Since

https://www.anybodytex.com/software/

https://opensim.stanford.edu/

Fast and Realistic Approach to Virtual Muscle Deformation

225

then, it has been further developed (e.g., (Macklin

et al., 2019) proposed recently some speed and ac-

curacy improvements) and has found many (close to)

real-time applications, not only in computer graph-

ics but even in other domains. For example, Kotsalos

et. al. use PBD to model blood cells (Kotsalos et al.,

2019). As far as we know, however, there is no PBD-

based method for muscle modelling even though one

could expect a good compromise between speed and

accuracy from such a method.

A mass-spring system (MSS) is another approach

to consider. Janak et al. use MSS to approxi-

mate muscle (Janak, 2012), showing promising, sim-

ple method with visually plausible results. How-

ever, there are some issues in the approach they pro-

posed. First, to avoid penetration between muscles

and bones, the authors choose a particle-based colli-

sion detection method requiring many particles to get

reasonable results, which, however, causes high time

and memory complexity. Secondly, and more impor-

tantly, the main issue is that muscle volume is not pre-

served during deformation. This could be probably

solved using the approach described in (Hong et al.,

2006), however, it would increase computational time

dramatically. Finally, our experiments show that al-

though this method retains the smooth shape of ili-

acus muscle during ﬂexion, it twists the part of the

muscle close to the insertion. This is because, un-

like our method, the particles are in the entire volume

of the muscle, which results in a model that is much

more rigid, and as anisotropy is not exploited, rigid in

all directions. Our method supports anisotropy, pre-

serves the volume and runs in a fraction of time while

requiring no extra parameter or input in comparison

with this method.

On the contrary to line segment approximation,

ﬁnite element method (FEM) is the most complex

method. Well discretized muscle provides a phys-

ically very accurate result (see e.g., (Delp, 2005)).

However, computational complexity is high, mean-

ing the FEM-based methods are unsatisfactorily slow.

Therefore, it is quite impractical for real-time appli-

cation or even clinical assessments. Next issue is a

difﬁcult set up of FEM methods, making them un-

suitable for personalised musculoskeletal method de-

formation. Despite these facts, these methods can be

seen in the movie industry, see e.g. Ziva VFX

plu-

gin for Maya, and in muscle physiology research, see

e.g. (Oberhofer et al., 2009) or (Kojic et al., 1998). In

comparison with these methods, our method is quite

simple to set up and runs fast providing the promising

results in most cases.

https://zivadynamics.com/

7 CONCLUSION & FUTURE

WORK

The proposed muscle deformation technique is capa-

ble to do fast and relatively accurate simulation. De-

spite problems with muscle trapped in the hip joint,

we believe that a better collision detection can ﬁx the

issue.

Moreover, the method is ready to be included in

OpenSim (a state-of-the-art simulation software) as

a plugin, allowing common users to use the method

more intuitively. Its source code is available at https:

//github.com/cervenkam/muscle-deformation-PBD.

In this paper, we veriﬁed the method, but to prove

correctness, the method needs to be validated in real

life. There are some works (e.g. (Modenese et al.,

2018)) providing correct momentum values during

muscle movement, which can be useful for validation.

ACKNOWLEDGMENT

Authors would like to thank their colleagues and stu-

dents for valuable discussion, worthful suggestions

and constructive comments. Authors would like to

thank also anonymous reviewers for their hints and

notes provided.

REFERENCES

Arnold, E., Ward, S., Lieber, R., and Delp, S. (2009). A

model of the lower limb for analysis of human move-

ment. Annals of biomedical engineering, 38:269–79.

Audenaert, A. and Audenaert, E. (2008). Global optimiza-

tion method for combined spherical-cylindrical wrap-

ping in musculoskeletal upper limb modelling. Com-

puter methods and programs in biomedicine, 92:8–19.

Bergmann, G., Deuretzbacher, G., Heller, M., Graichen, F.,

Rohlmann, A., Strauss, J., and Duda, G. (2001). Hip

contact forces and gait patterns from routine activities.

Journal of Biomechanics, 34(7):859 – 871.

Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M.,

Ganovelli, F., and Ranzuglia, G. (2008). Meshlab:

an open-source mesh processing tool. Computing,

1:129–136.

Delp, S. (2005). Three-dimensional representation of com-

plex muscle architectures and geometries 1. Annals

of Biomedical Engineering - ANN BIOMED ENG,

33:1134–1134.

Delp, S. L., Loan, J. P., Hoy, M. G., Zajac, F. E., Topp,

E. L., and Rosen, J. M. (1990). An interactive

graphics-based model of the lower extremity to study

orthopaedic surgical procedures. IEEE Transactions

on Biomedical Engineering, 37(8):757–767.

HEALTHINF 2020 - 13th International Conference on Health Informatics

226

Hong, M., Jung, S., Choi, M.-H., and Welch, S. (2006). Fast

volume preservation for a mass-spring system. IEEE

computer graphics and applications, 26:83–91.

Janak, T. (2012). Fast soft-body models for musculoskele-

tal modelling. Technical Report DCSE/TR-2012-5,

University of West Bohemia, Faculty of Applied Sci-

ences.

Kohout, J. and Cholt, D. (2017). Automatic reconstruc-

tion of the muscle architecture from the superﬁcial

layer ﬁbres data. Computer Methods and Programs

in Biomedicine, 150.

Kohout, J., Clapworthy, G., Zhao, Y., Tao, Y., Gonzalez-

Garcia, G., Dong, F., Wei, H., and Kohoutov

a, E.

(2013). Patient-speciﬁc ﬁbre-based models of muscle

wrapping. Interface focus, 3:20120062.

Kohout, J. and Kukacka, M. (2014). Real-time modelling of

ﬁbrous muscle. Computer Graphics Forum, 33(8):1–

15.

Kojic, M., Mijailovic, S., and Zdravkovic, N. (1998).

Modelling of muscle behaviour by the ﬁnite element

method using hill’s three-element model. Interna-

tional Journal for Numerical Methods in Engineering,

43(5):941–953.

Kotsalos, C., Latt, J., and Chopard, B. (2019). Bridging

the computational gap between mesoscopic and con-

tinuum modeling of red blood cells for fully resolved

blood ﬂow. Journal of Computational Physics, 398.

cited By 0.

Macklin, M., Storey, K., Lu, M., Terdiman, P., Chentanez,

N., Jeschke, S., and M

uller, M. (2019). Small steps in

physics simulation. In Proceedings of the 18th Annual

ACM SIGGRAPH/Eurographics Symposium on Com-

puter Animation, SCA ’19, pages 2:1–2:7, New York,

NY, USA. ACM.

Modenese, L., Monteﬁori, E., Wang, A., Wesarg, S., Vice-

conti, M., and mazz

a, C. (2018). Investigation of the

dependence of joint contact forces on musculotendon

parameters using a codiﬁed workﬂow for image-based

modelling. Journal of Biomechanics.

uller, M., Heidelberger, B., Hennix, M., and Ratcliff, J.

(2007). Position based dynamics. Journal of Visual

Communication and Image Representation, 18:109–

118.

Oatis, C. (2013). Kinesiology: The mechanics and path-

omechanics of human movement: Second edition.

Lippincott Williams & Wilkins.

Oberhofer, K., Mithraratne, K., Stott, N. S., and Ander-

son, I. A. (2009). Anatomically-based musculoskele-

tal modeling: prediction and validation of muscle de-

formation during walking. Vis. Comput., 25(9):843–

851.

Shao, X., Liao, E., and Zhang, F. (2017). Improving sph

ﬂuid simulation using position based dynamics. IEEE

Access, PP:1–1.

Valente, G., Martelli, S., Taddei, F., Farinella, G., and

Viceconti, M. (2012). Muscle discretization affects

the loading transferred to bones in lower-limb muscu-

loskeletal models. Proc. Inst. Mech. Eng. H J. Eng.

Med., 226(2):161–169.

Van Sint Jan, S. (2005). Introducing anatomical and physi-

ological accuracy in computerized anthropometry for

increasing the clinical usefulness of modeling sys-

tems. Critical Reviews in Physical and Rehabilitation

Medicine, 17:149–174.

Viceconti, M., Clapworthy, G., and Van Sint Jan, S. (2008).

The virtual physiological human — a european initia-

tive for in silico human modelling —. The journal of

physiological sciences : JPS, 58:441–6.

Wade, S. W., Strader, C., Fitzpatrick, L. A., Anthony, M. S.,

and O’Malley, C. D. (2014). Estimating prevalence of

osteoporosis: examples from industrialized countries.

Archives of Osteoporosis, 9(1):182.

Zhang, J., Fernandez, J., Hislop-Jambrich, J., and Besier,

T. F. (2016). Lower limb estimation from sparse land-

marks using an articulated shape model. Journal of

Biomechanics, 49(16):3875 – 3881.

Fast and Realistic Approach to Virtual Muscle Deformation

227