Fractional Order Analysis of the Activator Model for Gene
Regulation Process
Hisham H. Hussein
1
, Shaimaa A. Kandil
2
and Khadeeja Amr
3
1
Mathematics Department, The German University in Cairo (GUC), Egypt
2
Department of Power and Electrical Machines Engineering, Faculty of Engineering, Helwan University, Cairo, Egypt
3
Department of Biochemistry and Molecular Biology, Faculty of Biotechnology, The German University in Cairo, Egypt
Keywords: Gene Regulation, Transcription, Translation, Activator and Fractional Modeling.
Abstract: Mathematical modeling for gene regulation process is very important for future prediction and control of
diseases on the hereditary level. This paper presents a complete fractional dynamical analysis for an activator
gene regulation model. The study of the system's phase planes portraits and the variables' transient responses
starting from different initial points are presented and discussed. The effect of the fractional parameter within
the differential operator is investigated. The simulation results show that the fractional parameter
(
𝛼
)
is
effective in the process of synthesizing proteins and the gene regulation process stability.
1 INTRODUCTION
Mathematical modeling is becoming a vital tool for
molecular cell biology (MCB). Thus, it is of
paramount importance for life scientists to have a
solid background in the relevant mathematical
techniques, to enable them to participate in the
construction, analysis, and critique of published
models.
Biological systems are complex systems and the
higher levels of complexity emerge from collective
behaviour and rising properties at multiple levels. At
initial stages, this requires the analysis of large
quantities of low level data, which is either acquired
by direct measurements or by accessing a variety of
sources. It is very important to understand and clarify
the dynamic of gene regulatory networks. Various
mathematical models have been developed to clarify
those complex biochemical systems. Each modeling
technique has its focal points and drawbacks and that
has to be taken into consideration when creating
mathematical model, where the proposed model has
to provide good insight into gene regulation process
and be valuable for predicting of some possible
mutations or any other change (Ahmet and David,
2011), (Santo and Francesco, 2012).
Gene expression is the process by which the
hereditary code of a gene is used for synthesizing
proteins and producing the structures of the cell.
Genes that code for amino acid sequences are named
as 'structural genes'. Gene expression process
includes two main stages known as 'Transcription and
translations'. Transcription is the creating of
messenger RNA (mRNA) by the enzyme RNA
polymerase, and the processing of the resulting
mRNA molecule. But, translation is the use of mRNA
to direct synthesizing proteins, and the subsequent
posttranslational preparing for the protein molecule.
There are some genes are responsible for the
production of other forms of RNA and play a role in
translation, including transfer RNA (tRNA) and
ribosomal RNA (rRNA) (Donald and Charlotte,
2016).
The mathematical model to be studied is a
fractional mathematical model. The concept of
Fractional Calculus (FC) is basically a generalization
of ordinary differentiation to the non integer case,
where the integrals and derivatives are of an arbitrary
order. First introduced by (Ross, 1975), FC was soon
regarded as a major research point by scientists from
various fields. This is because it proved to be
exceptionally well suited in modeling and describing
the complex nature of real world problems
(Kilbas, and
Trujillo, 2006
) (e.g. MCB), in comparison to local
derivatives.
The main contribution of this paper is introducing
a fractional model for the gene expression process. A
complete mathematical analysis of the fractional
296
Hussein, H., Kandil, S. and Amr, K.
Fractional Order Analysis of the Activator Model for Gene Regulation Process.
DOI: 10.5220/0009149402960300
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 4: BIOSIGNALS, pages 296-300
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

differential operator for the gene regulation process
with the effect of activators is presented. The exact
solution of the fractional model and studying the
stability conditions are discussed. The effect of the
fractional parameter 𝛼 on the system performance is
taken into consideration.
This paper is organized as follows: Section 2
introduces the gene expression process, Transcription
and translation. Section 3 presents a fractional
analysis model for the gene regulation process using
activator. The results and discussion are shown in
section 4. Finally, section 5 concludes this work.
2 GENE EXPRESSION PROCESS
The main principle of molecular biology is describing
the structure of deoxyribonucleic acid (DNA) and the
process of synthesizing proteins. These proteins are
synthesized in a process called gene expression. The
gene expression process is performed in two steps
known as transcription (DNA → RNA) and
translation (RNA → Proteins) as shown in figure 1(a).
In transcription process, enzymes use one of the
strands of DNA within a gene as a template to create
a messenger RNA (mRNA). This process can be
executed in four steps (Ana and Želimir, 2012): (i)
promoter recognition (ii) chain initiation (iii) mRNA
chain elongation and (iii) chain termination and
regulation can occur at each step. Producing RNA
polymerase using proteins is named as transcription
factors (TF), binds to a specific sequence within the
gene, which is called the promoter and prices the two
strands apart. One of the strands acts as a template
strand, or antisense strand, which means that it will be
used to produce the mRNA. The other strand is a non-
template strand or a sense strand (
Ana and Želimir,
2012).
RNA polymerase does not need a primer; it
simply initiates mRNA generation at the start codon,
and then moves downstream along the gene in a
process called elongation. This is very similar to the
way DNA polymerase synthesizes DNA as it moves
along the template strand, the main difference here is
that RNA is being produced. Termination occurs
when RNA polymerase reaches the end of the gene,
and the enzyme withdraws from the gene and the
DNA with it the data encoded within the gene, and
after a few quick adjustments during RNA processing
it will leave the nucleus, where all the hereditary
material or chromatin is and move into the cytoplasm,
where it will meet a ribosome. This is where
translation happens (Ana and Želimir, 2012).
(a)
𝐺𝑒𝑛𝑒
.

⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯

𝑚𝑅𝑁𝐴
.

⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯

𝑃𝑟𝑜𝑡𝑒𝑖𝑛
𝑚𝑅𝑁𝐴
.

⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯

𝜙
𝑃𝑟𝑜𝑡𝑒𝑖𝑛
.

⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯

𝜙
(b)
Figure 1: (a) transcription and translation (Martha, 2017)
(b) Gene expression.
During translation the mRNA acts as a code for a
particular protein, this occurs since each set of three
bases on the mRNA, which known as codons, will be
coded for a particular transfer RNA (tRNA), and
match the mRNA sequence by the complementary
sequence of amino acids carried by another sort of
RNA called transfer RNA (tRNA). They are utilized
to encode the 20 standard amino acids. The generated
amino acids add together to form a peptide chain
shaping the desired protein, then the mRNA molecule
corrupts. The same produced mRNA can be
translated many times (Samar, 2018).
3 FRACTIONAL MODELING
The constitutive gene expression has been
summarized in figure 1(b). When gene expression is
unregulated, it is said to be constitutive, and the gene
is always on. Using the law of mass action, a model
for constitutive expression as in (Guy, 2018) given as:
𝑚
.
=𝑘

−𝑑

𝑚
(1)
𝑝
.
=𝑘

𝑚−𝑑

𝑝
Where 𝑚 and 𝑝 represent the produced mRNA and
protein, respectively. 𝑘

and 𝑘

are the constitutive
transcription and translation rates, respectively.
Also,𝑑

and 𝑑

are the mRNA and protein degradation
rates, respectively.
Fractional Order Analysis of the Activator Model for Gene Regulation Process
297

The constitutive transcription rate in case of the
gene whose transcription is activated by the
activator 𝐴

(
𝑘

+𝐴

)⁄
; which is known as the hill
function. It is found that the shape of the hill function
for modeling the transcriptional activation of the gene
expression analysis is a function of the amount of the
activator 𝐴. This function appears in the dynamics of
𝑚
.
; and it can be derived from considering it to very
quickly reach its steady state.
The following model is commonly used to
describe activator controlled gene transcription
(Samar, 2018), (Guy, 2018).
𝑚
.
=𝑘

𝐴

𝑘

+
𝐴

−𝑑

𝑚
(2)
𝑝
.
=𝑘

𝑚−𝑑

𝑝
Where 𝑘 is the activation coefficient and 𝑛 is the
number of the activators that need cooperatively bind
the promoter to trigger the activation of the gene
expression.
The usual Caputo fractional time derivative of
order 𝛼, is given as in (Miller and Ross, 1993),
(Caputo, 1967
) by:
𝐷




𝑓
(
𝑡
)
=
1
Γ
(
𝛼−1
)

𝑓
(
𝜏
)
(
𝑡−𝜏
)

𝑑𝜏


(3)
The aim of the current work is to solve the
fractional version of the above dynamical system,
given by:
𝐷


𝑚
(
𝑡
)
𝑝
(
𝑡
)
=
−𝑑

0
𝑘

−𝑑


𝑚
(
𝑡
)
𝑝
(
𝑡
)
+𝑘


𝑎

0

(4)
where 𝑎

=






. This system can be written in a
matrix form:
𝐷

𝑿
(
𝑡
)
=
𝐴
𝑿
(
𝑡
)
+𝑩 (5)
where 𝛼 is the fractional order of the fractional
system and it is equal to a real number between 0 and
1. The general solution of the fractional dynamical
system (4) as in (Odibat, 2010), has the following
form:
𝑿
𝑮
(
𝑡
)
=𝑿
𝑷
(
𝑡
)
+𝑿
𝑪
(
𝑡
)
(6)
First, to find the particular solution 𝑿
𝑷
(
𝑡
)
, which
is assumed to be constant, depending on the constant
non-homogeneous part,
𝐷

𝑿
𝑷
(
𝑡
)
=
𝐴
𝑿
𝑷
(
𝑡
)
+𝑩 (7)
Due to the previous Caputo definition (3), 𝐷

𝑿
𝑷
=
0, then,
𝑿
𝑷
=−
𝑎

𝑑


1
𝑘

𝑑

⁄

(8)
Second, the homogeneous solution of the
fractional order of the studied dynamical system with
two dimensions can be calculated from the following
equation (Odibat, 2010),
𝑿
𝑪
(
𝑡
)
=𝐶

𝒖

𝐸

(
𝜆

𝑡

)
+𝐶

𝒖

𝐸

(
𝜆

𝑡

)
(9)
where 𝒖
,
and 𝜆
,
are the eigenvectors and the
eigenvalues of the coefficient matrix 𝑨, respectively.
The arbitrary constants depend on the initial
conditions of the system, 𝑚
(
0
)
=0 and 𝑝
(
0
)
=0.
Ultimately, the general solution takes the form:
𝑚
(
𝑡
)
=
𝑎

𝑑

−
𝑎

𝑑

−𝑚
(
0
)
𝐸

(
−𝑑

𝑡

)
(10a)
𝑝
(
𝑡
)
=
𝑎

𝑘

𝑑

𝑑

+
𝑎

𝑑

−𝑚
(
0
)

𝑘

(
𝑑

−𝑑

)
𝐸

(
−𝑑

𝑡

)
+
𝑝
(
0
)
𝑑

𝑑

−𝑝
(
0
)
𝑑


−𝑎

𝑘

+𝑚
(
0
)
𝑑

𝑘

𝑑

(
𝑑

−𝑑

)
𝐸

(
−𝑑

𝑡

)
(10b)
4 RESULTS AND DISCUSSION
The general solution of the mRNA ( 𝑚) and the
protein (𝑝) are plotted in Figure 2 at the parameter
values as in [8], such that 𝑎

= 416.7, 𝑑

=41.6,
𝑑

=83.3 and 𝑘

= 41.6, for 𝛼 =

0.3,0.5,0.7,1.0

.
4.1 Stability Analysis
The stability of the fractional gene regulation system
can be deduced from the stability conditions τ

−
4Δ > 0 , τ>0 and Δ>0. The parameter τ=
−d

−d

is the trace of the coefficient matrix 𝐀 and
Δ=d

d

is the value of the determinant 𝐀. The
stability analysis has been studied for different values
of 𝛼 and for different initial points.
The system's phase plane portrait and the
variables’ transient responses starting from different
initial points are shown in figure 2. Figure 2 shows
that the system reaches the same fixed point,
(
𝑚
∗
=𝑎

𝑑

⁄
,𝑝
∗
=𝑎

𝑘

𝑑

𝑑

⁄)
for different
values of 𝛼 and for different initial points
𝑚
(
0
)
,𝑝
(
0
)
. Also, the figure shows that as the value
of 𝛼 decreased, the relation curve between 𝑚 and 𝑝
near to be linear.
BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing
298

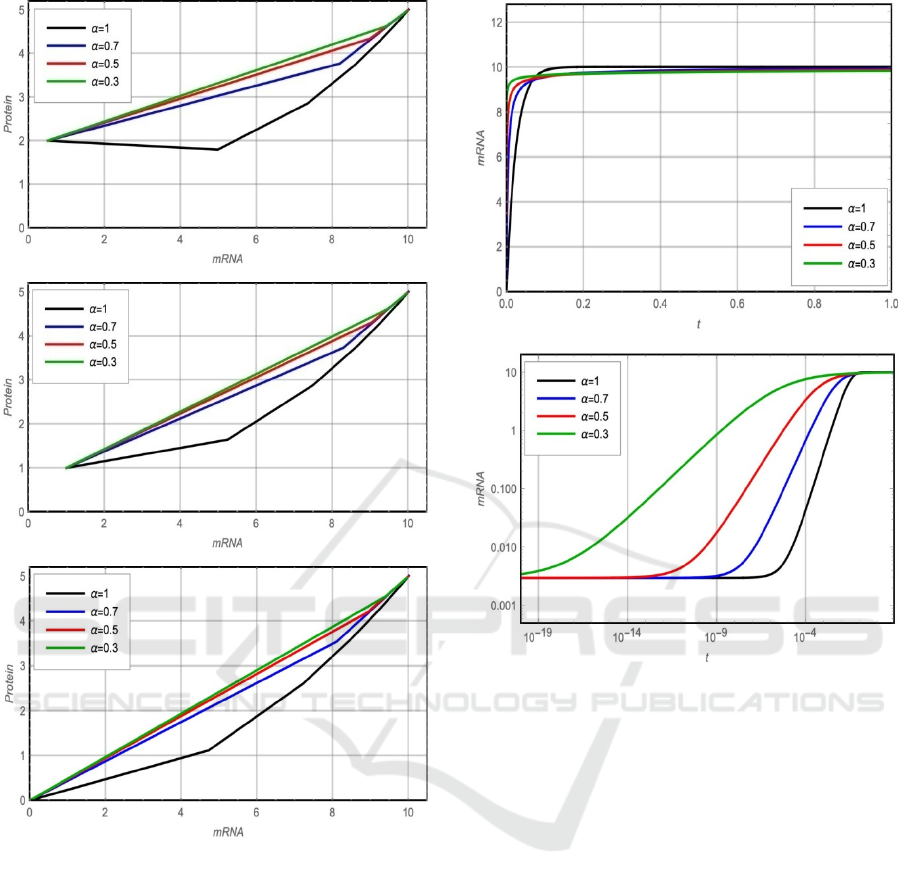
(a)
(b)
(c)
Figure 2: Phase plane portrait (a) m(0)=0 and p(0)=0. (b)
m(0)=1 and p(0)=1.(c) m(0)=0.5 and p(0)=2.
4.2 Fractional Parameter Analysis
Studying the effect of the fractional parameter 𝛼 on
the system behavior is presented in figures 3 and 4.
To study the behaviour of mRNA and protein at
small-time interval 𝑡 , the graphs are plotted for
log
(
𝑚
)
and log
(
𝑃
)
in figure 3 and figure 4
respectively. From figure 3(b) and figure 4(b), it is
clear that the rising time of mRNA (𝑚) and protein
(𝑃) decreases with increasing the value of 𝛼 which
improves the system stability.
(a)
(b)
Figure 3: Fractional solution of m(t). (a) Linear plot (b)
Logarithmic plot.
5 CONCLUSIONS
This paper presents the modeling of a fractional
differential operator on the gene regulation process.
A complete fractional dynamical system for an
activator gene regulation model using the exact
solution of the fractional model is introduced and
discussed. The study of the systems’ phase plane
portrait and the variables’ transient responses starting
from different initial points are discussed. Moreover,
the effect of the fractional parameter α on the system
stability and its transient response is presented.
Results show that the parameter α is effective in
describing mRNA and Protein , and it causes
variance especially at a small interval of t. These
results and analysis may be helpful for the future
genetic studies in case of availability of laboratory
data.
Fractional Order Analysis of the Activator Model for Gene Regulation Process
299

(a)
(b)
Figure 4: Fractional solution of p(t). (a) Linear plot (b)
Logarithmic plot.
REFERENCES
Ahmet Ay and David N. Arnosti, 2011. Mathematical
Modeling of Gene Expression: A guide for the
perplexed biologist, Critical Reviews in Biochemistry
and Molecular Biology; vol. 46, no. 2, pp. 137-151.
Santo Motta and Francesco Pappalardo, 2012.
Mathematical Modeling of Biological Systems,
briefings in bioinformatics, vol. 14, no. 4, pp. 411-422.
Donald Voet, Judith G Voet, Charlotte W. Pratt, 2016.
Fundamentals of Biochemistry Life At The Molecular
Level, Wiley, The United States of America 5
th
edition.
B.Ross, 1975. A brief history and exposition of the
fundamental theory of fractional calculus, fractional
calculus and its applications, Springer, pp. 1-36.
A.A.A. Kilbas, H.M.Sirivastava, and J.J.Trujillo, 2006.
Theory and applications of fractional differential
equations, Elsevier science limited, vol. 204.
Ana Tušek and Želimir Kurtanjek 2012. Mathematical
Modelling of Gene Regulatory Networks, Applied
Biological Engineering - Principles and Practice, Dr.
Ganesh R. Naik (Ed.), ISBN: 978-953-51-0412-4,
InTech,
Martha R. Taylor, Eric J. Simon, Jean L. Dickey, Kelly A.
Hogan and Jane B. Reece, 2017. Campbell Biology:
Concepts & Connections (9th Edition), Pearson,
London.
Samar M. Ismail, Lobna A. Said, Ahmed G. Radwan,
Ahmed H. Madian and Mohamed F. Abu-ElYazeed,
2018 "Mathematical Analysis of Gene Regulation
Activator Model," 7th International Conference on
Modern Circuits and Systems Technologies
(MOCAST), IEEE, 7-09 May, Thessaloniki, Greece.
Guy-Bart Stan, 2018. Modelling in Biology, Lectures in
Imperial College London.
K.S. Miller, B. Ross, 1993. An Introduction to fractional
calculus and fractional differential equations, Wiley ,
New York.
M. Caputo, 1967. Linear Models of Dissipation Whose Q
Is Almost Frequency Independent-II, Geophysical
Journal of the Royal Astronomical Society,, vol.13, no.
2, pp. 361-370.
Z.M. Odibat, 2010. Analytic study on linear systems of
fractional differential equations, Computers &
Mathematics with Applications, vol. 59, no. 3, pp.
1171-1183.
BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing
300