
Interactive Axis-based 3D Rotation Specification using Image Skeletons
Xiaorui Zhai
1 a
, Xingyu Chen
1,2 b
, Lingyun Yu
1 c
and Alexandru Telea
3 d
1
Bernoulli Institute, University of Groningen, The Netherlands
2
School of Computer and Communication Engineering, University of Science and Technology, Beijing, China
3
Utrecht University, The Netherlands
Keywords:
Skeletonization, 3D Interaction, Image-based Techniques.
Abstract:
Specifying 3D rotations of shapes around arbitrary axes is not easy to do. We present a new method for this
task, based on the concept of natural local rotation axes. We define such axes using the 3D curve skeleton
of the shape of interest. We compute effective and efficient approximations of such skeletons using the 2D
projection of the shape. Our method allows users to specify 3D rotations around parts of arbitrary 3D shapes
with a single click or touch, is simple to implement, works in real time for large scenes, can be easily added to
any OpenGL-based scene viewer, and can be used on both mouse-based and touch interfaces.
1 INTRODUCTION
Interactive manipulation of 3D scenes is a key part
of many applications such as CAD/CAM modeling,
computer games, and scientific visualization (Jackson
et al., 2013). 3D rotations are an important manip-
ulation type, as they allow examining scenes from
various viewpoints to e.g. select the most suitable one
for the task at hand. Two main 3D rotation types ex-
ist – rotation around a center and rotation around an
axis. The first one can be easily specified via classi-
cal (mouse-and-keyboard) (Zhao et al., 2011) or touch
interfaces (Yu et al., 2010) by well-known metaphors
such as the trackball. The latter is also easy to specify
if the rotation axis coincides with one of the world-
coordinate axes. Rotations around arbitrary axes are
considerably harder to specify, as this requires a total
of 7 degrees of freedom (6 for specifying the axis and
one for the rotation angle around the axis).
Users often do not need to rotate around any 3D
axis. Consider the case when one wants to examine
a (complex) 3D shape such as a statue: It can be ar-
gued that a good viewpoint will display the statue in a
‘natural’ position, i. e., with the head upwards. Next, a
‘natural’ way to rotate this shape is around its vertical
symmetry axis. This keeps the shape’s global orienta-
a
https://orcid.org/0000-0002-4244-9485
b
https://orcid.org/0000-0002-3770-4357
c
https://orcid.org/0000-0002-3152-2587
d
https://orcid.org/0000-0003-0750-0502
tion (which helps understanding the shape) but allows
one to examine it from all viewpoints.
Several methods support the above exploration
scenario by first aligning a shape’s main symmetry
axis with one of the world coordinate axes and then
using a simple-to-specify rotation around this world
axis (Duffin and Barrett, 1994). This scenario falls
short when (a) the studied shape does not admit a
global symmetry axis, although its parts may have
local symmetry axes; (b) computing such (local or
global) symmetry axes is not simple; or (c) we do not
want to rotate along an axis which is first aligned with
a world axis.
To address the above, we propose a novel inter-
action mechanism: Given a shape viewed from an
arbitrary 3D viewpoint, we allow the user to choose a
part of interest of the shape. Next, we propose a fast
and generic method to compute an approximate 3D
symmetry axis for this part. Finally, we interactively
rotate the shape around this axis by the desired angle.
This effectively allows one to rotate the viewpoint to
examine shapes around a multitude of symmetry axes
that they can easily select. Our method can handle any
3D shape or scene, e.g., polygon mesh or polygon soup,
point-based or splat-based rendering, or combination
thereof; is simple to implement and works at interac-
tive rates even for scenes of hundreds of thousands
of primitives; requires no preprocessing of the 3D ge-
ometry; and, most importantly, allows specifying the
rotation axis and rotation angle by a single click, there-
fore being suitable for both classical (mouse-based)
Zhai, X., Chen, X., Yu, L. and Telea, A.
Interactive Axis-based 3D Rotation Specification using Image Skeletons.
DOI: 10.5220/0009149901690178
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages
169-178
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
169

and touch interfaces. We demonstrate our method on
several types of 3D scenes and exploration scenarios.
2 RELATED WORK
Rotation Specification.
Many mechanisms for
specifying 3D scene rotation exist. The trackball
metaphor (Bade et al., 2005; Zhao et al., 2011) is one
of the oldest and likely most frequently used. Given a
3D center-of-rotation
x
, the scene is rotated around an
axis passing through
x
and determined by the projec-
tions on a hemisphere centered at
x
of the 2D screen-
space locations
p
1
and
p
2
corresponding to a mouse
pointer motion. The rotation angle
α
is controlled
by the amount of pointer motion. Trackball rotation
is simple to implement and allows freely rotating a
shape to examine it from all viewpoints. Yet, control-
ling the actual axis around which one rotates is hard,
as this axis constantly changes while the user moves
the mouse. At the other extreme, world-coordinate-
axis rotations allow rotating a 3D scene around the
x
,
y
, or
z
axes (Zhao et al., 2011; Jackson et al., 2013).
The rotation axis and rotation amount
α
can be cho-
sen by simple click-and-drag gestures in the viewport.
This method works best when the scene is already pre-
aligned with a world axis, so that rotating around that
axis provides meaningful viewpoints.
Pre-alignment of 3D models is a common prepro-
cessing stage in visualization (Chaouch and Verroust-
Blondet, 2009). Principal Component Analysis (PCA)
does this by computing a shape’s eigenvectors
e
1
,
e
2
and
e
3
, ordered by the respective eigenvalues
λ
1
≥
λ
2
≥ λ
3
, so that the coordinate system
{e
i
}
is right-
handed. Next, the shape can be suitably aligned with
the viewing coordinate system
x
1
,x
2
,x
3
by a simple
3D rotation around the shape’s barycenter (Tangelder
and Veltkamp, 2008; Kaye and Ivrissimtzis, 2015).
3D rotations can be specified by classical (mouse-
and-keyboard) (Zhao et al., 2011) but also touch inter-
faces. Yu et al. (Yu et al., 2010) presented a direct-
touch exploration technique for 3D scenes called
Frame Interaction with 3D space (FI3D). Guo et
al. (Guo et al., 2017) extended FI3D with constrained
rotation, trackball rotation, and rotation around a user-
defined center. (Yu and Isenberg, 2009) used trackball
interaction to control rotation around two world axes
by mapping it to single-touch interaction.
Medial Descriptors.
Medial descriptors, also
known as skeletons, are used for decades to capture
the symmetry structure of shapes (Siddiqi and Pizer,
2008). For shapes
Ω ⊂ R
n
,
n ∈ {2, 3}
with boundary
∂ Ω, skeletons are defined as
S
Ω
={x ∈ Ω|∃f
1
∈ ∂ Ω,f
2
∈ ∂ Ω : f
1
6= f
2
∧
||x −f
1
|| = ||x − f
2
|| = DT
Ω
(x)} (1)
where
f
i
are called the feature points of skeletal point
x
and
DT
Ω
is the distance transform (Rosenfeld and
Pfaltz, 1968) of skeletal point x, defined as
DT
Ω
(x ∈ Ω) = min
y∈∂ Ω
kx −yk. (2)
The feature points define the so-called feature trans-
form (Hesselink and Roerdink, 2008)
FT
Ω
(x ∈ Ω) = argmin
y∈∂ Ω
kx −yk. (3)
In 3D, two skeleton types exist (Tagliasacchi et al.,
2016): Surface skeletons, defined by Eqn 1 for
Ω ⊂ R
3
,
consist of complex intersecting manifolds with bound-
ary, and hence are hard to compute and utilize. Curve
skeletons are curve-sets in
R
3
that locally capture the
tubular symmetry of shapes. They are structurally
much simpler than surface skeletons and enable many
applications such as shape segmentation (Rodrigues
et al., 2018) and animation (Bian et al., 2018). Yet,
they still cannot be computed in real time, and require
a well-cured definition of
Ω
as either a watertight, non-
self-intersecting, fine mesh (Sobiecki et al., 2013), or
a high-resolution voxel volume (Reniers et al., 2008).
3 PROPOSED METHOD
We construct a 3D rotation in five steps (Fig. 1) which
can be integrated into any OpenGL-based 3D scene
viewer. We start by loading the scene of interest into
the viewer (a). Next, the user can employ any standard
mechanisms offered by the viewer, e.g. trackball rota-
tion, zoom, or pan, to choose a viewpoint of interest,
from which the viewed scene shows a detail around
which one would like to further rotate to explore the
scene. In our example, such a viewpoint (b) shows the
horse’s rump, around which we next want to rotate the
horse to view it from different angles.
3.1 Rotation Axis Computation
From the above-mentioned initial viewpoint, we next
perform three image-space operations to compute the
3D rotation axis. These steps, denoted A, B, and C
next, are as follows.
A. Silhouette Extraction.
This is the first operation
in step (d) in Fig. 1. We render the shape with Z
buffering on and using the standard
GL LESS
OpenGL
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
170

click
to start
e) rotation axis estimation
sihouette boundary ∂Ω
skeleton S
Ω
distance field DT
S
Ω
clicked point p
skeleton
anchor s
p
skeleton
neighbors N(s
p
)
rotation
axis a
||p-s
p
|| = rotation speed
(single click mode)
p
s
p
b) free
manipulation
c) viewpoint
of interest
d) image-space computations
(silhouette, skeleton, Z-buffers)
f) rotation along
local axis
move
to control
release
to end
a) initial
pose
_
_
d
n×a
d (n×a)
rotation angle
(click & drag mode)
Figure 1: Skeleton-based local rotation pipeline. Blue boxes indicate tool states. Green boxes indicates user actions.
depth-test. Let
Ω
near
be the resulting Z buffer. We next
find the silhouette
Ω
of the rendered shape as all pixels
that have a value in
Ω
near
different from the default
(the latter being 1 for standard OpenGL settings).
B. Skeleton Computation.
We next compute the sil-
houette skeleton
S
Ω
following Eqn. 1. This is the
second operation in step (d) in Fig. 1. To eliminate
spurious skeletal branches caused by small-scale noise
along
∂ Ω
, we regularize
S
Ω
by using the salience-
based metric in (Telea, 2011). Briefly put, this regular-
ization works as follows. For every point
x ∈ S
Ω
of the
full skeleton computed by Eqn. 1, we compute first the
so-called importance
ρ(x) ∈ R
+
, defined as the short-
est path along
∂ Ω
between the two feature points
f
1
and
f
2
of
x
. As shown in (Telea and van Wijk, 2002),
ρ
monotonically increases along skeletal branches from
their endpoints to the skeleton center, and equals, for a
skeleton point
x
, the amount of boundary length which
is captured (described) by
x
. Next, the saliency of
point x is defined as
σ(x) =
ρ(x)
DT
Ω
(x)
. (4)
As shown in (Telea, 2011), the saliency is overall
low on skeleton branches caused by small-scale de-
tails along
∂ Ω
and overall high on skeleton branches
caused by important (salient) protrusions of
∂ Ω
.
Hence, we can regularize
S
Ω
simply by removing all
its pixels having a salience value lower than a fixed
threshold
σ
0
. Following (Telea, 2011), we set
σ
0
= 1
.
Figure 2 illustrates the regularization process by show-
ing the raw skeleton
S
Ω
and its regularized version
S
Ω
for a noisy shape. As visible in image (b), the salience
regularization removes all spurious branches created
by surface noise, but leaves the main skeleton branches,
corresponding to the animal’s limbs, rump, and tail,
intact. Salience regularization is simple and automatic
to use, requiring no parameters to be controlled by the
user – for details, we refer to (Telea, 2011).
a) noisy (non-regularized)
skeleton S
Ω
b) regularized
skeleton S
Ω
_
Figure 2: Raw skeleton
S
Ω
with noise-induced branches (a)
and saliency-based regularized version S
Ω
(b).
C. Rotation Axis Computation.
This is step (e) in
Fig. 1. Let
p
be the pixel under the user-manipulated
pointer (blue in Fig. 1e). We first find the closest
skeleton point s
p
= argmin
y∈S
Ω
kp −yk by evaluating
the feature transform (Eqn. 3)
FT
S
Ω
(p)
of the regu-
larized skeleton
S
Ω
at
p
. Figure 1d shows the related
distance transform
DT
S
Ω
. In our case,
s
p
is a point
on the horse’s rump skeleton (cyan in Fig. 1e). Next,
we find the neighbor points
N(s
p
)
of
s
p
by searching
depth-first from
s
p
along the pixel connectivity-graph
of
S
Ω
up to a maximal distance set to
10%
of the
viewport size.
N(s
p
)
contains skeletal points along
a single branch in
S
Ω
, or a few connected branches,
if
s
p
is close to a skeleton junction. In our case,
N(s
p
)
contains a fragment of the horse’s rump skele-
ton (red in Fig. 1e). For each
q ∈ N(s
p
)
, we next
estimate the depth
q
z
as the average of
Ω
f ar
(q)
and
Ω
near
(q)
. Here,
Ω
f ar
is the Z buffer of the scene
rendered with front-face culling on and the standard
GL LESS
OpenGL depth-test, giving thus the depth of
the nearest backfacing-polygons to the view plane.
Figure 3 illustrates this. First (a), the user clicks
above the horse’s rump and drags the pointer upwards.
Image (b) shows the resulting rotation. As visible,
the rotation axis (red) is centered inside the rump, as
its depth
q
z
is the average of the near and far rump
Interactive Axis-based 3D Rotation Specification using Image Skeletons
171

faces. Next (c), we consider a case of overlapping
shape parts. The user clicks left to the horse’s left-
front leg, which overlaps the right-front one. Image
(d) shows the resulting rotation. Again, the rotation
axis (red) is centered inside the left-front leg. In this
case,
Ω
f ar
(q)
contains the Z value on the backfacing
part of the left-front leg, so
(Ω
near
(q) + Ω
f ar
(q))/2
yields a value roughly halfway this leg along the Z
axis. Separately, we handle non-watertight surfaces as
follows: If
Ω
f ar
(q)
contains the default (maximal) Z
value, this means there’s no backfacing surface under
a given pixel
q
, so the scene is not watertight at that
point. We then set q
z
to Ω
near
(q).
a) b)
c) d)
clicked
point p
clicked
point p
rotation
rotation
Figure 3: Depth estimation of rotation axis for (a,b) non-
overlapping part and (c,d) overlapping parts. In both cases,
the rotation axis (red) is nicely centered in the shape.
We now have a set
N
3D
= {(q ∈ N(s
p
),q
z
)}
of 3D
points that approximate the 3D curve skeleton of our
shape close to the pointer location
p
. We set the 3D
rotation axis
a
to the line passing through the average
point of
N
3D
and oriented along the largest eigenvector
of N
3D
’s covariance matrix (Fig. 1e, red dotted line).
3.2 Controlling the Rotation
We offer three interactive mechanisms to control the
rotation (step (f) in Fig. 1), as follows.
Indication.
As the user moves the pointer
p
, we con-
tinuously update the display of
a
. This shows along
which axis the scene would rotate if the user initiated
the rotation from
p
. If
a
is found suitable, one can start
rotating by a click following one of the two modes
listed next; else one can move the pointer
p
to find a
more suitable axis;
Single Click.
In this mode, we compute a rotation
speed
σ
equal to the distance
kp −s
p
k
and a rotation
direction
δ
(clockwise or anticlockwise) given by the
sign of the cross-product
(s
p
− p)× n
, where
n
is the
viewplane normal. We next continuously rotate (spin)
the shape around a with the speed σ in direction δ ;
Click and Drag.
Let
d
be the drag vector created by
the user as she moves the pointer
p
from the current
to the next place in the viewport with the control, e.g.
mouse button, pressed. We rotate the scene around
a
with an angle equal to d ·(n ×a) (Fig. 1e).
We stop rotation when the user release the control
(mouse button, touchpad, or touch screen). In single-
click mode, clicking closer to the shape rotates slowly,
allowing to examine the shape in detail. Clicking far-
ther rotates quicker to e.g. explore the shape from the
opposite side. The rotation direction is given by the
side of the skeleton where we click: To change from
clockwise to counterclockwise rotation in the example
in Fig. 1, we only need to click below, rather than
above, the horse’s rump. In click-and-drag mode, the
rotation speed and direction is given by the drag vector
d
: Values
d
orthogonal to the rotation axis
a
create
corresponding rotations clockwise or anticlockwise
around
a
; values
d
along
a
yield no rotation. This
matches the intuition that, to rotate along an axis, we
need to move the pointer across that axis.
a) b)
c) d)
wrong skeleton
branches
s
p
s
p
s
p
Figure 4: Two problems of estimating rotation axes from
skeletons. (a) Zoomed-in scene. (b-d) Anchor points close
to a skeleton junction. See Sec. 3.3.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
172

The skeleton-based construction of the rotation axis is
key to the effectiveness of our approach: If the shape
exhibits some elongated structure in the current view
(e.g. rump or legs in Fig. 1c), this structure will yield a
skeleton branch. Clicking closer to this structure than
to other structures in the same view – e.g., clicking
closer to the rump than to the horse’s legs or neck –
selects the respective skeleton branch to rotate around.
This way, the 3D rotation uses the ‘natural’ structure
of the viewed shape. We argue that this makes sense
in an exploratory scenario, since, during rotation, the
shape parts we rotate around stay fixed in the view, as
if one ‘turns around’ them.
The entire method requires a single click and, op-
tionally, a pointer drag motion to execute. This makes
our method simpler than other 3D rotation methods
that rotate around freely specifiable 3D axes, and also
directly applicable to contexts where no second but-
ton or modifier keys are available, e.g., touch screens.
Moreover, our method does not require any complex
(and/or slow) 3D curve-skeleton computation: We
compute only 2D (silhouette) skeletons, which are
fast and robust to extract (Telea and van Wijk, 2002;
Ersoy et al., 2011). We can handle any 3D input ge-
ometry, e.g., meshes, polygon soups, point clouds, or
mixes thereof, as long as such primitives render in the
Z buffer (see Sec. 4 for examples hereof).
3.3 Improvements of Basic Method
We next present three improvements of the basic local-
axis rotation mechanism described above.
Zoom Level.
A first issue regards computing the
scene’s 2D silhouette
Ω
(Sec. 3.1A). For this to work
correctly, the entire scene must be visible in the cur-
rent viewport. If this is not the case, the silhouette
boundary
∂ Ω
will contain parts of the viewport bor-
ders. Figure 4a shows this for a zoomed-in view of the
horse model, with the above-mentioned border parts
marked purple. This leads to branches in the skeleton
S
Ω
that do not provide meaningful rotation axes. We
prevent this to occur by requiring that the entire scene
is visible in the viewport before initiating the rotation-
axis computation. If this is not the case, we do not
allow the skeleton-based rotation to proceed, but map
the user’s interaction to a traditional trackball-based
rotation.
Skeleton Junctions.
If the user selects
p
so that the
skeleton anchor
s
p
is too close to a skeleton junction,
then the neighbor-set
N(s
p
)
will contain points belong-
ing to more than two branches. Estimating a line from
such a point set (Sec. 3.1C) is unreliable, leading to
possibly meaningless rotation axes. Figures 4b-d illus-
trates the problem. The corresponding skeleton points
N(s
p
)
used to estimate the axis are shown in yellow,
and the resulting axes in red. When
s
p
is relatively far
from the junction (Figs. 4b,d),
N(s
p
)
contains mainly
points from a single skeleton branch, so the estimated
rotation axes are reliable. However, when
s
p
is very
close to the junction (Fig. 4c),
N(s
p
)
contains points
from all three meeting branches, so, as the user moves
the pointer
p
, the estimated axis ‘flips’ abruptly and
can even assume orientations that do not match any
skeleton branch.
We measure the reliability of the axis
a
by
the anisotropy ratio
γ = λ
1
/λ
3
of the largest to
smallest eigenvalue of
N
3D
’s covariance matrix.
Other anisotropy metrics can be used equally well,
e.g. (Emory and Iaccarino, 2014). High
γ
values in-
dicate elongated structures
N
3D
, from which we can
reliably compute rotation axes. Low values, empiri-
cally detected as
γ < 5
, indicate problems to find a
reliable rotation axis. When this occurs, we prevent
executing the axis-based rotation.
Selection Distance.
A third issue concerns the po-
sition of the point
p
that initiates the rotation: If one
clicks too far from the silhouette
Ω
, the rotation axis
a
may not match what one expects. To address this, we
forbid the rotation when the distance
d
from
p
to
Ω
exceeds a given upper limit
d
max
. That is, if the user
clicks too far from any silhouette in the viewport, the
rotation mechanism does not start. This signals to the
user that, to initiate the rotation, she needs to click
closer to a silhouette.
We compute
d
as
DT
Ω
(p)
, where
Ω
is the view-
point area outside
Ω
, i.e., all viewport pixels where
Ω
near
equals the default Z buffer value (see Sec. 3.1A).
We studied two methods for estimating
d
max
(see
Fig. 5). First, we set
d
max
to a fixed value, in practice
10% of the viewport size. Using a constant
d
max
is
however not optimal: We found that, when we want
to rotate around thick shape parts, such as the horse’s
rump in Fig. 5b, it is intuitive to select
p
even quite
far away from the silhouette. This is the situation of
point
p
1
in Fig. 5b. In contrast, when we want to
rotate around thin parts, such as the horse’s legs, it is
not intuitive to initiate the rotation by clicking too far
away from these parts. This is the situation of point
p
2
in Fig. 5b. Hence,
d
max
depends on the scale of the
shape part we want to rotate around; selecting large
parts can be done by clicking farther away from them
than selecting small parts.
We model this by setting
d
max
to the local shape
thickness (see Fig. 5c). We estimate this thickness
as follows: Given the clicked point
p
, we find the
closest point to it on the silhouette boundary
∂ Ω
as
Interactive Axis-based 3D Rotation Specification using Image Skeletons
173
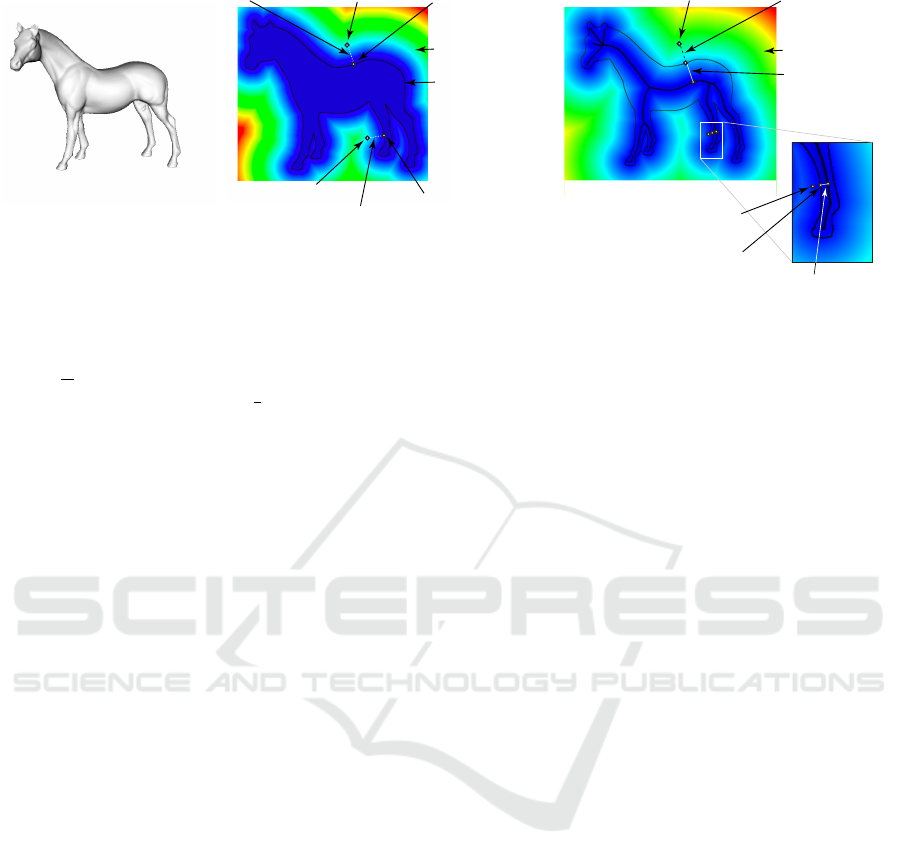
sihouette
boundary ∂Ω
siho
boun
clicked point p
1
closest silhouette
point q
1
to p
1
distance to silhouette d
1
clicked point p
2
distance to silhouette d
2
closest silhouette
point q
2
to p
2
distance field DT
Ω
_
clicked point p
1
closest silhouette
point q
1
to p
1
distance field DT
S
Ω
_
shape thickness
at q
1
closest silhouette
point q
2
to p
2
clicked point p
2
shape thickness at q
2
a)
b)
c)
Figure 5: Improvements of axis-based rotation method. (a) A view of the shape to be rotated. (b) Fixed maximum-distance
setting for two clicked points p
1
and p
2
. (c) Thickness-based maximum-distance setting for two clicked points p
1
and p
2
.
q = FT
Ω
(p)
. The shape thickness at location
q
is the
distance to the skeleton, i.e.,
DT
S
Ω
(q)
. Here, the point
p
1
is the farthest clickable point around the location
q
1
to the silhouette that allows initiating a rotation around
the rump. If we click further from the silhouette than
the distance
d
max
from
p
1
to
q
1
, no rotation is done.
For the leg part, the farthest clickable point around
the location
q
2
has, however, to be much closer to
the silhouette (see Fig. 5c), since here the local shape
thickness, i.e., the distance
d
max
from
p
2
to
q
2
, is much
smaller.
4 RESULTS
Figure 6 shows our 3D skeleton-based rotation applied
to two 3D mesh models. For extra insights, we rec-
ommend also watching the demonstration videos (The
Authors, 2019). First, we consider a 3D mesh model
of a human hand (100K faces), which is not water-
tight (open at wrist). We start from a poor viewpoint
from which we cannot easily examine the shape (a).
We click close to the thumb (b) and drag to rotate
around it (b-e), yielding a better viewpoint (e). Next,
we want to rotate around the shape to see the other
face, but keeping the shape roughly in place. Using
a trackball or world-coordinate axis rotation cannot
easily achieve this. We click on a point close to the
shape-part we want to keep fixed during rotation (f),
near the the wrist, and start rotation. Images (g-j) show
the resulting rotation.
Figure 6(k-ad) show a more complex ship object
(380K polygons). This mesh contains multiple self-
intersecting and/or disconnected parts, some very thin
(sails, mast, ropes) (Kustra et al., 2014). Comput-
ing a 3D skeleton for this shape is extremely hard
or even impossible, as Eqn. 1 requires a watertight,
non-self-intersecting, connected shape boundary
∂ Ω
.
Our method does not suffer from this, since we com-
pute the skeleton of the 2D silhouette of the shape.
We start again from a poor viewing angle (k). Next,
we click close to the back mast to rotate around it,
showing the ship from various angles (l-o). Images
(p-u) show a different rotation, this time around an
axis found by clicking close to the front sail, which
allows us to see the ship from front. Note how the
2D skeleton has changed after this rotation – compare
images (p) with (v). This allows us to select a new
rotation axis by clicking on the main sail, to see the
ship’s stern from below (w-z). Finally, we click on the
ship’s rump (aa) to rotate the ship and make it verti-
cal (ab-ad). The entire process of three rotations took
around 20 seconds.
Figure 7 shows a different dataset type – a 3D
point cloud that models a collision simulation be-
tween the Milky Way and the nearby Andromeda
Galaxy (Dubinski, 2001; J. Dubinski et al., 2006). Its
160K points describe positions of the stars and dark
matter in the simulation. Image (a) uses volume ren-
dering to show the complex structure of the cloud,
for illustration purposes – we do not use this render-
ing in our method. Rather, we render the cloud in our
pipeline using 3D spherical splats (b). Image (c) shows
the cloud, rendered with half-transparent splats, so that
opacity reflects local point density. Since we render a
3D sphere around each point, this results in a front and
back buffer
Ω
near
and
Ω
f ar
, just as when rendering a
3D polygonal model. From these, we can compute
the 2D skeleton of the cloud’s silhouette, as shown in
the figure. Images (d-f) show a rotation around the
central tubular structure of the cloud, which reveals
that the could is relatively flat when seen from the last
viewpoint (f). Image (g) shows the new 2D skeleton
corresponding to the viewpoint after this rotation. We
next click close to the upper high-density structure (f)
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
174

(a) (b) (c) (d) (e)
(f) (g) (h) (i) (j)
click
drag
drag
drag
click
drag
drag
drag
drag
(k) (l) (m) (n) (o)
click
drag
drag
(p) (q) (r) (s) (t) (u)
click
drag
drag
click
drag
drag
click
drag
drag
(v) (w) (x) (y) (z)
(aa) (ab) (ac) (ad)
Legend
pointer
clicked point p
pointer move d
rotation axis a
3D neighbors N
3D
rotation direction
Figure 6: Examples of two rotations (a-e), (f-j) for the hand shape and four rotations (k-o), (p-u), (v-z), (aa-ad) for the ship.
and rotate around it. Images (h-j) reveal a spiral-like
structure present in the lower part of the cloud, which
was not visible earlier. To explore this structure bet-
ter, we next click on its local symmetry axis (l) and
rotate around it. Images (l-n) reveal now better this
structure. As for the earlier examples, executing these
three rotations took roughly 15 seconds. Scientists
involved with studied this dataset for roughly a decade
appreciated positively the ease of use of the skeleton-
based rotation as compared to standard trackball and
multi-touch gestures.
Interactive Axis-based 3D Rotation Specification using Image Skeletons
175

(b) (c) (d) (e) (f)
click
drag
drag
click
drag
drag
click
drag
drag
(g) (h) (i) (j)
(k) (l) (m) (n)
(a)
Figure 7: Exploration of astronomical point cloud dataset. (a) Volume-rendered overview (J. Dubinski et al., 2006). Rotations
around three 3D axes (b-f), (g-j), (k-n).
5 DISCUSSION
We next outline our method’s advantages and limita-
tions:
Ease of Use.
We can rotate around 3D axes locally
aligned with the scene’s features with a single click
and optionally pointer drag motion. This makes our
method usable to contexts where no second button,
modifier keys, or multi-touch input is available. Find-
ing the axis works with even inexact click locations
as we use a set of closest 2D-skeleton points for that
(N(s
p
), Sec. 3).
Genericity.
We handle 3D meshes, polygon soups,
and point clouds; our only requirement is that these
generate fragments with a depth value. This contrasts
using 3D curve skeletons for interaction, which heav-
ily constrain the input scene quality, and cannot be
computed in real time, as already mentioned.
Novelty.
To our knowledge, this is the first time
when 2D image-based skeletons have been used to
perform interactive manipulations of 3D shapes. Com-
pared to view-based reconstructions of 3D curve skele-
tons from their 2D silhouettes (Kustra et al., 2013),
our method requires a single viewpoint to compute an
approximate 3D curve skeleton.
Simplicity and Speed.
Our method consists of ba-
sic OpenGL 1.1 operations (primitive rendering and
Z-buffer reading) plus the 2D image-based skeletoniza-
tion method in (Ersoy et al., 2011). This skeletoniza-
tion method delivers us the skeleton
S
Ω
, its regulariza-
tion
S
Ω
, and the feature transform
FT
S
Ω
. This method
is efficiently implemented in NVidia’s CUDA and C++,
so it handles scenes of hundreds of thousands of poly-
gons rendered onto
1000
2
pixel viewports in a few
milliseconds on a consumer-grade GPU, e.g. GTX
660. Its computational complexity is linear in the num-
ber of silhouette pixels, i.e.,
O(|Ω|)
. This is due to the
fact that the underlying distance transform used has
the same linear complexity. For details on this, we
refer to the original algorithm (Cao et al., 2010).
Implementing the two improvements presented in
Sec. 3 is also computationally efficient: The skele-
ton’s distance transform
DT
S
Ω
is already computed
during the rotation axis estimation (Sec. 3.1C). The
distance
DT
Ω
and feature transforms
FT
Ω
require one
extra skeletonization pass of the background image
Ω
. All in all, our interaction method delivers frame
rates over 100 frames-per-second on the aforemen-
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
176

tioned consumer-grade GPU. For replication purposes,
the full code of the method is provided online (The
Authors, 2019).
Limitations.
Since 3D rotation axes are computed
from 2D silhouette skeletons, rotations are not, strictly
speaking, invertible: Rotating from a viewpoint
v
1
with an angle
α
around a 3D local axis
a
1
computed
from the silhouette
Ω
1
leads to a viewpoint
v
2
in which,
from the corresponding silhouette
Ω
2
, a different axis
a
2
6= a
1
can be computed. This is however a problem
only if the user releases the pointer (mouse) button
to end the rotation; if the button is not released, the
computation of a new axis
a
2
is not started, so mov-
ing the pointer can reverse the first rotation. Another
limitation regards the measured effectiveness of our
rotation mechanism. While our tests show that one can
easily rotate a scene around its parts, it is still unclear
which specific tasks are best supported by this rotation,
and by how much so, as compared to other rotation
mechanisms such as trackball. We plan to measure
these aspects next by organizing several controlled
user experiments in which we select a specific task
to be completed with the aid of rotation and quanti-
tatively compare (evaluate) the effectiveness of our
rotation mechanism as compared to other established
mechanisms such as trackball.
6 CONCLUSION
We proposed a novel method for specifying interac-
tive rotations of 3D scenes around local axes using
image skeletons. We compute local 3D rotation axes
out of the 2D image silhouette of the rendered scene,
using heuristics that combine the silhouette’s image
skeleton and depth information from the rendering’s
Z buffer. Specifying such local rotation axes is simple
and intuitive, requiring a single click and drag ges-
ture, as the axes are automatically computed using
the closest scene fragments rendered from the current
viewpoint. Our method is simple to implement, us-
ing readily-available distance and feature transforms
provided by modern 2D skeletonization algorithms;
can handle 3D scene consisting of arbitrarily complex
polygon meshes (not necessarily watertight, connected,
and/or of good quality) but also 3D point clouds; can
be integrated in any 3D viewing system that allows ac-
cess to the rendered Z buffer; and works at interactive
frame-rates even for scenes of hundreds of thousands
of primitives. We demonstrate our method on sev-
eral polygonal and point-cloud 3D scenes of varying
complexity.
Several extension directions are possible as follows.
More cues can be used to infer more accurate 3D curve
skeletons from image data, such as shading and depth
gradients. Separately, we plan to execute a detailed
user study to measure the effectiveness and efficiency
of the proposed skeleton-based 3D rotation for specific
exploration tasks of spatial datasets such as 3D meshes,
point clouds, and volume-rendered data.
REFERENCES
Bade, R., Ritter, F., and Preim, B. (2005). Usability com-
parison of mouse-based interaction techniques for pre-
dictable 3D rotation. In Proc. Smart Graphics (SG),
pages 138–150.
Bian, S., Zheng, A., Chaudhry, E., You, L., and Zhang, J. J.
(2018). Automatic generation of dynamic skin defor-
mation for animated characters. Symmetry, 10(4):89.
Cao, T.-T., Tang, K., Mohamed, A., and Tan, T.-S. (2010).
Parallel banding algorithm to compute exact distance
transform with the GPU. In Proc. ACM SIGGRAPH
Symp. on Interactive 3D Graphics and Games, pages
83–90.
Chaouch, M. and Verroust-Blondet, A. (2009). Alignment
of 3D models. Graphical Models, 71(2):63–76.
Dubinski, J. (2001). When galaxies collide. Astronomy Now,
15(8):56–58.
Duffin, K. L. and Barrett, W. A. (1994). Spiders: A
new user interface for rotation and visualization of
N-dimensional point sets. In Proc. IEEE Visualization,
pages 205–211.
Emory, M. and Iaccarino, G. (2014). Visualizing turbulence
anisotropy in the spatial domain with componental-
ity contours. Center for Turbulence Research Annual
Research Briefs, pages 123–138.
Ersoy, O., Hurter, C., Paulovich, F., Cantareiro, G., and
Telea, A. (2011). Skeleton-based edge bundling for
graph visualization. IEEE TVCG, 17(2):2364 – 2373.
Guo, J., Wang, Y., Du, P., and Yu, L. (2017). A novel multi-
touch approach for 3D object free manipulation. In
Proc. AniNex, pages 159–172. Springer.
Hesselink, W. H. and Roerdink, J. B. T. M. (2008). Eu-
clidean skeletons of digital image and volume data in
linear time by the integer medial axis transform. IEEE
TPAMI, 30(12):2204–2217.
J. Dubinski et al. (2006). GRAVITAS: Portraits of a universe
in motion. https://www.cita.utoronto.ca/
∼
dubinski/
galaxydynamics/gravitas.html.
Jackson, B., Lau, T. Y., Schroeder, D., Toussaint, K. C., and
Keefe, D. F. (2013). A lightweight tangible 3D inter-
face for interactive visualization of thin fiber structures.
IEEE TVCG, 19(12):2802–2809.
Kaye, D. and Ivrissimtzis, I. (2015). Mesh alignment using
grid based PCA. In Proc. CGTA), pages 174–181.
Kustra, J., Jalba, A., and Telea, A. (2013). Probabilistic
view-based curve skeleton computation on the GPU.
In Proc. VISAPP. SCITEPRESS.
Interactive Axis-based 3D Rotation Specification using Image Skeletons
177

Kustra, J., Jalba, A., and Telea, A. (2014). Robust segmenta-
tion of multiple intersecting manifolds from unoriented
noisy point clouds. Comp Graph Forum, 33(4):73–87.
Reniers, D., van Wijk, J. J., and Telea, A. (2008). Computing
multiscale skeletons of genus 0 objects using a global
importance measure. IEEE TVCG, 14(2):355–368.
Rodrigues, R. S. V., Morgado, J. F. M., and Gomes, A.
J. P. (2018). Part-based mesh segmentation: A survey.
Comp Graph Forum, 37(6):235–274.
Rosenfeld, A. and Pfaltz, J. (1968). Distance functions in
digital pictures. Pattern Recognition, 1:33–61.
Siddiqi, K. and Pizer, S. (2008). Medial Representations:
Mathematics, Algorithms and Applications. Springer.
Sobiecki, A., Yasan, H., Jalba, A., and Telea, A. (2013).
Qualitative comparison of contraction-based curve
skeletonization methods. In Proc. ISMM. Springer.
Tagliasacchi, A., Delame, T., Spagnuolo, M., Amenta, N.,
and Telea, A. (2016). 3D skeletons: A state-of-the-art
report. Comp Graph Forum, 35(2):573–597.
Tangelder, J. W. H. and Veltkamp, R. C. (2008). A survey of
content based 3D shape retrieval methods. Multimedia
Tools and Applications, 39(441).
Telea, A. (2011). Feature preserving smoothing of shapes
using saliency skeletons. In Proc. VMLS, pages 136–
148. Springer.
Telea, A. and van Wijk, J. J. (2002). An augmented fast
marching method for computing skeletons and center-
lines. In Proc. VisSym, pages 251–259. Springer.
The Authors (2019). Source code and videos of interactive
skeleton-based axis rotation. http://www.staff.science.
uu.nl/
∼
telea001/Shapes/CUDASkelInteract.
Yu, L. and Isenberg, T. (2009). Exploring one- and two-
touch interaction for 3D scientific visualization spaces.
Posters of Interactive Tabletops and Surfaces.
Yu, L., Svetachov, P., Isenberg, P., Everts, M. H., and Isen-
berg, T. (2010). FI3D: Direct-touch interaction for the
exploration of 3D scientific visualization spaces. IEEE
TVCG, 16(6):1613–1622.
Zhao, Y. J., Shuralyov, D., and Stuerzlinger, W. (2011).
Comparison of multiple 3D rotation methods. In Proc.
IEEE VECIMS, pages 19–23.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
178
