
Distributed Information Integration in Convolutional Neural Networks
Dinesh Kumar
a
and Dharmendra Sharma
b
Faculty of Science & Technology, University of Canberra, 11 Kirinari Street, Canberra, ACT 2617, Australia
Keywords:
Distributed Information Integration, Central Processor, Local Processor, Convolutional Neural Network,
Filter Pyramid, Scale-invariance.
Abstract:
A large body of physiological findings has suggested the vision system understands a scene in terms of its local
features such as lines and curves. A highly notable computer algorithm developed that models such behaviour
is the Convolutional Neural Network (CNN). Whilst recognising an object in various scales remains trivial for
the human vision system, CNNs struggle to achieve the same behaviour. Recent physiological findings are
suggesting two new paradigms. Firstly, the visual system uses both local and global features in its recognition
function. Secondly, the brain uses a distributed processing architecture to learn information from multiple
modalities. In this paper we combine these paradigms and propose a distributed information integration model
called D-Net to improve scale-invariant classification of images. We use a CNN to extract local features and,
inspired by Google’s INCEPTION model, develop a trainable method using filter pyramids to extract global
features called Filter Pyramid Convolutions (FPC). D-Net locally processes CNN and FPC features, fuses the
outcomes and obtains a global estimate via the central processor. We test D-Net on classification of scaled
images on benchmark datasets. Our results show D-Net’s potential effectiveness towards classification of
scaled images.
1 INTRODUCTION
Evolution has made our vision system a state-of-the-
art biological object detector, recognition engine and
classifier. This allows us to perform with ease sev-
eral vision tasks such as object detection, classifica-
tion and recognition. Even if the appearance of the
object of interest in a scene has changed for exam-
ple in terms of its relative size and position our vi-
sual system still achieves a high recognition accu-
racy. Making computer vision algorithms achieve bi-
ological vision-like behaviour has resulted in various
techniques such as the Convolutional Neural Network
(CNN) (LeCun et al., 1998). Since then CNNs have
achieved great success in numerous computer vision
tasks. However, the generalisation capability of CNN
diminishes when classifying objects that are altered
by transformations such as translations, scaling, rota-
tion and reflection (Jaderberg et al., 2015; Kauderer-
Abrams, 2017; Lenc and Vedaldi, 2015).
Recent physiological findings are suggesting two
new paradigms. Firstly, the visual system uses both
local and global features in its recognition function
a
https://orcid.org/0000-0003-4693-0097
b
https://orcid.org/0000-0002-9856-4685
(Huang et al., 2017; Su et al., 2009). Local fea-
ture information is used where global features can-
not be determined. Here global features are not the
same as global features obtained by aggregating lo-
cal features from CNN models. Secondly instead of a
dedicated multi-sensory integration brain area, there
exists many multisensory brain areas that simultane-
ously process information from multiple modalities
(Zhang et al., 2016b). This suggests our neural sys-
tem uses a distributed information processing and in-
tegration architecture to learn information from dif-
ferent modalities. These paradigms provide the po-
tential for improving transformation invariance prob-
lems in CNNs.
In this paper we combine these paradigms and
propose a distributed information integration model
for CNNs called D-Net. D-Net allows us to test these
paradigms by locally processing local and global fea-
tures of test images and then centrally processing the
outcomes of local processors. We use a CNN to ex-
tract local features. In order to extract global fea-
tures, we apply the concept of large filters (kernels)
to spatially cover broader areas of an image (Peng
et al., 2017). We achieve this by creating a convolu-
tion layer with pyramids of stacked filters (filter pyra-
Kumar, D. and Sharma, D.
Distributed Information Integration in Convolutional Neural Networks.
DOI: 10.5220/0009150404910498
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
491-498
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
491

mids) of different sizes similar to Google’s INCEP-
TION model (Szegedy et al., 2015). Through the
process of convolution these filters generate multi-
scale features maps. These feature maps are down-
sampled via pooling and used as global features. We
use max pooling as research indicates max pooling
help achieve some translation and rotation invariance
(Xu et al., 2014) in CNNs. In our work we refer to
this layer as Filter Pyramid Convolution (FPC) layer.
We test D-Net on classification of scaled images on
benchmark datasets. Our results show D-Net outper-
forms traditional CNN on raw train and test statistics.
D-Net also shows promising results in classification
of scaled images.
The main contributions of this paper are to im-
prove CNNs towards classification of scaled images
by showing the effectiveness of a) using both global
and local features as different aspects of information
for an image and b) applying the distributed process-
ing architecture of the neural system in the artificial
CNN.
The rest of the paper is organised as follows: Sec-
tion 2 reviews related work while Section 3 introduces
our model. Section 4 describes our experiment design
and results are presented in Section 5. We summarise
and point to future directions in Section 6.
2 BACKGROUND
Given our research is related to topics on global fea-
ture extraction using CNNs, the distributed informa-
tion integration architecture of the biological neural
system and filter and feature pyramid based design of
CNNs, we cover review them briefly in the following
sub-sections.
Global Features: Experiments on behaving mon-
keys by (Huang et al., 2017) showed detecting a dis-
tinction or change in the global feature (such as a
hole in a circle) was faster than detecting a distinc-
tion or change in a local feature (solid shapes such
as a circle). This means the visual system uses spa-
tial and semantic information present in global fea-
tures to identify objects prior to using local features
(Park and Lee, 2016). In some studies, global fea-
tures have been applied in CNNs but are limited to
using feature descriptors such as histogram of gradi-
ents (HOG) (Zhang et al., 2016a). In another work,
SIFT is combined with CNN (Zheng et al., 2017) but
we note SIFT is classified as a local feature descriptor
instead. An examination of how pre-trained Alex-Net
and VGG-19 networks process local and global fea-
tures is presented in (Zheng et al., 2018). These meth-
ods however have not been tested on how the network
handles scaled images.
Distributed Information Integration: Anatomical
evidence and experimental observations on the func-
tioning of neural systems suggest the existence of
dense clusters of neurons referred to as multisensory
brain areas (Tononi and Edelman, 1998). To process
different aspects of information about the same en-
tity, a combined effort of several multisensory brain
areas is needed (Zhang et al., 2016b; Ma and Pouget,
2008). Thus, the integration of information from
multisensory brain areas form a reliable description
of an underlying object of interest. (Zhang et al.,
2016b) describe three principle architectures namely
central, distributed and decentralised. We adopt the
distributed architecture (Figure 1) in our work where
we introduce multiple processing areas in the form of
fully connected neural networks. We also show with
some evidence the effectiveness of this design on clas-
sification of scaled images. Here our design contrasts
with designs of most CNNs which use a dedicated
multisensory integration area in the form of a single
fully connected neural network.
A notable model to handle transformation invari-
ance in CNNs is proposed by (Jaderberg et al., 2015)
called Spatial Transformer networks. This model is
built using 3 major components called a localisation
network, grid generator and sampler to spatially trans-
forms feature maps. The localisation network in the
model contains a feed-forward network which gen-
erates and learns the parameters of the spatial trans-
formation that should be applied to the input feature
map. A limitation of this technique is that it limits the
number of objects that can be modelled in the feed-
forward network. We refer to this work as another
evidence of the use of small networks embedded with
the CNN pipeline.
Filter Pyramid: Neuroscience models by (Poggio
et al., 2014; Han et al., 2017; Dicarlo et al., 2012)
essentially describe the vision system as having a
conical neuronal architecture with increasing recep-
tive field sizes in the form of an inverted pyramid of
neurons. Visual stimuli processed by each horizontal
slice of the neuronal pyramid allows the visual system
to become robust to scale changes. Inspired by these
models the approach of using differently sized convo-
lutional filters in parallel to capture more context is in-
creasingly being explored by researchers (Gong et al.,
2014; Zagoruyko and Komodakis, 2015). Google’s
INCEPTION family of models uses this approach
(Szegedy et al., 2015; Szegedy et al., 2016; Szegedy
et al., 2017). Based on the INCEPTION model simi-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
492
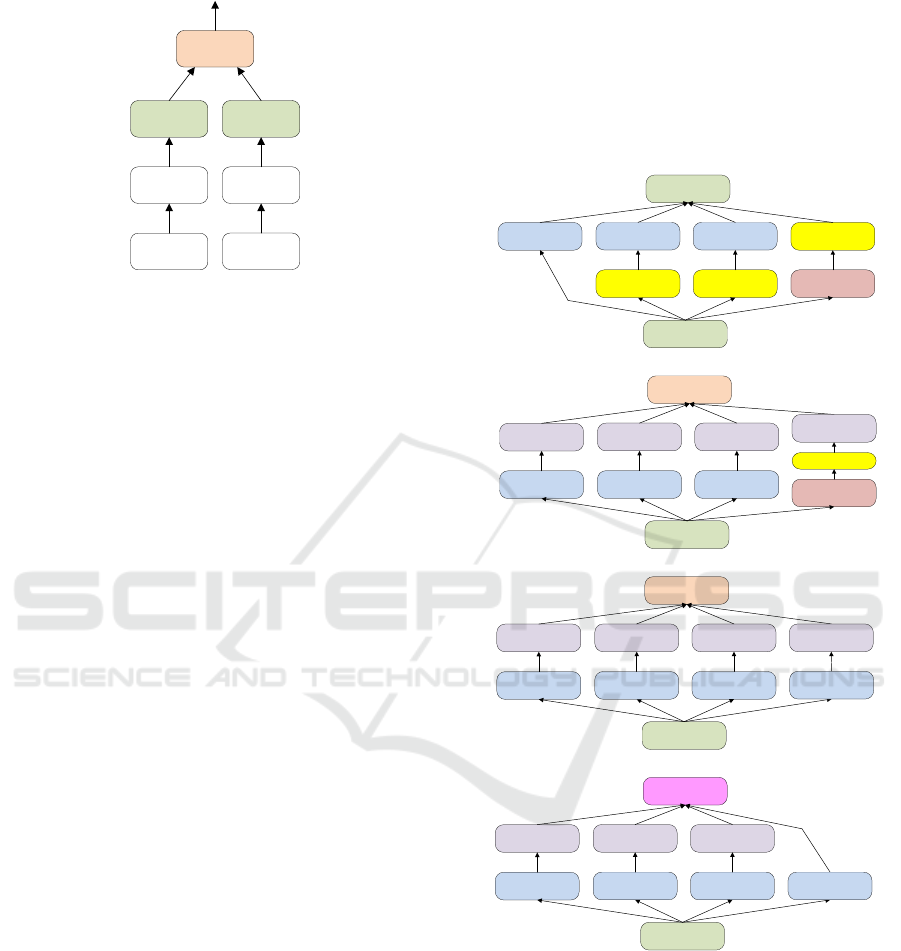
Central
processor
Local
processor
Local
processor
Local
sensor
Local
sensor
Stimulus
Stimulus
global estimate
(a) (b)
Figure 1: Distributed architecture adopted from (Zhang
et al., 2016b). Dedicated local processors in each pipeline
((a) and (b)) compute local estimates which are then inte-
grated by a central processor to obtain a global estimate.
lar models are proposed in (Liao and Carneiro, 2015;
Wang et al., 2019). The FPC layer in D-Net adopts a
similar approach as in the INCEPTION model. How-
ever what makes FPC different when compared to the
original INCEPTION model (Szegedy et al., 2015)
is a) FPC is uses much larger filters, b) is designed
to operate on input images directly to capture global
features and c) before filter concatenation, outputs
from large filters are selectively maxpooled to gen-
erate uniform-sized feature maps. In a similar fash-
ion, the use of maxpooling at the end of each par-
allel multi-scale pipeline makes FPC different when
compared with competitive INCEPTION model and
competitive multi-scale convolution model (Liao and
Carneiro, 2015). In addition, FPC does not use Max-
out (Goodfellow et al., 2013). Figure 2 shows the
comparison of FPC with the INCEPTION family of
models.
Image and Feature Pyramid: Pyramid based
methods used to address scale-invariance in CNNs
and can be categorised into image pyramids and fea-
ture map pyramids. For example, an image pyramid-
based method is proposed by (Kanazawa et al., 2014)
where they apply the same kernels on multi-scaled
version of the target image. In another work (Xu
et al., 2014) propose a scale-invariant CNN (SiCNN)
by applying a similar process of convolving a filter
on different image scales. (Lin et al., 2017) in their
work develop lateral connections between the feature
maps that are generated in deep convolutional net-
works through successive convolution and maxpool-
ing operations. They argue connections between fea-
ture maps establish scale-invariance in the network as
a change in an object’s scale is offset by shifting its
level in the pyramid. (Kim et al., 2018; Zhao et al.,
2019; Kong et al., 2018; Yu et al., 2018) propose
similar architectures. A commonality in these archi-
tectures is that features from different resolutions are
fused by either concatenation or summation. What
makes FPC different is that features from different
resolutions are normalised by mandatory maxpooling
operations except for the smallest-sized block of fea-
ture maps.
(a) Original inception module
1x1 convolutions 3x3 max pooling
5x5 convolutions
Filter
concatenation
Previous layer
1x1 convolutions
3x3 convolutions
1x1 convolutions 1x1 convolutions
(b) Competitive inception module
3x3 convolutions
3x3 max pooling
Batch
normalisation
Maxout
Previous layer
5x5 convolutions
Batch
normalisation
Batch
normalisation
1x1 convolutions
1x1 convolutions
Batch
normalisation
(c) Competitive multi-scale convolution module
3x3 convolutions
Batch
normalisation
Maxout
Previous layer
5x5 convolutions
Batch
normalisation
Batch
normalisation
1x1 convolutions
Batch
normalisation
7x7 convolutions
(d) FPC module
15x15
convolutions
2x2 max pooling
Feature
concatenatation
Input image
21x21
convolutions
3x3 max pooling
4x4 max pooling
9x9 convolutions
27x27
convolutions
Figure 2: Comparison of FPC with INCEPTION family of
models (Szegedy et al., 2015; Liao and Carneiro, 2015).
3 MODEL
In this section we propose a novel neural network
model called D-Net that combines local features from
CNN and global features from FPC. The design of D-
Net is inspired by a) (Huang et al., 2017) who show
that biological visual system utilizes global features
Distributed Information Integration in Convolutional Neural Networks
493

CNN [Convolution + ReLU + Maxpool]
(a) LOCAL FEATURE EXTRACTOR
p2
p3
p1
Multisensory processor
i
j
k
l
Final
classification
Local processor
classifications
Input image
i
j
k
l
i
j
k
l
(d)
(c)
Global features vector
CNN features vector
Local processor
classifications
(b) GLOBAL FEATURE EXTRACTOR
filters
features
downsampled
features
FPC [Filter Pyramids Convolution]
(f) CENTRAL PROCESSOR
LOCAL PROCESSOR
LOCAL PROCESSOR
(e)
FLATTEN
Figure 3: Architecture of D-Net which is explained in Section 3.
prior to local features in detection and recognition, b)
(Poggio et al., 2014) who show the conical architec-
ture of the visual system contains neurons packed in
groups of different sizes in the form of an inverted
pyramid of neurons and c) (Zhang et al., 2016b) who
describe the distributed information integration archi-
tecture of the neural system. The ensemble D-Net
model comprises of six main parts ((a)-(f)) as shown
in Figure 3. They are explained in the following sub-
sections.
3.1 Distributed Information Integration
Model for CNNs (D-Net)
Dual Pipeline Architecture: The hallmark of D-
Net is the dual channel pipeline in its architecture
that enables integration of local processors and merg-
ing outputs in the central processor. The parallel
pipelines are dedicated to extracting global and local
features respectively. This design makes D-Net dif-
ferent from multi-scale parallel processing channels
in CNNs such as in the INCEPTION family of models
(Figure 2). Such models use a single linear feedfor-
ward processing channel despite the multi-scale chan-
nels. D-Net allows examination of input image data in
two different aspects, in terms of its local and global
features.
Local Feature Extractor: D-Net uses standard
CNN as local feature extractor method. The operation
of the CNN processes input image through several
successive convolution, ReLU and maxpooling lay-
ers. The major advantage of CNN is the ability to pro-
cess large datasets and extract features automatically,
hence eliminating the need to manually extract fea-
tures for learning. CNN uses lower layers to extract
features such as lines and curves, while higher level
features may identify shapes relevant to the dataset
such as actual digits, faces or natural objects. As such
CNNs are widely used in image and video processing.
Global Feature Extractor (FPC): The FPC layer
in D-Net contains multiple stacks of filters of vary-
ing sizes. This forms a pyramidal structure of stacked
filters similar to the biological structure of the visual
system proposed in (Poggio et al., 2014) and the IN-
CEPTION model (Szegedy et al., 2015). The dimen-
sions ((k
0
h
, k
0
w
), (k
1
h
, k
1
w
), ...,(k
n
h
, k
n
w
)) of each filter in
the stack is manually chosen where n is the number
of filters in a stack and (k
0
h
, k
0
w
) is the largest filter. In
addition, the size of each filter in the stack is deter-
mined by the output size of its resultant feature map
(( f
0
h
, f
0
w
), ( f
1
h
, f
1
w
), ..., ( f
n
h
, f
n
w
)) and where dimensions
of feature maps ( f
1
, ..., f
n
) can be become equal to f
0
when pooled by an integer factor. Subsequently, sizes
of other filters are identified using a similar process.
For downscaling we use the technique of maxpooling.
Local Processor: In D-Net we use fully connected
neural networks as local processors. The goal of lo-
cal processor is to assimilate information flowing into
it from each channel independently. In this way we
can decentralise the learning of local and global fea-
tures and obtain a reliable description for the underly-
ing object of interest (image) in terms of information
from the two modalities.
Global Processor: Information integration is facil-
itated by the central processor in D-Net. Here we
represent the central processor by a fully connected
neural network. Inputs in terms of local estimates
from local processors feed into the central processor
and are integrated to reach the final global estimate.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
494

The probabilistic outputs from the central processor
become the final classification results of D-Net.
3.2 D-Net Forward Propagation
Our goal is to combine extracted features from CNN
and FPC for learning in distributed local processors
and integrate the outcomes in the central processor.
To achieve the forward pass function, an input image
is processed in the local (CNN) and global feature ex-
tractor (FPC) pipelines respectively. The CNN part
of the network obtains local-global features as output.
Meanwhile in FPC, multi-scale filters produce multi-
scale outputs. They are pooled to generate a set of
uniform-sized downsampled feature maps which are
concatenated and returned as final outputs of FPC.
Both CNN and FPC outputs are then forward propa-
gated through the respective local processors. Finally,
classification outputs from local processors are com-
bined and reshaped into a vector form in the flatten
layer (Figure 3 (e)). This vector forms the input to
fully connected neural network central processor in
D-Net (Figure 3 (f))
3.3 D-Net Backward Propagation
Model loss is calculated on the outputs of the central
processor. The backward function in the flatten layer
receives gradients from the central processor. Since
there are two pipelines in D-Net, the flatten layer re-
turns two sets of gradients - CNN gradients and FPC
gradients. The backward function in FPC layer takes
the FPC gradients and updates the multi-scale filter
weights in the respective filter pyramids. In a similar
fashion CNN gradient are back propagated in the lo-
cal feature extractor pipeline using chain rule deriva-
tive algorithm as well.
4 THE EXPERIMENTS
We describe the datasets, D-Net model component ar-
chitectures and our experimental design in the follow-
ing sub-sections.
4.1 Dataset Descriptions
We test D-Net on both color and grey-scale images. In
practice color images are preferred, however we wish
to ascertain the effectiveness of D-Net on both. For
color images we use the CIFAR10 dataset (described
in (Krizhevsky et al., 2009)). For grey-scale images
we use the Fashion-MNIST dataset (FMNIST) (de-
scribed in (Xiao et al., 2017)). Both datasets have 10
Table 1: Architecture of FPC in D-Net.
# of pyramids 16
# of filters in pyramid 4
On CIFAR10 dataset
Sizes of filters in pyramid
(9x9), (15x15),
(21x21), (27x27)
Final Output size (64x6x6)
On FMNIST dataset
Sizes of filters in pyramid
(5x5), (11x11),
(17x17), (23x23)
Final Output size (64x6x6)
classes and have equal distribution of samples in each
class.
4.2 CNN and FPC Architectures
CNN: For benchmarking and local feature extrac-
tor part of D-Net we used LeNet5 CNN structure as
proposed by (LeCun et al., 1998).
FPC Parameters: Table 1 describes the architec-
ture of FPC in terms of filter sizes in each filter pyra-
mid and the number of filter pyramids used. Since
the dimensions of images in CIFAR10 and FMNIST
dataset are different, filter sizes are adjusted accord-
ingly.
Local and Central Processor Networks: Table 2
describes the layers present in our distributed process-
ing modules. The fully connected neural networks
comprise of two hidden layers. This is in line with
suggestions by (Heaton, 2008) that a) two hidden lay-
ers can represent functions with any kind of shape
and b) the optimal size of the hidden layer is recom-
mended to be between the size of its input and output.
4.3 Training Process
End-to-end training was performed on all models.
For networks trained on both CIFAR10 and FMNIST
datasets we start with a warm-up strategy for 4 epochs
with a learning rate of 10
−2
, 10
−3
from epochs 5 −50
and decreasing it to 10
−4
for the rest of training.
Training on all models were stopped at 100 epochs.
Stochastic gradient decent and cross-entropy were
used as learning and loss function respectively. We
use weight decay of 10
−4
and momentum of 0.9. For
training we use batch size of 8 and 4 for testing. We
implement our models using PyTorch version 1.2.0 on
a Dell Optiplex i5 48GB RAM computer with Cuda
support using NVIDIA GeForce GTX 1050 Ti 4GB
graphics card.
Distributed Information Integration in Convolutional Neural Networks
495

Table 2: Layers in the distributed information processors.
Processor Layers
Local (c)
(fc 480) → (relu) → (fc 84) →
(relu)
Local (d)
(fc 2304) → (relu) → (fc 400) →
(relu)
Central (f)
(fc 20) → (relu) → (fc 12) →
(softmax)
Figure 4: An example of scaled test image from datasets CI-
FAR10 - airplane (top) and FMNIST - ankle boot(bottom).
The numbers indicate percentage image is scaled to. 100
indicates no scaling.
4.4 Scaled Images for Testing
We establish 7 scale categories -
[150, 140, 120, 100, 80, 60, 50] to test our models.
The numbers indicate percentage an image is scaled
to. In this paper we consider both reduction and
enlargement of image size from the original. We
select at random 100 images per class from the
datasets. These images are scaled as per the scale
category percentages. In this fashion for a single
test image of a class we generate 7 scaled test
images amounting to 1000 scaled images per scale
category. We further combine images from all 7 scale
categories into an ensemble scale dataset resulting
in 7000 scaled images combined. We analyse our
models on scaled images from each of these scale
categories independently (Section 5.2) as well as on
the ensemble dataset. Figure 4 shows an example
image from each dataset and its corresponding scaled
versions for testing.
4.5 Evaluation Metrics
We use metrics accuracy to analyse results of D-Net
on scale categories. Accuracy is an intuitive perfor-
mance measure to simply evaluate the generalisation
capability D-Net by finding out the total number of
scaled images that were correctly classified in the re-
spective scale categories.
5 RESULTS AND DISCUSSION
5.1 Comparing Train and Test Statistics
on Regular Images
Table 3 compares the train losses and test accuracy
for all networks used in our experiments on regu-
lar images from the test datasets. These are evalua-
tions on images that have not been subjected to any
form of scale transformations. Our ensemble D-Net
model outperforms the traditional LeNet5 network
on all train and test metrics (indicated in bold). We
record lower train losses on D-Net networks on both
datasets. The highest test accuracy increases of 5.3%
is recorded on D-Net combining LeNet5 and FPC on
CIFAR10 dataset. Similarly, we record a 1.0% in-
crease in test accuracy on FMNIST dataset. These
baseline results provide some evidence that combin-
ing global feature information in network training is
useful in improving the overall generalisation capa-
bility of the models studied, more so on color images.
5.2 Improvements on Classification of
Scaled Images
The classification results of our models on differ-
ent scale categories and on different datasets can be
viewed in Table 4. The column hit-rate indicates
the number of scale categories D-Net outperformed
the benchmark. For purposes of our study hit-rate of
>= 60% is desirable, that is D-Net should at least per-
form better on 60% of the scale categories compared
to the benchmark LeNet5 only network. Since the en-
semble test dataset combines all scaled images in one
batch it is excluded from this ratio. Classifications ac-
curacies are obtained by testing the studied models on
scaled images from each scale category. Our results
show D-Net using LeNet5 with FPC performed better
on most scale categories, where hit rate achieved is
greater than 60% on both datasets. This means D-Net
was able to identify a high number of samples from
most scale bins in it correct class despite the images
being scale transformed.
We compare accuracy scores of D-Net
with LeNet5 on upscaled images (categories
150, 140, 120). For these categories on CIFAR10
dataset average D-Net accuracy score is 5.0% higher
than LeNet5. A similar performance of D-Net over
LeNet5 on FMNIST dataset is shown where average
accuracy is 1.5% higher. Comparing accuracy scores
on downscaled images (categories 80, 60, 50), we
note promising performance of D-Net over LeNet5
on both datasets. Here average accuracy score is
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
496
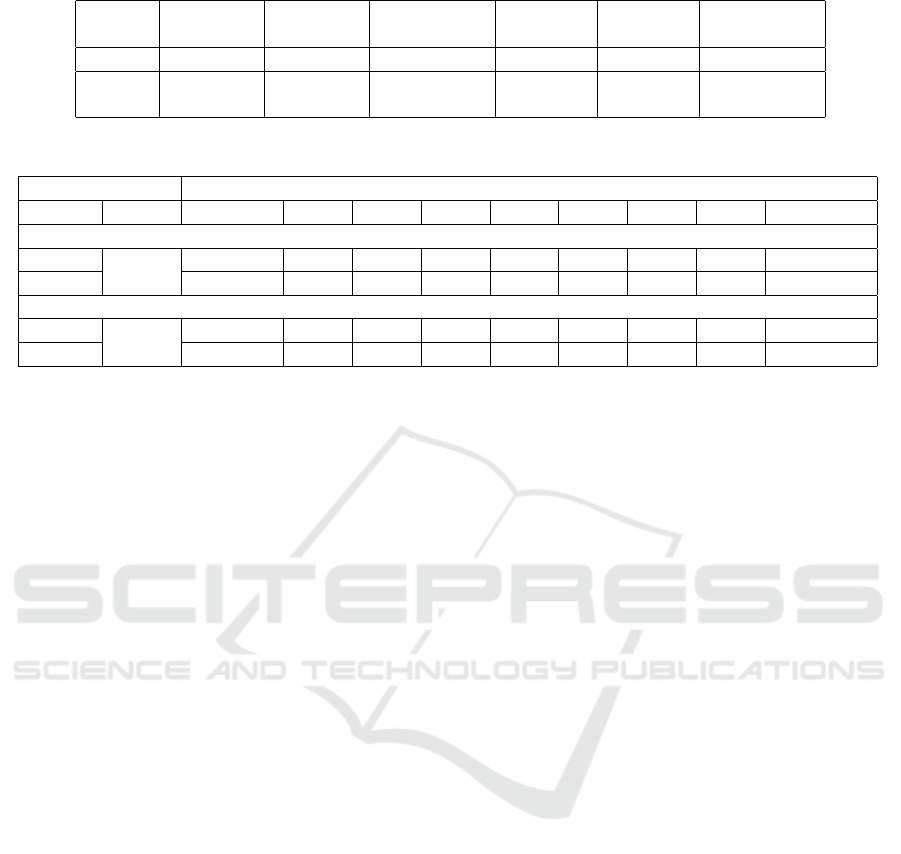
Table 3: Train losses and test accuracy for all models used in our experiments.
Model
train loss
CIFAR10
test acc
CIFAR10
difference
train loss
FMNIST
test acc
FMNIST
difference
LeNet5 1.734 0.568 1.535 0.899
D-Net 1.692 0.621
-0.042 (loss)
+5.3% (acc)
1.527 0.909
-0.008 (loss)
+1.0% (acc)
Table 4: Performance summarization (accuracy) of the studied models on all the scale categories.
scale categories
Model metric ensemble 150 140 120 100 80 60 50
hit rate
CIFAR10 dataset
LeNet5
acc
0.381 0.449 0.478 0.531 0.577 0.265 0.217 0.149
D-Net 0.419 0.481 0.532 0.594 0.637 0.277 0.214 0.195
0.857 (6/7)
FMNIST dataset
LeNet5
acc
0.611 0.575 0.654 0.785 0.895 0.703 0.373 0.295
D-Net 0.629 0.570 0.685 0.804 0.922 0.712 0.410 0.303
0.857 (6/7)
higher by 1.8% and 2.0% in favour of D-Net on
CIFAR10 and FMNIST datasets respectively. Scale
category 100 is where images are in their original
state (unscaled). In this category test accuracy of
D-Net surpasses benchmark LeNet5 by 6.0% on
CIFAR10 dataset and by 2.7% on FMNIST dataset.
Further, higher D-Net accuracy scores over
LeNet5 are recorded on all combined scaled images
in the ensemble test dataset. In this the best D-Net
performance is shown on CIFAR10 dataset where ac-
curacy is higher by 3.8% than LeNet5. This equates
to 266 more images classified correctly from the total
7000 samples in the ensemble dataset compared to
LeNet5 only network.
From the above analysis we arrive at two obser-
vations. First, distributed information processing and
integration has a positive impact on improving CNNs
ability to classify scaled images. Second, we note in
general accuracy scores of both D-Net and LeNet5
decline as images are blown-up as well as reduced
in size. In other words, the classification accuracy
of images closer to original image dimensions are
higher. This shows CNN based architectures are task
specific where they perform well when deviations in
test images from the learnt samples are small.
6 CONCLUSION
In this paper we propose a novel model to improve
classification of scaled images in CNNs by fusing
global and local features in a distributed information
integration neural network architecture called D-Net.
We study the effects of using global features on im-
age classification by combining FPC and CNN fea-
tures and testing on scaled images. Our experimen-
tal results indicate using distributed information inte-
gration architecture with CNNs is an effective way to
combine information from different modalities. We
conclude adding global feature information in CNN
models are beneficial in addressing scaled images.
Problems and opportunities that require further in-
vestigations are a) to evaluate other downsampling
methods in FPC such as using interpolation instead of
max pooling, b) test this technique to evaluate other
forms of transformations such as rotations and trans-
lations, c) apply FPC layer with other benchmark
network configurations using larger and more com-
plex datasets and d) experiment distributed proces-
sors with other classifiers such as Support Vector Ma-
chines (SVM). Finally making CNNs learn features
which are invariant to transformation remains a chal-
lenge and thus requires further investigation.
REFERENCES
Dicarlo, J., Zoccolan, D., and C Rust, N. (2012). How does
the brain solve visual object recognition? Neuron,
73:415–34.
Gong, Y., Wang, L., Guo, R., and Lazebnik, S. (2014).
Multi-scale orderless pooling of deep convolutional
activation features. In European conference on com-
puter vision, pages 392–407. Springer.
Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville,
A., and Bengio, Y. (2013). Maxout networks. arXiv
preprint arXiv:1302.4389.
Han, Y., Roig, G., Geiger, G., and Poggio, T. A. (2017).
Is the human visual system invariant to translation
and scale? In 2017 AAAI Spring Symposia, Stanford
University, Palo Alto, California, USA, March 27-29,
2017.
Heaton, J. (2008). Introduction to Neural Networks for
Distributed Information Integration in Convolutional Neural Networks
497

Java, 2Nd Edition. Heaton Research, Inc., 2nd edi-
tion.
Huang, J., Yang, Y., Zhou, K., Zhao, X., Zhou, Q., Zhu, H.,
Yang, Y., Zhang, C., Zhou, Y., and Zhou, W. (2017).
Rapid processing of a global feature in the on visual
pathways of behaving monkeys. Frontiers in Neuro-
science, 11:474.
Jaderberg, M., Simonyan, K., Zisserman, A., and
Kavukcuoglu, K. (2015). Spatial transformer net-
works. In Cortes, C., Lawrence, N. D., Lee, D. D.,
Sugiyama, M., and Garnett, R., editors, Advances
in Neural Information Processing Systems 28, pages
2017–2025. Curran Associates, Inc.
Kanazawa, A., Sharma, A., and Jacobs, D. W. (2014). Lo-
cally scale-invariant convolutional neural networks.
CoRR, abs/1412.5104.
Kauderer-Abrams, E. (2017). Quantifying translation-
invariance in convolutional neural networks. arXiv
preprint arXiv:1801.01450.
Kim, S.-W., Kook, H.-K., Sun, J.-Y., Kang, M.-C., and Ko,
S.-J. (2018). Parallel feature pyramid network for ob-
ject detection. In Proceedings of the European Con-
ference on Computer Vision (ECCV), pages 234–250.
Kong, T., Sun, F., Tan, C., Liu, H., and Huang, W. (2018).
Deep feature pyramid reconfiguration for object de-
tection. In Proceedings of the European Conference
on Computer Vision (ECCV), pages 169–185.
Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple
layers of features from tiny images. Technical report,
Citeseer.
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P., et al. (1998).
Gradient-based learning applied to document recogni-
tion. Proceedings of the IEEE, 86(11):2278–2324.
Lenc, K. and Vedaldi, A. (2015). Understanding image
representations by measuring their equivariance and
equivalence. CVPR.
Liao, Z. and Carneiro, G. (2015). Competitive multi-scale
convolution. arXiv preprint arXiv:1511.05635.
Lin, T.-Y., Doll
´
ar, P., Girshick, R., He, K., Hariharan, B.,
and Belongie, S. (2017). Feature pyramid networks
for object detection. In Proceedings of the IEEE con-
ference on computer vision and pattern recognition,
pages 2117–2125.
Ma, W. J. and Pouget, A. (2008). Linking neurons to be-
havior in multisensory perception: A computational
review. Brain research, 1242:4–12.
Park, H. and Lee, K. M. (2016). Look wider to match im-
age patches with convolutional neural networks. IEEE
Signal Processing Letters, 24(12):1788–1792.
Peng, C., Zhang, X., Yu, G., Luo, G., and Sun, J. (2017).
Large kernel matters–improve semantic segmentation
by global convolutional network. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 4353–4361.
Poggio, T. A., Mutch, J., and Isik, L. (2014). Computational
role of eccentricity dependent cortical magnification.
CoRR, abs/1406.1770.
Su, Y., Shan, S., Chen, X., and Gao, W. (2009). Hierar-
chical ensemble of global and local classifiers for face
recognition. IEEE Transactions on image processing,
18(8):1885–1896.
Szegedy, C., Ioffe, S., Vanhoucke, V., and Alemi, A. A.
(2017). Inception-v4, inception-resnet and the impact
of residual connections on learning. In Thirty-First
AAAI Conference on Artificial Intelligence.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,
Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-
novich, A. (2015). Going deeper with convolutions.
In Proceedings of the IEEE conference on computer
vision and pattern recognition, pages 1–9.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wo-
jna, Z. (2016). Rethinking the inception architecture
for computer vision. In Proceedings of the IEEE con-
ference on computer vision and pattern recognition,
pages 2818–2826.
Tononi, G. and Edelman, G. M. (1998). Consciousness and
complexity. science, 282(5395):1846–1851.
Wang, H., Kembhavi, A., Farhadi, A., Yuille, A. L., and
Rastegari, M. (2019). Elastic: Improving cnns with
dynamic scaling policies. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 2258–2267.
Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-
mnist: a novel image dataset for benchmarking ma-
chine learning algorithms. Technical report, arXiv.
Xu, Y., Xiao, T., Zhang, J., Yang, K., and Zhang, Z. (2014).
Scale-invariant convolutional neural networks. CoRR,
abs/1411.6369.
Yu, F., Wang, D., Shelhamer, E., and Darrell, T. (2018).
Deep layer aggregation. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 2403–2412.
Zagoruyko, S. and Komodakis, N. (2015). Learning to com-
pare image patches via convolutional neural networks.
In Proceedings of the IEEE conference on computer
vision and pattern recognition, pages 4353–4361.
Zhang, T., Zeng, Y., and Xu, B. (2016a). Hcnn: A neu-
ral network model for combining local and global fea-
tures towards human-like classification. International
Journal of Pattern Recognition and Artificial Intelli-
gence, 30(01):1655004.
Zhang, W.-H., Chen, A., Rasch, M. J., and Wu, S. (2016b).
Decentralized multisensory information integration in
neural systems. Journal of Neuroscience, 36(2):532–
547.
Zhao, Q., Sheng, T., Wang, Y., Tang, Z., Chen, Y., Cai, L.,
and Ling, H. (2019). M2det: A single-shot object de-
tector based on multi-level feature pyramid network.
In Proceedings of the AAAI Conference on Artificial
Intelligence, volume 33, pages 9259–9266.
Zheng, L., Yang, Y., and Tian, Q. (2017). Sift meets cnn:
A decade survey of instance retrieval. IEEE trans-
actions on pattern analysis and machine intelligence,
40(5):1224–1244.
Zheng, Y., Huang, J., Chen, T., Ou, Y., and Zhou, W. (2018).
Processing global and local features in convolutional
neural network (cnn) and primate visual systems. In
Mobile Multimedia/Image Processing, Security, and
Applications 2018, volume 10668, page 1066809. In-
ternational Society for Optics and Photonics.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
498
