Geometric Deep Learning on Skeleton Sequences for 2D/3D Action

Recognition

Rasha Friji

1,2

, Hassen Drira

and Faten Chaieb

CRISTAL Lab, National University of Computer Science ENSI, Manouba University Campus, Manouba, Tunisia

Talan Innovation Factory, Talan, Tunisia

IMT Lille Douai, Univ. Lille, CNRS, UMR 9189,

CRISTAL – Centre de Recherche en Informatique Signal et Automatique de Lille, F-59000 Lille, France

Ecole Nationale des Sciences de l’Informatique INSAT, Tunisia

https://talan.com/

Keywords:

Geometric Deep Learning, Action Recognition, Abnormal Gait Recognition.

Abstract:

Deep Learning models, albeit successful on data deﬁned on Euclidean domains, are so far constrained in many

ﬁelds requiring data which underlying structure is a non-Euclidean space, namely computer vision and imag-

ing. The purpose of this paper is to build a geometry aware deep learning architecture for skeleton based action

recognition. In this perspective, we propose a framework for non-Euclidean data classiﬁcation based on 2D/3D

skeleton sequences, speciﬁcally for Parkinson’s disease classiﬁcation and action recognition. As a baseline,

we ﬁrst design two Euclidean deep learning architectures without considering the Riemannian structure of the

data. Then, we introduce new architectures that extend Convolutional Neural Networks (CNNs) and Recur-

rent Neural Networks(RNNs) to non-Euclidean data. Experimental results show that our method outperforms

state-of-the-art performances for 2D abnormal behavior classiﬁcation and 3D human action recognition.

1 INTRODUCTION

Geometric deep learning is a terminology, initiated by

Bronstein et al. (Bronstein et al., 2017), and used to

refer to deep learning approaches to generalize deep

neural networks to non-Euclidean domains such as

manifolds (e.g action recognition) and graphs (image

analysis). Skeleton sequences is an example of non-

Euclidean data which has been increasingly standing

out (Du et al., 2015; Shahroudy et al., 2016; Vemula-

palli et al., 2014; Ke et al., 2017) given the availability

of huge datasets and the multitude of possible appli-

cations. In this paper, we focus on skeleton-based 2D

Parkinson’s disease classiﬁcation and 3D skeleton-

based action recognition. CNNs (LeCun and Ben-

gio, 1998) have proven distinguished performance in

image classiﬁcation (Krizhevsky et al., 2012; Cohen

et al., 2018; Xiong et al., 2015; Ke and Li, 2014;

Ciresan et al., 2012). In our work, we propose a

ﬁrst CNN based architecture validated for the Parkin-

son’s disease classiﬁcation. But, instead of directly

applying CNN on video images, we primarily iden-

tify the sequence of performed actions, by tracking

the trajectories of human skeleton joints. We rep-

resent then every action with a sequence of joints’

2D coordinates and perform spherical modelling fol-

lowed by a projection in the tangent space. Nonethe-

less, as far as video action recognition is concerned,

even deep CNNs are still not capable of modelling

the temporal correlation between the video frames

(Wang et al., 2016). In order to address this limitation

and to exploit the dynamics of human movements,

the joints’ series have been used in recurrent neu-

ral networks (RNNs) with Long-Short Term Memory

(LSTM) neurons (Graves, 2012; Graves et al., 2013)

for action recognition (Du et al., 2015; Veeriah et al.,

2015; Zhu et al., 2016). Motivated by these works, we

propose a second non-Euclidean architecture based

on CNN and LSTM combination for action recogni-

tion, tested on NTU RGB+D dataset. At the ﬁrst layer

of the network, we used a deep CNN for features ex-

traction. At the second layer, features are then passed

to LSTM which makes the network temporally-

aware. The contributions of this work are 1) Novel

non-Euclidean deep neural networks architectures for

2D/3D skeletal sequences based action recognition.

2) Actions are recognized with respect to the geom-

etry of the manifold of skeletal sequences and with

196

Friji, R., Drira, H. and Chaieb, F.

Geometric Deep Learning on Skeleton Sequences for 2D/3D Action Recognition.

DOI: 10.5220/0009161701960204

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages

196-204

ISBN: 978-989-758-402-2; ISSN: 2184-4321

respect to the temporal dependencies between these

sequences 3) Ablation studies for the classiﬁcation of

Parkinson’s disease and action recognition. Experi-

ments are conducted on two benchmark datasets to

prove the competitiveness of the proposed method.

The rest of the paper is organized as follows. In

section 2, we brieﬂy review existing geometry-aware

deep learning models applied on non linear manifolds

using CNNs and RNNs networks. Section 3 intro-

duces the spherical modelling of skeletal data and the

mapping to the tangent space. In section 4, we de-

scribe the proposed method. Experimental settings

and results are reported in section 5, and lastly sec-

tion 6 concludes the paper.

2 RELATED WORK

In this section, we brieﬂy review the relevant lit-

erature of geometry-aware deep learning architec-

tures for skeleton sequences based classiﬁcation using

CNNs and RNNs networks.

2.1 CNNs based Methods

Unlike the common deep learning architectures that

have been widely used in many applications, only lim-

ited efforts have been spent on non-linear deep learn-

ing. In the past few years, the interest for CNNs

adapted to manifolds has grown exponentially. The

ﬁrst generalized CNNs to manifolds was proposed

by (LeCun and Bengio, 1998) who used local in-

trinsic patches to deﬁne the convolution operation.

Yann LeCun and M.Bronstein proposed in (Bronstein

et al., 2017) an overview of the mainly used non-

Euclidean deep learning architectures. In problems

like shape description, retrieval, and correspondence,

a Geodesic Convolutional Neural Network (GCNN)

was designed in (Masci et al., 2015) to learn invariant

shape features. GCNN is an intrinsic version of CNN

on manifolds where Masci, Jonathan, et al proposed

an application of ﬁlters on local patches represented

in geodesic polar coordinates. In (Cohen et al., 2018),

Cohen, Taco S., et al., proposed spherical CNNs using

a generalized Fast Fourier Transform (FFT).

2.2 CNN and RNNs Combination based

Methods

Recently, RNNs (Baccouche et al., 2011; Lefebvre

et al., 2013; Zhu et al., 2016) have been used for ac-

tion recognition. However, vanishing gradient prob-

lems often occurred because of the large number of

parameters computations and the neglect of initial in-

put effect after few layers. As a solution, LSTM net-

works (Donahue et al., 2017a; Ng et al., 2015; Srivas-

tava et al., 2015) were deployed since they integrate

memory units and they are subsequently capable of

capturing long-term dependencies. Based on the ex-

tension of CNNs to 3D, Baccouche et al. (Baccouche

et al., 2011) propose a unidirectional model with only

one hidden layer LSTM-RNN for action recognition.

Lefebvre et al. (Lefebvre et al., 2013) propose a bidi-

rectional LSTM-RNN with one forward hidden layer

and one backward hidden layer for gesture classiﬁca-

tion. In (Zhu et al., 2016), in order to learn the in-

herent co-occurrence features of skeleton joints, these

joints are fed to a regularized deep LSTM at each time

interval. In (Shahroudy et al., 2016), Shahroudy et al.

propose to learn the long-term context representations

of the body parts with a part-aware LSTM (P-LSTM).

In (Liu et al., 2016), a spatial temporal LSTM is used

to learn both the spatial and temporal information of

skeleton sequences and a Trust Gate is introduced to

omit noisy joints. This approach achieves the state-

of-the-art performance on the NTU RGB+D dataset

(Shahroudy et al., 2016).

3 MODELLING OF 2D/3D

SKELETAL DATA

Actions captured by visual sensors and cameras are

often subject to scale variations. This is due to the

change of distance between the camera and the person

performing the action. As a result, the same actions

can be interpreted very differently. In order to avoid

this problem, sequences of skeletons should be invari-

ant to global scaling. For this purpose, a modeling

is done on the input of our architecture to normalize

skeletons.

3.1 Spherical Modelling

Let X ∈ R

n×k

be a body skeleton, where n indicates

the number of body joints and k denotes the dimen-

sion of X. To remove scale, we propose to model

skeletons as elements on a (n × k−1) dimension Rie-

mannian manifold, more speciﬁcally, the unit sphere

S embedded in R

n×k

. To do so, we divide every skele-

ton X by its Frobenius norm given by Eq.1:

kXk

∑

i, j=1

i j

1/2

(1)

With this process, we consequently get skeletons

representations as well as their temporal evolution,

Geometric Deep Learning on Skeleton Sequences for 2D/3D Action Recognition

197

called trajectories on the unit sphere S embedded in

n×k

. Accordingly, each motion sequence of a mov-

ing skeleton is represented with a trajectory on the

unit sphere S embedded in R

n×k

as shown in Fig.1

(for visualization purposes the trajectory is shown in

2D, however, it lies, in fact, on a space of (n × k−1)

dimensions).

Figure 1: Spherical modelling of the skeleton sequence

data.

3.2 Inverse Exponential Map

The input fed to our CNNs network lies on a Rieman-

nian manifold which is the Unit Sphere S embedded

in R

n×k

. Unlike the Euclidean space which is a vec-

tor space characterized by translation invariance and

operations like vector addition and scalar multiplica-

tion, the non- Euclidean structure of our input implies

that there are no such properties. Consequently, even

basic operations like convolution can’t be applied on

the Unit Sphere S embedded in R

n×k

, since they are

not deﬁned. However, manifolds, including Rieman-

nian manifold, are topological spaces that can be lo-

cally assimilated to an Euclidean space. Given that

the unit sphere S embedded in R

n×k

has a Rieman-

nian manifold structure, the manifold can be assim-

ilated, locally around each point x, to an Euclidean

space known as the tangent space T

(S).

Following, we deﬁne the tangent space shown in

Fig.2 and the inverse exponential map layer used to

map data from the Riemannian manifold which is the

unit sphere embedded in R

n×k

to a tangent space.

A differentiable d-dimensional manifold X is a

topological space where each point x has a neighbor-

hood, which is homeomorphic to a d-dimensional Eu-

clidean space, a.k.a the tangent space and denoted by

(X). In other words, at each point x on the manifold

X, it is possible to associate a linear space T

(X). The

space T

(X) is a local Euclidean representation of the

manifold X around x. This space is called the tangent

space of the manifold X at the point x. Considering

that the tangent space is linear and hence equipped

Figure 2: Examples of two tangent spaces: T

(X) at a point

x of the manifold X and T

(X) at a point x’ of the manifold

with the inner product, the Riemannian metric on S is

deﬁned by Eq.2:

< X

>= trace(X

),X

∈ T

(S) (2)

Figure 3: Unit Sphere S embedded in R

n×k

, the trajectories

α1 and α2 of two sequences of skeletons, the geodesic α(t)

connecting arbitrary points on α1 and α2, the tangent space

(S) at the skeleton X1 and skeletons X2 and X3 mapped

on T

(S).

The inverse exponential map shown in Fig.3, also

known as the logarithm map and uniquely deﬁned

around a small neighborhood of a point x on the man-

ifold X, is given by Eq.3:

exp

−1

) =

sinθ

− cos (θ)X

) (3)

With θ = cos

−1

(trace(X

)

). Here X

and X

represent skeletons on the unit S embedded in R

n×k

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

198

Figure 4: Architecture of the non-Euclidean CNN based proposed method: a) Input 2D skeletal joints coordinates b) Mod-

elling of skeletal data on the Riemannian manifold c) Skeletal data mapping on tangent space d) Feature Extraction with CNN

e) Classiﬁcation.

4 PROPOSED METHOD

Overall architecture of the proposed methods are de-

picted in Fig.4 and Fig.5. Both models have simi-

lar global structure components with the difference

that in the ﬁrst architecture, feature extraction is per-

formed with CNN only, while the second architec-

ture is based on CNN-LSTM, taking into account se-

quence dependencies.

4.1 Non-Euclidean CNN based Model

In this section, we present a general framework al-

lowing to design CNN architectures on non-Euclidean

domains. For this purpose, we build a network struc-

ture where each input is an element of the unit sphere

S embedded in R

n×k

. As shown in Fig.5, this ar-

chitecture is composed of classical convolution layer,

pooling layer, and fully connected layer, subsequent

to a spherical modelling and an inverse exponen-

tial map layer to address the problem of the non-

Euclidean structure of the input data.

After spherical modelling of the skeleton se-

quence data, we use Eq.3 to map each skeleton X

from the sphere S to the tangent space T

(S) at the

skeleton X

. We choose a skeleton X

as a reference

and map all the other skeletons to the tangent space

of X

as shown in Fig.2. Since the tangent space is an

Euclidean space, the input is no more a trajectory on a

manifold. It lies however on an Euclidean Space and

hence can be fed into any regular CNN layer.

4.2 Non-Euclidean CNN-LSTM based

Model

Fig.5 depicts the non Euclidean CNN-LSTM pro-

posed method. This architecture is an extension of

the previous one, aiming to improve and consolidate

the obtained results using a better performing model

and tested on a larger dataset. As far as the overall

building components are concerned, the two archi-

tectures are basically identical: input skeletal joints

coordinates, spherical modelling, mapping to tangent

space, feature extraction and action recognition. The

only difference is the introduction of LSTM to cap-

ture global sequence dependencies of the input data.

CNN-LSTM (Donahue et al., 2017b) architecture in-

volves using CNN layers for feature extraction from

input data combined with LSTMs for sequential fea-

tures interpretation. In our approach, we implement

this architecture using two consecutive CNN layers

ahead of dropout and a max pooling layer. The whole

CNN model is wrapped in a "TimeDistributed" layer.

The extracted features are next ﬂattened and provided

to the LSTM model before a dense mapping to an ac-

tion is performed.

5 EXPERIMENTS

In this section, we introduce the testing datasets, the

evaluation protocols and the experimental results ob-

tained by our methods with comparison to state of the

art and baseline models.

5.1 Datasets

The ﬁrst proposed architecture has been tested on

Parkinson’s Vision-Based Pose Estimation Dataset(Li

et al., 2017). The second architecture has been tested

on NTU RGB+D dataset. In this part, we introduce

the two datasets on which we performed our experi-

ments.

Geometric Deep Learning on Skeleton Sequences for 2D/3D Action Recognition

199

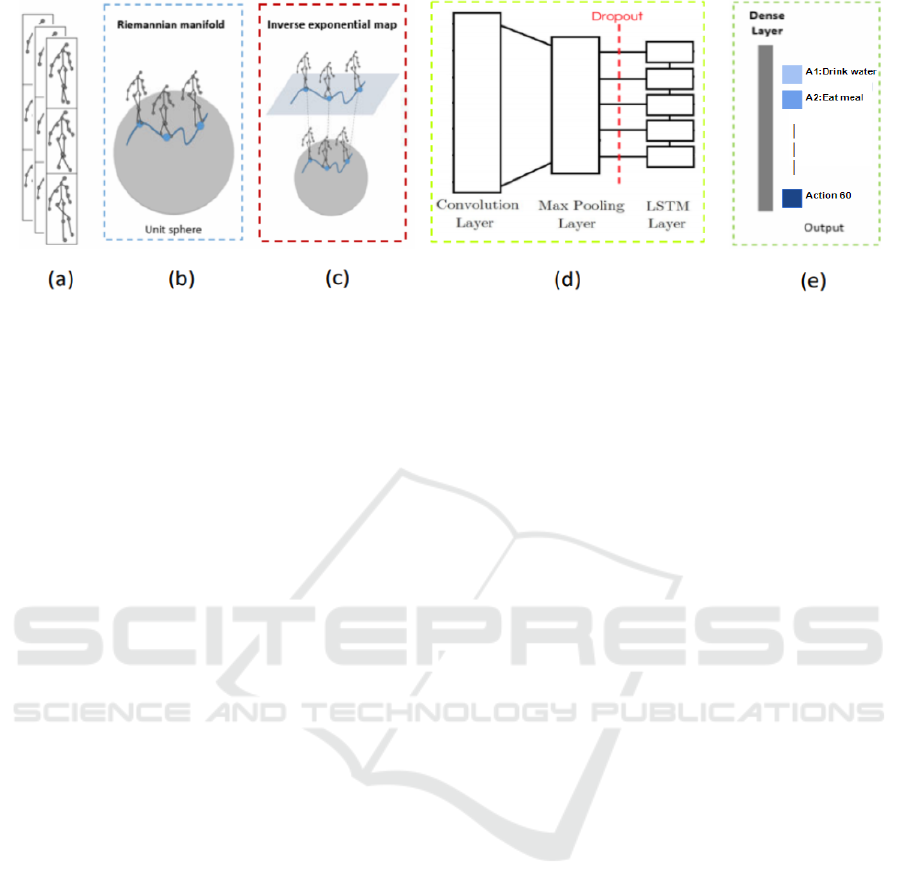
Figure 5: Architecture of the non-Euclidean CNN-LSTM based proposed method: a) Input 3D skeletal joints coordinates b)

Modelling of skeletal data on the Riemannian manifold c) Skeletal data mapping on tangent space d) Feature Extraction with

CNN combined with LSTM neurons to support sequence prediction e) Action recognition.

Parkinson’s Dataset. Parkinson’s Disease (PD) is

a progressive neurodegenerative disease (Nussbaum

and Ellis, 2003). It causes a decrease of dopamine

neurons in the brain and therefore a reduction of

dopamine levels that these neurons produce. The

“Parkinson’s Vision-Based Pose Estimation Dataset”

(Li et al., 2017) contains movement trajectories ex-

tracted from 526 videos of 9 participants (5 men and

4 women) with an average age of 64 years and di-

agnosed with idiopathic Parkinson’s diseases. Par-

ticipants completed a two hour Levodopa infusion

protocol followed by a two hour observation during

which they were asked to do various tasks like drink-

ing from a cup, communication tasks (describing an

image, talking with another person, recalling some-

thing and mental math ), leg agility(stomping of the

leg vertically with the maximum possible amount of

speed and amplitude) and toe-tapping. Communi-

cation and drinking from a cup tasks were used to

evaluate the Dyskinesia whereas leg agility and toe-

tapping were used to evaluate Parkinsonism. Videos

were recorded using a consumer grade video camera

and then a 2D human pose estimation was done us-

ing Convolutional Pose Machines (CPM) (Wei et al.,

2016). Since the CPM algorithm gives only an anno-

tation of the head which is not adapted for tracking

head turning movements, an object tracker algorithm

was used to estimate the face position. Finally, skele-

tons with 15 joints are obtained. Since this dataset has

action-sequences of variable lengths, we split every

sequence into 100-frame sequences, which makes, in

total, a number of 30859 sequences. After data sam-

pling, every sequence is composed of 100 skeletons

represented with 15 joints. Every joint has two coor-

dinates. The sequences used have therefore a dimen-

sion of 100 × 30 each: 100 indicates the number of

skeletons in a sequence and 30 denotes the number of

joint-coordinates of each skeleton. For the designed

CNN architecture, we transform those sequences into

a 1D signal by concatenating all the skeletons in a se-

quence.

NTU RGB+D Dataset. This dataset (Shahroudy

et al., 2016) is one of the largest skeleton-based hu-

man action datasets, consisting of more than 56000

sequences and 4 million frames. It covers 60 classes

of actions performed by 40 distinct subjects, in-

cluding both individual daily actions (e.g. read-

ing,clapping, writing,(sneezing, staggering, falling

down, etc) and interaction actions (e.g. hugging,

handshaking, pointing).

- Data Modalities: To collect this dataset, Mi-

crosoft Kinect v2 sensors were utilized. Four major

data modalities were collected: depth maps, 3D joint

information, RGB frames, and IR sequences. Joint

information, which is the data modality used in this

work, consists of 3-dimensional locations of 25 major

body joints for detected and tracked human bodies in

the scene. The conﬁguration of body joints is illus-

trated in Fig.6.

- Views: Three cameras were used at the same

time to capture three different horizontal views from

the same action. For each setup, the three cameras

were located at the same height but from three differ-

ent horizontal angles: −45°, 0°, +45°. Each subject

was asked to perform each action twice, once towards

the left camera and once towards the right camera.

Hence, two front views, one left side view, one right

side view, one left side 45 degrees view, and one right

side 45 degrees view are captured. The three cameras

are assigned consistent camera numbers. Camera 1

always observes the 45 degrees views, while camera

2 and 3 observe front and side views.

NTU RGB+D dataset is considered very challeng-

ing given the large view points, the intra-class non

uniformity and the variation of sequence length. To

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

200

Figure 6: Conﬁguration of 25 body joints in our dataset.

The labels of the joints are: 1-base of the spine 2-middle of

the spine 3-neck 4-head 5-left shoulder 6-left elbow 7-left

wrist 8- left hand 9-right shoulder 10-right elbow 11-right

wrist 12- right hand 13-left hip 14-left knee 15-left ankle

16-left foot 17- right hip 18-right knee 19-right ankle 20-

right foot 21-spine 22- tip of the left hand 23-left thumb

24-tip of the right hand 25- right thumb. (Shahroudy et al.,

2016).

overlap the complication of this variation, we con-

sider the same length of sequence for all the subjects,

which is the length of the shortest sequence.

5.2 Evaluation Protocols

As a means to standardize the assessment of the

results of our work, we deﬁne in this section, the

adopted evaluation setups for each of the two datasets.

5.2.1 Protocol on Pakinson’s dataset

Our goal is to classify sequences into three different

classes: normal, Parkinson’s disease (PD) or Parkin-

son’s disease with Levodopa-induced dyskinesia (PD

with LID). Given that only the communication se-

quences have ratings for PD and LID and that the

communication task had the best performance accord-

ing to (Li et al., 2017), we only use those sequences

for our multi-classiﬁcation problem. In all experi-

ments, we adopt the leave-one-out cross validation

protocol which means using, for N times (N is the

number of instances), the sequences of one person as

the validation set and the remaining sequences as the

training set.

5.2.2 Protocols for NTU RGB+D

To get standard evaluations for all the reported results

on this benchmark, we deﬁne precise criteria for two

types of action classiﬁcation evaluation, as described

in this section.

Cross-subject Protocol. For the cross-subject eval-

uation protocol, we split the 40 subjects into training

and testing sets, each is composed of 20 subjects. The

training and testing groups are made up of 40,320 and

16,560 samples, respectively. In our work, we use for

training, the subjects which IDs are among the follow-

ing list of values: 1, 2, 4, 5, 8, 9, 13, 14, 15,16, 17,

18, 19, 25, 27, 28, 31, 34, 35, 38. The 20 remaining

subjects are reserved for testing.

Cross-view Protocol. In cross-view protocol, we

select the samples from cameras 2 and 3 for train-

ing and the samples from camera 1 for testing. The

training set consists then of the front and two side

views of the actions,whilst testing set incorporates left

and right 45 degree views of the action performances.

For this assessment, the training and testing sets have

37,920 and 18,960 samples, respectively.

5.3 Results

This section summarizes the experimental results for

both non Euclidean architectures, each tested on a

separate benchmark dataset. The classiﬁcation accu-

racy reported in the results sections is in percentage.

5.3.1 Results of CNN Only based Architecture

Table.1 reports the resulting accuracy values of

2D skeletal sequences classiﬁcation on “Parkinson’s

Vision-Based Pose Estimation Dataset” for different

methods. In line with the state of the art approach (Li

et al., 2017) based on random forest tree algorithm,

we compare results achieved using only the commu-

nication sequences and adopting leave-one-out cross

validation. The Euclidean CNN architecture shown

Table 1: Results on Parkinson’s Vision-Based Pose Estima-

tion Dataset.

Method Leave-one-out

cross validation

Accuracy

State of the art (Li et al.,

2017)

71.4%

Euclidean CNN (Baseline) 68%

Non Euclidean CNN 72%

Geometric Deep Learning on Skeleton Sequences for 2D/3D Action Recognition

201

Figure 7: Architecture of the baseline Euclidean CNN based proposed method: a) Input 2D skeletal joints coordinates b)

Modelling of skeletal data on the Riemannian manifold c) Feature Extraction with CNN d) Classiﬁcation.

Figure 8: Architecture of the baseline Euclidean CNN-LSTM based proposed method: a) Input 3D skeletal joints coordinates

b) Modelling of skeletal data on the Riemannian manifold c) Feature Extraction with CNN combined with LSTM neurons to

support sequence prediction d) Action recognition.

in Fig.7 is used as a baseline method to point out the

contribution of inverse exponential map layer.

In Table.1, it can be seen that the non-Euclidean

CNN architecture, with 72% accuracy, outperforms

the baseline architecture which accuracy is 68%. This

improvement can highlight the importance of the

mapping of the skeletal data to tangent space. Com-

pared with the state of the art results, the performance

of our proposed method improved by 0.6%. This im-

proved performance is due to the fact that our method

takes into account the non-Euclidean structure of the

skeletal data.

5.3.2 Results of CNN-LSTM based Architecture

The results of action recognition on NTU RGB+D

dataset for the two evaluation protocols: cross-subject

and cross-view are reported in Table.2. The ﬁrst two

lines refer to the accuracy values obtained by the two

state of the art approaches(Shahroudy et al., 2016)

which deploy respectively, one layer and two layers

Table 2: Results on NTU RGB+D dataset using two evalu-

ation protocols: cross-subject and cross-view. The two ﬁrst

lines refer to the state of the art results(Shahroudy et al.,

2016).

Method Cross-

Subject

Accuracy

Cross-

View

Accuracy

1 Layer P-

LSTM(Shahroudy

et al., 2016)

62.05% 69.40%

2 Layer P-

LSTM(Shahroudy

et al., 2016)

62.93% 70.27%

Euclidean CNN-

LSTM (Baseline)

56.61% 62.32%

Non Euclidean

CNN-LSTM

61.45% 71.03%

of part-aware extension of the long short-term mem-

ory (P-LSTM). Similarly to CNN based architecture,

we used a baseline euclidean CNN-LSTM architec-

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

202

ture, as shown in Fig.7, for the purpose of pointing

out the contribution of inverse exponential map layer.

With reference to this architecture, the performance

of our proposed method improves with 4.84% using

cross-subject protocol and with 8.71% using cross-

view protocol.

Table.2 shows also that our non-Euclidean CNN-

LSTM based model achieves competitive result to the

state of the art (Shahroudy et al., 2016) in terms of

cross-subject accuracy. In fact, our model reaches

61.45% accuracy versus 62.93% in (Shahroudy et al.,

2016). For cross-view accuracy, our method outper-

forms the state of the art with 0.76% increase.

6 CONCLUSIONS

In this paper, we have proposed, for action recogni-

tion, to map skeleton sequences from the Riemannian

manifold to linear spaces, previous to feature extrac-

tion and learning layers. We proposed a ﬁrst non-

Euclidean architecture based on CNNs to extract a

compact representation of each skeletons frame.We

then propose a second non-Euclidean temporally-

aware architecture based on CNN-LSTM networks.

We have tested the proposed approaches using two

datasets, namely Parkinson’s Vision-Based Pose Es-

timation dataset and NTU RGB+D dataset. Exper-

imental results have shown the effectiveness of the

proposed architectures compared to state of the art

models. However, for future work, we are working

1) on integrating our method with state of the art ar-

chitectures to consolidate its performance and 2) on

improving the geometry awareness of deep learning

architecture for action recognition by modifying the

inner operations of the CNN network.

ACKNOWLEDGEMENTS

This work has been jointly supported by Talan In-

novation Factory, Talan Tunisia, Talan Group. Talan

is a French digital transformation Consulting Group,

based in Paris, with ofﬁces in London, Geneva,

Madrid, Luxembourg, New York, Chicago, Montreal,

Toronto,Tunis, Rabat and Singapore. Talan Innova-

tion Factory provides expertise relative to disruptive

technologies such as Blockchain, Artiﬁcial Intelli-

gence, Data Science and Internet of Things. In the

frame of an academic-industry collaboration, Talan

has been persistently contributing to this work by pro-

viding Hardware resources (Deep learning platform),

mentoring and ﬁnancial support.

REFERENCES

Baccouche, M., Mamalet, F., Wolf, C., Garcia, C., and

Baskurt, A. (2011). Sequential deep learning for hu-

man action recognition. In Human Behavior Un-

derstanding - Second International Workshop, HBU

2011, Amsterdam, The Netherlands, November 16,

2011. Proceedings, pages 29–39.

Bronstein, M. M., Bruna, J., LeCun, Y., Szlam, A., and

Vandergheynst, P. (2017). Geometric deep learning:

Going beyond euclidean data. IEEE Signal Process.

Mag., 34(4):18–42.

Ciresan, D. C., Meier, U., and Schmidhuber, J. (2012).

Multi-column deep neural networks for image classiﬁ-

cation. In 2012 IEEE Conference on Computer Vision

and Pattern Recognition, Providence, RI, USA, June

16-21, 2012, pages 3642–3649.

Cohen, T. S., Geiger, M., Koehler, J., and Welling, M.

(2018). Spherical cnns.

Donahue, J., Hendricks, L. A., Rohrbach, M., Venugopalan,

S., Guadarrama, S., Saenko, K., and Darrell, T.

(2017a). Long-term recurrent convolutional networks

for visual recognition and description. IEEE Trans.

Pattern Anal. Mach. Intell., 39(4):677–691.

Donahue, J., Hendricks, L. A., Rohrbach, M., Venugopalan,

S., Guadarrama, S., Saenko, K., and Darrell, T.

(2017b). Long-term recurrent convolutional networks

for visual recognition and description. IEEE Trans.

Pattern Anal. Mach. Intell., 39(4):677–691.

Du, Y., Wang, W., and Wang, L. (2015). Hierarchical recur-

rent neural network for skeleton based action recog-

nition. In IEEE Conference on Computer Vision and

Pattern Recognition, CVPR 2015, Boston, MA, USA,

June 7-12, 2015, pages 1110–1118.

Graves, A. (2012). Supervised Sequence Labelling with Re-

current Neural Networks, volume 385 of Studies in

Computational Intelligence. Springer.

Graves, A., Mohamed, A., and Hinton, G. E. (2013).

Speech recognition with deep recurrent neural net-

works. In IEEE International Conference on Acous-

tics, Speech and Signal Processing, ICASSP 2013,

Vancouver, BC, Canada, May 26-31, 2013, pages

6645–6649.

Ke, Q., An, S., Bennamoun, M., Sohel, F. A., and Boussaïd,

F. (2017). Skeletonnet: Mining deep part features for

3-d action recognition. IEEE Signal Process. Lett.,

24(6):731–735.

Ke, Q. and Li, Y. (2014). Is rotation a nuisance in shape

recognition? In 2014 IEEE Conference on Computer

Vision and Pattern Recognition, CVPR 2014, Colum-

bus, OH, USA, June 23-28, 2014, pages 4146–4153.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Advances in Neural Information Pro-

cessing Systems 25: 26th Annual Conference on Neu-

ral Information Processing Systems 2012. Proceed-

ings of a meeting held December 3-6, 2012, Lake

Tahoe, Nevada, United States, pages 1106–1114.

LeCun, Y. and Bengio, Y. (1998). The handbook of brain

theory and neural networks. chapter Convolutional

Geometric Deep Learning on Skeleton Sequences for 2D/3D Action Recognition

203

Networks for Images, Speech, and Time Series, pages

255–258. MIT Press, Cambridge, MA, USA.

Lefebvre, G., Berlemont, S., Mamalet, F., and Garcia, C.

(2013). BLSTM-RNN based 3d gesture classiﬁcation.

In Artiﬁcial Neural Networks and Machine Learning

- ICANN 2013 - 23rd International Conference on Ar-

tiﬁcial Neural Networks, Soﬁa, Bulgaria, September

10-13, 2013. Proceedings, pages 381–388.

Li, M. H., Mestre, T. A., Fox, S. H., and Taati, B.

(2017). Vision-based assessment of parkinsonism and

levodopa-induced dyskinesia with deep learning pose

estimation. CoRR, abs/1707.09416.

Liu, J., Shahroudy, A., Xu, D., and Wang, G. (2016).

Spatio-temporal LSTM with trust gates for 3d human

action recognition. In Computer Vision - ECCV 2016

- 14th European Conference, Amsterdam, The Nether-

lands, October 11-14, 2016, Proceedings, Part III,

pages 816–833.

Masci, J., Boscaini, D., Bronstein, M. M., and Van-

dergheynst, P. (2015). Geodesic convolutional neu-

ral networks on riemannian manifolds. In 2015 IEEE

International Conference on Computer Vision Work-

shop, ICCV Workshops 2015, Santiago, Chile, De-

cember 7-13, 2015, pages 832–840.

Ng, J. Y., Hausknecht, M. J., Vijayanarasimhan, S., Vinyals,

O., Monga, R., and Toderici, G. (2015). Beyond

short snippets: Deep networks for video classiﬁcation.

In IEEE Conference on Computer Vision and Pattern

Recognition, CVPR 2015, Boston, MA, USA, June 7-

12, 2015, pages 4694–4702.

Nussbaum, R. L. and Ellis, C. E. (2003). Alzheimer’s dis-

ease and parkinson’s disease. New england journal of

medicine, 348(14):1356–1364.

Shahroudy, A., Liu, J., Ng, T., and Wang, G. (2016). NTU

RGB+D: A large scale dataset for 3d human activity

analysis. In 2016 IEEE Conference on Computer Vi-

sion and Pattern Recognition, CVPR 2016, Las Vegas,

NV, USA, June 27-30, 2016, pages 1010–1019.

Srivastava, N., Mansimov, E., and Salakhutdinov, R.

(2015). Unsupervised learning of video representa-

tions using lstms. In Proceedings of the 32nd Interna-

tional Conference on Machine Learning, ICML 2015,

Lille, France, 6-11 July 2015, pages 843–852.

Veeriah, V., Zhuang, N., and Qi, G. (2015). Differential

recurrent neural networks for action recognition. In

2015 IEEE International Conference on Computer Vi-

sion, ICCV 2015, Santiago, Chile, December 7-13,

2015, pages 4041–4049.

Vemulapalli, R., Arrate, F., and Chellappa, R. (2014). Hu-

man action recognition by representing 3d skeletons

as points in a lie group. In 2014 IEEE Conference

on Computer Vision and Pattern Recognition, CVPR

2014, Columbus, OH, USA, June 23-28, 2014, pages

588–595.

Wang, L., Xiong, Y., Wang, Z., Qiao, Y., Lin, D., Tang, X.,

and Gool, L. V. (2016). Temporal segment networks:

Towards good practices for deep action recognition. In

Computer Vision - ECCV 2016 - 14th European Con-

ference, Amsterdam, The Netherlands, October 11-14,

2016, Proceedings, Part VIII, pages 20–36.

Wei, S., Ramakrishna, V., Kanade, T., and Sheikh, Y.

(2016). Convolutional pose machines. In 2016 IEEE

Conference on Computer Vision and Pattern Recog-

nition, CVPR 2016, Las Vegas, NV, USA, June 27-30,

2016, pages 4724–4732.

Xiong, Y., Zhu, K., Lin, D., and Tang, X. (2015). Recog-

nize complex events from static images by fusing deep

channels. In IEEE Conference on Computer Vision

and Pattern Recognition, CVPR 2015, Boston, MA,

USA, June 7-12, 2015, pages 1600–1609.

Zhu, W., Lan, C., Xing, J., Zeng, W., Li, Y., Shen, L.,

and Xie, X. (2016). Co-occurrence feature learning

for skeleton based action recognition using regular-

ized deep LSTM networks. In Proceedings of the

Thirtieth AAAI Conference on Artiﬁcial Intelligence,

February 12-17, 2016, Phoenix, Arizona, USA, pages

3697–3704.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

204