Predicting Function Related Pain Outcomes using Comorbidity and Age

Dependent Model

Aleksandar Jeremic

, Dejan Nikolic

2,3

, Milena Kostadinovic

and Milena Santric Milicevic

2,5

Department of Electrical and Computer Engineering, McMaster University, Hamilton, ON, Canada

Faculty of Medicine, University of Belgrade, Belgrade, Serbia

Physical Medicine and Rehabilitation Department, University Children’s Hospital, Belgrade, Serbia

Clinical Center of Serbia, Belgrade, Serbia

Institute of Social Medicine, Faculty of Medicine, University of Belgrade, Belgrade, Serbia

Keywords:

Pain Prediction, Logistic Regression.

Abstract:

Effective pain management can signiﬁcantly improve quality of life and outcomes for various types of patients

(e.g. elderly, adult, young). In order to improve our understanding of patients’ response to pain we need to

develop adequate signal processing techniques that would enable us to understand underlying interdependen-

cies. To this purpose in this paper we develop several different algorithms that can predict function related

pain outcomes using a large database obtained as a part of the national health survey. As a part of the survey

the respondents provided detailed information about general health care state, acute and chronic problems as

well as personal perception of pain associated with performing two simple talks: walking on the ﬂat surface

and walking upstairs. We model the correspondent responses using parametric and non-parametric models and

use health indicators (both chronic and acute) as explanatory variables. For the binomial model we propose

parametric age dependent model and then compare its performance to the performance of the multinomial and

histogram models.

1 INTRODUCTION

The presence of pain is associated with various de-

grees of disability, leading to an impaired quality

of life(McCarberg, 2008). It affects both mental

and physical aspects of the quality of life (Carma-

ciu, 2007), leading to the deconditioning, gait ab-

normalities, accidents and cognitive decline (Kaye,

2010). In a sample of elderly persons in aged care

rehabilitation units only chronic physical pain, and

not the intensity of pain, has an independent associa-

tion with a decrease in performance (Pereira, 2014)],

while in a sample of older adults attending primary

health care centers, pain intensity is associated with

both performance-based disability and self-reported

disability (Silva, 2014). The impact of pain in older

individuals may limit functioning due to the fact that

activity may exacerbate the pain or the elderly are

afraid of repeated injuries and falling (Molton, 2014).

In (McCarberg, 2008), above 80% of older veterans

with chronic pain reported that the pain has an inﬂu-

ence on one or more higher order physical activities,

while 3% reported the inﬂuence of pain on basic ac-

tivities.

It is of great importance to timely assess the

proper management of pain, since it has numerous

consequences namely in aged population, with dys-

functions in different degrees of functional, social and

cognitive dimensions (Schoﬁeld, 2007), deteriorating

individual’s overall health, with the increase of the ne-

cessity for institutionalization, and thus increasing the

health care costs. Therefore, the complexity of pain

suggests an interdisciplinary approach both in diag-

nosis and treatment.

The survey outcomes are often modelled using the

logistic (logit) models which are commonly used for

statistical modelling of survey data consisting of de-

pendent data (outcomes of the survey) and explana-

tory data. We propose age dependent logit model in

which the regression coefﬁcients are modelled as age

dependent and apply this model to the third national

study data set of Serbia. We then evaluate the perfor-

mance of the proposed model by using a half of the

data for training the model and using the other half as

testing. We compare the performance of the proposed

model to the empirical model based on the multivari-

Jeremic, A., Nikolic, D., Kostadinovic, M. and Milicevic, M.

Predicting Function Related Pain Outcomes using Comorbidity and Age Dependent Model.

DOI: 10.5220/0009167403190323

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 4: BIOSIGNALS, pages 319-323

ISBN: 978-989-758-398-8; ISSN: 2184-4305

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

319

ate histogram estimation of the conditional probabili-

ties.

2 SIGNAL MODEL

2.1 Data Set

The performed investigation included participants

from the third national study in Serbia “National

Health Status Survey in 2013” that was performed

by the Ministry of Health of the Republic of Ser-

bia (Silva, 2014). It followed the methodology and

instruments of the European Health Interview Sur-

vey wave 2 (EHIS wave 2) (Silva, 2014), (Molton,

2014). For the purpose of this study, chronic dis-

eases and conditions were grouped in seven groups:

cardiovascular diseases (myocardial infarct, stroke

and coronary artery disease); pulmonary disease

(chronic bronchitis and asthma); diseases of muscu-

loskeletal system (lower back disorder, neck disor-

der, arthrosis); diabetes; hyperlipidemia; hyperten-

sion and other chronic diseases (depression, cancer,

urinary incontinence, kidney problems and liver cir-

rhosis) (Schoﬁeld, 2007). We used SF-36 version 2.0

(SF-36v2) in evaluation of pain presence and its de-

gree (Hawker, 2019). We classiﬁed pain in four cate-

gories (none; mild; moderate and severe) (Schoﬁeld,

2007). The walking difﬁculty was assessed by dif-

ﬁculty in walking up or down 12 steps. The asked

question was: Do you have difﬁculty walking up or

down 12 steps?; and proposed answers were: no dif-

ﬁculty, some difﬁculty, a lot of difﬁculty and cannot

do at all/unable to do ((Molton, 2014),(Kostadinovic,

2019)). According to the age of participants they were

grouped into three age groups (65–74 years; 75–84

years and older than 85 years) (Radosavljevic, 2013).

2.2 Age Dependent Binary Logit Model

First we deﬁne the outcome variables y

as pain eval-

uation variables and propose to model them using sur-

vey responses related to chronic pain questions as ex-

planatory variables X

. Then we model the outcome

probabilities using the odds ratio (Engel, 1988)

log



1− p



∑

j=0

(θ)x

(1)

where p

= Pr{y

= 1} and the unknown regression

coefﬁcients are modelled using age dependent poly-

nomial basis functions

(θ) =

∑

l=1

i,l,l

l−1

(2)

and α

i, j,l

are the unknown polynomial coefﬁcients

that will be estimated.

Then the unknown parameters are obtained by ﬁt-

ting the above model with the empirical counts using

by minimizing the mean square error i.e. using a least

squares estimates. The probabilities of pain outcomes

are then estimated as

ˆp

|(x

, . . . , x

) =

∑

j=0

(

θ)x

1+ e

∑

j=0

(

θ)x

(3)

2.3 Age Independent Multinomial Logit

Model

Note that the functional pain outcomes in the afore-

mentioned study include measurements of respon-

dents’ pain for two tasks: walking on the ﬂat surface

and walking upstairs. These outcomes are most likely

correlated i.e. the respondents experiencing pain

when walking on a ﬂat surface are expected to ex-

perience even higher pain when walking upstairs. In

order to account for possible correlation we propose

to model the join probability density (mass) function

by combining the pain outcomes into a single vector

consisting of two binary scalar components. There-

fore our lumped vector y has four possible states. Al-

though one of the states is not very likely ( ﬂat walk

pain 0, upstairs walk pain 1) we keep it for the com-

pleteness of the model as well as a semi-validation as

the probability of that state is expected to be low.

Then the proposed logit model is given by (Dar-

roch and Ratcliff, 1972)

log





= β

x+ z

(4)

log





= β

x+ z

(5)

log





= β

x+ z

(6)

= 1− p

− p

(7)

where probability of outcome (0,0) was chosen as

pivot variable and β

and z

are unknown model co-

efﬁcients. Similarly to the previous case using empir-

ical estimates of probability mass function based on

the event frequency we estimate the unknown coef-

ﬁcients using the least squares ﬁt. Using these esti-

mates we estimate the probabilities as

ˆp

1+ β

x+ z

+ β

x+ z

11+β

x+z

(8)

ˆp

= ˆp

x+ ˆz

(9)

ˆp

= ˆp

x+ ˆz

(10)

ˆp

= ˆp

x+ ˆz

(11)

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

320

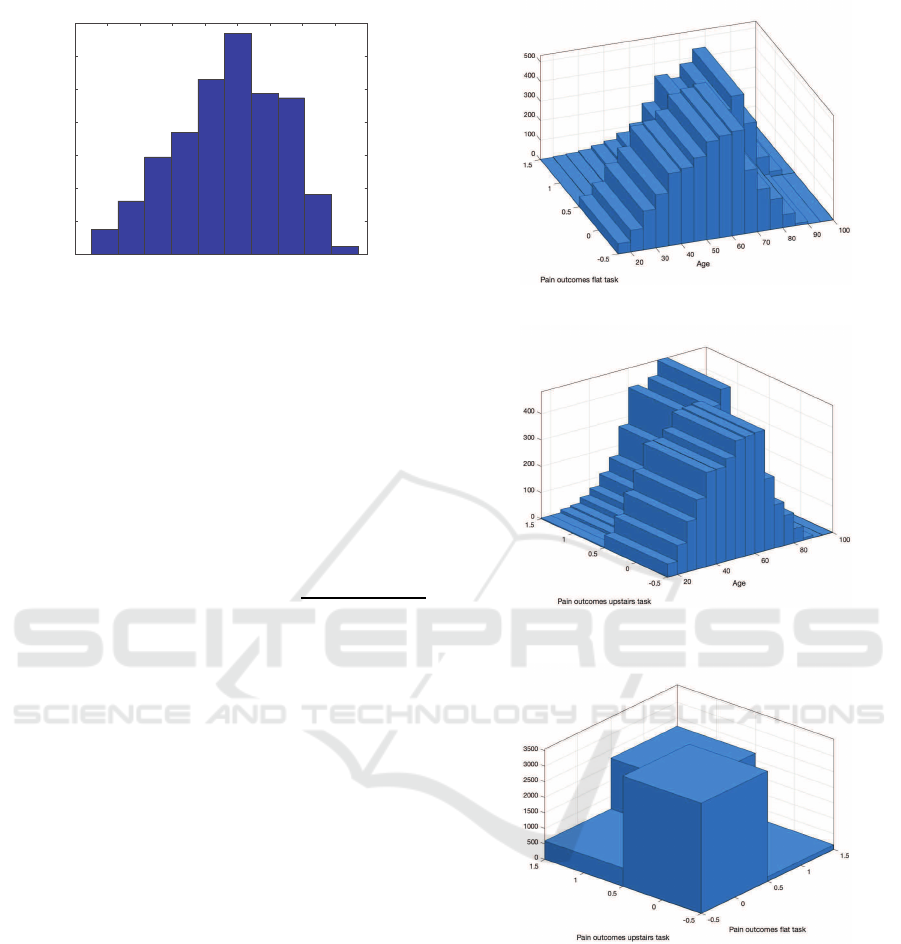
10 20 30 40 50 60 70 80 90 100

200

400

600

800

1000

1200

1400

Figure 1: Age Histogram.

2.4 Empirical Histogram

Finally, for comparison purposes we propose to esti-

mate the pain outcomes using so called ”naive” esti-

mator in which conditional probabilities are obtained

from the corresponding frequency counts. Namely,

let n

, . . . , x

be the number of instances for which

= i and y

= j when x = [x

, . . . , x

]. Then we esti-

mate conditional probability

ˆp(y

= i, y

= j|X

= x

, . . . X

= x

) =

, . . . , x

∑

i, j

, . . . , x

(12)

Note that each of the explanatory variables has

one of 4 possible states and hence our explanatory

vector has maximum of 64 possible values. In our

data set we have all the possible combinations and

hence can use the aforementioned empirical estima-

tor without any adjustments. In general, it is possible

that some of the possible combinations will not ap-

pear in the training data set. In these cases, it is pos-

sible to perform estimation of conditional probabili-

ties using a basis functions approach similar to kernel

smoothing of the probability density function estima-

tion. Namely the pmf estimates have conﬁdence inter-

vals and missing data could be interpolated based on

the estimates and conﬁdence intervals of the nearest

neighbours.

3 RESULTS

In order to evaluate the performance we divide the

available data set in two parts. We use the ﬁrst part for

estimating the unknown coefﬁcients in the parametric

models and conditional pmfs in the non-parametric

model. Then we count the number of incorrect classi-

ﬁcations i.e. for each respondent we calculate model

based prediction of the most likely pain outcomes and

Figure 2: Histogram of age and pain outcome - ﬂat task.

Figure 3: Histogram of age and pain outcome - upstairs

task.

Figure 4: Histogram of pain outcomes.

compare it to the actual outcomes. Using these counts

we calculate so called probabilities of anomalies ε

for age dependent model and ε

ij,i

′

for multinomial

and empirical histogram models where ij refers to the

binomial vector estimate and i

′

to the observed vec-

tor. In order to make results comparable, we calculate

the corresponding overall probability of error.

In Figures 2-4 we illustrate the statistical proper-

ties of the data using the histograms. As expected the

Figure 4 illustrates correlation between the pain out-

comes. We removed all the patients who failed to at

least one of the questions which resulted in the ﬁnal

Predicting Function Related Pain Outcomes using Comorbidity and Age Dependent Model

321

Table 1: Goodness of ﬁt - parametric models.

Binomial Multinomial model

Group 1 0.141 0.163

Group 2 0.121 0.134

Group 3 0.101 0.987

Group 4 0.098 0.081

Table 2: Probabilities of error binomial model.

ﬂat task upstairs task

Group 1 0.101 0.143

Group 2 0.087 0.076

Group 3 0.075 0.081

Group 4 0.072 0.061

Table 3: Probabilities of error multinomial model.

ﬂat task upstairs task

Group 1 0.121 0.152

Group 2 0.101 0.92

Group 3 0.082 0.115

Group 4 0.088 0.072

Table 4: Probabilities of error histogram model.

ﬂat task upstairs task

Group 1 0.132 0.141

Group 2 0.085 0.094

Group 3 0.099 0.101

Group 4 0.102 0.098

number of respondents being equal to 6524.

In Table 1 we illustrate the goodness-of-ﬁt for two

parametric models and all age groups. As it can be

seen the parametric models seem to perform better

for older patients. In Tables 2 - 4 we illustrate the

overall probabilities of errors for all of the proposed

models. The performance of the proposed models in-

creases with the age of respondents and as expected

this improvementis best for the age dependent model.

4 CONCLUSIONS

In this paper we proposed several models that can be

used to predict pain outcomes using health indicators

and demonstrated their performance using a real data

set obtained from the national health survey. From the

academic standpoint the proposed models can provide

additional insight into intricate multidimensional de-

pendencies between pain and health indicators. From

the clinical standpoint it could enable practicians to

attempt to manage pain effectively by focusing on the

parameters of interest. Therefore, further studies are

advised on multidimensional levels of pain and its ef-

fects on physical functioning in patients with param-

eters that could have effects not only on pain severity

degree but disability degree as well. Furthermore, ad-

equate detection of potential patients with this model

will effect decision making policies for diagnosis and

treatment of both components of disability (pain and

physical functioning). An effort should be placed on

deﬁning similarity measures that would enable us to

create homogeneous groups of patients and then eval-

uate our ability to predict the pain within those ho-

mogenous groups. To this purpose we also plan to

develop fully multinomial models including both ex-

planatory and outcome variables. Since perception of

pain is rather subjective, this model would enable us

to identify parameters of interest and thus design sur-

veys that will be focused on particular groups of pa-

tients. Ultimately we expect that it would create mod-

els that would enable us to study personal biases and

potentially remove them from outcomes thus enabling

health care system to deliver optimized pain manage-

ment to the general population.

In addition we plan to compare our results to the

performance of machine learning techniques such as

support vector machines (SVM) and random forrest

(RF). Since the accuracy of these techniques depend

on availability of large data sets we expect to be able

to obtain a good benchmark. Furthermore, since the

number of respondents is large we expect to be able to

deﬁne a deep learning model by by using more than

half of the data for the neural network training. We

plan to compare the performance as a function of the

training set size.

REFERENCES

Carmaciu, C. (2007). Health risk appraisal in older people

3: Prevalence, impact and context of pain and their

implications for gps. Br. J. Gen. Pract, 1(57):630–

635.

Darroch, J. and Ratcliff, D. (1972). Generalized iterative

scaling for log-linear models. The Annals of Mathe-

matical Statistics., 43(5):1470–1480.

Engel, J. (1988). polytomous logistic regression. Statistica

Neerlandica, 42(1):233–252.

Hawker, G. (2019). Measures of adult pain: Visual analog

scale for pain (vas pain), numeric rating scale for pain

(nrs pain), mcgill pain questionnaire (mpq), short-

form mcgill pain questionnaire (sf-mpq), chronic pain

grade scale (cpgs), short form-36 bodily pain scale (sf-

36 bps), and measure of intermittent and constant os-

teoarthritis pain (icoap). Arthritis Care R, 9(2):47.

Kaye, A. (2010). Pain management in the elderly popula-

tion: A review. Ochsner J., 10:179–187.

Kostadinovic, M. (2019). A national health survey. Int J

Environ Res Public Health, 19(1):37.

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

322

McCarberg, B. (2008). The impact of pain on quality of

life and the unmet needs of pain management: Results

from pain sufferers and physicians participating in an

internet survey. Am. J. Ther, 15(1):213–220.

Molton, I. (2014). Overview of persistent pain in older

adults. Am. Psychol., 69:197–207.

Pereira, M. (2014). Self-reported chronic pain is associated

with physical performance in older people leaving

aged care rehabilitation. Clin. Interv. Aging, 9:259–

265.

Radosavljevic, N. (2013). Estimation of functional recovery

in patients after hip frac-ture by berg balance scale re-

garding the sex, age and comorbidity of participants.

Geriatr Gerontol Int, 13(1):365–371.

Schoﬁeld, P. (2007). Pain in older adults: Epidemiology,

impact and barriers to management. Rev. Pain, 1:12–

14.

Silva, A. (2014). Pain intensity is associated with both

performance-based disability and self-reported dis-

ability in a sample of older adults attending primary

health care centers. Disabil. Health J., 7:457–465.

Predicting Function Related Pain Outcomes using Comorbidity and Age Dependent Model

323