Visualizing Learning Space in Neural Network Hidden Layers

Gabriel D. Cantareira

, Fernando V. Paulovich

and Elham Etemad

Universidade de S

ao Paulo, Brazil

Dalhousie University, Canada

Keywords:

Machine Learning, Neural Network Visualization, Deep Neural Networks.

Abstract:

Analyzing and understanding how abstract representations of data are formed inside deep neural networks is a

complex task. Among the different methods that have been developed to tackle this problem, multidimensional

projection techniques have attained positive results in displaying the relationships between data instances,

network layers or class features. However, these techniques are often static and lack a way to properly keep a

stable space between observations and properly convey ﬂow in such space. In this paper, we employ different

dimensionality reduction techniques to create a visual space where the ﬂow of information inside hidden layers

can come to light. We discuss the application of each used tool and provide experiments that show how they

can be combined to highlight new information about neural network optimization processes.

1 INTRODUCTION

Given their ability to abstract high-level patterns and

model data beyond most heuristics (LeCun et al.,

2015), deep neural networks (DNNs) are currently

among the state-of-the-art techniques for the analysis

of large-scale, complex datasets. Despite the preva-

lence of DNNs in different domains, such as natu-

ral language processing, face and speech recognition,

and generation of artiﬁcial data, its success heavily

depends on the right choice of hyperparameters and

architecture.

In recent years, visualization strategies have be-

come increasingly popular in the research commu-

nity to help analysts interpret the results and support

the improvement of DNNs. One of the most popular

visualization strategies, multidimensional projection

techniques (Nonato and Aupetit, 2018) have report-

edly attained relative success in helping users to ex-

plore and explain what happens inside DNNs (Rauber

et al., 2017; Mahendran and Vedaldi, 2015; Srivastava

et al., 2014). These techniques aim to generate lower-

dimensional visual representations of the data capable

of preserving data structure, such as relationships be-

tween data instances or the presence of clusters. How-

ever, the currently available techniques are somewhat

limited when exploring sequential processes inside

the network, such as the state of hidden layers during

training or the shaping of high-level representations

as data ﬂows through different layers of a network.

In this paper, we present a novel approach to visu-

alize the hidden structure of DNNs that aids in under-

standing the generated abstract high-level represen-

tations and how they are formed during the training

process. In our approach, we employ different tech-

niques to project data extracted from various states

of a neural network and estimate a common space

that can show how these projections relate to one an-

other by computing a vector ﬁeld from the projected

data. Based on these methods, we show possibili-

ties in identifying ﬂow and tracking down meaningful

changes in the neural network as abstract representa-

tions of data are formed.

Our main contributions are:

• A projection-based visual representation better

suited to represent sequential aspects of DNNs,

eliminating movement clutter while keeping dis-

tances meaningful;

• A visual transition space between two or more

sequential projections that is not restricted by a

varying number of dimensions of the input data.

2 RELATED WORK

Artiﬁcial neural networks (ANNs) are structures com-

posed of groups of simple and complex cells. Sim-

ple cells are responsible for extracting basic features,

while complex ones combine local features producing

110

Cantareira, G., Paulovich, F. and Etemad, E.

Visualizing Learning Space in Neural Network Hidden Layers.

DOI: 10.5220/0009168901100121

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 3: IVAPP, pages

110-121

ISBN: 978-989-758-402-2; ISSN: 2184-4321

abstract representations (Scherer et al., 2010). This

structure hierarchically manipulates data through lay-

ers (complex cells), each one using a set of process-

ing units or neurons (simple cells) to extract local

features. In classiﬁcation tasks, each neuron divides

input data space using a linear function (i.e., hyper-

plane), which is positioned to obtain the best sepa-

ration as possible between labels of different classes.

Thus, the connections among processing units are re-

sponsible for combining the half-spaces built up by

those linear functions to produce nonlinear separabil-

ity of data spaces (LeCun et al., 2015). Deep neural

networks (DNNs) are artiﬁcial neural network mod-

els that contain a large number of layers between in-

put and output, generating more complex representa-

tions. Such networks are called convolutional neural

networks (CNNs) when convolutional ﬁlters are em-

ployed.

In the past few years, the use of visualization tools

and techniques to support the understanding of neu-

ral network models has become more proliﬁc, with

many different approaches focusing on exploring and

explaining different aspects of DNN training, topol-

ogy, and parametrization (Hohman et al., 2018). As

deep models grow more complex and sophisticated,

understanding what happens to data inside these sys-

tems is quickly becoming key to improving their efﬁ-

ciency and designing new solutions.

When exploring layers of a DNN, a common

source of data is the hidden layer activations: the out-

put value of each neuron of a given layer when sub-

jected to a data instance (input). Many DNN visual-

ization approaches are focused on understanding the

high-level abstract representations that are formed in

hidden layers. This is often attained by transferring

the activations of hidden layer neurons back to the

feature space, as deﬁned by the Deconvnet (Zeiler and

Fergus, 2014) and exempliﬁed by applications such as

the Deep Dream (Szegedy et al., 2015). Commonly

associated with CNNs, techniques based on this ap-

proach often try to explain and represent which fea-

ture values in a data object generate activations in

certain parts of hidden layers. The Deconvnet is capa-

ble of reconstructing input data (images) at each CNN

layer to show the features extracted by ﬁlters, support-

ing the detection of incidental problems based on user

inspections.

Other techniques focus on identifying content that

activates ﬁlters and hidden layers. Simonyan et

al. (Simonyan et al., 2013) developed two visualiza-

tion tools based on Deconvnet to support image seg-

mentation, allowing feature inspection and summa-

rization of produced features. Zintgraf et al. (Zintgraf

et al., 2017) introduced a feature-based visualization

tool to assist in determining the impact of ﬁlter size

on classiﬁcation tasks and identifying how the deci-

sion process is conducted. Erhan et al. (Erhan et al.,

2009) proposed a strategy to identify features detected

by ﬁlters after their activation functions, allowing the

visual inspection of the impact of network initializa-

tion as well as if features are humanly understandable.

Similarly, Mahendran et al. (Mahendran and Vedaldi,

2016) presented a triple visualization analysis method

to inspect images. Babiker et al. (Babiker and Goebel,

2017) also proposed a visual tool to support the iden-

tiﬁcation of unnecessary features ﬁltered in the layers.

Liu et al. (Liu et al., 2017) present a system capable

of showing a CNN as an acyclic graph with images

describing each ﬁlter.

Other methods aim to explore the effects of differ-

ent parameter conﬁgurations in training, such as reg-

ularization terms or optimization constraints (Srivas-

tava et al., 2014). These can also be connected to dif-

ferent results in layer activations or classiﬁcation out-

comes. Some techniques are designed to help evalu-

ate the effectiveness of speciﬁc network architectures,

estimating what kind of abstraction can be learned

in each section, such as the approach described by

Yosinki et al. (Yosinski et al., 2015).

The research previously described is focused on

identifying and explaining what representations are

generated. However, it is also important to under-

stand how those representations are formed, regard-

ing both the training process and the ﬂow of infor-

mation inside a network. Comprehending these as-

pects can lead to improvements in network archi-

tecture and the training process itself. The Deep-

Eyes framework, developed by Pezzotti et al.(Pezzotti

et al., 2018), provides an overview of DNNs, being

capable of identifying when a network architecture

requires more or fewer ﬁlters or layers, employing

scatterplots and heatmaps to show ﬁlter activations

and allowing the visual analysis of the feature space.

Kahng et al. (Kahng et al., 2018) introduce a method

to explore the features produced by CNNs project-

ing activation distances and presenting a neuron ac-

tivation heatmap for speciﬁc data instances. These

techniques are, however, not designed for projecting

multiple transition states and their projection methods

require complex parametrization to show the desired

information.

Multidimensional projections (or dimensionality

reduction techniques) (Nonato and Aupetit, 2018) are

popular tools to aid the study of how abstract rep-

resentations are generated inside ANNs. Speciﬁc

projection techniques, such as the UMAP (McInnes

et al., 2018), were developed particularly with ma-

chine learning applications in mind. While dimen-

Visualizing Learning Space in Neural Network Hidden Layers

111

sionality reduction techniques are generally used in

ANN studies to illustrate model efﬁcacy (Donahue

et al., 2014; Srivastava et al., 2014; Hamel and Eck,

2010; Mohamed et al., 2012; Mahendran and Vedaldi,

2015), Rauber et Al (Rauber et al., 2017) showed their

potential on providing valuable visual information on

DNNs to improve models and observe the evolution

of learned representations. Projections were used to

reveal hidden layer activations for test data before and

after training, highlighting the effects of training, the

formation of clusters, confusion zones, as well as the

neurons themselves, using individual activations as

attributes. Despite offering insights on how the net-

work behaves before and after training, the visual rep-

resentation presented by the authors for the evolution

of representations inside the network or the effects

of training between epochs displays a great deal of

clutter; when analyzing a large number of transition

states, information such as the relationships between

classes or variations that occur only during intermedi-

ate states may become difﬁcult to infer. Additionally,

the method used to ensure that all projections share

a similar 2D space is prone to problems in alignment

and performance. In this paper, we propose a visual-

ization scheme that employs a ﬂow-based approach to

offer a representation better suited to show transition

stated and evolving data in DNNs. We also brieﬂy

address certain pitfalls encountered when visualizing

neuron activation data using standard projection tech-

niques, such as the t-SNE (Van Der Maaten and Hin-

ton, 2008), and discuss why these pitfalls are relevant

to our application.

3 VISUALIZING LEARNING

SPACE

Our visual representation is based on gathering layer

activation data from a sequence of ANN outputs, then

projecting them onto a 2D space while sharing infor-

mation to ensure semantically similar data remain in

similar positions between projections. The movement

of the same data instance between projections gener-

ate trajectories, which are then condensed into vector

ﬁelds that reﬂect how data ﬂows throughout the differ-

ent outputs. These outputs consist of layer activations,

either from a speciﬁc layer during different epochs of

training (to visualize how training changes data rep-

resentations), or from different layers from the same

instance of a network (to visualize how data represen-

tations evolve as layers propagate information.

To build this representation, we ﬁrst extract acti-

vation sets A(1), A(2), . . . , A(T ) representing the net-

work outputs from T sequential steps of the process

we want to explore. In this paper, we either a) save

the network model at different epochs of training,

choose a slicing layer, feed the same set of input data

to the saved models, and then save the outputs from

the layer, or b) pick a given network model, slice it at

different layers, feed the input data set, and save the

output from these layers as activation sets.

Once the activation data is extracted, it is pro-

jected onto a 2D space using a multidimensional pro-

jection technique, obtaining A

[1], A

[2], . . . , A

[T ].

Then, the positions of the same points in two sub-

sequent projections form movement vectors that de-

scribe how data instances in one output changed to

the next. This movement data is joined for all out-

put transitions, generating trajectories for each data

instance across the sequential steps we wanted to ex-

plore. Finally, all trajectories are used to compute a

vector ﬁeld to explain and visualize how and what the

network has learned in the training process. The 2D

space shared by all projections is our visual learning

space, and the vector ﬁeld describes how network out-

puts ﬂow through it. Figure 1 summarizes this pro-

cess.

The following sections show in detail how data is

projected and how the vector ﬁeld is generated in our

model.

3.1 Projecting Data

Although we can compare any set of projections to

produce vector ﬁelds, we need to eliminate changes

between projections that do not reﬂect variations

in the high-dimensional data as much as possible.

Therefore, the projection technique itself must share

information between all observations to ensure the

generation of a synchronized view. Although precise

and popular, non-linear projection techniques gener-

ally do not guarantee consistent visual spaces when

comparing two distinct projections since the axis (di-

mensions) of the original space are not projected into

straight lines on the visual spaces, and, therefore, can-

not be considered equivalent in the projections. Some

techniques offer a certain degree of control, such as

ﬁxing control points (Joia et al., 2011) or selecting

the same initialization parameters (Van Der Maaten

and Hinton, 2008), but often this means a trade-off

between local and global distance preservation.

For two distinct projections to be compared, they

need to be aligned as best as possible, i.e., the pro-

jected distances must be as similar as possible to the

original data while keeping the projections as simi-

lar as possible with each other. Currently, there are

two techniques able to generate multiple aligned pro-

jections of the same data: the Dynamic t-SNE (Dt-

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

112

Figure 1: Overview of the learning space vector ﬁeld generation. From the DNN model, we obtain sequential data, in the

form of hidden layer activations. From this highly multivariate data, we compute projections, sharing information between all

activation sets (dashed lines) to ensure that the obtained projections are synchronized. The differences between each pair of

projections in the sequence are then processed to obtain vector ﬁelds that represent the changes in data.

SNE) (Rauber et al., 2016) and the Visual Feature Fu-

sion (VFF) (Hilasaca and Paulovich, 2019).

The Dt-SNE is a variation of the t-SNE capable

of minimizing data variability in successive projec-

tions to a certain degree in order to observe changes

in multiple DNN states. This is achieved by adding a

term to the t-SNE’s cost function to approach points

representing the same instance in different projections

close to each other. Although attaining better results

if compared to the original t-SNE in terms of align-

ing subsequent projections, it inherits a major prob-

lem: the misleading effect of cluster distance and

shape in t-SNE projections resulted from the local

nature of the optimization and how hyperparameters

are set up (Wattenberg et al., 2016) – the observed

distance between clusters is unreliable and sensitive

to parametrization (perplexity parameter), conﬂicting

with our design goals.

Given that, we opt to use the VFF technique. VFF

is next described.

3.1.1 Aligning Projections

The VFF technique was originally developed to fuse

different feature representations of data with the aim

of building a new, user-driven representation. Here,

we use it to generate 2D projections that align differ-

ent feature representations of the same data.

This process consists of obtaining samples

, ..., F

from the activation sets A[1]...A[T ] with the

same indexes (i.e., the samples contain data related

to the same points) and then calculating representa-

tions R

, ..., R

∈ R

that preserves the relationships

in each set F

as best as possible while aligning the

projections. In this process, two restrictions are con-

sidered for optimization. The ﬁrst is responsible for

ensuring that the projection matches the original data

and is given by

stress

) =

∑

δ( f

, f

)

max

−



− r



(1)

where f

and f

are instances in F

, δ



, f



is the

distance between them on their original space, δ

max

the maximum pairwise distance between instances in

, and r

and r

are the representations of f

and f

on the m-dimensional space, respectively. The second

restriction is responsible for the alignment between

projections, given by

alignment

) =

∑



d(¯r

, ¯r

) −



¯r

− r





(2)

where d (¯r

, ¯r

) is the average distance between

two instances in all representations. Our experi-

ments were performed using Euclidian distances and

−norm, as we intend to visually examine distance

relations in the 2D space. This technique is, however,

designed to be able to merge features from different

distance metrics. Joining the two equations, the ﬁnal

optimization problem is described by the equation

E(F

) = λ · E

stress

) + (1 − λ) · E

alignment

) (3)

where λ is a parameter used to control the importance

of each aspect of the optimization. This equation is

minimized using stochastic gradient descent.

Visualizing Learning Space in Neural Network Hidden Layers

113

3.2 Vector Field Generation

The vector ﬁelds contained in our visualization are

generated using an adapted version of the Vector Field

K-means technique, proposed by Ferreira et al. (Fer-

reira et al., 2013). This technique uses a distance mea-

sure d(X , a) between a discrete grid representation of

a vector ﬁeld X and a trajectory a, composed by pairs

of time and spatial position (t, a(t)). Once this dis-

tance function is deﬁned, it is minimized to ﬁnd dis-

crete vector ﬁelds that provide the best approximation

to a group of trajectories and match each trajectory to

a ﬁeld, similar to the k-means algorithm.

In this approach, a trajectory is represented by a

path written as α : [t

, t

] → R

and a vector ﬁeld is de-

ﬁned in a domain Ω ⊂ R

, i.e., a function X : Ω → R

So that, ﬁnding the vector ﬁeld that best matches a set

of trajectories φ can be described as the optimization

problem

E = min

∑

∈φ



X (α

(t)) −



(t)





dt (4)

where α

(t) is the velocity vector of the trajectory α

on instant t. Also included in this problem is a regu-

larization restriction

E = min

∆X

(1 − λ

)

∑

∈φ



(α

(t)) −



(t)





(5)

where ∆ is the Laplace operator. This restriction en-

sures the smoothness of the resulting vector ﬁeld, with

parameter λ

controlling the weight of each term in

the minimization equation and therefore determining

if the optimization should prioritize smoothness or

matching the vector ﬁeld to the trajectories.

In the Vector Field k-Means technique, vector

ﬁelds are generated from trajectory groups, so that

trajectories can be reassigned to the most similar vec-

tor ﬁelds in the next half of the iteration. Since our

focus is to generate only one vector ﬁeld that approx-

imates a set of trajectories, our simpliﬁed version of

this technique only ﬁts the vector ﬁeld to the trajec-

tory set, with no need for reassignment.

4 RESULTS

One typical application of DNNs is data classiﬁca-

tion, which consists of inferring some model f : X →

Y to correctly label unknown data based on a set

of known labelled examples (x

, y

) ∈ X × Y (LeCun

et al., 2015). This learning process is known as su-

pervised learning, in which the model is iteratively

adapted according to training examples.

Although it is well established in the literature

that DNNs yield outstanding results in classiﬁcation

tasks for different domains, training the network and

choosing appropriate parameters can still be a com-

plex, time-consuming process. In this section, we

visualize the projected learning space on MLPs and

CNNs performing classiﬁcation tasks with the objec-

tive of gaining insights on the training process and on

how conclusions are drawn when performing classiﬁ-

cation.

It is important to clarify that these visualization

methods are not restricted to a speciﬁc architecture or

application. These network conﬁgurations were cho-

sen due to their pervasiveness on literature, and be-

cause the classiﬁcation problem offers an easy way to

keep track of instances by coloring the points repre-

senting them using the assigned classes.

4.1 Experimental Setup

In order to allow the comparison between our

approach and the results reported by Rauber et

al.(Rauber et al., 2017), we used the same network

conﬁguration described in their experiments:

• An MLP with four fully-connected layers of

1, 000 rectiﬁed linear processing units (ReLU ac-

tivation) each, a 10 unit softmax output, and

dropout regularization of 0.2 − 0.5 on each hid-

den layer;

• A CNN consisting of two sequential convolu-

tional layers of 32 3 × 3 ﬁlters, a 2 × 2 max-

pooling layer (dropout 0.25), two convolutional

layers with 64 3 × 3 ﬁlters, another 2 × 2 max-

pooling layer (dropout 0.25), a fully-connected

layer with 4, 096 processing units (dropout 0.5),

a fully connected layer with 512 processing units,

and a softmax output with 10 units. All layers (ex-

cept the output) use ReLU activation.

Our experiments were conducted using the

CIFAR-10 and the MNIST datasets. Training opti-

mization was conducted using stochastic gradient de-

scent in both networks. In the MLPs, the employed

parameters were batch size equal to 16, learning

rate = 0.01, momentum coefﬁcient = 0.9, and learn-

ing decay = 10

−9

. In the CNNs, the parameters were

batch size = 32, learning rate = 0.01, momentum coef-

ﬁcient = 0.9, and learning decay = 10

−6

. We extracted

network snapshots after 0, 5, 10, and 100 training

epochs. The models for comparison between layers

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

114

are all based on networks after 100 training epochs.

Implementation is coded on CUDA-enabled Tensor-

Flow, using Keras

, NumPy

, and SciKit Learn

li-

braries. The vector ﬁeld generation is based on the

code provided by Ferreira et al. (Ferreira et al., 2013),

and the visualization system was built using D3.js

For the projections, 2, 000 data instances were ran-

domly sampled from the test data of each dataset. We

used the same sample for all tests of the same dataset

to provide consistency. We produced hidden layer ac-

tivations by predicting the classes for the data sample

on all the snapshots of different training epochs and

capturing the results on the last hidden layer (1, 000

processing units on the MLP, 512 processing units on

the CNN). To compare different layers, we used the

trained network snapshots after 100 epochs and cap-

tured the results of each hidden layer on the MLP. On

the CNN, we captured results from 4 different layers:

the ﬁrst max-pooling layer, the second max-pooling

layer, the ﬁrst fully-connected layer, and the second

fully-connected layer. The ﬁlter information from the

convolutional layers was ﬂattened and read as a vec-

tor. To project data, we used λ = 0.5.

Accuracy results for all training experiments can

be seen in Tables 1 and 2. There was a quick con-

vergence in the experiments done using the MNIST

dataset. The CIFAR10 experiments took longer and

got worse results, showing drops in accuracy due to

overﬁtting by epoch 100. It is important to mention

that in this paper, we do not seek the best accuracy

results in these tests - our goal is to explain why these

results happen. Therefore, while changes in accuracy

may seem small, we can explore these networks and

observe the ﬁne tuning that is applied over the course

of 100 training epochs.

4.2 Evolution of Representations with

Training

Our ﬁrst analysis was to observe hidden layer acti-

vations during training. We generated four visualiza-

tions, one for each dataset/network combination, each

composed by four projections, one for each training

epoch snapshot. Our goal was to compare the projec-

tions and identify useful information about the train-

ing process from the vector ﬁeld model.

The results of the projections obtained for the

MNIST dataset can be seen in Figure 2. The MNIST

dataset is well-behaved compared to other image clas-

siﬁcation sets, and both networks achieved positive

keras.io

www.numpy.org

scikit-learn.org

www.d3js.org

Table 1: MNIST dataset accuracy using different network

architectures after e epochs.

network e = 5 e = 10 e = 100

MLP 0.9812 0.9823 0.9841

CNN 0.9933 0.9952 0.9954

rMLP 0.9806 0.9823 0.9849

Table 2: CIFAR10 dataset accuracy using different network

architectures after e epochs.

network e = 5 e = 10 e = 100

MLP 0.3260 0.3555 0.2803

CNN 0.6673 0.7538 0.7344

results (classiﬁcation accuracy of 98% for the MLP

and 99% for the CNN). the projections show a high

level of separation right from the start: this is due to

the separability inherent to the data, even when mul-

tiplied by random weights. While the alignment pro-

cess also forces the ﬁrst projection to be similar to the

later, better segmented ones, we also observed simi-

lar behavior even with very small λ values. The quick

optimization is reﬂected in the vector ﬁelds by a clear

outwards expansion as data instances are clustered in

their respective classes. It is possible to notice that

the expansion in the CNN is slightly more expressive

than the one observed in the MLP. This indicates a

quicker optimization process, as the CNN approaches

a high accuracy plateau slightly faster. The results of

this experiment are simple but demonstrate how our

approach can be used to show that both networks are

capable of solving the problem quite quickly, prob-

ably indicating that the employed architectures may

be excessive for the task. As further iterations group

the data in ever smaller sections of the visual space,

more caution should be advised to avoid overﬁtting.

As the number of instances and projection snapshots

increase in datasets, this visualization is able to pro-

vide information regarding convergence, transition

density, and temporal ﬂow of data in a simpler and

cleaner way, compared to previous approaches.

Figure 3 shows the analysis of the CIFAR-10

dataset using both networks. The CIFAR-10 dataset is

much more complex and, therefore, more difﬁcult to

classify when compared to the MNIST. The classiﬁca-

tion results reﬂect this (accuracy of 35% for the MLP

and 75% for the CNN). The fact that the networks did

not yield particularly good results can lead to some

interesting observations. For instance, the clear out-

wards expansion observed in the vector ﬁelds on pre-

vious tests is absent in the MLP model and much less

pronounced in the CNN. Data still expands to a larger

area, but in a much more disorganized manner. Tra-

jectories of points heading in opposite directions may

Visualizing Learning Space in Neural Network Hidden Layers

115

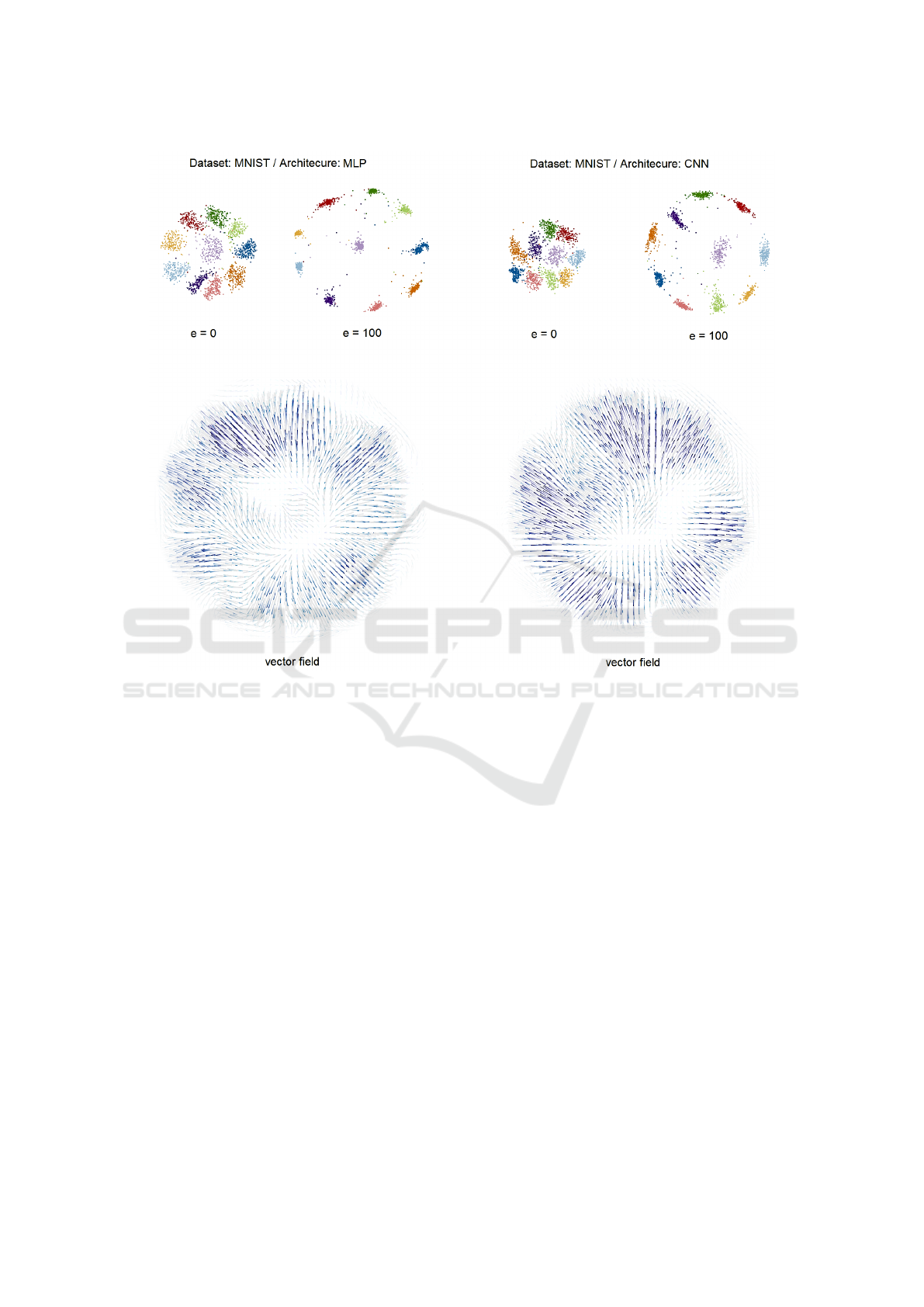
Figure 2: Last hidden layer activation projections for the MNIST dataset on MLP (left) and CNN (right), with the obtained

vector ﬁelds on the lower part. The upper area shows the projections of activations from the last hidden layer after different

numbers of training epochs. The lower area shows the resulting vector ﬁelds of the transitions between the four projections.

As MNIST is a simpler, more well-behaved dataset, both networks adapt to perform classiﬁcation without issues, as can be

seen from the groups formed in the projected data. The vector ﬁelds show subtle differences. The lines are drawn with

transparency and color according to the vector intensity (norm of the vector at the given point) for each point on the grid.

The lines on the CNN vector ﬁeld are slightly more intense, indicating a faster jump towards convergence. In the MLP vector

ﬁeld, it is possible to notice that the upper-left part of the image is more intense, indicating that one class (red) gets separated

more quickly than the others.

result in a neutral vector ﬁeld, with no strong pull to-

wards any direction. This is more evident on the MLP

model, which has the worst classiﬁcation results. The

MLP projection on epoch 100 also shows a concen-

tration of data points in the same area, which is also

unwanted behavior since the points contained in this

area do not belong to the same class. This is an indi-

cator that, while an optimization process did happen,

the model’s view of the data did not advance much

towards an organized structure. The hidden layers vi-

sualization section will further explore this issue.

Both results indicate that these networks are not

quite up for the task. The few areas in which the

vector ﬁeld shows some activity correspond to a few

instances that do get some degree of separation, as

can be seen in the blue dots on the right side and

the red dots on the left side. The CNN model shows

an amount of evolution: classes get somewhat sepa-

rated by their color around the circle, with strong or-

ganized movement towards the lower external parts.

This movement indicates that the objects in this area

were better perceived by the model, something that

would be more difﬁcult to notice simply by observing

a sequence of projections.

4.3 Hidden Activations throughout the

Network

Our second analysis was to observe the evolution of

representations inside the network. We extracted acti-

vation data from several different layers and gener-

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

116

Figure 3: Last hidden layer activation projections for the CIFAR10 dataset on MLP (left) and CNN (right), with the obtained

vector ﬁelds on the lower part. The upper area shows the projected data along 100 training epochs and the lower area shows

the generated vector ﬁeld for the transition data. The CIFAR10 is a more complex dataset, and the trained classiﬁers were

not so efﬁcient. The training was still effective on the CNN to a certain degree, as can be seen by the outwards expansion in

the vector ﬁeld that, while not as expressive as the previous ones, still indicates relationships between instances being formed

with time. In the MLP, the effect is much more muted. This is because, while an expansion can be noticed, it is chaotic, with

points moving in opposite directions and therefore generating a somewhat neutral vector ﬁeld. A quick glance is enough to

inform that, while the CNN does some progress, the MLP is getting nowhere.

ated the projections with the goal of observing the

ﬂow of data throughout the network.

Figure 4 shows the activations for the MNIST

dataset, in both networks. It is possible to notice

that clusters are formed right at the ﬁrst projection,

but while the CNN clusters data in a more gradual

manner along the four projections, the MLP separates

data instances much more quickly. This can also be

observed in the vector ﬁelds. The vector ﬁeld from

the MLP is much smoother and more muted than the

other ﬁelds observed so far. This indicates that there

is little ﬂow of abstract information between the lay-

ers; the ﬁrst ones are already capable of separating

the data. The vector ﬁeld from the CNN is also quite

muted but shows more intensity, especially regard-

ing the center-top areas of the projection. As for the

projections themselves, much of the intra-class dis-

tance in the CNN is reduced between hidden layers

3 and 4. Since the last observed layer on the CNN

is fully connected, we notice that both networks tend

to rely more on fully connected layers to make sense

of the MNIST dataset. Both networks are clearly

overequipped for the task, and their topology can be

trimmed with the aim of improving performance and

generalization. Reducing complexity and amount of

the convolutional ﬁlters for the CNN and the overall

number of neurons and layers for the MLP should be

the obvious areas to attack. As a simple example, we

set up a reduced MLP network containing only the

ﬁrst layer and ran the same training to observe accu-

racy. Table 1 shows that the results for this reduced

conﬁguration (referred to as rMLP) are virtually the

Visualizing Learning Space in Neural Network Hidden Layers

117

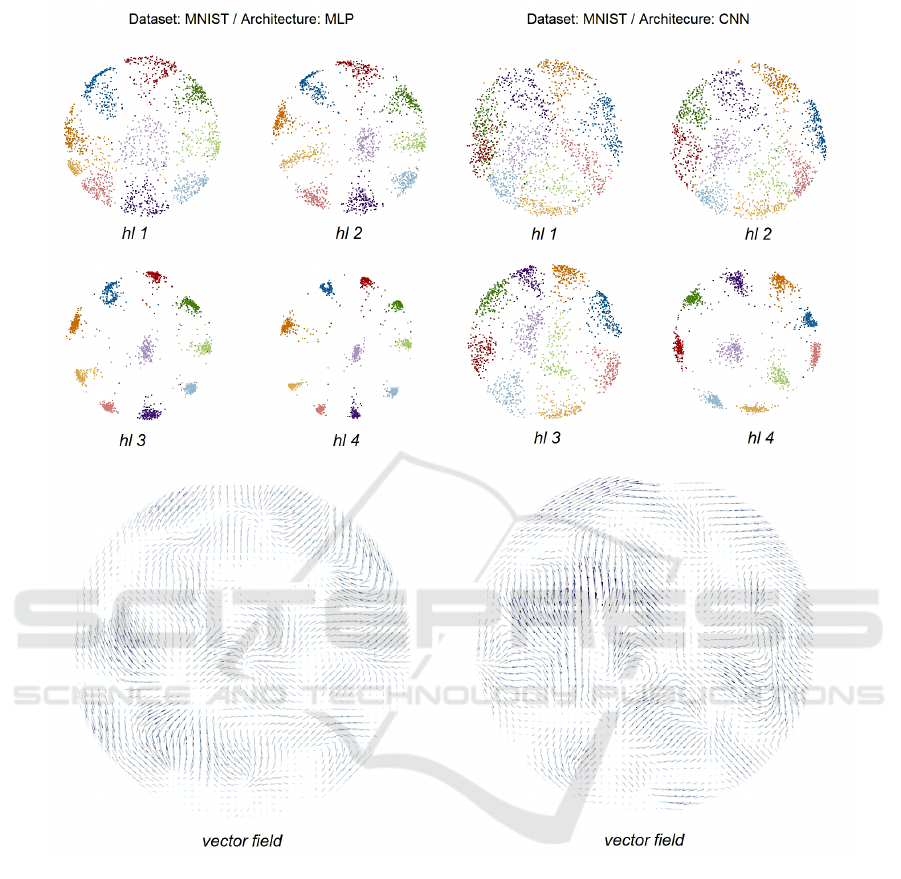
Figure 4: Hidden layer activation projections for the MNIST dataset on MLP(left) and CNN(right), with the obtained vector

ﬁelds. The upper area shows the projections of the 4 hidden layers of the fully trained MLP and 4 sampled hidden layers from

the fully trained CNN. While both networks are capable of achieving quite an amount of segmentation on the ﬁrst layer, the

MLP achieves separation much faster, since the data is pretty much already shown in clusters in the projection of the second

sampled hidden layer. The fact that the vector ﬁelds are so muted shows that there is little extra knowledge being generated as

data ﬂows through the layers. The vector ﬁeld representing the CNN is slightly more intense at the middle, indicating more

movement between layers, which could indicate a class that is taking the network more effort to ﬁgure out.

same to those of the original MLP, conﬁrming that

the other layers were in fact unnecessary for this task.

This may indicate, however, that the less immediate

representations of the CNN are more able to adapt and

generalize to different data.

Figure 5 shows the activation projections for the

CIFAR-10 dataset. While the classiﬁcation results

are worse compared to those of the MNIST, it is in-

stantly clear that there is more action on the vector

ﬁelds. There is no smooth expansion: while there is

a clear ﬂow in sections of the ﬁeld, it is convoluted,

with twists and waves. This means representations are

being formed, but their meaning changes as they are

passed forward through the layers, as instances gen-

erate activations that seem to be oscillating between

being close by or distant in the layer projections. The

intuitive idea is that, in an ideal model, progressing

through layers would mean that instances either get

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

118

Figure 5: Hidden layer activation projections for the CIFAR10 dataset on MLP(left) and CNN(right), with the obtained vector

ﬁelds. The upper area shows projections of 4 hidden layers of the MLP and the 4 sampled layers of the CNN (please see

Experiment Details). The movement happening in these pictures is more twisted and convoluted than before, lacking the

regular expansion we expect to see in ideal results. This movement still means there is information ﬂow through the network,

as more abstract representations are obtained and the relations between objects change, but these representations shift in

meaning and the model seems to fail to make use of the representations it learned.

gradually closer or further apart. That does not hap-

pen here, especially in the MLP model. The CNN

gets to a point where it is possible to see class sepa-

ration (colored zones in the last projections) match-

ing its 75% accuracy value, and this is highlighted

by a smoother vector ﬁeld. This experiment shows

cases where representations are being formed despite

poor classiﬁcation results. Going back to the data, it is

possible to search for trajectories most responsible for

deﬁning the vector ﬁelds in a certain place (i.e. low

dissimilarity to the vector ﬁeld, high velocity) and see

which data objects were responsible for that strain of

knowledge in particular, or even identifying trajecto-

ries that are outliers and don’t quite match the approx-

imated vector ﬁeld.

5 LIMITATIONS

The work described in this paper has certain limita-

tions: one of them is the fact that our projections are

Visualizing Learning Space in Neural Network Hidden Layers

119

forced to be aligned; the visual learning space can

generate distortions in the projected data, as a result of

the matching process between different projections.

As an optimization technique, the method employed

to generate the projections also has random factors,

that need to be accounted for if different sequences of

projections are to be compared as the resulting vector

ﬁelds can vary. Additionally, a single vector ﬁeld may

not be enough to display subtleties of some networks.

There is the possibility of generating a visualization

from multiple vector ﬁelds, in order to estimate and

explore more complex visual learning spaces.

6 CONCLUSION

In this paper, we presented a new approach for

projection-based ANN hidden layer visualization that

uses different techniques to provide insights on how

knowledge is generated in a DNN through training

and how abstract representations are formed between

layers. Our focus was to a) adopt a ﬂow-based model

to represent a transition space between projections to

remove point-based clutter and b) present a projection

system capable of holding an aligned view for several

projections, a limitation found in most t-SNE based

techniques. Our approach has other useful character-

istics, namely the ability to compare different data and

to align them using a common feature (e.g., compar-

ing the results of different models applied over the

same objects, or how different parts of a same system

process data) and the generation of a space that tie

different projections together, that may support other

visualization aids in the future. Using this visualiza-

tion, we performed experiments that aim to show how

they can be used to generate knowledge. Our analysis

was able to go further in certain aspects of the training

process of neural networks, attempting to explain sub-

tle aspects of how knowledge is generated in a DNN

system. There are many future research directions re-

garding the work depicted in this paper: as an intro-

ductory study using these methods, the network archi-

tectures used and experiments conducted are the ones

commonly depicted in literature, and more complex

systems and datasets should provide other interesting

analysis opportunities. Additionally, the learning pro-

jection space and vector ﬁelds as deﬁned in this paper

assume data from a sequential nature, but there is no

hard restriction limiting them to this type of data.

ACKNOWLEDGMENTS

We would like to thank CAPES and FAPESP

(2017/08817-7, 2015/08118-6) for the ﬁnancial sup-

port.

REFERENCES

Babiker, H. K. B. and Goebel, R. (2017). An intro-

duction to deep visual explanation. arXiv preprint

arXiv:1711.09482.

Donahue, J., Jia, Y., Vinyals, O., Hoffman, J., Zhang, N.,

Tzeng, E., and Darrell, T. (2014). Decaf: A deep con-

volutional activation feature for generic visual recog-

nition. In International conference on machine learn-

ing, pages 647–655.

Erhan, D., Bengio, Y., Courville, A., and Vincent, P. (2009).

Visualizing higher-layer features of a deep network.

University of Montreal, 1341(3):1.

Ferreira, N., Klosowski, J. T., Scheidegger, C. E., and Silva,

C. T. (2013). Vector ﬁeld k-means: Clustering trajec-

tories by ﬁtting multiple vector ﬁelds. In Computer

Graphics Forum, volume 32, pages 201–210. Wiley

Online Library.

Hamel, P. and Eck, D. (2010). Learning features from mu-

sic audio with deep belief networks. In ISMIR, vol-

ume 10, pages 339–344. Utrecht, The Netherlands.

Hilasaca, G. and Paulovich, F. (2019). Visual feature fusion

and its application to support unsupervised clustering

tasks. arXiv preprint arXiv:1901.05556.

Hohman, F. M., Kahng, M., Pienta, R., and Chau, D. H.

(2018). Visual analytics in deep learning: An interrog-

ative survey for the next frontiers. IEEE Transactions

on Visualization and Computer Graphics.

Joia, P., Coimbra, D., Cuminato, J. A., Paulovich, F. V., and

Nonato, L. G. (2011). Local afﬁne multidimensional

projection. IEEE Transactions on Visualization and

Computer Graphics, 17(12):2563–2571.

Kahng, M., Andrews, P. Y., Kalro, A., and Chau, D. H. P.

(2018). A cti v is: Visual exploration of industry-scale

deep neural network models. IEEE transactions on

visualization and computer graphics, 24(1):88–97.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. nature, 521(7553):436.

Liu, M., Shi, J., Li, Z., Li, C., Zhu, J., and Liu, S. (2017).

Towards better analysis of deep convolutional neu-

ral networks. IEEE transactions on visualization and

computer graphics, 23(1):91–100.

Mahendran, A. and Vedaldi, A. (2015). Understanding deep

image representations by inverting them. In Proceed-

ings of the IEEE conference on computer vision and

pattern recognition, pages 5188–5196.

Mahendran, A. and Vedaldi, A. (2016). Visualizing

deep convolutional neural networks using natural pre-

images. International Journal of Computer Vision,

120(3):233–255.

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

120

McInnes, L., Healy, J., and Melville, J. (2018). Umap: Uni-

form manifold approximation and projection for di-

mension reduction. arXiv preprint arXiv:1802.03426.

Mohamed, A.-r., Hinton, G., and Penn, G. (2012). Under-

standing how deep belief networks perform acoustic

modelling. neural networks, pages 6–9.

Nonato, L. G. and Aupetit, M. (2018). Multidimensional

projection for visual analytics: Linking techniques

with distortions, tasks, and layout enrichment. IEEE

Transactions on Visualization and Computer Graph-

ics, pages 1–1.

Pezzotti, N., H

ollt, T., Van Gemert, J., Lelieveldt, B. P.,

Eisemann, E., and Vilanova, A. (2018). Deepeyes:

Progressive visual analytics for designing deep neu-

ral networks. IEEE transactions on visualization and

computer graphics, 24(1):98–108.

Rauber, P. E., Fadel, S. G., Falcao, A. X., and Telea, A. C.

(2017). Visualizing the hidden activity of artiﬁcial

neural networks. IEEE transactions on visualization

and computer graphics, 23(1):101–110.

Rauber, P. E., Falc

ao, A. X., and Telea, A. C. (2016). Vi-

sualizing time-dependent data using dynamic t-sne. In

Proceedings of the Eurographics/IEEE VGTC Confer-

ence on Visualization: Short Papers, pages 73–77. Eu-

rographics Association.

Scherer, D., M

uller, A., and Behnke, S. (2010). Evaluation

of pooling operations in convolutional architectures

for object recognition. In International conference on

artiﬁcial neural networks, pages 92–101. Springer.

Simonyan, K., Vedaldi, A., and Zisserman, A. (2013).

Deep inside convolutional networks: Visualising im-

age classiﬁcation models and saliency maps. arXiv

preprint arXiv:1312.6034.

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,

and Salakhutdinov, R. (2014). Dropout: A simple way

to prevent neural networks from overﬁtting. The Jour-

nal of Machine Learning Research, 15(1):1929–1958.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,

Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-

novich, A. (2015). Going deeper with convolutions.

In Proceedings of the IEEE conference on computer

vision and pattern recognition, pages 1–9.

Van Der Maaten, L. and Hinton, G. (2008). Visualizing

high-dimensional data using t-sne. journal of machine

learning research. J Mach Learn Res, 9:26.

Wattenberg, M., Vi

egas, F., and Johnson, I. (2016). How to

use t-sne effectively. Distill, 1(10):e2.

Yosinski, J., Clune, J., Nguyen, A., Fuchs, T., and Lipson,

H. (2015). Understanding neural networks through

deep visualization. arXiv preprint arXiv:1506.06579.

Zeiler, M. D. and Fergus, R. (2014). Visualizing and under-

standing convolutional networks. In European confer-

ence on computer vision, pages 818–833. Springer.

Zintgraf, L. M., Cohen, T. S., Adel, T., and Welling,

M. (2017). Visualizing deep neural network deci-

sions: Prediction difference analysis. arXiv preprint

arXiv:1702.04595.

Visualizing Learning Space in Neural Network Hidden Layers

121