
Two-step Multi-spectral Registration Via Key-point Detector and
Gradient Similarity: Application to Agronomic Scenes for Proxy-sensing
Jehan-Antoine Vayssade
a
, Gawain Jones
b
, Jean-Noel Paoli
c
and Christelle Gee
d
Agro
´
ecologie, AgroSup Dijon, INRA, Univ. Bourgogne-Franche-Comt
´
e, F-21000 Dijon, France
Keywords:
Registration, Multi-spectral Imagery, Precision Farming, Feature Descriptor.
Abstract:
The potential of multi-spectral images is growing rapidly in precision agriculture, and is currently based on the
use of multi-sensor cameras. However, their development usually concerns aerial applications and their pa-
rameters are optimized for high altitudes acquisition by drone (UAV ≈ 50 meters) to ensure surface coverage
and reduce technical problems. With the recent emergence of terrestrial robots (UGV), their use is diverted
for nearby agronomic applications. Making it possible to explore new agronomic applications, maximizing
specific traits extraction (spectral index, shape, texture . . . ) which requires high spatial resolution. The prob-
lem with these cameras is that all sensors are not aligned and the manufacturers’ methods are not suitable for
close-field acquisition, resulting in offsets between spectral images and degrading the quality of extractable
informations. We therefore need a solution to accurately align images in such condition.
In this study we propose a two-steps method applied to the six-bands Airphen multi-sensor camera with (i)
affine correction using pre-calibrated matrix at different heights, the closest transformation can be selected via
internal GPS and (ii) perspective correction to refine the previous one, using key-points matching between en-
hanced gradients of each spectral bands. Nine types of key-point detection algorithms (ORB, GFTT, AGAST,
FAST, AKAZE, KAZE, BRISK, SURF, MSER) with three different modalities of parameters were evaluated
on their speed and performances, we also defined the best reference spectra on each of them. The results show
that GFTT is the most suitable methods for key-point extraction using our enhanced gradients, and the best
spectral reference was identified to be the band centered on 570 nm for this one. Without any treatment the
initial error is about 62 px, with our method, the remaining residual error is less than 1 px, where the man-
ufacturer’s involves distortions and loss of information with an estimated residual error of approximately 12
px.
1 INTRODUCTION
Modern agriculture is changing towards a system that
is less dependent on pesticides (Lechenet et al., 2014)
(herbicides remain the most difficult pesticides to re-
duce) and digital tools are of great help in his mat-
ter. The development of imaging and image process-
ing have made it possible to characterize an agricul-
tural plot (Sankaran et al., 2015) (crop health sta-
tus or soil characteristics) using non-destructive agro-
nomic indices (Jin et al., 2013) replacing traditional
destructive and time-consuming methods. In recent
years, the arrival of miniaturized multi-spectral and
hyper-spectral cameras on Unmanned Aerial Vehicles
a
https://orcid.org/0000-0002-7418-8347
b
https://orcid.org/0000-0002-5492-9590
c
https://orcid.org/0000-0002-0499-9398
d
https://orcid.org/0000-0001-9744-5433
(UAVs) has allowed spatio-temporal field monitoring.
These vision systems have been developed for precise
working conditions (flight height 50 m). Although,
very practical to use, they are also used for proxy-
sensing applications. However, the algorithms offered
by manufacturers to co-register multiple single-band
images at different spectral range, are not optimal for
low heights. It thus requires a specific close-field im-
age registration.
Image registration is the process of transforming
different images of one scene into the same coordi-
nate system. The spatial relationships between these
images can be rigid (translations and rotations), affine
(shears for example), homographic, or complex large
deformation models (due to the difference of depth
between ground and leafs) (Kamoun, 2019). The
main difficulty is that multi-spectral cameras have low
spectral coverage between bands, resulting in a loss of
Vayssade, J., Jones, G., Paoli, J. and Gee, C.
Two-step Multi-spectral Registration Via Key-point Detector and Gradient Similarity: Application to Agronomic Scenes for Proxy-sensing.
DOI: 10.5220/0009169301030110
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
103-110
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
103

characteristics between them. Which is caused by (i)
plant leaves have different aspect depending on the
spectral bands (ii) there are highly complex and self-
similar structures in our images (Douarre et al., 2019).
It therefore affects the process of detecting common
characteristics between bands for image registration.
There are two types of registration, feature based and
intensity based (Zitov
´
a and Flusser, 2003). Feature
based methods works by extracting point of interest
and use feature matching, in most cases a brute-force
matching is used, making those techniques slow. For-
tunately these features can be filtered on the spatial
properties to reduce the matching cost. A GPGPU
implementation can also reduce the comparisons cost.
Intensity-based automatic image registration is an it-
erative process, and the metrics used are sensitive
to determine the numbers of iteration, making such
method computationally expensive for precise regis-
tration. Furthermore multi-spectral implies different
metrics for each registered bands which is hard to
achieve.
Different studies of images alignment using multi-
sensors camera can be found for acquisition using
UAV at medium (50 − 200 m) and high (200 − 1000
m) distance. Some show good performances (in term
of number of key-points) of feature based (Dantas
Dias Junior et al., 2019; Vakalopoulou and Karantza-
los, 2014) with strong enhancement of feature de-
scriptor for matching performances. Other prefer to
use intensity based registration (Douarre et al., 2019)
on better convergence metrics (Chen et al., 2018) (in
term of correlation), which is slower and not necessar-
ily robust against light variability and their optimiza-
tion can also fall into a local minimum, resulting in a
non-optimal registration (Vioix, 2004).
Traditional approach to multi-spectral image reg-
istration is to designate one channel as the target chan-
nel and register all the others on the selected one. Cur-
rently, only (Dantas Dias Junior et al., 2019) show
a method for selecting the best reference, but there
is no study who as defined the best spectral refer-
ence in agronomic scene. In all cases NIR (850
nm) or middle range spectral reference are conven-
tionally used without studying the others on preci-
sion agriculture. In addition those studies mainly pro-
pose features matching without large methods com-
parison (Dantas Dias Junior et al., 2019)(less than 4)
of their performance (time/precision), without show-
ing the importance of the spectral reference and the
interest of normalized gradients transformation (like
in Intensity-based methods).
However, despite the growing use of UGVs and
multi-spectal imaging, the domain is not very well
sourced, and no study has been found under agricul-
tural and external conditions in near field of view (less
than 10 meter) for multi-spectral registration.
Thus, this study propose a benchmark of popular
feature extractors inside normalized gradients trans-
formation and the best spectral reference was defined
for each of them. Moreover a pre-affine registration is
used to filter the feature matching, evaluated at differ-
ent spatial resolutions. So this study shows the impor-
tance of the selection of the reference and the features
extractor on normalized gradients in such registration.
2 MATERIAL AND METHOD
2.1 Material
2.1.1 Camera
The multi-spectral imagery is provided by the six-
band multi-spectral camera Airphen developed by
HiPhen. Airphen is a scientific multi-spectral cam-
era developed by agronomists for agricultural appli-
cations. It can be embedded in different types of plat-
forms such as UAV, phenotyping robots, etc.
Airphen is highly configurable (bands, fields
of view), lightweight and compact. The camera
was configured using interferential filter centered at
450/570/675/710/730/850 nm with FWHM
1
of 10
nm, the position of each band is referenced on fig-
ure 1. The focal lens is 8 mm for all wavelength. The
raw resolution for each spectral band is 1280 × 960
px with 12 bit of precision. Finally the camera also
provides an internal GPS antenna that can be used to
get the distance from the ground.
Figure 1: Disposition of each band on the Airphen multi-
sensors camera.
2.1.2 Datasets
Two datasets were taken at different heights with im-
ages of a chessboard (use for calibration) and of an
agronomic scene. We used a metallic gantry for po-
sitioning the camera at different heights. The size of
the gantry is 3 × 5 × 4 m. Due to the size of the chess-
board (57 × 57 cm with 14 × 14 square of 4 cm), the
1
Full Width at Half Maximum
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
104
limited focus of the camera and the gantry height, we
have bounded the acquisition heights from 1.6 to 5 m
with 20 cm steps, which represents 18 acquisitions.
The first dataset is for the calibration. A chess-
board is taken at different heights The second one is
for the alignment verification under real conditions.
One shot of an agronomic scene is taken at different
heights with a maximum bias set at 10 cm.
2.2 Methods
Alignment is refined in two stages, with (i) affine reg-
istration approximately estimated and (ii) perspective
registration for the refinement and precision. As ex-
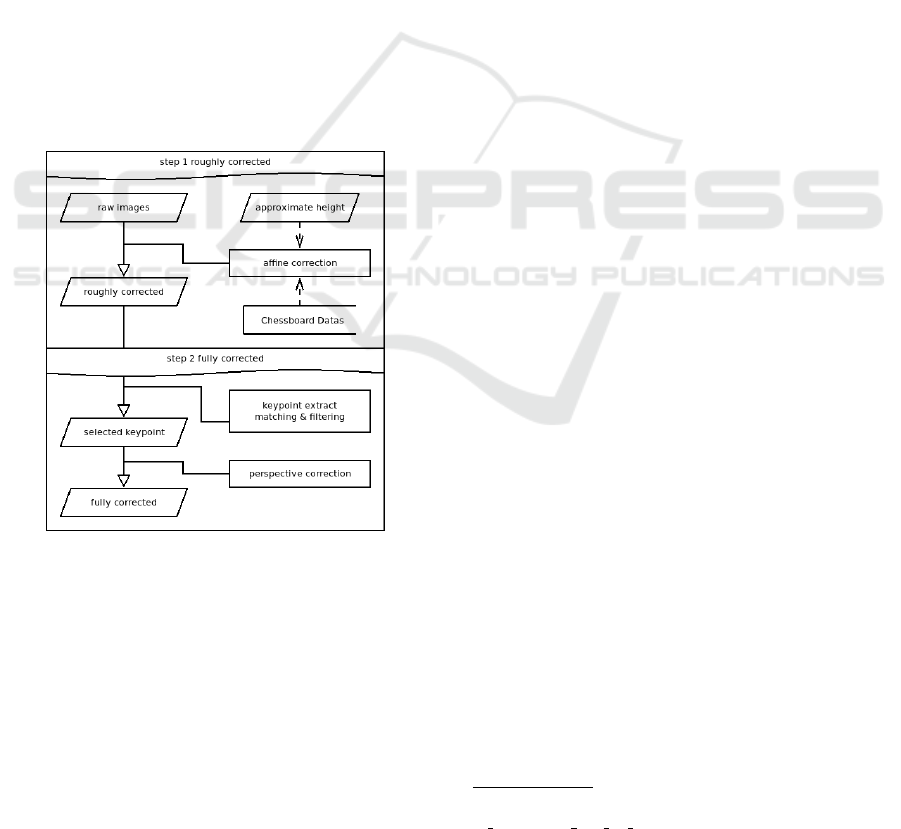
ample the figure 2 shows each correction step, where
the first line is for the (i) affine correction (section
2.2.1), the second is for (ii) perspective correction.
More precisely the second step is per-channel pre-
processed where feature detectors are used to de-
tect key-points (section 2.2.2). Each channel key-
points are associated to compute the perspective cor-
rection through homography, to the chosen spectral
band (section 2.2.2). These steps are explained on
specific subsections.
Figure 2: Each step of the alignment procedure, with (step
1) roughly corrected from affine correction and (step 2) en-
hancement via key-points and perspective.
2.2.1 Affine Correction
We make the assumption that closer we take the snap-
shot, the bigger the distance between each spectral
band is. On the other hand, at a distance superior
or equals to 5 m, the initial affine correction become
stable. A calibration is used to build a linear model
based on that assumption, which will allow the affine
correction to work at any height. The main purpose of
this step is to reduce the offset between each spectral
band, which allows the similarity between key-points
to be spatially delimited within a few pixels, making
feature matching more effective.
Calibration: Based on that previous assumption a
calibration is run over the chessboard dataset. We de-
tect the chessboard using the opencv calibration tool-
box (Bouguet, 2001) on each spectral image (nor-
malized by I = (I − min(I))/ max(I) where I is the
spectral image) at different heights (from 1.6 m to 5
m). We use the function findChessboardCorners how
attempts to determine whether the input image is a
view of the chessboard pattern and locate the inter-
nal chessboard corners. The detected coordinates are
roughly approximated. To determine their positions
accurately we use the function cornerSubPix as ex-
plained in the documentation
2
.
Linear Model: Using all the points detected for
each spectral band, we calculate the centroid grid
(each point average). The affine transform from each
spectral band to this centroid grid is estimated. The-
oretically, the rotation and the scale (A,B,C,D) do
not depend on the distance to the ground, but the
translation (X,Y ) does. Thus a Levenberg-Marquardt
curve fitting algorithm with linear least squares re-
gression (Mor
´
e, 1978) can be used to fit an equation
for each spectral band against X and Y independently
to the centroid grid. We adjust the following curve
t = αh
3
+ βh
2
+ θh + γ where h is the height, t is the
resulted translation and factors α,β,θ,γ are the model
parameters.
Correction: Based on the model estimated on the
chessboard dataset, we transpose them to the agro-
nomic dataset. To make the affine matrix correction,
we used the rotation and scale factors at the most ac-
curate height (1.6 m where the spatial resolution of
the chessboard is higher), because it does not theoret-
ically depend on the height. For the translation part,
the curve model is applied for each spectral band at
the given height provided by the user. Each spec-
tral band is warped using the corresponding affine
transformation. Finally, all spectral bands are cropped
to the minimal bounding box (minimal and maximal
translation of each affine matrix). This first correction
is an approximation. It provides some spatial proper-
ties that we will use on the second stage.
2
https://docs.opencv.org/2.4/modules/calib3d/doc/came
ra calibration and 3d reconstruction.html
Two-step Multi-spectral Registration Via Key-point Detector and Gradient Similarity: Application to Agronomic Scenes for Proxy-sensing
105

2.2.2 Perspective Correction
Each spectral band has different properties and values
by nature but we can extract the corresponding simi-
larity by transforming each spectral band into its ab-
solute derivative, to find similarities in gradient break
among them. As we can see in figure 3 gradients
can have opposite direction depending on the spectral
bands, making the absolute derivative an important
step for matching between different spectral band.
Figure 3: Gradient orientation in spectral band (Rabatel and
Labbe, 2016). Orientation of the gradient is not the same
depending to the spectral band.
The affine correction attempts to help the fea-
ture matching by adding properties of epipolar lines
(close). Thus, the matching of extracted features can
be spatially bounded, (i) we know that the maximum
translation is limited to a distance of a few pixels (less
than 10px thanks to affine correction), and (ii) the an-
gle between the initial and the matched one is limited
to [−1,1] degree.
Computing the Gradient: To compute the gra-
dient of the image with a minimal impact of the
light distribution (shadow, reflectance, specular, ...),
each spectral band is normalized using Gaussian blur
(Sage and Unser, 2003), the kernel size is defined by
next odd(image width
0.4
) (19 in our case) and the fi-
nal normalized images are defined by I/(G + 1) ∗ 255
where I is the spectral band and G is the Gaussian blur
of those spectral bands. This first step minimizes the
impact of the noise on the gradient and smooth the
signal in case of high reflectance. Using this normal-
ized image, the gradient I
grad
(x,y) is computed with
the sum of absolute Sharr filter (Seitz, 2010) for hori-
zontal S
x
and vertical S
y
derivative, noted I
grad
(x,y) =
1
2
|S
x
| +
1
2
|S
y
|. Finally, all gradients I
grad
(x,y) are nor-
malized using CLAHE (Zuiderveld, 1994) to locally
improve their intensity and increase the number of
key-points detected.
Key-points Extractor: A key-point is a point of in-
terest. It defines what is important and distinctive in
an image. Different types of key-point extractors are
available and the following are tested :
(ORB) Oriented FAST and Rotated BRIEF
(Rublee et al., 2011), (AKAZE) Fast explicit diffu-
sion for accelerated features in nonlinear scale spaces
(Alcantarilla and Solutions, 2011), (KAZE) A novel
multi-scale 2D feature detection and description algo-
rithm in nonlinear scale spaces (Ordonez et al., 2018),
(BRISK) Binary robust invariant scalable key-points
(Leutenegger et al., 2011), (AGAST) Adaptive and
generic corner detection based on the accelerated seg-
ment test (Mair et al., 2010), (MSER) maximally sta-
ble extremal regions (Donoser and Bischof, 2006),
(SURF) Speed-Up Robust Features (Bay et al., 2006),
(FAST) FAST Algorithm for Corner Detection (Tra-
jkovi
´
c and Hedley, 1998) and (GFTT) Good Features
To Track (Shi et al., 1994).
These algorithms are largely described across
multiple studies (Dantas Dias Junior et al., 2019;
Tareen and Saleem, 2018; Zhang et al., 2016; Ali
et al., 2016), they are all available and easily usable
in OpenCV. Thus we have studied them by varying
the most influential parameters for each of them with
three modalities, the table 1 in appendix shows all
modalities.
Table 1: list of algorithms with 3 modalities of their param-
eters.
ABRV parameters modality 1 modality 2 modality 3
ORB nfeatures 5000 10000 15000
GFTT maxCorners 5000 10000 15000
AGAST threshold 71 92 163
FAST threshold 71 92 163
AKAZE nOctaves, nOctaveLayers (1, 1) (2, 1) (2, 2)
KAZE nOctaves, nOctaveLayers (4, 2) (4, 4) (2, 4)
BRISK nOctaves, patternScale (0, 0.1) (1, 0.1) (2, 0.1)
SURF nOctaves, nOctaveLayers (1, 1) (2, 1) (2, 2)
MSER None None None None
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
106
Key-point Detection: We use one of the key-point
extractors mentioned above between each spectral
band gradients (all extractors are evaluated). For each
detected key-point, we extract a descriptor using ORB
features. We match all detected key-points to a ref-
erence spectral band (all bands are evaluated). All
matches are filtered by distance, position and angle,
to eliminate a majority of false positives along the
epipolar line. Finally we use the function findHomog-
raphy between the key-points detected/filtered with
RANSAC (Fischler and Bolles, 1981), to determine
the best subset of matches to calculate the perspective
correction.
Correction: The perspective correction between
each spectral band to the reference is estimated and
applied. Finally, all spectral bands are cropped to the
minimum bounding box, which is obtained by apply-
ing a perspective transformation to each corner of the
image.
3 RESULTS AND DISCUSSION
Firstly the results will focus on affine corrections and
then on the effects of the perspective correction. Fig-
ure 4 shows a closeup inside at 1.6 m (4a) raw images
acquisition, (4c & 4d) registred image of each correc-
tion steps and (4b) the manufacturer results.
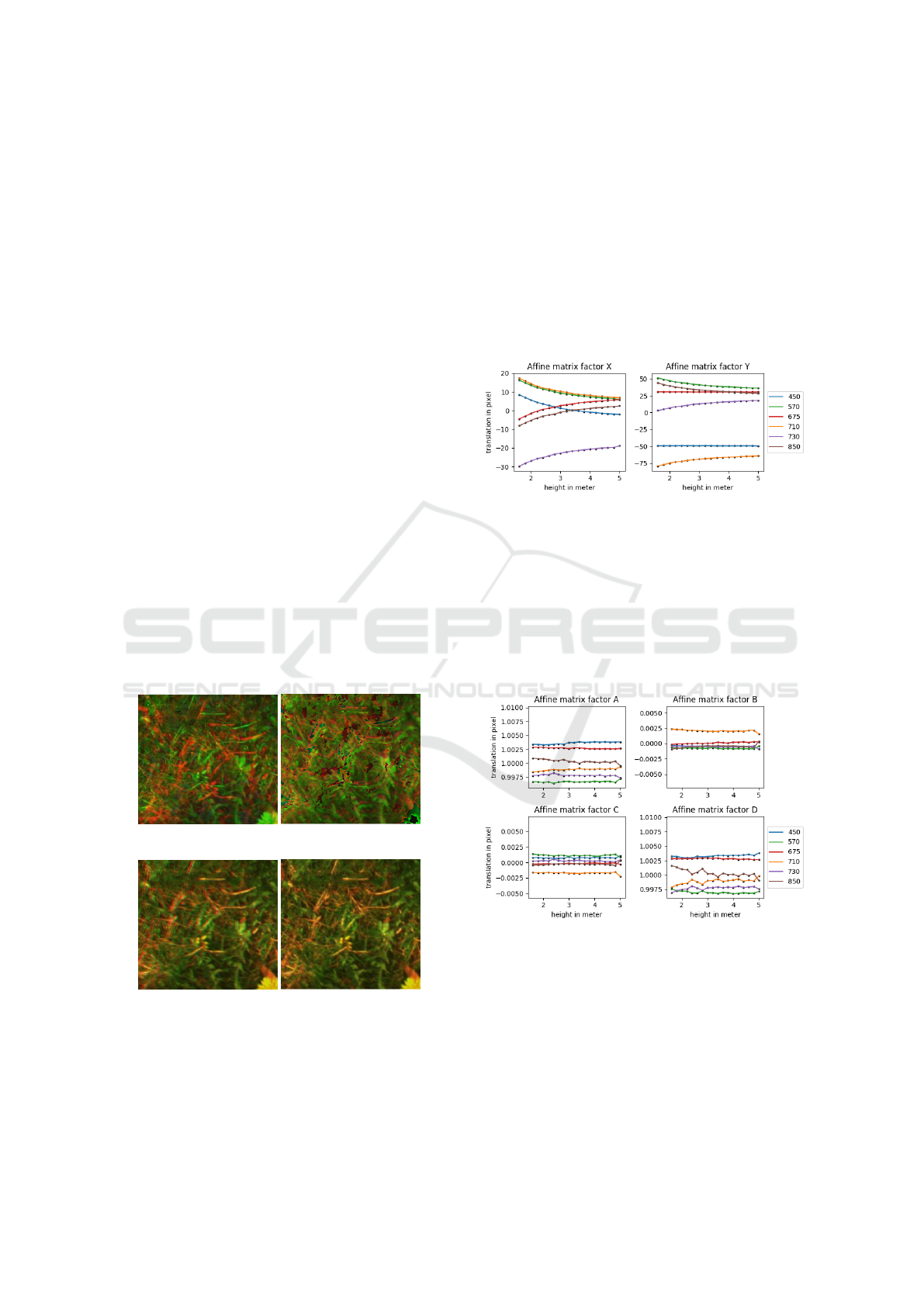
(a) raw image (b) manufacturer’s
(c) roughly corrected (d) fully corrected
Figure 4: Example of each correction and the manufacturers
results.
3.1 Affine Correction
The affine correction model is based on the calibration
dataset (where the chessboard are acquired). The 6
coefficients (A,B,C,D, X,Y ) of the affine matrix were
studied according to the height of the camera in or-
der to see their stability. It appears that the translation
part (X,Y ), depends on the distance to the field (ap-
pendix figure 5) according to the initial assumption.
On this part the linear model is used to estimate the
affine correction from an approximated height.
Figure 5: Affine matrix value by height.
Rotation and scale do not depend on the ground
distance (figure 6) according to the theory. These fac-
tors (A,B,C, D) are quite stable and close to identity,
as expected (accuracy depends on the spatial resolu-
tion of the board). As result, single calibration can be
used for this part of the matrix, and the most accurate
are used (i.e where the chessboard has the best spatial
resolution).
Figure 6: Affine matrix value by height.
After the affine correction, the remaining residual
distances have been extracted, it is computed using
the detected, filtered and matched key-point to the ref-
erence spectral band, figure 9 (up) shows an example
using 570 nm as reference before the perspective cor-
rection. The remaining distance between each spec-
tral band to the reference varies according to the dis-
tance between the real height and the nearest selected
(through linear model). Remember that a bias of +/-
Two-step Multi-spectral Registration Via Key-point Detector and Gradient Similarity: Application to Agronomic Scenes for Proxy-sensing
107
10cm was initially set to show the error in the worst
case, so the difference of errors between each of them
are due to the difference of sensors position in the
array to the reference and the provided approximate
height.
3.2 Perspective Correction
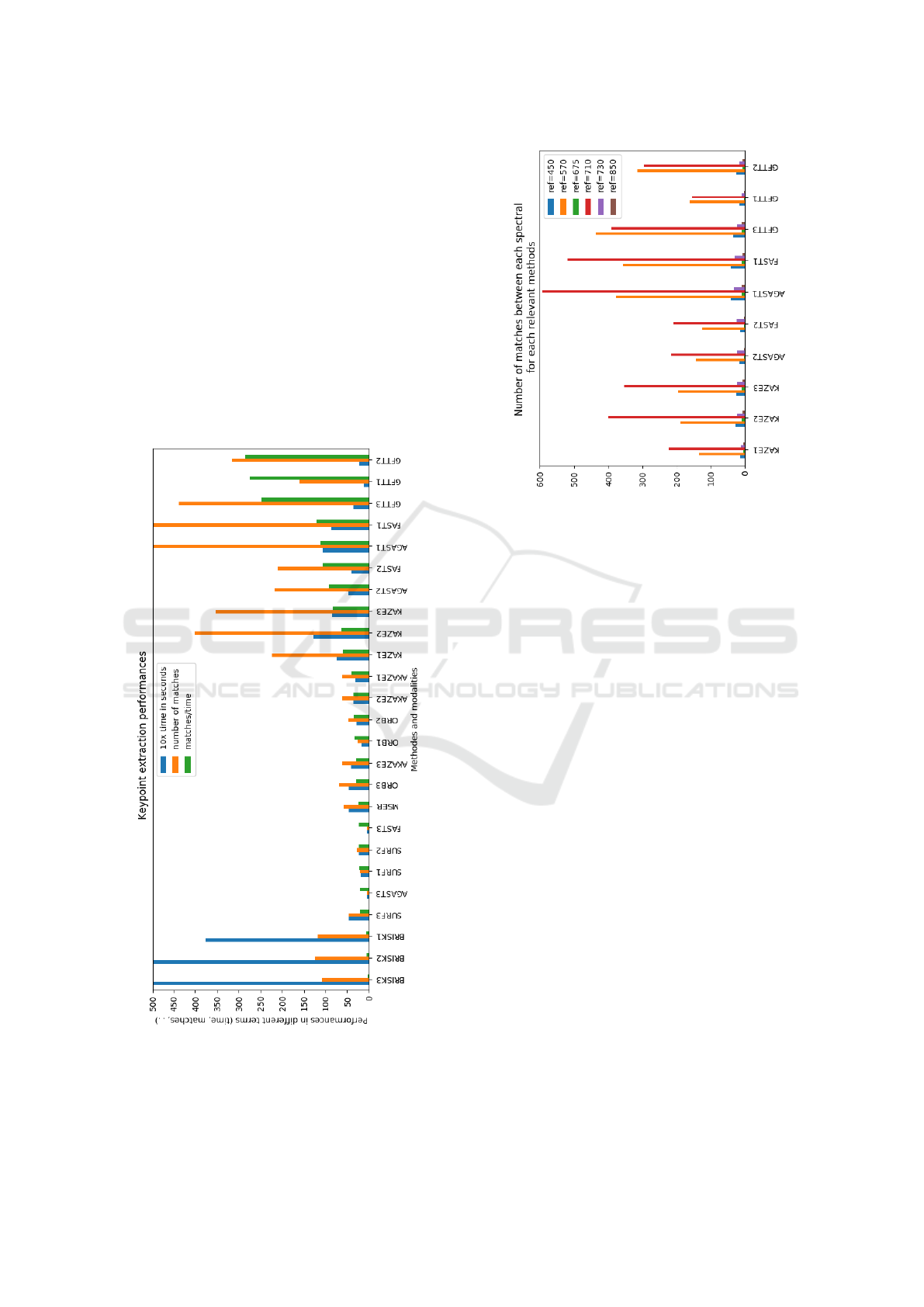
The figures 7 shows the numbers of key-points after
filtering and homographic association (minimum of
all matches) as well as the computation time and per-
formance ratio (matches/time) for each method. The
performance ratio is used to compare methods be-
tween them, bigger he is, greater is the method (bal-
anced between time and accuracy), making lower of
them unsuitable.
Figure 7: Features extractor performances after filtering and
homography association.
All these methods offer interesting results, the
choice of method depends on application needs be-
Figure 8: Key-point extractor performances.
tween computation time and accuracy, three methods
stand out in all of there modality:
• GFTT shows the best overall performance in both
computation time and number of matches
• FAST and AGAST1 are quite suitable too, with
acceptable computation time and greater matches
performances.
The other ones did not show improvement in term
of time or matches (especially compared to GFTT),
some of them show a small number of matches which
can be too small to ensure the precision. Increasing
the number of key-points matched allows a slightly
higher accuracy (Dantas Dias Junior et al., 2019). For
example, switching from SURF (30 results) to FAST
(130 results) reduces the final residual distances from
≈ 1.2 to ≈ 0.9 px but increases the calculation time
from ≈ 5 to ≈ 8 seconds.
All methods show that the best spectral band is
710 nm (in red), with an exception for SURF and
GFTT which is 570 nm. The figure 8 shows the
minimum number of matches between each reference
spectrum and all the others, for each relevant meth-
ods and modalities (KAZE, AGAST, FAST GFTT).
Choosing the right spectral reference is important, as
we can see, no correspondence is found in some cases
between 675-850 nm, but correspondences are found
between 675-710 nm and 710-850 nm, making the
710 nm more appropriate, the same behavior can be
observed for the other bands and 570 nm as the more
appropriate one. This is visible on the figure for all
methods, 570 nm and 710 nm have the best minimum
number of matches where all the other are quite small.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
108
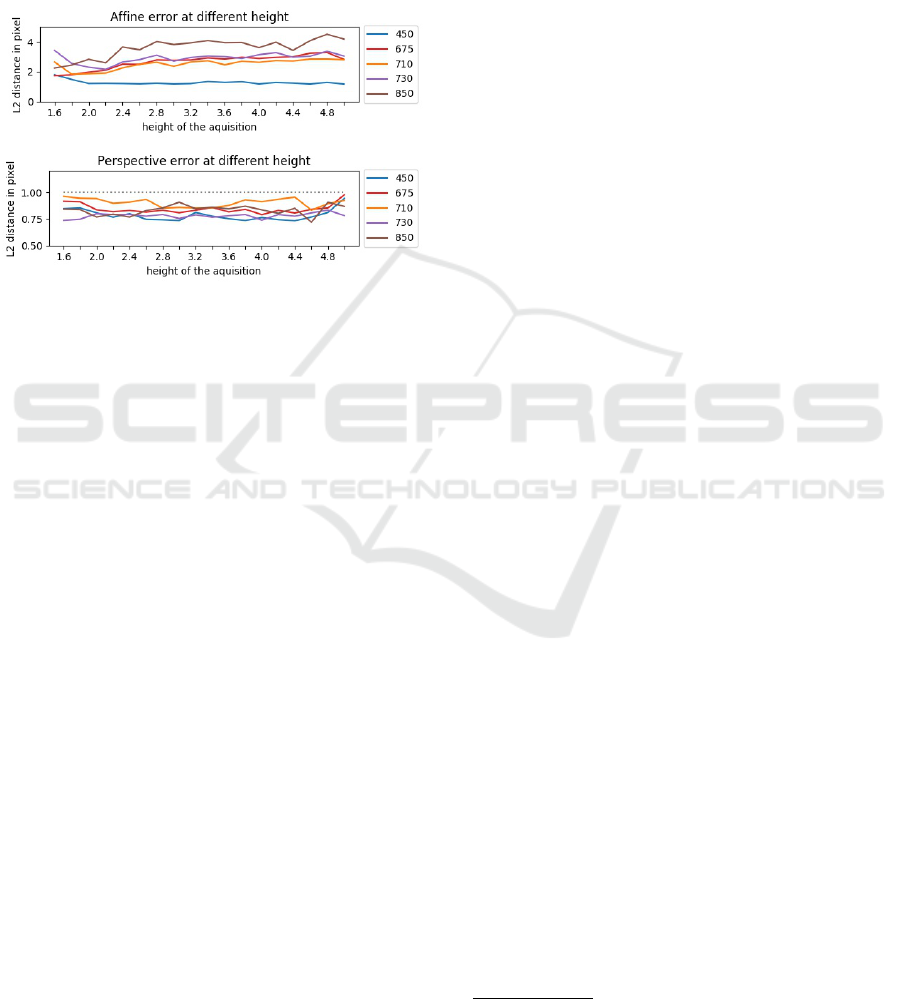
Residues of the perspective correction show that
we have correctly registered each spectral band, the
figure 9 (down) shows the residual distance at differ-
ent ground distances. In comparison the affine correc-
tion error are between [1.0 −4.8] px where the combi-
nation of affine and perspective correction the resid-
ual error are between [0.7 − 1.0] px. On average the
perspective correction enhance the residual error by
(3.5 − 0.9)/3.5 ≈ 74%.
Figure 9: (up) The mean distance of detected key-point be-
fore perspective correction with 570 nm as spectral refer-
ence (down) Perspective re-projection error with GFTT us-
ing the first modality and 570 nm as reference.
3.3 General Discussion
Even if the relief of the scene is not taken into ac-
count due to the used deformation model, in our case,
with flat ground, no difference arise. However, more
complex deformation models (Lombaert et al., 2012;
Bookstein, 1989) could be used to improve the re-
maining error. But could also, in some case, create
large angular deformations caused by the proximity
of key-points, of course, it’s possible to filter these
key-points, which would also reduce the overall accu-
racy.
Further research can be performed on each pa-
rameter of the feature extractors, for those who need
specific performance (time/precision), we invite any-
one to download the dataset and test various combina-
tions. Otherwise feature matching can be optimized,
at this stage, we use brute-force matching with post
filtering, but a different implementation that fulfill our
spatial properties should greatly enhance the number
of matches by reducing false positives.
4 CONCLUSION
In this work, the application of different techniques
for multi-spectral image registration was explored us-
ing the Airphen camera. We have tested nine type
of key-points extractor (ORB, GFTT, AGAST, FAST,
AKAZE, KAZE, BRISK, SURF, MSER) at different
heights and the number of control points obtained. As
seen in the method, the most suitable method is the
GFTT (regardless of modalities 1, 2 or 3) with a sig-
nificant number of matches 150 − 450 and a reason-
able calculation time 1.17 s to 3.55 s depending on the
modality.
Furthermore, the best spectral reference was de-
fined for each method, for example 570 nm for GFTT.
We have observed a residual error of less than 1 px,
supposedly caused by the difference of sensors nature
(spectral range, lens).
ACKNOWLEDGMENTS
The authors acknowledge support from European
Union through the project H2020 IWMPRAISE
3
(Integrated Weed Management: PRActical Im-
plementation and Solutions for Europe) and from
ANR Challenge ROSE through the project ROSEAU
4
(RObotics SEnsorimotor loops to weed AU-
tonomously).
We would like to thanks Combaluzier Quentin,
Michon Nicolas, Savi Romain and Masson Jean-
Benoit for the realization of the metallic gantry that
help us positioning the camera at different heights.
REFERENCES
Alcantarilla, P. F. and Solutions, T. (2011). Fast ex-
plicit diffusion for accelerated features in nonlinear
scale spaces. IEEE Trans. Patt. Anal. Mach. Intell,
34(7):1281–1298.
Ali, F., Khan, S. U., Mahmudi, M. Z., and Ullah, R. (2016).
A comparison of fast, surf, eigen, harris, and mser fea-
tures. International Journal of Computer Engineering
and Information Technology, 8(6):100.
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. In European conference
on computer vision, pages 404–417. Springer.
Bookstein, F. L. (1989). Principal warps: thin-plate splines
and the decomposition of deformations. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
11(6):567–585.
Bouguet, J.-Y. (2001). Camera calibration toolbox for mat-
lab.
Chen, S., Shen, H., Li, C., and Xin, J. H. (2018). Normal-
ized total gradient: A new measure for multispectral
image registration. IEEE Transactions on Image Pro-
cessing, 27(3):1297–1310.
3
https://iwmpraise.eu/
4
http://challenge-rose.fr/en/projet/roseau-2/
Two-step Multi-spectral Registration Via Key-point Detector and Gradient Similarity: Application to Agronomic Scenes for Proxy-sensing
109

Dantas Dias Junior, J., Backes, A., and Escarpinati,
M. (2019). Detection of control points for uav-
multispectral sensed data registration through the
combining of feature descriptors. pages 444–451.
Donoser, M. and Bischof, H. (2006). Efficient maximally
stable extremal region (mser) tracking. In 2006 IEEE
Computer Society Conference on Computer Vision
and Pattern Recognition (CVPR’06), volume 1, pages
553–560. Ieee.
Douarre, C., Crispim-Junior, C. F., Gelibert, A., Tougne,
L., and Rousseau, D. (2019). A strategy for mul-
timodal canopy images registration. In 7th Interna-
tional Workshop on Image Analysis Methods in the
Plant Sciences, Lyon, France.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: A paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Commun. ACM, 24(6):381–395.
Jin, X.-l., Diao, W.-y., Xiao, C.-h., Wang, F.-y., Chen,
B., Wang, K.-r., and Li, S.-k. (2013). Estimation of
wheat agronomic parameters using new spectral in-
dices. PLOS ONE, 8(8):1–9.
Kamoun, E. (2019). Image registration: From sift to deep
learning.
Lechenet, M., Bretagnolle, V., Bockstaller, C., Boissinot,
F., Petit, M.-S., Petit, S., and Munier-Jolain, N. M.
(2014). Reconciling pesticide reduction with eco-
nomic and environmental sustainability in arable
farming. PLOS ONE, 9(6):1–10.
Leutenegger, S., Chli, M., and Siegwart, R. (2011). Brisk:
Binary robust invariant scalable keypoints. In 2011
IEEE international conference on computer vision
(ICCV), pages 2548–2555. Ieee.
Lombaert, H., Grady, L., Pennec, X., Ayache, N., and
Cheriet, F. (2012). Spectral demons – image registra-
tion via global spectral correspondence. In Fitzgib-
bon, A., Lazebnik, S., Perona, P., Sato, Y., and
Schmid, C., editors, Computer Vision – ECCV 2012,
pages 30–44, Berlin, Heidelberg. Springer Berlin Hei-
delberg.
Mair, E., Hager, G. D., Burschka, D., Suppa, M., and
Hirzinger, G. (2010). Adaptive and generic corner de-
tection based on the accelerated segment test. In Euro-
pean conference on Computer vision, pages 183–196.
Springer.
Mor
´
e, J. J. (1978). The levenberg-marquardt algorithm:
Implementation and theory. In Watson, G., editor,
Numerical Analysis, volume 630 of Lecture Notes in
Mathematics, pages 105–116. Springer Berlin Heidel-
berg.
Ordonez, A., Arguello, F., and Heras, D. B. (2018). Align-
ment of hyperspectral images using kaze features. Re-
mote Sensing, 10(5).
Rabatel, G. and Labbe, S. (2016). Registration of visi-
ble and near infrared unmanned aerialvehicle images
based on Fourier-Mellin transform. Precision Agri-
culture, 17(5):564–587.
Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.
(2011). Orb: An efficient alternative to sift or surf. In
Proceedings of the 2011 International Conference on
Computer Vision, ICCV ’11, pages 2564–2571, Wash-
ington, DC, USA. IEEE Computer Society.
Sage, D. and Unser, M. (2003). Teaching image-processing
programming in java. IEEE Signal Processing Maga-
zine, 20(6):43–52. Using “Student-Friendly” ImageJ
as a Pedagogical Tool.
Sankaran, S., Khot, L. R., Espinoza, C. Z., Jarolmasjed,
S., Sathuvalli, V. R., Vandemark, G. J., Miklas, P. N.,
Carter, A. H., Pumphrey, M. O., Knowles, N. R., and
Pavek, M. J. (2015). Low-altitude, high-resolution
aerial imaging systems for row and field crop pheno-
typing: A review. European Journal of Agronomy,
70:112 – 123.
Seitz, H. (2010). Contributions to the minimum linear ar-
rangement problem.
Shi, J. et al. (1994). Good features to track. In 1994 Pro-
ceedings of IEEE conference on computer vision and
pattern recognition, pages 593–600. IEEE.
Tareen, S. A. K. and Saleem, Z. (2018). A comparative
analysis of sift, surf, kaze, akaze, orb, and brisk. 2018
International Conference on Computing, Mathemat-
ics and Engineering Technologies (iCoMET), pages
1–10.
Trajkovi
´
c, M. and Hedley, M. (1998). Fast corner detection.
Image and vision computing, 16(2):75–87.
Vakalopoulou, M. and Karantzalos, K. (2014). Automatic
descriptor-based co-registration of frame hyperspec-
tral data. Remote Sensing, 6.
Vioix, J.-B. (2004). Conception et r
´
ealisation d’un dispositif
d’imagerie multispectrale embarqu
´
e : du capteur aux
traitements pour la d
´
etection d’adventices.
Zhang, H., Wohlfeil, J., and Grießbach, D. (2016). Exten-
sion and evaluation of the agast feature detector.
Zitov
´
a, B. and Flusser, J. (2003). Image registration meth-
ods: A survey. Image and Vision Computing, 21:977–
1000.
Zuiderveld, K. (1994). Contrast limited adaptive histogram
equalization. In Graphics gems IV, pages 474–485.
Academic Press Professional, Inc.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
110
