
A Contrario Elliptical Arc, Circular Arc and Line Segment Detection
Boshra Rajaei
1,2
and Rafael Grompone von Gioi
2
1
Sadjad University of Technology, Mashhad, Iran
2
CMLA, ENS Paris-Saclay, France
Keywords:
Ellipse Detection, Line Segment Detection, A Contrario Theory.
Abstract:
In this paper, we propose a joint elliptical arc, circular arc, and line segment detector based on the a contrario
statistical approach. Our method is an extension of the ELSDc method, recently proposed for line segment
and elliptical arc detection. The main contribution is a more general geometrical model, which allows the
joint evaluation of the best combination of elliptical arcs, circular arcs, and line segments that corresponds to
a given contour. Different interpretations in terms of these elements are tried for the whole contour, instead
of locally as it is done in ELSDc. In addition, several minor improvements were performed to the heuristic
algorithm used to propose candidates. The performance of the proposed method is compared to the original
one on synthetic and real images.
1 INTRODUCTION
The extraction of geometrical primitives correspond-
ing to edges is a compact way of representing the ge-
ometrical contents of a digital image. Several such
algorithms were proposed in the past, among others,
for full lines and line segment detection (Bonci et al.,
2005; Ji et al., 2011; Alpatov et al., 2015), for cir-
cles and circular arc detection (Goulermas and Liat-
sis, 1999; Yao and Yi, 2016), and for ellipses and el-
liptical arc detection (Lu and Tan, 2008; Chia et al.,
2010; Arellano and Dahyot, 2016; Grbi
´
c et al., 2016).
Naturally, this kind of methods are exposed to both
false positive and false negative, due to the inevitable
noise of real images and the difficulty in defining
these primitives and especially their interactions.
In the past decade, Desolneux et al. (Desolneux
et al., 2000; Desolneux et al., 2008) proposed the so-
called a contrario methodology to set automatically
the detection thresholds in order to control the num-
ber of false detections. This statistical approach is
based on multiple testing procedures (Gordon et al.,
2007) and the main idea is that an observed structure
is meaningful only when the relation between its parts
is too regular to be the result of an accidental arrange-
ments of independent parts. This approach led to
several automatic feature detectors which are robust
to image noise. This includes detectors of line seg-
ments (Grompone von Gioi et al., 2010; Akinlar and
Topal, 2011), circles (Akinlar and Topal, 2013), sym-
metric patches (P
˘
atr
˘
aucean et al., 2013), regular ar-
rangement of line segments (Rajaei et al., 2016), sub-
jective contours (Rajaei et al., 2017), or point align-
ments (Lezama et al., 2014), to mention a few. In all
these cases, the a contrario approach was used to set
the detection thresholds for a single kind of geometric
primitive.
Recently, an a contrario method was proposed
for joint detection of line segments and elliptical
arcs (P
˘
atr
˘
aucean et al., 2017; P
˘
atr
˘
aucean et al., 2012).
The number of false detections is controlled by using
a contrario models for both, line segments and ellip-
tical arcs. When these two interpretations both satisfy
the detection threshold on the same part of the image,
the same modeling is also used to compare them and
to select the interpretation which corresponds better to
the observation. Therefore, this model selection step
helps to reduce the error of misinterpreting one primi-
tive by another. More precisely, the ELSDc algorithm
first uses some heuristics to propose detection candi-
dates. The aim of these heuristics is to obtain a high
recall without spending too much computational time;
rejecting false detections due to noise is the task of
the a contrario validation step. Three types of events,
polygonal line, elliptical arc and circular arc, are con-
sidered. A separate a contrario validation criterion is
used for each of these events, and a Number of False
Alarms (NFA) is assigned to each one, indicating its
degree of accidentalness in a random model. Finally,
if more than one event is declared meaningful, the one
538
Rajaei, B. and von Gioi, R.
A Contrario Elliptical Arc, Circular Arc and Line Segment Detection.
DOI: 10.5220/0009172005380545
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
538-545
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
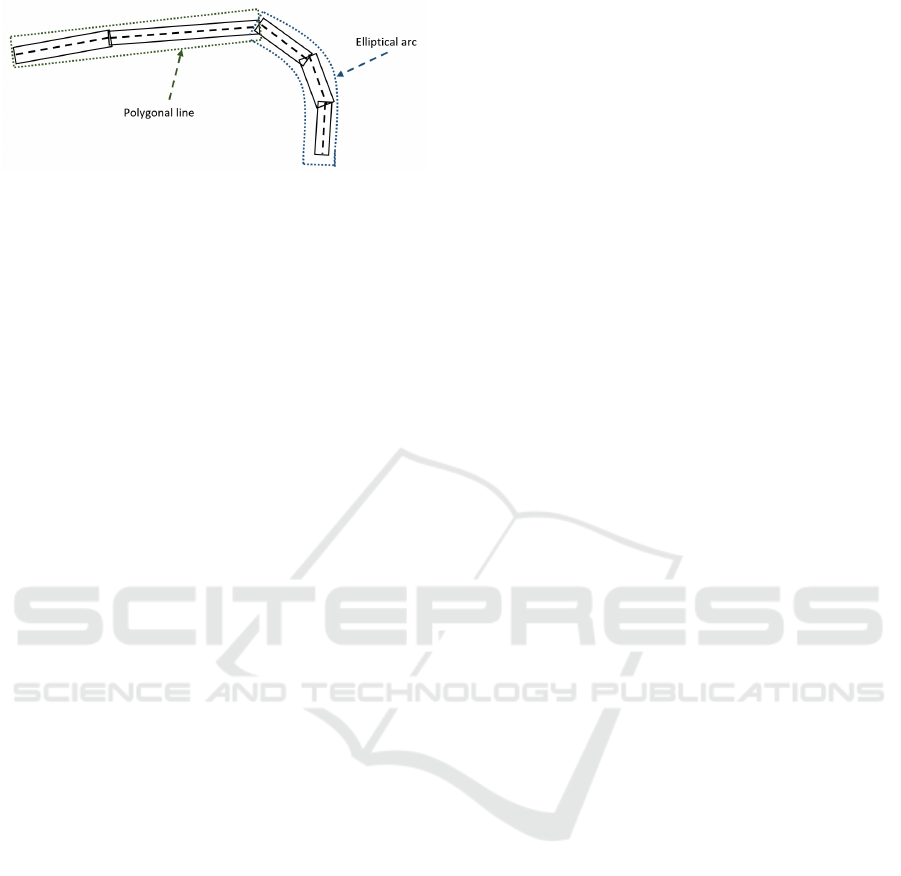
Figure 1: A sequence of rectangles and a candidate arcline
event composed of one line segment (a polygonal line of
one part) and an elliptical arc.
with best NFA value is kept as the detected primitive.
In practice, the ELSDc algorithm does not always
manage to produce the expected result. This is mainly
due to the fact that it starts by cutting a curve into parts
that does not change the curvature sign, i.e., the curve
is cut at inflection points. Then, each of those parts is
evaluated as either one polygonal line, one elliptical
arc, or as one circular arc. But a piece of curve with-
out curvature sign changes is not necessarily compose
of just one of those primitives. For example, a line
segment concatenated to an elliptical arc can share the
same curvature sign, see Figure 1. In such cases, the
polygonal approximation would usually get the best
fit and be kept. As a result, ELSDc has a tendency
to prefer the polygonal interpretation over circular or
elliptical arcs.
In this paper we propose an algorithm that follows
the same general scheme of ELSDc but using a richer
geometrical event. A whole curve (possibly includ-
ing curvature sign changes) is interpreted by what we
call an arcline, namely a sequence of line segments,
circular arcs and elliptical arcs. Again, heuristics are
used to propose candidate arcline events, i.e., different
ways of cutting the curve into line segments, circular
arcs and elliptical arcs. As in ELSDc, an a contrario
validation step rejects false detections due to noise,
and the valid interpretation with the best NFA value
is selected. As it is classic in model selection, this
step takes into consideration the complexity of the in-
terpretation and how well it fits the image data.
Wolters et al. (Wolters and Koch, 2017) also pro-
posed a detector for combined extraction of line seg-
ments and elliptical arcs which, by modeling the
topological relationships of the individual features in
a graph, describes more complex geometric struc-
tures over multiple connected primitives. The authors
showed that their algorithm outperforms ELSDc over
edges with multiple structures. However, on simple
edges the experimental results show that ELSDc has
a better performance. Our experiments will compare
the proposed method to the ELSDc (P
˘
atr
˘
aucean et al.,
2017) and to Wolters et al.’s method (Wolters and
Koch, 2017).
This paper is organized as follows. The next sec-
tion outlines the a contrario approach and section 3
summarizes the ELSDc algorithm. The main contri-
bution of this paper is introduced in section 4, where
the a contrario formulation for the arcline event is
presented. Then, the proposed algorithm is described
in section 5 and the experimental results are discussed
in section 6. Finally, section 7 concludes the paper.
2 THE A Contrario APPROACH
The a contrario theory (Desolneux et al., 2000; Des-
olneux et al., 2008) is a statistical framework used to
set detection thresholds automatically in order to con-
trol the number of false detections. It is based on the
non-accidentalness principle (Witkin and Tenenbaum,
1983; Lowe, 1985) which informally states that there
should be no detection in noise. In the words of
D. Lowe, “we need to determine the probability that
each relation in the image could have arisen by acci-
dent, P(a). Naturally, the smaller that this value is,
the more likely the relation is to have a causal inter-
pretation” (Lowe, 1985, p. 39).
A stochastic background model H
0
needs to be
defined, where the structure of interest is not present
and can only arise as an accidental arrangement. For
example, the ELSDc algorithm, as well as the algo-
rithm proposed here, is based on the orientation of the
image gradient. Thus, the background model H
0
as-
sumes that the gradient orientations at each pixel are
independent random variables, uniformly distributed
in [−π, π); under such model, a region of the image
where the gradient orientation follows a regular struc-
ture would be a rare accident.
We also need to define a family of events of in-
terest T . For feature detection the family of events is
the set of all the geometrical events considered, i.e.,
all the line segments, circular arcs, etc., considered
in the image domain. Then, we need to assess the
accidentalness of a candidate feature. For example,
if a line segment is present in an image, the gradient
orientation at the corresponding position would be or-
thogonal to the line segment. Then, given a candidate
line segment, one measures how well the image gradi-
ent corresponds to the candidate event, and we need to
evaluate the probability of observing by chance such
a good agreement. A rough agreement could arise
just by chance and thus does not correspond to an
interesting event; inversely, a good agreement would
be rare and suggest a casual reason instead of just a
lucky accident. In other words, when this probability
is small enough, there exists evidence to reject the null
hypothesis and declare the event meaningful. How-
A Contrario Elliptical Arc, Circular Arc and Line Segment Detection
539
ever, one needs to consider that multiple candidates
are tested. If 100 tests were performed, for example,
it would not be surprising to observe among them one
event that appears with probability 0.01 under random
conditions. The number of tests N
T
needs to be in-
cluded as a correction term, as it is done in the statis-
tical multiple hypothesis testing framework (Gordon
et al., 2007).
Following the a contrario methodology (Desol-
neux et al., 2000; Desolneux et al., 2008), we define
the Number of False Alarms (NFA) of an event e ob-
served up to an error k(e) as:
NFA(e) = N
T
·P
h
K
H
0
(e) ≤ k(e)
i
, (1)
where it is evaluated the probability of obtaining in
the background model H
0
an error K
H
0
(e) smaller
or equal to the observed one k(e). The smaller the
NFA value, the more unlikely the event e is to be ob-
served by chance in the background model H
0
; thus,
the more meaningful. The a contrario approach pre-
scribes to accept as valid detections the candidates
with NFA ≤ ε, for a predefined ε value. It can be
shown (Desolneux et al., 2000; Desolneux et al.,
2008) that under H
0
, the expected number of tests
with NFA ≤ ε is bounded by ε. As a result, ε corre-
sponds to the mean number of false detections under
H
0
. In most practical applications the value ε = 1 is
suitable and we will set it once and for all.
3 THE ELSDc ALGORITHM
The ELSDc algorithm (P
˘
atr
˘
aucean et al., 2017) em-
ploys the a contrario approach to detect more than
one image structure simultaneously. The method con-
siders polygonal line, elliptical arc, and circular arc as
three geometrical primitives. The detection strategy
goes through three main steps: 1) candidate genera-
tion; 2) candidate validation; and 3) model selection.
Candidate Generation. A heuristic procedure is
used to propose candidates instead of testing all possi-
ble ones, which would requires too much time. Start-
ing from one seed pixel, a region growing procedure
recursively merges all neighboring pixels sharing the
same gradient orientation up to a precision; this step
is based on the heuristics used in (Grompone von Gioi
et al., 2010). A rectangle covering the region of pixels
found determines a line segment with a given width.
Then, a second region is started from a new seed pixel
at one end-point of the rectangle. This procedure is
repeated until no new region is found. The result is a
chain of rectangles roughly following an image con-
tour. The chain of rectangles is then cut into parts
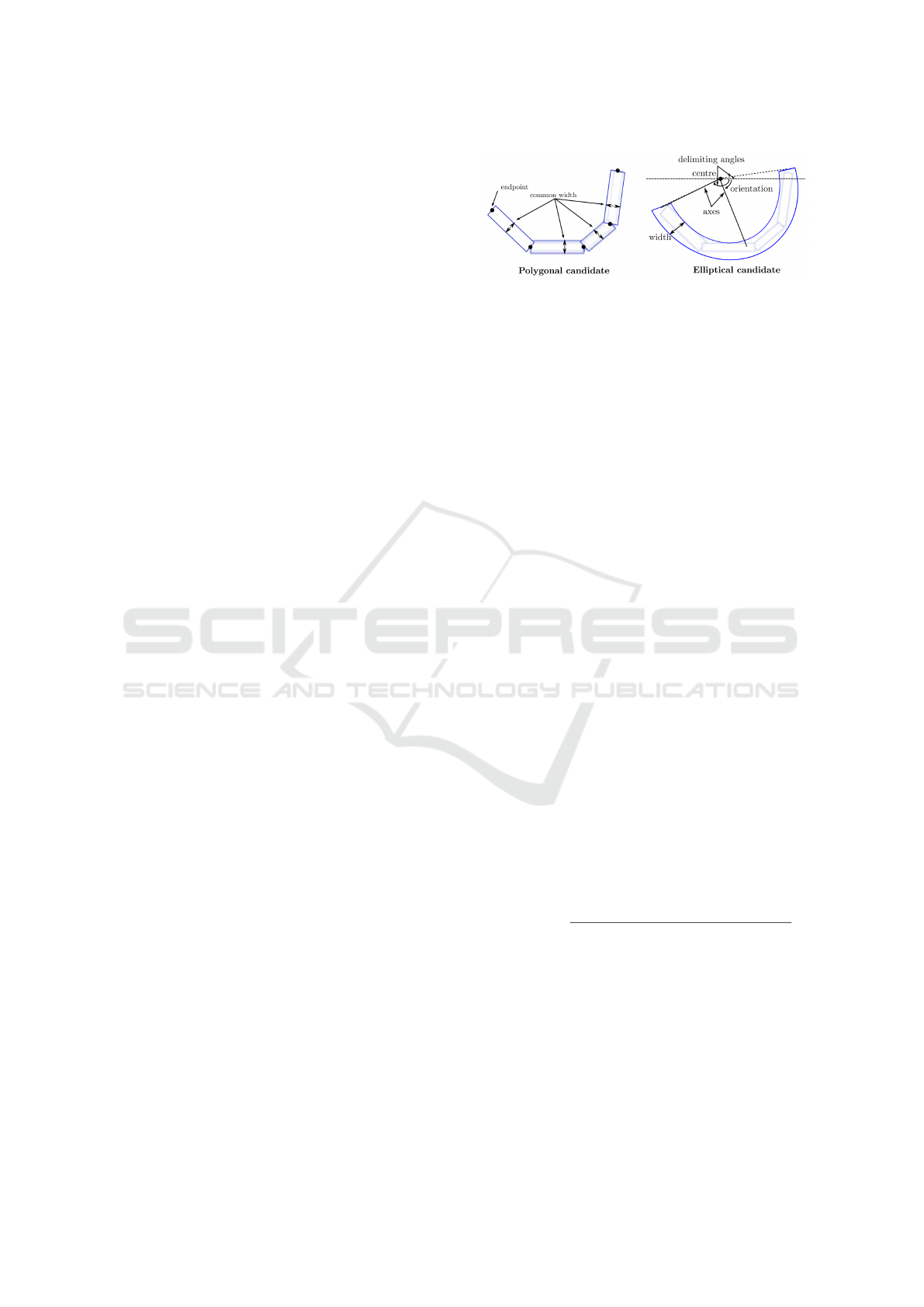
Figure 2: ELSDc polygonal line and elliptical arc candi-
dates. A polygonal line is defined as a sequence of rectangle
end-points with a common width. An elliptical arc is de-
termined by eight degrees of freedom: ellipse center, axes,
orientation, delimiting angles and width. (Figure reprinted
from (P
˘
atr
˘
aucean et al., 2017)).
such that consecutive rectangles in one part turn in the
same direction; this leaves parts which have the same
curvature sign. Finally, three candidates are generated
for each chain part: a polygonal line p
d
composed of
d line segments, determined by the central lines of
the rectangles in the chain; a circular arc c obtained
by fitting the gradient orientations on the pixels cor-
responding to the rectangles; and an elliptical arc t,
similarly obtained by fitting the gradient orientations
to an elliptical arc. Figure 2 shows an example of
a part of a chain of rectangles, corresponding to a
polygonal candidate and a fitted elliptical candidate.
See (P
˘
atr
˘
aucean et al., 2017) for more details.
Candidate Validation. After candidate generation,
the ELSDc algorithm employs an a contrario valida-
tion step to reject non-meaningful candidates accord-
ing to equation 1. Let us call I the input image of size
n ×m. Let S(e) denotes the set of pixels supporting
an event e, that is, the set of pixels in the correspond-
ing positions of the image. Let l(e) be the size of the
support region S(e). The agreement error between a
candidate event e and the image I is measured by the
sum of the normalized angle difference between the
gradient orientation and the normal direction to the
event at each pixel of the support region S(e):
k(e) =
∑
i∈S(e)
AngleDifference
∇I(i), dir
⊥e
(i)
π
,
(2)
where the sum is over all pixels i belonging to the
support region S(e), ∇I(i) is the gradient of the im-
age at pixel i, and dir
⊥e
(i) corresponds to the normal
direction to the geometrical event e at position i. The
agreement error k(e) takes values between zero (when
there is a perfect agreement between the event and the
image gradient) and l(e) (for the worst possible agree-
ment) (P
˘
atr
˘
aucean et al., 2017).
Under the background model H
0
defined in sec-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
540

tion 2, the normalized angle differences at each pixel
are independent random variables following a uni-
form distribution in [0, 1]. Thus, K
H
0
(e) follows
an Irwin-Hall distribution of l(e) parameters, which
leads to the probability term in Eq. 1 given by
P
h
K
H
0
(e) ≤ k(e)
i
=
1
l(e)!
bk(e)c
∑
j=0
(−1)
j
l(e)
j
(k(e) − j)
l(e)
,
(3)
where bxc is the largest integer not greater than x
and
a
b
is the binomial coefficient. To simplify the
presentation, we will use the upper-bound given by
first term, P
h
K
H
0
(e) ≤ k(e)
i
≤
[k(e)]
l(e)
l(e)!
, which allows
a more compact formula and is accurate enough for
our needs, see (P
˘
atr
˘
aucean et al., 2017).
We will focus here on the main two events: polyg-
onal lines (p
d
) and elliptical arcs (t) (circular arcs
are treated as a particular case of elliptical event).
In each case, the agreement error en Eq. 2 is com-
puted relative to the corresponding primitive, polyg-
onal line or elliptical arc. The difference in formu-
lation is in the number of events (N
T
) considered in
each family. The number of tests are approximated by
2
d+1
(mn)
(d+1)+
1
2
for a polygonal line of d segments,
and 18(mn)
4
for an elliptical event (recall that the im-
age size is n ×m), see (P
˘
atr
˘
aucean et al., 2017). Then,
the NFA values for polygonal line and elliptical arc
events are obtained from Eq. 1:
NFA(p
d
) = 2
d+1
(mn)
(d+1)+
1
2
[k(p
d
)]
l(p
d
)
l(p
d
)!
, (4)
NFA(t) = 18(mn)
4
[k(t)]
l(t)
l(t)!
. (5)
As usual, an event with NFA ≤ ε is considered as a
detection, with ε = 1.
Model Selection. For some sequence of rectangles,
it could happen that more than one candidate (p
d
, c,
or t) obtain NFA ≤ ε and are thus meaningful. As
stated in section 2, the smaller the NFA value, the
more meaningful the event. Thus, the ELSDc algo-
rithm simply selects and keeps, among those three,
the interpretation with the smallest NFA value.
4 THE ARCLINE EVENT
As explained in section 3, the first step of the ELSDc
algorithm cuts a chain of rectangles into parts in
which there is no change of curvature sign; then, each
of these parts is evaluated as either a polygonal line, a
circular arc, or an elliptical arc. But a piece of curve
without curvature sign changes can corresponds to a
sequence of line segments and elliptical arcs, see fig-
ure 1 for an example. In such cases, ELSDc would
produce either one elliptical arc with a rough fit or,
more often, a polygonal line.
To overcome this issue, we define a new event
which we call an arcline that consists in a sequence
of line segments, circular arcs, and elliptical arcs:
Definition 1. An arcline a
g,h
f
is an ordered set of f
primitives, where g of them are circular arcs, h are
elliptical arcs and the remaining f −g −h are line
segments, and such that consecutive elements in the
chain share end-points. The geometrical configura-
tion is completed with a width value, defining a region
of pixels inside each geometrical primitive.
The rest of this section is dedicated to the presen-
tation of the a contrario formulation to validate ar-
cline events. Next section will describe an algorithm
similar to ELSDc but using arclines as geometrical
primitives.
The same background model H
0
defined in sec-
tion 2 is used and the agreement error k(a
g,h
f
) between
an arcline a
g,h
f
and the image is measured as in Eq. 2,
where dir
⊥a
g,h
f
(i) corresponds to the normal direction
to the primitive of a
g,h
f
at position i, i.e., either a line
segment, a circular arc, or an elliptical arc. Again, the
only difference in the formulation is in the number of
test N
T
in Eq. 1.
The number of elements in the family must in-
clude any relevant arcline event. First, we start by
dividing the family according to the number of ele-
ments in the chain, f , and dividing the total number
of allowed false detection ε accordingly. The arclines
with just one primitive would be allowed
ε
2
false de-
tections in H
0
; the arclines composed of two primi-
tives would be allowed
ε
2
2
false detections in H
0
; gen-
erally, the arclines composed of f primitives would
be allowed
ε
2
f
false detections in H
0
. Thus, an arcline
composed of f primitives would be declared mean-
ingful when
N
T
( f ) ·P
h
K
H
0
(a
g,h
f
) ≤ k(a
g,h
f
)
i
≤
ε
2
f
, (6)
where N
T
( f ) is the number of arclines composed of
f primitives. As a consequence, the total number of
false detections in H
0
would be bounded, as desired,
by
∞
∑
f =1
ε
2
f
= ε. (7)
The condition in Eq. 6 is equivalent to
2
f
·N
T
( f ) ·P
h
K
H
0
(a
g,h
f
) ≤ k(a
g,h
f
)
i
≤ ε, (8)
A Contrario Elliptical Arc, Circular Arc and Line Segment Detection
541
where 2
f
appears as a factor in the number of tests.
In an arcline composed of f primitives, each of
the f primitives can be either a line segment, a circu-
lar arc, or an elliptical arc. Thus, there are 3
f
possi-
ble configurations. Again, we can divide ε among all
these 3
f
configurations, what is equivalent, as before,
to including a factor 3
f
in the number of tests.
Now, for an arcline composed f primitives in one
of the 3
f
possible configurations, there are f + 1 end-
points in the chain, and considering pixel precision
in an n ×m image, there are (nm)
f +1
possibilities.
For each of the g circular arcs (whose end-points are
determined), there is still one degree of freedom to
determine its curvature. Assuming roughly
√
mn op-
tions for each one, this adds a factor (nm)
g
2
. Similarly,
an elliptical arc still has three degrees of freedom once
the end-points are determined, adding a factor (nm)
3
2
h
for the h elliptical arcs. Finally, we need to determine
the arcline width; again, we will assume that there
are about
√
mn possible values. Then, there are about
(nm)
f +
3+g+3h
2
arclines to be considered.
All in all, the NFA for the arcline event is given by
NFA(a
g,h
f
) = 2
f
3
f
(nm)
f +
3+g+3h
2
h
k(a
g,h
f
)
i
l(a
g,h
f
)
l(a
g,h
f
)!
.
(9)
As usual, an arcline a
g,h
f
is declared meaningful when
NFA(a
g,h
f
) ≤ ε. Also, the smaller the NFA(a
g,h
f
)
value, the more meaningful the arcline. Thus, the
model selection step will keep the arcline with the
smallest NFA value as the best interpretation.
5 THE ALD ALGORITHM
The ArcLine Detector (ALD) shares the same three
step strategy of ELSDc: 1) candidate generation; 2)
candidate validation; and 3) model selection. Here all
the candidates are arclines with different configura-
tions. Note that the candidate generation step aims at
avoiding false negatives while not spending too much
computational time; missing detections are in part due
to this heuristic step, when failing to propose the right
candidate. However, accepted detections must satisfy
the statistical test imposed by the a contrario theory;
the same is true for the model selection step.
Algorithm 1 outlines the main steps of the ALD
method. Starting from seed pixels, a sequence of rect-
angular regions r is obtained by an iterative region
growing procedure (steps 1 to 4). Then, all different
ways of partitioning the sequence into line segments,
circular arcs, and elliptical arcs are examined (steps 5
to 12). For each configuration a
g,h
f
, the NFA value is
computed, which evaluates its agreement with the in-
put image I (step 9). Model selection is performed by
keeping the arcline a
?
with the smallest NFA value
(steps 10 to 12). Finally, the arcline a
?
is stored if it
is meaningful, i.e., if NFA ≤ ε with ε = 1 (steps 13
to 15). The supporting pixels of a validated arcline
are prevented from being used again to avoid spend-
ing time on data already handled.
Algorithm 1: Arcline detector algorithm.
input : image I
output: a set of validated arclines A
1 I
g
← G
σ
? I Gaussian blur
2 Seeds ←{s, |∇I
g
(s)| > ρ} set of seed pixels
3 for s ∈ Seeds do loop on seed pixels
4 r ← RegionGrowing(s,∇I
g
, θ, γ, δ)
5 P ← GeneratePartitions(r)
6 nfa
?
← ∞
7 for partition ∈ P do loop on partitions
8 a
g,h
f
← FitArcline(partition, r, ∇I
g
, α)
9 nfa ← NFA(a
g,h
f
) NFA of arcline, Eq. 9
10 if nfa < nfa
?
then
11 nfa
?
← nfa keep best NFA
12 a
?
← a
g,h
f
keep best arcline
13 if nfa
?
≤ 1 then meaningful arcline found
14 add a
?
to A
15 remove supp. pixels of a
?
from Seeds
Given the richness of the arcline event, generat-
ing relevant candidates is quite challenging; a set of
heuristic methods are used. The main ideas are simi-
lar to the ones in the ELSDc algorithm, but some im-
provements were introduced. As in ELSDc, a Gaus-
sian blurred version I
g
of the input image is com-
puted (step 1) to be used for candidate generation;
this makes the region growing process more robust
to noise and small irregularities. However, the NFA
value used for validation (step 9) is computed on the
non-blurred input image I. To select good starting
points which probably belongs to edges, the seeds are
selected as pixels with gradient magnitude larger than
a fixed value ρ (step 2).
The region growing procedure (step 4) groups to-
gether pixels that share the same gradient orientation
up to a tolerance θ. Those pixels must, nevertheless,
also satisfy the condition that their gradient magni-
tude be larger than γ. In ELSDc, ρ and γ have the same
value, but here ρ is more strict for selecting good seed
pixels, while allowing a more relaxed condition γ on
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
542

Figure 3: An instance of an edge with two low contrast re-
gions. The region growing algorithm used in ELSDc splits
the support region into three regions. This kind of regions
are better handled by the hysteresis-like approach with two
gradient thresholds proposed here: a week threshold for re-
gion growing to pass the gaps and a stronger one for actual
candidate generation and validation.
the neighbor pixels. Figure 3 shows a simple example
were the new strategy helps to improve the result. A
small gap in edge points, that happens frequently in
real images due to changes in intensity, stops the re-
gion growing; the more permissive threshold γ, there-
fore allows to jump gaps.
As in ELSDc, the rectangles are cut until a min-
imum density of support pixels of δ is reached. But
here, only pixels with gradient magnitude larger than
α times gradient magnitude of the seed pixel s are
considered when fitting the arcline a (step 8) to make
sure that only strong edge points determine the final
detection. Besides this improvement, the fitting of el-
liptical and circular arcs to the region r is performed
by the method proposed in (P
˘
atr
˘
aucean et al., 2012).
Several strategies are used to reduce the computa-
tional burden. An upper bound to the number of parts
in the partitions is imposed, currently set to 10. Also,
the validation step is straightforwardly parallelized.
The parameter of the candidate generation heuristics
are set to σ = 1, θ = 22.5
◦
, ρ = 10, γ = 5, δ = 0.3
and α = 0.2. For more details, we refer the reader
to (P
˘
atr
˘
aucean et al., 2017) and to the publicly avail-
able source code of the proposed method (see below).
6 EXPERIMENTS
In this section, we examine the ALD algorithm over
a few synthetic and real images. The interested read-
ers may refer to the web page of the article
1
and use
the online demo for trying out the algorithm on ar-
bitrary images. For comparison purposes, two recent
1
http://dev.ipol.im/
∼
jirafa/ald/
algorithms which both detect straight lines and ellipti-
cal arcs simultaneously are used, ELSDc (P
˘
atr
˘
aucean
et al., 2017) and Wolters et al (Wolters and Koch,
2017).
Figure 4 shows the detections of ELSDc and ALD
algorithms on three images with multiple line seg-
ment and elliptical arc primitives along edges. Here,
the ELSDc algorithm is executed using the public
available source code of the authors. On edges con-
taining both, straight and non-straight structures, the
ELSDc algorithm is forced to choose between either
an elliptical arc or a polygonal line. In many cases the
decrease in agreement error in polygonal line event
dominates over the increased number of tests. There-
fore, the ELSDc algorithm chooses polygonal line
and, comparing to ALD, misses many curvy struc-
tures. This effect is visible in, for instance, the inner
contour in parking sign image and in the outer circular
arc in the dolphin image.
Additionally, the double gradient thresholds (ρ
and γ) in the region growing and validation steps
in ALD result in longer regions and give the algo-
rithm the chance of using a more suitable primitive
to model the edge. This happen in the clocks im-
age where ELSDc misses some curves from the outer
clock boundaries and groups the pixels in different re-
gions.
The second experiment compares the algorithms
using the three real images from (Wolters and Koch,
2017)
2
, see Figure 5. The ALD algorithm produces
a good synthesis between both methods, detecting as
many good line segment structures as ELSDc, and as
many good elliptical or circular arcs as Wolters et al.’s
method.
7 CONCLUSIONS
We proposed an a contrario model for line segment,
circular arc, and elliptical arc detection in digital im-
ages. The arcline geometrical event is used to express
an edge in terms of those primitives and select the
best interpretation for the whole edge. An heuristic
algorithm is also proposed to cope with the computa-
tional burden of finding good candidates. The results
compares favorably to state-of-the-art methods. Fu-
ture work will concentrate on improving the ellipse
fitting step, which in some cases leads to small local-
ization offsets.
2
We did not have access to the source code of the
method by Wolters et al.; to have a fair comparison, the re-
sults of that algorithm are reprinted from the original paper.
A Contrario Elliptical Arc, Circular Arc and Line Segment Detection
543

Figure 4: Detected image structures on the synthetic ‘parking sign’ image, and real ‘dolphin’ and ‘clocks’ images. From left
to right are the input images, the result of ELSDc (P
˘
atr
˘
aucean et al., 2017), and the result of the proposed ALD algorithm
(red: elliptical or circular arcs, blue: line segments and, green: cut points).
Figure 5: Detected image structures on the images ‘building’, ‘window’ and ‘roof’. From left to right are the input images,
the results of ELSDc (P
˘
atr
˘
aucean et al., 2017), Wolters et al. (Wolters and Koch, 2017) (reprinted from (Wolters and Koch,
2017)), and the proposed ALD algorithm (red: elliptical or circular arcs, blue: line segments, and green: cut points).
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
544

REFERENCES
Akinlar, C. and Topal, C. (2011). Edlines: A real-time line
segment detector with a false detection control. Pat-
tern Recognition Letters, 32(13):1633–1642.
Akinlar, C. and Topal, C. (2013). Edcircles: A real-time
circle detector with a false detection control. Pattern
Recognition, 46(3):725–740.
Alpatov, B. A., Babayan, P. V., and Shubin, N. Y. (2015).
Weighted radon transform for line detection in noisy
images. Journal of Electronic Imaging, 24(2):023023.
Arellano, C. and Dahyot, R. (2016). Robust ellipse detec-
tion with gaussian mixture models. Pattern Recogni-
tion, 58:12–26.
Bonci, A., Leo, T., and Longhi, S. (2005). A bayesian ap-
proach to the hough transform for line detection. IEEE
Transactions on Systems, Man, and Cybernetics-Part
A: Systems and Humans, 35(6):945–955.
Chia, A. Y.-S., Rahardja, S., Rajan, D., and Leung, M. K.
(2010). A split and merge based ellipse detector with
self-correcting capability. IEEE Transactions on Im-
age Processing, 20(7):1991–2006.
Desolneux, A., Moisan, L., and Morel, J.-M. (2000). Mean-
ingful alignments. International Journal of Computer
Vision, 40(1):7–23.
Desolneux, A., Moisan, L., and Morel, J.-M. (2008). From
gestalt theory to image analysis: a probabilistic ap-
proach, volume 34. Springer.
Gordon, A., Glazko, G., Qiu, X., and Yakovlev, A. (2007).
Control of the mean number of false discoveries, Bon-
ferroni and stability of multiple testing. The Annals of
Applied Statistics, 1(1):179–190.
Goulermas, J. Y. and Liatsis, P. (1999). Incorporating gradi-
ent estimations in a circle-finding probabilistic hough
transform. Pattern Analysis & Applications, 2(3):239–
250.
Grbi
´
c, R., Grahovac, D., and Scitovski, R. (2016). A
method for solving the multiple ellipses detection
problem. Pattern Recognition, 60:824–834.
Grompone von Gioi, R., Jakubowicz, J., Morel, J.-M., and
Randall, G. (2010). LSD: A fast line segment detector
with a false detection control. IEEE transactions on
pattern analysis and machine intelligence, 32(4):722–
732.
Ji, J., Chen, G., and Sun, L. (2011). A novel hough trans-
form method for line detection by enhancing accumu-
lator array. Pattern Recognition Letters, 32(11):1503–
1510.
Lezama, J., Morel, J.-M., Randall, G., and Grompone von
Gioi, R. (2014). A contrario 2d point alignment de-
tection. IEEE transactions on pattern analysis and
machine intelligence, 37(3):499–512.
Lowe, D. (1985). Perceptual Organization and Visual
Recognition. Kluwer Academic Publishers.
Lu, W. and Tan, J. (2008). Detection of incomplete el-
lipse in images with strong noise by iterative ran-
domized hough transform (irht). Pattern Recognition,
41(4):1268–1279.
P
˘
atr
˘
aucean, V., Grompone von Gioi, R., and Ovsjanikov,
M. (2013). Detection of mirror-symmetric image
patches. In Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition Workshops,
pages 211–216.
P
˘
atr
˘
aucean, V., Gurdjos, P., and Grompone von Gioi, R.
(2012). A parameterless ellipse and line segment de-
tector with enhanced ellipse fitting. In Proc. of ECCV.
P
˘
atr
˘
aucean, V., Gurdjos, P., and von Gioi, R. G. (2017).
Joint a contrario ellipse and line detection. IEEE
transactions on pattern analysis and machine intelli-
gence, 39(4):788–802.
Rajaei, B., Grompone von Gioi, R., Facciolo, G., and
Morel, J.-M. (2017). Straight subjective contour de-
tector. In Proceedings of the 10th International Sym-
posium on Image and Signal Processing and Analysis,
pages 183–188. IEEE.
Rajaei, B., Grompone von Gioi, R., and Morel, J.-M.
(2016). From line segments to more organized
gestalts. In 2016 IEEE Southwest Symposium on Im-
age Analysis and Interpretation (SSIAI), pages 137–
140. IEEE.
Witkin, A. P. and Tenenbaum, J. M. (1983). On the role of
structure in vision. In Beck, J., Hope, B., and Rosen-
feld, A., editors, Human and Machine Vision, pages
481–543. Academic Press.
Wolters, D. and Koch, R. (2017). Combined precise ex-
traction and topology of points, lines and curves in
man-made environments. In German Conference on
Pattern Recognition, pages 115–125. Springer.
Yao, Z. and Yi, W. (2016). Curvature aided hough transform
for circle detection. Expert Systems with Applications,
51:26–33.
A Contrario Elliptical Arc, Circular Arc and Line Segment Detection
545
