
Artificial Neural Networks for Quantitative Microwave Breast Imaging
M. Ambrosanio
a
, S. Franceschini
b
, F. Baselice
c
and V. Pascazio
d
Department of Engineering, University of Naples Parthenope, Naples, Italy
Keywords:
Microwave Imaging, Inverse Scattering, Artificial Neural Network, MIMO Systems, Biomedical Imaging.
Abstract:
This paper is focused on the use of artificial neural networks (ANNs) for biomedical microwave imaging of
breast tissues in the framework of advanced breast cancer imaging techniques. The proposed scheme processes
the scattered field collected at receivers locations of a multiview-multistatic system and aims at providing an
estimate of the morphological and dielectric features of the breast tissues, which represents a strongly non-
linear scenario with several challenging aspects. In order to train the network, a simulated data set has been
created by implementing the forward problem and an automatic randomly-shaped breast profile generator
based on the statistical distribution of complex permittivity of breast biological tissues was developed. Some
numerical tests were carried out to evaluate the performance of the proposed method and, in conclusion, we
found that the use of ANNs for quantitative biomedical imaging purposes seems to be very promising.
1 INTRODUCTION
Inverse scattering (IS) techniques represent a valuable
imaging modality for several applications in which
a non-destructive testing is required (Massa et al.,
2005; Persico et al., 2018; Ambrosanio and Pascazio,
2015), especially for biomedical diagnostics (Bevac-
qua et al., 2019; Ambrosanio et al., 2016). The capa-
bility of these approaches to retrieve physical as well
as geometrical properties of the objects under test lo-
cated in an inaccessible domain by exploiting electro-
magnetic waves makes them very attractive.
In order to detect inhomogeneities in a medium,
the scattered field related to these targets is collected
and processed in a coherent fashion. Nevertheless,
the intrinsic ill-posedness and strong non-linearity of
the inverse problem at hand still represent a big issue
(Colton and Kress, 2012; Isernia et al., 1997). Classi-
cal approaches exploit some linear and nonlinear ap-
proximations to handle the non-linearity issue, such
as the iterative Born method, the distorted Born iter-
ative method (Ahsan et al., 2018) and others (Bevac-
qua and Isernia, 2018; Estatico et al., 2016). There-
fore, by minimising a proper functional, the mismatch
between estimated and measured data is evaluated at
each step of the iterative procedure in order to provide
a
https://orcid.org/0000-0003-3669-8183
b
https://orcid.org/0000-0002-7608-6686
c
https://orcid.org/0000-0002-5964-8667
d
https://orcid.org/0000-0002-5403-5482
a recovery of the unknown object.
Unfortunately, these approaches are time-
consuming and computationally expensive, and thus
not suitable for real-time applications. However,
some non-iterative methods are available to provide
reconstructed images in a fast fashion, but they are
still not accurate in the recoveries, especially if strong
scatterers are present in the region of interest.
In this framework, some recent methodologies
based on artificial neural networks (ANNs) and more
in general on machine learning may be very bene-
ficial to face the drawbacks related to classical ap-
proaches (Lucas et al., 2018). Recently, machine
learning has attracted attention with interesting results
for image classification and segmentation, but ANNs
have proven to provide good results also in case of ill-
posed inverse problems (Caorsi and Gamba, 1999).
In this paper, we propose an approach based on
neural networks for the quantitative biomedical imag-
ing of breast profiles via a direct inversion scheme.
Thus, the output of the network consists in an estimate
of the complex permittivity profile given the scattered
field as input.
2 MATHEMATICAL
BACKGROUND
For the sake of simplicity, a bounded and simply-
connected investigation domain Ω is considered in
204
Ambrosanio, M., Franceschini, S., Baselice, F. and Pascazio, V.
Artificial Neural Networks for Quantitative Microwave Breast Imaging.
DOI: 10.5220/0009172802040208
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 2: BIOIMAGING, pages 204-208
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Ω
Γ
𝜖
𝑠
1
𝒓
𝜖
𝑠
2
𝒓
𝑇𝑥
𝑅𝑥
Figure 1: Sketch of the multiview-multistatic imaging sys-
tem for the non-invasive testing of the imaging domain Ω.
The antennas are locate on a measurement curve Γ.
a homogeneous background medium whose electro-
magnetic features (ε
b
, σ
b
) or an estimate of theirs
are assumed to be known a priori. All the scatter-
ers, as well as the background medium, are assumed
to have a constant magnetic permeability equal to
µ
0
= 4π · 10
−7
H/m.
In the considered scattering experiments, an im-
pinging time-harmonic wave illuminates the objects
of interest at a certain frequency by a transmitting an-
tenna, and the corresponding scattered field generated
by the interaction of the incident field with the targets
is collected by some receivers located on a measuring
curve which surrounds the imaging domain. In or-
der to simplify the mathematical formulation, a scalar
two-dimensional (2D) scenario will be considered in
the following.
The incident fields are modelled as transverse-
magnetic (TM) polarised with respect to z axis which
represents the symmetry direction and all the scatter-
ers located in the domain Ω are assumed to have a
constant section along this axis, as shown in Fig. 1.
Under these hypotheses and by omitting the time fac-
tor e
jωt
, the scattering problem can be stated as a 2D
scalar equation, known as electric field integral equa-
tion (EFIE), i.e. (Colton and Kress, 2012):
E
s
(r
r
r
R
, r
r
r
T
, ω) =
= k
2
b
Z
Ω
G(r
r
r
R
− r
r
r
0
, ω)χ(r
r
r
0
, ω)E
t
(r
r
r
0
, r
r
r
T
, ω)dr
r
r
0
=
= A
e
[χE
t
], r
r
r
0
∈ Ω, r
r
r
T
, r
r
r
R
∈ Γ, (1)
with:
χ(r
r
r, ω) =
ε
s
(r
r
r, ω)
ε
b
(ω)
− 1, (2)
being the contrast function relating the electric prop-
erties of the objects inside the imaging domain ε
s
to those of the homogeneous hosting medium ε
b
at
the working frequency ω, k
b
is the wavenumber in
the background medium, ε
s
(r
r
r, ω) = ε
0
s
(r
r
r) − j
σ
s
(r
r
r)
ωε
0
and
ε
b
(ω) = ε
0
b
− j
σ
b
ωε
0
are the complex permittivities of
the targets and background medium, respectively. Fi-
nally, E
t
, E
s
are the total and scattered electric fields
and G(r
r
r
R
− r
r
r
0
, ω) is the Green’s function for the case
of homogeneous background and observation points
located along the measurement line. Under this as-
sumption, the relationship between contrast and elec-
tric field becomes quite easy since it is a convolution;
therefore, fast Fourier transform (FFT) codes can be
adopted for its evaluation (Isernia et al., 1997).
The aforementioned problem, whose model is
depicted in Eq. (1), aims at retrieving the un-
known contrast function χ(·) from the measurements
of the scattered field collected at receivers loca-
tions and for different incident angles E
s
(·). Thus,
the proposed framework represents a multiple-input-
multiple-output (MIMO) system, commonly referred
to as multiview-multistatic. As most inverse prob-
lems, the attempt of retrieving the contrast function
χ(r
r
r, ω), or equivalently the complex permittivity of
the targets ε
s
(r
r
r, ω), from the measurement samples
represents an ill-posed problem which needs proper
regularisation strategies to obtain reliable solutions
(Colton and Kress, 2012). Moreover, the problem
at hand is also strongly nonlinear, and the degree of
non-linearity (DNL) of the considered integral model
depends on the electromagnetic and geometrical fea-
tures of the targets embedded in the scattering region.
Therefore, the higher the DNL, the harder the prob-
lem at hand and thus the difficulty of solving the in-
verse scattering problem as well as its computational
burden.
In order to face these drawbacks and provide an
efficient, almost real-time imaging strategy also in
complicated, strongly non-linear scenarios, in the fol-
lowing a machine-learning-based approach is pro-
posed.
3 ARTIFICIAL NEURAL
NETWORK FOR
QUANTITATIVE IMAGING
The reconstruction of the inner part of an unknown
object from scattered field measurements is computa-
tionally expensive in both time and memory require-
ments. Thus, there is a strong interest in the devel-
opment of online techniques for quantitative imag-
ing purposes, whose reconstructions are obtained in
a short time after the acquisition.
Artificial Neural Networks for Quantitative Microwave Breast Imaging
205
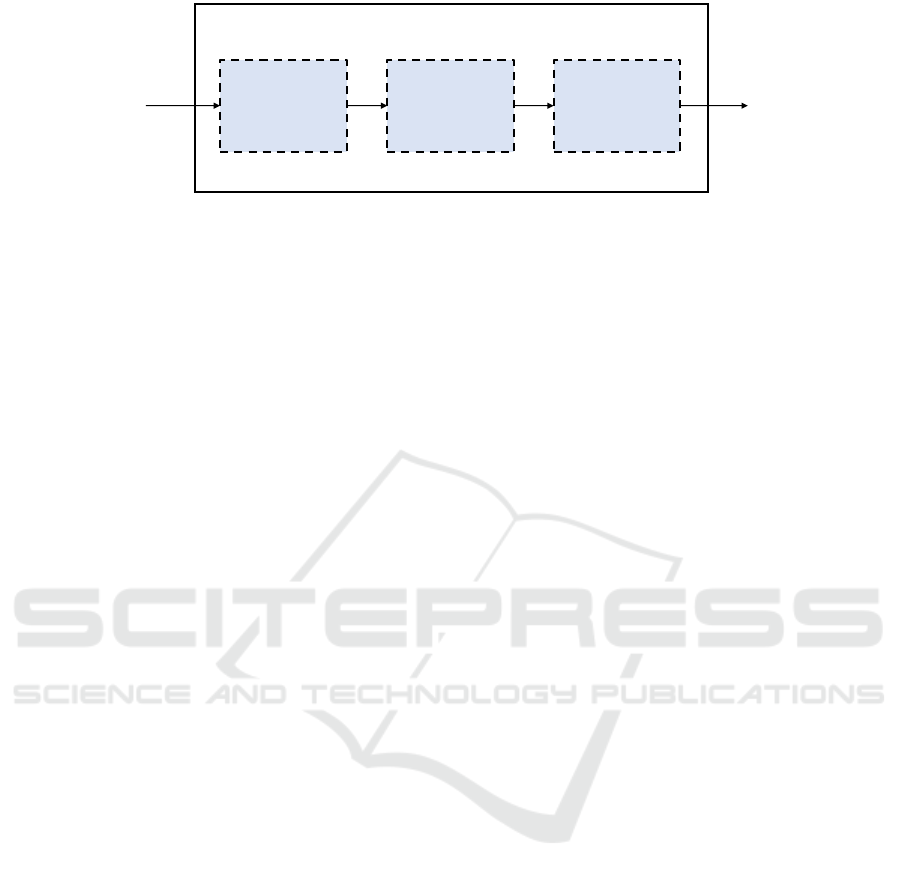
Fully-
connected
Layer
Fully-
connected
Layer
Fully-
connected
Layer
Retrieved
Prole
Scaered
Field
Acial Neural Network
Figure 2: Architecture of the proposed network. This direct inversion scheme has the samples of the scattered field as input
and provides an estimate of unknown complex permittivity profile maps as output.
The use of ANNs for imaging purposes goes
back till to the nineties for simple imaging scenar-
ios (Caorsi and Gamba, 1999), but nowadays has be-
come more and more attractive due to the improve-
ment in the computational power of modern technol-
ogy as well as to the innovative network architec-
tures proposed in the scientific literature. Most arti-
cles propose the use of machine learning either for the
imaging of simple scenarios or as a complementary
strategy in the inversion procedure for regularisation
and super-resolution issues (Shah and Moghaddam,
2017)–(Ashtari et al., 2010).
In this framework, ANNs based on multilayer per-
ceptrons could be very promising for online imaging
purposes. Firstly, they act as universal function ap-
proximators, and secondly they prove to be robust in
presence of noise and fast, since after a training step
they are able to implement a direct mapping between
data and unknowns without any analysis of the phys-
ical rules associated with these data.
Due to these interesting capabilities, they have
been exploited for remote sensing (Vitale et al., 2019;
Aghababaee et al., 2013) as well as for inverse scatter-
ing applications. Most of the research articles focus
on the use of machine learning techniques in order to
find a more stable solution, i.e. as an efficient regular-
isation (Shah and Moghaddam, 2017)-(Ashtari et al.,
2010), as well as a hybrid strategy with some analyti-
cal information.
A critical issue in the use of ANNs resides in the
choice of a properly large data set for the training of
the network, since it is fundamental for the estima-
tion of its weights. After an initial training proce-
dure, which represents the bottleneck of this kind of
approaches due to the required computational burden,
a direct mapping between data (i.e., the scattered field
samples) and unknowns (i.e., the geometrical and di-
electric features of the targets) can be obtained, which
speeds up the imaging procedure considerably.
In this manuscript, the authors want to propose an
ANN architecture in order to provide a quantitative
online imaging of the electric properties of female
breast tissues starting from measures of the scattered
field. The universal approximation theorem (Hornik
et al., 1990) states that any arbitrary nonlinear func-
tion can be approximated via a proper network archi-
tecture. Based on it, in this manuscript a three-layer
network is proposed. Each hidden layer combines all
of the features (local information) learned by the pre-
vious layers across the image to identify the largest
patterns. Fig. 2 provides a sketch of the considered
ANN architecture.
4 NUMERICAL BREAST
PHANTOMS GENERATION
The selection of a proper training data set is of rel-
evant importance for the learning procedure since
the choice of the weights involved in the network is
strongly related to the considered pairs in the data
set. As a matter of fact, large pairs of scattered data
and reference profiles are required to build a data set
which is relevant in order to obtain good recovery per-
formance. To this aim, a numerical 2D randomly-
shaped breast profile generator has been exploited in
order to create the reference profiles, and the forward
problem has been implemented in order to create the
related scattered data, obtaining the training data set
required by the network.
Due to the relatively simple geometry of the breast
shape, and since the biological tissues can be mainly
grouped into fibro-glandular, transitional and adipose
tissues (Lazebnik et al., 2007), the authors proposed
an automatic numerical breast generator which allows
to obtain ellipsoidal-shaped phantoms with a variable
percentage of fibro-glandular internal tissue. The skin
thickness is modelled as a uniform random variable in
the range [1.5, 2.5] mm whose dielectric permittivity
is equal to 36 and conductivity to 0.86 S/m. Regard-
ing the complex permittivity of the breast inner tis-
sues, the statistical distributions reported in (Lazebnik
et al., 2007) have been considered.
In order to model the spatial variability of the
BIOIMAGING 2020 - 7th International Conference on Bioimaging
206
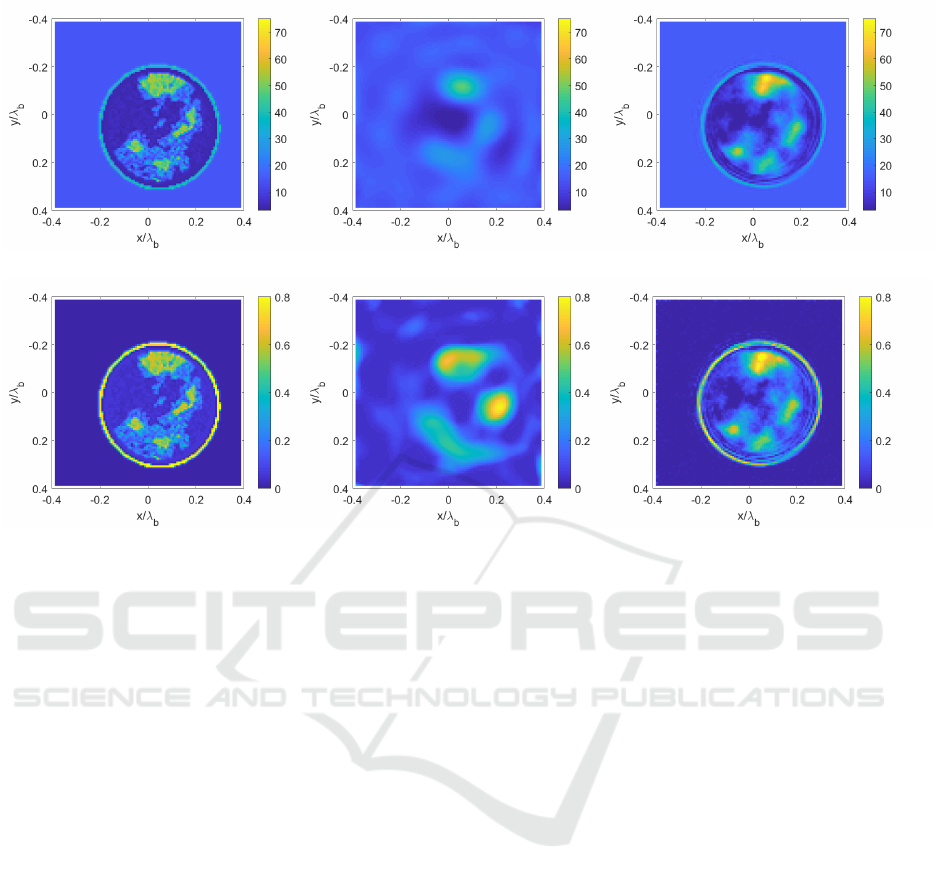
(a) (b) (c)
(d) (e) (f)
Figure 3: Numerical results (a),(d) real and imaginary parts of the reference complex permittivity, respectively; (b),(e):
retrieved profiles via a classical non-linear approach (distorted-Born iterative method) and (c),(f) via the proposed neural
network architecture.
fibro-glandular tissue, a random-shape generation
based on a universal multi-fractal random field gen-
erator proposed in (Schertzer and Lovejoy, 1989) has
been adopted. The profile generator can be controlled
via setting three different parameters which govern
the level of sparsity of the fibro-glandular tissue as
well as the ruggedness or smoothness of the profile.
5 NUMERICAL RESULTS
The scattered field related to the numerical breast
phantoms was evaluated via a method of moments
(MoM) forward solver. This information was ex-
ploited for the training phase of the network. To test
the performance of the proposed ANN, 50.000 breast
profiles were generated and split into training (80%),
testing (15%) and validation (5%) data sets.
The ANN architecture proposed in Section 3 was
trained by employing the stochastic gradient descent
algorithm with momentum which updates the net-
work parameters by taking small steps in the direction
of the negative gradient of the loss. The default values
of the initial weights belong to a Gaussian distribution
with zero-mean and standard deviation equal to 0.01,
and initial bias equal to zero. Finally, a regularisation
term for the weights of the loss function is added to
reduce the overfitting.
Regarding the geometry of the problem at hand,
the investigated area is 15 cm
2
. The matching fluid
employed as background medium is lossless with
ε
0
r,b
= 15 in order to maximise the matching with the
skin layer and, thus, the amount of field reaching the
breast internal tissues (Catapano et al., 2010).
The operating frequency is fixed at 1 GHz and the
circle on which the receivers and transmitters are lo-
cated has radius equal to 22.5 cm. Regarding the
number of antennas, thirty elements acting as trans-
mitters/receivers in a multiview-multistatic fashion
have been assumed. Reconstruction results related to
one case are reported in Fig. 3 in comparison with
classical distorted-Born iterative method (DBIM) es-
timation.
6 CONCLUSION
In the this paper, a novel and computationally fast ap-
proach based on ANNs for the quantitative microwave
imaging of breast tissues has been presented. A pre-
liminary performance assessment was proposed in a
Artificial Neural Networks for Quantitative Microwave Breast Imaging
207

simplified 2D scenario which can be easily gener-
alised to the more complete and realistic case of three-
dimensional breast.
In the framework of imaging techniques,
microwave-based tomographic breast imaging may
represent a valid alternative or a complementary
medical exam, since it is safe compared to the
standard mammography and less expensive rather
than magnetic resonance imaging.
For the generation of the training data set, a
randomly-shaped breast profile generator has been
proposed whose tissues electric parameters were se-
lected according to proper statistical distributions as
reported in the scientific literature (Lazebnik et al.,
2007). Regarding the network design, a three fully-
connected layers network architecture was proposed
and compared with a classical inversion scheme
(DBIM). It is worth to underline the capability of the
proposed approach to retrieve the imaginary part of
complex permittivity with a good accuracy compared
with classical approaches, as well as the capability of
correctly estimating the thickness of the skin layer.
Future work will focus on testing new network ar-
chitectures and on the proper design of the training
data set.
REFERENCES
Aghababaee, H., Amini, J., and Tzeng, Y.-C. (2013). Im-
proving change detection methods of sar images using
fractals. Scientia Iranica, 20(1):15–22.
Ahsan, S., Guo, Z., Miao, Z., Sotiriou, I., Koutsoupidou,
M., Kallos, E., Palikaras, G., and Kosmas, P. (2018).
Design and experimental validation of a multiple-
frequency microwave tomography system employing
the dbim-twist algorithm. Sensors, 18(10):3491.
Ambrosanio, M., Kosmasy, P., and Pascazio, V. (2016). An
adaptive multi-threshold iterative shrinkage algorithm
for microwave imaging applications. In 2016 10th
European Conference on Antennas and Propagation
(EuCAP), pages 1–3. IEEE.
Ambrosanio, M. and Pascazio, V. (2015). Numerical analy-
sis of a compressive sensing approach for ground pen-
etrating radar applications. In 2015 16th International
Radar Symposium (IRS), pages 410–415. IEEE.
Ashtari, A., Noghanian, S., Sabouni, A., Aronsson, J.,
Thomas, G., and Pistorius, S. (2010). Using a-priori
information for regularization in breast microwave
image reconstruction. IEEE Transactions on Biomed-
ical Engineering, 57(9):2197–2208.
Bevacqua, M. T., Bellizzi, G. G., Crocco, L., and Iser-
nia, T. (2019). A method for quantitative imaging
of electrical properties of human tissues from only
amplitude electromagnetic data. Inverse Problems,
35(2):025006.
Bevacqua, M. T. and Isernia, T. (2018). Boundary indica-
tor for aspect limited sensing of hidden dielectric ob-
jects. IEEE Geoscience and Remote Sensing Letters,
15(6):838–842.
Caorsi, S. and Gamba, P. (1999). Electromagnetic detection
of dielectric cylinders by a neural network approach.
IEEE transactions on geoscience and remote sensing,
37(2):820–827.
Catapano, I., Crocco, L., Di Donato, L., Angiulli, G., Is-
ernia, T., Morabito, A., Tringali, S., and Bucci, O.
(2010). Guidelines for effective microwave breast
imaging: a numerical assessment against 3d anthro-
pomorphic phantoms. In Proceedings of the Fourth
European Conference on Antennas and Propagation,
pages 1–5. IEEE.
Colton, D. and Kress, R. (2012). Inverse acoustic and elec-
tromagnetic scattering theory, volume 93. Springer
Science & Business Media.
Estatico, C., Fedeli, A., Pastorino, M., and Randazzo, A.
(2016). A banach space regularization approach for
multifrequency microwave imaging. International
Journal of Antennas and Propagation, 2016.
Hornik, K., Stinchcombe, M., and White, H. (1990). Uni-
versal approximation of an unknown mapping and
its derivatives using multilayer feedforward networks.
Neural networks, 3(5):551–560.
Isernia, T., Pascazio, V., and Pierri, R. (1997). A non-
linear estimation method in tomographic imaging.
IEEE Transactions on Geoscience and Remote Sens-
ing, 35(4):910–923.
Lazebnik, M., Popovic, D., McCartney, L., Watkins, C. B.,
Lindstrom, M., Harter, J., Sewall, S., Ogilvie, T.,
Magliocco, A., Breslin, T. M., et al. (2007). A large-
scale study of the ultrawideband microwave dielec-
tric properties of normal, benign and malignant breast
tissues obtained from cancer surgeries. Physics in
Medicine & Biology, 52(20):6093.
Lucas, A., Iliadis, M., Molina, R., and Katsaggelos, A. K.
(2018). Using deep neural networks for inverse prob-
lems in imaging: beyond analytical methods. IEEE
Signal Processing Magazine, 35(1):20–36.
Massa, A., Donelli, M., Pastorino, M., and Rosani, A.
(2005). Microwave imaging for non-destructive evalu-
ation of civil structures. Insight-Non-Destructive Test-
ing and Condition Monitoring, 47(1):11–14.
Persico, R., Ludeno, G., Soldovieri, F., De Coster, A., and
Lambot, S. (2018). Improvement of ground penetrat-
ing radar (gpr) data interpretability by an enhanced
inverse scattering strategy. Surveys in Geophysics,
39(6):1069–1079.
Schertzer, D. and Lovejoy, S. (1989). Nonlinear variabil-
ity in geophysics: Multifractal simulations and analy-
sis. In Fractals’ Physical Origin and Properties, pages
49–79. Springer.
Shah, P. and Moghaddam, M. (2017). Super resolution for
microwave imaging: A deep learning approach. In
2017 IEEE International Symposium on Antennas and
Propagation & USNC/URSI National Radio Science
Meeting, pages 849–850. IEEE.
Vitale, S., Ferraioli, G., and Pascazio, V. (2019). A new
ratio image based cnn algorithm for sar despeckling.
arXiv preprint arXiv:1906.04111.
BIOIMAGING 2020 - 7th International Conference on Bioimaging
208
