
A Novel Dispersion Covariance-guided One-Class Support Vector
Machines
Soumaya Nheri
1
, Riadh Ksantini
1,2
, Mohamed-B
´
echa Ka
ˆ
aniche
1
and Adel Bouhoula
1
1
Higher School of Communication of Tunis, Research Lab: Digital Security, University of Carthage, Carthage, Tunisia
2
University of Windsor, 401, Sunset Avenue, Windsor, ON, Canada
Keywords:
Support Vector Machine, Kernel Covariance Matrix, One-Class Classification, Outlier Detection, Low
Variances, Subclass Information.
Abstract:
In order to handle spherically distributed data, in a proper manner, we intend to exploit the subclass informa-
tion. In one class classification process, many recently proposed methods try to incorporate subclass informa-
tion in the standard optimization problem. We presume that we should minimize the within-class variance,
instead of minimizing the global variance, with respect to subclass information. Covariance-guided One-Class
Support Vector Machine (COSVM) emphasizes the low variance direction of the training dataset which results
in higher accuracy. However, COSVM does not handle multi-modal target class data. More precisely, it does
not take advantage of target class subclass information. Therefore, to reduce the dispersion of the target data
with respect to newly obtained subclass information, we express the within class dispersion and we incorpo-
rate it in the optimization problem of the COSVM. So, we introduce a novel variant of the COSVM classifier,
namely Dispersion COSVM, that exploits subclass information in the kernel space, in order to jointly mini-
mize the dispersion within and between subclasses and improve classification performance. A comparison of
our method to contemporary one-class classifiers on numerous real data sets demonstrate clearly its superiority
in terms of classification performance.
1 INTRODUCTION
The important motivation of one-class classification
(OCC) has been studied under three main frame-
works. First, generally, it is assumed that information
from normal operation (targets) are easy to collect
during a training process, but most faults (outliers)
are not available or very costly to measure. For in-
stance, it is possible to measure the necessary features
for a nuclear power plant operating under normal cir-
cumstances. But, in case of accident, it is too dan-
gerous or impossible to measure the same features.
Second, outliers are badly represented and poorly dis-
tributed for training. This appears mainly in tumour
detection or rare medical diseases, where a limited
number of outliers are available during the training
process. Third, for many learning tasks, many ob-
jects are unlabeled and few labeled examples are al-
ways available, but they are badly represented with
unknown prior and ill-defined distributions. For these
reasons, OCC problem can be found in many prac-
tical applications, such as, medical analysis (Gard-
ner et al., 2006), anomaly detection, face recognition
(Zeng et al., 2006) and web page classification (Qi
and Davison, 2009).
In OCC problems, to classify future data points
as targets or outliers, three different categories of
OCC method can be used: density-based methods,
boundary-based methods and reconstruction-based
methods. Density-based methods, like Parzen density
estimator (Muto and Hamamoto, 2001) and Gaussian
distribution (Parra et al., 1996), are based on the es-
timation of the probability density function (PDF) of
the target class. In boundary-based classifiers, only
the boundary points around the target class are used to
classify data (Vapnik, 1998). The Support Vector Ma-
chine (SVM) (Cristianini and Shawe-Taylor, 2000) is
a popular two-class classification method based on
this philosophy. It aims to maximize the distance mar-
gin between the two considered classes using support
vectors. It also found its application in OCC prob-
lem as One-Class SVM (OSVM) (Sch
¨
olkopf et al.,
2001) and Support Vector Data Description (SVDD)
(Sadeghi and Hamidzadeh, 2018). Reconstruction-
based classifiers like k-means clustering (Ahmad and
Dey, 2011), have been introduced to model the data
546
Nheri, S., Ksantini, R., Kaâniche, M. and Bouhoula, A.
A Novel Dispersion Covariance-guided One-Class Support Vector Machines.
DOI: 10.5220/0009174205460553
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
546-553
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

rather than resolving classification problem. During
classification, a reconstruction error for the incoming
data point is calculated. The less the error, the more
accurate is the model. The main problems with these
three categories of one-class classification methods
are that none of them consider the full scale of in-
formation available for classification. For instance,
the density-based methods focus only on high den-
sity area and neglect areas with lower training data
density. In boundary-based methods, the solutions
are only calculated based on the points near the deci-
sion boundary, regardless the spread of the remaining
data. A more reasonable method would be to simul-
taneously make use of the maximum margin criterion
(Cristianini and Shawe-Taylor, 2000), while control-
ling the spread of data. Besides, unlike multi-class
classification problems, the low variance directions
of the target class distribution are crucial for OCC.
In (Kwak and Oh, 2009), it has been shown that pro-
jecting the data in the high variance directions (like
PCA) will result in higher error (bias), while retain-
ing the low variance directions will lower the total
error. Boundary-based methods privilege separating
data along large variance directions and do not put
special emphasis on low variance directions (Shiv-
aswamy and Jebara, 2010). Moreover, we need to re-
duce the estimation error by taking projections along
some variance directions and the estimated covari-
ance is not accurate due to the limited number of train-
ing samples.
However, taking these projections before train-
ing leads to an important loss of characteristics.
Some powerful classifiers have been proposed to take
the overall structural information of the training set
into account through the incorporation of the co-
variance matrix into the objective OSVM function
then we can mention the most relevant among them:
The Mahalanobis One-class SVM (MOSVM) (Tsang
et al., 2006), the Relative Margin Machines (RMM)
(Shivaswamy and Jebara, 2010) and the Discrimi-
nant Analysis via Support Vectors(SVDA) (Gu et al.,
2010). In the one-class domain, the most relevant
work is the Covariance-guided One-class Support
Vector Machine (COSVM) (Khan et al., 2014). The
principal motivation behind COSVM method is to put
more emphasis on the low variance directions by in-
corporates the covariance matrix into object function
of the OSVM (Sch
¨
olkopf et al., 2001). In fact, before
training, we want to keep all data characteristics and
use the maximum margin based solution, while taking
projections in specific directions. In terms of classi-
fication performance, COSVM was shown to be very
competitive with SVDD, OSVM and MOSVM.
However, there are still some difficulties asso-
ciated with COSVM application in real case prob-
lems, where data are highly dispersed and the tar-
get class can be divided into subclasses. In order to
handle spherically distributed data, in a proper man-
ner, we intend to exploit the subclass information. In
one class classification process, many recently pro-
posed methods try to incorporate subclass informa-
tion in the standard optimization problem. We can
mention among them: The Subclass One-Class Sup-
port Vector machine (SOC-SVM) (Mygdalis et al.,
2015) and the Kernel Support Vector Description
(KSVDD) (Mygdalis et al., 2016). The basic prin-
ciple of the SOC-SVM method is to introduce a novel
variant of the OSVM classifier that exploits subclass
information, in order to minimize the data disper-
sion within each subclass and determine the optimal
decision function. Experimental results denote that
(SOC-SVM) approach is able to outperform OSVM
in video segments selection. On the other hand,
KSVDD method modifies the standard SVDD opti-
mization process and extends the proposed method
to work in feature spaces of arbitrary dimensional-
ity. Comparative results of KSVDD with the OSVM,
the standard SVDD and the minimum variance SVDD
(MV-SVDD)(Zafeiriou and Laskaris, 2008) demon-
strate the superiority of KSVDD. We presume that we
should minimize the within-class variance, instead of
minimizing the global variance, with respect to sub-
class information. Thus, a clustering step is achieved
in order to estimate the existing subclasses into the
target class. Furthermore, It has been shown in (Zhu
and Martinez, 2006) that the clustering does not have
a major impact in the classification accuracy. Hence,
any clustering algorithm can work in this approach.
Then, to reduce the dispersion of the target data with
respect to newly obtained subclass information, we
express the within class dispersion and we incorpo-
rate it in the optimization problem of the COSVM.
In this paper, we propose a novel Dispersion
COSVM (DCOSVM), which incorporates a dis-
persion matrix into the objective function of the
COSVM, in order to reduce the dispersion of the tar-
get data with respect to newly obtained subclass in-
formation and improve classification accuracy. Un-
like the SOC-SVM and the KSVDD methods, the
DCOSVM has the advantage of minimizing not only
the data dispersion within each subclass, but also data
dispersion between subclasses, in order to improve
classification performance. Moreover, the DCOSVM
utilizes a trade off controlling parameter to fine-tune
the effect of the dispersion matrix on the classifica-
tion accuracy. The proposed method is still based on
a convex optimization problem, where a global op-
A Novel Dispersion Covariance-guided One-Class Support Vector Machines
547

timal solution could be estimated easily using exist-
ing numerical methods. The rest of the paper is orga-
nized as follows: The next section describes in details
a novel subclass method based on COSVM. Section
3 presents a comparative evaluation of our method to
other state of the art relevant one-class classifiers, on
several common datasets. Finally, Section 4 contains
some concluding remarks.
2 THE NOVEL DISPERSION
COSVM
In this section we describe in details our proposed
method. First, we present the COSVM method which
provides more importance towards the low variance
directions by incorporating the estimated covariance
matrix of target class.
2.1 The COSVM Method
The estimated covariance matrix of the training data
contains all projectional directions, from high vari-
ance to low variance. Thus, to keep the robustness
of the OSVM classifier intact while emphasizing the
small variance directions, (Khan et al., 2014) incor-
porate the kernel covariance matrix into the objective
function of the OSVM optimization problem. So, us-
ing the kernel trick, the convex optimization problem
of COSVM method can be described as follows:
min
α
α
T
(ηQ + (1 − η)∆)α (1)
s.t. 0 ≤ α
i
≤
1
vN
,
N
∑
i=1
α
i
= 1,
where
∆ = Q(I − 1
N
)Q
T
. (2)
For clarity, we have used the vectorized form of α =
(α
1
,.. .,α
N
) and v ∈ (0, 1] is the key parameter that
controls the fraction of outliers and that of support
vectors (SVs). Q is the kernel matrix as defined in
Eq. (3):
Q(i, j) = K (x
i
,x
j
), (3)
i = 1, ... ,N; j = 1, ... ,N.
I is the identity matrix and 1
N
is a matrix with all en-
tries
1
N
, and η is the tradeoff parameter that controls
the balance between the kernel matrix Q and the dual
kernel covariance matrix ∆. According to (Khan et al.,
2014), by controlling the value of v in the training
phase, one can control the confidence on the training
dataset directly. If the training dataset is very reliable,
v can be set to a low value so that the whole training
dataset is considered. On the other hand, if it is not
known whether or not the training dataset truly rep-
resents the target class, v can be set to some higher
value.
2.2 Derivation of Dispersion COSVM
(DCOSVM)
The DCOSVM takes into account the subclass dis-
tribution in order to provide more efficient and ro-
bust solutions than standard COSVM. The whole idea
is based onto projecting the training data set of N
samples, X = {x
i
}
N
i=1
to a higher dimensional fea-
ture space F = {Φ(x
i
)}
N
i=1
by the function Φ, where
linear classification might be achieved. In practice,
F is not calculated directly. The kernel trick (Vap-
nik, 1998) is used to calculate the mapping, where
a kernel function K calculates the inner products of
the higher dimensional data samples: K (x
i
,x
j
) =<
Φ(x
i
),Φ(x
j
) >,∀i, j ∈ {1, 2,.. ., N}. After mapping
to feature space, since the entire training set belongs
to one class only, we cluster all the training vec-
tors in order to determine K clusters {C
d
}
K
d=1
, where
|C
d
| = N
d
,∀d ∈ {1, 2,.. .,K}. Let m
d
Φ
denotes the
mean of the cluster C
d
samples calculated in feature
space:
m
d
Φ
=
1
N
d
N
d
∑
i=1
Φ(x
i
). (4)
We used m
d
Φ
to calculate the kernel covariance matrix
Σ
d
Φ
of the training cluster C
d
:
Σ
d
Φ
=
N
d
∑
i=1
(Φ(x
i
) − m
d
Φ
)(Φ(x
i
) − m
d
Φ
)
T
. (5)
Considering the case where K subclasses are formed
within the target class, the within subclass scatter ma-
trix (dispersion of the training vectors) can be ex-
pressed as follows:
S
w
Φ
=
K
∑
d=1
(
N
d
N
Σ
d
Φ
). (6)
Where
N
d
N
is the prior probability of the d − th sub-
class. The between scatter matrix can be defined as
follows:
S
B
Φ
=
K
∑
d=1
K
∑
b=1,b6=d
(m
d
Φ
− m
b
Φ
)(m
d
Φ
− m
b
Φ
)
T
. (7)
Using this definition, we incorporate the within sub-
class and between subclass scatter matrices as an ad-
ditional w
T
S
w
Φ
w and w
T
S
B
Φ
w, respectively, into the
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
548

objective function of the optimization problem of
COSVM Eq. (1). In fact, the term w
T
S
w
Φ
w is used to
minimize the dispersion within subclasses, whereas
the term w
T
S
B
Φ
w has the advantage of minimizing
the dispersion between subclasses. However, the
dual problem is the one that is solved through some
optimization algorithm for COSVM, not the primal
one. Thus, it is more appropriate to incorporate the
subclass scatter matrix directly in the dual problem.
Therefore, we have to use the kernel trick to repre-
sent the additional term w
T
S
w
Φ
in terms of dot prod-
ucts only. From the theory of reproducing kernels, we
know that any solution w must lie in the span of all
training samples. Hence, we can find an expansion of
w of the form:
w =
N
∑
i=1
α
i
Φ(x
i
). (8)
By using the definitions of Σ
d
Φ
Eq. (5), m
d
Φ
Eq. (4)
and the kernel function K (x
i
,x
j
) =< Φ(x
i
),Φ(x
j
) >
,∀i, j ∈ {1,2,.. .,N}, we derive the dot product form
in Eq. (9), where Q is the kernel matrix as defined in
Eq. (3). I is the identity matrix and 1
N
is a matrix
with all entries
1
N
.
∆
d
is the transformed version of Σ
d
Φ
to be used in the
dual form:
∆
d
= Q
d
(I − 1
N
)Q
d
T
. (10)
This form of kernel covariance matrix ∆
d
is only in
terms of the kernel function and can be calculated
easily using the kernel trick. Let M
d
is the “kernel
mean of cluster C
d
”, which is an N
d
dimensional vec-
tor. Each component of M
d
is defined as:
(M
d
)
j
=
1
N
N
d
∑
i=1
K (x
i
,x
j
), ∀ j = 1,. .., N. (11)
Using this definition, the between scatter matrix S
B
Φ
is
defined in Eq. (12).
Hence, our target term to incorporate into the
COSVM dual problem is:
α
T
K
∑
d=1
N
d
N
∆
d
+
K
∑
d=1
K
∑
b=1,b6=d
(M
d
− M
b
)(M
d
− M
b
)
T
α.
(13)
With this replacement, our proposed Dispersion
COSVM method can be described by the optimiza-
tion problem defined in Eq. (14).
w
T
S
W
Φ
w =
N
∑
i=1
α
i
Φ
T
(x
i
)
K
∑
d=1
(
N
d
N
Σ
d
Φ
)
N
∑
k=1
α
k
Φ(x
k
)
(9)
=
N
∑
i=1
N
∑
k=1
K
∑
d=1
N
d
∑
j=1
N
d
N
α
i
Φ
T
(x
i
)(Φ(x
j
) − m
d
Φ
)(Φ(x
j
) − m
d
Φ
)
T
α
k
Φ(x
k
)
=
N
∑
i=1
N
∑
k=1
K
∑
d=1
N
d
∑
j=1
N
d
N
α
d
i
K (x
i
,x
j
) −
1
N
d
N
d
∑
l=1
α
d
i
K (x
i
,x
l
)
α
d
k
K (x
k
,x
j
) −
1
N
d
N
d
∑
m=1
α
d
k
K (x
k
,x
m
)
=
N
∑
i=1
N
∑
k=1
K
∑
d=1
N
d
∑
j=1
N
d
N
α
d
i
α
d
k
K (x
i
,x
j
)K (x
k
,x
j
) −
2α
d
i
α
d
k
N
d
N
d
∑
l=1
K (x
i
,x
j
)K (x
k
,x
l
) +
α
d
i
α
d
k
N
d
2
N
d
∑
l=1
N
d
∑
m=1
K (x
i
,x
l
)K (x
k
,x
m
)
=
N
∑
i=1
N
∑
k=1
K
∑
d=1
N
d
∑
j=1
N
d
N
α
d
i
α
d
k
K (x
i
,x
j
)K (x
k
,x
j
) −
α
d
i
α
d
k
N
d
N
d
∑
l=1
K (x
i
,x
j
)K (x
k
,x
l
)
=
K
∑
d=1
N
d
N
α
d
T
Q
d
T
Q
d
α
d
− α
d
T
Q
d
T
1
N
d
Q
d
α
d
=
K
∑
d=1
N
d
N
α
d
T
Q
d
T
(I − 1
N
d
)Q
d
α
d
= α
T
K
∑
d=1
N
d
N
∆
d
α
w
T
S
B
Φ
w =
N
∑
i=1
α
i
Φ
T
(x
i
)
K
∑
d=1
K
∑
b=1,b6=d
(m
d
Φ
− m
b
Φ
)(m
d
Φ
− m
b
Φ
)
T
N
∑
k=1
α
k
Φ(x
k
)
(12)
= α
T
K
∑
d=1
K
∑
b=1,b6=d
(M
d
− M
b
)(M
d
− M
b
)
T
α.
A Novel Dispersion Covariance-guided One-Class Support Vector Machines
549
min
α
α
T
ηQα + α
T
(1 − η)
K
∑
d=1
N
d
N
∆
d
+
N
∑
d=1
K
∑
b=1,b6=d
(M
d
− M
b
)(M
d
− M
b
)
T
α (14)
s.t. 0 ≤ α
i
≤
1
vN
,
N
∑
i=1
α
i
= 1.
The proposed method still results in a convex op-
timization problem since both the kernel matrix Q
and the covariance matrix ∆ are positive definite
(Michelli, 1986; Horn and Charles, 1990). As a re-
sult, the solution to this optimization problem will
have one global optimum solution and can be solved
efficiently using numerical methods.
However, we control the balance between the disper-
sion matrix and the Kernel matrix through our control
parameter η.
2.3 The Impact of the Tradeoff
Parameter η
One important step for achieving better classification
with DCOSVM is finding the appropriate value for η.
The contribution of our kernel matrix Q, the between
scatter matrix S
B
Φ
and the within subclass scatter ma-
trix S
w
Φ
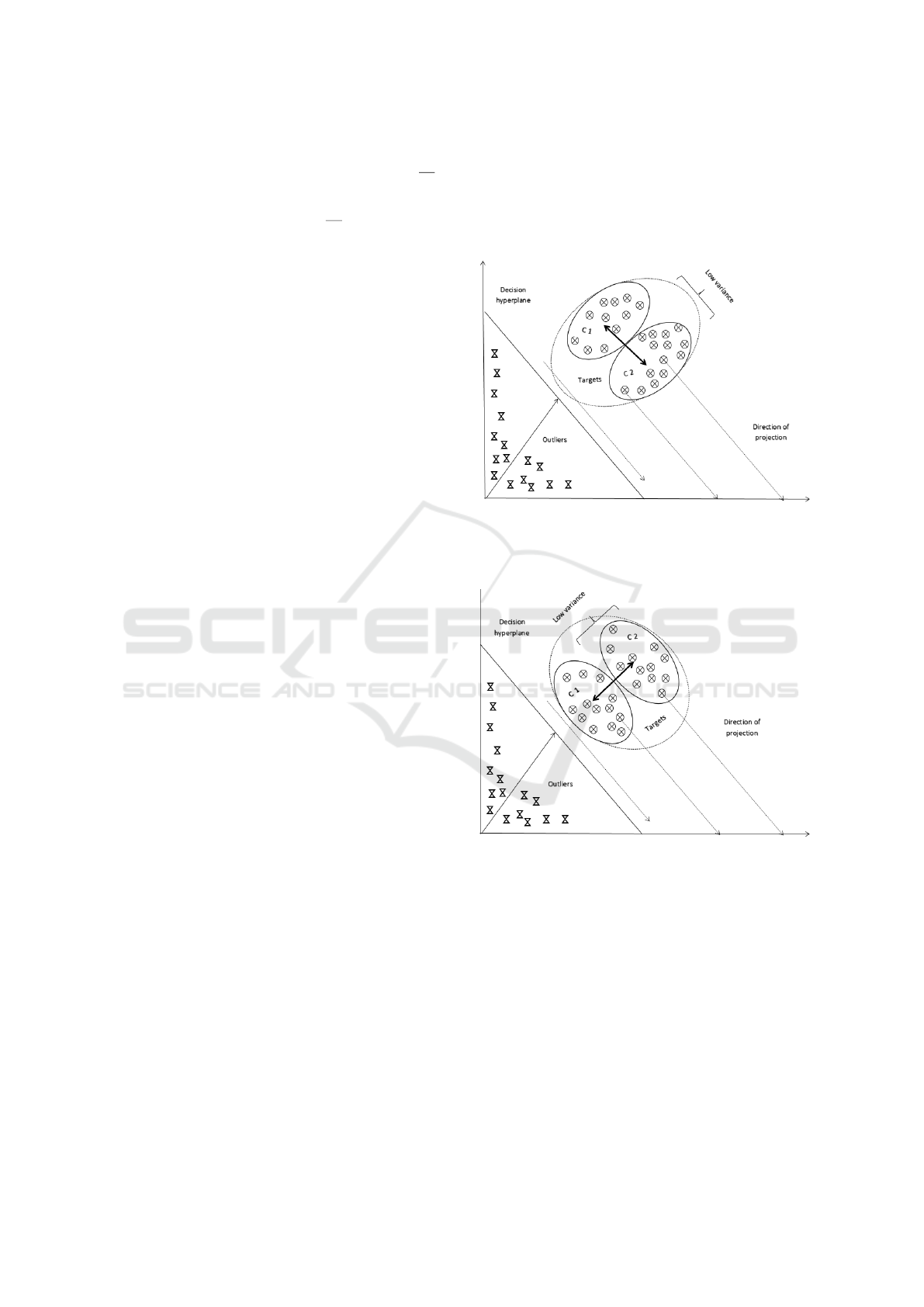
is controlled using the parameter η. Figure 1
shows the case where the optimal decision hyperplane
for the example target data is on the same direction
as the high variance. The control parameter η is set
equal to 1 which means the low variance directions
will not be given any special consideration in this
case. On the other hand, Figure 2 is the case when
the direction optimal of decision hyperplane and the
low variance are parallel. In this case, η can be set to
0. However, in real world cases (0 < η < 1), the op-
timal decision hyperplane is highly unlikely to be en-
tirely parallel to the direction of low variance or high
variance. For this reason, the value of η needs to be
tuned so that we have less overlap between the linear
projections of the target data and the outlier data. We
use an indirect approach to optimize η which will be
explained in detail in the next section.
2.4 Schematic Depictions
In this section, Figure 3 presents schematic depic-
tions to show the advantage of our DCOSVM method
over the unimodal COSVM.
3 EXPERIMENTAL RESULTS
This section presents the detailed experimental anal-
ysis and results for our proposed method, performed
on both artificial and benchmark real-world one-class
Figure 1: Case 1: Schematic depiction of the decision hy-
perplane for DCOSVM when the optimal linear projection
would be along the direction of high variance. In this case,
the optimal control parameter value for DCOSVM is η = 1.
Figure 2: Case 2: Schematic depiction of the decision hy-
perplane for DCOSVM when the optimal linear projection
would be along the direction of low variance. In this case,
the optimal control parameter value for DCOSVM is η = 0.
datasets, compared against contemporary one-class
classifiers.
3.1 Data Sets Used
In our experiments, to test the robustness of our pro-
posed method in different scenarios, we have used
both artificially generated datasets and real world
datasets. For the experiments on artificially gener-
ated data, we have created several sets of 2D four-
class data drawn from two different sets of distribu-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
550

Figure 3: Comparison between COSVM and DCOSVM:
The value of the tradeoff parameter is set equal to 0 (η = 0),
to only consider the dispersion term.
tions: 1) Gaussian distributions with different covari-
ance matrices. 2) Gamma distributions with differ-
ent shape and scale parameters. For each distribution,
two different sets were created, one with low overlap
and the other with high overlap. Figure 4 shows the
plots of these generated data sets. We had a total 4
classes, one of the class is designated target and the
other ones as outlier. For the real world case, most of
these datasets were originally collected from the UCI
machine learning repository (Blake and Merz, 1999).
We have primarily focused on one of the important
fields of one-class classification, such as, medical di-
agnosis (Fazli and Nadirkhanlou, 2013). Since these
datasets are originally multi- class, one of the class is
designated target and the other ones as outlier. Some
of the target and outlier sets were too trivial to clas-
sify. We have omitted those sets from our results. We
have also used varying size and dimensions of data
sets to test the robustness of our method against dif-
ferent feature sizes. As we can see from Table 1, the
dimensions vary from 3 to 300, while the training set
sizes vary from 21 to 288.
3.2 Experimental Protocol
The performance of the DCOSVM has been
compared to Covariance guided One-class SVM
(COSVM), One-class SVM (OSVM), Support Vec-
tor Data Description (SVDD), K Nearest Neighbors
(K-NN), Parzen, Gaussian. The classifiers are imple-
mented with the help of DDtools (Tax, 2012), and the
radial basis kernel was used for kernelization. This
kernel is calculated as K (x
i
,x
j
) = e
−kx
i
−x
j
k
2
/σ
, where
σ represents the positive “width” parameter. For all
data sets used, we set the number of clusters C
min
= 2
and C
max
= 10 with the assumption that each data sets
Table 1: Description of Real Data Sets.
Data Number Number Number Number
set of of of of
Name Targets Outliers Features clusters
Haberman’s 81 225 3 2
Survival
Biomedical 67 127 5 4
(diseased)
Biomedical 127 67 5 4
(healthy)
SPECT Images 95 254 44 2
(normal)
Balance-scale 288 337 4 5
left
Balance-scale 288 337 4 4
right
waveform 21 600 300 3
target has a minimum of 2 clusters (sub-class) to a
maximum of 10 clusters. The number of subclasses is
determined by applying a clustering technique and the
validity index proposed in (Bouguessa et al., 2006),
on the samples belonging to each of the classes inde-
pendently. Second, we used 10-fold stratified cross
validation. In fact, we added 10% randomly selected
data to the outliers for testing, and the remaining was
used as the training data. To build different training
and testing sets, this approach was repeated 10 times.
The final result was achieved by averaging over these
10 models. This ensures that the achieved results were
not a coincidence. Besides, to evaluate the methods,
we have used the Area Under the ROC Curve (AUC)
(Fawcett, 2006) produced by the ROC curves, and we
presented them in the results Table2. Consequently,
the AUC criterion must be maximized in order to ob-
tain a good separation between targets and outliers.
3.3 Results and Discussion
Table 2 and Table 4 contain the average AUC val-
ues obtained for the classifiers on the artificial and
real data sets. As we can see, the DCOSVM is su-
perior to all the other classifiers and provides best
results on almost data sets, in terms of the obtained
unbiased AUC values by averaging over 10 different
models. In fact, the DCOSVM has the advantage of
minimizing dispersion within and between subclasses
of the target class, thereby reducing overlapping and
improving classification accuracy. In general, we see
that for real-world datasets (Table 4), the performance
of k-NN, Gaussian and Parzen classifiers are poor
when compared to the SVM-based classifiers (SVDD,
OSVM, COSVM). This is because of the limitations
inherent in these classifiers. Since k-NN classifies a
data point solely based on its neighbors, it is sensi-
tive to outliers (Jiang and Zhou, 2004). The Gaussian
classifier has some obvious limitations from the as-
A Novel Dispersion Covariance-guided One-Class Support Vector Machines
551

sumption that the underlying distribution is Gaussian,
which is not always the case for real datasets. The
Parzen classifier is prone to degraded performance in
case of high-dimensional data or small sample size
(Muto and Hamamoto, 2001). We can easily see this
limitation of the Parzen classifier from the poor re-
sults on the Gene Expression datasets which has a
very high dimension. The SVM-based classifiers are
free from all these assumptions and, hence, leads to
better result in majority of the cases. However, in case
of the artificial datasets (Table 2), we see that these
three classifiers (i.e. k-NN, Gaussian and Parzen) are
competitive with the SVM-based methods, sometimes
even better. This is because the artificial datasets are
generated from a pre-defined regular distribution. We
see that the Gaussian method performs well for the
cases where the dataset was generated from a Gaus-
sian distribution, which is expected. It also performs
comparatively well for the datasets generated from the
banana distribution. This is because the banana dis-
tribution is actually generated by superimposing an
underlying Gaussian distribution on a banana shape.
However, in case of Gamma distribution, it performs
poorly since the distribution does not match with the
assumption of the classifier.
Table 2: Average AUC of each method for the 4 artificial
data sets (best method in bold).
Dataset COSVM DCOSVM
Gauss. (low overlap) 95.66 96.88
Gauss. (high overlap) 88.29 91.10
Gamma (low overlap) 91.27 93.03
Gamma (high overlap) 98.17 98.69
In terms of training computational complexity,
the DCOSVM has almost the same complexity as
COSVM. In fact, the computation of dual kernel
covariance matrix can be done as part of the pre-
processing and re-used throughout the training phase.
The DCOSVM algorithm uses sequential minimal op-
timization to solve the quadratic programming prob-
lem, and therefore scales with is O(N
3
), where N is
the number of training data points (Sch
¨
olkopf et al.,
2001). Table 3 shows the average training times for
both the artificial and the real-world datasets. As we
−5 0 5 10 15 20
−5
0
5
10
15
20
25
30
−5 0 5 10 15 20
−5
0
5
10
15
20
25
30
(a) Gaussian (low overlap) (b) Gaussian (high overlap)
0 50 100 150 200
20
40
60
80
100
120
140
160
180
200
220
0 50 100 150 200 250 300 350
0
50
100
150
200
250
300
(c) Gamma (low overlap) (d) Gamma (high overlap)
Figure 4: Four artificial four-class datasets used for com-
parison. The blue class represents the target class (in each
subfigure caption).
Table 3: Average training times in milliseconds for COSVM
and DCOSVM for the experiments on the artificial and real-
world datasets.
Experiment COSVM DCOSVM
Artificial Datasets 7.4 8.5
Real-world Datasets 127.7 131.2
expect, DCOSVM has almost the same training time
as COSVM.
4 CONCLUSIONS
In this paper, we have improved COSVM classifica-
tion approach by taking advantage of target class sub-
class information.The novel variant of the COSVM
classifier, namely, Dispersion COSVM (DCOSVM),
minimizes the dispersion within and between sub-
classes and improves classification performance. We
have compared our method against contemporary
one-class classifiers on several artificial and real-
world benchmark datasets. The results show the su-
Table 4: Average AUC of each method for the 7 real-world data sets (best method in bold, second best emphasized).
Dataset k-NN Parzen Gaussian SVDD OSVM COSVM DCOSVM
Biomedical (healthy) 36.83 40.02 64.66 81.38 82.65 85.80 89.81
Biomedical (diseased) 89.42 90.09 89.60 90.28 91.04 91.04 92.16
SPECT (normal) 84.28 96.45 93.90 92.32 95.29 96.79 97.81
Balance-scale left 87.78 91.23 92.09 94.20 96.13 97.19 98.51
Balance-scale right 87.76 91.23 91.95 94.72 97.57 97.69 98.82
Haberman’s Survival 66.49 67.97 60.09 68.87 69.62 69.59 70.28
waveform 87.78 97.02 92.10 97.20 97.19 97.23 98.36
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
552

periority of DCOSVM which provides significantly
improved performance over the other classifiers. In
future work, we will validate the proposed DCOSVM
on security applications, such as, face recognition,
anomaly detection, etc.
REFERENCES
Ahmad, A. and Dey, L. (2011). A k-means type clustering
algorithm for subspace clustering of mixed numeric
and categorical datasets. Pattern Recognition Letters,
32(7):1062–1069.
Blake, C. and Merz, C. (1999). UCI repos-
itory of machine learning data sets.
http://www.ics.uci.edu/∼mlearn/MLRepository.html.
Bouguessa, M., Wang, S., and Sun, H. (2006). An objective
approach to cluster validation. Pattern Recognition
Letters, 27(13):1419–1430.
Cristianini, N. and Shawe-Taylor, J. (2000). An Introduction
to Support Vector Machines and Other Kernel-based
Learning Methods. Cambridge University Press, 1
edition.
Fawcett, T. (2006). An introduction to ROC analysis. Pat-
tern Recognition Letters, 27(8):861–874.
Fazli, S. and Nadirkhanlou, P. (2013). A novel method
for automatic segmentation of brain tumors in mri im-
ages. CoRR, abs/1312.7573.
Gardner, A. B., Krieger, A. M., Vachtsevanos, G. J., and
Litt, B. (2006). One-class novelty detection for seizure
analysis from intracranial eeg. Journal of Machine
Learning Research, 7:1025–1044.
Gu, S., Tan, Y., and He, X. (2010). Discriminant anal-
ysis via support vectors. Neurocomputing, 73(10-
12):1669–1675.
Horn, R. and Charles, R. (1990). Matrix Analysis. Cam-
bridge University Press.
Jiang, Y. and Zhou, Z.-H. (2004). Editing Training Data for
k-NN Classifiers with Neural Network Ensemble. In
International Symposium on Neural Networks, pages
356–361. IEEE Press.
Khan, N. M., Ksantini, R., Ahmad, I. S., and Guan, L.
(2014). Covariance-guided one-class support vector
machine. Pattern Recognition, 47(6):2165–2177.
Kwak, N. and Oh, J. (2009). Feature extraction for one-
class classification problems: Enhancements to biased
discriminant analysis. Pattern Recognition, 42(1):17–
26.
Michelli, C. (1986). Interpolation of Scattered Data: Dis-
tance Matrices and Conditionally Positive Definite
Functions. Constructive Approximation, 2:11–22.
Muto, Y. and Hamamoto, Y. (2001). Improvement of the
Parzen classifier in small training sample size situa-
tions. Intelligent Data Analysis, 5(6):477–490.
Mygdalis, V., Iosifidis, A., Tefas, A., and Pitas, I. (2015).
Exploiting subclass information in one-class support
vector machine for video summarization. In ICASSP,
pages 2259–2263. IEEE.
Mygdalis, V., Iosifidis, A., Tefas, A., and Pitas, I. (2016).
Kernel subclass support vector description for face
and human action recognition. In SPLINE, pages 1–5.
IEEE.
Parra, L., Deco, G., and Miesbach, S. (1996). Statisti-
cal independence and novelty detection with informa-
tion preserving nonlinear maps. Neural Computation,
8:260–269.
Qi, X. and Davison, B. D. (2009). Web page classifica-
tion: Features and algorithms. ACM Comput. Surv.,
41(2):12:1–12:31.
Sadeghi, R. and Hamidzadeh, J. (2018). Automatic support
vector data description. Soft Comput., 22(1):147–158.
Sch
¨
olkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J.,
and Williamson, R. C. (2001). Estimating the support
of a high-dimensional distribution. Neural Computa-
tion, 13(7).
Shivaswamy, P. K. and Jebara, T. (2010). Maximum relative
margin and data-dependent regularization. Journal of
Machine Learning Research, 11:747–788.
Tax, D. (2012). DDtools, the Data Description Toolbox for
Matlab. version 1.9.1.
Tsang, I. W., Kwok, J. T., and Li, S. (2006). Learning the
kernel in mahalanobis one-class support vector ma-
chines. In IJCNN, pages 1169–1175. IEEE.
Vapnik, V. N. (1998). Statistical Learning Theory. Wiley,
New York, NY, USA.
Zafeiriou, S. and Laskaris, N. A. (2008). On the improve-
ment of support vector techniques for clustering by
means of whitening transform. IEEE Signal Process.
Lett., 15:198–201.
Zeng, Z., Fu, Y., Roisman, G. I., Wen, Z., Hu, Y., and
Huang, T. S. (2006). Spontaneous emotional facial
expression detection. Journal of Multimedia, 1(5):1–
8.
Zhu, M. and Martinez, A. M. (2006). Subclass discrimi-
nant analysis. IEEE Trans. Pattern Anal. Mach. Intell.,
28(8):1274–1286.
A Novel Dispersion Covariance-guided One-Class Support Vector Machines
553
