
Metagenomic Clustering in Search of Common Origin
Jolanta Kawulok and Michal Kawulok
Institute of Informatics, Silesian University of Technology, Gliwice, Poland
Keywords:
Metagenome, Metagenomic Reads, Hierarchical Clustering, Urban Microbiome, k-mers.
Abstract:
Analysis of metagenomic samples is aimed at extracting relevant information on these samples, including their
composition and origin. To determine where a sample comes from, it is commonly compared with a set of
reference samples extracted from known locations. However, if such reference samples are unavailable or
when the origins of the investigated samples are not covered by the reference set, it may be helpful to identify
groups of similar samples that may have a common origin. In this paper, we tackle this problem with hierar-
chical clustering applied to analyse a matrix of mutual similarities obtained using the Mash and our CoMeta
programs. We report initial, yet encouraging results of our experimental study performed for the metagenomic
data extracted from two large metropolises, downloaded from the Sequence Read Archive repository. The ob-
tained results indicate that the proposed approach is effective, which justifies further exploration of the topic
using more extensive data.
1 BACKGROUND
In recent years, analysis of metagenomic reads (col-
lections of genome fragments derived from microbes
living in a given location) has become a hot research
topic. Such analysis has a large potential, as it is
no longer necessary to isolate and culture organisms
in laboratory conditions to study them (Simon and
Daniel, 2011; Handelsman, 2004). The majority of
the research works are aimed at discovering the com-
position of the metagenomic samples. They consist
in identifying the species of the organisms (taxonomic
classification) or in determining the functions that can
be performed by the microorganisms from the sample
(functional classification) (Bengtsson-Palme, 2018).
There are many metagenomic software tools for 16S
analysis and shotgun metagenomic analysis (Oulas
et al., 2015). The latter data can be analyzed follow-
ing two kinds of methodological approaches: read-
based and assembly-based (Breitwieser et al., 2017).
Metagenomic reads may also be subject to binning
(Li et al., 2012; Wang et al., 2015), which commonly
consists in clustering the reads. This process is aimed
at identifying artificial duplicates or grouping simi-
lar sequences into species or operational taxonomic
units.
Furthermore, metagenomic analysis can be used
to predict the place where the samples come from
and to create a profile of that place. Walker et al.
(2018) used the 16S gene profile for taxonomic clas-
sification prior to building the city profiles. Taxo-
nomic analysis for classifying samples to the most
probable environment was proposed by Qiao et al.
(2018), whose MetaBinG2 program allows for de-
composing the complete genome sequence into short
substrings composed of k symbols (k-mers). The use
of functional classification was explored by Casimiro-
Soriguer et al. (2019) and Zhu et al. (2019). Zolfo
et al. (2018) used both taxonomic and functional clas-
sification for this purpose. For the metagenomic clas-
sification, various machine learning techniques are
also tested, including random forests, linear discrim-
inant analysis, and support vector machines (Harris
et al., 2019; Walker and Datta, 2019).
The aforementioned research works were focused
on comparing the query samples with those extracted
from known locations. In addition to that, dimension-
ality reduction techniques, including principal com-
ponent analysis and t-distributed stochastic neighbor
embedding, were employed to visualize the relation
between the samples based on their identified species
or functions (treated as highly-dimensional features
of these samples).
In this paper, we are focused on clustering the
metagenomic samples to identify those that may have
a common origin. Recently, we investigated such an
unsupervised scenario (Kawulok et al., 2019) with
no reference samples available, and we exploited our
218
Kawulok, J. and Kawulok, M.
Metagenomic Clustering in Search of Common Origin.
DOI: 10.5220/0009177702180225
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 218-225
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

CoMeta program (Kawulok and Deorowicz, 2015) to
determine mutual similarities between the samples. In
our earlier research (Kawulok and Kawulok, 2018),
we demonstrated that CoMeta can be successfully
used to classify the samples by comparing them with
entire metagenomic collections derived from refer-
ence samples, which allowed us to determine their
origin. Contrary to other approaches, we proposed
to compare the metagenomic samples by measuring
their similarity directly in the space of the reads,
which means that it is not necessary to identify the
species of organisms that are present in the samples to
compute their similarity—hence a reference database
with species or functions of microorganisms is not re-
quired. After obtaining the mutual similarities, we
formed the groups of similar samples manually. The
metagenomic samples are a mixture of diverse DNA
fragments. Thus, for a number of samples derived
from several different locations, it may be expected
that appropriate clustering would help identify those
that come from the same location.
Compared to our earlier research (Kawulok et al.,
2019), here we perform automatic (rather than man-
ual) clustering of the samples to determine those that
have a common origin. For this purpose, we employ
hierarchical clustering (Rokach and Maimon, 2005)
(its important advantage is that it does not require the
number of clusters to be provided in advance), and
we consider two different approaches toward analyz-
ing the similarity matrix. Furthermore, in addition to
using CoMeta, we also exploit the Mash program to
determine the similarities between the samples. The
reported results indicate that the clusters can be cor-
rectly identified in an automatic way without the ne-
cessity of performing taxonomic or functional classi-
fication.
2 MATERIALS AND METHODS
2.1 Metagenomic Data
In our experiments, our intention was to verify, if
we could cluster the samples, even if their origins
are geographically similar to each other. There-
fore, we aimed at selecting samples extracted from
large cities located relatively close to each other, in
which there are many travellers carrying microbes
from other places. From the Sequence Read Archive
repository
1
(SRA), we selected two projects that pro-
vide data of urban metagenome. The first dataset was
derived from New York City MTA subway (Afshin-
1
https://www.ncbi.nlm.nih.gov/sra
nekoo et al., 2015). For our experiments, we have
chosen 100 samples from them, each of which con-
tains 0.8 − 11.7 million paired-end reads (together
105.2G bases). The dataset from the second project
contains sequences from train cars and subway sta-
tions across the Boston subway system (Hsu et al.,
2016). For our experiments, we used 23 samples,
each of which contains 0.9 − 58.6 million paired-end
reads with 102 bp length.
2.2 Data Preprocessing
The SRA repository stores raw sequencing data,
therefore it can be expected that the samples ac-
quired from various cities contain highly-similar frag-
ments of the human genome. Therefore, we re-
moved human DNA from the investigated samples.
The GRCh38 latest genomic.fna.gz file (containing
human reference genome) was downloaded from the
NCBI Website. We filter each metagenome sample
using the kmc tools software (Deorowicz et al., 2015)
—if at least one human k-mer (k = 24) appears in a
read, then that read is removed from the sample.
2.3 Research Methodology
The clustering of the metagenomic samples is per-
formed on the basis of their mutual distances. For
determining the distances between the samples, we
have considered two programs.
The first one is the Mash program which estimates
the similarity between two genomes or metagenomes.
The program uses the MinHash dimensionality re-
duction technique to compress k-mer sets of whole
genomes (Ondov et al., 2019). In the program, the
reads in the sample (S) must be first sketched with s
hashes (s is termed the sketch size). Then, the simi-
larity between two samples is determined using these
sketched files by counting the number of overlapping
k-mers among all the s hashes.
Apart from Mash, we also used the our CoMeta
program to determine the similarities between the
samples. First, CoMeta creates k-mer databases for
all the reference samples that the query sample is to
be compared against. Subsequently, each read derived
from a query sample is compared against each other
sample (represented by a k-mer database). For each
ith read and jth sample, their similarity is computed
as the number of the nucleotides in the k-mers which
are present both in the read and in the database (asso-
ciated with that sample), divided by the length of the
query read. For clustering, a k-mer database must be
built for every sample, and then the similarity of each
sample (treated as a set of reads) to other sample (rep-
Metagenomic Clustering in Search of Common Origin
219
Comparison using CoMeta or Mash
S
1
S
2
S
3
S
N
Removal of human DNA from the
samples using the kmc tools software
S
0
1
S
0
2
S
0
3
S
0
N
S
H
— SIMS
2
S
1
SIMS
3
S
1
. . . SIMS
N
S
1
SIMS
1
S
2
— SIMS
3
S
2
. . . SIMS
N
S
2
SIMS
1
S
3
SIMS
2
S
3
— . . . SIMS
N
S
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SIMS
1
S
N
SIMS
2
S
N
SIMS
3
S
N
. . . —
Hierarchical clustering
Grouping of the most similar samples
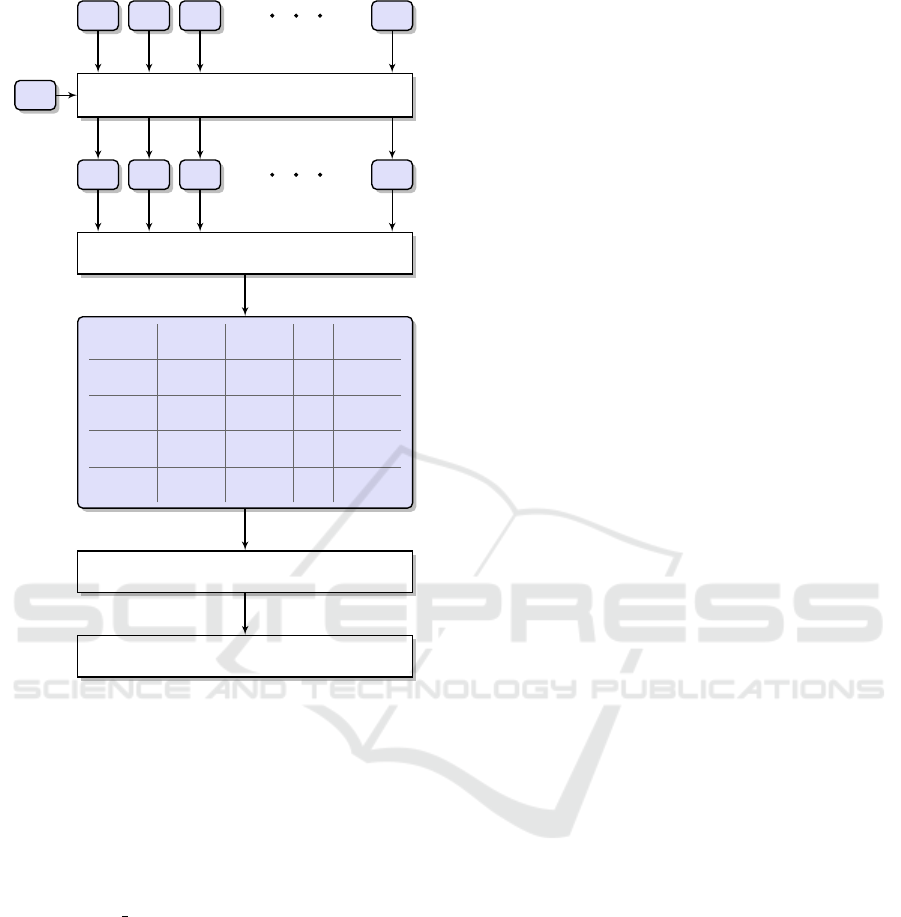
Figure 1: The processing pipeline for metagenomic reads
clustering.
resented by a k-mer database) is determined as a sum
of single-read similarities.
A simplified diagram of our clustering scheme is
shown in Figure 1. At the beginning (as described
in Section 2.2), the human fragments (S
H
) are sub-
tracted from the original metagenomic samples (S
0
i
)
using the kmc tools software. As a result, we ob-
tain N samples (S
i
) which are smaller than the orig-
inal ones. The next step is to compare the samples
between each other using CoMeta or Mash. From
these comparisons, we build a square matrix of sim-
ilarities (SSM) between the samples. It is worth not-
ing that the Mash program compares the samples us-
ing two sketched files, therefore the similarity is sym-
metrical (SIMS
1
S
2
= SIMS
2
S
1
). Contrary to that, the
CoMeta algorithm compares each sample in a read-
wise manner to a k-mer database built from another
sample. Hence, the similarities are not symmetrical
(SIMS
1
S
2
6= SIMS
2
S
1
).
The Mash program sketches each file using the
same size of a sketch, so despite the fact that the
files with reads are of different sizes, the size of each
sample is the same after sketching. The CoMeta pro-
gram builds a k-mer database using the whole sample,
therefore the sizes of these databases differ signifi-
cantly from each other. In the reported research, we
test CoMeta program using whole k-mer databases
and using reduced databases. The latter are built af-
ter reducing each sample to the size of 0.8 million
paired-end reads (which is the size of the smallest
sample), therefore each sample is represented by a k-
mer database of the same size.
For each sample, we obtain a set of N similari-
ties between that sample and the remaining samples.
However, the distributions of the similarity values dif-
fer significantly for individual samples. This is par-
ticularly visible for the scores obtained with CoMeta,
where even the values of self-similarity (i.e., the simi-
larity between the sample and a k-mer database cre-
ated from that sample) are varied. To address that
problem, we normalize the similarities in the follow-
ing way. First, we substitute each value on the di-
agonal (which contains the self-similarities) with the
highest value from the given row:
SIMS
i
S
i
← max{SIMS
i
S
j
: i, j ∈ h1,Ni,i 6= j}. (1)
Subsequently, each value in the row is divided by that
highest value to obtain the distance (DST) between the
samples:
DSTS
i
S
k
= 1 − SIMS
i
S
k
/SIMS
i
S
i
: i,k ∈ h1,Ni. (2)
In this way, we convert the SSM matrix into the
square distance matrix (SDM). While for CoMeta we
always exclude the self-similarities (1), we treat it as
an optional step for Mash, considering two versions
here: with self-similarities (WSS) and after excluding
self-similarities (ESS).
The distance matrix is subsequently used to iden-
tify the groups of samples which are supposed to have
the same origin. We consider two variants of ex-
ploiting the hierarchical clustering, namely: (origi-
nal dst)—the distances from the SDM are used as
an input for clustering; (recomputed dst)—the values
in columns are treated as individual attributes for the
samples in the rows (hence each sample is represented
with an N-dimensional feature vector containing the
distances of that sample to all the samples). In the lat-
ter variant, the Euclidean distances between the sam-
ples’ feature vectors are treated as the distances be-
tween the samples, which forms a new SDM that is
subject to hierarchical clustering.
Then, the samples are grouped using hierarchi-
cal clustering analysis (HCA). The HCA algorithm
starts by treating each sample as a singleton clus-
ter. Then, the following two steps are repeatedly exe-
cuted: (1) determine a pair of the closest clusters, and
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
220
CoMeta (whole kmer db)
BOS
NY
NY
NY
NY
NY
BOS
NY
NY
NY
NY
NY
10
20
30
40
50
60
70
80
90
100
CoMeta (reduced kmer db )
BOS
NY
NY
NY
NY
NY
BOS
NY
NY
NY
NY
NY
10
20
30
40
50
60
70
80
90
100
(a) (b)
Mash (WSS)
BOS
NY
NY
NY
NY
NY
BOS
NY
NY
NY
NY
NY
0
100
200
300
400
500
600
700
800
900
1000
Mash (ESS)
BOS
NY
NY
NY
NY
NY
BOS
NY
NY
NY
NY
NY
0
10
20
30
40
50
60
70
80
90
100
(c) (d)
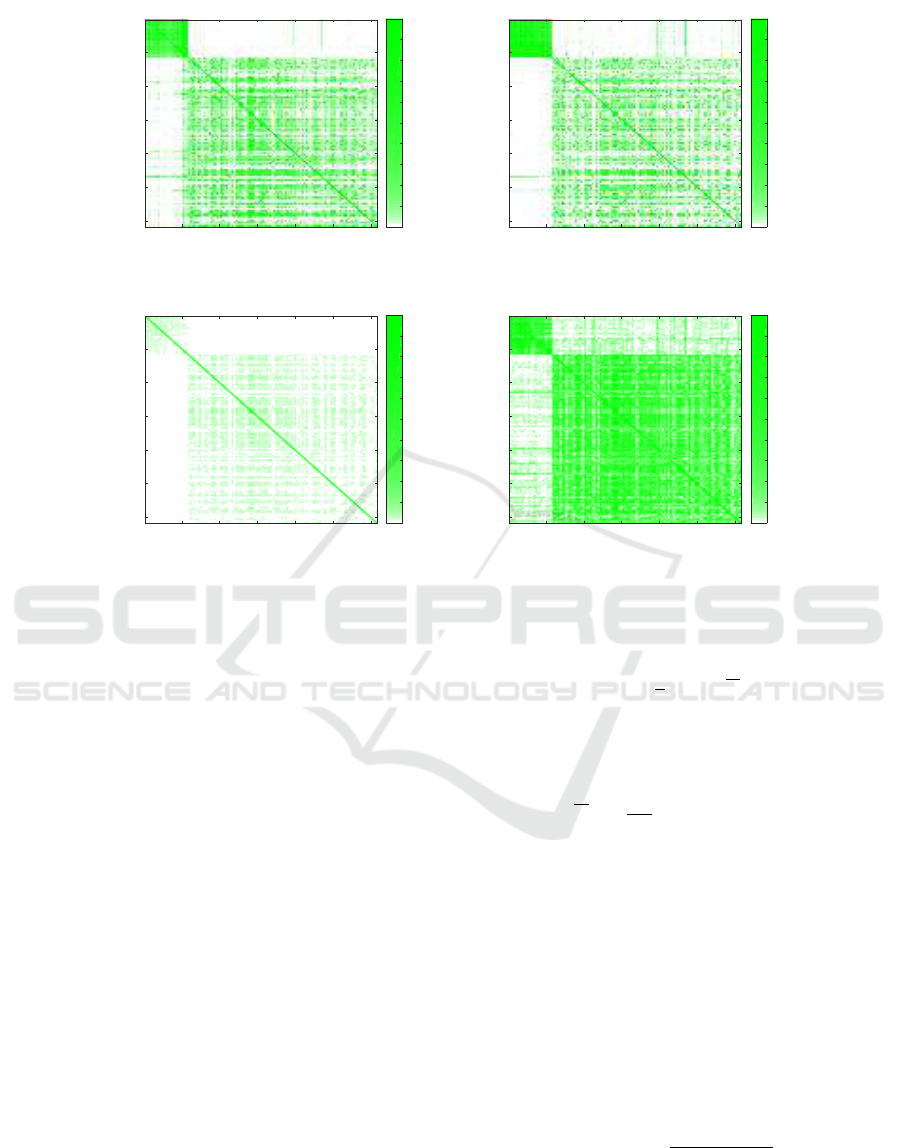
Figure 2: The square matrices of similarities between the samples.
(2) merge them together. This searching-and-merging
process is continued until all the clusters (samples)
are merged together. The relationship between the
clusters is represented by the dendrogram plot of the
hierarchical binary cluster tree. In our work, for deter-
mining the distances between sets of samples, we use
single-linkage clustering criteria, which is the shortest
distance.
3 EXPERIMENTAL VALIDATION
Our experimental study was performed using two pro-
grams: CoMeta and Mash. For the CoMeta pro-
gram, we use whole k-mer databases and reduced k-
mer databases, as explained earlier in this paper. The
SSM matrix is normalized for both programs, and for
Mash we report the results obtained without and with
excluding the self-similarities. For HCA, we use orig-
inal SDM, as well as the recomputed distance matrix.
3.1 Evaluation of Clustering
The clustering outcome can be evaluated taking into
account internal or external criteria (Rokach and Mai-
mon, 2005). As an internal quality criterium, for
M clusters, we use a sum of squared error (SSE):
D =
1
2
M
∑
m=1
N
m
D
m
, (3)
where N
m
= |C
m
| is the number of instances (here,
samples) belonging to the cluster C
m
, and:
D
m
=
1
N
2
m
∑
S
i
,S
j
∈C
m
d
2
(S
i
,S
j
), (4)
where d(S
i
,S
j
) is the distance between the samples S
i
and S
j
.
The external quality criteria can be useful for ex-
amining whether the structure of the clusters matches
some predefined classification of the samples. One
of the simplest metrics here is the Rand index, which
consists in determining the ratio between matched
and unmatched observations among two clustering
structures—C1, which is an induced clustering struc-
ture and C2, which is a given (ground-truth) clustering
structure. This index is defined as:
RAND =
a + d
a + b + c + d
, (5)
where a is the number of pairs of samples that are
assigned to the same cluster in both structures (C1 and
C2); b is the number of pairs of samples that are in the
Metagenomic Clustering in Search of Common Origin
221
Samples
50
100
150
200
Distance
CoMeta (whole kmer db, original dst)
Samples
100
200
300
400
500
Distance
CoMeta (whole kmer db, recomputed dst)
(a) (b)
Samples
0
50
100
150
200
250
300
Distance
CoMeta (reduced kmer db, original dst)
Samples
0
500
1000
1500
Distance
CoMeta (reduced kmer db, recomputed dst)
(c) (d)
Samples
1200
1250
1300
1350
1400
Distance
Mash (WSS, original dst)
Samples
1700
1750
1800
1850
1900
1950
Distance
Mash (WSS, recomputed dst)
(e) (f)
Samples
50
100
150
200
250
300
Distance
Mash (ESS, original dst)
Samples
200
400
600
800
1000
1200
Distance
Mash (ESS, recomputed dst)
(g) (h)
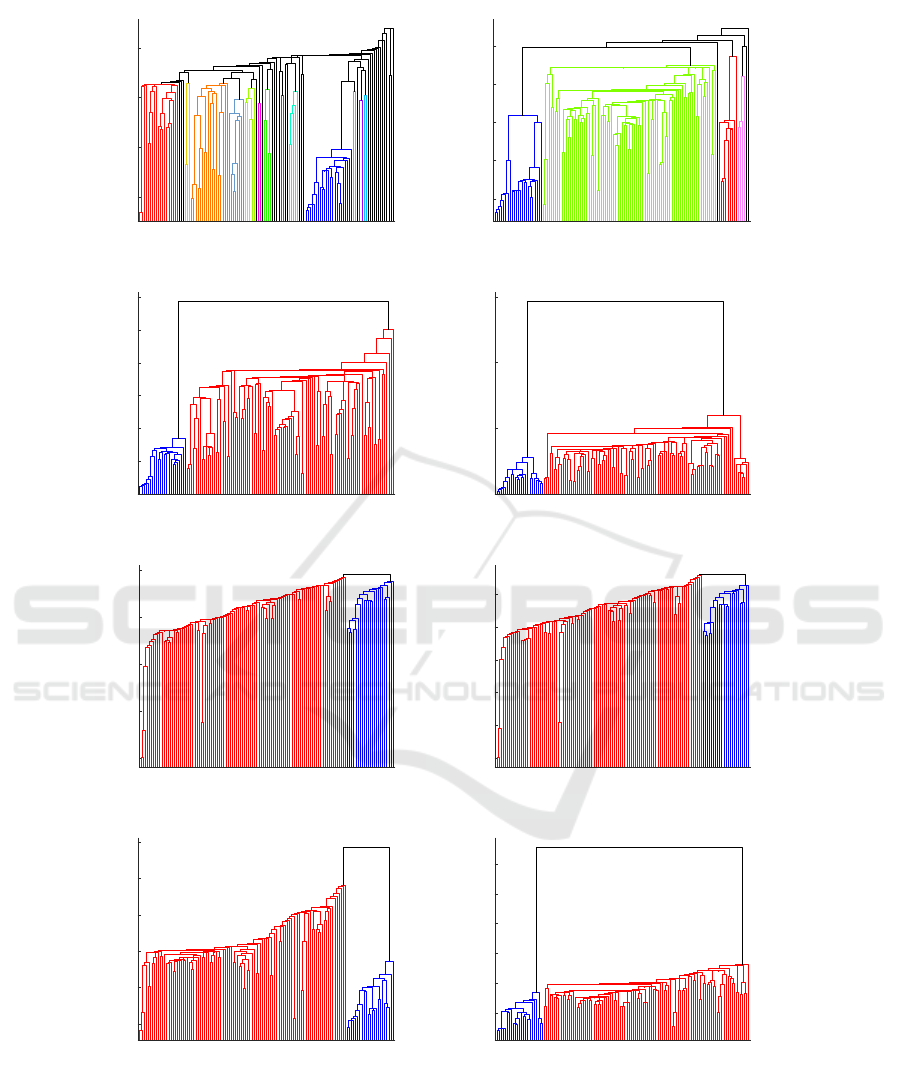
Figure 3: The dendrogram plots for hierarchical clustering. The dark blue color indicates the samples from Boston, the other
colors indicate the samples from New York.
same cluster in C1, but not in the same cluster in C2;
c is the number of pairs of samples that are in the same
cluster in C2, but not in the same cluster in C1; and
d is the number of pairs of samples that are available
in different clusters in C1 and C2. The Rand index
value lies between 0 and 1, and it equals 1 when the
samples are perfectly separated.
In addition, we inspect the appearance of the ob-
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
222
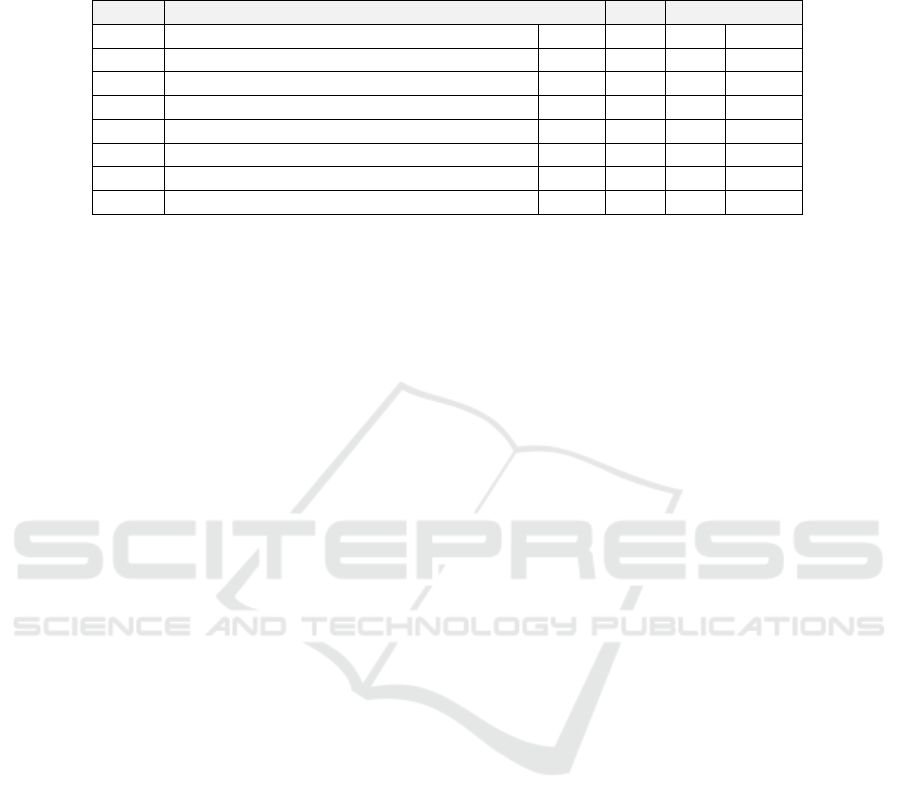
Table 1: The clustering quality scores. D
BOS
and D
NY
are cluster-wise SSEs (4), computed for individual clusters of Boston
and New York samples, respectively; D is the overall SSE (3); and RAND is the Rand index (5). The three best scores in each
column are bolded.
Fig 3: Name: D
BOS
D
NY
D RAND
(a) CoMeta (whole kmer db, original dst) 0.23 0.44 0.33 0.68
(b) CoMeta (whole kmer db, recomputed dst) 0.09 0.23 0.16 0.68
(c) CoMeta (reduced kmer db, original dst) 0.19 0.44 0.32 1.00
(d) CoMeta (reduced kmer db, recomputed dst) 0.08 0.23 0.15 1.00
(e) Mash (WSS, original dst) 0.47 0.49 0.48 1.00
(f) Mash (WSS, recomputed dst) 0.45 0.47 0.46 1.00
(g) Mash (ESS, original dst) 0.26 0.34 0.30 1.00
(h) Mash (ESS, recomputed dst) 0.12 0.22 0.17 1.00
tained SSM matrices and dendrograms, taking into
account how the classes are separated—we assess
whether it is easy to separate the individual clusters
based on the graphs.
3.2 Results and Discussion
Figure 2 shows the square matrixes of similarities be-
tween the samples for various cases. The results for
samples from Boston are shown in the top left cor-
ner, and it can be seen that in all cases two clusters
are formed, and they correspond with the ground truth
(i.e., with the Boston and New York samples). How-
ever, on the plot obtained with CoMeta using a whole
database (Figure 2(a)), two additional clusters can be
noticed in the bottom right corner. For Mash, ex-
cluding the self-similarities (Figure 2(d)) allowed for
strengthening the scores, and the clusters appear to be
visually better than when obtained with CoMeta.
Figure 3 shows dendrogram plots for hierarchi-
cal clustering obtained from four SDMs from Fig-
ure 2. Two methods of providing the distance matrix
to HCA were investigated—the original matrix (orig-
inal dst) and a modified matrix (recomputed dst). The
dendrograms in the left column in Figure 3(a, c, e, g)
were obtained from original distance matrices, and in
the right column (b, d, f, h) using the recomputed ma-
trices. The dark blue color indicates the samples from
Boston, and the red color indicates the samples from
New York. In the dendrograms (a, b), some additional
clusters are visible (presented with different colors in
the plots)—they show the results retrieved with the
CoMeta program, when the whole k-mer databases
are used. The dendrograms (c, d) are built using the
reduced k-mer databases in CoMeta algorithm which
balances the size of the samples. In Figure 3(g, h), the
dendrograms show the outcome obtained with Mash
after excluding the self-similarities from the SSM ma-
trix, while the dendrograms (e, f) present the results
obtained with the self-similarities.
The clustering quality scores obtained using data
shown in Figure 3 are reported in Table 1. The SSE
is the sum of squared error defined in (3). It is com-
puted using additional minimum variance criteria (4),
whose values for single clusters are D
BOS
and D
NY
for Boston and New York, respectively. The smaller
the value is, the greater is the homogeneity within the
cluster. RAND is the Rand index defined in (5). The
best scores for each parameter are bolded.
Analyzing all plots, we can observe that the use
of small k-mer databases as opposed to the whole
ones allows for correct identification of clusters for
the CoMeta program. When whole k-mer databases
are used, then some additional clusters are induced
within the New York samples which can be seen in
Figures 2(a) and 3(a, b). Hence, for these two sets of
data, the value of Rand index is below 1 in Table 1.
This means that unbalanced samples lead to identify-
ing false positive clusters in the results.
From the plots obtained for Mash, we can notice
that excluding the self-similarities allows us to sepa-
rate the samples from both cities more clearly. This
could also be noticed in Table 1—the values of D
BOS
,
D
NY
and SSE are smaller for the Mash data after ex-
cluding the self-similarities. For more sophisticated
data with more ground-truth clusters, this can be cru-
cial for correct cluster identification, as it could be
difficult to clearly separate the individual clusters.
Comparing the left and right dendrograms in Fig-
ure 3, it can be seen that the recomputed distances be-
tween the samples reduce the distances between the
samples within each cluster, and it has a similar ef-
fect to excluding the self-similarities for Mash. These
observations are also confirmed by the scores in Ta-
ble 1—the homogeneity within the clusters is larger
when the distances are refined taking into account the
distance features of each sample.
Overall, the presented work clearly indicates that
it is possible to automate the process of clustering the
samples without identifying the microorganisms de-
Metagenomic Clustering in Search of Common Origin
223

rived from them. The best results have been obtained
using Mash based on the recomputed distances after
excluding the self-similarities (Figure 3(h)). Also, the
operation of balancing the samples by reducing the
size of the databases allows for obtaining similar re-
sults with the CoMeta program (Figure 3(d)). It is
worth noting here that such an operation is indirectly
performed by Mash, as it builds sketches of a constant
size, independently on the sample size.
4 CONCLUSIONS AND FUTURE
WORK
In this paper, we proposed a new approach toward
clustering metagenomic reads in search of the sam-
ples that have common origin. The results of our ex-
perimental study indicate that the presented method
allows for separating the samples based on their mu-
tual similarity.
An important advantage of the reported approach
lies in determining the sample similarity at the reads
level without the necessity to understand the contents
of these samples. Therefore, our methodology does
not require large databases (taxonomical and func-
tional) of annotated reads. Here, we used two pro-
grams (CoMeta and Mash) for comparing the sam-
ples prior to clustering, and the results obtained for
the best variants of both programs were similar. Im-
portantly, we show that clustering of the metagenomic
samples can be automated, which may be extremely
important when a larger number of samples is to be
processed.
In the presented preliminary research, we used the
samples from two large cities located relatively close
to each other—Boston and New York. While based on
that limited dataset it is difficult to indicate which pro-
gram is more suitable for clustering, we have demon-
strated how important it is to deal with the problem
of imbalanced data as well as to preprocess the sim-
ilarity scores. In our future work, we will extend the
database used for evaluation to verify this approach
for a larger number of clusters (i.e., ground-truth lo-
cations) and increase their diversity.
ACKNOWLEDGEMENTS
This work was supported by the Polish Na-
tional Science Centre under the project DEC-
2015/19/D/ST6/03252. This research was supported
in part by PL-Grid Infrastructure.
REFERENCES
Afshinnekoo, E., Meydan, C., Chowdhury, S., Jaroudi, D.,
Boyer, C., Bernstein, N., Maritz, J. M., Reeves, D.,
Gandara, J., Chhangawala, S., et al. (2015). Geospa-
tial resolution of human and bacterial diversity with
city-scale metagenomics. Cell systems, 1(1):72–87.
Bengtsson-Palme, J. (2018). Strategies for taxonomic and
functional annotation of metagenomes. In Metage-
nomics, pages 55–79. Elsevier.
Breitwieser, F. P., Lu, J., and Salzberg, S. L. (2017). A re-
view of methods and databases for metagenomic clas-
sification and assembly. Briefings in bioinformatics.
Casimiro-Soriguer, C. S., Loucera, C., Perez Florido, J.,
L
´
opez-L
´
opez, D., and Dopazo, J. (2019). Antibi-
otic resistance and metabolic profiles as functional
biomarkers that accurately predict the geographic ori-
gin of city metagenomics samples. Biology Direct,
14(1):15.
Deorowicz, S., Kokot, M., Grabowski, S., and Debudaj-
Grabysz, A. (2015). KMC 2: fast and resource-frugal
k-mer counting. Bioinformatics, 31(10):1569–1576.
Handelsman, J. (2004). Metagenomics: application of ge-
nomics to uncultured microorganisms. Microbiol Mol
Biol Rev., 68(4).
Harris, Z. N., Dhungel, E., Mosior, M., and Ahn, T.-H.
(2019). Massive metagenomic data analysis using
abundance-based machine learning. Biology Direct,
14(1):12.
Hsu, T., Joice, R., Vallarino, J., Abu-Ali, G., Hartmann,
E. M., Shafquat, A., DuLong, C., Baranowski, C.,
Gevers, D., Green, J. L., et al. (2016). Urban tran-
sit system microbial communities differ by surface
type and interaction with humans and the environ-
ment. Msystems, 1(3):e00018–16.
Kawulok, J. and Deorowicz, S. (2015). CoMeta: Clas-
sication of metagenomes using k-mers. PLoS ONE,
10(4):e0121453.
Kawulok, J. and Kawulok, M. (2018). Environmen-
tal metagenome classification for soil-based forensic
analysis. In BIOINFORMATICS, pages 182–187.
Kawulok, J., Kawulok, M., and Deorowicz, S. (2019). Envi-
ronmental metagenome classification for constructing
a microbiome fingerprint. Biology Direct, 14(1).
Li, W., Fu, L., Niu, B., Wu, S., and Wooley, J. (2012). Ultra-
fast clustering algorithms for metagenomic sequence
analysis. Briefings in bioinformatics, 13(6):656–668.
Ondov, B. D., Starrett, G. J., Sappington, A., Kostic,
A., Koren, S., Buck, C. B., and Phillippy, A. M.
(2019). Mash screen: High-throughput sequence con-
tainment estimation for genome discovery. BioRxiv,
page 557314.
Oulas, A., Pavloudi, C., Polymenakou, P., Pavlopoulos,
G. A., Papanikolaou, N., Kotoulas, G., Arvanitidis,
C., and Iliopoulos, l. (2015). Metagenomics: tools
and insights for analyzing next-generation sequencing
data derived from biodiversity studies. Bioinformatics
and biology insights, 9:BBI–S12462.
Qiao, Y., Jia, B., Hu, Z., Sun, C., Xiang, Y., and Wei, C.
(2018). MetaBinG2: a fast and accurate metagenomic
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
224

sequence classification system for samples with many
unknown organisms. Biology direct, 13(1):15.
Rokach, L. and Maimon, O. (2005). Clustering methods.
In The Data Mining and Knowledge Discovery Hand-
book, pages 321–352.
Simon, C. and Daniel, R. (2011). Metagenomic Analyses:
Past and Future Trends. Applied and Environmental
Microbiology, 77(4):1153–1161.
Walker, A. R. and Datta, S. (2019). Identification of city
specific important bacterial signature for the metasub
camda challenge microbiome data. Biology Direct,
14(1):11.
Walker, A. R., Grimes, T. L., Datta, S., and Datta, S.
(2018). Unraveling bacterial fingerprints of city sub-
ways from microbiome 16s gene profiles. Biology di-
rect, 13(1):10.
Wang, Y., Hu, H., and Li, X. (2015). Mbbc: an efficient ap-
proach for metagenomic binning based on clustering.
BMC bioinformatics, 16(1):36.
Zhu, C., Miller, M., Lusskin, N., Mahlich, Y., Wang, Y.,
Zeng, Z., and Bromberg, Y. (2019). Fingerprinting
cities: differentiating subway microbiome functional-
ity. Biology Direct, 14:19.
Zolfo, M., Asnicar, F., Manghi, P., Pasolli, E., Tett, A.,
and Segata, N. (2018). Profiling microbial strains in
urban environments using metagenomic sequencing
data. Biology direct, 13(1):9.
Metagenomic Clustering in Search of Common Origin
225
