
3D Spatial Dependencies Study in the Hawk and Dove Model
Andrzej Swierniak
a
, Marek Bonk and Damian Borys
b
Silesian University of Technology, Faculty of Automatic Control, Electronics and Computer Science,
Akademicka 16, Gliwice, Poland
Keywords:
Evolutionary Games, Game Theory, Spatial, 3D Grid.
Abstract:
The aim of the research was to check spatial dependencies in evolutionary games in 3D grids and compare
them with simulation results (2D) and theoretical or analytical considerations obtained from the replicator
dynamics equations. In order to compare the results, the classic Hawk and Dove model was used and a series
of simulations for both v < c and v > c cases was performed using our own software. The results are almost
the same as the theoretical analysis of this model, but some small differences were observed and discussed. It
seems, however, that the 3D model better reflects the behaviour of the population than 2D simulations.
1 INTRODUCTION
The theory of evolutionary game theory (EGT) initi-
ated by JM. Smith and G. Price (Sigmund and Nowak,
1999; Smith, 1982) allow expressing the idea of Dar-
win’s matching of genres and their evolution with the
elegant mathematical apparatus of game theory. This
field of knowledge has allowed the creation of meth-
ods for simulation and analysis of the dynamics of the
population of individuals observed in the biological
world. The players in those games are characterised
by strategies or phenotypes that can compete or coop-
erate to achieve their evolutionary goals. Unlike stan-
dard game theory, players are instinct-based rather
than particularly rational, and the expected outcome
of the game is a better fit for the environment, thereby
gaining food, partner, or living space. In the results of
individual interactions, the population may be stable,
monomorphic or multi-morphic. This state is called
evolutionary stable, and the phenotype recognised as
an evolutionary stable strategy (ESS) cannot be re-
placed by another (Smith and Price, 1973). The EGT
methodology allows us to predict the behaviour of the
population, e.g. whether one of the strategies will
be dominant. Additional information about dynamics
can be obtained from the so-called replicator dynam-
ics equations (Hofbauer et al., 1979). Still, all this
concerns the whole population and does not allow for
the analysis of its spatial structure. The use of spatial
evolutionary game theory (SEGT) (Bach et al., 2003)
a
https://orcid.org/0000-0002-5698-5721
b
https://orcid.org/0000-0003-0229-2601
allows us to supplement the missing knowledge. Each
new state of the population is obtained by perform-
ing the following steps: updating payoffs, removing
cells, reproducing. Such models have been used e.g.
in modelling cancer development (Bach et al., 2003),
modelling inter-cellular interactions including avoid-
ance of apoptosis and production of angiogenic fac-
tors (Tomlinson and Bodmer, 1997), modelling the
production of the cytotoxic substances (Tomlinson,
1997), modelling production of growth factors (Bach
et al., 2001), invasion and metastasis (Mansury et al.,
2006), tumor-environment interactions (Gatenby and
Vincent, 2003), interaction between osteoclasts and
osteoblasts (Dingli et al., 2009), tumor-stroma in-
teraction (Gerstung et al., 2011), neighbourhood ef-
fect modelling (Krzeslak and Swierniak, 2011), resis-
tance to chemotherapy (Basanta et al., 2012a) or in-
teraction of different types of cancer (Basanta et al.,
2012b). An overview of the models can be found in
the works (Basanta et al., 2008; Swierniak and Krzes-
lak, 2013). Until now, spatial analysis has been pre-
sented and analysed only in two dimensions (Krzes-
lak and Swierniak, 2016; Swierniak and Krzeslak,
2016; Swierniak and Krzeslak, 2013; Krzeslak and
Swierniak, 2011) or the third dimension meant addi-
tional resources (Swierniak et al., 2018). To relate the
models to any real, biological population, it seems
necessary to examine spatial relationships in three-
dimensional space, analysing whether the behaviour
of the studied population will show significant differ-
ences. In this paper, we examine the spatial model
of evolutionary games for the three-dimensional gam-
Swierniak, A., Bonk, M. and Borys, D.
3D Spatial Dependencies Study in the Hawk and Dove Model.
DOI: 10.5220/0009180102330238
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 233-238
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
233
ing space on the example of the Hawk-Dove model
known in the literature. The results of 3D simula-
tions were compared compare them with 2D simu-
lation results and theoretical or analytical consider-
ations obtained from the replicator dynamics equa-
tions. Both cases of parameter settings (for v < c and
v > c) were taken into account in the research. The in-
fluence of the choice of different settings in a spatial
game was investigated and simulations for ordinary
and mixed games (MSEG - multidimensional spa-
tial evolutionary game), proposed in (Swierniak and
Krzeslak, 2016; Krzeslak et al., 2016; Krzeslak and
Swierniak, 2016; Swierniak et al., 2016), in which
each cell contains information about the composition
of different phenotypes, were carried out. Thus, a
heterogeneous subpopulation within individual cells
is represented.
2 MATERIALS AND METHODS
The game Hawk and Dove is one of the first evo-
lutionary models proposed by John Maynard Smith
(Smith, 1982). It includes two types of phenotypes
or behaviour: combat (Hawks) or avoidance (Doves),
within the population of a single species. This pop-
ulation is a symbolic representation of the ritual con-
flicts between two different strategies that evolved in
the process of evolution.
This game has two players, and each player has
his own set of decisions, which we call strategy here.
Each pair of strategies for players will result in some
game result for each player, which we call a payoff.
These values, saved in the matrix form, can be treated
as a profit or the cost of choosing a particular strat-
egy. These values can also be used to model for e.g.
Darwinians fitness. The payoff matrix (presented in
general form in Table 1) has two parameters: v - the
benefit of the competition and c - the cost of escala-
tion.
In this model the replicator dynamics equation is
as follows:
˙x = cx (x − 1)(x −
v
c
). (1)
For Hawk and Dove game stable polymorphism
(coexistence between all phenotypes) is defined by
the following evolutionarily stable strategy (ESS):
(v/c,1 − v/c) if v < c. This conditions can be
found directly from the definition of ESS or from
the Bishop-Canning theorem (Bishop and Cannings,
1978). To achieve a stable polymorphic result v must
be less than c, otherwise the population is dominated
by Hawks. The results for this model are independent
of the initial frequencies of occurrence and the plot of
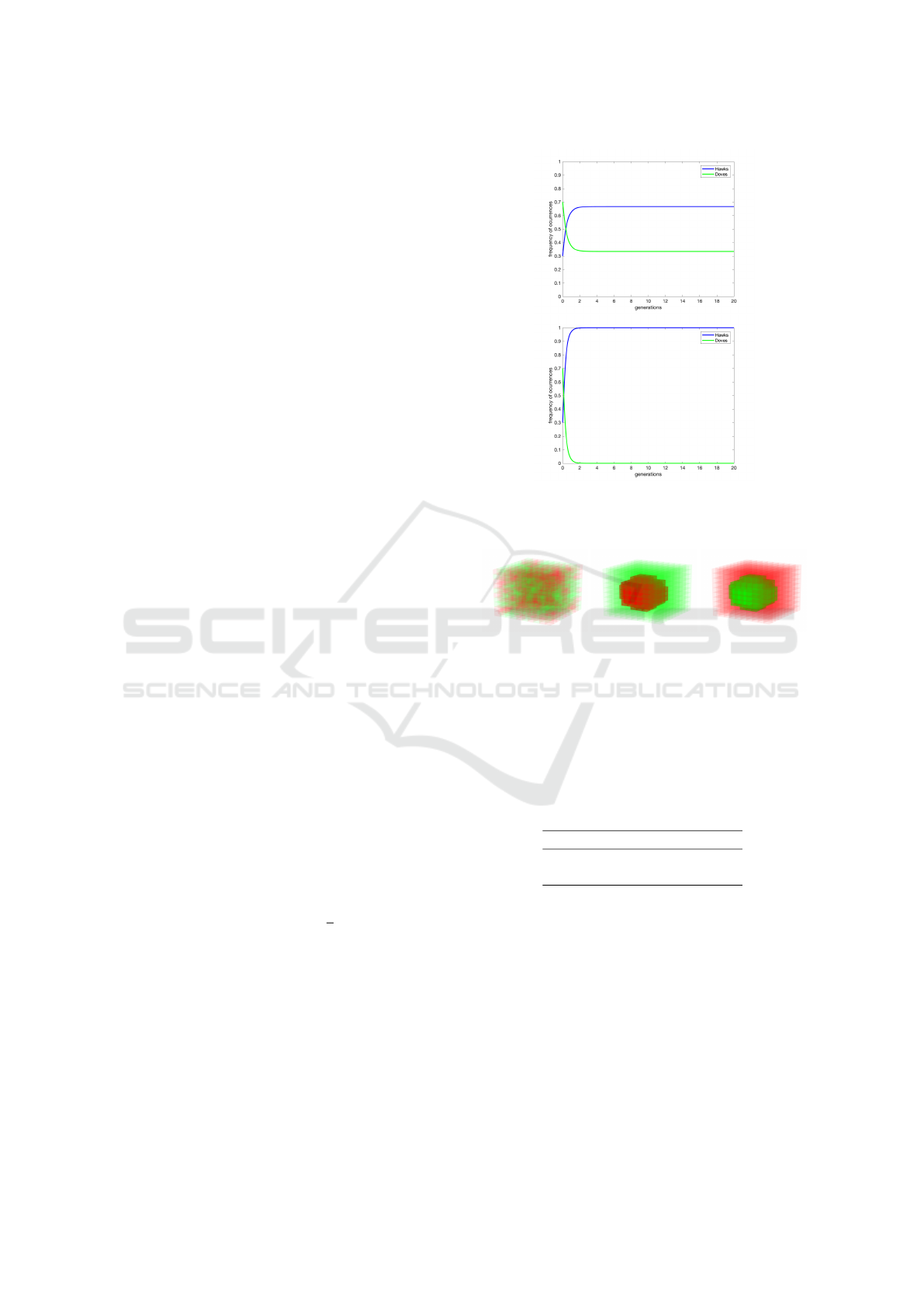
Figure 1: Result of mean-field (replication equations) dy-
namics for v=6, c=9 (v < c) in the top and v=9, c=6 (v > c)
in the bottom.
Figure 2: Initial conditions tested for Hawk and Dove
model: random (init0), Hawks in the middle (init1), Doves
in the middle (init2).
both cases (v < c and v > c) are presented on Figure
1). Those plots are the result of solving the Equation
1. Any further plots in this work are the averaged re-
sult of simulation performed in 2D or 3D grid.
Table 1: The payoff matrix for original Hawk and Dove
model.
Phenotypes Hawk Dove
Hawk v-c 2v
Dove 0 v
In this paper, we have focused on the comparison
of 2D and 3D game results, examining the impact of
the initial condition and referring these simulations to
the plots obtained from the replicator dynamic equa-
tions. The simulations were performed for three dif-
ferent initial conditions, which also gave a different
share of particular phenotypes. These were: random
distribution of individuals in the participation of 50/50
(called by us init0), Hawks concentration in the center
of the area (as init1) and Doves concentration (init2).
All those initial conditions are presented in Figure 2.
The in-house software was created to perform
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
234

Figure 3: Result of mean 2D spatial game presented for
v=6, c=9 (v < c) and appropriately for init0, init1 and init2
conditions.
Figure 4: Averaged 2D spatial game dynamics presented in
mean-field like plot for v=6, c=9 (v < c) and appropriately
for init0, init1 and init2 conditions.
simulations in 2D and 3D cases. Exact steps of simu-
lations were explained first by Bach et al. (Bach et al.,
2003) and later in our previous works (Swierniak
and Krzeslak, 2013; Swierniak and Krzeslak, 2016;
Krzeslak et al., 2016; Krzeslak and Swierniak, 2016;
Swierniak et al., 2018). All simulations were per-
formed for 2D or 3D torus of size 32x32 or 10x10x10
cells. Results were analysed on spatial maps, aver-
age mean-field like plots and averaged spatial maps.
Those averaged spatial images were analysed to show
the areas occupied by particular phenotype during the
simulation. Green colour represents Doves, and red
represents Hawks in all plots that presents the simula-
tion results.
3 RESULTS
In this section results for v=6, c=9 (v < c) and v=9,
c=6 (v > c) will be presented in Figures 3-6 for dif-
ferent initial conditions and for 2D games. Averaged
map as one in Figure 3 tells us where are areas of an
increased occurrence of a specific phenotype. For ex-
ample, pixels with almost pure red colour represents
areas where almost all the time were observed Hawks
phenotype, and vice versa - the greener the more often
Doves was in that specific location: the more mixed
colour, the more random occurrence of a specific phe-
notype.
In next section results for v=6, c=9 (v < c) are pre-
sented in Figures 7-9 for different initial conditions
and summary mean image in Figure 10.
In the last section, results for v=9, c=6 (v > c) are
presented in Figures 12-14 for different initial condi-
tions and summary mean image in Figure 15.
Figure 5: Result of mean 2D spatial game presented for
v=9, c=6 (v > c) and appropriately for init0, init1 and init2
conditions.
Figure 6: Averaged 2D spatial game dynamics presented in
mean-field like plot for v=9, c=6 (v > c) and appropriately
for init0, init1 and init2 conditions.
4 DISCUSSION AND
CONCLUSIONS
Observation of average graphs (for example Fig. 4,
Fig. 6 etc.) allows us to state that the results of spatial
games on average overlap with theoretical considera-
tions and replicator dynamics (Fig. 1). At this level,
there were no significant differences between 2D and
3D simulations. Only it can be noticed that for the
case v < c, where the coexistence of both popula-
tions occurs, we expected (referring to Figure 1 and
the solution of ESS) a slightly better adaptation of the
Hawks for the given parameters. However, for 2D
spatial games, the Doves phenotype showed a slightly
better adaptation. This may suggest that games sim-
ulated on 3D grids better reflect the behaviour of the
population. Otherwise, in the opposite case (v > c), in
each situation the results coincided with the theoreti-
Figure 7: Result of 3D spatial game presented for the mid-
dle layer for v=6, c=9 (v < c), init0 and appropriately in
generations : 0 (left-top), 50 (right-top), 200 (left-bottom)
and 500(right-bottom).
3D Spatial Dependencies Study in the Hawk and Dove Model
235
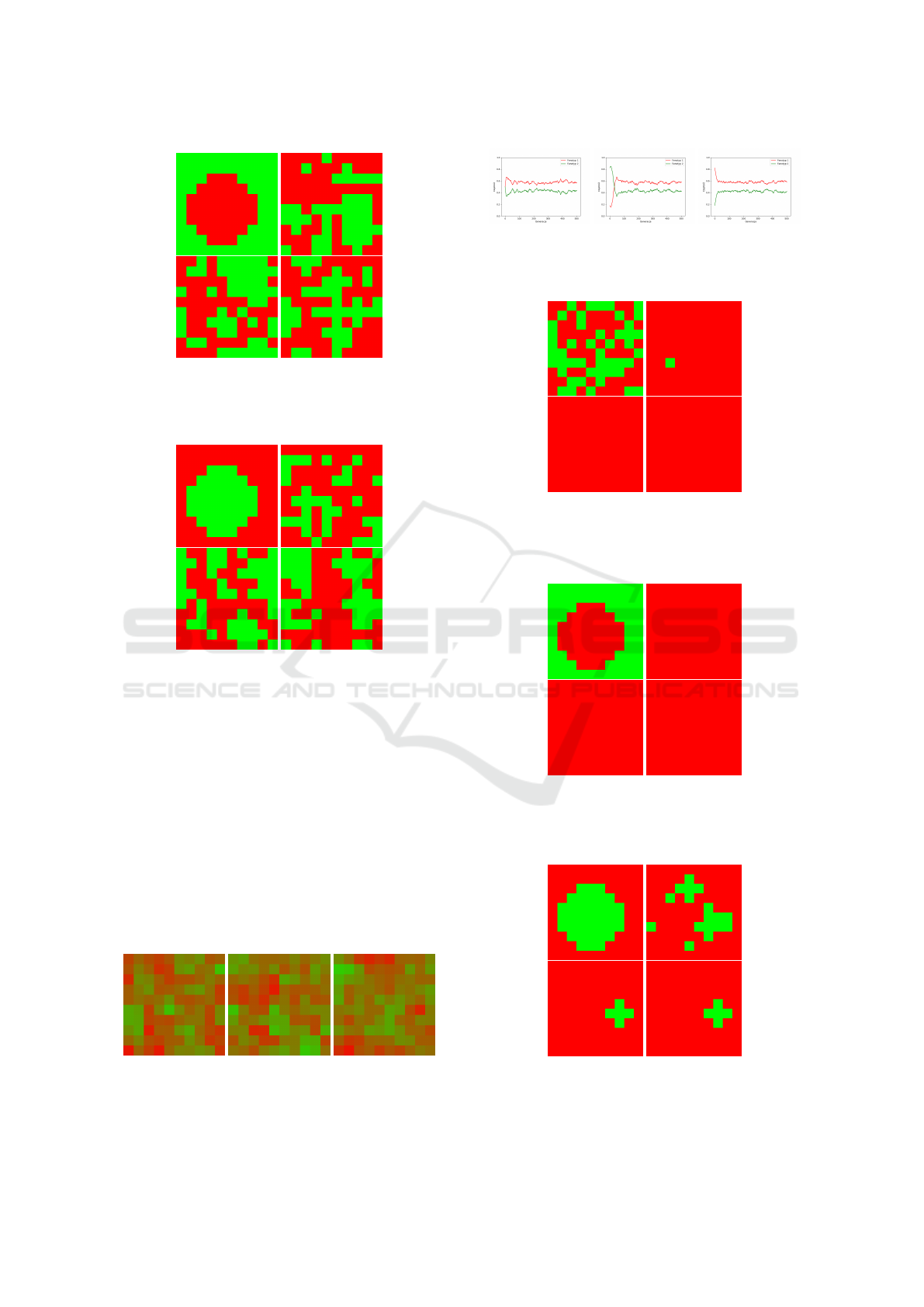
Figure 8: Result of 3D spatial game presented for the mid-
dle layer for v=6, c=9 (v < c), init1 and appropriately in
generations : 0 (left-top), 50 (right-top), 200 (left-bottom)
and 500(right-bottom).
Figure 9: Result of 3D spatial game presented for the mid-
dle layer for v=6, c=9 (v < c), init2 and appropriately in
generations : 0 (left-top), 50 (right-top), 200 (left-bottom)
and 500(right-bottom).
cal, quickly following the dominance of Hawks. The
analysis of spatial results showed that even if, in the
initial stage, the populations show some structure, the
spatial distribution quickly starts to resemble a ran-
dom one. On the average graphs in 2D, one can see a
delicate structure, where particular phenotypes were
grouped. This is not so clear for the 3D case (and
v < c), although it is possible that this is due to the
small size of the grid. An interesting structure was
observed in the results of the 3D simulations, which
seemed not to show much. After all, we expect a
Figure 10: Result of mean 3D spatial game presented for
the middle layer for v=6, c=9 (v < c) and appropriately for
init0, init1 and init2 conditions.
Figure 11: Averaged 3D spatial game dynamics presented
in mean-field like plot for v=6, c=9 (v < c) and appropri-
ately for init0, init1 and init2 conditions.
Figure 12: Result of 3D spatial game presented for the mid-
dle layer for v=9, c=6 (v > c), init0 and appropriately in
generations : 0 (left-top), 50 (right-top), 200 (left-bottom)
and 500(right-bottom).
Figure 13: Result of 3D spatial game presented for the mid-
dle layer for v=9, c=6 (v > c), init1 and appropriately in
generations : 0 (left-top), 50 (right-top), 200 (left-bottom)
and 500(right-bottom).
Figure 14: Result of 3D spatial game presented for the mid-
dle layer for v=9, c=6 (v > c), init2 and appropriately in
generations : 0 (left-top), 50 (right-top), 200 (left-bottom)
and 500(right-bottom).
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
236

Figure 15: Result of mean 3D spatial game presented for
the middle layer for v=9, c=6 (v > c) and appropriately for
init0, init1 and init2 conditions.
Figure 16: Averaged 3D spatial game dynamics presented
in mean-field like plot for v=9, c=6 (v > c) and appropri-
ately for init0, init1 and init2 conditions.
quick elimination of Doves. In spatial games, it turns
out that the full elimination of Doves does not take
place, and there is always a small number of repre-
sentatives of this phenotype. What is more, on the
Figure 14 one can see a formed structure in the form
of a cross (corresponding to the settings of the sim-
ulations, i.e. Moore’s neighbourhood), where Doves
remain all the time. This trend is also clearly shown
in Figure 15 (the mean of 3D spatial game result). On
the basis of the carried out calculations, we can sug-
gest that 3D simulations seem to reflect the population
dynamics better, although the results are slightly more
demanding for analysis. So concluding this study we
suggest to perform spatial simulations of any game
theoretical model using 3D grids.
ACKNOWLEDGEMENTS
The study was partly supported by National Sci-
ence Centre, Poland, grant n. 2016/21/B/ST7/02241
(AS) and by Silesian University of Technology, grant
n. BK-18/0102 (DB). Calculations were performed
on the Ziemowit computer cluster in the Labo-
ratory of Bioinformatics and Computational Biol-
ogy, created in the EU Innovative Economy Pro-
gramme POIG.02.01.00-00-166/08 and expanded in
the POIG.02.03.01-00-040/13 project.
REFERENCES
Bach, L., Bentzen, S., Alsner, J., and Christiansen, F.
(2001). An evolutionary-game model of tumour-cell
interactions: possible relevance to gene therapy. Eu-
ropean Journal of Cancer, 37(16):2116–2120.
Bach, L. A., Sumpter, D. J. T., Alsner, J., and Loeschcke,
V. (2003). Spatial evolutionary games of interaction
among generic cancer cells. Journal of Theoretical
Medicine, 5(1):47–58.
Basanta, D., Gatenby, R. A., and Anderson, A. R. A.
(2012a). Exploiting evolution to treat drug resistance:
combination therapy and the double bind. Molecular
pharmaceutics, 9(4):914–21.
Basanta, D., Hatzikirou, H., and Deutsch, A. (2008). Study-
ing the emergence of invasiveness in tumours using
game theory. The European Physical Journal B,
63:393–397.
Basanta, D., Scott, J. G., Fishman, M. N., Ayala, G., Hay-
ward, S. W., and Anderson, A. R. A. (2012b). Inves-
tigating prostate cancer tumour-stroma interactions:
clinical and biological insights from an evolutionary
game. British journal of cancer, 106(1):174–81.
Bishop, D. T. and Cannings, C. (1978). A generalized war
of attrition. Journal of theoretical biology, 70(1):85–
124.
Dingli, D., Chalub, F. A. C. C., Santos, F. C., Van Seg-
broeck, S., and Pacheco, J. M. (2009). Cancer pheno-
type as the outcome of an evolutionary game between
normal and malignant cells. British journal of cancer,
101(7):1130–6.
Gatenby, R. A. and Vincent, T. L. (2003). An evolu-
tionary model of carcinogenesis. Cancer research,
63(19):6212–20.
Gerstung, M., Eriksson, N., Lin, J., Vogelstein, B., and
Beerenwinkel, N. (2011). The temporal order of ge-
netic and pathway alterations in tumorigenesis. PloS
one, 6(11):e27136.
Hofbauer, J., Schuster, P., and Sigmund, K. (1979). A note
on evolutionary stable strategies and game dynamics.
Journal of Theoretical Biology, 81(3):609–612.
Krzeslak, M., Borys, D., and Swierniak, A. (2016). An-
giogenic switch - mixed spatial evolutionary game ap-
proach. Intelligent Information and Database Sys-
tems, 9621:420–429.
Krzeslak, M. and Swierniak, A. (2011). Spatial evolu-
tionary games and radiation induced bystander effect.
Archives of Control Sciences, 21(2).
Krzeslak, M. and Swierniak, A. (2016). Multidimensional
extended spatial evolutionary games. Computers in
biology and medicine, 69:315–27.
Mansury, Y., Diggory, M., and Deisboeck, T. S. (2006).
Evolutionary game theory in an agent-based brain tu-
mor model: exploring the ’genotype-phenotype’ link.
Journal of theoretical biology, 238(1):146–56.
Sigmund, K. and Nowak, M. A. (1999). Evolutionary game
theory. Current Biology, 9(14):R503–R505.
Smith, J. M. (1982). Evolution and the theory of games.
Smith, J. M. and Price, G. R. (1973). The logic of animal
conflict. Nature, 246:15–18.
Swierniak, A. and Krzeslak, M. (2013). Application
of evolutionary games to modeling carcinogenesis.
Mathematical biosciences and engineering : MBE,
10(3):873–911.
3D Spatial Dependencies Study in the Hawk and Dove Model
237

Swierniak, A. and Krzeslak, M. (2016). Cancer heterogene-
ity and multilayer spatial evolutionary games. Biology
direct, 11(1):53.
Swierniak, A., Krzeslak, M., Borys, D., and Kim-
mel, M. (2018). The role of interventions in the
cancer evolution-an evolutionary games approach.
Mathematical biosciences and engineering : MBE,
16(1):265–291.
Swierniak, A., Krzeslak, M., Student, S., and Rzeszowska-
Wolny, J. (2016). Development of a population of
cancer cells: Observation and modeling by a mixed
spatial evolutionary games approach. Journal of theo-
retical biology, 405:94–103.
Tomlinson, I. (1997). Game-theory models of interactions
between tumour cells. European Journal of Cancer,
33(9):1495–1500.
Tomlinson, I. and Bodmer, W. (1997). Modelling the conse-
quences of interactions between tumour cells. British
Journal of Cancer, 75(2):157–160.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
238
