Different Modal Stereo: Simultaneous Estimation of Stereo Image

Disparity and Modality Translation

Ryota Tanaka, Fumihiko Sakaue and Jun Sato

Nagoya Institute of Technology, Gokiso Showa, Naogya, 466-8555, Japan

Keywords:

Multi-modal Images, Stereo Reconstruction, Deep Neural Networks, Modal Translation.

Abstract:

We propose a stereo matching method from the different modal image pairs. In this method, input images

are taken in different viewpoints by different modal cameras, e.g., an RGB camera and an IR camera. Our

proposed method estimates the disparity of the two images and translates the modality of the input images to

different modality simultaneously. To achieve this simultaneous estimation, we utilize two networks, i.e., a

disparity estimation method from a single image and modality translation method. Both methods are based on

the neural networks, and then we train the network simultaneously. In this training, we focus on several con-

sistencies between the different modal images. By these consistencies, two kinds of networks are effectively

trained. Furthermore, we utilize image synthesis optimization on conditional GAN, and the optimization pro-

vides quite good results. Several experimental results by open databases show that the proposed method can

estimate disparity and translate the modality even if the modalities of the input image pair are different.

1 INTRODUCTION

3D reconstruction using a stereo camera system is one

of the most important techniques in the ﬁeld of com-

puter vision, and then, various kinds of methods are

studied extensively. In these methods, feature points

such as SIFT are detected at ﬁrst. After that, a cor-

responding point is determined in the other image.

These techniques are based on the assumption that

image feature points in the image pair are similar to

each other. Thus, in the stereo camera systems, the

same modality, representatively RGB, image pair is

used.

On the other hand, various modal cameras, as

shown in Fig.1 are often used for speciﬁc purposes

in recent years. For example, IR (infrared) cameras

are used for such as surveillance systems and driving

assist systems at night with IR light sources. Since

the human eyes can not observe IR light, these sys-

tems do not disturb human visual systems. Also,

FIR (far infrared) thermal camera is often utilized for

night surveillance since most of the humans and an-

imals emit FIR light by body temperature. In these

surveillance systems, not only these unique cameras

but also conventional RGB cameras are combinedly

used since RGB images are familiar to the human vi-

sual systems. In addition, traditional computer vision

techniques are for the RGB images, and thus the RGB

images are required to apply these techniques.

Furthermore, these systems often require 3D in-

formation in the scene. However, conventional stereo

camera systems require the same modality cameras,

and then additional cameras arenecessary to construct

the stereo system in existing techniques.

In this paper, we propose a stereo matching

method from different modal image pairs. Our pro-

posed method is based on two techniques. One of

them is the modality translation using a neural net-

work. Although different modal image pairs taken in

the same viewpoint by the different modal cameras

are required to train the deep neural networks in ex-

isting methods, our method achieves training of the

network using image set taken from different view-

points. The other one is a disparity estimation from a

single image. In this technique, different modal im-

ages assist the estimation of disparities. By using

these techniques, we achieve a stereo matching and

modality translation simultaneously from a different

modal image pair.

2 RELATED WORKS

Recently, techniques for multi-modal imaging are

widely studied. Especially, multi-spectral imaging is

one of the most important techniques because of its

wide applications. In general, light spectral informa-

554

Tanaka, R., Sakaue, F. and Sato, J.

Different Modal Stereo: Simultaneous Estimation of Stereo Image Disparity and Modality Translation.

DOI: 10.5220/0009180205540560

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages

554-560

ISBN: 978-989-758-402-2; ISSN: 2184-4321

(a) IR image (b) Thermal image

Figure 1: Different modal images taken by special cameras.

tion is taken by a special multispectral camera with a

long capturing time. Thus, the imaging by this cam-

era cannot be applied to dynamic scenes. To avoid

the problem, Kiku et al.(Kiku et al., 2014; Monno

et al., 2014) propose a special camera that equipped a

special Bayer ﬁlter. The special Bayer pattern in this

method ﬁlter different band light pixel by pixel, and

then, several spectral information can be captured si-

multaneously by a single camera. Since the captured

spectral information by the ﬁlter is sparse, the infor-

mation is interpolated to dense information by image

demosaicing technique using a guide image. This

kind of special Bayer pattern can be applied to not

only multi-spectral imaging but also HDR imaging,

IR imaging and so on(Raskar et al., 2006; Levin et al.,

2008; Fergus et al., 2006). Although these methods

can capture multi-modal information from dynamic

scenes, special and expensive camera systems are re-

quired.

Stereo matching of different modal images is also

studied since the stereo matching is one of the essen-

tial problems in the ﬁeld of computer vision. Zbon-

tar et al.(Zbontar and LeCun, 2016) propose a stereo

matching method based on similarity learning using

CNN. Although the method can be applied multi-

modal image pair as well as the same modal image

pair, the method may not work well when the modal-

ities of input images are much different, such as ther-

mal and RGB(Treible et al., 2017).

In our approach, we do not require correspon-

dences between different modal images to train the

network. This is large advantage because our method

require just stereo camera pair in different modals to

train the network. In addition, our method can ap-

ply to greatly different modal image pairs such as

RGB images and thermal images. Thus, applicable

ﬁeld can become wider. Furthermore, our method

estimates not only the disparity of the image pair

but also modality translated images from each view-

point. Therefore, a multi-modal image from a single

viewpoint can be virtually obtained from the different

viewpoints camera pair without any special devices.

In the following sections, the detail of our proposed

method is explained.

3 NETWORKS FOR DISPARITY

ESTIMATION AND MODALITY

TRANSLATION

3.1 Disparity Estimation from Single

Image

As described in the previous section, our method uti-

lizes two methods using deep neural networks. In this

section, we summarize these methods before a detail

explanation of our proposed method.

We ﬁrst explain the disparity estimation from a

single image(Luo et al., 2018). In this method, dis-

parity maps are predicted from the texture informa-

tion of the input images. As larger A large advantage

of the method is that this method does not require cor-

rect disparity data to train the disparity estimation net-

work. This method requires only a set of stereo im-

age pairs to train the network. Let I

and I

denote the

image taken by the right camera and the left camera,

respectively. The disparity map V(i, j) shows a dis-

parity at point (i, j) in the left image. In this case, the

left image can be translated to the right image

follows:

(i, j) = I

((i, j) +V(i, j)) (1)

When the disparity map V is correct, the estimated

right image close to the real right image I

. Therefore,

the disparity map can be evaluated as follows:

= k

− I

k (2)

By minimizing the ε

, an appropriate disparity map

can be estimated.

To estimate the disparity map V efﬁciently, not

a direct disparity map V but probability maps V

)

is estimated from the image. The probability map

(i, j) denote a probability that the disparity at (i, j)

is d. When the I

(d)

denotes the shifted image I((i, j)+

d), the viewpoint changed image

can be estimated

as follows:

′

∑

(d)

) (3)

This equation compute expected values of each point.

The loss function can be deﬁned as follows:

′

= k

′

− I

k (4)

By minimizing the loss ε

′

, an appropriate estimation

function of the V

can be estimated. Details of the

network architecture and this method are in their pa-

per(Luo et al., 2018).

Note that although the method does not require the

correct disparity, modalities of the images should be

the same since the technique uses the similarity of the

image pair.

Different Modal Stereo: Simultaneous Estimation of Stereo Image Disparity and Modality Translation

555

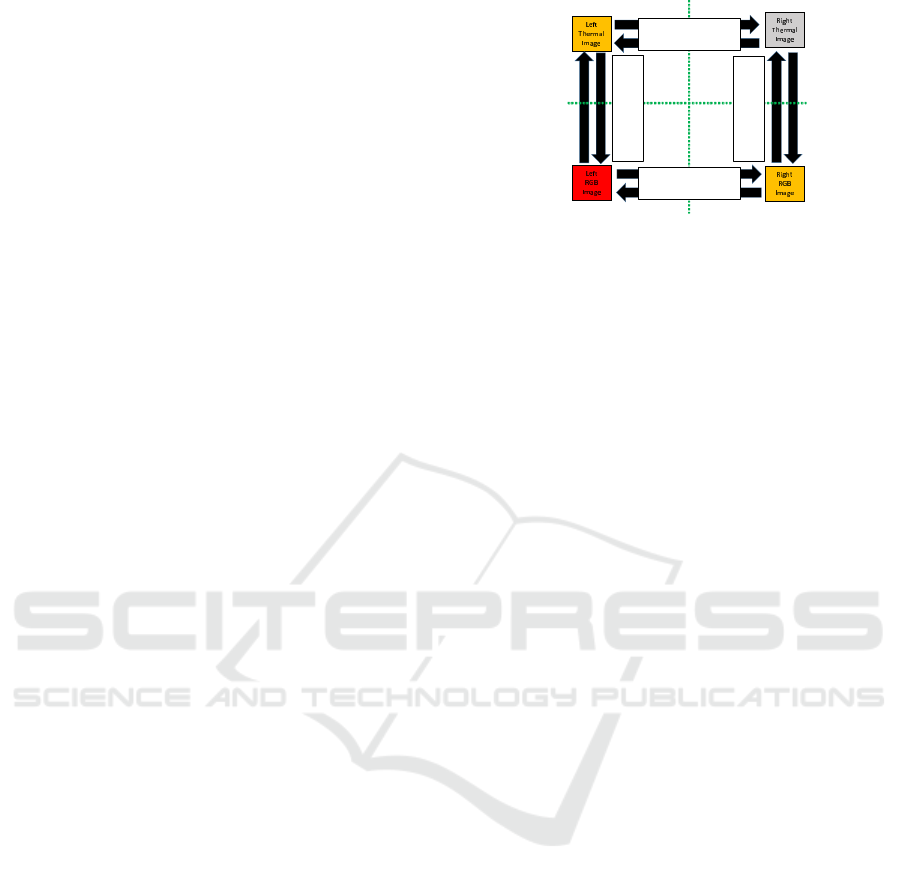
3.2 Modality Translation using

Conditional GAN

We next consider the modality translation of the in-

put image. In this translation, we utilize a framework

of the conditional GAN to synthesize different modal

image. Especially, pix2pix(Isola et al., 2017) pro-

vides effective image translation in a framework of

conditional GAN (cGAN), and we utilize the pix2pix

in our research.

The pix2pix is one of the representative networks

to synthesize different characteristic images from the

input image. Several image translation examples,

such as an edge image to a color image, are reported

based on the framework. In this method, a genera-

tor network and a discriminator network is used. The

generator network synthesizes the translated image,

and the discriminator network decides the image syn-

thesized by the generator is valid or not. By training

these two adversarial networks simultaneously, the

generator accomplishes pretty useful image synthesis.

An objective function of the cGAN can be ex-

pressed as follows:

cGAN

(G, D) = E

x,y

[logD(x, y)]

x,z

[log(1− D(x, G(x, z))]

(5)

where G is a generator and the generator synthesize

the image from the noise z under the condition x .

D(x, y) is a discriminator and it provides a probabil-

ity that y can be translated from y. In addition, the

pix2pix uses a similarity between objective image y

and a synthesized image G(x, z) as follows:

(G) = E

x,y,z

[ky− G(x, z)k] (6)

From these, an optimized generator is computed as

follows:

∗

= argmin

min

cGAN

(G, D) + λL

(G) (7)

Network architecture is in their paper(Isola et al.,

2017).

Note that the pix2pix requires a set of correspond-

ing image pairs. For example, when thermal images

are translated to the RGB image, a thermal image set

and an RGB image set taken the same scenes from

the same viewpoints are required. In our research, the

viewpoints of the cameras are different, and then, we

cannot utilize the pix2pix directly in our method.

>ĞĨƚ ZŝŐŚƚ

ŝŶƉƵƚ

dŚĞƌŵĂů

Z'

DŽĚĂůŝƚǇdƌĂŶƐůĂƚŝŽŶ

ǇĐ'E

sŝĞǁƉŽŝŶƚǆĐŚĂŶŐĞ

ďǇ ŝƐƉĂƌŝƚǇ DĂƉ

sŝĞǁƉŽŝŶƚǆĐŚĂŶŐĞ

ďǇ ŝƐƉĂƌŝƚǇ DĂƉ

DŽĚĂůŝƚǇdƌĂŶƐůĂƚŝŽŶ

ǇĐ'E

Figure 2: Overview of our proposed network. All networks

are trained simultaneously based on several loss functions.

4 SIMULTANEOUS ESTIMATION

OF IMAGE DISPARITY AND

MODALITY TRANSLATION

4.1 Overview

Let us explain our proposed method in this section.

As described in 1, we have two images that have dif-

ferent modalities and taken from different viewpoints.

In this section, we consider the case when a thermal

image I

is taken from the left camera, and an RGB

image I

is taken from the right camera. From these

images, we synthesize a viewpoint changed of modal-

ity translated images

and

, and estimate a dispar-

ity map D.

Figure 2 shows an overview of our proposed

method. As shown in this ﬁgure, we utilize a disparity

estimation method shown in 3.1 and image translation

method shown in 3.2. However, these networks can-

not be trained directly in our environment. Therefore,

we deﬁne several losses to train the networks and es-

timate results. We explain the losses in the following

sections.

4.2 cGAN Loss

We ﬁrst deﬁne a cGAN loss. This loss evaluates that

the translated image is valid or not by discrimina-

tors for cGAN. Let V

) and V

) denote viewpoint

changing by the disparity map D. And let G

, z)

and G

, z

′

) denote modality translation from RGB

images to thermal images and thermal images to RGB

images. Discriminators D(I

, I

) and D(I

, I

) com-

pute probability that the images I

and I

are corre-

spond to the images I

and I

, respectively. By using

the functions, The cGAN loss is deﬁned as follows:

lr1

= E[logD(I

, I

)]

+E[log(1− D(G

(V(I

), z)))]

+E[kI

− G

(V(I

), z)k

]

(8)

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

556

lr2

= E[logD(I

, I

)]

+E[log(1− D(V(G(I

, z))))]

+E[kI

−V(G(I

, z))k

]

(9)

In these losses, a left image is translated to a right

image with the modality translation. In L

lr1

, the

modality of the I

is translated at ﬁrst. After that,

the viewpoint is changed from the left to the right.

In L

lr2

, the order of the image transformation is re-

versed. As same as the left to right translation, losses

for the right to left is deﬁned as L

rl1

and L

rl2

. These

losses are very similar to the loss of the cGAN used in

pix2pix because discriminator decides the translated

image is valid or not based on the training images. A

difference from the pix2pix is that the generator in-

cludes viewpoint exchange as well as modality trans-

lation.

4.3 Image Consistency Loss

We next deﬁne an image consistency loss. In this loss,

we assume that the translated images should be the

same even if exchanging order is different. Therefore,

we deﬁne the loss as follows:

= E[kV(G(I

, z)) − G

(V(I

), z)k

] (10)

for the right to left translation is also deﬁned in

this loss.

Furthermore, we assume that synthesized images

in the same modality and the same viewpoint should

be the same even if the original images are different.

For example,

from the I

by viewpoint exchange

and

from the I

by the modality translation should

be the same under this assumption. Thus, the second

image consistency loss is deﬁned as follows:

= E[kV(I

) − G

, z)k

]

+E[kV(I

) − G

, z)k

]

(11)

4.4 Cycle Loss

We next deﬁne a cycle loss. This loss is based on the

loss of the cycle GAN(Zhu et al., 2017). This loss fo-

cus on the similarity between an original image and

a synthesized image by a combination of translation

and inversed translation. In the computation of this

loss, an input image is translated to the different im-

age at ﬁrst, and back to the original domain by in-

versed translation. By this combined translation, the

input image should be back to the original image if the

translation is valid. That is, the loss can be deﬁned as

follows:

= E[log(D

))]

+E[log(1− D

, z)))]

+E[kI

− G

, z), z)k

]

(12)

where D

denotes a discriminator computing a prob-

ability that the image is the RGB image or not. This

loss is combination of the original GAN and cycle im-

age consistency.

4.5 Attention Loss

As described above, our networks for estimating the

disparity map and modality translation are trained si-

multaneously using a training dataset that is taken in

different modalities and different viewpoints. How-

ever, networks often cannot be trained appropriately.

This is because the image translation networks G have

a signiﬁcant redundancy. Therefore, the network G

often includes not only modality translation but also

viewpoint changing even if the losses shown in the

previous sections are minimized. If the networks G

include the viewpoint exchange V, we cannot esti-

mate the disparity appropriately.

To avoid this excessive image translation, we de-

ﬁne the attention loss for modality translation. For

the attention loss, we assume that an image region

that includes essential information is the same, even

if the modality of the image is changed. There-

fore, we extract a degree of attention by using Grad-

CAM(Selvaraju et al., 2017) and evaluate the image

translation based on the attentions. The difference be-

tween the Grad-CAM result from each image is used

as the attention loss. Therefore, attention loss is de-

ﬁned as follows:

⊣

= E[kA(I

) − A(V(I

))k

]

E[kA(l

) − A(V(I

]

(13)

where A denote attention extraction by Grad-CAM.

As this equation indicates, the attention loss does not

include the image translation G, and thus the disparity

exchange V and the image translation G can be sepa-

rated by minimizing the attention loss.

By minimizing all losses mentionedabove, dispar-

ity map estimation and image translation are accom-

plished simultaneously.

5 IMAGE ESTIMATION USING

THE DEEP NEURAL

NETWORKS

We last describe image synthesis techniques using the

deep neural networks trained in the previous sections.

In fact, the disparity map and modality translation re-

sults are not determined uniquely by the described

networks. Because the generator G requires not only

an input image but also noise in a latent space as input

Different Modal Stereo: Simultaneous Estimation of Stereo Image Disparity and Modality Translation

557

(a) IR image (b) RGB image

Figure 3: Examples of input IR and RGB image pair.

data. Thus, the estimated result can changes accord-

ing to the noise z in the latent space.

Therefore, we optimize the noise z in the latent

space to synthesize an appropriate image. In this op-

timization, the losses used for network training can be

used because the losses represent consistencies of the

estimated data. Therefore, we compute the optimized

noise z

∗

which minimizes all the losses with ﬁxed net-

works as follows:

∗

= argmin

∑

(14)

where L

denote a loss explained in the previous sec-

tion. From the optimized noise z

∗

and input images,

a disparity map and modality translated images are

synthesized. Thus, we accomplish the disparity esti-

mation and the modality translation from the different

modal and different viewpoint image pairs.

6 EXPERIMENTAL RESULTS

6.1 IR Image and RGB Image

In this section, we show several experimental re-

sults. We ﬁrst show the results when the input im-

age pair is an IR image and an RGB image. In

this experiment, we utilized the PittsStereo-RGBNIR

dataset(Zhi et al., 2018) for training and testing. This

dataset includes stereo pairs of IR images and RGB

images Size of these images is 582× 429. These im-

ages were rectiﬁed, and then the epipolar line in the

images are parallelized to the horizontal axis. By us-

ing the rectiﬁed images, a disparity map and modality

translated images, i.e., from IR to RGB and RGB to

IR, are estimated by our proposed method. Examples

of rectiﬁed input images are shown in Fig.3

Figure 4 and 5 shows the estimated results by our

proposed method. In this ﬁgure, images (a) and (b)

shows input images, and (c) and (d) show modality

translated results by our proposed method. In this ﬁg-

ure, the viewpoints of the images in the same column

are the same. The image (e) shows the estimated dis-

parity. In the disparity image, colors in each pixel

(a) input IR image (b) input RGB image

(e) Estimated disparity

Figure 4: Input images and estimated results: (a) and (b) are

input images, and (c) and (d) are translated results. The im-

ages in the same column were (virtually) taken in the same

viewpoint. An image (e) shows estimated disparity by color

indicated in the right color bar.

show the value of the disparity, and the values are col-

orized by the right color bar.

In both results, the modality translated images are

pretty good. Positions of the objects in the input im-

age and the translated image are much similar. Fur-

thermore, the translated images are very natural, and

we could not discriminate which image was the trans-

lated image by ourselves. Also, the disparity maps

gradually change according to the depth of the image.

In these images, the upper region of the image has far

depth, and the lower region has close depth. The es-

timated disparity represents the change of this dispar-

ity. Furthermore, the depth of the region, including

the vehicle is different from the other region, and it

indicates that the depth changes by the vehicle.

These results indicate that our proposed method

can estimate the disparity maps and modality trans-

lated images from the IR and the RGB image pair.

6.2 Results from Thermal Image and

RGB Image

We next show the results from thermal images and

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

558

(a) input IR image (b) input RGB image

(e) Estimated disparity

Figure 5: The other input images and estimated results.

RGB images. In this experiment, we utilized VAP

Trimodal people segmentation dataset(Treible et al.,

2017). The dataset includes pair of thermal images

and RGB images with a disparity of them. Size of

images is 680 × 480. Examples of the input images

are shown in the Fig.6(a), (b).

From these results, we estimated the modality

translated images and the disparity maps. Figure 6

and 7 shows input images and estimated results. As

same as the Fig 4 and 5 image (a) ∼ (e) shows input

images and estimated results. The image (f) shows

the ground truth of the disparity map.

In these results, modality translation makes clear

images in both the thermal to RGB and RGB to ther-

mal. The brightness of the estimated thermal images

is slightly differentfrom the input image. We consider

that the difference was occurred by the difference of

the intensity in each input image. However, the differ-

ence can be suppressed easily by ordinary image pro-

cessing techniques such as brightness normalization.

In the disparity image, several regions have different

disparity from the ground truth. In this region, tex-

tures of the image are very slight, and it might occur

open aperture problems. However, disparities could

be estimated in textured regions and edges of the ob-

jects, and then, our method can estimate the dispar-

ity if the input image provides sufﬁcient information.

(a) input RGB image (b) input thermal image

(e) Estimated disparity (f) Ground truth

Figure 6: Input images and estimated results: (a) and (b) are

input images, and (c) and (d) are translated results. Images

(e) and (f) shows estimated disparity and ground truth, re-

spectively. RMSE between the estimated disparity and the

ground truth was 3.22[pix].

RMSE of the two estimated results were 3.22[pix]

and 3.25[pix]. These values are relatively small to the

whole image disparity. These results indicate that our

proposed method can accomplish simultaneous com-

putation of modality translation and disparity estima-

tion even if the modality of the input image pair is

drastically different.

7 CONCLUSION

In this paper, we propose simultaneous computation

of image modality translation and disparity estimation

from the different modal images based on the neural

networks. In this method, we utilize two kinds of net-

works. The ﬁrst one is for estimating the disparity,

and the second one is for modality translation. We

deﬁne several losses to optimize the network simul-

taneously and appropriately. In addition, we propose

the optimal image synthesis technique by minimiz-

ing the loss functions on the GAN. Several exper-

imental results show that our proposed method can

translate the modality of images and estimate dispar-

ity from the different modal image pairs. Notably,

even if the modalities of the image pair are far from

Different Modal Stereo: Simultaneous Estimation of Stereo Image Disparity and Modality Translation

559

(a) input RGB image (b) input thermal image

(e) Estimated disparity

(f) Ground truth

Figure 7: Input images and estimated results. RMSE

between the estimated disparity and ground truth was

3.25[pix].

each other such as RGB and thermal, our method

can estimate modality translated image and disparity.

Although the qualitative evaluation of our proposed

method is good, it is not enough because we cannot

use a sufﬁcient number of images, including ground

truth. Thus, we construct the database for evaluation

and evaluate our proposed method extensively in fu-

ture work.

REFERENCES

Fergus, R., Singh, B., Hertzmann, A., Roweis, S. T., and

Freeman, W. T. (2006). Removing camera shake from

a single photograph. In ACM Transactions on Graph-

ics (TOG), volume 25, pages 787–794. ACM.

Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. (2017). Image-

to-image translation with conditional adversarial net-

works. In Proc. CVPR2017.

Kiku, D., Monno, Y., Tanaka, M., and Okutomi, M. (2014).

Simultaneous capturing of rgb and additional band im-

ages using hybrid color ﬁlter array. In Digital Pho-

tography X, volume 9023, page 90230V. International

Society for Optics and Photonics.

Levin, A., Sand, P., Cho, T. S., Durand, F., and Freeman,

W. T. (2008). Motion-invariant photography. In ACM

Transactions on Graphics (TOG), volume 27. ACM.

Luo, Y., Ren, J., Lin, M., Pang, H., Sun, W., Li, H., and

Lin, L. (2018). Single view stereo matching. In Proc.

CVPR2018, pages 155 – 163.

Monno, Y., Kiku, D., Kikuchi, S., Tanaka, M., and Oku-

tomi, M. (2014). Multispectral demosaicking with

novel guide image generation and residual interpola-

tion. In Image Processing (ICIP), 2014 IEEE Interna-

tional Conference on, pages 645–649. IEEE.

Raskar, R., Agrawal, A., and Tumblin, J. (2006). Coded

exposure photography: motion deblurring using ﬂut-

tered shutter. In ACM Transactions on Graphics

(TOG), volume 25, pages 795–804. ACM.

Selvaraju, R., Cogswell, M., Das, A., Vedantam, R., Parikh,

D., and Batra, D. (2017). Grad-cam: Visual explana-

tions from deep networks via gradient-based localiza-

tio. In Proc. ICCV2017.

Treible, W., Saponaro, P., Sorensen, S., Kolagunda, A.,

ONeal, M., Phelan, B., Sherbondy, K., and Kamb-

hamettu, C. (2017). Cats: A color and thermal stereo

benchmark. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

2961–2969.

Zbontar, J. and LeCun, Y. (2016). Stereo matching by train-

ing a convolutional neural network to compare im-

age patches. Journal of Machine Learning Research,

17(1-32):2.

Zhi, T., Pires, B., Hebert, M., and Narasimhan, S. (2018).

Deep material-aware cross-spectral stereo matching.

In Proc. CVPR2018.

Zhu, J.-Y., Park, T., Isola, P., and Efros, A. A. (2017).

Unpaired image-to-image translation using cycle-

consistent adversarial networks. In Proc. ICCV2017.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

560