Mining Patient Flow Patterns in a Surgical Ward

Christoffer O. Back

1 a

, Areti Manataki

2 b

and Ewen Harrison

2 c

Department of Computer Science, University of Copenhagen, Denmark

Usher Institute, University of Edinburgh, U.K.

Keywords:

Bayesian Network, Data Mining, Patient Flows, Process Mining, Surgery, Surgical Workﬂow.

Abstract:

Surgery is a highly critical and costly procedure, and there is an imperative need to improve the efﬁciency in

surgical wards. Analyzing surgical patient ﬂow and predicting cycle times of different peri-operative phases

can help improve the scheduling and management of surgeries. In this paper, we propose a novel approach

to mining temporal patterns of surgical patient ﬂow with the use of Bayesian belief networks. We present

and compare three classes of probabilistic models and we evaluate them with respect to predicting cycle times

of individual phases of patient ﬂow. The results of this study support previous work that surgical times are

log-normally distributed. We also show that the inclusion of a clustering pre-processing step improves the

performance of our models considerably.

1 INTRODUCTION

Surgery is a cornerstone of the healthcare system, and

critical in terms of time and resources. Ensuring efﬁ-

ciency, timeliness and safety are crucial for providing

high quality service while controlling costs (Lalys and

Jannin, 2014), (Denton, 2007). While many processes

surrounding surgery are well structured, the dynamic

nature of patient arrivals combined with the complex-

ity of coordinating large numbers of specialized staff

and facilities, means that delays and misalignments

can have cascading effects leading to last-minute can-

cellations. This leads not only to an under-utilization

of expensive resources, but causes stress and upheaval

for patients.

The well-deﬁned, yet dynamic; and high-cost,

high-impact nature of surgical patient ﬂows, suggests

it is an area amenable to improvements via data ori-

ented process modeling. Advances in forecasting

long and short term dynamics of the surgical ward

can help inform intelligent surgery sequencing, staff

scheduling and workﬂow management systems.

This paper presents a preliminary investigation

into methods for modeling patient ﬂows in surgi-

cal wards, with outset in a data set following pa-

tients from admission to discharge at the Royal In-

https://orcid.org/0000-0001-7998-7167

https://orcid.org/0000-0003-3698-8535

https://orcid.org/0000-0002-5018-3066

ﬁrmary of Edinburgh. We focus our present in-

vestigation on temporal aspects of individual patient

ﬂows, which are key to improving efﬁciency. Results

from this study can then inform the investigation of

other aspects of patient ﬂows such as positioning, as

well as high-level dynamics between multiple patient

ﬂows competing for shared resources at the level of

ward/hospital.

After an exploratory investigation of the data, we

present and compare three probabilistic models de-

scribing cycle times of individual phases in patient

ﬂows prior to, during and following surgery. We eval-

uate these w.r.t. to predicting cycle times of individ-

ual phases of patient ﬂows, from the time patients

are sent for, through anesthesia and surgery, and until

they leave recovery.

Speciﬁcally, we employ a type of probabilistic

model called a Bayesian network. Aside from their

capacity to easily incorporate domain knowledge,

Bayesian networks have the advantage that they can

be queried in complex ways even with incomplete ev-

idence, which is invaluable in the uncertain hospital

environment. Crucially, we show that by incorporat-

ing a pre-processing step based on simple clustering

of ﬂows w.r.t. cycle times, we can improve the perfor-

mance of our models noticeably.

The structure of the sequel is as follows. In Sec-

tion 2 we review existing literature. Our subsequent

analysis of the data follows the classic data analyt-

ics workﬂow of Describe → Diagnose → Predict. In

Back, C., Manataki, A. and Harrison, E.

Mining Patient Flow Patterns in a Surgical Ward.

DOI: 10.5220/0009181302730283

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 5: HEALTHINF, pages 273-283

ISBN: 978-989-758-398-8; ISSN: 2184-4305

273

Section 3 we introduce the domain, the data set, and

the data cleaning process. In Section 4, we present a

descriptive analysis of the data set using process min-

ing tools and standard statistical tools to identify in-

formative features of the data. This informs the pro-

cess of building predictive models which we describe

and evaluate in Section 5. In Section 6 we discuss our

results and in Section 7 we conclude.

2 RELATED WORK

Improving efﬁciency in surgical wards, speciﬁcally

improving utilization of operating rooms, has re-

ceived growing interested nationally and internation-

ally for a number of years now (Lalys and Jannin,

2014). The National Theatres Project in Scotland

states as its objective, “appropriately increasing pa-

tient throughput, thereby using resources more pro-

ductively and efﬁciently”(Scotland, 2006). The met-

rics for improvement include: reducing unutilized

(operating room) hours; reducing over/under-runs,

late-starts, cancellations and delayed discharges; and

avoiding unnecessary out-of-hours and nighttime pro-

cedures. Many of these objectives are strongly related

to appropriate scheduling, and would thereby beneﬁt

from more accurate, data-informed, models of patient

ﬂows.

A signiﬁcant amount of research exists in model-

ing processes in the surgical domain. The modeling

scope of much existing work tends to fall on two ends

of a spectrum in terms of granularity: the level of sur-

gical procedures at one end and broader care ﬂows

beyond the surgical ward at the other.

In (Lalys and Jannin, 2014), 46 publications on

surgical process modeling are categorized into a tax-

onomy ranging from the level of the surgical pro-

cedure at the lowest level of granularity, to low-

level physical movements at the highest. At the lat-

ter level, which is typically concerned with robot-

assisted surgery or training and assessment of sur-

geons, we see research on phase detection (Stauder,

2014) and detailed models of individual tool usage

patterns based on sensor data (Ahmadi, 2009). In-

dividual hand motions from video data are automat-

ically identiﬁed in (Lin, 2006) and (Haro, 2012). A

number of models based on sensor data collected dur-

ing Cholecystectomies (a highly standardized proce-

dure), were developed in (Blum, 2008), (Bouarfa and

Dankelman, 2012), (Bouarfa, 2011), and (Neumuth,

2011). All of these studies have the surgical proce-

dure at the highest level of abstraction. Our present

investigation lies above this level of granularity, with

only the procedure name and some other basic details

being present in the data.

Above the level of individual procedures, we see

work such as (Stahl, 2006) which describes the work-

ﬂow within an operating room, including anesthesia,

surgery, and early recovery. Other studies also ad-

dress the process surrounding surgery, from admis-

sion to recovery (Funkner, 2017), which matches the

scope of our data set. Taking a view beyond the oper-

ating room is important, since activities downstream

from the actual surgical procedure can interrupt pa-

tient ﬂows as shown in the case of ICU bottlenecks in

(Akkerman and Knip, 2004). Some studies have also

incorporated diagnosis and follow-up after surgery

such as (Mans, 2012) and (Huang, 2013).

Bayesian networks were used to model several as-

pects of stays in an emergency department in (Acid,

2004). While overall stay duration was one attribute

included in the model, the scope was at higher level

of abstraction, and not focused speciﬁcally on surgi-

cal patient ﬂows. Furthermore, the main focus was

the comparison of structure learning algorithms.

Some work has looked speciﬁcally at model-

ing variance in surgery durations (Strum, 2000) and

incorporating this into sequencing and scheduling

strategies (Denton, 2007). In (Kayis, 2012), regres-

sion modeling is employed to predict surgery dura-

tion based on clinical, operational and temporal data.

Stochastic balancing of bed capacity based on ﬂuctu-

ating demand patterns was explored in (Cochran and

Bharti, 2006) and length of stay patterns in (Akker-

man and Knip, 2004). Resource allocation and patient

admission was addressed in (Hulshof, 2013).

In summary, the scope of patient ﬂows ranging

from admission, through surgery to recovery, is one

which has been less thoroughly addressed: most work

is positioned at a lower or higher level of abstrac-

tion. In regards to the distribution of surgery times,

our work has the corollary contribution of conﬁrm-

ing previous ﬁndings. In terms of the more nuanced

conditional models we present of cycle times, specif-

ically the integration of patient clusters to Bayesian

networks, we believe our approach to be novel.

3 DOMAIN & DATA

PREPARATION

The Royal Inﬁrmary of Edinburgh is the largest in

Scotland, housing 900 beds and with its 24-hour ac-

cident and emergency department, providing a full

range of acute medical and surgical services. The hos-

pital IT system is integrated with the Operating Room

Scheduling Ofﬁce System (ORSOS), a surgery man-

agement and scheduling system.

HEALTHINF 2020 - 13th International Conference on Health Informatics

274

The data set analyzed stems from the ORSOS sys-

tem and involves records ranging from 2010 until

2018 inclusive. Over 1700 types of procedures are

recorded in the data set with about half of cases classi-

ﬁed as emergency cases. It is oriented around individ-

ual surgical procedures, such that any time a patient

receives surgical treatment, a new entry is created and

each such entry has a unique case ID. This means that

the same patient may have multiple unique case IDs,

potentially for the same hospital stay. Unique patient

IDs, as well as electronic health record identiﬁers,

make it possible to follow patients’ overall treatment

ﬂows, though this was out of scope of this investiga-

tion.

Data regarding patient ﬂows are entered manually

by surgical support personnel, with the system requir-

ing the entry of timestamps for each event in the pa-

tient ﬂow. Figure 1 illustrates the proscribed sequence

of events, and also shows the authors’ aggregation

of activities into logical phases (pre-op, anesthesia,

surgery, recovery). The system enforces a simple lin-

ear ordering of events, though it can be overridden. If

users attempt to enter timestamps out of sequence, a

warning is given, but can be entered upon conﬁrma-

tion. Summaries of cases with anomalous entries are

later sent in batches to staff for review.

Aside from the 11 timestamp attributes, the data

schema contains 34 other attributes, though some

are empty for many cases, such as “reason for de-

lay”. Information regarding the procedure performed

is included in two different coding schemes, one

providing more detail such as location on body.

Other case attributes such as the case type (emer-

gency/scheduled), its urgency classiﬁcation

, the

ASA patient status rating

, and whether the patient

is registered as a day-case or inpatient. Stafﬁng de-

tails include names of the main and supervising sur-

geon and anesthetist as well as the consultant as-

signed to the case. The source of admission (emer-

gency room, etc.), the operating room number, as well

as intended and actual destination following surgery

(ICU, etc.) are also included. Further details include

the diabetic status of the patient, types of anesthetics

administered, whether antibiotics were administered,

and whether pre-session brieﬁngs and surgical pauses

were held.

Cleaning and Preparation. The data set contains

a number of anomalous entries, comprising roughly

10% of the 38,728 entries. These entries were re-

NCEPOD Classiﬁcation of Intervention (NCEPOD,

2019).

American Society of Anesthesiologists physical status

classiﬁcation system. (Dripps, 1963)

Table 1: Anomalous cases removed prior to analysis.

ANOMALY COUNT % OF TOTAL

Duplicate entries 58 0.15

Missing values 31 0.08

Dates out-of-range 475 1.23

Zero timestamps 3089 7.98

Bad ordering 443 1.44

Total 4096 10.58

moved prior to further analysis. Table 1 provides an

overview.

Duplicate entries may have been due to an at-

tempt to correct a data entry error. The column

anaesthetic start time was the only timestamp

column to contain <NA> values. A larger number of

cases have clearly anomalous values in the case date

column, e.g. dates much too far in the past (1800) or

future (3206).

Process mining techniques helped quickly reveal

that despite the de-jure linear ordering of activities,

many anomalous, and decidedly implausible, event

orderings exist in the data. Figure 4 shows the re-

sult of running the SIMPLE version of the Alpha

miner(Van der Aalst, 2004) from the pm4py package

(Berti, 2019) on the top 20 sequence variants. The

Alpha miner takes as input an event log and outputs a

Petri net (speciﬁcally a workﬂow net): a type of pro-

cess model. Running the Alpha miner on the entire

log results in a ﬂower model

. A further a analy-

sis of the directly-follows graph indicated that nearly

all possible pairwise event orderings occurred at least

once in the data.

One of the aspects of the Petri net in Figure 4 that

stands out is that it permits incision start time to

occur before anaesthetic start time. While this

was to an extent the result of anomalous timestamps

in the data, upon further inquiry with surgical staff,

we learned that it is indeed legal for these activities to

be recorded with the same timestamp in cases where

the surgeon administers a local anesthetic.

Timestamps in the data set are rounded to

the minute, and that for many cases, two or

more events are recorded with the same times-

tamp. For example, enter theatre time and

incision start time are sometimes identi-

cal, and in fact leave theatre time and are

enter recovery time identical for all cases. This

needed to be addressed prior to applying process

mining techniques, since they assume sequential

orderings in event traces. For this, the de-jure model

was used as a tiebreaker in cases of simultaneity.

A ﬂower model is a process model which permits any

event to be executed at any stage of the process.

Mining Patient Flow Patterns in a Surgical Ward

275

PREOP

ANESTHESIA SURGERY

RECOVERY

Send

for

patient

Enter

depart-

ment

Into

anesthetic

room

Anesth

-etic

start

Into

operating

room

Incision

start

Incision

stop

Leave

operating

room

Enter

recovery

Ready

to leave

recovery

Leave

recovery

Figure 1: The patient ﬂow proscribed by the ORSOS system. Activities are linearly ordered, but can occur “simultaneously”.

That is, some activities (such as Leave Operating Room) can have the same timestamp as the “succeeding” activity (Enter

Recovery), but should not occur after it.

Many of the implausible cases had zero times-

tamps associated with the out-of-order events (times-

tamps of the the form YY-MM-DDT00:00:00). We sus-

pect that these entries may be the result of users spec-

ifying only a date without a timestamp. A further 443

cases had anomalous event orderings, likely due to an

incorrect entry such as failing to increment the date

when a patient ﬂow stretched from one day to the

next. All cases with invalid orderings were removed

prior to subsequent analysis of cycle time patterns.

Plotting event occurrences on a “dotted chart” (see

Figure 2) also reveals several outlying events (occur-

ring months or years from the rest of the ﬂow). The

dotted chart simply plots the events from an event by

the case id along the y-axis and by time along the x-

axis, such that events associated with the same case

fall along a horizontal line.

In the remainder of the analysis, we have removed

data points with cycle times in the 99

percentile of

values, having observed the presence of events oc-

curring months, even years apart, which for a single

surgical case are almost certainly due to data entry

mistakes. The chart also makes immediately obvious

that a gap exists in the data, and gives an indication

of the development in the throughput of cases over

time, which remains nearly constant, perhaps increas-

ing slightly.

The number of anomalous cases discovered de-

spite the ORSOS system’s compliance measures,

demonstrate the importance of data quality measures,

especially if such data are to form the basis of pre-

scriptive models and policies. While many of these

anomalies would in principle be discoverable by man-

ually querying the data, the use of process mining

techniques helped reveal these anomalies quickly and

intuitively, serving as a springboard for more detailed

analysis.

4 ANALYSIS

In this section, we describe the empirical distributions

of individual and aggregate cycle times, and compare

how well various parametric distributions ﬁt the data.

Then, we identify the most informative features of

the data set, which will be used as astarting point for

model building in 5.

Marginal Cycle Time Distributions. Fitting an ap-

propriate distribution to data can be a powerful ap-

proach to building a predictive model, despite its sim-

plicity. These models consider only the marginal dis-

tribution, i.e. they consider outcome across all cases,

without conditioning the distribution on case-speciﬁc

attributes. Table 2 displays the results of ﬁtting seven

different distributions to the cycle times of both the

original “low-level” events, as well as the aggregated

process phases.

As indicated by goodness-of-ﬁt statistics, aggre-

gating individual event cycle times results in more

well-formed distributions, with the one slight excep-

tion of the recovery stage. While information is

clearly lost by reducing 9 cycle times to 4, this is jus-

tiﬁed by the fact that any implications of cycle times

on resource utilization is captured by the aggrega-

tions. For example, an operating theatre, will have

the status of being occupied and unavailable for other

patients during each of the events Into theatre, Inci-

sion start, Incision stop, and until Leave theatre com-

mences. This effect on resource availability is equiva-

lently captured in the aggregations of these events into

one Surgery event and its corresponding cycle time.

Previous research has indicated that surgical cycle

times are log-normally distributed (Strum, 2000). Our

observations are consistent with this, but it should be

noted that the Kolmogorov-Smirnov goodness-of-ﬁt

does not achieve statistical signiﬁcance.

Mutual Information. To get an overview of corre-

lation between attributes, the mutual information be-

HEALTHINF 2020 - 13th International Conference on Health Informatics

276

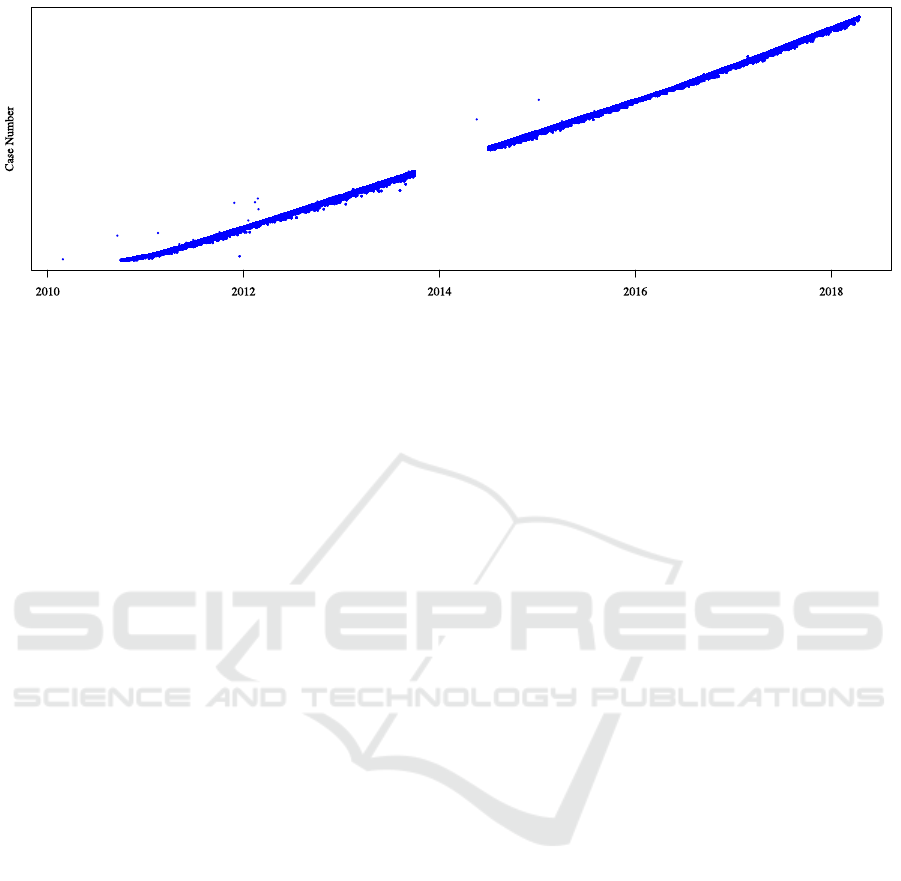
Figure 2: A “dotted chart” helps give a quick overview of the event log. Each data point represents the occurrence of an

event, plotted by time on the x-axis and by a numerical case identiﬁer on the y-axis which are incremented by time. At this

level of granularity we cannot see the dynamics of individual process instances, but aspects such as arrival rate, outliers and

missing values become clear. In our data set, there is a prominent gap from October 2013 to July 2014, something one would

otherwise need to actively investigate, but is immediately noticeable here . Furthermore, several events lie weeks or years

from the rest of the events in a case, suggesting anomalous values.

tween attributes was computed, a selection of which

are visualized as heatmap in Figure 5. As a nonpara-

metric correlation metric, mutual information is more

suitable for our data than parametric estimators such

as χ

since we cannot conﬁdently assume normality

for all attributes. Intuitively, mutual information mea-

sures the expected decrease in uncertainty regarding

the outcome of y upon learning the outcome of x.

Speciﬁcally, it measures the reduction in entropy of

the resulting conditional probability distribution.

For continuous values, namely cycle times, it was

necessary to discretize the data. This was done such

that each of 7 bins contained was of equal widths such

that the distribution of cases amongst bins roughly ap-

proximates their original distribution. Using this ap-

proach, correlations between attributes other than cy-

cle times were the strongest, while attributes inﬂuenc-

ing cycle times were more weakly correlated, though

still observable. Especially intended destination and

source of admission standout as informative w.r.t. cy-

cle times. Mutual information can tend to hide im-

portant nuances since it reﬂects the expected value of

the pointwise mutual information for individual val-

ues of a variable. Lead us to do a more detailed ex-

ploration of how different attributes inﬂuence cycle

times speciﬁcally.

Conditional Cycle Time Distributions. By explor-

ing the conditional distributions of cycle times for the

individual values attributes, we were able to get a bet-

ter idea of what inﬂuences cycle times. By visualizing

conditional distributions on the same plot, one gets a

quick impression of the whether an attribute is infor-

mative in this respect, or not. Albeit somewhat of a

time-consuming, brute-force approach, exploring the

data in this way is quite informative. This was an im-

portant factor for us in choosing which variables to

include in the models we present in Section 5. See

Figure 6 for examples of some of the most informa-

tive attributes.

Principle Components Analysis. Based on the in-

tuition that cases likely fall into some sort of group-

ing w.r.t cycle times, we investigated the presence of

clusters in the data. For example, cases with a long

anesthetic cycle time may also tend to have a long

surgery or recovery time - this likely being related to

the procedure performed or the patient’s condition.

A visual exploration of the raw, as well as log-

transformed, data gives the impression that no clear

groupings exist. One method for revealing sepa-

rable clusters in data that are not clearly separable

in the original data is via transformation techniques

such as Principle Components Analysis (PCA). PCA

projects the original data onto a linear subspace which

maximizes the resulting variability of the data along

the resulting bases, or principle components (Bishop,

2006). It is perhaps most commonly used as a method

for dimensionality reduction, by redeﬁning the data

on a subset of the principal components which cap-

ture most of the variance in the data.

Applying PCA to the log-transformed data reveals

that the data does in fact fall into distinct clusters.

This can be seen in Figure 3 which shows the data

w.r.t to top 3 (of 4) principle components.

Mining Patient Flow Patterns in a Surgical Ward

277

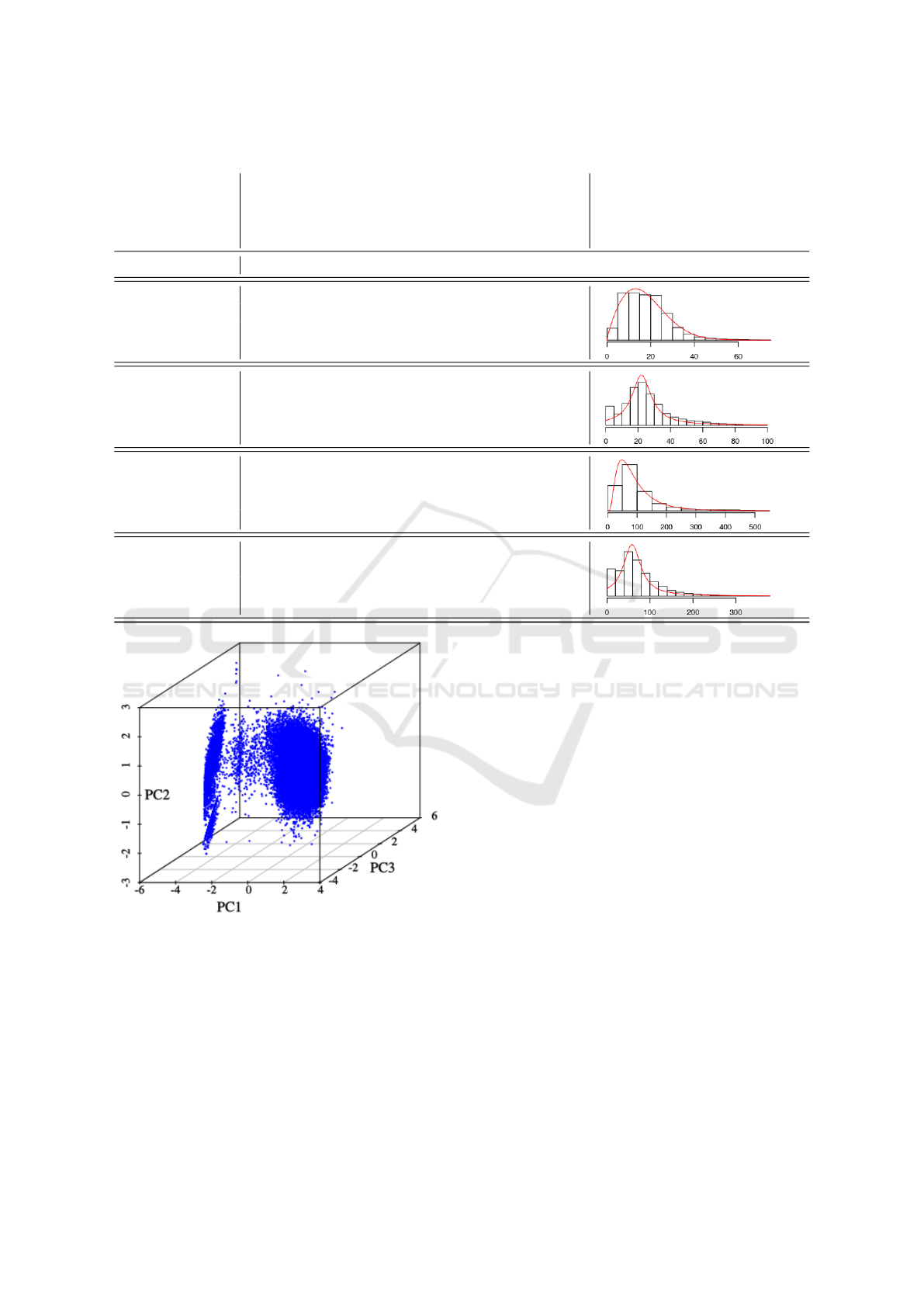
Table 2: Best ﬁts for marginal distributions of cycle times. Goodness-of-ﬁt statistic used is the Kolmogorov-Smirnov criterion.

Gaussian

Cauchy

Logistic

Log-Normal

Gamma

Weibull

Exponential

EVENT GOODNESS-OF-FIT (KS) PLOT (Best ﬁt for aggregate)

Send for patient 0.147 0.113 0.139 0.169 0.126 0.104 0.267

Enter department 0.161 0.147 0.197 0.205 0.171 0.157 0.184

Pre-op 0.094 0.087 0.123 0.127 0.09 0.062 0.24

Into anesthetic 0.226 0.166 0.168 0.153 0.133 0.15 0.19

Anesthetic start 0.146 0.098 0.134 0.171 0.112 0.096 0.189

Anesthetic 0.124 0.077 0.106 0.188 0.132 0.106 0.244

Into theatre 0.16 0.094 0.143 0.111 0.093 0.114 0.298

Incision start 0.164 0.122 0.144 0.061 0.06 0.07 0.132

Incision stop 0.187 0.145 0.168 0.111 0.144 0.128 0.25

Surgery 0.16 0.11 0.134 0.036 0.071 0.087 0.193

Enter recovery 0.083 0.079 0.126 0.243 0.174 0.139 0.198

Ready to leave 0.285 0.277 0.266 0.184 0.144 0.144 0.22

Recovery 0.099 0.083 0.127 0.244 0.17 0.136 0.19

Figure 3: Top 3 principle components for (log-transformed)

aggregate cycle times.

5 PREDICTION

In order to facilitate improved resource utilization

through more accurate scheduling and dynamic re-

source allocation, we suggest using Bayesian belief

networks (Koller and Friedman, 2009). The reason

for this choice of model lies in its ﬂexibility. Not

limited to one target feature, Bayesian networks can

be queried on any attribute, using whatever evidence

is currently available. A scheduler can pose queries

concerning, for example, the probability of a surgery

taking more than x minutes given the case type and

condition of patient, or the likely destination of the

patient given other evidence.

A Bayesian belief network is a directed acyclic

graph with an associated parametrization and repre-

sents a joint probability distribution and its condi-

tional independence relations between variables, rep-

resented as nodes. Both of these aspects, the graph

structure and its parametrization need to be either

hand modeled, learned automatically, or a combina-

tion of the two. We restricted this investigation to

automatically learned models. This can sometimes

lead to what may seem counterintuitive models, but

it should be kept in mind that an edge between two

nodes does not necessarily indicate a causal relation-

ship between source and target.

We present a comparison of 3 classes of models,

the latter 2 hybrid discrete/(log)-Gaussian models:

Marginal Model: an unconnected graph, equivalent

to the distributions in Table 2.

10 Variable Model: 4 aggregate cycle times, ASA,

CaseType, Intended Destination, Management In-

HEALTHINF 2020 - 13th International Conference on Health Informatics

278

Send for patient

Anesthetic start Into anesthetic room Enter department

Incision stop

Into operating room

Incision start

Enter recovery

Leave operating room

Ready to leave recovery

Leave recovery

Figure 4: A Petri net generated by the Alpha miner on the

top 20 trace variants observed in the event log. This model

clearly allows implausible behavior, such as Incision start

preceding Anesthetic start.

tent, NCEPOD Category, Source of Admission.

22 Variable Model: 4 aggregate cycle times, ASA,

CaseType, Intended Destination, Management In-

tent, NCEPOD Category, Source of Admission,

Diabetic, Operating Room, 10 Anaesthetic Type

variables.

Figure 5: Heatmap of the mutual information between at-

tributes. The “bright” spots indicate that learning the out-

come of the corresponding variable on the x-axis decreases

the uncertainty about the outcome of the corresponding

variable on the y-axis. Destination denotes the intended

destination following the procedure, NCEPOD denotes the

urgency classiﬁcation, and Intent denotes whether the case

is a day-case or inpatient case.

Feature Selection. The choice of variables was

based on analysis in Section 4, as well as the cardinal-

ity of variables. Variables with very large cardinality

often fail to improve results due to sparse represen-

tation in the data. One solution to allow the incor-

poration of these is to perform dimensionality reduc-

tion on these variables prior to training the network.

This is left for future work. For the largest model,

we started by including all features, removing those

which had no effect on performance.

Clustering. In order to explicitly incorporate the

clusters observed in Section 4, we performed simple

k-means clustering on the PCA transformed data and

added a Cluster attribute to each case. This new at-

tribute was then included as a node in some variants

of the Bayesian networks. Speciﬁcally, we added 4

variants of both the 10- and 22-variable model us-

ing different numbers of clusters: 5, 10, 15, 20. For

comparison a model without clusters added is evalu-

ated as well. These values were chosen to illustrate

the improvement in model performance upon adding

more clusters and the eventual appearance of an el-

bow of diminishing improvement usually around 15

to 20 clusters. We experimented with values ranging

between 2 and 40.

Mining Patient Flow Patterns in a Surgical Ward

279

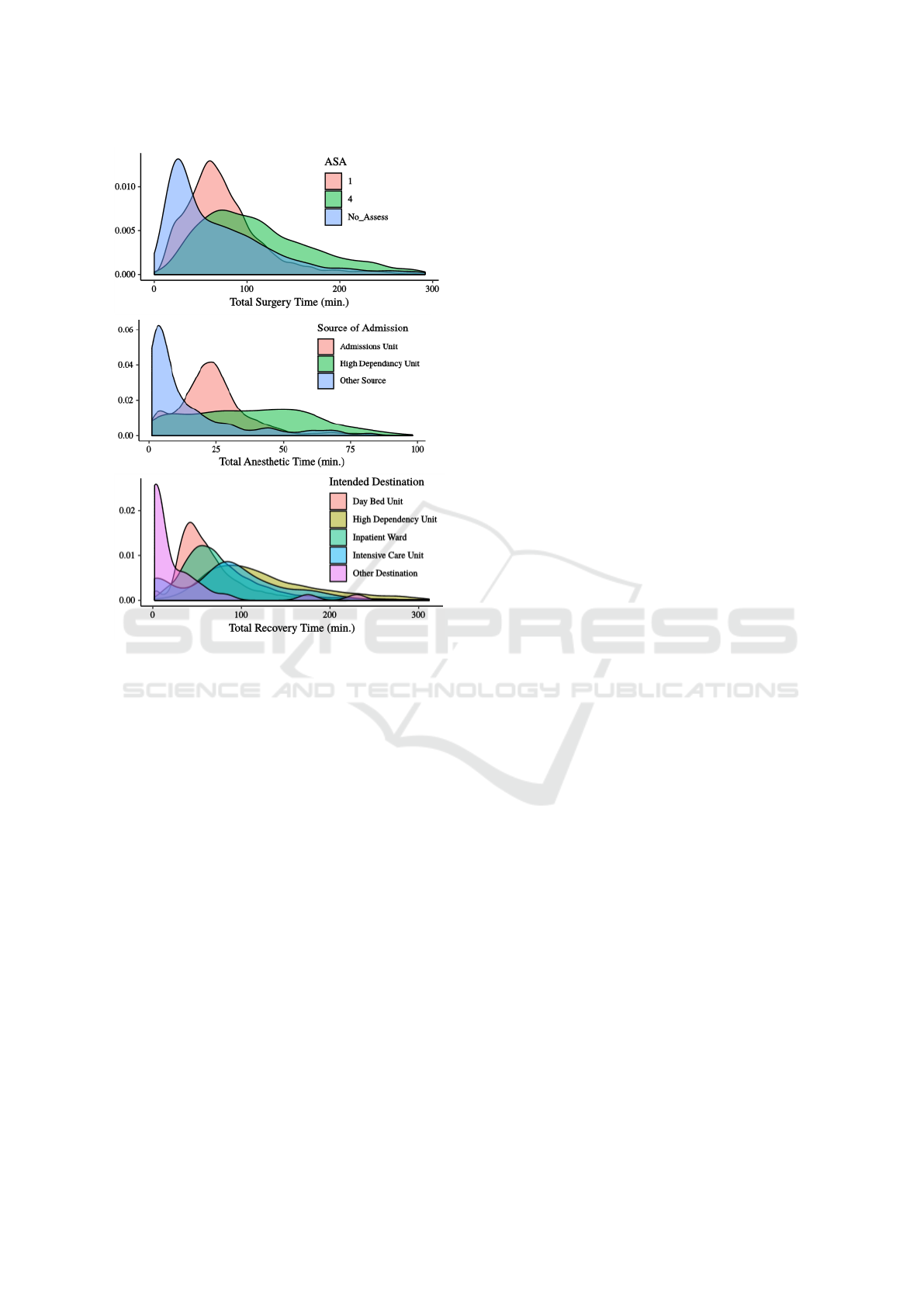
Figure 6: Examples of conditional cycle time distributions.

Top: conditioned on ASA status. Middle: Source of Ad-

mission. Bottom: Intended Destination.

We found that performing clustering on the PCA

transformed data gave slightly better results than clus-

tering on the original data. Note that we used all 4

principal components, hence the data was only trans-

formed and not reduced in dimensionality. It turns

out that PCA and k-means are in fact closely linked:

in (Ding and He, 2004) it is shown that PCA effec-

tively performs clustering w.r.t. the k-means objective

function. While performing PCA prior to k-means is a

widespread practice, it should be noted that it does not

always lead to improved results (Yeung and Ruzzo,

2001). We did observe a small improvement over per-

forming k-means on the untransformed data.

Learning Algorithms. Structure learning was per-

formed using score-based methods, speciﬁcally Hill

Climbing and TABU search, using Akaike Informa-

tion Criterion (AIC), Bayesian Information Criteron

(BIC) scores. We were unable to obtain models us-

ing log-likelihood scoring within a reasonable time.

An example of the graph structure of the learned

Bayesian network is shown in Figure 8. Parameter

learning was performed using the standard maximum

likelihood estimation, partly due to the unavailability

of Bayesian estimation techniques for hybrid models

in the chosen inference library.

Smoothing & Priors. Simple smoothing was ap-

plied to avoid zero probabilities for outcomes not ob-

served in the training data. This was done by simply

adding 0.01% to all probabilities and subsequently re-

normalizing. For continuous nodes with discrete par-

ents, the marginal distribution was assigned in case

a combination of the parents’ values was observed in

the training data.

Evaluation. Evaluation of Bayesian networks is of-

ten based on quantifying how closely the probabil-

ity distribution represented by the network matches

the empirical distribution (data). Typical metrics in-

clude log likelihood, Akaike information criterion,

Bayesian information criterion, and Kullback-Liebler

divergence.

One can also consider a speciﬁc target variable for

prediction and measure the error rate. Since we are

speciﬁcally interested in predicting cycle times, we

report results of the mean absolute error of predic-

tions for these 4 target variables. We chose to report

this metric rather than the more standard (root) mean

squared error (RMSE), since it gives a more imme-

diate sense of how far predictions were from actual

cycle times in terms of the original time units (min-

utes). Results for RMSE follow very nearly the same

pattern between models. Results are reported for 5

runs of 10-fold cross-validation, see Figure 7.

A crucial point regarding our approach to cross

validation concerns which attributes were considered

observed at each phase of the process. When predict-

ing a given cycle time, clearly any future cycle times

will not have been observed and should not be in-

cluded as inputs to the model. So when predicting the

Preop cycle time, Anesthesia, Surgery, and Recovery

should not be including as inputs. However, once the

patient has reached the Recovery phase, the preceding

cycle times are at least theoretically known and can

be used as inputs. This was our approach, motivated

by the assumption that even if patient ﬂow monitor-

ing systems do not presently integrate such real-time

information they will likely do so in the near future.

6 DISCUSSION

Our preliminary analysis of the ORSOS data set has

demonstrated three points. First, the importance of

data quality assurance, cleaning and the usefulness

HEALTHINF 2020 - 13th International Conference on Health Informatics

280

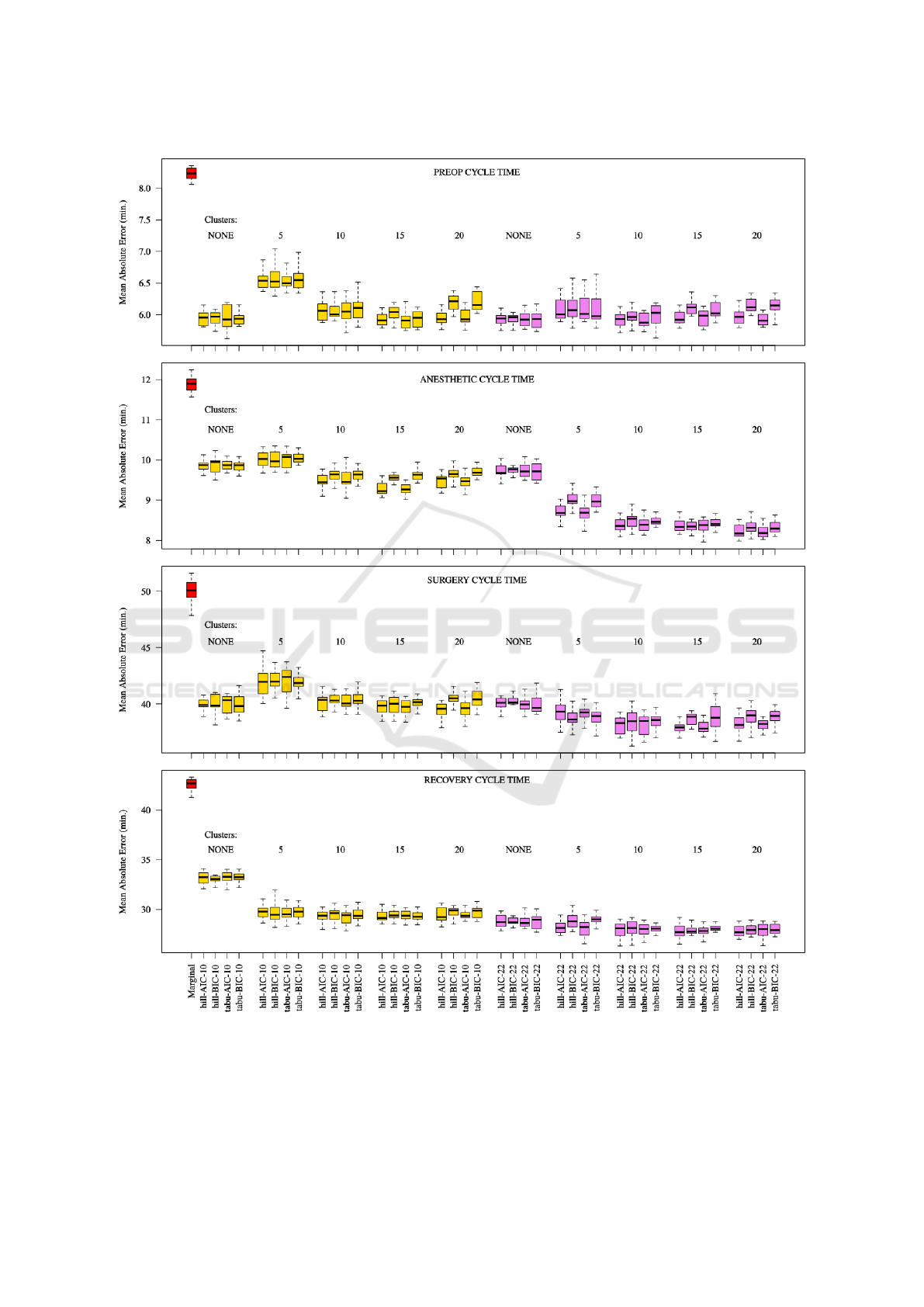
Figure 7: 5 runs of 10-fold cross-validation based on mean absolute error on the 4 cycle time target variables: preop, anesthetic,

surgery, and recovery. Red: Marginal baseline model. Gold: 10-variable model. Violet: 22-variable model. Within each

boxplot grouping are results for models learned with the Hill Climbing and TABU structure learning algorithms using Akaike

Information Criterion (AIC) and Bayesian Information Criterion (BIC) respectively.

Mining Patient Flow Patterns in a Surgical Ward

281

Source

CaseType

A_SED

IntendedDest

Intent

NCEPOD A_MINNB

A_IVMON

Cluster

OperatingRoom

A_EPI

A_LA

A_MAJNBSurgeryTime PreopTime

AnestheticTime

Diabetic ASA

A_GA

RecoveryTime A_SP

A_IVRA

A_CAU

Figure 8: The overall best performing model. The 22 variable model using TABU with BIC scoring and 20 clusters. Node

labels preﬁxed by Ane. denote anaesthetic types. NCEPOD indicates urgency classiﬁcation, ASA patient condition and Intent

indicates day-case/inpatient.

of process mining techniques in this respect. Sec-

ond, that a reasonably accurate predictive model of

event cycle times in the form of a simple Bayesian

belief network can be built which signiﬁcantly out-

performs simple marginal distribution ﬁtting. Third,

that by clustering the target variables and including

these cluster labels as attribute in the model and train-

ing data improves accuracy yet further. Furthermore,

we describe how mutual information, tools for explor-

ing conditional probability distributions and principle

components analysis can not only give insight into the

data, but also guide model building

The choice of Bayesian networks was motivated

by their ﬂexibility and interpretability. The fact that

they can be queried in such a versatile manner, based

on whatever data is available at the time, suggests they

would be a strong component of a predictive model in

a decision support and scheduling systems in surgery.

This allows for queries of the form, “what is the prob-

ability that case c will be in surgery for more than

m minutes given it has the following attributes, and

took n minutes to complete anesthesia?”. Speciﬁcally,

these could form the basis for probabilistic scheduling

systems.

7 CONCLUSION & FUTURE

WORK

We have demonstrated the utility of combining sev-

eral data analysis tools, including from process min-

ing and machine learning, to begin building a useful

model of a very complex set of processes in a sur-

gical ward. This approach would be also applica-

ble in other areas of the healthcare system in which

under-utilization of expensive resources calls for pre-

cise scheduling to avoid down-time.

In terms of the full data analytics workﬂow, often

summarized by Describe → Diagnose → Predict →

Prescribe, we have only just begun the Predict phase.

The incorporation of more aspects of the data set is

a clear next step - the huge cardinality of some at-

tributes, such as procedures and staff, should be ad-

dressed by incorporating domain knowledge and/or

dimensionality reduction. Considering the notable

improvements in precision we achieved with a rela-

tively limited data set, it is likely that incorporating

patient ﬂow attributes across domains would lead to

yet more precise models.

A thorough comparison with learning algorithms

other than simple distribution ﬁtting to conﬁrm the

suitability of Bayesian networks to this application

is also important. Finally, while we have focused

on individual patient ﬂows here, more comprehensive

HEALTHINF 2020 - 13th International Conference on Health Informatics

282

models which take into account ward level dynam-

ics such as patient arrival rates, resource constraints,

and resulting inter-patient dynamics are a natural ex-

tension. In such a system-wide model, the work pre-

sented here would serve as a component to more ac-

curately model local event timings and subsequent

downstream arrival rates.

REFERENCES

Acid, S., e. a. (2004). A comparison of learning algorithms

for bayesian networks: a case study based on data

from an emergency medical service. Artiﬁcial intel-

ligence in medicine, 30(3):215–232.

Ahmadi, S.A., e. a. (2009). Motif discovery in or sen-

sor data with application to surgical workﬂow analysis

and activity detection. In M2CAI workshop, MICCAI,

London. Citeseer.

Akkerman, R. and Knip, M. (2004). Reallocation of beds to

reduce waiting time for cardiac surgery. Health care

management science, 7(2):119–126.

Berti, A., e. a. (2019). Process Mining for Python (PM4Py):

Bridging the Gap Between Process-and Data Science.

In ICPM Demo Track (CEUR 2374).

Bishop, C. M. (2006). Pattern recognition and machine

learning. Springer Science+ Business Media.

Blum, T., e. a. (2008). Workﬂow mining for visualization

and analysis of surgeries. Int. journal of computer as-

sisted radiology and surgery, 3(5):379–386.

Bouarfa, L., e. a. (2011). Discovery of high-level tasks in

the operating room. Journal of biomedical informat-

ics, 44(3):455–462.

Bouarfa, L. and Dankelman, J. (2012). Workﬂow mining

and outlier detection from clinical activity logs. Jour-

nal of biomedical informatics, 45(6):1185–1190.

Cochran, J. K. and Bharti, A. (2006). Stochastic bed balanc-

ing of an obstetrics hospital. Health care management

science, 9(1):31–45.

Denton, B., e. a. (2007). Optimization of surgery se-

quencing and scheduling decisions under uncertainty.

Health care management science, 10(1):13–24.

Ding, C. and He, X. (2004). K-means clustering via prin-

cipal component analysis. In Proc. of the twenty-ﬁrst

int. conference on Machine learning, page 29. ACM.

Dripps, R. (1963). American society of anesthesiologists.

New classiﬁcation of physical status. Anesthesiology,

24(1):111.

Funkner, A. A., e. a. (2017). Towards evolutionary discov-

ery of typical clinical pathways in electronic health

records. Procedia computer science, 119:234–244.

Haro, B.B., e. a. (2012). Surgical gesture classiﬁcation from

video data. In Int. Conf. on Medical Image Comput-

ing and Computer-Assisted Intervention, pages 34–

41. Springer.

Huang, Z., e. a. (2013). Summarizing clinical pathways

from event logs. Journal of biomedical informatics,

46(1):111–127.

Hulshof, P. J. H., e. a. (2013). Tactical resource allocation

and elective patient admission planning in care pro-

cesses. Health care management science, 16(2):152–

166.

Kayis, E., e. a. (2012). Improving prediction of surgery

duration using operational and temporal factors. In

AMIA Annual Symposium Proc., volume 2012, page

456. American Medical Informatics Association.

Koller, D. and Friedman, N. (2009). Probabilistic graphical

models: principles and techniques. MIT press.

Lalys, F. and Jannin, P. (2014). Surgical process modelling:

a review. Int. journal of computer assisted radiology

and surgery, 9(3):495–511.

Lin, H.C., e. a. (2006). Towards automatic skill evaluation:

Detection and segmentation of robot-assisted surgical

motions. Computer Aided Surgery, 11(5):220–230.

Mans, R., e. a. (2012). Mining processes in dentistry. In

Proc. of the 2nd ACM SIGHIT Int. Health Informatics

Symposium, pages 379–388. ACM.

NCEPOD (2019). NCEPOD classiﬁcation of interven-

tion. https://www.ncepod.org.uk/classiﬁcation.html.

Accessed: 2019-11-22.

Neumuth, T., e. a. (2011). Analysis of surgical interven-

tion populations using generic surgical process mod-

els. Int. Journal of Computer Assisted Radiology and

Surgery, 6(1):59–71.

Scotland, N. (2006). National theatres project re-

port. https://www.isdscotland.org/Health-Topics/

Quality-Indicators/National-Benchmarking-Project/

National-Theatres-Project/. Accessed: 2019-11-22.

Stahl, J. E., e. a. (2006). Reorganizing patient care and

workﬂow in the operating room: a cost-effectiveness

study. Surgery, 139(6):717–728.

Stauder, R., e. a. (2014). Random forests for phase detec-

tion in surgical workﬂow analysis. In Int. Conf. on In-

formation Processing in Computer-Assisted Interven-

tions, pages 148–157. Springer.

Strum, D., e. a. (2000). Modeling the uncertainty of sur-

gical procedure times: comparison of log-normal and

normal models. Anesthesiology, 92(4):1160–1167.

Van der Aalst, W. e. a. (2004). Workﬂow mining: Dis-

covering process models from event logs. IEEE

Transactions on Knowledge and Data Engineering,

16(9):1128–1142.

Yeung, K. and Ruzzo, W. L. (2001). An empirical study

on principal component analysis for clustering gene

expression data. Bioinformatics, 17(9):763–774.

Mining Patient Flow Patterns in a Surgical Ward

283