Possibilities of Predicting Arterial Pressure by Means of Heart Rate

Variability

Anton Yu Dolganov

Ural Federal University Yekaterinburg, Russian Federation

Keywords: Arterial Pressure, Heart Rate Variability, Machine Learning, Genetic Programming, Regression.

Abstract: The paper shows results of the study which aims to predict values of arterial pressure by means of heart rate

variability features. A total list of 64 features was tested, which included features in time and frequency

domain, as well as non-linear features. As a means of feature selection, the genetic programming was used.

In particular binary encoding was used for generation of features in combinations as well as degree of the

polynomial. Data of 50 students-volunteers recorded in sitting position was used. Results of the study suggests

that certain heart rate variability features can be used for prediction of the change of arterial pressure.

Perspectives and future plans for results improvement were described.

1 INTRODUCTION

Arterial hypertension is one of the most common

diseases of the cardiovascular system worldwide.

Sharp fluctuations in blood pressure can lead to a

deterioration in the patient's condition. It is especially

worth noting that the rate of change of pressure has a

great influence. Therefore, the task of continuous

monitoring of blood pressure becomes extremely

important and in demand (WHO, 2018).

Currently used long-term monitoring systems are

usually invasive (and can only be carried out under

clinical conditions), or intrusive (and do not allow

continuous measurements due to the influence of

residual occlusion). Therefore, methods of indirect,

non-invasive and non-intrusive assessment of blood

pressure are becoming more common.

Blood pressure depends on several factors, heart

rate is one of them. However, many other variables

also affect blood pressure, such as arterial stiffness,

blood viscosity, volume of blood pumped into the

aorta, microcirculation impedance, etc. Artificial

intelligence methods based on using the capabilities

of machine learning can help solve this problem. Such

an approach allows not only to formalize the

description of complex living systems and conduct

prognostic analysis, but also to find implicit patterns

in the data.

https://orcid.org/0000-0003-2318-9144

Most of the work in this area comes down to using

plethysmogram signals or a combination of

plethysmograms with an electrocardiogram, where

standard parameters are calculated, such as the arrival

time of the pulse, the period of the pulse ejection, the

pulse propagation time, and the pulse wave velocity

(Anisimov et al., 2014; Kurylyak et al., 2013;

Sannino et al., 2015). However, approaches that

combine several signals are not practical for everyday

use.

At the same time, the possibilities of using only

electrocardiogram signals in the task of indirectly

assessing blood pressure have not been sufficiently

studied. Available works, as a rule, are limited to a

rough prediction of the level of pressure (high, normal

or low) and do not allow to obtain accurate estimates

(Simjanoska et al., 2018, 2019).

In previous works, a study was carried out of the

found complexes of significant parameters of heart

rate variability to assess the effectiveness of

treatment, which showed the consistency of the

calculated estimates with blood pressure

measurements (Vladimir Kublanov & Dolganov,

2019). This indicates the prospects of using the

parameters of heart rate variability signals in the task

of indirect estimation of blood pressure.

348

Dolganov, A.

Possibilities of Predicting Arterial Pressure by Means of Heart Rate Variability.

DOI: 10.5220/0009183203480354

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 4: BIOSIGNALS, pages 348-354

ISBN: 978-989-758-398-8; ISSN: 2184-4305

2 MATERIALS AND METHODS

2.1 Biomedical Signals Data

Pilot study was performed in Research Medical and

Biological Engineering Centre of High Technologies

(Ural Federal University, Russian Federation). A total

of 50 students volunteers have performed in the study.

Prior to the biomedical signals acquisition the

participants were informed of the study paradigm and

gave the consent to participate in the study.

The diagram of the study is presented on Figure 1.

Figure 1: Study Timeline.

All subjects were sitting during the whole Study.

Initially, the Arterial Pressure (AP) is measured using

a professional tonometer OMRON HEM-907

(Omron Healthcare, Japan). The measurement of AP

takes around 30 sec. After that the

ElectroCardioGraphy (ECG) signals were registered

in the first limb lead by the “Encephalan-131-03”

device (manufactured by “Medicom-MTD”

company, Russian Federation) for 300 sec. After that

the AP is measured again. Follows 300 sec of ECG

signals recording. In the end the AP is measured

again.

Overall, for each person there were 3

measurements of AP and 2 measurements of ECG

signals. The first measurement of ECG is used for

Training and Testing, the second measurement is

used for the Validation.

The software of “Encephalan-131-03” device

allows one to automatically derive the signals of

Heart Rate Variability (HRV) from the ECG signals.

2.2 Heart Rate Variability Features

Present work involves list of 64 HRV features, that

were in detail described in (Vladimir Kublanov &

Dolganov, 2019). Briefly, that list includes

commonly used time- and frequency-domain

features, non-linear features as well as certain

features of wavelet transform. The in-house software

in Python was used to evaluate these 64 features.

All these features are presented and briefly

described below:

Statistical Features

• M, the mean value of the NN time series;

• HR, the Heart Rate, an inverse ratio to the M;

• SDNN, the standard deviation of the NN intervals;

• the skewness of the dataset;

• the kurtosis of the dataset (Zwillinger & Kokoska,

1999);

• CV, the coefficient of variation;

• RMSSD is the square root of mean of squares of

differences between successive elements (Stein et al.,

1994);

• NN5O, the number of pairs of successive elements

that differ by more than 50 ms;

• pNN50, is normalized NN50 by length;

• SDSD is the standard deviation of differences

between successive elements (Stein et al., 1994);

• Zero-crossing rate, ZCR, the rate of sign-changes.

For evaluation of this feature, M is substracted from

the HRV time-series.

Geometric Features

• М

, the mode;

• VR, the variation range;

• АМ

, the amplitude of the mode.

These three main geometric features comprises

following indexes:

• SI, the Stress Index

SI = AM

/(2·M

·VR)

• IAB, the Index of the Autonomic Balance

IAB = AM

/VR

• ARI, the Autonomic Rhythm Index

ARI = 1/(M

·VR)

• IARP, the Index of Adequate Regulation

Processes

IARP = AM

/(2·M

·VR)

• Triangular Index, also know as St. George Index

(Malik, 1996).

Non-linear Features

The list of nonlinear methods studied in this work

includes: Shannon Entropy, Aproximate Entropy

(ApEn), Sample Entropy (SampEn) and Poincare plot

features.

Fourier Spectral Features

Spectral analysis is used to quantify periodic

processes in the heart rate by the means of the Fourier

transform. The main spectral components of the HRV

signal are High Frequency – HF (0.4 – 0.15 Hz), Low

Frequency – LF (0.15 – 0.04 Hz), Very Low

Frequency – VLF (0.04 – 0.003 Hz) (Malik, 1996;

Ushakov et al., 2013). Features include spectral

power of component, normalized power of

component, maximal power and corresponding

frequency.

Wavelet Spectral Features

The wavelet transform can be used as an alternative

to the Fourier analysis (Addison, 2005). For

AP1

AP2

AP3ECG1

ECG2

30 sec

300 sec

Possibilities of Predicting Arterial Pressure by Means of Heart Rate Variability

349

evaluation of the continious wavelet transfrom the

Gaus wavelet of 8-th order was used (Mallat, 2009).

The wavelet transform allows to obtain continious

time series, in this case of HFwt(t), LFwt(t) and

VLFwt(t) - time series of the HF, LF and VLF spectral

components, respectively. The spectral features

obtained by the wavelet transform include mean,

standard deviation and Shannon Entropy of the

wavelet time series.

Moreover, one can study continious function of

the LF/HF ratio – (LF/HF)[t]. In current study the

following features of (LF/HF)[t] were used:

• Nd - the number of dysfunctions;

• pNd - the propotion of the number of dysfunctions

divided by the length of the (LF/HF)[t].

• (LF/HF)

max

the maximal value of dysfunction

• (LF/HF)

int

the intensity of dysfunction (Egorova

et al., 2014).

Prior to the application of genetic programming

the features were normalized using z-normalisation.

2.3 Genetic Programming

In the course of the previous study, the genetic

programming approach has proven itself to search for

significant parameters and select the optimal machine

learning method. However, the work was devoted to

classification problems. Therefore, during the

implementation of this study, solutions will be

proposed for the use of genetic programming in

regression problems.

For regression task the sklearn library was used.

In particular, LinearRegression module was used to

evaluate the linear regression models. The

polynomial models were evaluated using

combination of PolynomialFeatures and Pipeline

modules.

The main points that should be determined when

using genetic algorithms are the encoding, the initial

population, the selection criterion, and the

evolution strategy.

In this paper, we used the simplest binary

encoding. Each “chromosome” consists of 66 genes.

For first 64 genes a value of "1" in the chromosome

means that a particular HRV feature is included in the

combination, a value of "0" means that a particular

HRV feature is not included in the combination. Last

2 genes are used to code the degree of Polynomial

(from 1 to 5). Empirical evidence had shown that

polynomials of higher order were ineffective. Overall

each “chromosome” represents list of features in

combination and degree of polynomial for a particular

combination of features.

As the initial population, it was decided to choose

100 randomly generated chromosomes. It was

ensured that first 64 genes contain at least single "1"

(there is at least one feature in combination).

Additionally, all duplicate chromosomes were

removed.

The selection criterion was a minimizing of the

following fitness function f with the leave-one-out

cross validation (LOOCV):

f=a*Train+b*Test+c*Validate

where Train is a term related to a training error

(obtained on train using .score method on each

iteration of LOOCV), Test is a term related to a test

error (obtained on test point on each iteration of

LOOCV), Validate is a term related to a validation

error (obtained on a validation measurement on each

iteration of LOOCV), a, b, c are the weight constants,

which are 1, 2, 2 respectfully. Each term consists of

median, maximum, minimum and standard deviation

of absolute errors.

As a rule, the strategy of evolution is determined

by the ratio of the three main genetic operations -

copying, crossover and mutation.

In case of copying, the descendant is an exact

copy of the ancestor. In our case, 10 representatives

of the current generation who have the best ratings by

the selection criterion are directly copied to the next

generation. In case of crossover, the chromosomes of

a child are determined by the interaction between the

chromosomes of their parents. In our case, each

chromosome is a normalized sum of both parents. 10

representatives of the current generation randomly

form 30 pairs of parents, which as a result form 30

descendants with cross chromosomes. Mutations are

manifestations of random changes in the

chromosome. In our case, the mutation changes the

gene to the opposite - “1” to “0” and “0” to “1”,

respectively. Each gene on the chromosome has a 5%

chance of mutating. In total, 60 mutants obtained

from the 10 best representatives of the current

generation pass into each subsequent generation.

Prior to the further evaluations repeated

chromosomes are excluded.

The maximum number of generations in the work

is 10. For a greater account of various probabilities,

the Genetic algorithm was applied 25 times. Overall

diagram of the algorithm is presented on Figure 2.

The algorithm starts with generation of 100

randomly generated chromosomes. After removal of

duplicate chromosomes, for remaining chromosomes

fitness function f is evaluated. All chromosomes are

sorted by the value of the f. Best 10 chromosomes are

used for Copy, Crossover and Mutation operations.

As the result, the next generation is formed, and

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

350

fitness function f is evaluated again. The process of

next generation formation and evaluation is repeated

for 10 times. The algorithm is repeated 25 times.

Figure 2: Genetic Programming Diagram (V. Kublanov et

al., 2017).

3 RESULTS

At the first step data of AP1 and ECG1 is used for

training. Data of AP2 and ECG2 is used for

validation. The results of applying the genetic

algorithm for all 25 implementations are given in

Figures 3 and 4 for Systolic (APS) and Diastolic

(APD) AP. Each line represents change of minimal

fitness function f within a single evolution. Each

column represents step of generation within a single

evolution. Different lines represent 25

implementations of genetic programming. The value

itself is the minimal value of the fitness function f for

each evolution for each generation.

Relative errors for best representatives among all

evolutions are presented in Tables 1 and 2.

Figure 3: Genetic Programming Results for APS.

Table 1: Errors for APS.

median max min std

test 8.23% 24.09% 0.62% 6.15%

validate 7.93% 33.97% 0.00% 7.68%

Table 2: Errors for APD.

median max min std

test 5.60% 26.35% 0.18% 6.71%

validate 6.32% 34.45% 0.01% 7.05%

As it can be seen, the best median results on test

data is around 8% for APS and 6% for APD. In

addition, alternative variant was considered: to the

feature vector values of HRV features of arterial

pressure on a previous segment were added. In

4,02 3,82 3,74 3,33 3,33 3,33 3,31 3,30 3,21 3,17

3,85 3,69 3,64 3,57 3,50 3,40 3,24 3,17 3,07 3,07

4,00 3,55 3,52 3,52 3,41 3,25 3,04 3,04 3,04 2,98

4,21 3,84 3,78 3,42 3,20 3,20 3,19 3,16 3,16 3,10

3,77 3,60 3,47 3,27 3,24 3,24 3,24 3,20 3,16 3,13

3,98 3,60 3,35 3,16 3,16 3,16 3,16 3,02 3,02 3,02

4,00 3,59 3,34 3,21 3,18 3,18 3,16 3,12 3,08 3,08

4,14 3,95 3,56 3,49 3,28 3,28 3,08 3,06 3,01 2,99

4,08 3,79 3,71 3,40 3,32 3,32 3,32 3,26 3,26 3,13

3,95 3,95 3,71 3,56 3,54 3,41 3,29 3,24 3,17 3,00

4,10 3,86 3,86 3,74 3,63 3,48 3,43 3,43 3,21 3,11

4,15 3,80 3,80 3,54 3,54 3,38 3,36 3,34 3,34 3,34

3,99 3,85 3,83 3,69 3,69 3,65 3,51 3,51 3,31 3,31

4,07 3,70 3,50 3,28 3,05 3,05 2,97 2,86 2,86 2,86

4,05 3,85 3,76 3,56 3,50 3,31 3,27 3,13 3,11 2,84

4,07 3,77 3,74 3,74 3,58 3,51 3,30 3,30 3,30 3,30

3,98 3,90 3,76 3,55 3,49 3,33 3,29 3,24 3,19 3,09

4,05 3,57 3,57 3,45 3,31 3,23 3,23 3,23 3,22 3,11

4,08 3,94 3,68 3,55 3,55 3,52 3,50 3,37 3,37 3,19

3,97 3,59 3,41 3,40 3,21 3,02 2,94 2,94 2,94 2,82

3,93 3,69 3,49 3,47 3,08 3,08 3,08 3,04 3,02 2,95

4,12 3,80 3,34 3,34 3,34 3,08 3,08 2,89 2,89 2,89

3,68 3,60 3,22 3,22 3,07 3,07 3,07 3,01 3,01 3,00

4,02 3,76 3,47 3,44 3,35 3,31 3,16 3,14 3,10 3,10

3,64 3,57 3,47 3,22 3,20 3,20 3,05 3,02 3,02 3,02

Start

Initial population

Start

evolution

Fitness function

Copy Crossover

Mutation

Next generation

Maximal

eneration is

reached?

end

Yes

Possibilities of Predicting Arterial Pressure by Means of Heart Rate Variability

351

particular AP1 and ECG1 were used for prediction of

AP2. At the same time validation was performed on

data of AP2 and ECG2 for prediction of AP3.

Results of such alternative approach are presented

on Figures 5 and 6, and on Tables 3 and 4.

Figure 4: Genetic Programming Results for APD.

It can be seen that alternative approach can

significantly improve results. It can be concluded that

task of predicting AP by means of only HRV features

can be too ambitious. At the same time the proposed

approach can be used to evaluate change in AP after

a certain time, when the original “calibration” value

is known.

It was noted that the best result was obtained for

the linear regression (polynomial of 1

degree). Best

combinations consist of around 20 features. Which

coupled with 1 degree lessen overtraining.

The results, presented in current work are

comparable with ones obtained using Pulsation Wave

propagation time (Anisimov et al., 2014). In that work

authors reported that for a 1/3 of validation set error

was less than 1 mmHg, average error was 9%.

Figure 5: Alternative Genetic Programming Results for

APS.

Table 3: Alternative Errors for APS.

median max min std

test 2.65% 10.07% 0.06% 2.58%

validate 4.04% 13.77% 0.00% 3.62%

Table 4: Alternative Errors for APD.

median max min std

test 4.72% 13.12% 0.05% 3.46%

validate 5.91% 21.38% 0.00% 4.84%

Results of the current work are also comparable

with results application of genetic algorithms for

symbolic regression (Dolganov, 2019). Although

additional comparison is required.

3,34 3,34 3,26 3,26 3,23 3,15 3,01 2,95 2,86 2,74

3,48 3,38 3,27 3,14 3,03 3,03 3,03 3,03 2,92 2,88

3,46 3,24 3,21 3,21 3,18 3,09 3,09 3,09 3,08 3,08

3,50 3,41 3,14 3,14 3,14 3,12 2,90 2,90 2,89 2,87

3,37 3,37 3,29 3,26 3,18 3,18 3,00 2,92 2,92 2,92

3,43 3,24 3,24 3,05 3,05 3,05 3,05 3,05 3,00 3,00

3,42 3,38 3,27 3,27 3,15 2,92 2,92 2,92 2,92 2,92

3,35 3,23 3,13 3,07 2,97 2,92 2,84 2,84 2,84 2,82

3,42 3,29 3,25 3,17 3,10 3,10 3,10 3,10 3,10 3,10

3,30 3,09 3,05 2,91 2,77 2,55 2,55 2,54 2,48 2,48

3,34 3,17 3,16 3,11 3,03 3,03 2,99 2,95 2,86 2,83

3,42 3,32 3,23 3,16 3,14 3,05 3,04 2,99 2,98 2,74

3,30 3,16 3,16 3,16 3,07 3,05 3,05 2,93 2,93 2,93

3,21 3,21 3,21 3,21 3,20 3,19 3,13 3,02 2,90 2,90

3,44 3,34 3,27 3,27 3,13 3,07 3,04 3,04 3,04 2,93

3,44 3,23 3,21 2,75 2,64 2,56 2,53 2,53 2,50 2,50

3,46 3,23 3,07 3,07 3,06 2,96 2,96 2,96 2,92 2,92

3,35 3,26 3,26 2,98 2,98 2,98 2,86 2,82 2,81 2,77

3,43 3,22 3,22 3,21 3,02 2,97 2,97 2,70 2,70 2,70

3,29 3,26 3,20 3,16 3,16 3,14 3,13 3,13 3,07 3,07

3,33 3,22 3,22 3,14 3,14 3,03 3,03 3,01 2,94 2,94

3,37 3,26 3,17 3,10 2,92 2,92 2,72 2,72 2,72 2,71

3,36 3,28 3,18 3,12 3,06 3,03 3,03 3,03 3,02 2,96

3,43 3,33 3,33 3,27 3,27 3,20 3,20 3,17 3,11 3,11

3,33 3,07 3,06 2,86 2,81 2,81 2,81 2,81 2,81 2,81

1,16 1,10 1,09 1,05 1,05 1,05 1,05 1,05 1,05 1,05

1,21 1,15 1,13 1,08 1,07 1,05 1,05 1,05 1,04 1,04

1,17 1,12 1,11 1,10 1,05 1,05 1,05 1,05 1,04 1,03

1,21 1,18 1,16 1,14 1,12 1,12 1,12 1,09 1,09 1,05

1,15 1,14 1,11 1,11 1,11 1,08 1,06 1,05 1,03 1,03

1,19 1,18 1,15 1,15 1,15 1,10 1,10 1,10 1,08 1,07

1,12 1,07 1,05 1,02 1,01 1,01 1,01 1,01 1,01 0,99

1,18 1,17 1,16 1,10 1,10 1,10 1,10 1,10 1,08 1,08

1,18 1,16 1,15 1,09 1,07 1,05 1,05 1,05 1,05 1,05

1,19 1,14 1,09 1,08 1,06 1,06 1,06 1,06 1,06 1,03

1,19 1,15 1,11 1,07 1,07 1,06 1,06 1,02 1,02 1,01

1,19 1,16 1,16 1,14 1,12 1,12 1,12 1,10 1,10 1,06

1,20 1,16 1,12 1,12 1,11 1,07 1,07 1,06 1,04 1,04

1,21 1,17 1,13 1,13 1,12 1,12 1,07 1,05 1,05 1,05

1,14 1,10 1,09 1,07 1,07 1,04 1,03 1,01 1,00 1,00

1,22 1,18 1,15 1,11 1,11 1,09 1,06 1,05 1,04 1,02

1,18 1,17 1,13 1,05 1,02 1,00 1,00 0,98 0,98 0,98

1,19 1,13 1,12 1,12 1,03 1,03 1,03 1,03 1,03 1,03

1,20 1,17 1,14 1,11 1,08 1,07 1,06 1,06 1,04 1,04

1,18 1,13 1,10 1,09 1,08 1,08 1,07 1,07 1,02 1,01

1,18 1,15 1,12 1,04 1,02 1,02 1,02 1,02 1,02 1,02

1,19 1,14 1,12 1,12 1,10 1,09 1,08 1,08 1,07 1,02

1,13 1,01 1,01 1,00 1,00 0,99 0,99 0,99 0,99 0,96

1,17 1,15 1,11 1,11 1,09 1,07 1,07 1,07 1,07 1,06

1,23 1,22 1,16 1,12 1,11 1,09 1,04 1,03 1,03 1,03

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

352

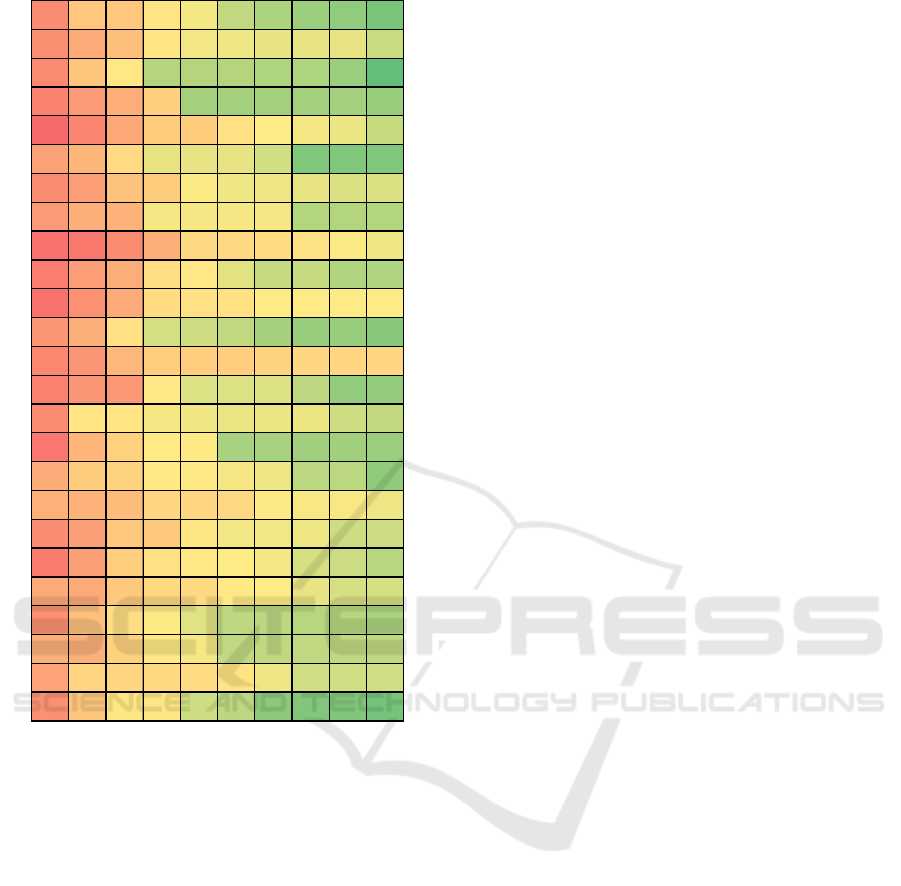
Figure 6: Alternative Genetic Programming Results for

APD.

4 DISCUSSION AND

CONCLUSIONS

The paper describes investigation testing possibility

of the indirect AP measurement by means of HRV

features. For such task a pilot study was performed on

50 student-volunteers. The study consisted of

simultaneous record of ECG signals and

measurements of AP. In the following, HRV time-

series were derived from ECG signals by software

application. A list of 64 HRV was tested.

Proposed modification of previously used

approach of genetic programming (V. Kublanov et

al., 2017).

Previously the approach was used for the

classification task in task of arterial hypertension

express-diagnosing. In the paper the approach was

modified to be applied in the regression task.

Preliminary results have shown that the error of

AP prediction using only features of HRV can be

relatively high. At the same time, when we add

“calibration” data to the HRV features it is possible

to predict change of the AP with relatively low error.

Even though the results, presented in the paper,

are relatively low, they show that there is a certain

relation between HRV features and AP data. It is

worthy to point out that no additional data was used

in current study. In particular, no data on gender,

anthropomorphic features, age was used. In addition,

features of raw ECG signals (morphology, features of

P-QRS-T complex) were also not yet tested. Addition

of such features might improve the results in the

proposed approach.

Among the possible future works directions are

application of deep neural networks (Belo et al.,

2017) in the task which proved to effective in the

biomedical signals synthesis.

REFERENCES

Addison, P. S. (2005). Wavelet transforms and the ECG: A

review. Physiological Measurement, 26(5), R155–

R199. Scopus. https://doi.org/10.1088/0967-

3334/26/5/R01

Anisimov, A. A., Yuldashev, Z. M., & Bibicheva, Yu. G.

(2014). Non-occlusion Monitoring of Arterial Pressure

Dynamics from Pulsation Wave Propagation Time.

Biomedical Engineering, 48(2), 66–69.

https://doi.org/10.1007/s10527-014-9420-7

Belo, D., Rodrigues, J., Vaz, J. R., Pezarat-Correia, P., &

Gamboa, H. (2017). Biosignals learning and synthesis

using deep neural networks. Biomedical Engineering

Online, 16(1), 115.

Dolganov, A. (2019). Indirect Measurement of Arterial

Pressure by Means of Heart Rate Variability Signals.

2019 Ural Symposium on Biomedical Engineering,

Radioelectronics and Information Technology

(USBEREIT), 156–158. https://doi.org/10.1109/

USBEREIT.2019.8736632

Egorova, D. D., Kazakov, Y. E., & Kublanov, V. S. (2014).

Principal Components Method for Heart Rate

Variability Analysis. Biomedical Engineering, 48(1),

37–41. Scopus. https://doi.org/10.1007/s10527-014-

9412-7

Kublanov, V., Dolganov, A., & Gamboa, H. (2017).

Genetic programming application for features selection

in task of arterial hypertension classification.

Proceedings - 2017 International Multi-Conference on

Engineering, Computer and Information Sciences,

SIBIRCON 2017, 561–565. Scopus. https://doi.org/

10.1109/SIBIRCON.2017.8109954

Kublanov, Vladimir, & Dolganov, A. (2019). Development

of a decision support system for neuro-

electrostimulation: Diagnosing disorders of the

1,81 1,67 1,67 1,60 1,57 1,52 1,50 1,48 1,47 1,44

1,81 1,74 1,69 1,60 1,57 1,57 1,56 1,56 1,56 1,53

1,82 1,68 1,60 1,51 1,51 1,51 1,50 1,50 1,48 1,42

1,84 1,78 1,74 1,65 1,49 1,49 1,49 1,49 1,49 1,47

1,90 1,83 1,75 1,66 1,66 1,61 1,59 1,57 1,57 1,52

1,76 1,71 1,63 1,56 1,56 1,56 1,54 1,45 1,45 1,45

1,81 1,77 1,68 1,66 1,58 1,57 1,57 1,56 1,55 1,55

1,78 1,73 1,72 1,57 1,57 1,57 1,57 1,50 1,50 1,50

1,88 1,86 1,82 1,73 1,63 1,63 1,62 1,61 1,58 1,57

1,85 1,77 1,73 1,62 1,60 1,56 1,52 1,52 1,50 1,50

1,87 1,80 1,74 1,62 1,61 1,61 1,59 1,59 1,59 1,59

1,79 1,73 1,61 1,54 1,53 1,52 1,49 1,47 1,47 1,46

1,82 1,79 1,71 1,66 1,66 1,66 1,64 1,64 1,64 1,64

1,84 1,79 1,79 1,59 1,55 1,55 1,55 1,52 1,47 1,47

1,82 1,60 1,60 1,57 1,57 1,56 1,56 1,56 1,53 1,52

1,87 1,72 1,65 1,59 1,58 1,49 1,49 1,48 1,48 1,48

1,74 1,66 1,64 1,59 1,59 1,57 1,57 1,51 1,51 1,47

1,72 1,72 1,70 1,64 1,64 1,63 1,58 1,58 1,58 1,57

1,81 1,77 1,67 1,67 1,60 1,57 1,57 1,57 1,53 1,53

1,85 1,77 1,66 1,61 1,59 1,59 1,57 1,54 1,53 1,51

1,74 1,74 1,67 1,63 1,63 1,59 1,59 1,56 1,54 1,54

1,80 1,69 1,62 1,58 1,55 1,51 1,51 1,51 1,51 1,49

1,73 1,73 1,65 1,59 1,57 1,52 1,52 1,52 1,52 1,52

1,76 1,64 1,64 1,63 1,62 1,60 1,57 1,54 1,54 1,54

1,81 1,68 1,60 1,60 1,53 1,51 1,46 1,45 1,45 1,44

Possibilities of Predicting Arterial Pressure by Means of Heart Rate Variability

353

cardiovascular system and evaluation of the treatment

efficiency. Applied Soft Computing, 77, 329–343.

https://doi.org/10.1016/j.asoc.2019.01.032

Kurylyak, Y., Lamonaca, F., & Grimaldi, D. (2013). A

Neural Network-based method for continuous blood

pressure estimation from a PPG signal. 2013 IEEE

International Instrumentation and Measurement

Technology Conference (I2MTC), 280–283. https://

doi.org/10.1109/I2MTC.2013.6555424

Malik, M. (1996). Heart rate variability: Standards of

measurement, physiological interpretation, and clinical

use. Circulation, 93(5), 1043–1065. Scopus.

Mallat, S. (2009). A Wavelet Tour of Signal Processing.

Scopus.

Sannino, G., Falco, I. D., & Pietro, G. D. (2015). Indirect

Blood Pressure Evaluation by Means of Genetic

Programming. Biomedical Engineering Systems and

Technologies, 75–92. https://doi.org/10.1007/978-3-

319-27707-3_6

Simjanoska, M., Gjoreski, M., Bogdanova, A. M., Koteska,

B., Gams, M., & Tasič, J. (2018). ECG-derived Blood

Pressure Classification using Complexity Analysis-

based Machine Learning. 282–292. https://www.

scitepress.org/PublicationsDetail.aspx?ID=I16nQUpZj

Dw=&t=1

Simjanoska, M., Papa, G., Seljak, B., & Eftimov, T. (2019).

Comparing Different Settings of Parameters Needed

for Pre-processing of ECG Signals used for Blood

Pressure Classiﬁcation. 62–72. https://www.

scitepress.org/PublicationsDetail.aspx?ID=tgp8l7PfXk

w=&t=1

Stein, P. K., Bosner, M. S., Kleiger, R. E., & Conger, B. M.

(1994). Heart rate variability: A measure of cardiac

autonomic tone. American Heart Journal, 127(5),

1376–1381.

Ushakov, I. B., Orlov, O. I., Baevskii, R. M., Bersenev, E.

Y., & Chernikova, A. G. (2013). Conception of health:

Space-Earth. Human Physiology, 39(2), 115–118.

Scopus. https://doi.org/10.1134/S0362119713020175

WHO. (2018). World health statistics 2018: Monitoring

health for the SDGs sustainable development goals.

World Health Organization.

Zwillinger, D., & Kokoska, S. (1999). CRC standard

probability and statistics tables and formulae. Crc

Press.

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

354