
Scene Adaptive Structured Light 3D Imaging
Tomislav Pribanic
1a
, Tomislav Petkovic
1b
, David Bojanic
1c
, Kristijan Bartol
1d
and Mohit Gupta
2
1
Faculty of Electrical Engineering and Computing, University of
Zagreb, Unska 3, Zagreb, Croatia
2
Department of Computer Science, University of Wisconsin, Madison, WI, U.S.A.
Keywords: 3D Imaging, Structured Light, Time-of-Flight, Depth Precision.
Abstract: A 3D structured light (SL) system is one powerful 3D imaging alternative which in the simplest case is
composed of a single camera and a single projector. The performance of 3D SL system has been studied
considering many aspects, for example, accuracy and precision, robustness to various imaging factors,
applicability to a dynamic scene capture, hardware and image processing complexity, to name but a few. In
this work we consider the spatial projector-camera set up and its influence on the uncertainty of points’ depth
reconstruction. In particular, we show how a depth precision is in a great extent determined by the angle of
pattern projection and the angle of imaging from a projector and a camera, respectively. For a fixed camera
projector configuration, those angles are scene dependent for various points in space. Consequently, the
attainable depth precision will typically vary considerably across the volume of reconstruction which is not a
desirable property. To that end, we study a scene dependent 3D imaging approach during which we propose
how to conveniently detect points with a lower depth precision and to influence other factors of a depth
precision, in order to improve a depth precision in scene parts where necessary.
1 INTRODUCTION
The study on 3D imaging system design has attracted
a great deal of attention in computer vision. There has
been many methods and systems proposed (Chen,
Brown, & Song, 2000). A particularly interesting
ones are active illumination 3D imaging systems
where, besides a camera, an active source of
illumination is introduced. The most representative
ones are photometric systems (Barsky & Maria,
2003), time-of-flight (ToF) cameras (Hansard, Lee,
Choi, & Horaud, 2012) and structured light (SL)
systems (Geng, 2011). SL has proven to be one of the
most accurate and robust methods proposed and
analyzed (Salvi, Fernandez, Pribanic, & Xavier,
2010). In SL an illumination source is typically a
projector. The main task of a projector is to project
pattern(s) in the scene. That is especially beneficial
when a natural scene has a low texture since SL is
triangulation-based 3D imaging system and, in order
to triangulate 3D point position, it is necessary to find
a
https://orcid.org/0000-0002-5415-3630
b
https://orcid.org/0000-0002-3054-002X
c
https://orcid.org/0000-0002-2400-0625
d
https://orcid.org/0000-0003-2806-5140
the correspondent projector and camera image
coordinates. Having basically two different pieces of
hardware HW, i.e. a camera and a projector, opened
an additional vast amount of research possibilities to
study the performance of SL systems. Naturally, the
reconstruction accuracy and precision aspects have
been given perhaps the most attention. To that end,
different factors and system design issues have been
analyzed and various measures have been proposed in
order to improve the accuracy and precision.
However, somewhat surprisingly and to the best of
our knowledge, there is relatively less work about the
spatial geometrical set up between a camera and a
projector (Liu & Li, 2014). We note that besides a
camera projector baseline, two other most obvious
factors defining a geometry of 3D reconstruction are
the angle of projector’s pattern projection and the
angle of camera imaging (angles α and β in Figure 1).
In this work our main contributions are related to
those two angles and to their influence on the depth
precision. First, we derive an expression clearly
576
Pribanic, T., Petkovic, T., Bojanic, D., Bartol, K. and Gupta, M.
Scene Adaptive Structured Light 3D Imaging.
DOI: 10.5220/0009189905760582
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
576-582
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

showing the various factors determining the depth
precision of a SL system, two of which are the afore
mentioned angles of pattern projection and imaging.
We further demonstrate how those two angles change
across the scene, thus having a significant impact on
the expected depth precision throughout the scene.
Obviously, the pair of such angles are scene
dependent and for a general scene cannot be
anticipated in advance. we also provide a simple
measure on improving the depth precision for those
points in space where the particular angles cause an
unsatisfactory depth precision. In turn, the proposed
strategy allows scene dependent 3D imaging.
The remainder of this work is structured as
follows. We next briefly cover the related work on 3D
active imaging. Afterwards we derive an expression
for SL system depth precision, followed by the
experimental simulations of depth precision
dependency on angles of pattern projection and
imaging. In the same section we discuss possible
measures of improving the depth precision. At the end
we reflect on the possible future work and draw the
main paper conclusions.
2 RELATED WORK
A common approach to classify 3D imaging systems
is to divide them in the following three groups:
triangulation, interferometry and time-of flight
(Büttgen, Oggier, Lehmann, Kaufmann, &
Lustenberger, 2015). An even simpler classification
would be only in two groups: passive and active 3D
imaging systems. Within the active ones two most
notable representatives, and closely related to this
work, are structured light systems and time of flight
cameras which will be, therefore, in brief jointly
overviewed.
Due to a fact that an active source of illumination
has been utilized, a significant deal of work was
devoted to the performance error analyses where
multiple illuminations sources (3D imaging systems)
are simultaneously used. To prevent either interfering
one SL projector with another or one ToF LED (laser)
source with another several approaches have been
proposed: space division-multiple access (Jia, Wang,
Zhou, & Meng, 2016), wavelength-division multiple
access (Bernhard & Peter, 2008), time-division
multiple access, frequency-division multiple access )
(Petković, Pribanić, & Đonlić, 2017), and finally, in
the case of ToFs, a code-division multiple access
(Whyte, Payne, Dorrington, & Cree, 2010).
When analyzing the performance of a single 3D
imaging system, a significant work was done, mostly
in the field of ToFs, studying hardware itself w.r.t. to
various factors such as power budget, quantum noise
and thermal noise (Lange & Seitz, 2001); or
integration time related error and built-in pixel related
error (Foix, Alenya, & Torras, 2011). On the other
hand, SL system performance has been analyzed
mainly in the hardware agnostic manner, i.e. more in
the image processing sense by trying to identify
potential errors during pattern(s) (de)coding process
(Horn & Kiryati, 1997) and/or by finding the optimal
coding scheme (Gupta & Nakhate, A Geometric
Perspective on Structured Light Coding, 2018). That
is in a way understandable since in terms of signal
processing ToF is generally based on two or three
principles: continuous/discrete and direct time of
flight (Horaud, Hansard, Evangelidis, & Ménier,
2016). On the other hand, SL has richer alternatives
regarding the various types of patterns to be projected
and subsequently processed, particularly using color
patterns for dynamic scenarios (Petković, Pribanić, &
Đonlić, 2016). In that sense a high emphasis was put
on a design of patterns to be projected (Mirdehghan,
Chen, & Kutulakos, 2018). Interestingly, certain
hardware design proposed solutions for ToF, e.g.
epipolar time of flight imaging (Achar, Bartels,
Whittaker, Kutulakos, & Narasimhan, 2017), are
applicable for SL too.
One of the main differences between ToF and SL
is the former does not have the baseline involved
since ToF illumination source and camera are
generally assumed to be collocated. In terms of the
baseline, an interesting work has been done in SL
when the baseline is very small which simplifies the
process of finding a projected code in cameras images
(Saragadam, Wang, Gupta, & Nayar, 2019).
Moreover, a close work to ours is the one analyzing
the influence of the short projector-camera baseline
on the performance (Liu & Li, 2014). Similarly
(Bouquet, Thorstensen, Bakke, & Risholm, 2017)
compares the performance 3D SL and ToF systems,
but without any relation to the geometrical
configuration between the camera and the projector.
To the best of our knowledge none of the mentioned
works are specially concentrated on the analyses of
the pattern projection angle and the camera imaging
angle and their impact on the estimated depth
precision.
Scene Adaptive Structured Light 3D Imaging
577

3 DEPTH PRECISION OF SL 3D IMAGING SYSTEM
Figure 1 A: 3D point T, at the depth D from the camera (C), is projected in the camera (C) image at (u
c
, v
c
) and in the projector
(P) image at (u
p
, v
p
). Backprojected rays to the point T from the projector and the camera form with the baseline B the angles
α and β, respectively. FOV stands for a projector’s field of view. f
x
and f
y
are the effective focal lengths in the horizontal and
vertical direction, receptively.
We start by introducing the basic principle behind
phase shifting (PS) method which is very likely the
most notable SL pattern strategy (Salvi, Fernandez,
Pribanic, & Xavier, 2010). PS consists of sequentially
projecting a number (N≥3) of periodic sine patterns,
shifted by some phase shift 𝜑
=
∙
∙𝑖, where i=0, 1,
… N-1. The projected patterns are imaged by a
camera and then processed to compute a wrapped
phase φ, based on which the correspondence between
projector and camera image pixels can be established.
The intensity I
i
observed at some camera pixel can be
modeled as follows:
𝐼
=
𝐴
∙sin
(
𝜑+𝜑
)
+𝐶
(1)
where A is the brightness when projector projects its
full intensity (A is related to 3D points reflectivity and
propagation loss), φ is the unknown phase, φ
i
is the
known relative phase shift at which a particular pattern
was projected, and C represents the contribution from
a background illumination. Evidently having three
unknowns (A, φ and C) there are at least N=3 shifts
(projected patterns) needed to recover all three
unknowns. In practice to cope with the noise at least
four shifts are normally used, both in SL and ToF
systems also (Büttgen, Oggier, Lehmann, Kaufmann,
& Lustenberger, 2015), which allows to recover the
unknowns:
𝐴
=
(𝐼
−𝐼
)
+(𝐼
−𝐼
)
2
𝜑=tan
𝐼
−𝐼
𝐼
−𝐼
𝐶=
𝐼
+𝐼
+𝐼
+𝐼
4
(2)
We next derive a depth precision of the SL
system. Figure shows rectified, but still a very
general relationship between a projector, a camera
and some triangulated point in space. Using the law
of sines, we derive an expression for the depth D:
𝐷=
𝐵∙sin
(
𝛼
)
sin
(
𝛼+𝛽
)
(3)
where B is projector-camera baseline, and given some
point T, α is projector pattern projection angle with
the respect to baseline B and β is a camera imaging
angle with the respect to baseline B too. Depth
precision can be quantitively estimated as a depth
uncertainty where the cause of uncertainty can be
attributed to the noise in measurements I
i
of Eq. (1).
In particular, a standard deviation σ
D
of depth is
commonly estimated using the expression for the
error propagation:
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
578

𝜎
=
𝜕𝐷
𝜕𝐼
∙𝑉𝑎𝑟
(
𝐼
)
𝑖=0
(4)
where the variance Var(I
i
) is modeled as being equal
to the signal level (Lange & Seitz, 2001). According
to the expression (3), the depth D is explicitly
dependent on the angles α and β. However, angle α
can be expressed as a function of the phase φ (2)
which in turn provides a relationship to the
measurements I
i
. Hence, using the chain rule the
partial derivative
can be expressed as:
𝜕𝐷
𝜕𝐼
=
𝜕𝐷
𝜕𝛼
·
𝜕𝛼
𝜕𝜑
·
𝜕𝜑
𝜕𝐼
(5)
Based on Eq. (3), the first factor in Eq. (5) is readily
computed:
𝜕𝐷
𝜕𝛼
=
𝐵·sin𝛽
𝑠𝑖𝑛
(
𝛼+𝛽
)
(6)
The actual relationship between the angle α and the
phase φ is less obvious. According to Figure 1, the
vector v
P
pointing back in space in the direction of the
spatial point T can be computed based on the
projector calibration matrix K
P
and on the projector
image point p=[u
p
v
P
1]
T
:
𝐾
=
𝑓
0𝑢
0
𝑓
𝑣
001
𝑣
=𝐾
∙𝑝=
⎣
⎢
⎢
⎢
⎡
𝑢
−𝑢
𝑓
𝑣
−𝑣
𝑓
1
⎦
⎥
⎥
⎥
⎤
(7)
where (u
P
, v
P
) are projector image coordinates,
(u
0
, v
0
) is the position of the principal point in the
projector image. f
x
and f
y
are effective focal lengths
in horizontal and vertical direction, respectively. For
the simplicity of exposition and without loss of
generality we can set an image component coordinate
u as being identical to the wrapped phase φ. Next, the
angle α is immediately determined by a dot product
between the vector v
P
and the baseline B direction
vector v
B
, where v
B
can be taken as a unit vector.
cos𝛼=
𝑑𝑜𝑡(𝑣
,𝑣
)
|
𝑣
|
∙
|
𝑣
|
=
𝑑𝑜𝑡(𝑣
,𝑣
)
|
𝑣
|
(8)
Evidently this poses a nonlinear relationship between
the angle α and the wrapped phase φ. Fortunately, the
angle α typically spans values where the cos𝛼 𝑖𝑠
fairly linear w.r.t. its argument (unless a wide-angle
optics for a projector is used). Therefore, similarly as
in (Bouquet, Thorstensen, Bakke, & Risholm, 2017),
we approximate the relationship between the angle α
and the wrapped phase φ with a linear function. Using
fairly straightforward geometry relations, depicted on
Figure , it can be shown that:
𝛼≈-FOV/φ_MAX ∙𝜑+
(9)
where FOV is projector’s field of view. Eq. (9) finally
determines the partial derivative
=−
and
simplifies the original (4) to.
𝜎
=
𝐵·sin𝛽∙𝐹𝑂𝑉
sin
(
𝛼+𝛽
)
∙𝜑
∙
𝜕𝜑
𝜕𝐼
∙𝐼
𝑖=0
(10)
The sum of partial derivatives under the square root
from (10), using the relations (1) and (2), will yield
√
√∙
and will ultimately define the final expression for
the depth standard deviation σ
D
:
𝜎
=
𝐷
·𝐹𝑂𝑉∙
√
𝐶
𝐵∙𝜑
∙√2∙𝐴
∙
sin𝛽
𝑠𝑖𝑛
𝛼
𝜎
=
𝐵·𝐹𝑂𝑉∙
√
𝐶
𝜑
∙
√
2∙
𝐴
∙
sin𝛽
𝑠𝑖𝑛
(
𝛼+𝛽
)
(11)
Here we point out the dependence of σ
D
on the part
we call the angle factor 𝐴𝐹=
(
)
. In the next
section we show how AF affects the amount of
standard deviation σ
D
across the reconstruction whole
volume.
4 RESULTS AND DISCUSSION
In this section we first show how the angle factor AF
varies across a 3D imaging scene. Then we use Monte
Carlo approach in the synthetic experiments to
estimate the depth standard variation σ
D
for various
points in the 3D space. Finally we propose and
discuss strategies to improve depth precision for the
desired portion of space, in order to achieve a more
uniform depth precision values across the volume. To
that end, and without loss of generality, we assume
one plausible projector-camera set up where projector
and camera images are epipolary rectified (Fusiello,
Trucco, & Verri, 2000) and with the following
parameters: the baseline B=300mm, the effective
focal lengths in pixels f
x
=fy=1000, image resolution
Scene Adaptive Structured Light 3D Imaging
579
(u, v)=(1024, 768), the principal point coordinates
(u
0
, v
0
)=(512, 384).
Figure 2 visualizes the change of AF for a given
volume and at the standoff distance 400mm from the
3D SL scanner. In the case of this rectified projector-
camera set up, AF factor increases (a depth precision
becomes worse) almost linearly along the volume
depth. However, besides volume depth alone, which
can be fairly arbitrary defined, we are even more
interested about AF dependency of the depth D wrt to
the camera itself.
Figure 2: The relative change of AF across the 3D imaging
volume 800mm×800mm×1000mm(width×depth×height).
3D scanner standoff distance is 400mm.
Figure 3 shows, for a sequence of constant depths
D, how AF changes as the angle α changes, spanning
the entire projector’s FOV angle. Given the current
projector-camera arrangement it turns out that at
some constant depth D, AFs become worse and worse
as the angle α increases. In fact, the relative
discrepancy between points having a small AF and
points having a big AF is more evident as the depth D
is smaller.
Figure 3: Each solid curve corresponds to a constant depth.
Going from the top curve to the bottom, depth D changes
from 350mm to 1000mm. Values within each curve are
normalized on the smallest AF value for that curve (depth).
Figure 4: A camera image of the 3D plane of points, parallel
to the projector-camera image plane, where the intensity
represents the values of AF.
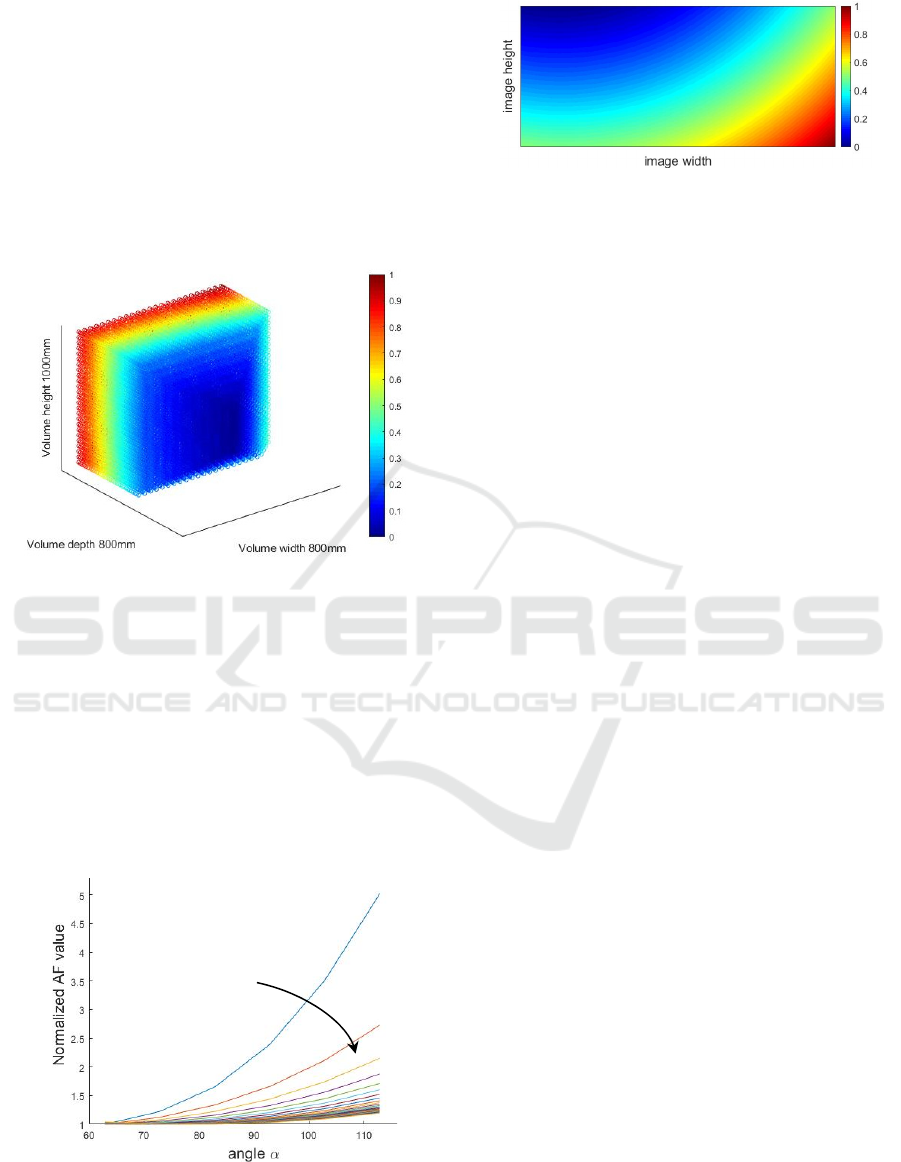
Figure 4 presents another alternative overlook on
the issue. In this case points in 3D plane, at the
standoff distance of about 300mm and parallel to the
projector-camera image planes, are projected to the
camera image where for each point the value AF is
shown as the intensity. Going from the upper left
corner to the lower right corner, a diversity of AF
values is witnessed, even though the points are in the
plane parallel to the projector/camera images. Thus,
one must not conclude, as may seem at the first glance
based solely on the previous Figure 2, that in planes
parallel to the projector-camera image plane there are
no notable changes in the AF values. Therefore, in the
case of a general scene it is reasonable to expect
points having different values for the angles α and β
not only at different depths D, but also within the
same depth D as well. In turn, a diverse set of AF
values is expected to be present. The fact is that
having point clouds reconstructed with the
significantly different precision values per individual
points may impair further processing on the point
cloud itself.
The natural question raises on how to improve the
depth precision for a desired portion of 3D points or
even for individual points. Examining the expression
(11) we notice the depth standard variation σ
D
is
controlled by several parameters. The one most
convenient to control is likely to be the value A
dictated by the strength of the illumination source.
Using the illumination source with an adjustable
illumination power over different portion of projector
images/patterns, such as in (Gupta, Yin, & Nayar,
Structured Light In Sunlight, 2013), it is possible to
relatively easily decrease or increase the value of A
during the scanning (pattern projection). In turn this
assures a seamless approach to directly impact the
depth standard variation σ
D
in the areas where needed.
Our proposed approach initially scans 3D scene
simply to get an estimate on AF values. This intial
scan is done in practice using the fewest number of
patterns possible since we just need a rough estimate
of AF values which does not require highly accurate
and precise 3D reconstruction. Afterward, the scene
de
p
th D increases
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
580
is re-scanned using the full set of patterns and with
the appropriate strengths of the illuminations across
the scene.
In attempt to verify the crucial part of our
approach we perform the following simulation. We
randomly sample M=100 points from the volume as
defined in Figure 2. Such point set will exhibit a
significantly different AF values. For each of these
3D points we estimate the depth standard variation σ
D
using the Monte Carlo simulation. That is, we assume
an additive Gaussian noise on the image values I
i
from Eq.(1), with noise variance equal to I
i
, and
generate such random noise values in order to
compute the phase φ from Eq.( 2). Knowing φ we can
eventually estimate noisy depth D. Repeating the
experiment a number of times (N=10000) for each
known 3D point, allows us to estimate directly the
depth standard deviation σ
D
. According to our theory
we expect to see a proportional relation between the
estimated depth standard deviation and the
corresponding AF of a certain point. In another
words, the ratios between the different depth standard
deviations σ
D
should be the same as the ratios of AF’s.
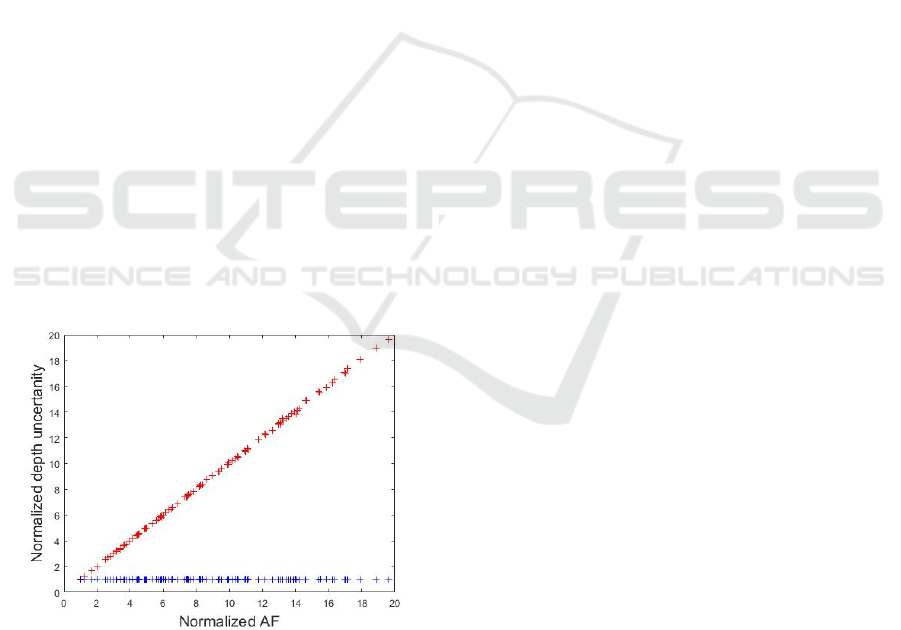
Following the above-mentioned simulation, Figure 5
presents on the vertical axis the estimated depth
standard deviations normalized to the smallest one in
the randomly chosen set of the above mentioned
M=100 points. On the horizontal axis the
corresponding AF’s are normalized to the AF of the
smallest estimated depth standard deviation. In Figure
5 emerges (almost) a straight diagonal (red) line
which confirms our predicted theory.
Figure 5: Diagonal (red) line: Verification of the
relationship between the depth precision and AF.
Horizontal (blue) line: After the proposed adjustment of
illuminations source strength, depth precision becomes
invariant w.r.t. AF.
Next, we look for the ratio of AF’s with the
respect to the point having the smallest (within
randomly chosen set of M=100 points) estimated
depth standard deviation and we aim to appropriately
increase the illuminations strength of all other points
in order to achieve the same depth precision. Thus,
we run another Monte Carlo simulation for estimation
of standard deviations, but this time with the suitably
increased value A for each of the remaining points.
Figure 5 shows a straight horizontal (blue) line
proving that after the proposed adjustment of the
illumination strength a depth precision (an estimated
depth standard variation) is uniform across all 3D
points, i.e. it is independent of the AF.
5 CONCLUSIONS
In this work we have proposed a method for scene
dependent 3D imaging aimed at improving the depth
precision at various 3D points in space. We have
begun by developing a theoretical framework
explaining the depth precision in 3D imaging system
based on the SL principle. Within this framework we
have identified several key factors determining a
depth precision, among which are the projector’s
angle of pattern projection and the camera’s angle of
imaging. We have proposed to analyze jointly the
influence of these two angles through a proposed
angle factor AF. Having established a clear
dependence of AF on the depth precision, we have
further proposed a simple approach to improve the
depth precision on the desired set of points, by
manipulating the strength of the illumination source.
The foreseen future work will include the
implementation and evaluation using the actual
hardware. In addition, we plan to consider the
improvement of depth precision using other factors
such as the number of phase shifts undertaken during
the phase shifting procedure.
ACKNOWLEDGEMENTS
This work has been supported in part by Croatian
Science Foundation under the project IP-2018-01-
8118, in part by the European Regional Development
Fund under the grant KK.01.1.1.01.0009
(DATACROSS) and in part by the Fulbright U.S.
Visiting Scholar Program.
Scene Adaptive Structured Light 3D Imaging
581

REFERENCES
Achar, S., Bartels, J. R., Whittaker, W. L., Kutulakos, K.
N., & Narasimhan, S. G. (2017). Epipolar time-of-flight
imaging. ACM Transactions on Graphics (TOG), 36(4),
371:1-37:8. doi:10.1145/3072959.3073686
Barsky, S., & Maria, P. (2003). The 4-Source Photometric
Stereo Technique for Three-Dimensional Surfaces in
the Presence of Highlights and Shadows. IEEE
Transactions on Pattern Analysis and Machine
Intelligence, 25(10), 1239-1252.
Bernhard, B., & Peter, S. (2008). Robust Optical Time-of-
Flight Range Imaging Based on Smart Pixel Structures.
IEEE Transactions on Circuits and Systems I, 55(6),
1512 - 1525.
Bouquet, G., Thorstensen, J., Bakke, K. A., & Risholm, P.
(2017). Design tool for TOF and SL based 3D cameras.
Optics Express, 25(22), 27758-27769. doi:10.1364/
OE.25.027758
Büttgen, B., Oggier, T., Lehmann, M., Kaufmann, R., &
Lustenberger, F. (2015). CCD/CMOS lock-in pixel for
range imaging: Challenges, Limitations and State-of-
the-Art. In In Proceedings of 1st Range Imaging
Research Day (pp. 21-32).
Chen, F., Brown, G., & Song, M. (2000). Overview of
three-dimensional shape measure- ment using optical
methods. Optical Engineering, 31(1), 10-22.
Foix, S., Alenya, G., & Torras, C. (2011). Lock-in Time-of-
Flight (ToF) Cameras: A Survey. 11(3), IEEE Sensors
Journal. doi:10.1109/JSEN.2010.2101060
Fusiello, A., Trucco, E., & Verri, A. (2000). A Compact
Algorithm for Rectification of Stereo Pairs. Machine
Vision and Applications, 12(1), 16-12. doi:doi.org/
10.1007/s001380050
Geng, J. (2011). Structured-light 3D surface imaging: a
tutorial. Advances in Optics and Photonics, 3(2), 128-
160. doi:doi.org/10.1364/AOP.3.000128
Gupta, M., & Nakhate, N. (2018). A Geometric Perspective
on Structured Light Coding. European Conference on
Computer Vision (pp. 90-107). Munich: Springer,
Cham. doi:10.1007/978-3-030-01270-0_6
Gupta, M., Yin, Q., & Nayar, S. K. (2013). Structured Light
In Sunlight. IEEE International Conference on
Computer Vision (ICCV), (pp. 1-8). Sydney.
Hansard, M., Lee, S. L., Choi, O. C., & Horaud, R. (2012).
Time of Flight Cameras: Principles, Methods, and
Applications. London: Springer. doi:10.1007/978-1-
4471-4658-2
Horaud, R., Hansard, M., Evangelidis, G., & Ménier, C.
(2016). An Overview of Depth Cameras and Range
Scanners Based on Time-of-Flight Technologies. (S.
Verlag, Ed.) Machine Vision and Applications, 27(7),
1005-1020. doi:10.1007/s00138-016-0784-4
Horn, E., & Kiryati, N. (1997). Toward optimal structured
light patterns. Proceedings. International Conference
on Recent Advances in 3-D Digital Imaging and
Modeling (pp. 28-35). Ottawa: IEEE. doi:10.1109/
IM.1997.603845
Jia, T., Wang, B., Zhou, Z., & Meng, H. (2016). Scene
depth perception based on omnidirectional structured
light. IEEE Transactions on Image Processing, 25(9),
4369 - 4378. doi:10.1109/TIP.2016.2590304
Lange, R., & Seitz, P. (2001). Solid-State Time-of-Flight
Range Camera. IEEE Journal of Quantum Electronics,
37(3), 390-397. doi:10.1109/3.910448
Liu, J., & Li, Y. (2014). Performance analysis of 3-D shape
measurement algorithm with a short baseline projector-
camera system. Robotics and Biomimetics, 1-10.
doi:doi.org/10.1186/s40638-014-0001-8
Mirdehghan, P., Chen, W., & Kutulakos, K. N. (2018).
Optimal Structured Light a la Carte. Computer Vision
and Pattern Recognition (CVPR, (pp. 6248-6257). Salt
Lake City. doi:10.1109/CVPR.2018.00654
Petković, T., Pribanić, T., & Đonlić, M. (2016). Single-Shot
Dense 3D Reconstruction Using Self-Equalizing De
Bruijn Sequence. IEEE Transactions on Image
Processing, 25(11), 5131-5144. doi:10.1109/TIP.2016.
2603231
Petković, T., Pribanić, T., & Đonlić, M. (2017). Efficient
Separation between Projected Patterns for Multiple
Projector 3D People Scanning. International
Conference on Computer Vision (ICCV): Workshop on
Capturing and Modeling Human Bodies, Faces and
Hands., (pp. 815-823). Venice.
Salvi, J., Fernandez, S., Pribanic, T., & Xavier, L. (2010).
A state of the art in structured light patterns for surface
profilometry. Pattern Recognition, 43(8), 2666-2680.
doi:doi.org/10.1016/j.patcog.2010.03.004
Saragadam, V., Wang, J., Gupta, M., & Nayar, S. (2019).
Micro-Baseline Structured Light. International
Conference on Computer Vision (ICCV), (str. 4049-
4058). Seoul.
Whyte, R. Z., Payne, A. D., Dorrington, A. A., & Cree, M.
J. (2010). Multiple range imaging camera operation
with minimal performance impact. IS&T/SPIE
Electronic Imaging, 7538, pp. 75380I-1-10. San Jose.
doi:10.1117/12.838271
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
582
