
Towards Keypoint Guided Self-supervised Depth Estimation
Kristijan Bartol
1 a
, David Bojani
´
c
1 b
, Tomislav Petkovi
´
c
1 c
, Tomislav Pribani
´
c
1 d
and Yago Diez Donoso
2 e
1
University of Zagreb, Faculty of Electrical Engineering and Computing, Zagreb, Croatia
2
Yamagata University, Faculty of Science, Yamagata, Japan
Keywords:
Monocular Depth Estimation, Self-supervised Learning, Keypoint Similarity Loss.
Abstract:
This paper proposes to use keypoints as a self-supervision clue for learning depth map estimation from a
collection of input images. As ground truth depth from real images is difficult to obtain, there are many
unsupervised and self-supervised approaches to depth estimation that have been proposed. Most of these
unsupervised approaches use depth map and ego-motion estimations to reproject the pixels from the current
image into the adjacent image from the image collection. Depth and ego-motion estimations are evaluated
based on pixel intensity differences between the correspondent original and reprojected pixels. Instead of
reprojecting the individual pixels, we propose to first select image keypoints in both images and then reproject
and compare the correspondent keypoints of the two images. The keypoints should describe the distinctive
image features well. By learning a deep model with and without the keypoint extraction technique, we show
that using the keypoints improve the depth estimation learning. We also propose some future directions for
keypoint-guided learning of structure-from-motion problems.
1 INTRODUCTION
Monocular depth estimation is a long-standing, ill-
posed computer vision problem. A depth map esti-
mated from a monocular image describes an infinite
amount of scenes due to the scale ambiguity. Never-
theless, monocular depth estimation is a very popular
topic, especially in the deep learning era. A partic-
ularly interesting approach is the joint, unsupervised
learning of monocular depth and pose (Garg et al.,
2016). The model has two convolutional networks,
one which outputs a depth map and one which outputs
the transformation matrices representing pose trans-
formations between the target and the source views
(Figure 1). Assuming the intrinsic matrix is known,
depth and pose estimations are sufficient to reproject
the pixels from the source views to the target view
(Hartley and Zisserman, 2003). The sum of differ-
ences between the original (target) and the reprojected
(source) pixel intensities is called a photometric loss.
a
https://orcid.org/0000-0003-2806-5140
b
https://orcid.org/0000-0002-2400-0625
c
https://orcid.org/0000-0002-3054-002X
d
https://orcid.org/0000-0002-5415-3630
e
https://orcid.org/0000-0003-4521-9113
The supervision clue in case of unsupervised
learning comes from time component between the im-
ages in a collection. The idea of the photometric
loss is to learn to warp the source image to match
with the target image. Another way to look at this
is that the photometric loss is used to learn the model
to find the correct pixel correspondences between the
images. Of course, pixel intensities are not unique,
so even though the correspondent pixel intensities are
the same, it does not guarantee that they are truly cor-
respondent. For example, the pixels of the white wall
will perfectly match, even though they might not be
correspondent in 3D.
There are many ways to cope with the correspon-
dence problem. Unsupervised depth estimation mod-
els like (Mahjourian et al., 2017) estimate depth maps
on multiple scales. The pixel on a lower scale is
aggregated from the square of pixels on the original
scale. It is therefore expected that the lower scale
pixels will match better in case of low or repeating
textures. In classical structure-from-motion, for ex-
ample, in COLMAP (Sch
¨
onberger and Frahm, 2016),
the correspondences are found by matching the se-
lected image keypoints. Our proposal is therefore to
select and reproject the keypoints from the source to
the target images and then compare these keypoints
Bartol, K., Bojani
´
c, D., Petkovi
´
c, T., Pribani
´
c, T. and Donoso, Y.
Towards Keypoint Guided Self-Supervised Depth Estimation.
DOI: 10.5220/0009190005830589
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
583-589
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
583
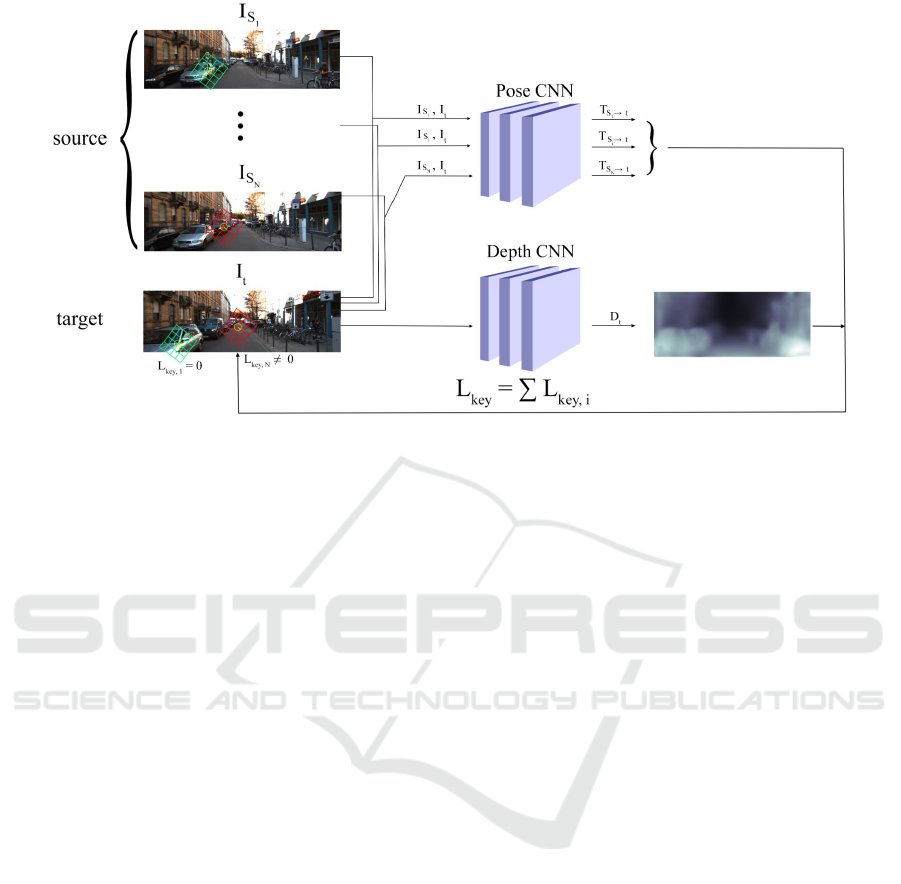
Figure 1: Overview of the model. The model contains separate depth and pose networks that jointly learn as in (Garg et al.,
2016) and (Mahjourian et al., 2017). Instead of source images’ pixels, the keypoints of the source images are reprojected to
the target image. The keypoints shown in green is the correct reprojection and the keypoints in red is the incorrect one. Note
that the reprojection is done for all the source-target image pairs separately.
to determine their similarity. If the values are similar,
it means that the keypoints of both images are proba-
bly representing the same part of the 3D scene, so the
loss function value should be low, and vice versa. To
the best of our knowledge, the keypoints have not yet
been utilitized for learning structure-from-motion.
We use SIFT keypoint descriptors by (Lowe,
2004) to compare the original and the reconstructed
image. Keypoints have many beneficial properties.
First, they preserve and enforce distinctiveness of im-
age regions. In (Bojani
´
c et al., 2019), it is shown
that the SIFT descriptors are still among the best op-
tions in state-of-the-art of keypoint descriptors. Sec-
ond, the selected keypoints are expected to be more
important and informative than other image regions.
Third, SIFT keypoints are assigned varying sizes that
are, in general, reversely proportional to the poten-
tial information in the pixel neighbourhood. For ex-
ample, low texture region might be assigned a large
sized keypoint whose boundary reaches some distinc-
tive edges, also making this low texture region more
distinctive, carrying greater information. Large sized
keypoint regions offer an elegant solution to handling
low or repeating texture areas compared to multi-scale
depth estimation. Finally, by selecting the keypoints,
the model also ignores the regions that are not ben-
eficial, for example, very large textureless areas like
sky, road or walls. Learning models like (Mahjourian
et al., 2017) cope with this by learning the explain-
ability mask that assigns weights to each pixel based
on their estimated importance.
The aim of this work is to show that using the
keypoints provide a beneficial clue for self-supervised
learning of depth estimation. To summarize, we pro-
pose a keypoint similarity loss between the original
and the reprojected image keypoints as an improve-
ment to the unsupervised loss components’ stack and
as a replacement for the explainability mask loss and
multi-scale depth map estimation.
2 RELATED WORK
There is a lot of work dedicated to depth estimation.
In this section we will give a brief overview over the
recent attempts which are mostly focused on deep
learning.
Unsupervised Structure-from-motion. The pio-
neering unsupervised learning of monocular depth es-
timation work is done by (Garg et al., 2016). The
authors propose an image warping technique, the
same as the one used in this work. They also pro-
pose a smooth loss function that minimizes the dif-
ferences between the neighbouring values of an es-
timated depth map. It is shown that smoothing the
depth map greatly improves the estimation accuracy
and serves as a regularization for the photometric loss.
Instead of using time as a supervision clue, they use a
stereo pair and compare between the real and the re-
constructed image. A similar approach is proposed by
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
584

Figure 2: The keypoint similarity loss. The selected keypoint on the left (source) image is reprojected to the right (target)
image using the depth and pose estimations. The red keypoint indicates that the reprojection is incorrect. The difference
between the keypoint descriptors is labeled as L
key,i
and is a keypoint similarity loss for a given pair of keypoints.
(Godard et al., 2016) to enable left-right consistency
check.
A model by (Mahjourian et al., 2017) learns to
predict both the depth map and pose estimations be-
tween the views, exploiting the time component, as
done in this paper. The photometric loss uses the im-
age warping technique and compares the target image
with its reconstructions sampled from the source im-
ages. The model architecture is composed of depth
and pose estimation networks which are coupled dur-
ing training as shown in Figure 1, but which can be
applied independently in test time. They also propose
to learn the explainability mask whose goal is learn-
ing to ignore the parts of the image that might degrade
the photometric loss performance. For example, oc-
cluded or moving objects are ideally ignored using the
explainability mask. Finally, they output depth maps
on multiple scales to enable pixels of smaller scale to
see larger patches of the original image and in that
way cope with low textured regions.
The authors of (Godard et al., 2018) improve the
depth estimation results by focusing on the pose es-
timation network. The authors propose to share the
encoder weights between the depth and pose network.
Also, they use the improved, edge-aware smooth loss
that accounts less for the differences between the
neighbouring depth map values if their correspond-
ing, original image difference is also higher. Instead
of directly utilizing the depth maps on smaller scale,
they simply upscale these depth maps to the origi-
nal image size and then apply the photometric error,
which is shown to reduce the texture-copy artifacts.
That way they improve on the multi-scale depth map
estimation.
Keypoint Similarity. LF-Net (Ono et al., 2018) is
a self-supervised model for learning keypoint detec-
tion and description. Similar to us, they also use
SIFT keypoints. On top of the keypoints supervi-
sion, SfM algorithm is used to estimate the transfor-
mations between the image pairs so that the LF-Net
model is not directly supervised by SIFT (otherwise,
it would perform as SIFT at best). The model predicts
the keypoints for the reference image and then these
keypoints are transformed to the ground truth image
where the detections and the corresponding descrip-
tions are compared. The difference between LF-Net
and our proposal is that LF-Net uses SIFT and SfM
self-supervision to learn to generate keypoints. Our
model directly uses SIFT keypoints to learn SfM, i.e.,
the keypoints help the model to verify the keypoint
correspondence, which is the core problem in SfM
(Furukawa and Hern
´
andez, 2015). We further reflect
on LF-Net in section 5.
3 KEYPOINT SIMILARITY LOSS
Let I
t
denote a target image, I
s
i
one of the source
images, D
t
a depth map estimated for the target im-
age, matrix K the camera intrinsics and T
s
i
→t
a rigid
transformation between the views (pose). The stan-
dard photometric loss evaluates the depth estimation
of the target view, D
t
, by measuring how well the
pixels from the source image reproject to the target
image. Precisely, I
t
is reconstructed by warping I
s
i
based on D
t
and T
s
i
→t
:
ˆ
I
ij
t
= I
uv
s
i
= I
u
∗
v
∗
s
i
= KT
s
i
→t
(D
ij
t
K
−1
I
ij
s
i
), (1)
where
ˆ
I
ij
t
is the reconstructed target image sam-
pled from the image I
s
i
in the coordinates (u, v) →
I
uv
s
i
. Note that the pixel (i, j) reprojects to the sub-
pixel (u
∗
, v
∗
). To assign the exact (u, v) pixel’s in-
tensity, the (u
∗
, v
∗
) subpixel reprojection is used to
sample the four closest pixel intensities using bilin-
ear interpolation. The difference between the pixel
intensities of the original image I
t
and of the recon-
structed image
ˆ
I
t
is the photometric loss L
photo
=
Towards Keypoint Guided Self-Supervised Depth Estimation
585

Figure 3: The keypoints are precomputed in every pixel location. The green keypoints represent the keypoints selected by the
detector. The keypoints have predefined sizes and orientations.
P
ij
||
ˆ
I
ij
t
− I
ij
t
||
1
. Instead of reprojecting and com-
paring all the pixel intensities, we propose to only re-
project and compare the keypoints selected by SIFT.
The overview of the proposal is shown in Figure 1.
Let K
k
s
i
denote k-th keypoint in the source image
and K
k
t
its correspondent keypoint in the target im-
age (Figure 2). We define the keypoint similarity loss
function between the two images I
t
and I
s
i
as a sum
over the differences between the correspondent key-
point vectors:
L
key,i
=
X
k
X
l
||K
k
t
(l) − K
k
s
i
(l)||
1
, (2)
where k represents k-th keypoint of the source im-
age I
s
i
and l ∈ 1...128 the index of an element in
the k-th SIFT keypoint vector. For the source key-
point K
s
i
and its perfectly reprojected, corresponding
counterpart K
k
g t
, the loss should be zero (Figure 2).
The total keypoint similarity loss is the sum of key-
point similarity losses for all the source-target image
pairs, L
key
=
P
i
L
key,i
.
For the experimental purposes, we also use other
loss components previously proposed and used by
(Mahjourian et al., 2017), (Godard et al., 2018), etc.,
for example, smooth loss and explainability mask
loss. When all these components are included, our
loss function looks like:
L = αL
key
+ βL
photo
+ γL
smooth
+ δL
expl
, (3)
where α, β, γ and δ are the loss hyperparameters
that balance the dynamics between the loss compo-
nents. The best hyperparameter values determined by
the experiments are: α = 2.0, β = 1.0, γ = 0.5 and
δ = 0.2.
4 EXPERIMENTS
The purpose of the experiments is to provide a step to-
wards the keypoint guided self-supervision for learn-
ing depth estimation. For this purpose, we choose
the KITTI dataset (Geiger et al., 2013) and the model
based on (Mahjourian et al., 2017), but the similar ap-
proach can be applied to other structure-from-motion
environments and datasets. Instead of using the orig-
inal smooth loss, we use the improved, edge-aware
smoothness from (Godard et al., 2016). To enable the
keypoint similarity loss, we add it as a loss compo-
nent, based on the Eq. 2 from section 3.
The SIFT keypoints are precomputed in every
pixel (Figure 3), for two reasons. First, by precom-
puting the keypoints in all the pixel locations (i, j),
we make sure that the keypoint reprojections in (u, v)
will have its correspondent pair, for every (u, v) in-
side the image boundaries. Second, by precomput-
ing the keypoints in every pixel, we are able to test
two different approaches - learning with and without
the keypoint selection mechanism. In case learning is
done without the keypoint detector, keypoints calcu-
lated from every source image pixel’s neighbourhood
reproject to the target image, which boils down to us-
ing keypoint descriptions instead of pixel intensities
as a supervision clue.
When using the keypoint detector, the gradients
in backward pass are applied only on the selected
keypoints and the rest are masked as shown in Fig-
ure 3. As expected, we show that keypoint detection
improves learning, compared to the model that does
not select the keypoints. We explain this by the fact
that the SIFT descriptions of the keypoints are simply
better for the selected keypoints, but it also indicates
that the selectivity increases the quality of the back-
ward passed gradients. To compute the keypoint for a
specific pixel location (i, j), the orientation and patch
size need to be specified upfront by hand. We choose
to provide zero angled orientations and the patches of
size 15x15.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
586

Table 1: Quantitative comparison of the experimental results. The first column displays the experiments’ names. The second
and third show absolute relative and squared relative error (the lower the better). The last three columns show the accuracy
metrics, where δ denotes the ratio between the estimates and the ground truth (the higher the better). The first part of the table
shows the results obtained when keypoint similarity loss was used.
Experiment / Metric Abs Rel Sq Rel δ < 1.25 δ < 1.25
2
δ < 1.25
3
No det + expl (ours) 0.309 3.813 0.603 0.818 0.912
Det + expl (ours) 0.284 3.275 0.620 0.822 0.914
No det + no expl (ours) 0.282 3.160 0.605 0.815 0.911
Det + no expl (ours) 0.277 3.275 0.633 0.829 0.917
SfMLearner 0.286 3.072 0.629 0.829 0.916
SfMLearner (full) 0.181 1.341 0.733 0.901 0.964
4.1 Quantitative Comparison
The first row of the Table 1 shows the used metrics’
names. The first part of the table shows the results
of four of our different experiments and the second
part shows the results of the base model (without the
keypoint similarity loss). The four experiments are
done by learning the model with and without the key-
point detector and with and without the explainability
mask.
Looking at the first part of the Table 1, it is shown
that the model learn better without the explainabil-
ity mask. As expected, the more selective mod-
els (the ones in third and fifth row of the table) are
shown to learn better than their non-selective counter-
parts (second and fourth row). Our selective keypoint
model without the explainability mask slightly out-
performs SfMLearner. This is an indication that key-
point guidance help to improve the overall learning
performance. The last row shows the results reported
by (Mahjourian et al., 2017) after training on KITTI
and fine-tuning on Cityscapes dataset (Cordts et al.,
2016). Even though we outperform the base model
using the keypoint similarity loss, the model needs to
be further fine-tuned to reach the results in the last
row of Table 1.
4.2 Qualitative Comparison
The overview of the qualitative results is shown in the
Figure 4 where the first column shows the input im-
ages and the rest of the columns follow the second to
sixth row of the Table 1. The fifth column contains
the sharpest depth maps which corresponds with the
quantitative results. Interestingly, the three people are
most precisely reconstructed in the fourth row, when
the keypoint selection was not used. Comparing the
depth maps the models using the explainability mask
with the ones not using it (first part of the qualita-
tive results with the second), we confirm the quanti-
tative results. The results from the models not using
explainability mask are generally sharper and more
precise and than the ones using the explainability. Fi-
nally, the last column is worse than the fifth column,
both in terms of precision and sharpness. Moreover,
the three people are not clearly visible at all in the last
column.
4.3 Implementation Details
The model is an extension of the PyTorch (Paszke
et al., 2019) implementation of SfMLearner by
(Mahjourian et al., 2017). Our experiments were run
on a single NVidia GeForce RTX 2080 GPU, 12GB
VRAM. SIFT keypoints generated from the KITTI
dataset are stored using about 400GB of HDD. We
only generated SIFT patches of size 15x15 and it
took around 40 hours on Intel(R) Core(TM) i7-8700K
CPU @ 3.70GHz. For larger sizes, it takes even more
time. Hard disk reads are the implementation bot-
tleneck which prevented us from running more than
20 training epochs of batch size 4 in the learning ex-
periments. There are multiple ways to cope with the
latter problem. One is to generate compressed SIFT
descriptors to reduce the overall dataset size. Another
way is to use a GPU implementation of SIFT com-
piled as PyTorch node and the SIFT keypoints can
then be calculated on-demand. However, the com-
pression takes even more time to generate the descrip-
tors. We therefore aim for the second improvement.
4.4 Other Experiments
An interesting question is whether the keypoint simi-
larity loss could be used alone, with all the other loss
function components’ weights set to zero. We ran the
experiment with and without the smooth loss com-
ponent. When run with the smooth loss component,
the produced depth maps after an epoch of learning
are completely smooth, which means that the model
have converged too early. In this case, the smooth-
ness loss was too dominant over the keypoint simi-
larity loss, which might be mitigated by lowering the
smooth weight hyperparameter. However, when the
Towards Keypoint Guided Self-Supervised Depth Estimation
587

Figure 4: The overview of the qualitative results. The three input images (in the first column) are randomly selected from the
KITTI dataset.
smoothness loss was completely turned off, the model
was unable to significantly move from the starting
point. All this suggests that the keypoint similarity
loss in this form can not be solely used as a loss func-
tion. Surprisingly, multi-scale depth estimation did
not outperform its single-scale counterpart so we do
not mention it in the analysis.
5 FUTURE WORK
The mandatory step towards reaching state-of-the-art
results is further model fine-tuning. It is also worth
examining SIFT’s parameters further. The most im-
portant parameter for the experiments is the size of the
keypoint. By using larger patches, low or repeating
texture image regions should be learned better. In the
experiments, it is shown that the keypoint guided self-
supervision replaces the explainability mask. Larger
keypoint patches might also serve as an elegant re-
placement for multi-scale depth map estimations. Ide-
ally, we will wrap SIFT as a computational node,
which would enable SIFT to choose the size an ori-
entation of keypoints itself.
However, all these approaches largely depend on,
and are limited by, the SIFT performance. Taking a
step further, it seems reasonable to try a joint learning
of image keypoints and depth estimation in a similar,
self-supervised learning fashion.
5.1 Learning the Keypoints
Encouraged by LF-Net presented in (Ono et al.,
2018), we plan to learn the keypoints instead of di-
rectly using the ones selected and described by SIFT.
The keypoints learning model should implicitly cap-
ture the depth properties of a scene. We propose the
following high-level pipeline:
• Select and describe N SIFT keypoints for every
source image.
• Use the keypoints network to find N keypoints on
the target image.
• Reproject the estimated target image keypoints to
the source images based on depth (and pose) esti-
mation.
• Assign the correspondent source image keypoint
to every reprojected target keypoint reprojected
and compare them.
Note that the correspondences now need to be
determined, because they not known upfront. This
makes the task much harder, so we decide to sim-
plify it by using the pose ground truths. The dataset
in which the camera parameters are known is, for ex-
ample, an InteriorNet by (Li et al., 2018). The subset
of structure-from-motion problems where the camera
parameters are known is called a multi-view-stereo
or MVS (Furukawa and Hern
´
andez, 2015) and it is
a possible future direction for joint learning of geom-
etry and keypoints.
6 CONCLUSION
The aim of our work is to propose a step towards key-
point guided learning of depth estimation. The model
performance is still not on the state-of-the-art level
on KITTI dataset, but the experimental results sug-
gest that the presented approach improves the learn-
ing. The future goals are to wrap SIFT as a PyTorch
node and try learning joint keypoint and depth estima-
tion, completely removing the SIFT dependency. To
make the joint learning of depth and keypoints easier,
we propose to learn under camera parameters semi-
supervision, i.e., in a multi-view-stereo configuration.
ACKNOWLEDGEMENT
This work has been supported by Croatian Sci-
ence Foundation under the grant number HRZZ-
IP-2018-01-8118 (STEAM) and by European Re-
gional Development Fund under the grant number
KK.01.1.1.01.0009 (DATACROSS).
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
588

REFERENCES
Bojani
´
c, D., Bartol, K., Pribani
´
c, T., Petkovi
´
c, T., Donoso,
Y. D., and Mas, J. S. (2019). On the comparison
of classic and deep keypoint detector and descriptor
methods. 11th Int’l Symposium on Image and Signal
Processing and Analysis.
Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler,
M., Benenson, R., Franke, U., Roth, S., and Schiele,
B. (2016). The cityscapes dataset for semantic urban
scene understanding. CoRR, abs/1604.01685.
Furukawa, Y. and Hern
´
andez, C. (2015). Multi-view stereo:
A tutorial. Foundations and Trends in Computer
Graphics and Vision.
Garg, R., G, V. K. B., and Reid, I. D. (2016). Unsupervised
CNN for single view depth estimation: Geometry to
the rescue. CoRR, abs/1603.04992.
Geiger, A., Lenz, P., Stiller, C., and Urtasun, R. (2013).
Vision meets robotics: The kitti dataset. I. J. Robotic
Res., 32(11):1231–1237.
Godard, C., Aodha, O. M., Firman, M., and Brostow, G.
(2018). Digging into self-supervised monocular depth
estimation. The International Conference on Com-
puter Vision (ICCV).
Godard, C., Mac Aodha, O., and Brostow, G. J. (2016). Un-
supervised monocular depth estimation with left-right
consistency. CoRR, abs/1609.03677.
Hartley, R. and Zisserman, A. (2003). Multiple View Geom-
etry in Computer Vision. Cambridge University Press,
USA, 2 edition.
Li, W., Saeedi, S., McCormac, J., Clark, R., Tzoumanikas,
D., Ye, Q., Huang, Y., Tang, R., and Leutenegger, S.
(2018). Interiornet: Mega-scale multi-sensor photo-
realistic indoor scenes dataset. In British Machine Vi-
sion Conference (BMVC).
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision.
Mahjourian, R., Wicke, M., and Jun, C. (2017). Unsuper-
vised learning of depth and ego-motion from video.
CVPR.
Ono, Y., Trulls, E., Fua, P., and Yi, K. M. (2018). Lf-
net: Learning local features from images. CoRR,
abs/1805.09662.
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,
Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,
Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-
Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,
Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).
Pytorch: An imperative style, high-performance deep
learning library. In Wallach, H., Larochelle, H.,
Beygelzimer, A., d'Alch
´
e-Buc, F., Fox, E., and Gar-
nett, R., editors, Advances in Neural Information Pro-
cessing Systems 32, pages 8024–8035. Curran Asso-
ciates, Inc.
Sch
¨
onberger, J. L. and Frahm, J.-M. (2016). Structure-
from-motion revisited. 2016 IEEE Conference on
Computer Vision and Pattern Recognition (CVPR),
pages 4104–4113.
Towards Keypoint Guided Self-Supervised Depth Estimation
589
