
Segmentation and Visualization of Crowd Flows in Videos using Hybrid
Force Model
Shreetam Behera
1
, Debi Prosad Dogra
1
, Malay Kumar Bandyopadhyay
2
and Partha Pratim Roy
3
1
School of Electrical Sciences, Indian Institute of Technology Bhubaneswar, Odisha, India
2
School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Odisha, India
3
Department of Computer Science and Engineering, Indian Institute of Technology Roorkee, Uttarakhand, India
Keywords:
Crowd Flow, Smooth Particle Hydrodynamics, Langevin Equation, Crowd Phenomena, Crowd Behavior,
Crowd Flow Segmentation.
Abstract:
Understanding crowd phenomena is a challenging task. It can help to monitor crowds to prevent unwanted
incidents. Crowd flow is one of the most important phenomena that describes the motion of people in crowded
scenarios. Crowd flow analysis is popular among the computer vision researchers as this can be used to
describe the behavior of the crowd. In this paper, a hybrid model is proposed to understand the flows in
densely crowded videos. The proposed method uses the Smooth Particle Hydrodynamics (SPH)-based method
guided by the Langevin-based force model for the segmentation of linear as well as non-linear flows in crowd
gatherings. SPH-based model identifies the coherent motion groups. Their behavior is then analyzed using
the Langevin equation guided force model to segment dominant flows. The proposed method, based on the
hybrid force model, has been evaluated on public video datasets. It has been observed that the proposed hybrid
scheme is able to segment linear as well as non-linear flows with accuracy as high as 91.23%, which is 4-5%
better than existing crowd flow segmentation algorithms. Also, our proposed method’s execution time is better
than the existing techniques.
1 INTRODUCTION
In the last few decades, many researchers have put
their interests in understanding collective motion be-
havior and analysis. Analyzing collective motion can
help understand human behavior in groups in the con-
text of visual surveillance. Understanding crowd be-
havior can help develop systems for monitoring and
managing people in crowded scenarios. According
to (Junior et al., 2010), computer vision-based tech-
niques are highly popular for such surveillance pur-
poses. Automation of visual surveillance can results
in efficient crowd monitoring and management with
higher accuracy, better information fusion, and, most
importantly, reduction in human efforts to a greater
extent. Automated visual surveillance-based systems
can be used for identifying unusual behavior or activ-
ity in the crowd. This feature can help law-enforcing
bodies to plan and take the necessary steps to avoid
undesirable incidents.
In developing automatic crowd surveillance sys-
tems, flow detection, and segmentation are two in-
strumental elements in understanding crowd move-
ments. According to (Zhang et al., 2018), crowd flows
can be found using physical modeling-based meth-
ods or signal processing and machine learning-based
methods. Physical modeling-based methods can be
physics-based or particle-based techniques. These
methods consider the crowd as fluid or system and
process similar movement patterns contained within
the flows.
In (Ali and Shah, 2007), Lagrange particle dynam-
ics have been used to segment crowd flows. The au-
thors have also done a stability analysis of the seg-
mented crowd flows. However, their method is com-
putationally intensive. The authors in (Ali and Shah,
2008) have proposed a force model based on static,
dynamic, and boundary floor fields of the crowd.
However, the method is sensitive to camera shake.
Zhang et al. in (Zhang et al., 2017) have developed
a streak-lines-based model to describe high-density
crowd behaviors. In (Wu et al., 2017), bi-linear inter-
action of curl and divergence of the flows are analyzed
for understanding crowd behaviors. The method pro-
posed in (Lim et al., 2014) detects temporal flow vari-
ations in the crowd. In (Su et al., 2013), a spatio-
Behera, S., Dogra, D., Bandyopadhyay, M. and Roy, P.
Segmentation and Visualization of Crowd Flows in Videos using Hybrid Force Model.
DOI: 10.5220/0009328708610867
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
861-867
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
861

temporal viscous fluid field-based technique has been
proposed to recognize the large-scale crowd behav-
ior from appearance and driven factor perspectives.
An agent-based simulation method to monitor crowd
density has been mentioned in (Basak and Gupta,
2017). Mehran et al. (Mehran et al., 2010) com-
bined social force graph technique and streaklines
to understand crowd flows in a video. In (Zhang
et al., 2015), the social attributes-aware force model
has been used for analyzing crowd movements. The
social force model, in terms of attractive and repul-
sive forces, is used for crowd analysis in (Andrade
and Fisher, 2005). A hybrid social influence model
(HSIM) proposed in (Ullah et al., 2018) segments
pedestrian motion in crowds. In (Lin et al., 2013), a
heat map-based method has been proposed to under-
stand group activities in crowd videos. Smooth Par-
ticle Hydrodynamics-based model, along with multi-
layer spectral clustering, has been proposed to under-
stand and detect coherent regions in density varying
crowd scenarios in (Ullah et al., 2017). However, the
method doesn’t perform finer-level crowd flow seg-
mentation.
None of the aforementioned addresses flow seg-
mentation in terms of randomness in the crowd. Also,
there is no such method that addresses the crowd in
terms of hydrodynamics and random particles. This
has been the primary motivation behind the work pro-
posed in this paper. In this paper, a hybrid model is
proposed for crowd flow segmentation. This hybrid
model consists of two parts. The first part presents
a Smooth Particle Hydrodynamics-based model that
segments out the initial coherent regions, followed by
a Langevin-theory guided force model that segments
crowd flows irrespective of the randomness present in
the system.
The paper is organized as follows. In Section 2,
we explain the proposed hybrid force model and the
relevant foundations. In Section 3, we present the out-
puts of the proposed model evaluated on two video
datasets. Conclusion and Future directions are pre-
sented in Section 4.
2 PROPOSED HYBRID MODEL
In this section, we present the proposed hybrid model
to segment motion flows in dense crowd videos.
Crowd flow movements in videos can be represented
analogously to fluid particles moving with different
velocities in the fluid. While their movement, the
particles experience different forces due to viscosity
of the fluid, hydrodynamic interactions, and random
events occurring within the fluid. In (Ullah et al.,
2017), the authors have modeled coherency regions
in the crowd. However, the model doesn’t address
the randomness in the crowd and only accounts for
interactions similar to hydrodynamics interactions.
The proposed hybrid model is a combination of two
models, as illustrated in Figure 1. The first part of
the model is based on Smooth Particle Hydrodynam-
ics, which is used for coherence motion detection in
videos. The coherent regions provide initial segmen-
tation information that is then fed to the Langevin-
based force model. This forms the second part of the
hybrid system for performing crowd flow segmenta-
tion and accounts for the randomness in the crowd.
As a result, both hydrodynamics and random behav-
ior of motion particles are maintained in the proposed
hybrid model.
Figure 1: Block diagram representation of the proposed hy-
brid crowd flow segmentation model.
2.1 Smooth Particle Hydrodynamics
Guided Grouping
Smooth-particle hydrodynamics (SPH) is a compu-
tational fluid dynamics method used for understand-
ing fluid flows (Monaghan, 1992). It is a mesh-free
method that does not need a mesh for spatial deriva-
tive calculations. A set of ordinary differential equa-
tions can describe the equations of momentum and
energy of the fluid particles. According to the Navier-
Stokes equation, the movement of fluid particles is
guided by the force model presented in (1),
dv
dt
= − ∇P + ρg + µ∇
2
V (1)
where ∇, P, ρ, g, µ, and V are derivative operator,
pressure, density, acceleration, viscosity, and velocity,
respectively.
The first term of (1) represents pressure force
(F
pressure
), the second term (F
external
) represents exter-
nal force due to other particles in the fluid and the
third term represents viscosity force (F
viscosity
). In
a more generalization form, the equation (1) can be
written as (2),
dv
dt
= F
pressure
+ F
external
+ F
viscosity
(2)
where
F
pressure
= m
∑
i,N
K(r
c
− r
i
,λ) (3)
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
862

F
external
= m
∑
i,N
∇K(r
c
− r
i
,λ) (4)
F
viscosity
= m
∑
i,N
γv∇
2
K(r
c
− r
i
,λ) (5)
In the above equations, m represents the mass of
the particle, v is the average velocity of the particle
with respect to its neighboring particles, N represents
the neighboring particles (r
1
, ..., r
N
) surrounding the
central particle r
c
and γ is the viscosity coefficient.
K(r
c
− r
i
,λ) is the smoothed kernel function that de-
scribes the physical properties of the central particle
(r
c
) by considering the relevant properties of the par-
ticles (r
i
) falling in the range of the kernel. Here,
the distance and density are considered as the rele-
vant properties of the particles. Mathematically, the
kernel function is represented using (6),
K(r
c
−r
i
,λ) =
|
K
t
(r
c
− r
i
,λ) − K
t−1
(r
c
− r
i
,λ)
|
(6)
where λ is the set of neighboring particles influencing
r
c
. The term K
t
(r
c
− r
i
,λ) signifies the influence of
the center particle r
c
with the neighboring particles at
time instant t.
K
t
(r
c
− r
i
,λ) =
315
64π(λ)
9
((λ)
2
−
k
r
c
− r
i
k
2
)
3
(7)
By rearranging (2), a hydrodynamics-based magni-
tude represented in (8) can be obtained which is used
for segregating the fluid particles with similar proper-
ties representing the group coherency among the par-
ticles.
Hydrodynamics
mag
= (
F
external
F
pressure
+
F
viscosity
F
pressure
)K (8)
2.2 Langevin Theory Guided Force
Model
In physics, the Langevin equation is used to de-
scribe the dynamics of a Brownian particle (Langevin,
1908; Coffey and Kalmykov, 2004). According to
(Schweitzer, 2007), the motion of the Brownian par-
ticle can be described as a combination of forces that
are represented in (9).
m
i
¨
−→
r
i
= −γ
˙
−→
r
i
+
−→
F
i
+
−→
R
i
(t) (9)
where m
i
is the mass of the particle,
−→
r
i
is the position
of the particle,
˙
−→
r
i
represents the velocity of the par-
ticle,
¨
−→
r
i
is the acceleration acting upon the particle,
−γ
˙
−→
r
i
is the drag force responsible for removing force
caused due to friction with γ as the viscosity coeffi-
cient (satisfying
K
B
T
D
), F
i
is the force exerted on the
i
th
particle, and R
i
(t) is the random force describes
the randomness of the particle and it should satisfy
(10). The above equation (9) holds good for passive
systems with Brownian particles,
h
−→
R
i
(t)i = 0, h
−→
R
i
(t)
−→
R
j
(t
0
)i = 6K
B
T γδ
i j
δ(t −t
0
) (10)
where h
−→
R
i
(t)i represents an average value considered
with respect to the distribution of the realizations of
the variable
−→
R
i
(t), and K
B
is Boltzmann’s constant,
T is the temperature, D is the dissipation coefficient
and δ is the delta function. Upon these particles, (9)
can thus be applied to estimate the dynamics of the
particle in terms of position and velocity.
2.3 Crowd Flow Segmentation
This section discusses the implementation of a hy-
brid flow segmentation model. The proposed crowd
flow model works on a windowing scheme. The win-
dowing scheme ensures periodic re-initialization of
the process. This reduces the load of tracking of the
flow changes happening in the temporal domain. For
a given window W , the first two consecutive frames
are used for dense optical flow calculation to generate
magnitude and orientation maps.
For a certain magnitude threshold, the orientation
map is quantized into four different bins within the
range of 0-2π. This step is useful in two ways. Firstly,
magnitude-based thresholding removes motion noise.
Secondly, the orientation is generalized into fixed val-
ues for these points.
Then, the hydrodynamics-based magnitude is cal-
culated, as mentioned in (8). The motion points
flowing in the same quantized directions and over a
particular Hydrodynamics
mag
threshold are then re-
tained and grouped based on the connected compo-
nent analysis. This step identifies the coherent re-
gions in the crowd. The coherent points are then
fed to the Langevin-based force model for perform-
ing segmentation in the remaining frames in the win-
dow. The parameters like γ and λ have been set to
0.3 and 5 during empirical evaluation. The magni-
tude and Hydrodynamics
mag
thresholds are set to be
0.4 and 0.1 based on empirical study. F is basically
a group force which is computed as the cumulative
sum of acceleration of the particles within a specific
neighborhood as mentioned in (11),
F
dri f t/con f inement
= m
∑
i
dv
i
dt
(11)
where v represents the velocity of the particle, and m
is initialized to unity throughout the experiment. In
this work, we calculate F using (11) as drift force
causing the particle to drift along x direction, and F
is a confinement force causing the particle to be con-
fined along y direction. We assume drift movement to
Segmentation and Visualization of Crowd Flows in Videos using Hybrid Force Model
863

Figure 2: Proposed Implementation of the hybrid crowd flow segmentation model.
be a positive phenomenon and particle confinement to
be a negative phenomenon, thus assigning the polar-
ity of forces accordingly. The random force is gener-
ated within (0 − 1). The block diagram of the hybrid
model is presented in Figure 2.
3 RESULTS AND DISCUSSIONS
The evaluation of the proposed model has been car-
ried out on two video datasets. One is a publicly avail-
able dataset, i.e., Marathon Video used in (Shao et al.,
2014) and the other dataset contains more than ten
hours of video recording of a popular event known
as Puri Rath Yatra that happens at Puri, Odisha every
year in India during the month of July. The Intersec-
tion over Union (IoU) metric presented in (12) is used
to quantify the percent overlap between the ground
truth and segmentation output.
The Marathon dataset is a dense crowd video,
where people are running in an elliptical path. The
path formed is non-linear in different directions. The
output of the proposed method can be seen as seg-
mented flows of four different directions represented
by four different colors, indicating the four different
directional flows, similar to the ground truths, as dis-
played in Figure 3.
The Rath Yatra video is a semi-dense crowd video
with a certain degree of randomness. In this video,
both structured and unstructured motions can be ob-
served. People can be seen pulling the car (Rath)
that can be considered as a structured linear motion.
Along the sides of the linear flow, people can be seen
moving towards different directions, thus forming un-
structured motion. The proposed method is able to
segment such linear flow to a greater extent, matching
closely with the ground truths, as evident in Figure 4.
Accuracy has been calculated using (12).
Accuracy =
Area(S
w
∩ G
T
)
Area(S
w
∪ G
T
)
(12)
where S
w
is the segmented image, and G
T
is the
ground truth image. It has been found that the pro-
posed method outperforms the basic SPH method pro-
posed in (Ullah et al., 2017). The proposed hybrid
method shows good improvement in both accuracy
and execution time which is represented in Table 1,
Figure 5 and Figure 6, respectively. This happens
because the proposed method estimates the position
and velocity of the particles using the Langevin-based
model. Therefore, there is no need to apply optical
flow in every frame. As a result, a significant amount
of computation time can be saved.
Table 1: Comparison of the proposed hybrid model with ba-
sic SPH method proposed in (Ullah et al., 2017). The com-
parison has been done with respect to accuracy and average
time taken per frame in seconds.
#Videos
Accuracy
(in %)
Time Taken
for execution
per frame (in seconds)
SPH Method
(Ullah et al., 2017)
Proposed
Method
SPH Method
(Ullah et al., 2017)
Proposed
Method
Marathon 90.37 91.23 3.89 2.32
Rath Yatra 77.12 81.29 2.69 1.97
The proposed hybrid force model can segment
both linear and non-linear crowd flows. The hybrid
force model detects the coherent motion regions in
the video frames. The Langevin-based force model
is able to trace the segmented flows within each win-
dow. This approach makes the proposed model faster
than the method proposed in (Ullah et al., 2017) since
it is not necessary to apply the Smooth Particle Hy-
drodynamics on every frame. The reliability of the
Langevin-based force model can be observed in the
temporal segmented maps presented in Figure 3 and
Figure 4, respectively. The segmented regions can be
used as input data for machine learning models in or-
der to detect abnormal activities in the crowd.
4 CONCLUSION AND FUTURE
DIRECTIONS
Crowd flows are essential components in crowd anal-
ysis to understand crowd movements. Thus, under-
standing crowd movement behavior can help law-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
864

(a) (b) (c) (d)
(e) (f) (g) (h)
(i) (j) (k) (l)
(m) (n) (o) (p)
Figure 3: (a-d) Original Frames (361-364) of the Marathon video (e-h) Ground Truth Frames, (i-l) represent outputs of method
proposed in (Ullah et al., 2017), (m-p) represent outputs of the proposed segmentation method, respectively. (Best viewed in
color).
(a) (b) (c) (d)
(e) (f) (g) (h)
(i) (j) (k) (l)
(m) (n) (o) (p)
Figure 4: (a-d) Original Frames (31-34) of the Rath Yatra video (e-h) Ground Truth Frames, (i-l) represent outputs of method
proposed in (Ullah et al., 2017), (m-p) represents the output of the proposed method, respectively. (Best viewed in color).
enforcing agencies to take necessary actions to avoid
unwanted accidents. Therefore, it is essential to seg-
ment the crowd flows efficiently. The proposed seg-
mentation method based on a hybrid method can seg-
Segmentation and Visualization of Crowd Flows in Videos using Hybrid Force Model
865
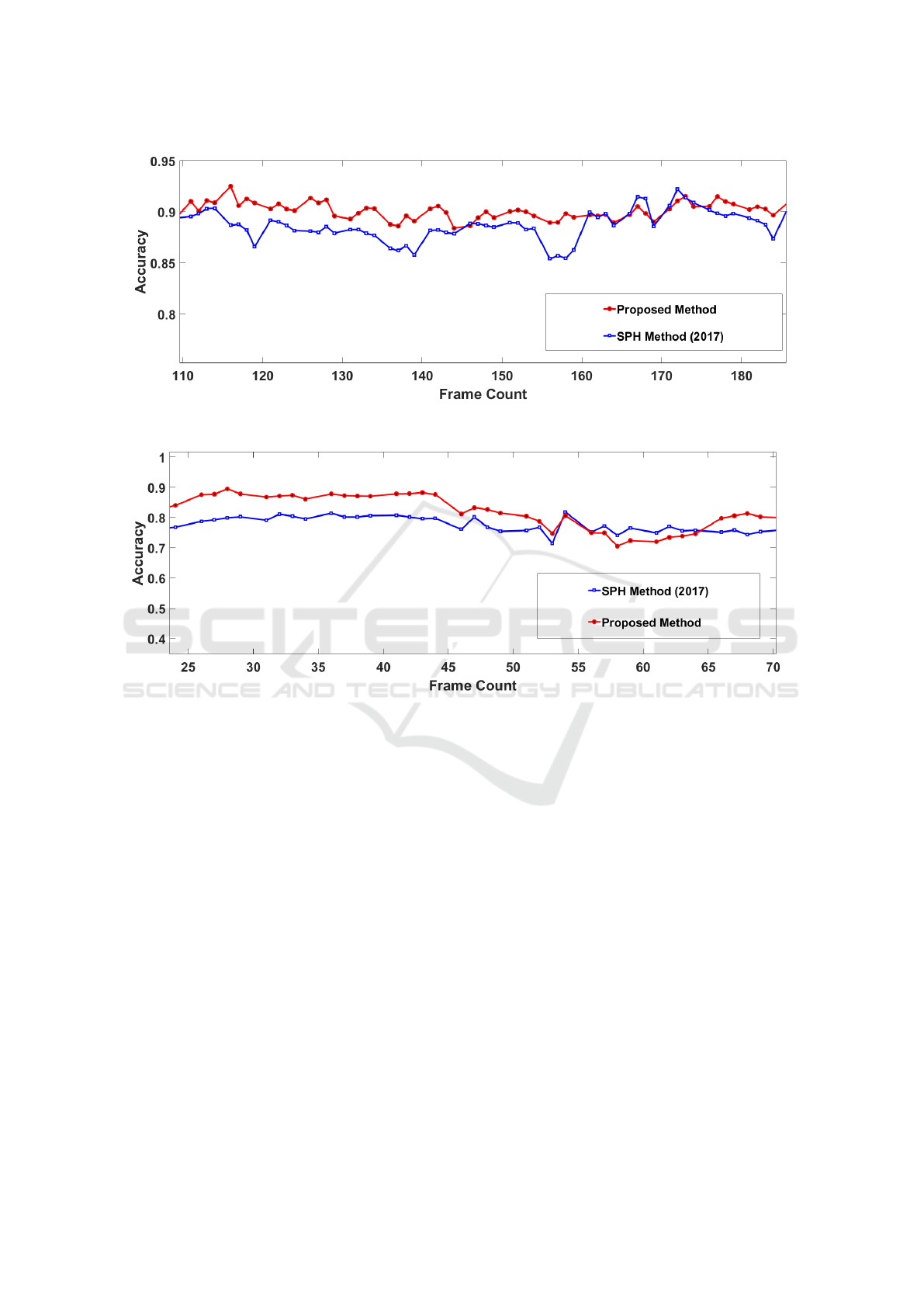
Figure 5: Segmentation Accuracy for the proposed method (red) and the SPH method (Ullah et al., 2017) (blue) for Marathon
Video.
Figure 6: Segmentation Accuracy for the proposed method (red) and the SPH method (Ullah et al., 2017) (blue) for Rath
Yatra Video.
ment both linear, and non-linear motion flows with
considerable accuracy. The proposed hybrid model
comprises of particle-based and physics-based force
models. The particle-based force model segments the
coherent regions effectively. The physics-based force
model then uses these regions for flow segmentation
in the successive frames. As a result, the proposed
model is better in terms of accuracy and speed when
compared to existing SPH-based methods.
The model also ensures robustness in the segmen-
tation of the flows, even in the presence of a high de-
gree of randomness in the crowd. There are a few
possible extensions of the present work. For exam-
ple, the SPH model of our proposed system can be re-
placed with advanced mesh-free methods to increase
the robustness and efficiency of the flow segmenta-
tion algorithm. Moreover, the method can be amalga-
mated with machine learning techniques for anomaly
detection and classification.
ACKNOWLEDGEMENTS
The authors would like to thank the Science and
Engineering Research Board (SERB), Department
of Science and Technology, Government of India
for funding this research work through the grant
YSS/2014/000046.
REFERENCES
Ali, S. and Shah, M. (2007). A lagrangian particle dynam-
ics approach for crowd flow segmentation and stabil-
ity analysis. In IEEE Conference on Computer Vision
and Pattern Recognition, pages 1–6.
Ali, S. and Shah, M. (2008). Floor fields for tracking in
high density crowd scenes. In European Conference
on Computer Vision, pages 1–14. Springer.
Andrade, E. L. and Fisher, R. B. (2005). Simulation of
crowd problems for computer vision. In First Inter-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
866

national Workshop on Crowd Simulation, volume 3,
pages 71–80.
Basak, B. and Gupta, S. (2017). Developing an agent-
based model for pilgrim evacuation using visual in-
telligence: A case study of ratha yatra at puri. Com-
puters, Environment and Urban Systems, 64:118–131.
Coffey, W. T. and Kalmykov, Y. P. (2004). The Langevin
equation: with applications to stochastic problems in
physics, chemistry and electrical engineering. World
Scientific.
Junior, J. C. S. J., Musse, S. R., and Jung, C. R. (2010).
Crowd analysis using computer vision techniques.
IEEE Signal Processing Magazine, 27(5):66–77.
Langevin, P. (1908). Sur la th
´
eorie du mouvement brown-
ien. CR Acad. Sci. Paris, 146:530–533.
Lim, M. K., Chan, C. S., Monekosso, D., and Remagnino,
P. (2014). Detection of salient regions in crowded
scenes. Electronics Letters, 50(5):363–365.
Lin, W., Chu, H., Wu, J., Sheng, B., and Chen, Z. (2013). A
heat-map-based algorithm for recognizing group ac-
tivities in videos. IEEE Transactions on Circuits and
Systems for Video Technology, 23(11):1980–1992.
Mehran, R., Moore, B. E., and Shah, M. (2010). A streak-
line representation of flow in crowded scenes. In Euro-
pean Conference on Computer Vision, pages 439–452.
Springer.
Monaghan, J. J. (1992). Smoothed particle hydrodynam-
ics. Annual review of astronomy and astrophysics,
30(1):543–574.
Schweitzer, F. (2007). Brownian agents and active par-
ticles: collective dynamics in the natural and social
sciences. Springer.
Shao, J., Change Loy, C., and Wang, X. (2014). Scene-
independent group profiling in crowd. In Proceedings
of the IEEE Conference on Computer Vision and Pat-
tern Recognition, pages 2219–2226.
Su, H., Yang, H., Zheng, S., Fan, Y., and Wei, S. (2013).
The large-scale crowd behavior perception based on
spatio-temporal viscous fluid field. IEEE Transactions
on Information Forensics and Security, 8(10):1575–
1589.
Ullah, H., Ullah, M., and Uzair, M. (2018). A hybrid social
influence model for pedestrian motion segmentation.
Neural Computing and Applications, pages 1–17.
Ullah, H., Uzair, M., Ullah, M., Khan, A., Ahmad, A., and
Khan, W. (2017). Density independent hydrodynam-
ics model for crowd coherency detection. Neurocom-
puting, 242:28–39.
Wu, S., Su, H., Yang, H., Zheng, S., Fan, Y., and Zhou, Q.
(2017). Bilinear dynamics for crowd video analysis.
Journal of Visual Communication and Image Repre-
sentation, 48:461–470.
Zhang, D., Xu, J., Sun, M., and Xiang, Z. (2017). High-
density crowd behaviors segmentation based on dy-
namical systems. Multimedia Systems, 23(5):599–
606.
Zhang, X., Yu, Q., and Yu, H. (2018). Physics inspired
methods for crowd video surveillance and analysis: a
survey. IEEE Access.
Zhang, Y., Qin, L., Ji, R., Yao, H., and Huang, Q. (2015).
Social attribute-aware force model: exploiting rich-
ness of interaction for abnormal crowd detection.
IEEE Transactions on Circuits and Systems for Video
Technology, 25(7):1231–1245.
Segmentation and Visualization of Crowd Flows in Videos using Hybrid Force Model
867
