Hidden Markov Models for Pose Estimation

László Czúni and Amr M. Nagy

Department of Electrical Engineering and Information Systems, University of Pannonia,

Egyetem Street 10, Veszprém, Hungary

Keywords: Optical Object Recognition, Pose Estimation, Temporal Models, Hidden Markov Model, Deep Neural

Network.

Abstract: Estimation of the pose of objects is essential in order to interact with the real world in many applications such

as robotics, augmented reality or autonomous driving. The key challenges we must face in the recognition of

objects and their pose is due to the diversity of their visual appearance in addition to the complexity of the

environment, the variations of illumination, and possibilities of occlusions. We have previously shown that

Hidden Markov Models (HMMs) can improve the recognition of objects even with the help of weak object

classifiers if orientation information is also utilized during the recognition process. In this paper we describe

our first attempts when we apply HMMs to improve the pose selection of elementary convolutional neural

networks (CNNs).

1 INTRODUCTION

The recognition of 3D objects is an elementary

problem in many application fields such as robotics,

autonomous vehicles or augmented reality. However,

to interact with the objects of the environment, not

only specific or generic object recognition is

inevitable, but the determination of their pose is also

essential. Pose estimation is also a fundamental

problem in computer vision and large number of

algorithms have been proposed for the various

conditions and applications.

In recent years, the state of the art of convolutional

neural networks, like Regional CNN (Girshick,

Donahue, Darrell, & Malik, 2014), Fast R-CNN

(Redmon, Divvala, Girshick, & Farhadi, 2016), Mask

R-CNN (He, Gkioxari, Dollar, & Girshick, 2017),

(Redmon et al.,2016) and Single Shot Detectors (Liu

et al., 2016), have been proven to be very efficient for

object detection and recognition in RGB and depth

images, however these CNNs do not provide us

straightforward object pose estimation.

Similarly, the problem of the estimation of the 6-

DoF object pose was recently attacked by different

CNN approaches. Classical approaches can be

grouped ( Nöll, Pagani, & Stricker, 2011) as Direct

Linear Transformation, Perspective n-Point, and a

priori information estimators; they all suffer from the

problem of efficient feature selection,

correspondence generation and outlier filtering.

Contrary, CNN-based methods have the great

advantage to learn the combination of the best

possible features and classifiers or regressors.

Partially as a result of the Amazon Picking

Challenge (Correll et al., 2018), interest in object

manipulation has increased recently leading to the

development of several 6-DoF object estimation

methods. Many of these methods, such as PoseCNN

(Xiang, Schmidt, Narayanan, & Fox, 2018), SSD-6D

(Kehl, Manhardt, Tombari, Ilic, & Navab, 2017),

Real-Time Seamless Single Shot 6D Object Pose

Prediction (Tekin, Sinha, & Fua, 2018) and BB8 (Rad

& Lepetit, 2017), use convolution neural network

(CNNs) to estimate pose with high accuracy of

known objects in cluttered environments.

It is well-known that the general disadvantage of

neural network based methods is the dependency on

the training data and the utilized training methods.

For example, in (Xu, Bai, & Ghanem, n.d., 2019) the

performance drop caused by missing object labels is

analysed. Unfortunately, the generation of training

data is typically costly whether it is based on real or

syntactic data, especially if the pose is to be

represented (Rennie, Shome, Bekris, & De Souza,

2016).

We have previously shown that Hidden Markov

Models (HMMs) can improve the recognition of

objects from a sequence of images when weak object

classifiers are utilized (Czúni et al., 2017). Since our

598

Czúni, L. and Nagy, A.

Hidden Markov Models for Pose Estimation.

DOI: 10.5220/0009357505980603

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages

598-603

ISBN: 978-989-758-402-2; ISSN: 2184-4321

proposal utilized orientation sensors it is

straightforward to investigate whether it can improve

more sophisticated object recognizers (such as

CNNs) in pose estimation.

In this paper we show, that using a general object

classification network (namely VGG16), the

temporal inference generated by the HMM can

significantly increase the pose estimation

possibilities. The integration of our HMM approach

with more specific pose related networks is the task

of future.

In the following Section we shortly overview

some relevant papers then in Section 3 we describe

the details of our object pose estimation method. In

Section 4 our dataset and experiments are described

and finally in Section 5 we conclude our paper.

2 RELATED WORKS

6D object pose estimation methods can be

categorized roughly into feature-based, template-

based, and CNN-based methods.

Traditional local features (Collet, Martinez, &

Srinivasa, n.d, 2011.) utilize RGB images to extract

local keypoints and perform feature matching to

estimate the object pose. Local feature methods are

often fast and able to handle scene clutter and

occlusion, but the objects needed enough textures.

A 3D template model is built and used in

template-based methods (Hinterstoisser et al., 2013)

to scan various locations in the input image. A

similarity score is calculated at each position and the

best match is obtained by comparing these scores.

Template-based methods have great advantages on

texture-less objects however, they suffer from

occlusions.

In recent years, CNNs have started to dominate this

field either, so will review some of the most important

approaches.

A main concept behind PoseCNN (Xiang et al.,

2018) is to decouple the pose estimation into separate

components, allowing the network to identify the

dependencies and independence between them

explicitly. PoseCNN carries out three related tasks.

Starting from predicting an object label for each pixel

in the input image, estimating the 2D pixel

coordinates of the object, and estimating the 3D

Rotation by regressing convolutional features. There

are two levels in the network architecture of

PoseCNN. The first level is considered as the

backbone of the network consisting of 13 convolution

layers and 4 max pooling layers. Feature maps are

extracted with various resolution from the input

image. These features are spread across all the second

level tasks (i.e. semantic labelling, 3D translation

estimation, and 3D rotation regression) performed by

the network.

The SSD-6D (Kehl et al., 2017) approach is a

different method to detect instances of 3D objects and

estimate their 6D poses by a single shot from RGB

data only. It extends the common SSD paradigm to

cover the entire 6D pose space and these networks are

typically trained only on synthetic data. The network

produces six feature maps on multiple scales for each

input RGB image. To determine the object class, the

2D bounding box, and scores for possible viewpoints

and in-plane rotations, each map is convolved with

specifically trained kernels. After convolution, these

feature maps are analysed to create 6D pose

hypotheses. While SSD-6D can give very good

results it has its limitations, for example it is

necessary to find a suitable sampling of the viewing

space of the model to obtain the satisfactory results.

In the approach of (Sundermeyer, Marton,

Durner, & Triebel, 2019) augmented autoencoders

are used with single RGB images as inputs but

additionally depth maps may optionally be

incorporated to refine pose estimation. First SSD is

applied to detect the required object, to identify its

bounding box then Augmented Autoencoder (AAE)

is utilized to estimate the 3D orientation. Because the

Augmented Autoencoder is trained on 3D syntactic

models, they used a Domain Randomization (DR)

strategy to generalize from syntactic data to real.

3 THE PROPOSED METHOD

We follow the approach when a single CNN is to

recognize an object and its pose through several

observations then a statistical framework is applied to

evaluate the result of inferences and to make the final

object recognition and pose estimation. We have

chosen a well-known neural network, often used as a

backbone of more complex architectures, namely

VGG16 (Simonyan & Zisserman, 2015). We don’t

deal with the localization of the object within the

image frame. I. e. it gives no big stress for the

annotation procedure to generate training data but

makes it a hard work for the processing framework to

achieve good pose estimation.

In our view-centred representation, the outlook of

the object is modelled from different viewpoints with

multiple 2D images. It would be possible to make

these sample images from several elevations,

although in our experiments we implemented only a

Hidden Markov Models for Pose Estimation

599

single elevation methodology (since the used dataset

COIL contains only such data).

During the recognition consecutive queries, shots

taken from different viewing directions, are first

evaluated by VGG16 inference resulting in

confidence values. We assume that the relative pose

changes between the shots are recorded by easily

available IMU sensors (such as those built into most

mobile phone).

Using the image shots, the pre-built object

models, the trained VGG16 networks, and the change

in orientation between shots we use an HMM

framework to evaluate the image sequences and to

determine the most probable object and its pose series

generating the observations.

Since the order of sequential poses (the actual

changes of relative viewing directions) is determined

by the behaviour of the camera (or with other words

by the user) it cannot be generally modelled in the

model to determine the actual transition probabilities.

What we can do is to measure the real change in

relative poses query by query, with the help of IMU

sensors, and use geometric probabilities to evaluate

the chance of going from one state to another. For this

resolution of the problem of computing state

transitions, please see Subsection 3.2.

3.1 HMM Object Models

An HMM is defined by:

• its states S

• transition probabilities between states S

and S

(see Eq. 2),

• emission probabilities (P(o), see Eq. 7),

• initial state probabilities (π

To achieve object retrieval will need to build

HMM models for all elements of the set of objects

(M) where different poses (views made from different

orientations in our case) correspond to the states.

Then, based on the sequence of observations (o

), we

will find the most probable state sequence for all

object models. The state sequence among these,

which has the highest probability, will belong to the

object being recognized.

Traditionally, to build a Markov model means

learning its parameters (π, transition and emission

probabilities) by examining training examples.

However, our case is special: the probability of going

from one state to another severely depends on the

user’s behaviour and on the frame rate of the camera.

Thus, we can’t follow the traditional way, to use the

Baum-Welch algorithm for parameter estimation

based on several training samples but can directly

compute transition probabilities based on geometric

as described later. Observation probabilities will be

determined by the confidence values of the trained

CNN.

3.2 Object Poses as States in Hidden

Markov Models

Let S = {S

,…,S

} denote the set of N possible hidden

states of a model. In each step of an observation

process (denoted by index t) the model can be

described as being in one q

∈

S state, where t =

1,…,T.

In our approach the states can be considered as the

2D views (poses) of a given object model. This can

be easily imagined as a camera is targeting towards

and object from a given elevation and a given

azimuth. The number of possible states should be kept

low, otherwise the state transition matrix (A) would

contain too small numbers and finding the most

probable state sequence would be too uncertain. On

the other hand, small number of states would mean

that quite different appearances of objects should be

encoded by the same representation (now by a single

CNN for all objects and their poses) resulting in

decreased confidence again, thus the generation of

states should be designed carefully. In our

experiments we use static subdivision of the circle of

360º into 8º uniform sectors each with 45º opening.

We define the initial state probabilities π = {π

1≤i≤N based on the opening angle of the views:



=𝑃

(

𝑞



=𝑆



)

𝛼(𝑆



)

360

(1)

where α(S

) is the angle (given in degree) of

aperture of state S

3.3 State Transitions

Between two steps the model can undergo a change

of states according to a set of transition probabilities

associated with each state pairs. In general, the

transition probabilities are:

= P(q

= S

t−1

= S

) (2)

where now i and j indices refer to states of the HMM,

≥ 0, and for a given state

∑

𝑎

,





=1 holds. The

transition probability matrix is denoted by A = {a

1≤i,j≤N. The probability of going from one state to

another cannot be determined as part of the model but

we can directly compute transition probabilities based

on geometric probability as follows.

First define ∆

t−1,t

as the orientation difference

between two successive observations:

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

600

−

1,t

= α(o

) − α(o

−

)

(3)

Now define R

as the aperture interval angle

belonging to state S

by borderlines:

=[S

min

, S

max

) (4)

where S

min

and S

max

denotes the two (left and

right) terminal positions of state S

(one side is

specified with an open interval symbol). The back

projected aperture interval angle is the range of

orientation from where the previous observation

should originate:

(5)

Now, to estimate the transition probability we use

the geometrical probability concept applied on the

intersection of L

and R

𝑎



=𝑃𝑞



=𝑆



𝑞



=𝑆



=









∩















(6)

3.4 Recognition of Objects and Their

Poses

The emission probability of a particular observation

for state S

is defined as:

𝑏



(

𝑜



)

=𝑃

(

𝑜



𝑞



=𝑆



)



(7)

Applying VGG16 as a global object classifier, for all

poses of all objects, we can consider the confidence

values of inferences as b

-s. We assume that an

observation sequence contains only one class of

objects (possibly with several poses as the camera

moves on). Then for each possible object we

independently run the Viterbi algorithm to combine

the values of Eq. 2, Eq. 7, and π

-s to get the most

probable state sequences. Finally, we choose the

object with the highest probability value as the

recognized object and we can also determine the

poses selected for each query by the Viterbi path.

4 EVALUATION

4.1 Dataset

The COIL-100 dataset (Nene et al., 1996) includes

100 different objects each with 72 images taken by 5º

at the same elevation. We have chosen 40 objects

from the 100 for our experiments, see Fig. 1 for some

sample images. Each object was represented with 8

poses by equally divided sectors of 45º. Images are

originally with black background but to be more

realistic we have given different backgrounds,

selected from 200 random images, so the original

COIL images cover around 25% of the area of 128 ×

128 pixels (Fig. 1 bottom line). We believe that that

small adjacent black area around the objects does not

distort the results since it appears in all objects and

gives no advantage to the classifier. Thus, we got

2880 images (40 × 72) directly from COIL-100 and

11520 from augmentation. The dataset was cut into

training and testing parts so no queries of the

experiments could exactly match those images used

to train the CNN.

Figure 1: Top line: example objects from the COIL-100

dataset. Bottom line: test images with different

backgrounds.

4.2 Tests and Evaluations

A single VGG16 network was used to recognize all

320 (40 objects × 8 poses) classes. The network was

pre-trained with images of ImageNet (Russakovsky et

al., 2014). We did not refine the feature extraction

layers of the network, only the 4 end layers

responsible for classification, were replaced and re-

trained. During training image rotation, shift, shear,

zoom, and horizontal flip was applied as further

augmentation.

Figure 2: Average orientation error at different number of

queries for VGG16 only (yellow) and VGG+HMM (blue).

To get a general overview of the performance we

computed the pose error by averaging the orientation

error for each object and each pose estimated in 8

independent random experiments. As one could

expect the error may depend on the number of

Hidden Markov Models for Pose Estimation

601

observations (i.e. the number of queries). As Fig. 2

shows, increasing the number of queries results in the

decrease of average pose error from 67.18º to 44.78º.

As a reference, we computed the average error of the

VGG16 network illustrated by yellow in Fig. 2. These

values are ranging from 67.18º to 63.59º significantly

higher than the VGG+HMM technique. To highlight

the information added by the orientation sensor we

made tests where the transition probabilities were set

constant. This is named VGG+mHMM and shown by

green dotted lines in Fig. 2. There is no significant

difference between VGG16 and VGG+mHMM as

expected.

Interestingly, regarding the average object-level

recognition rate based on 4 queries, the VGG+HMM

method achieved 99.7% and the VGG16 resulted in

99.1%, which is a small difference thanks to the good

general recognition abilities of VGG16.

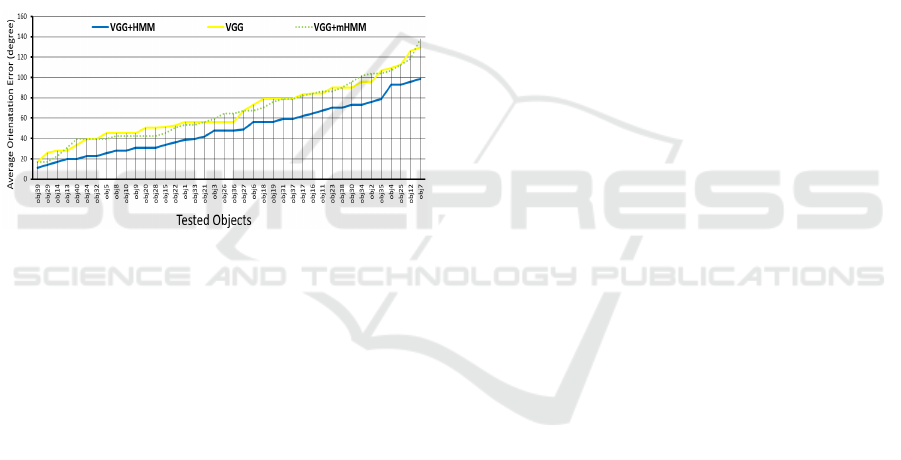
Figure 3: Average orientation error for each object, in case

of two queries, for VGG16 only (yellow), VGG+HMM

(blue), and VGG+mHMM with constant transition

probabilities (green dotted).

5 CONCLUSIONS

In our paper we discussed a probabilistic approach to

enhance the pose estimation capabilities of simple

classification networks such as VGG16. We utilized

the orientation sensor to estimate the transition

probabilities between poses thus HMMs could be

used to estimate the most probable pose sequences.

The improvement over the applied CNN is significant

as shown by experiments using 40 randomly chosen

objects of the COIL-100 dataset. In future we plan the

investigate how to fuse the model with more

sophisticated CNNs such as PoseCNN or SSD-6D.

ACKNOWLEDGEMENTS

We acknowledge the financial support of the

Széchenyi 2020 program under the project EFOP-

3.6.1-16-2016-00015, and the Hungarian Research Fund,

grant OTKA K 120367. We are grateful to the NVIDIA

Corporation for supporting our research with GPUs

obtained by the NVIDIA GPU Grant Program.

REFERENCES

Collet, A., Martinez, M., & Srinivasa, S. S. (2011). The

MOPED framework: Object recognition and pose

estimation for manipulation. International Journal of

Robotics Research, 30(10), 1284–1306.

Correll, N., Bekris, K. E., Berenson, D., Brock, O., Causo,

A., Hauser, K., … Wurman, P. R. (2018). Analysis and

observations from the first Amazon picking challenge.

IEEE Transactions on Automation Science and

Engineering, 15(1), 172–188.

Czúni, L., & Rashad, M. (2017). The Fusion of Optical and

Orientation Information in a Markovian Framework for

3D Object Retrieval. In International Conference on

Image Analysis and Processing, pp. 26–36.

Girshick, R., Donahue, J., Darrell, T., & Malik, J. (2014).

Rich feature hierarchies for accurate object detection

and semantic segmentation. Proceedings of the IEEE

Computer Society Conference on Computer Vision and

Pattern Recognition, 580–587.

He, K., Gkioxari, G., Dollar, P., & Girshick, R. (2017).

Mask R-CNN. Proceedings of the IEEE International

Conference on Computer Vision, 2980–2988.

Hinterstoisser, S., Holzer, S., Cagniart, C., Ilic, S.,

Konolige, K., Navab, N., & Lepetit, V. (2011).

Multimodal templates for real-time detection of

texture-less objects in heavily cluttered scenes.

Proceedings of the IEEE International Conference on

Computer Vision, 858–865.

Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski,

G., Konolige, K., & Navab, N. (2013). Model based

training, detection and pose estimation of texture-less

3D objects in heavily cluttered scenes. Lecture Notes in

Computer Science, 7724 LNCS(PART 1), 548–562.

Hodaň, T., Haluza, P., Obdrzalek, Š., Matas, J., Lourakis,

M., & Zabulis, X. (2017). T-LESS: An RGB-D dataset

for 6D pose estimation of texture-less objects.

Proceedings - 2017 IEEE Winter Conference on

Applications of Computer Vision, WACV 2017, 880–

888.

Kehl, W., Manhardt, F., Tombari, F., Ilic, S., & Navab, N.

(2017). SSD-6D: Making RGB-Based 3D Detection

and 6D Pose Estimation Great Again. Proceedings of

the IEEE International Conference on Computer

Vision, 1530–1538.

Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S.,

Fu, C. Y., & Berg, A. C. (2016). SSD: Single shot

multibox detector. Lecture Notes in Computer Science

(Including Subseries Lecture Notes in Artificial

Intelligence and Lecture Notes in Bioinformatics), 9905

LNCS, 21–37.

Nöll, T., Pagani, A., & Stricker, D. (2011). Markerless

camera pose estimation - An overview. OpenAccess

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

602

Series in Informatics, 19, 45–54. In Visualization of

Large and Unstructured Data Sets-Applications in

Geospatial Planning, Modeling and Engineering (IRTG

1131 Workshop). Schloss Dagstuhl-Leibniz-Zentrum

fuer Informatik.

Rad, M., & Lepetit, V. (2017). BB8: A Scalable, Accurate,

Robust to Partial Occlusion Method for Predicting the

3D Poses of Challenging Objects without Using Depth.

Proceedings of the IEEE International Conference on

Computer Vision, 3848–3856.

Redmon, J., Divvala, S., Girshick, R., & Farhadi, A. (2016).

You only look once: Unified, real-time object detection.

Proceedings of the IEEE Computer Society Conference

on Computer Vision and Pattern Recognition, 779–788.

Ren, S., He, K., Girshick, R., & Sun, J. (2017). Faster R-

CNN: Towards Real-Time Object Detection with

Region Proposal Networks. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 39(6),

1137–1149.

Rennie, C., Shome, R., Bekris, K. E., & De Souza, A. F.

(2016). A Dataset for Improved RGBD-Based Object

Detection and Pose Estimation for Warehouse Pick-

and-Place. IEEE Robotics and Automation Letters,

1(2), 1179–1185.

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,

Ma, S., … Fei-Fei, L. (2014). ImageNet Large Scale

Visual Recognition Challenge.

Simonyan, K., & Zisserman, A. (2015). Very deep

convolutional networks for large-scale image

recognition. 3rd International Conference on Learning

Representations, ICLR 2015 - Conference Track

Proceedings. International Conference on Learning

Representations, ICLR.

Sundermeyer, M., Marton, Z. C., Durner, M., & Triebel, R.

(2019). Augmented Autoencoders: Implicit 3D

Orientation Learning for 6D Object Detection.

International Journal of Computer Vision, 11210

LNCS, 712–729.

Tejani, A., Tang, D., Kouskouridas, R., & Kim, T. K.

(2014). Latent-class Hough forests for 3D object

detection and pose estimation. Lecture Notes in

Computer Science (Including Subseries Lecture Notes

in Artificial Intelligence and Lecture Notes in

Bioinformatics), 8694 LNCS(PART 6), 462–477.

Springer Verlag.

Tekin, B., Sinha, S. N., & Fua, P. (2018). Real-Time

Seamless Single Shot 6D Object Pose Prediction.

Proceedings of the IEEE Computer Society Conference

on Computer Vision and Pattern Recognition, 292–301.

Xiang, Y., Schmidt, T., Narayanan, V., & Fox, D. (2018,

November 1). PoseCNN: A Convolutional Neural

Network for 6D Object Pose Estimation in Cluttered

Scenes.

Xu, M., Bai, Y., & Ghanem, B. (2019). Missing Labels in

Object Detection. CVPR Workshop. In The IEEE

Conference on Computer Vision and Pattern

Recognition (CVPR) Workshops

Nene, S.A., Nayar, S.K., Murase, H. (1996). Columbia

Object Image Library (COIL-100), Technical Report

CUCS, Department of Computer Science, Columbia

University, New York, NY, USA

Hidden Markov Models for Pose Estimation

603