
3D Model-based 6D Object Pose Tracking on RGB Images using Particle
Filtering and Heuristic Optimization
Mateusz Majcher and Bogdan Kwolek
AGH University of Science and Technology, 30 Mickiewicza, 30-059 Krakow, Poland
Keywords:
6D Object Pose Tracking, Region-based Pose Estimation, Image Segmentation, Optimization.
Abstract:
We present algorithm for tracking 6D pose of the object in a sequence of RGB images. The images are acquired
by a calibrated camera. The object of interest is segmented by an U-Net neural network. The network is trained
in advance to segment a set of objects from the background. The 6D pose of the object is estimated through
projecting the 3D model to image and then matching the rendered object with the segmented object. The
objective function is calculated using object silhouette and edge scores determined on the basis of distance
transform. A particle filter is used to estimate the posterior probability distribution. A k-means++ algorithm,
which applies a sequentially random selection strategy according to a squared distance from the closest center
already selected is executed on particles representing multi-modal probability distribution. A particle swarm
optimization is then used to find the modes in the probability distribution. Results achieved by the proposed
algorithm were compared with results obtained by a particle filter and a particle swarm optimization.
1 INTRODUCTION
Estimating the 6-DoF pose (3D rotations + 3D trans-
lations) of an object with respect to the camera is very
important task. It is expected that in a near future the
robots will be used in larger scale in less structured
environments such as shops, households and hospi-
tals. In such applications, robots will need to be more
autonomous and have abilities to estimate 6 DOF pose
of objects randomly placed in environment. Due to
considerable applicability potential, considerable re-
search efforts have been devoted to tackling the 6D
pose estimation problem by computer vision commu-
nity (Brachmann et al., 2014), robotics community
(Hinterstoisser et al., 2013) and augmented reality
(Marchand et al., 2016). In virtual reality applications
a precise object pose is needed to perform interaction
with objects as well as to initialize tracking. In robotic
applications the robot pose is needed to avoid colli-
sions, to allow a robot to manipulate an object or to
avoid moving into the object.
Estimating the object pose using only a single
monocular camera is the most generic approach. In
context of robotics such monocular approaches are at-
tractive in grasping scenarios when single RGB cam-
era is usually attached to an arm of a robot. In con-
ventional approaches, the 6D pose of the object is re-
covered by optimizing the difference between the 2D
observation of the object in the current image and an
estimated synthetic 2D projection of a 3D model ab-
straction of the considered object, which is param-
eterized by the sought pose. Thus, the pose esti-
mate is recovered through selection the best match-
ing viewpoint onto the object or on the basis of 2D-
3D correspondences between such local features and
a Perspective-n-Point (PnP) algorithm (Fischler and
Bolles, 1981). In case of tracking, the object is as-
sumed to be seen in a sequence of consecutive im-
ages and the object motion is supposed to be rela-
tively small between two consecutive frames. The
correspondence-based approaches require rich tex-
ture features. They calculate the pose using the PnP
and recovered 2D-3D correspondences, often in a
RANSAC (Fischler and Bolles, 1981) framework for
outlier rejection. While PnP algorithms are usually
robust when the object is well textured, they can fail
when it is featureless or when in the scene there are
multiple objects occluding each other.
Another approaches consist in attaching artificial
markers or fiducials to objects of interest. Such ap-
proaches usually permit tracking by detection, mean-
ing that the object absolute pose can be determined
in each image in real-time without exploiting tempo-
ral continuity assumptions. However, having on re-
gard that the marker detection is based on high con-
trast edges in the image as well as overall high inten-
690
Majcher, M. and Kwolek, B.
3D Model-based 6D Object Pose Tracking on RGB Images using Particle Filtering and Heuristic Optimization.
DOI: 10.5220/0009365706900697
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
690-697
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sity contrast between the black and the white areas
of the marker, such methods are prone to motion blur
caused by fast marker or camera movement, mainly
due to unsharp or blurred edges (Marchand et al.,
2016). Active pose estimation approaches overcome
most of limitations related to passive markers or fea-
tures and are frequently used in conjunction with PnP
algorithms. When no marker and no additional light
sources can be used, the point correspondences can
be computed passively from so-called natural features
visible on the object. The most popular and com-
monly used natural features are so-called point and
edge features. A large variety of object pose estima-
tion approaches relying on natural point features have
been proposed in the past, e.g. (Lepetit et al., 2004;
Vidal et al., 2018), to enumerate only some of them.
In general, features can either be an encoding of
image properties or a result of learning. In recently
proposed algorithm (Brachmann et al., 2016), which
is based on learning so-called object coordinates, an
auto-context random forest processes the image to
predict object labels and object coordinates. As a re-
sult, pixel-wise distributions of object labels and ob-
ject coordinates are calculated. The distributions over
object labels are used to sample hypotheses for all ob-
jects at once. Then, pre-emptive RANSAC is used to
determine preliminary pose estimates. Finally, these
poses are refined on the basis of object coordinate
distributions. In (Hinterstoisser et al., 2011; Hinter-
stoisser et al., 2013), holistic template-based methods,
which can deal with texture-less objects in 6D pose
recovering in cluttered scenes have been introduced.
A first attempt to use a convolutional neural net-
work (CNN) for direct regression of 6DoF object
poses was PoseCNN (Xiang et al., 2018). In general,
two main CNN-based approaches to 6D pose object
pose estimation have emerged: either regressing the
6D object pose from the image directly (Xiang et al.,
2018) or predicting 2D key-point locations in the im-
age (Rad and Lepetit, 2017), from which the object
pose can be determined by the PnP algorithm.
There are several publicly available datasets for
benchmarking the performance of algorithms for 6D
object pose estimation, including OccludedLinemod
(Brachmann et al., 2014), YCB-Video (Xiang et al.,
2018). However, the current datasets do not focus
on 6D object tracking using RGB image sequences.
Most of the RGB image-based approaches to 6D pose
estimation focuses on accuracies as well as process-
ing times. As pointed out in recent work (Deng et al.,
2019), the majority of current techniques to 6D ob-
ject pose estimation ignore temporal information and
deliver only a single hypothesis for object pose. In
discussed work, a Rao-Blackwellized Particle Filter
(PoseRBPF) for object pose tracking has been pro-
posed. In this work we investigate the problem of 6-
DOF object pose tracking from RGB images, where
the object of interest is rigid and its 3D model is
known. At the beginning, the object is segmented
from the background using an U-Net convolutional
neural network. The network is trained in advance
using a small set of object images. A particle filter
(PF) (Doucet et al., 2000) combined with a particle
swarm optimization (PSO) (Kennedy and Eberhart,
1995; Sengupta et al., 2019) is then utilized to esti-
mate the 6D object pose by projecting the 3D object
model and then matching the projected image with the
image acquired by the camera. The tracking of 6D
object pose is formulated as a dynamic optimization
problem, where a particle filter is used to represent
the 6D pose probability distribution, the k-means++
is employed to find clusters in the probability distri-
bution, and a PSO is utilized to seek for the modes in
the probability distribution. In order to reduce work
needed to prepare the 3D object model as well as to
determine the ground-truth poses we employed an au-
tomated turntable setup.
2 OBJECT SEGMENTATION
The architecture of neural network has been based
on the U-Net (Ronneberger et al., 2015) in which
we can distinguish a down-sampling (encoding) path
and an up-sampling (decoding) path, see Fig. 1. In
the down-sampling path there are five convolutional
blocks. Each block has two convolutional layers with
3 × 3 filters and stride equal to 1. Down-sampling is
realized by max pooling with stride 2 × 2 that is ap-
plied on the end of every blocks except the last one.
In the up-sampling path, each block begins with a de-
convolutional layer with 3 × 3 filter and 2 × 2 stride,
which doubles the dimension of feature maps in both
directions and decreases the number of feature maps
by two. In each up-sampling block, two convolutional
layers decrease the number of feature maps, which
arise as a result of concatenation of deconvolutional
feature maps and the feature maps from correspond-
ing block in the encoding path. Finally, a 1 ×1 convo-
lutional layer is used. The neural network was trained
on RGB images of size 288 × 512. In order to reduce
training time, prevent overfitting and increase perfor-
mance of the U-Net we added Batch Normalization
(BN) (Ioffe and Szegedy, 2015) after each Conv2D.
BN is a kind of supplemental layer that adaptively
normalizes the input values of the following layer,
mitigating the risk of overfitting. Since it improves
gradient flow through the network, it reduces depen-
3D Model-based 6D Object Pose Tracking on RGB Images using Particle Filtering and Heuristic Optimization
691

dence on initialization and higher learning rates are
achieved. Data augmentation is useful for the reduc-
tion of overfitting and it has also been applied during
the network training.
Figure 1: Architecture of U-Net for object segmentation.
The pixel-wise cross-entropy has been used as the
loss function for object segmentation:
L = −
1
N
N
∑
i=1
[y
i
log( ˆy
i
) + (1 − y
i
)log(1 − ˆy
i
)] (1)
where N stands for the number of training samples, y
is true value and ˆy denotes predicted value.
3 6D OBJECT POSE TRACKING
At the beginning of this Section we discuss 6D object
pose tracking using PSO. Then, in Subsection 3.1.2
we present the fitness function. Afterwards, we
present 6D object pose tracking using particle filter-
ing. In Subsection 3.2.2 we outline observation and
motion models. Finally, in Subsection 3.3 we present
PF-PSO algorithm for 6D object pose tracking.
3.1 6D Object Pose Tracking using PSO
3.1.1 Particle Swarm Optimization
Particle swarm optimization (Kennedy and Eberhart,
1995; Sengupta et al., 2019) is an heuristic opti-
mization algorithm. It is derivative–free, stochastic
and population–based computational method, which
demonstrated a high optimization potential in un-
friendly non–convex, non–continuous spaces. The
swarm consists of a set of particles, and each swarm
member represents a potential solution of an opti-
mization task. The particles are placed in the search
space and move through such a space according to
rules, which take into account each particle’s personal
knowledge and the global knowledge of the swarm.
Every individual moves with its own velocity in the
multidimensional search space, determines its own
position and calculates its fitness using an objective
function f (x). On the basis of the fitness function the
particles determine the best locations and the global
best location.
The ordinary PSO algorithm begins by creating
particles at initial locations, and assigning them ini-
tial velocities (Kennedy and Eberhart, 1995). After-
wards, it determines the value of the objective func-
tion at each particle location, as well as determines
the best function value and the corresponding best lo-
cation. It determines new velocities, based on the cur-
rent velocity, the particles’s individual best locations,
and the best location of the entire swarm. In his work,
a topology with the global best has been selected due
to its faster convergence in comparison to neighbor-
hood best one.
At the beginning of optimization, each particle is
initialized with a random position and velocity. While
seeking the best fitness, every individual i is attracted
towards a position, which is affected by the best po-
sition p
(i)
found so far by itself and the global best
position p
g
found by the whole swarm. In every iter-
ation k, each particle’s velocity is first updated based
on the particle’s current velocity, the particle’s local
information and global information discovered by the
entire population. Then, each particle’s position is
updated using the velocity. In the ordinary PSO, the
position and velocity are calculated as follows:
v
(i)
k+1
= wv
(i)
k
+ c
1
r
(i)
1
(p
(i)
k
− x
(i)
k
) + c
2
r
(i)
2
(p
g,k
− x
(i)
k
)
(2)
x
(i)
k+1
= x
(i)
k
+ v
(i)
k+1
(3)
where w is the positive inertia weight, v
(i)
is the ve-
locity of particle i, r
(i)
1
and r
(i)
2
are uniquely generated
random numbers with the uniform distribution in the
interval [0.0, 1.0], c
1
, c
2
are positive constants, p
(i)
is
the best position that the particle i has found so far,
p
g
denotes the best position that was found by any
member of the swarm.
Equation (2), which updates the particle velocity
has three main components. The first component that
is frequently referred to as inertia models the parti-
cle’s tendency to keep it moving in the same direction
it was moving previously. In fact it controls the ex-
ploration of the search space. The second component,
called cognitive, attracts the particle towards the best
position p
(i)
that was found formerly. The last com-
ponent is referred to as social and it pulls the particle
towards the best position p
g
found by any particle.
The fitness value that corresponds to p
(i)
is called lo-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
692

cal best p
(i)
best
, whereas the fitness value corresponding
to p
g
is defined as g
best
. We implemented an asyn-
chronous PSO, where in a given iteration, each par-
ticle updates and communicates its state to particles
after its move to a new position, see pseudo-code of
PSO algorithm. This means that the particles that will
be updated in the same iteration can exploit the new
best position immediately, instead of using the global
best calculated in the previous iteration.
1 function PSO(X, iter)
2 for k = 0 to iter − 1 do
3 for each particle x
(i)
∈ X do
4 f x = f (x
(i)
)
5 if f x < p
(i)
best
then
6 p
(i)
= x
(i)
7 if f x < g
best
then
8 p
g
= x
(i)
9 v
(i)
← update velocity using (2)
10 x
(i)
← update position using (3)
11 endfor
12 endfor
13 return p
g
,X
The discussed algorithm is typically employed for
solving static optimization problems. The tracking of
the 6D object pose can be accomplished by dynamic
optimization and incorporating the temporal continu-
ity information into normal PSO. This means that
the 6D object pose can be estimated by a sequence
of static PSO-based optimizations, followed by re-
diversification of the particles to generate a search
area containing the potential object poses that can
arise in the next frame. The re-diversification of the
particle i can be obtained on the basis of normal dis-
tribution concentrated around the best particle loca-
tion p
g
in time t − 1, which can be expressed as:
x
(i)
← N (p
g
,Σ), where x
(i)
stands for particle’s lo-
cation in time t, Σ denotes the covariance matrix of
the Gaussian distribution, whose diagonal elements
are proportional to the expected movement.
3.1.2 Fitness Function
In recent years the PSO has been successfully applied
in several model-based applications, including object
detection (Ugolotti et al., 2013) and 3D pose refine-
ment via rendering and texture-based matching (Zab-
ulis et al., 2014). In 3D model-based tracking of 6D
object pose the most computationally demanding op-
eration is computing the objective function. A sub-
stantial speed-up of computation of the fitness func-
tion can be attained on modern GPU devices (Rymut
et al., 2013). In this work, more attention is paid to
reliable segmentation of the object of interest as well
as tracking accuracy of 6D object pose, and thus the
focus is on CPU implementation of fitness function to
simplify design and evaluation of various algorithms.
In PSO-based approach every particle represents
a hypothesis about likely 6D pose of the object. The
fitness score of the particle is calculated by project-
ing the 3D model and then matching the projected
model with the current image observations. Our fit-
ness score depends on the ratio of overlap between
rasterized 3D model in the hypothesized pose and the
segmented object. The overlap ratio is the sum of
the overlap degree from the object shape to the ras-
terized model and the overlap degree from the raster-
ized model to the object shape. The larger the over-
lap ratio is, the larger is the fitness value. Our fit-
ness function includes also the normalized distance
between the model’s projected edges and the closest
edges in the image. The discussed factor is calculated
on the basis of the edge distance map, see Fig. 2.
The fitness score is calculated as follows:
f
s
=
0.5 ∗
P
outside
P
model
+ 0.5 ∗
P
empty
P
seg
w
1
∗
K
P
K
w
2
(4)
where P
outside
stands for number of pixels projected
from model that are outside of segmented object on
image, see also Fig. 2 (left),
Figure 2: Fitness function.
P
model
denotes number of pixels in the projected
model, P
empty
is number of pixels of segmented object
on the image that are not covered by projected model,
P
seg
stands for number of pixels from segmented ob-
ject, K is sum of L2 distance transform values from
projected model’s edges to object edges on the image,
see Fig. 2 (right), P
K
denotes number of edge pixels in
the projected object outline, and w
1
= 0.4, w
2
= 0.6
are exponents that were determined experimentally.
3.2 6D Object Pose Tracking using PF
3.2.1 Particle Filtering
Particle filters permit estimating the state of partially
observable controllable Markov chains, i.e. dynami-
cal systems. For state estimation a probabilistic model
of the system and a probabilistic observation model
are needed. In this paper, the measurement at time t
3D Model-based 6D Object Pose Tracking on RGB Images using Particle Filtering and Heuristic Optimization
693

is denoted by z
t
, and x
t
denotes the state of the sys-
tem. Denoting by the superscript
t
all events leading
up to time t, the measurement can be expressed as:
z
t
= z
1
,z
2
,.. .,z
t
. where the subscript
t
stands for an
event at time t. Particle filters, like other Bayes fil-
ters, such as HMMs and Kalman filters, estimate the
posterior distribution p(x
t
|z
t
) of the dynamical sys-
tem state conditioned on the data. This is done via the
following recursive formula:
p(x
t
|z
t
) = η
t
p(z
t
|x
t
)
Z
p(x
t
|x
t−1
)p(x
t−1
|z
t−1
)dx
t−1
(5)
where η
t
is a normalization constant. To determine
the posterior three probability distributions, which are
referred as the probabilistic model of the dynamical
system are needed: (i) a measurement model p(z
t
|x
t
)
describing the probability of measuring z
t
when the
system is in state x
t
, (ii) a motion model p(x
t
|x
t−1
)
characterizing the probability of transiting from the
state x
t−1
to the state x
t
, (iii) an initial state distribu-
tion describing the initial system state.
A particle filter represents probability density
function (PDF) of nonlinear/non-Gaussian system by
a set of random samples. It is a common method to
cope with non-Gaussian noises. The posterior PDF
is approximated by a set of samples with associated
weights: X
t
= {x
[i]
t
}
i=1,...,m
. Such particle set approx-
imates the posterior p(x
t
|z
t
). Initially, at time t = 0,
the particles x
[i]
0
are drawn from the initial state distri-
bution p(x
0
). Given X
t−1
, the particle set X
t
is then
calculated recursively in the following manner:
1 function PF(X
t−1
)
2 set X
t
= X
s
t
=
/
0
3 for j = 1 to m do
4 pick the j-th sample x
[ j]
t−1
∈ X
t−1
5 draw x
[ j]
t
∼ p(x
t
|x
[ j]
t−1
)
6 set w
[ j]
t
= p(z
t
|x
[ j]
t
)
7 add hx
[ j]
t
,w
[ j]
t
i to X
s
t
8 endfor
9 for i = 1 to m do
10 draw x
[i]
t
from X
s
t
with prob. ∝ to w
[i]
t
11 add x
[i]
t
to X
t
12 endfor
13 return X
t
In lines 2 through 10 a new set of particles is gener-
ated on the basis of the estimate X
t−1
of the previous
time step through incorporating the probabilistic mo-
tion model, the probabilistic observation model and
a resampling. Thus, the particle filter estimates recur-
sively the particle set X
t
on the basis of X
t−1
. For large
m the resulting weighted particle set is asymptotically
distributed according to the desired posterior.
3.2.2 Motion and Observation Models
The probabilistic observation model is as follows:
p(z
t
|x
t
) = exp(− f
s
/σ
2
o
), where σ
o
is variance chosen
experimentally. Particles are propagated according to
a Gaussian distribution parameterized by σ
2
m
, which
was determined experimentally.
3.3 Proposed PF-PSO
The motivation is to improve the PSO by enabling
the algorithm dealing with multi-modal distributions.
At the beginning of each frame a PF is executed to
determine the posterior distribution. Then, samples
are clustered using k-means++ (Arthur and Vassilvit-
skii, 2007) algorithm, which applies a sequentially
random selection strategy according to a squared dis-
tance from the closest center already selected. Then,
a PSO with two sub-swarms consisting of samples as-
signed to the clusters is executed to find the modes in
the probability distribution. The number of the itera-
tions in the PSO is set to three. Afterwards, ten best
particles are selected to form a sub-swarm, see lines
#5-6 in below pseudo-code. Twenty iterations are ex-
ecuted by such a particle sub-swarm to find better par-
ticle positions. The best global position returned by
the discussed sub-swarm is used in visualization of
the best pose. Finally, an estimate of the probability
distribution is calculated by replacing the particle po-
sitions determined by the PF with corresponding par-
ticle positions, which were selected to represent the
modes in the probability distribution, see lines #5-6,
and particles refined by the sub-swarm, see line #8.
The initial probability distribution is updated by ten
particles with better positions found by the PSO algo-
rithms and ten particles with better positions found by
the sub-swarm, see lines #9-11.
1 function select(n best,X)
2 X
sorted
= quicksort(X) using f ()
3 return X
sorted
[1.. .n best]
1 X
t
= PF(X
t−1
)
2 X
c1
t
,X
c2
t
= k-means++(X
t
)
3 ∼,X
c1
t
= PSO(X
c1
t
,3)
4 ∼,X
c2
t
= PSO(X
c2
t
,3)
5 X
c1 best
t
= select(5,X
c1
t
)
6 X
c2 best
t
= select(5,X
c2
t
)
7 X
best
t
= X
c1 best
t
S
X
c2 best
t
8 g
best
,X
best
t
= PSO(X
best
t
,20)
9 substitute 5 x ∈ X
t
with corresp. x ∈ X
c1 best
t
10 substitute 5 x ∈ X
t
with corresp. x ∈ X
c2 best
t
11 substitute 10 x ∈ X
t
with corresp. x ∈ X
best
t
12 return g
best
,X
t
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
694
4 EXPERIMENTAL RESULTS
The experimental evaluation has been performed on
five objects: box, bottle, duck, clamp and drill. The
selected objects are almost entirely without any tex-
ture. 3D models of objects were created using the
Kinect 2.5D RGB-D camera (Izadi et al., 2011) and
SfM techniques. The OpenCV library (Bradski and
Kaehler, 2013) has been used to calibrate the RGB
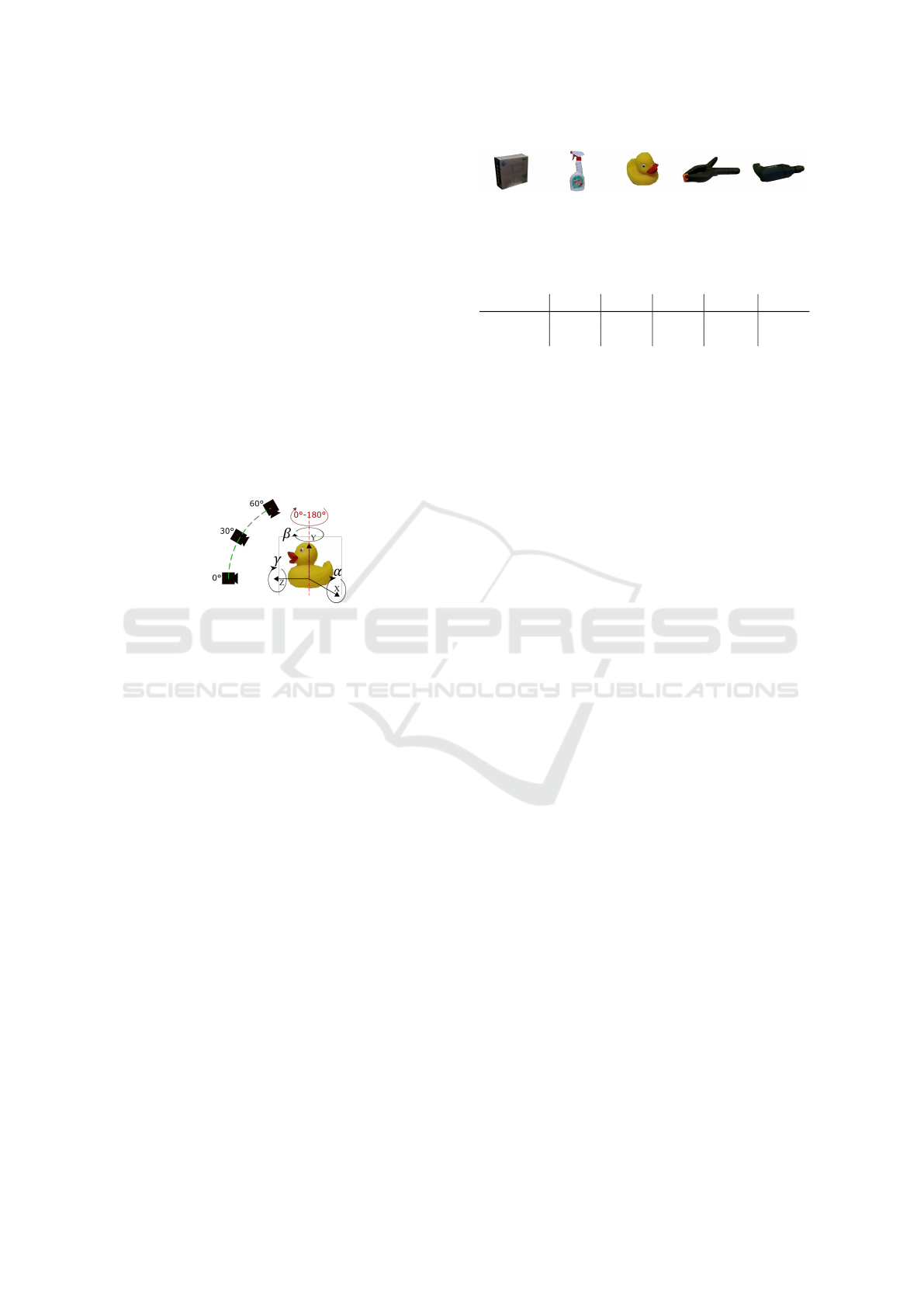
camera. The ground truths of the object poses have
been obtained by a turnable device, on which each
object has been placed and then observed from three
different camera views, see Fig. 3. For each camera
view the objects were rotated in range 0
◦
... 180
◦
, and
nineteen images were recorded. During object rota-
tion, an image has been acquired every ten degrees
with information about corresponding rotation angle.
Each experiment has been repeated three times, the
error metrics were calculated and then averaged.
Figure 3: Experiments setup.
In order to learn the segmentation model the con-
sidered objects were observed by the camera from dif-
ferent views. For each object more than one hun-
dred manual delineation of objects were done and
then used to train neural networks for object segmen-
tation. The models trained in such a way were then
used to segment the objects from the background. Af-
terwards, a dataset consisting of RGB images with the
corresponding ground truth data has been stored for
the evaluation of algorithms for 6D object pose esti-
mation and tracking.
4.1 Object Segmentation
A single U-Net neural network discussed in subsec-
tion 2 has been trained to segment the considered ob-
ject using the set of manually segmented images. Ta-
ble 1 presents the Dice scores achieved on the test
subset of the dataset. The test subset contains thirty
images for each object. As we can observe in Tab. 1,
promising segmentation results were achieved for U-
Net trained separately for each of the considered ob-
jects. Having on regard a better usefulness of a sin-
gle U-Net for segmentation of all five objects, in the
following subsections we present the experimental re-
sults achieved on the basis of the common U-Net for
all five objects, see sample results on Fig 4.
Figure 4: Segmented objects.
Table 1: Dice scores on the test sub-dataset (ind. stands for
individual U-Net for each object, whereas common means
a common U-Net for all objects.
U-Net box bottle duck clamp drill
ind. 0.985 0.964 0.974 0.971 0.928
common 0.946 0.972 0.978 0.968 0.965
4.2 Experimental Evaluation
We conducted experiments consisting in tracking the
6D object pose in sequences of RGB images. The ob-
jects were observed from different views. The exper-
iments were performed on sequences of RGB images
of size 288 × 512 acquired in advance and stored in
mp4 files. For every camera view, the 6D pose of each
object has been tracked on nineteen images. The ob-
jects were rotated about the vertical axis with poses
changed about ten degrees. We evaluated the qual-
ity of 6-DoF object pose estimation using ADD score
(Hinterstoisser et al., 2013). The 6D object pose esti-
mate is considered valid if the ADD is smaller than
ten percent of object’s diameter. Table 2 presents
scores [%] achieved by trackers on box [ADD < 3.5
cm], bottle [ADD < 2.6 cm], duck [ADD < 1.5 cm],
clamp [ADD < 2.2 cm] and drill [ADD < 3.0 cm].
The PF-PSO simple is a simplified version of the PF-
PSO, where no k-means++ clustering has been exe-
cuted, i.e. single PSO executing three iterations has
been employed. As we can notice in Tab. 2, the PF-
PSO achieves superior results on all objects except
the duck. The poses of symmetrical objects were
estimated with satisfactory accuracies with rotations
about vertical symmetry axes in range 0
◦
... 180
◦
.
The discussed results were achieved on the basis of
one thousand calls of the objective function in single
frame. The number of the calls of the fitness function
in PF-PSO has been identical to number of the calls
performed by the ordinary PF or the ordinary PSO. A
multinomial resampling has been used in the PF. The
state vector consists of 3D position and three Euler
angles describing rotation about axes, see Fig. 3.
Table 3 presents ADD scores [%] achieved by PF-
PSO in 6D object tracking in 0
◦
, 30
◦
and 60
◦
camera
views. As we can notice, the reason that the PF-PSO
achieves worse results for the duck are bigger errors
for 60
◦
camera view.
Figure 5 presents plots of angle tracking errors
over time, which were achieved by the algorithms for
the bottle and the drill. As we can observe, the parti-
3D Model-based 6D Object Pose Tracking on RGB Images using Particle Filtering and Heuristic Optimization
695

Table 2: Scores [%] achieved in 6D object tracking for box [ADD < 3.5 cm], bottle [ADD < 2.6 cm], duck [ADD < 1.5 cm],
clamp [ADD < 2.2 cm] and drill [ADD < 3.0 cm].
tracking score [%] box bottle duck clamp drill
PF, angle 0. . . 180
◦
0.345 0.222 0.246 0.281 0.450
PSO, angle 0. . . 180
◦
0.807 0.877 0.719 0.579 0.813
PF-PSO simple, ang. 0. . . 180
◦
0.889 0.912 0.351 0.520 0.614
PF-PSO, ang. 0. . . 180
◦
0.901 0.947 0.673 0.643 0.889
Table 3: Scores [%] achieved by PF-PSO in 6D object tracking.
tracking score [%] box bottle duck clamp drill
0
◦
camera view, angle 0. . . 90
◦
0.933 1.000 0.900 0.733 0.900
0
◦
camera view, angle 0. . . 180
◦
0.895 1.000 0.890 0.421 0.825
30
◦
camera view, angle 0. . . 90
◦
0.933 0.833 1.000 0.833 0.900
30
◦
camera view, angle 0. . . 180
◦
0.895 0.895 0.632 0.737 0.947
60
◦
camera view, angle 0. . . 90
◦
0.833 0.933 0.400 0.867 0.900
60
◦
camera view, angle 0. . . 180
◦
0.912 0.947 0.526 0.772 0.895
Average, angle 0. . . 90
◦
0.900 0.922 0.767 0.811 0.900
Average, angle 0. . . 180
◦
0.901 0.947 0.673 0.643 0.889
Figure 5: Pose errors over time for bottle and drill.
cle filter can continue tracking the object pose despite
currently larger errors in several consecutive frames,
see also errors about one hundred degrees for the bot-
tle. The errors achieved by the PF-PSO for specific
angle are smaller than 10
◦
, except the error in a few
frames for the drill, where in x axis, see Fig. 3, it is
slightly bigger than ten degrees.
In experiments with pose tracking algorithms we
noticed that the ordinary PSO can achieve promising
results. However, in tracking the 6D pose of more
complicated objects, the ordinary PSO can have dif-
ficulties with the tracking due to selecting in a given
frame a mode, which in next frames will not allow to
seek the optimal pose. On the other hand, the pro-
posed PF-PSO contains particles representing worse
mode in the given frame, which can be useful and can
give better results in forthcoming frames.
The complete system for 6D pose estimation and
tracking has been implemented in C/C++ and Python.
The system runs on an ordinary PC with a GPU card.
The images for training and evaluating the segmenta-
tion algorithm as well as extracted objects with cor-
responding ground-truth for evaluating the 6D ob-
ject pose estimation and tracking are freely available
for download at: http://home.agh.edu.pl/
∼
majcher/
src/visapp.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
696

5 CONCLUSIONS
We have presented a 3D model based algorithm for
6D object pose tracking in sequence of RGB images.
The object has been segmented using U-Net neural
network. The 6D object pose estimation has been
performed by particle filter combined with particle
swarm optimization algorithm. Owing to clustering
particles representing the probability distribution in
the PF, the extracted modes were processed by PSO
to represent them by a few representative particles in
the refined probability distribution. In future work we
are going to apply this algorithm for object manipula-
tion by Franka Emika. The initialization of the track-
ing will be done on the basis of pose regression neural
networks.
ACKNOWLEDGEMENTS
This work was supported by Polish National
Science Center (NCN) under a research grant
2017/27/B/ST6/01743.
REFERENCES
Arthur, D. and Vassilvitskii, S. (2007). K-means++: The
Advantages of Careful Seeding. In Proc. ACM-SIAM
Symp. on Discrete Algorithms, pages 1027–1035.
Brachmann, E., Krull, A., Michel, F., Gumhold, S., Shotton,
J., and Rother, C. (2014). Learning 6D object pose es-
timation using 3D object coordinates. In ECCV, pages
536–551. Springer.
Brachmann, E., Michel, F., Krull, A., Yang, M., Gumhold,
S., and Rother, C. (2016). Uncertainty-Driven 6D
Pose Estimation of Objects and Scenes from a Single
RGB Image. In IEEE Conf. on Computer Vision and
Pattern Recognition (CVPR), pages 3364–3372.
Bradski, G. and Kaehler, A. (2013). Learning OpenCV:
Computer Vision in C++ with the OpenCV Library.
O’Reilly Media, Inc., 2nd edition.
Deng, X., Mousavian, A., Xiang, Y., Xia, F., Bretl, T., and
Fox, D. (2019). PoseRBPF: A Rao-Blackwellized
Particle Filter for 6D Object Pose Tracking. In
Robotics: Science and Systems (RSS).
Doucet, A., Godsill, S., and Andrieu, C. (2000). On Se-
quential Monte Carlo Sampling Methods for Bayesian
Filtering. Statistics and Computing, 10(3):197–208.
Fischler, M. A. and Bolles, R. C. (1981). Random Sample
Consensus: A Paradigm for Model Fitting with Ap-
plications to Image Analysis and Automated Cartog-
raphy. Commun. ACM, 24(6):381–395.
Hinterstoisser, S., Holzer, S., Cagniart, C., Ilic, S., Kono-
lige, K., Navab, N., and Lepetit, V. (2011). Multi-
modal templates for real-time detection of texture-less
objects in heavily cluttered scenes. In Int. Conf. on
Computer Vision, pages 858–865.
Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski,
G., Konolige, K., and Navab, N. (2013). Model based
training, detection and pose estimation of texture-less
3D objects in heavily cluttered scenes. In Computer
Vision – ACCV 2012, pages 548–562. Springer.
Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-
celerating deep network training by reducing internal
covariate shift. In ICML - vol. 37, pages 448–456.
Izadi, S., Kim, D., Hilliges, O., Molyneaux, D., Newcombe,
R., Kohli, P., Shotton, J., Hodges, S., Freeman, D.,
Davison, A., and Fitzgibbon, A. (2011). KinectFu-
sion: Real-time 3D Reconstruction and Interaction
Using a Moving Depth Camera. In Proc. ACM Symp.
on User Interface Soft. and Techn., pages 559–568.
Kennedy, J. and Eberhart, R. (1995). Particle Swarm Opti-
mization. In Proc. of IEEE Int. Conf. on Neural Net-
works, pages 1942–1948. IEEE Press, Piscataway, NJ.
Lepetit, V., Pilet, J., and Fua, P. (2004). Point matching as a
classification problem for fast and robust object pose
estimation. In Proc. IEEE Conf. on Computer Vision
and Pattern Recognition, volume 2, pages II–II.
Marchand, E., Uchiyama, H., and Spindler, F. (2016).
Pose estimation for augmented reality: A hands-on
survey. IEEE Trans. on Vis. and Comp. Graphics,
22(12):2633–2651.
Rad, M. and Lepetit, V. (2017). BB8: A scalable, accurate,
robust to partial occlusion method for predicting the
3D poses of challenging objects without using depth.
In IEEE Int. Conf. on Comp. Vision, pages 3848–3856.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-
Net: Convolutional networks for biomedical image
segmentation. In MICCAI, pages 234–241. Springer.
Rymut, B., Kwolek, B., and Krzeszowski, T. (2013). GPU-
accelerated human motion tracking using particle fil-
ter combined with PSO. In Adv. Concepts Intell. Vi-
sion Syst., LNCS, vol. 8192, pages 426–437. Springer.
Sengupta, S., Basak, S., and Peters, R. A. (2019). Parti-
cle Swarm Optimization: A survey of historical and
recent developments with hybridization perspectives.
Machine Learning and Knowl. Extr., 1(1):157–191.
Ugolotti, R., Nashed, Y. S. G., Mesejo, P., Ivekovi
ˇ
c,
v., Mussi, L., and Cagnoni, S. (2013). Particle
Swarm Optimization and Differential Evolution for
Model-based Object Detection. Appl. Soft Comput.,
13(6):3092–3105.
Vidal, J., Lin, C., and Mart
´
ı, R. (2018). 6d pose estima-
tion using an improved method based on point pair
features. In Int. Conf. on Control, Automation and
Robotics (ICCAR), pages 405–409.
Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2018).
PoseCNN: A Convolutional Neural Network for 6D
Object Pose Estimation in Cluttered Scenes. In
Robotics: Science and Systems XIV (RSS).
Zabulis, X., Lourakis, M. I., and Stefanou, S. S. (2014).
3D pose refinement using rendering and texture-based
matching. In Computer Vision and Graphics, pages
672–679. Springer.
3D Model-based 6D Object Pose Tracking on RGB Images using Particle Filtering and Heuristic Optimization
697
