
Assessing Preferred Proximity between Different Types of Embryonic
Stem Cells
Minhong Wang
1 a
, Athanasios Tsanas
1 b
, Guillaume Blin
2 c
and Dave Robertson
3 d
1
Usher Institute, The University of Edinburgh, Edinburgh, U.K.
2
MRC Center for Regenerative Medicine, The University of Edinburgh, Edinburgh, U.K.
3
School of Informatics, The University of Edinburgh, Edinburgh, U.K.
Keywords:
Embryonic Stem Cells, Different Types of Stem Cells, Statistical Analysis, Minimum Spanning Tree.
Abstract:
Embryonic stem cells (ESCs) studies play an important role for understanding the molecular events that un-
derlie cell lineage commitment and serve as models for the development of disease. However, the interactions
between neighboring embryonic stem cells are not fully understood. Assessing proximity between different
types of embryonic stem cells might provide more information about distinct behaviors of embryonic stem
cells. In this study, we processed 186 cell colonies on disc constrained microdomains and 152 cell colonies on
ellipse. We grouped cell colonies based on different observed patterns and grouped cells by their locations. By
applying two measurements on embryonic stem cell colonies, minimum spanning tree and average distance to
the five closest objects, we investigated the difference of proximity between different types of embryonic stem
cells, the difference between grouped cell colonies and the difference between grouped cells. We found one
type of ESC has a smaller average path based on minimum spanning tree and higher proximity than the other
type. We report consistent results for different types of embryonic stem cells: these findings may be useful to
set benchmarks for empirical models which replicate ESC behaviors.
1 INTRODUCTION
Embryonic stem cells (ESCs) have shown potential
for regenerative medicine towards the development of
novel therapies for a wide range of diseases or injuries
(Wu and Hochedlinger, 2011). ESCs can self-renew
and differentiate into almost any type of mature cells.
Due to the special properties of ESCs, they are use-
ful for: 1) understanding the molecular events that
regulate stemness and cell lineage commitment (Ivey
et al., 2008)(Gan et al., 2007); 2) modeling develop-
ment of disease (Avior et al., 2016).
Previous work has demonstrated that stem cells
have the ability to socialize with their neigh-
bors while interacting with their micro-environment
(Fuchs et al., 2004). Recent studies illustrate that
different types of ESCs have distinct dynamic social
behaviors, such as variable migration speed and pre-
ferred number of neighbors (Phadnis et al., 2015).
a
https://orcid.org/0000-0001-7041-7045
b
https://orcid.org/0000-0002-0994-8100
c
https://orcid.org/0000-0002-9295-237X
d
https://orcid.org/0000-0001-9574-849X
However, the neighboring effects in ESCs are still
not fully understood as the underlying mechanisms of
their communication are highly complex (Madl and
Heilshorn, 2018)(Watt and Hogan, 2000). Under-
standing neighboring effects can benefit the investi-
gation of behaviors in ESCs, which would be helpful
for controlling differentiation and contribute towards
the development of new stem cell therapies.
Brachyury (T) is a marker of early mesendoder-
mal expression (Beddington et al., 1992)(Wilkinson
et al., 1990). T+ cells are early differentiated cells as
they are marked by Brachyury (T), while T- cells are
naive ESCs. The process of spatial pattern formation
in differentiated stem cells is essential for establish-
ing functional mammalian tissue. Blin and colleagues
demonstrated that T+ and T- cells prefer different
numbers of neighboring cells, with T- cells preferring
more neighbors than T+ cells (Blin et al., 2018).
In this study we extend on these findings and look
into the preferred proximity (closeness) of neighbors
between the two types of cells. We applied two new
measurements to quantify the proximity of T+ and
T- cells in ESC colonies and assess the difference of
proximity within different patterning constraints.
Wang, M., Tsanas, A., Blin, G. and Robertson, D.
Assessing Preferred Proximity Between Different Types of Embryonic Stem Cells.
DOI: 10.5220/0009368903770381
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 4: BIOSIGNALS, pages 377-381
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
377
2 METHODS
2.1 Empirical Data
We used previous data of ESC colonies consisting of
186 images for disc experiments and 152 images for
ellipse experiments (Blin et al., 2018)(Wang et al.,
2018). Each image corresponds to a single cell colony
that was captured 48 hours after the initial seeding
of the stem cells. Each colony was randomly seeded
with both T+ and T- cells. Populations of each cell
type were isolated in the images by thresholding la-
belled image data. We extracted the cells’ locations
(described by x and y values) based on the centers of
the nuclei. For disc experiments, we selected cells
within 95.5 µm from the center of the disc; for ellipse
experiments, we selected cells within the ellipse with
the semi-major axis as 193.5 µm and semi-minor axis
as 47 µm. Cells outside these defined constrained ar-
eas were considered as random noise and discarded.
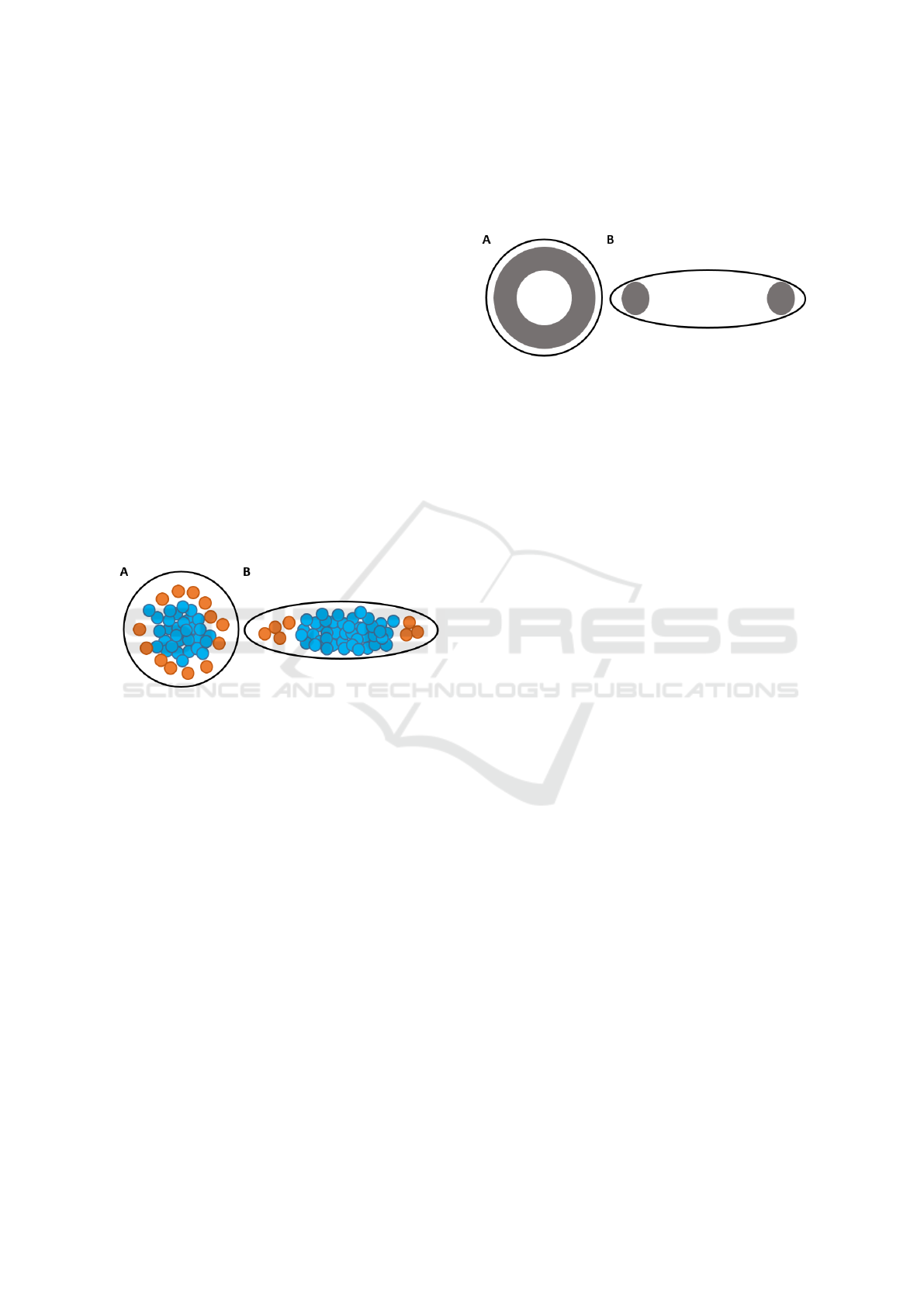
Figure 1 shows the indicative plots for disc and ellipse
experiments.
Figure 1: Indicative plots for A) disc and B) ellipse experi-
ments. Blue circles represent T- cells; orange circles repre-
sent T+ cells.
2.2 Pattern Grouping
For both disc and ellipse experiments, we applied 2D
kernel density estimation (Botev et al., 2010) to ob-
tain the density maps of aggregated T- and T+ cells
separately. Since we are interested in the locations of
T+ cells, we thresholded the aggregated density map
of T+ cells based on the mean of max and min density
of each pixel to obtain the areas with high density T+
cells. The borders of high density areas (HDA) were
smoothed by least squared circle or ellipse function.
Figure 2 shows indicative plots for HDA on the disc
and ellipse constrained microdomain. In the disc ex-
periments, the HDA is a ring shaped area due to the
symmetry of the disc. In the ellipse, the HDA is fo-
cused at the tips of the major axis of the ellipse. We
compared the ratio of HDA/non-HDA size to the ra-
tio of HDA/non-HDA cell number to get an indica-
tion of cell spacing. Subsequently we obtained three
distinct groups of different cell patterns based on the
grouping of T+ cells: 1) cell colonies with relatively
higher density of T+ cells on HDA; 2) cell colonies
with relatively low density of T+ cells on HDA; 3)
cell colonies with no T+ cells.
Figure 2: Indicative plots for HDA on A) disc and B) ellipse
experiments.
2.3 Measurements of Neighboring
Effects
2.3.1 Minimum Spanning Tree
We built a connected graph (Wilson, 1996) for T+ or
T- cells in each cell colony by taking each cell as a
node and connecting any two nodes with an edge. The
weight of each edge was defined as the Euclidean dis-
tance between the two nodes. A spanning tree is a
sub-graph that connects every node in the graph with-
out any cycles (Kruskal, 1956). As there are different
spanning trees for the graph, the minimum spanning
tree is the spanning tree connecting the nodes through
edges and has the smallest total weight (Prim, 1957).
Therefore, the minimum spanning tree calculates the
shortest path that connects all T+ or T- cells within the
colony. We calculated the average path distance be-
tween two nodes (cells) by dividing the path distance
of the minimum spanning tree by the number of T+ or
T- cells respectively. A smaller average path distance
indicates a higher proximity. Following this, we ap-
plied kernel density estimation (Botev et al., 2010) of
the average path distance we received from T+ and
T- cells from each cell colony. The number of mesh
points used in the kernel density estimation was 256.
We also calculated the minimum spanning tree for T+
and T- cells in each pattern group.
2.3.2 Quantifying Average Distance of Each
Query Object to Five Nearest Targets
For each T+ or T- cell (i.e., object) within disc and
ellipse experiments, we found the five closest T+ and
T- cells (i.e., targets). We calculated the average dis-
tance from each object to its targets (referred to as D).
The data presented four different cases of calculating
D: 1) the object is a T- cell with T- cell targets; 2) the
object is a T- cell with T+ cell targets; 3) the object
SERPICO 2020 - Special Session on Mining Self-reported Outcome Measures, Clinical Assessments, and Non-invasive Sensor Data
Towards Facilitating Diagnosis, Longitudinal Monitoring, and Treatment
378
is a T+ cell with T- cell targets; and 4) the object is a
T+ cell with T+ cell targets. For these four cases, we
applied kernel density estimation (Botev et al., 2010)
of D from all cells within each pattern group. Based
on the borders of the HDA, we applied kernel den-
sity estimation of the cells in the HDA and cells out-
side the HDA separately to investigate the difference
in proximity between the different cell type with both
regions.
3 RESULTS
3.1 Pattern Groups
Figure 3 shows the percentage of different patterns
observed in the disc and ellipse experiments. We de-
fined pattern 1 as a relatively higher density of T+
cells within the HDA. In pattern 2, the density of T+
cells within the HDA was lower than the density of T+
cells within the remaining areas. On pattern 3, there
were no T+ cells.
Figure 3: The percentage of the 3 different patterns ob-
served within the A) disc and B) ellipse experiments. Pat-
tern 1: high density of T+ cells within the HDA. Pattern 2:
density of T+ cells within the HDA was lower than the den-
sity of T+ cells within the remaining areas. Pattern 3: no
T+ cells.
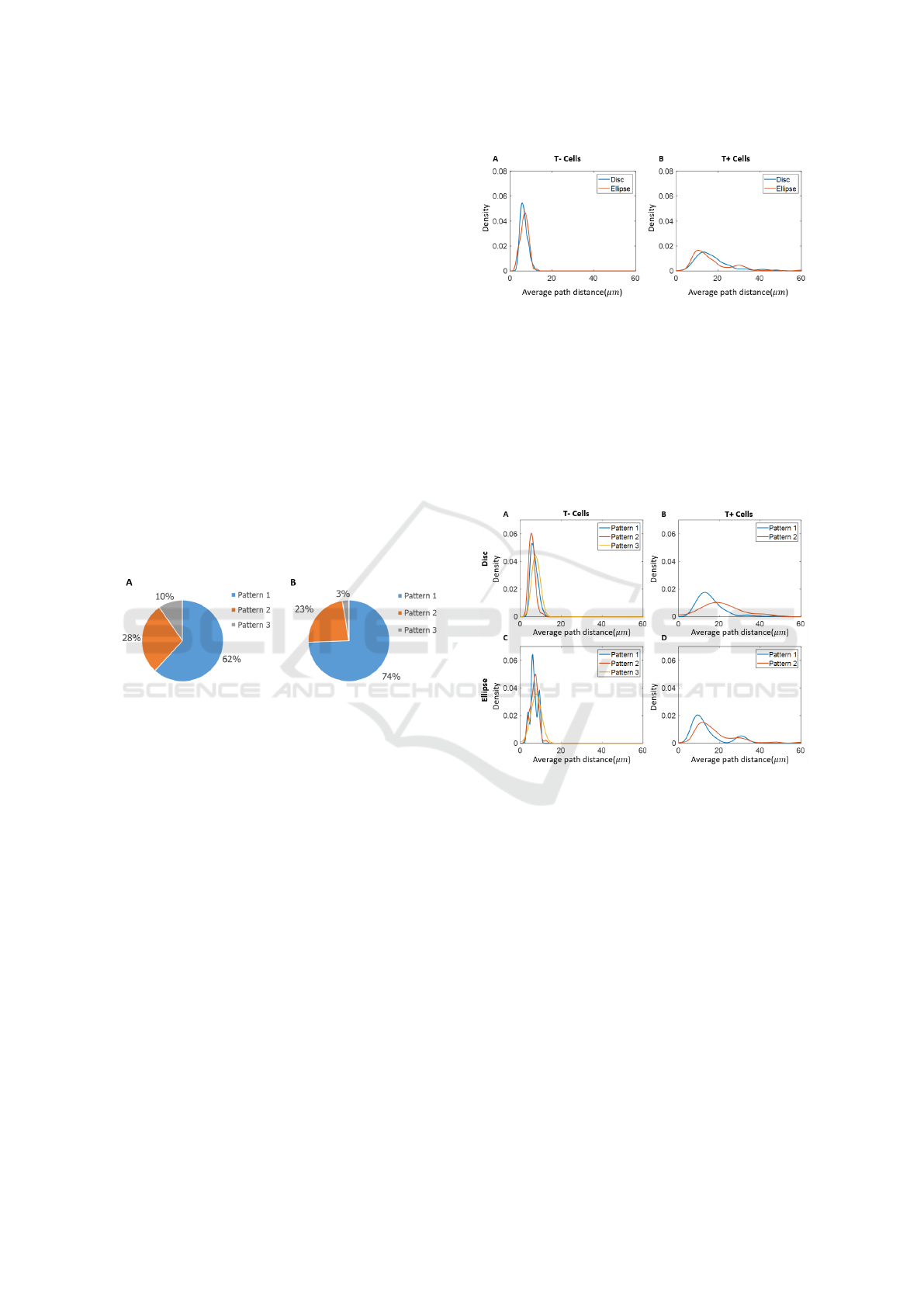
3.2 Minimum Spanning Tree Results
The results of the overall distribution of average path
distance based on the minimum spanning tree are
shown in Figure 4. The overall aggregate results for
the disc and the ellipse were consistent. It is note-
worthy that T- cells have much smaller average path
distance than T+ cells. The results indicate that T-
cells have a higher proximity than T+ cells, and the
variation in proximity of T+ cells was greater than in
T- cells.
Figure 5 shows the kernel density estimation re-
sults from the pattern groups described in 3.1. The
difference found in T- cells between the pattern
groups was relatively small. For Pattern 3, in which
there are no T+ cells, T- cells have the highest prox-
imity. T+ cells in Pattern 1 (more T+ cells on HDA)
Figure 4: Kernel density estimation of average path distance
(µm) of A) T- cells and B) T+ cells within disc and ellipse
experiments.
are slightly more compact than T+ cells in Pattern 2.
Again, the results from disc and ellipse experiments
are consistent. The double peaks of T+ cells on el-
lipse experiments might due to the fact that in some
colonies T+ cells were more dense at one tip of the el-
lipse and in some colonies T+ cells were more dense
at both tips.
Figure 5: Kernel density estimation of average path distance
of A) T- cells on disc experiments; B) T+ cells on disc ex-
periments; C) T- cells on ellipse experiments; D) T+ cells
on ellipse experiments.
3.3 Results of Average Distance of Each
Object to Five Nearest Targets
Figure 6 shows the kernel density estimation results
of average distance from the object to the five closest
targets (D) from the aggregated cells on disc and el-
lipse experiments. The case of T- as the object and T-
cells as the target results in the highest peak density
in both disc and ellipse experiments. This is consis-
tent with the results from the minimum spanning tree
which showed that T- cells have a high proximity. For
the case in which T- cells are taken as objects and T+
cells as targets the distribution of D has a high mean
value and a wide spread. This result could be due to
Assessing Preferred Proximity Between Different Types of Embryonic Stem Cells
379
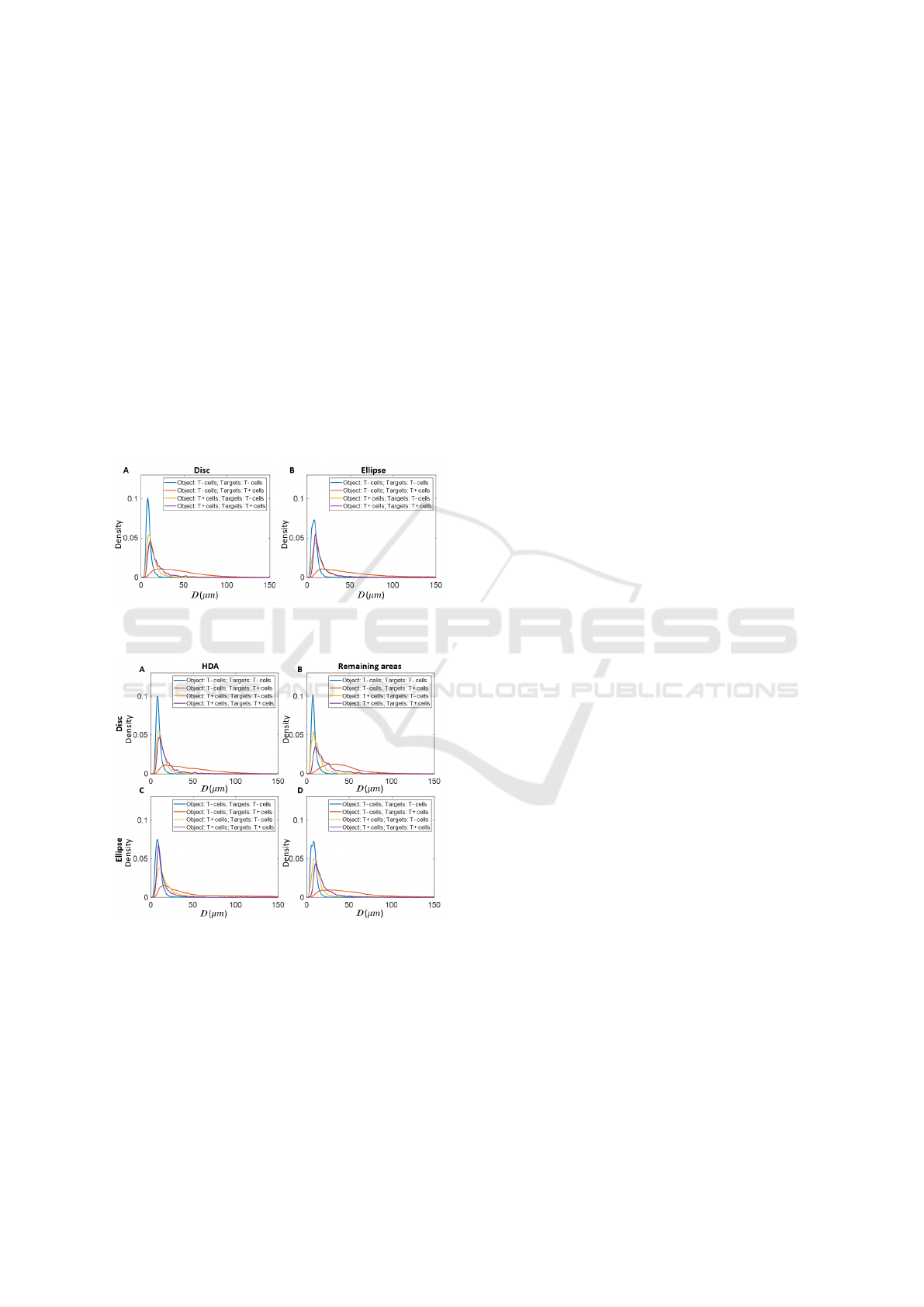
the fact that there are more T- cells than T+ cells on
the colonies. Hence, for T- cells it takes longer dis-
tance to retrieve for the closest T+ cells in average.
For T+ cells, the distribution of D to its five closest
T+ or T- cells are relatively similar.
Figure 7 shows the kernel density estimation re-
sults of D which is grouped by cell locations. It shows
for all object T- cells the average D of the five closest
T- cells showed relatively low variety whether con-
tained within the HDA or not. For T- cells not in the
HDA, the average distance to the five closest T+ cells
is higher than for T- cells in the HDA. Interestingly,
for the cases in which T+ cells are taken as objects,
and both T- or T+ cells as targets, the T+ cells in the
HDA have a higher average D than T+ cells not in the
HDA and the distribution of D is slightly more spread
out.
Figure 6: Kernel density estimation results of D from the
aggregated cells on A) disc and B) ellipse experiments.
Figure 7: Kernel density estimation results of D from the
aggregated A) object cells on HDA on disc; B) object cells
on remaining areas on disc; C) object cells on HDA on el-
lipse; D) object cells on remaining areas on ellipse.
4 DISCUSSION
In this study, we quantified the proximity of different
types of cells in ESC colonies on different shaped mi-
crodomains. We assessed cells’ proximity in different
patterns groups, and the difference of the proximity
between different types of cells depending on location
(as shown in Figure 5 and Figure 7). The obtained re-
sults are consistent across discs and ellipses, which
provides some confidence on the generalizability of
the extracted concepts (as shown in Figure 4 and Fig-
ure 6).
The results of the average path distance based
minimum spanning tree indicate that T- cells prefer
a higher proximity than T+ cells. The T+ cells in
colonies that formed the pattern with more cells in
the HDA (Pattern 1) have a higher proximity than the
T+ cells in the other pattern groups. The results from
D are consistent with the results from the minimum
spanning tree that T- cells have a higher proximity
than T+ cells. It also suggests that T+ cells have a
tendency to stay away from other cells as they have
a relatively low proximity to both T- and other T+
cells, compared to the high proximity we observed in
T- cells.
Compared to our previous work, we have provided
a more thorough analysis of the distribution of differ-
ent measurements by applying kernel density estima-
tion. We also analysed the difference between dif-
ferent observed patterns and different types of cells.
This information further improves our understanding
of the difference between types of stem cells, which
could be useful for controlling the differentiation in
ESCs. To the best of our knowledge, we are not aware
of other studies in literature which have investigated
the proximity in embryonic stem cells with the marker
Brachyury (T).
Currently, we are building diverse ESC compu-
tational models to reproduce the pattern formation
by investigating parsimonious, minimal sets of differ-
ent social behaviors of different types of ESCs which
replicate experimental data. This study is a step to-
wards informing the hypothesis that we can test in our
models as T+ cells tend to stay away from other cells.
In conclusion, we provided quantitative informa-
tion regarding the proximities of T- and T+ cells. T+
cells have a tendency to stay away from other cells
according to the results from the minimum spanning
tree and D. This finding could be useful in the analysis
of different social behaviors between different types
of ESCs.
ACKNOWLEDGEMENTS
MW would like to thank Sally Lab for supporting
data.
SERPICO 2020 - Special Session on Mining Self-reported Outcome Measures, Clinical Assessments, and Non-invasive Sensor Data
Towards Facilitating Diagnosis, Longitudinal Monitoring, and Treatment
380

REFERENCES
Avior, Y., Sagi, I., and Benvenisty, N. (2016). Pluripotent
stem cells in disease modelling and drug discovery.
Nature Reviews Molecular Cell Biology, 17(3):170–
182.
Beddington, R. S. P., Rashbass, P., and Wilson, V. (1992).
Brachyury - a gene affecting mouse gastrulation and
early organogenesis. Development, 116:157–165.
Blin, G., Wisniewski, D., Picart, C., Thery, M., Puceat,
M., and Lowell, S. (2018). Geometrical confine-
ment controls the asymmetric patterning of Brachyury
in cultures of pluripotent cells. Development,
145:dev.166025.
Botev, Z. I., Grotowski, J. F., and Kroese, D. P. (2010). Ker-
nel density estimation via diffusion. Annals of Statis-
tics, 38(5):2916–2957.
Fuchs, E., Tumbar, T., and Guasch, G. (2004). Socializing
with the neighbors: Stem cells and their niche. Cell,
116(6):769–778.
Gan, Q., Yoshida, T., McDonald, O. G., and Owens, G. K.
(2007). Concise Review: Epigenetic Mechanisms
Contribute to Pluripotency and Cell Lineage Determi-
nation of Embryonic Stem Cells. Stem Cells, 25(1):2–
9.
Ivey, K. N., Muth, A., Arnold, J., King, F. W., Yeh, R. F.,
Fish, J. E., Hsiao, E. C., Schwartz, R. J., Conklin,
B. R., Bernstein, H. S., and Srivastava, D. (2008).
MicroRNA Regulation of Cell Lineages in Mouse
and Human Embryonic Stem Cells. Cell Stem Cell,
2(3):219–229.
Kruskal, J. B. (1956). On the shortest spanning subtree of
a graph and the traveling salesman problem. Proceed-
ings of the American Mathematical Society, 7(1):48–
50.
Madl, C. M. and Heilshorn, S. C. (2018). Engineering
hydrogel microenvironments to recapitulate the stem
cell niche. Annual Review of Biomedical Engineer-
ing, 20(1):21–47. PMID: 29220201.
Phadnis, S. M., Loewke, N. O., Dimov, I. K., Pai, S.,
Amwake, C. E., Solgaard, O., Baer, T. M., Chen, B.,
and Reijo Pera, R. A. (2015). Dynamic and social
behaviors of human pluripotent stem cells. Scientific
Reports, 5(14209):1–12.
Prim, R. C. (1957). Shortest connection networks and some
generalizations. The Bell System Technical Journal,
36(6):1389–1401.
Wang, M., Robertson, D., Blin, G., Lowell, S., and Tsanas,
T. (2018). Agent-based modelling of pattern forma-
tion in pluripotent stem cells: initial experiments and
results. In 2018 11th International Congress on Im-
age and Signal Processing, BioMedical Engineering
and Informatics (CISP-BMEI), pages 1–5. IEEE.
Watt, F. M. and Hogan, B. L. (2000). Out of Eden: stem
cells and their niches. Science (New York, N.Y.),
287(5457):1427–1430.
Wilkinson, D. G., Bhatt, S., and Herrmann, B. G. (1990).
Expression pattern of the mouse T gene and its role
in mesoderm formation. Nature, 343(February):657–
659.
Wilson, R. J. (1996). Introduction to Graph Theory.
Wu, S. M. and Hochedlinger, K. (2011). Harnessing the
potential of induced pluripotent stem cells for regen-
erative medicine. Nature Cell Biology, 13(5).
Assessing Preferred Proximity Between Different Types of Embryonic Stem Cells
381
