The Comparison of Algorithms for Life-threatening Cardiac

Arrhythmias Recognition

Anatoliy P. Nemirko

, Liudmila A. Manilo, Boris E. Alekseev,

Anastasia A. Sokolova

and Zafar M. Yuldashev

Department of Biomedical Engineering, Saint-Petersburg Electrotechnical University "LETI",

Str. Professora Popova 5, 197376 Saint-Petersburg, Russian Federation

Keywords: Electrocardiogram, Arrhythmia, Spectrum, Classification, Fourier Transform.

Abstract: During the clinical monitoring of the human heart activity the main goal is to detect heart arrhythmias and

capture their precursors as early as possible. And we decided to apply 2 seconds gliding window for life-

threatening cardiac arrhythmias recognition. All types of arrhythmias were grouped into six classes depending

on their danger to the human life. And these classes were separated in two parts: threatening humans’ life and

others. As a classification features Fourier transform with spectrum up to 15 Hz were picked. In this paper we

describe the formed dataset of ECG fragments and compare efficiency of different simple classification

algorithms for this two-class problem. The following algorithms were tested: k-nearest neighbours, nearest

convex hull algorithm, nearest mean and SVMs with different kernels. The results appeared to be sufficiently

appropriate.

1 INTRODUCTION

Perspective intelligent outpatient monitoring systems

aim not only at long-term electrocardiogram

monitoring by also providing doctors and patients

with alarms based on the results of its online analysis.

Prominent applications of such systems include

detection of various life-threatening disorders such as

severe arrhythmia and/or ischaemia events as well as

signatures of such conditions as stroke and cardiac

arrest. Such as ventricular fibrillation (flutter) and

tachycardia in 40% of cases lead to cardiac arrest

(Wik et al., 2003). Electric defibrillation is only

effective therapy for these disorders. For the

successful implementation of life-threatening cardiac

arrhythmias recognition algorithms and their online

performance, the keynote requirements include

reliability and detection time (Moraes et al., 2002;

Meng et al., 2016). A large number of algorithms

have already been developed and tested using various

classifiers and features to solve this problem. In (Xu

et al., 2018), authors have made a review and

https://orcid.org/0000-0001-6459-626X

https://orcid.org/0000-0002-8380-4850

https://orcid.org/0000-0003-1075-3420

comparison of these algorithms and methods

proposed in the last decades.

Different features of life-threatening cardiac

arrhythmias (Cheng and Dong, 2017) were proposed

for the algorithms of their detection: morphology

analysis (Arafat et al., 2011; Amann et al., 2006;

Monte et al., 2011), spectral analysis (Barro et al.,

1989; Dzwonczyk et al., 1990), time-frequency

analysis (Millet-Roig et al., 1999), complexity

measure (Zhang et al., 1999; Roopaei et al., 2010),

wavelet analysis (Rasooli et al., 2015; Balasundaram

et al., 2013; Li et al., 2011), empirical mode

decomposition (EMD) (Arafat et al., 2009; Anas et

al., 2011; Kaur and Singh, 2013), sequential detection

methods (Anas et al., 2010; Thakor et al., 1990),

machine learning (Verma and Dong, 2016). However,

the authors used different databases and datasets for

their methods testing. In (Amann et al., 2005) the

majority of these methods were tested under the same

conditions by using open published annotated

databases, and it was shown that they could not

achieve the proclaimed performance.

402

Nemirko, A., Manilo, L., Alekseev, B., Sokolova, A. and Yuldashev, Z.

The Comparison of Algor ithms for Life-threatening Cardiac Arrhythmias Recognition.

DOI: 10.5220/0009374904020407

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 1: BIODEVICES, pages 402-407

ISBN: 978-989-758-398-8; ISSN: 2184-4305

The current standard for clinical monitoring

systems is to determine the onset of ventricular

fibrillation in 5 seconds after the episode starting

However, when it comes to such a dangerous heart

conditions, every second saved can have a huge

impact on a patient's health and life.

Based on these statements, the following task was

set: to reduce the detection time of the classification

algorithm of dangerous arrhythmias and,

additionally, to try to determine the occurrence of

non-dangerous violations that are highly likely to

evolve into dangerous ones. They are related to

precursors.

2 DATABASE AND

PPEPROCESSING

We used «The MIT-BIH Malignant Ventricular

Ectopy Database» (Goldberger et al., 2000). It

contains 22 two-channel annotated ECG recordings

each of about 30 minutes duration, with a sampling

frequency of 360 Hz. The recordings obtained from

the patients who experienced various types of heart

disorders: ventricular ectopic beats (bigeminy,

trigeminy, couples and groups), atrial tachycardia,

atrial fibrillation, pirouette tachycardia, ventricular

tachycardia, ventricular flutter and ventricular

fibrillation. For each of the signals, a set of

annotations was manually verified according to time

points of heart rhythm changing.

The recordings of this database were used as the

initial data for the formation set of two-second

segments in our own database. The process of this

database creation is described below.

The signals represented in the original database

are obtained using professional electrocardiographs

and are almost free of power grid noise or high-

frequency noises. However, there is still a noticeable

baseline drift corrupting some parts of the signal

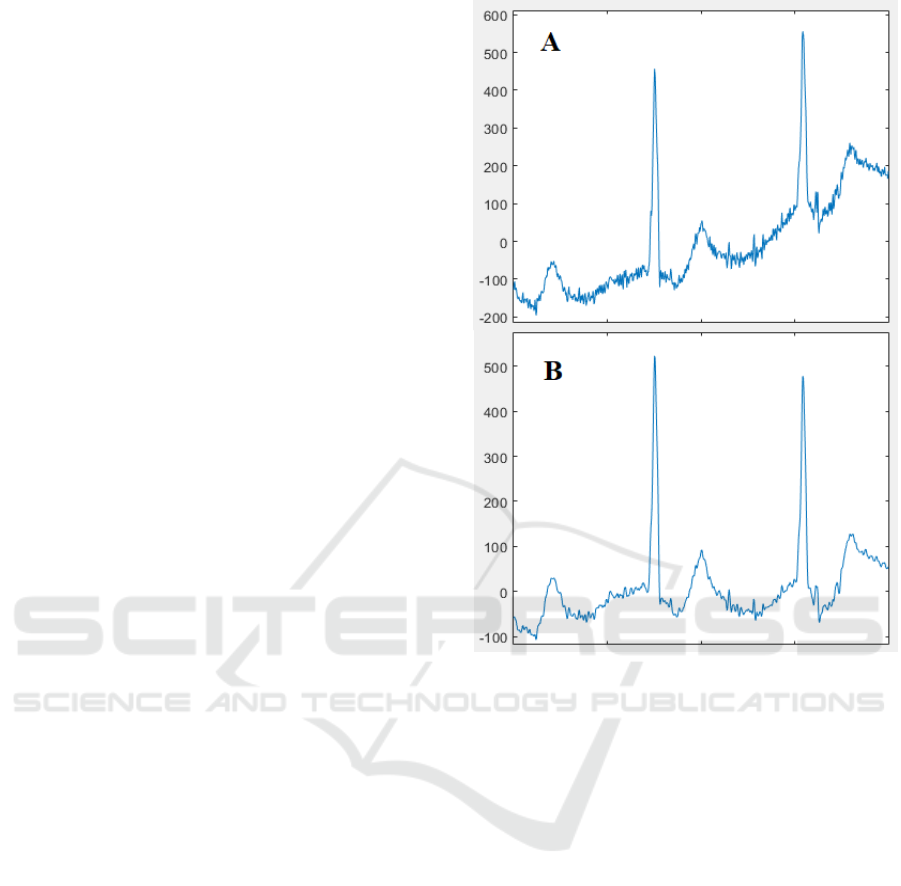
(fig. 1 A).

Before creating our database of two-second

fragments, the initial signals were processed using a

median filter with a window of 1.3 seconds, which

has removed the baseline drift. Remnants of electrical

network interference and high-frequency noise (such

as a myographic noise) with a frequency more than

50 Hz were removed using a high-order digital low-

pass filter with a cutoff frequency of 45 Hz. Figure 1

shows a fragment of ECG recording, which contains

the baseline drift and high-frequency interference (A)

and after their reductions (B).

Figure 1: ECG fragment before preprocessing (A) and

after (B).

3 NOVEL CLASSIFIER DATASET

ACCORDING TO

ARRHYTHMIA SEVERETY

The separation of ECG fragments into 6 classes was

proposed. The base for novel classifier set was their

potential danger to the life and health of the patient.

Classes are listening according to the descending

order of the danger:

• Class 1: ventricular flutter and ventricular

fibrillation.

• Class 2: pirouette tachycardia.

• Class 3: ventricular tachycardia.

• Class 4: bigeminy, high degree of ventricular

ectopic activity, ventricular rhythm.

• Class 5: atrial fibrillation, supraventricular

disorders, nodular rhythm.

• Class 6: normal rhythm, single extrasystoles.

The Comparison of Algorithms for Life-threatening Cardiac Arrhythmias Recognition

403

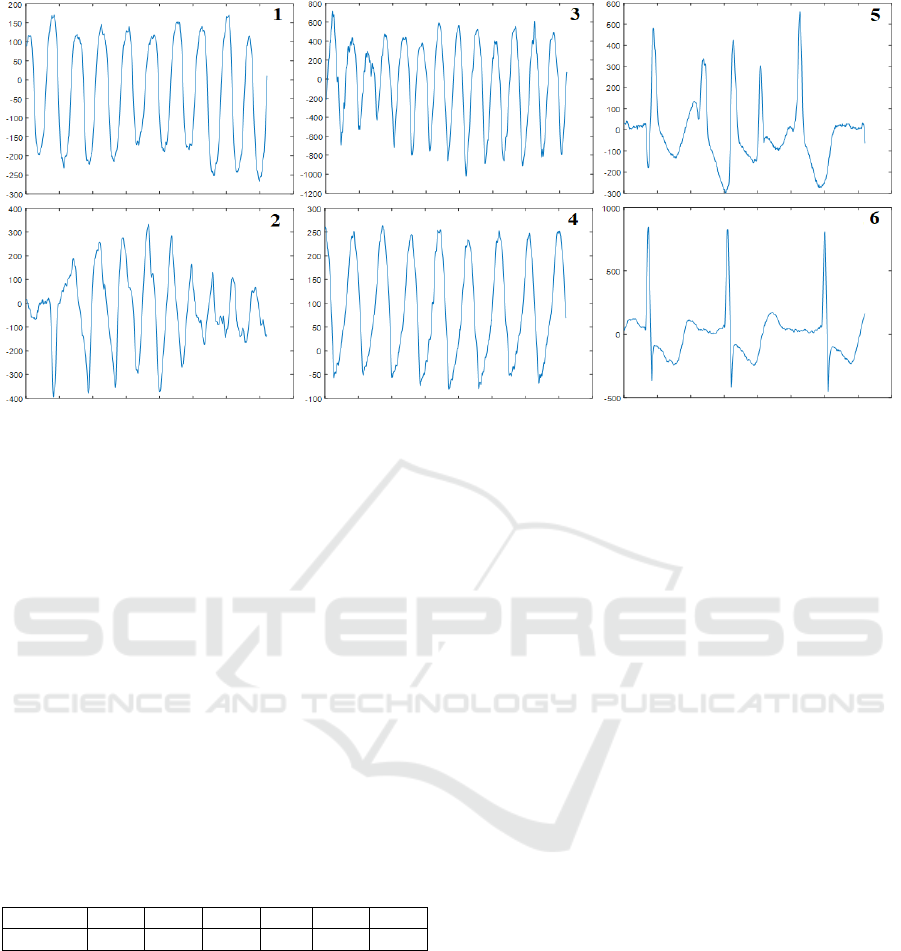
Figure 2: Examples of the representatives of each class.

Figure 2 shows typical ECG fragments for

representation of each class.

The aim of this research was the detection of life-

threatening arrhythmias in a much shorter time than

common practices.

We used 2 seconds window to analyze ECG

fragments for arrhythmias recognition. This window

time duration allows investigating at least two QRS

and RR interval between them for classes 4 and 6, and

several waves for classes 1-3 and 5.

During the creation of new sets of two-second

fragments from the original signals, 1000 fragments

were cut, so that in each of the six previously

designated classes there were at least 90 objects.

The table 1 presents number of two-second

nonoverlapping fragments from the MIT-BIH

database for each class.

Table 1: Number of analysed fragments.

Class 1 2 3 4 5 6

Quantit

220 113 183 90 133 261

Then we have consolidated above certain classes

in two groups: life-threatening arrhythmias (Classes

1-3) and their precursors (Classes 4-6).

Thus, the testing of all considered algorithms was

carried out on a two-class recognition – "life-

threatening violations" and "others".

To truthfully check the quality of classification

algorithms tested further, it was necessary to ensure

an equal number of objects of each class in the

training and test data sets. Thus, 90 fragments of six

classes were included in the set, forming 2 enlarged

groups of 270 objects.

The Fourier transform of the fragments was used

as the features supplied to the classifiers. It was

picked as a widely spread characteristics with high

interpretability. Since the duration of the studied

fragments is 2 seconds, the frequency step of the

spectrum is 0.5 Hz.

At the initial stage of the work it was planned to

use the union of harmonics in pairs to obtain a

reduced spectrum with a step of 1 Hz, but the first

results showed a significant decline in the accuracy of

the algorithms when combining harmonics and as a

result, 30 harmonics (up to 15 Hz) seemed to be the

best in terms of information amount/computing

difficulty ratio. Thus, they were used in the

experiments.

4 APPLIMENTATION

DIFFERENT ALGORITHMS TO

ARRHYTHMIAS

RECOGNITION AND RESULTS

4.1 Algorithms

Four classification algorithms were investigated in

the study.

The K nearest neighbour classifier (kNN) is based

on determining the most common class among the k

nearest known objects to the one being classified.

Testing different k’s revealed k = 6 to be the best

option.

NDNSNT 2020 - Special Session on Non-invasive Diagnosis and Neuro-stimulation in Neurorehabilitation Tasks

404

Light nearest convex hull classifier (LNCH)

represents classes in the form of convex hulls. The

classification algorithm determines the position of the

new object relative to these shells (Nalbantov and

Smirnov, 2010; Nemirko, 2019). This method

requires the biggest amount of computing among all

tested ones, since it requires the calculation of a large

number of projections of objects in n-dimensional

space for each classified object.

As for the nearest mean method, the decision on

whether an object belongs to a class is made on the

basis of the euclidean distances from the object to the

centres of the classes – their generalized objects.

Finally, the well-known method of support

vectors with several variants of kernels was used in

the study. Tested kernels are: linear, quadratic, cubic

and Gaussian one.

4.2 Results and Discussion

To avoid overfitting of some algorithms, cross-

validation was used during all tests.

Standard metrics of sensitivity (Se), specificity

(Sp) and overall accuracy (OA) were used to

determine the efficiency of the algorithms.

To test whether preprocessing has any impact on

accuracy, additional tests using not-preprocessed data

were conducted. The results are shown in the table 2.

The best results are marked bold.

Table 2: Quality metrics of investigated algorithms applied

to data without preprocessing.

orithm Se S

kNN, k = 6 91,1% 96,7% 93,3%

LNCH 86,7% 91,1% 88,9%

Nearest mean 78,9% 93,3% 86,1%

Linear SVM 91,5% 94,4% 93,0%

Quadratic SVM 95,9% 93,7% 94,8%

Cubic SVM 95,9% 93,7% 94,8%

Gaussian SVM 94,8% 94,4% 94,6%

Based on the obtained kNN results, we can

conclude the unequal dispersion of objects within the

studied classes: the low sensitivity of the algorithm is

explained by the presence of a large number of

outliers in the class of "life-threatening arrhythmias".

For the same reason the light nearest convex hull

classifier shows poor results, as its’s data quality

requirements are the biggest.

Accuracy of the same algorithms after signal

preprocessing are shown in the table 3.

It is interesting how the overall accuracy

decreased after removing the zero drift from the

signals. This is probably due to the much greater

Table 3: Quality metrics of investigated algorithms applied

to data after preprocessing.

Algorithm Se Sp OA

kNN, k = 6 89,6% 95,9% 92,8%

LNCH 85,6% 90,0% 88,8%

Nearest mean 78,5% 93,7% 86,1%

Linear SVM 91,1% 91,9% 91,5%

Quadratic

SVM

95,6% 93,3% 94,4%

Cubic SVM 95,9% 93,7% 94,8%

Gaussian SVM 94,1% 94,4% 94,3%

prevalence of zero drift precisely during occurrences

of life-threatening arrhythmias.

After reviewing the objects that gave an error on

most algorithms, 2 similar cases were identified that

could not be correctly classified in the frequency

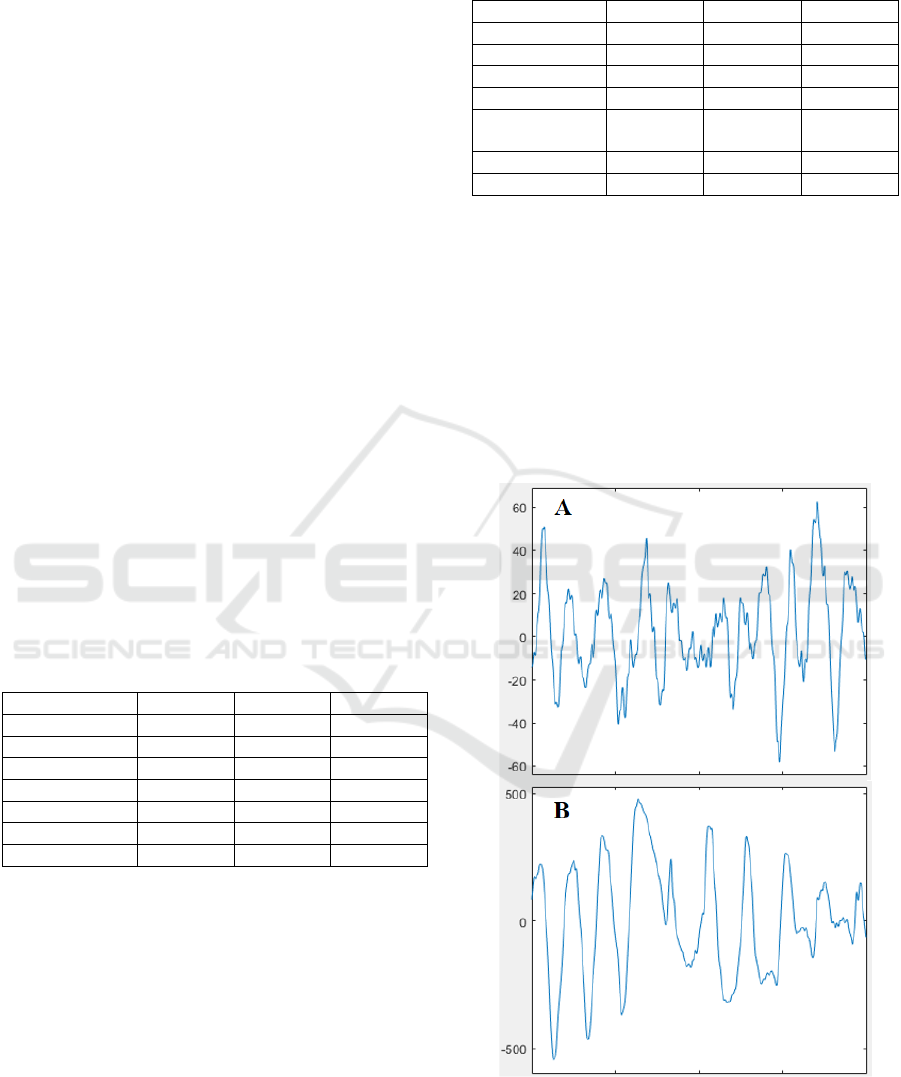
domain. Examples of such fragments are shown in

figure 3.

The first error source is significantly irregular

ventricular fibrillation, giving a blurred spectrum

similar to that of a normal ECG (figure 3A). The

second case is transitions within the analysed

Figure 3: The examples of most common error sources:

significantly irregular ventricular fibrillation (A) and

transitions between different rhythm types (B).

The Comparison of Algorithms for Life-threatening Cardiac Arrhythmias Recognition

405

segment. This situation is typical for episodes of the

pirouette form of ventricular tachycardia, appearing

for a very short period of time before the start of

ventricular tachycardia itself (figure 3B). Both of

these cases do not give a significant peak in their

Fourier transform, which is typical for "pure" life-

threatening arrhythmias.

To improve the quality of the features, describing

such aperiodic signals, the use of Wavelet transform

or high-order statistics can be a good choice.

5 CONCLUSIONS

The novel classifier dataset of two-second fragments

of electrocardiograms containing all of the most

common rhythm disorders has been created. The

fragments were grouped into 6 classes according to

the degree of their danger to human life.

Transition to two-class problem of separation of

life-threatening arrhythmias from background rhythm

and low-risk violations was made.

The resulting two-class problem was solved using

kNN, LNCH, nearest mean and SVM with different

kernels methods. As a result of the classification

quality assessment, the low sensitivity of non-SVM

methods was revealed.

After reviewing the objects that gave errors

regardless of the algorithm used, 2 types of fragments

were identified, which classification in the frequency

domain seems difficult.

ACKNOWLEDGEMENTS

This research was supported by Russian Foundation

for Basic Research (RFBR), research projects

19-29-01009 and 18-29-02036.

REFERENCES

Wik, L., Hansen, T. B., Fylling, F., Steen, T., Vaagenes, P.,

Auestad, B. H., & Steen, P. A., 2003. Delaying

defibrillation to give basic cardiopulmonary

resuscitation to patients with out-of-hospital ventricular

fibrillation: a randomized trial. Jama, 289(11): 1389-

1395.

Moraes, J. C. T. D. B., Blechner, M., Vilani, F. N., & Costa,

E. V., 2002. Ventricular fibrillation detection using a

leakage/complexity measure method. In Computers in

Cardiology, IEEE, pages 213-216.

Meng, O., Xia, D. E. L. I. N. G., Zhang, Q. I. A. N. G., &

Zhang, Z. A. I. G. U. O., 2016. Detection Ventricular

Tachycardia and Fibrillation using the Lempel-Ziv

complexity and Wavelet transform. WSEAS Trans.

Inform. Science and App, 13: 118-125.

Xu, Y., Wang, D., Zhang, W., Ping, P., & Feng, L., 2018.

Detection of ventricular tachycardia and fibrillation

using adaptive variational mode decomposition and

boosted-CART classifier. Biomedical Signal

Processing and Control, 39: 219-229.

Cheng, P., & Dong, X., 2017. Life-threatening ventricular

arrhythmia detection with personalized features. IEEE

access, 5: 14195-14203.

Arafat, M. A., Chowdhury, A. W., & Hasan, M. K., 2011.

A simple time domain algorithm for the detection of

ventricular fibrillation in electrocardiogram. Signal,

Image and Video Processing, 5(1): 1-10.

Amann, A., Tratnig, R., & Unterkofler, K., 2006. Detecting

ventricular fibrillation by time-delay methods. IEEE

Transactions on Biomedical Engineering, 54(1): 174-

177.

Monte, G. E., Scarone, N. C., & Liscovsky, P. O., 2011. A

novel time-domain signal processing algorithm for real

time ventricular fibrillation detection. In Journal of

Physics: Conference Series, (Vol. 332, No. 1,

p. 012015). IOP Publishing.

Barro, S., Ruiz, R., Cabello, D., & Mira, J., 1989.

Algorithmic sequential decision-making in the

frequency domain for life threatening ventricular

arrhythmias and imitative artefacts: a diagnostic

system. Journal of biomedical engineering, 11(4): 320-

328.

Dzwonczyk, R., Brown, C. G., & Werman, H. A., 1990.

The median frequency of the ECG during ventricular

fibrillation: its use in an algorithm for estimating the

duration of cardiac arrest. IEEE Transactions on

Biomedical Engineering, 37(6): 640-646.

Millet-Roig, J., Rieta-Ibanez, J. J., Vilanova, E., Mocholi,

A., & Chorro, F. J., 1999. Time-frequency analysis of a

single ECG: to discriminate between ventricular

tachycardia and ventricular fibrillation. In Computers in

Cardiology 1999, Vol. 26 (Cat. No. 99CH37004): 711-

714. IEEE.

Zhang, X. S., Zhu, Y. S., Thakor, N. V., & Wang, Z. Z.,

1999. Detecting ventricular tachycardia and fibrillation

by complexity measure. IEEE Transactions on

biomedical engineering, 46(5): 548-555.

Roopaei, M., Boostani, R., Sarvestani, R. R., Taghavi, M.

A., & Azimifar, Z., 2010. Chaotic based reconstructed

phase space features for detecting ventricular

fibrillation. Biomedical Signal Processing and Control,

5(4): 318-327.

Rasooli, M., Foomany, F. H., Balasundaram, K., Masse, S.,

Zamiri, N., Ramadeen, A., & Beheshti, S., 2015.

Analysis of electrocardiogram pre-shock waveforms

during ventricular fibrillation. Biomedical Signal

Processing and Control, 21: 26-33.

Balasundaram, K., Masse, S., Nair, K., & Umapathy, K.,

2013. A classification scheme for ventricular

arrhythmias using wavelets analysis. Medical &

biological engineering & computing, 51(1-2): 153-164.

NDNSNT 2020 - Special Session on Non-invasive Diagnosis and Neuro-stimulation in Neurorehabilitation Tasks

406

Li, Y., Bisera, J., Weil, M. H., & Tang, W., 2011. An

algorithm used for ventricular fibrillation detection

without interrupting chest compression. IEEE

Transactions on Biomedical Engineering, 59(1): 78-86.

Arafat, M. A., Sieed, J., & Hasan, M. K., 2009. Detection

of ventricular fibrillation using empirical mode

decomposition and Bayes decision theory. Computers

in Biology and Medicine, 39(11): 1051-1057.

Anas, E. M. A., Lee, S. Y., & Hasan, M. K., 2011.

Exploiting correlation of ECG with certain EMD

functions for discrimination of ventricular fibrillation.

Computers in biology and medicine, 41(2): 110-114.

Kaur, L., Singh, V., 2013. Ventricular fibrillation detection

using empirical mode decomposition and approximate

entropy. Intern. Journal of Emerging Technology and

Advanced Engineering, 3 (5): 260-268.

Anas, E. M. A., Lee, S. Y., & Hasan, M. K., 2010.

Sequential algorithm for life threatening cardiac

pathologies detection based on mean signal strength

and EMD functions. Biomedical engineering online,

9(1): 43.

Thakor, N. V., Zhu, Y. S., & Pan, K. Y., 1990. Ventricular

tachycardia and fibrillation detection by a sequential

hypothesis testing algorithm. IEEE Transactions on

Biomedical Engineering, 37(9): 837-843.

Verma, A., & Dong, X., 2016. Detection of ventricular

fibrillation using random forest classifier. Journal of

Biomedical Science and Engineering, 9(05): 259.

Amann, A., Tratnig, R., & Unterkofler, K., 2005.

Reliability of old and new ventricular fibrillation

detection algorithms for automated external

defibrillators. Biomedical engineering online, 4(1): 60.

Goldberger, A. L., Amaral, L. A., Glass, L., Hausdorff, J.

M., Ivanov, P. C., Mark, R. G., & Stanley, H. E., 2000.

PhysioBank, PhysioToolkit, and PhysioNet:

components of a new research resource for complex

physiologic signals. Circulation, 101(23): e215-e220.

Nalbantov, G., & Smirnov, E., 2010. Soft nearest convex

hull classifier. In Proceedings of the 2010 conference

on ECAI 2010: 19th European Conference on Artificial

Intelligence, pages 841-846. IOS Press.

Nemirko, A. P., 2019. Lightweight Nearest Convex Hull

Classifier. Pattern Recognition and Image Analysis,

29(3): 360-365.

The Comparison of Algorithms for Life-threatening Cardiac Arrhythmias Recognition

407