
Evaluating Deep Learning Uncertainty Measures in Cephalometric
Landmark Localization
Dušan Drevický and Old
ˇ
rich Kodym
Department of Computer Graphics and Multimedia, Brno University of Technology,
Keywords:
Landmark Localization, Cephalometric Landmarks, Deep Learning, Uncertainty Estimation.
Abstract:
Cephalometric analysis is a key step in the process of dental treatment diagnosis, planning and surgery. Local-
ization of a set of landmark points is an important but time-consuming and subjective part of this task. Deep
learning is able to automate this process but the model predictions are usually given without any uncertainty
information which is necessary in medical applications. This work evaluates three uncertainty measures ap-
plicable to deep learning models on the task of cephalometric landmark localization. We compare uncertainty
estimation based on final network activation with an ensemble-based and a Bayesian-based approach. We
conduct two experiments with elastically distorted cephalogram images and images containing undesirable
horizontal skull rotation which the models should be able to detect as unfamiliar and unsuitable for automatic
evaluation. We show that all three uncertainty measures have this detection capability and are a viable option
when landmark localization with uncertainty estimation is required.
1 INTRODUCTION
Cephalometric analysis provides clinicians with the
interpretation of the bony, dental and soft tissue struc-
tures in patients’ dental X-ray images. The analysis
results contain relationships between key points in the
radiogram. These landmark positions are then used
for treatment planning, clinical diagnosis, classifica-
tion of anatomical abnormalities and for surgery. This
procedure is time-consuming if performed manually
by experts and high interobserver variability is a sig-
nificant issue as well. Automatic landmark localiza-
tion helps to alleviate both of these problems (Wang
et al., 2016).
The existing solutions for landmark localiza-
tion can be classified into knowledge-based, pattern
matching-based, statistical learning-based and deep
learning-based. Knowledge-based methods automate
landmark localization by specifying rules based on
expert knowledge (Levy-Mandel et al., 1985). This is
problematic since rule complexity increases propor-
tional with image complexity.
Pattern matching-based methods search for a
specified pattern within the image. (Cardillo and
Sid-Ahmed, 1994) proposed to use template match-
ing and gray-scale morphological operators. (Grau
et al., 2001) showed that they can improve detection
accuracy by supplementing template matching with
edge detection and contour segmentation operators.
(Davis and Taylor, 1991) used features extracted from
the image to detect a set of candidate positions for
landmarks, and then analyzed the spatial relationships
among landmarks to select the best candidate points.
Statistical learning-based methods take into ac-
count both the local appearance of landmark locations
and global constraints specified by some model such
as an Active Shape Model (Cootes et al., 1995) or
an Active Appearance Model (Cootes et al., 2006).
Two public challenges for cephalometric landmark
detection were held in 2014 and 2015 at the IEEE
ISBI and the solutions were summarized in (Wang
et al., 2016). Best-performing methods used random
forests for classifying individual landmarks and sta-
tistical shape analysis for capturing the spatial rela-
tionship among landmarks.
Deep learning-based methods have achieved suc-
cess in many application domains and their usage
in medical image analysis has been consistently in-
creasing since 2015 (Litjens et al., 2017). (Payer
et al., 2016) found that convolutional neural networks
(CNNs) can be successful in localizing hand land-
marks. In the context of cephalometric landmark lo-
calization, (Pei et al., 2006) demonstrated the poten-
tial of bimodal deep Boltzmann machines and more
Drevický, D. and Kodym, O.
Evaluating Deep Learning Uncertainty Measures in Cephalometric Landmark Localization.
DOI: 10.5220/0009375302130220
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 2: BIOIMAGING, pages 213-220
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
213

recently (Arik et al., 2017) proposed to use deep
CNNs in combination with a shape-based model.
Deep learning-based methods show great poten-
tial but their shortcoming is that they are usually used
as deterministic models providing merely point es-
timates of predictions and model parameters with-
out any associated measure of uncertainty. Since the
models will produce a prediction for any input image,
this may lead to situations in which we cannot tell
whether the prediction is reasonable or just a random
guess (Gal, 2016). That is a problem since informa-
tion about the reliability of model predictions is a key
requirement for their incorporation into the medical
diagnostic systems (Widdowson and Taylor, 2016).
Deep learning models should thus provide each pre-
diction with an estimate of its uncertainty. This would
allow the diagnostic system to distinguish between
easy cases which can be handled automatically and
problematic ones which may instead be referred to a
supervising physician for review.
Models based on probability and uncertainty have
been extensively studied in the Bayesian machine
learning community. They provide a probabilistic
view that offers confidence bounds when performing
decision making (Gal, 2016) but usually come with
a prohibitive computational cost. To take advantage
of the qualities of deep learning models and still have
the option of assessing the uncertainty of their pre-
dictions, it has been suggested (Gal and Ghahramani,
2016) to recast them as Bayesian models using the
popular dropout (Hinton et al., 2012) technique often
used for regularization in neural networks. The poste-
rior distribution used by Bayesian models is approx-
imated in deep learning models using Monte Carlo
(MC) sampling and model uncertainty is given by the
prediction variance of the samples. The MC Dropout
method has already been applied in medical imag-
ing applications. (Leibig et al., 2017) used dropout-
based uncertainty when diagnosing diabetic retinopa-
thy from fundus images. (Eaton-Rosen et al., 2018)
and (Guha Roy et al., 2018) both applied it to seman-
tic segmentation of brain scan images.
Another option for estimating the uncertainty of
deep learning models comes from a recent non-
Bayesian line of research by (Lakshminarayanan
et al., 2017). While ensembles of machine learn-
ing models have long been known to increase per-
formance in terms of predictive accuracy, the authors
also suggest using the prediction variance of the en-
semble members as measure of the ensemble’s uncer-
tainty.
While (Gal, 2016) criticized the use of raw model
outputs as a measure of uncertainty estimation, that
conclusion was not based on experiments conducted
on a heatmap regression task (Payer et al., 2016).
Since we use that method to localize cephalometric
landmarks in this work, we also determine whether a
useful uncertainty measure can be derived from the
predictions of a CNN trained for the task of heatmap
regression.
The contribution of our work is in evaluating the
MC Dropout and ensemble methods of estimating
deep learning model uncertainty on the cephalometric
landmark localization task. To the best of our knowl-
edge, deep learning model uncertainty estimation has
not been studied on this task before. We further eval-
uate whether CNN activations can be used for esti-
mation of landmark uncertainty without multiple for-
ward passes required by other methods. We show that
all three uncertainty measures are able to detect out-
of-distribution data unsuitable for automatic evalua-
tion. Our experiments also hint at the possibility of
applying models trained on X-ray images to 2D CT
projections.
2 MATERIALS AND METHODS
2.1 Dataset
The dataset used for the landmark localization exper-
iments was released as a part of the 2014 and 2015
IEEE ISBI challenges (Wang et al., 2016). It consists
of 400 cephalograms from 400 subjects. All cephalo-
grams were acquired in the same format and from an
identical scanning machine. The resolution of the im-
ages is 1935 x 2400 pixels with a pixel spacing of 0.1
mm. Two orthodontists provided ground truth manual
annotations of 19 cephalometric landmark positions
and we used only the one from the senior physician
accuracy evaluation. For consistency with the proto-
col designed for the competition, we used only 150
images for training and the rest (which is split by the
competition authors into split test1 and test2) for eval-
uation.
2.2 Landmark Localization
We implemented landmark localization using
heatmap regression (Payer et al., 2016). In this
approach, the landmark positions are not regressed
directly as a pair of real coordinates but the model
learns to regress a separate heatmap for each land-
mark instead. For each training example, the CNN
receives a single-channel gray-scale image rescaled
to d × d dimensions. The corresponding ground truth
is a 19 × d × d volume of heatmaps. Each heatmap
corresponds to a single landmark and contains a
BIOIMAGING 2020 - 7th International Conference on Bioimaging
214
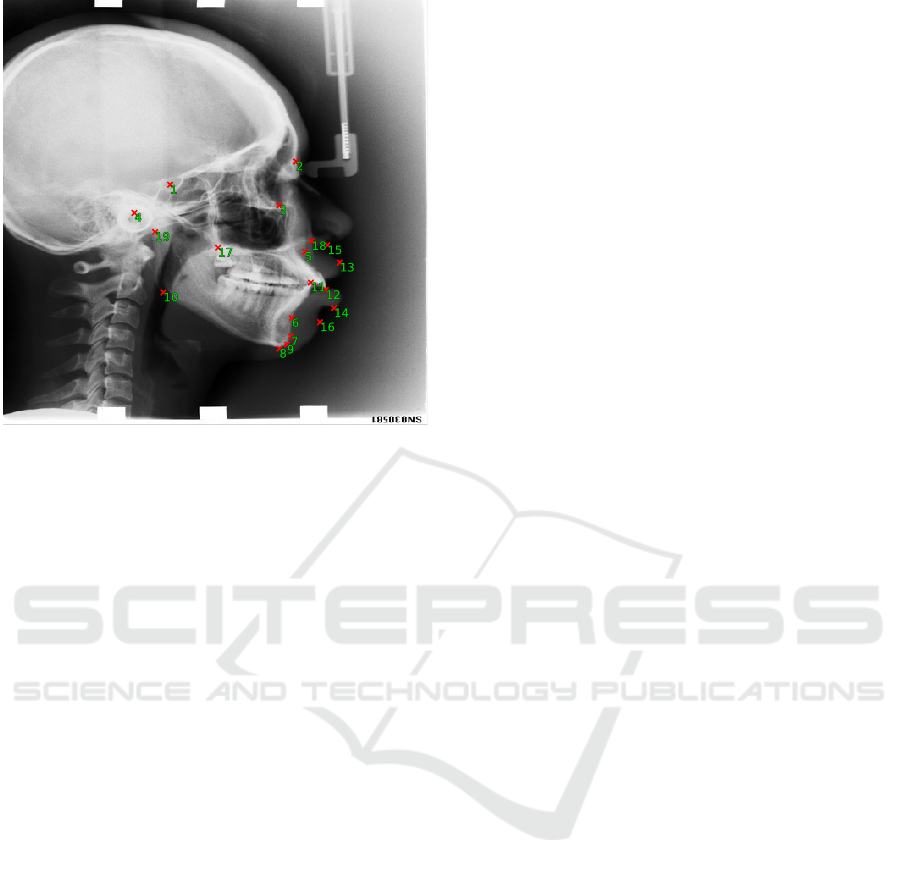
Figure 1: A rescaled image from the 2015 IEEE ISBI chal-
lenge dataset with 19 ground truth landmarks visualized.
Gaussian with a fixed variance and amplitude cen-
tered on the landmark position as annotated by the
physician. The output of the CNN is a 19 × d × d
volume of predicted heatmaps minimizing the mean
squared error loss. As a post-processing step, each
heatmap is convolved with a Gaussian filter of the
same variance as was used when creating the ground
truth heatmap. The position of the maximum value
in this activation map is chosen as the final predicted
landmark position.
2.3 CNN Architecture
The CNN architecture we used closely follows the
U-Net (Ronneberger et al., 2015) with some minor
modifications. U-Net contains a down-sampling path
followed by a symmetric up-sampling path and is de-
signed to be able to learn both global context (relative
landmark positions) and local characteristics of each
landmark.
The down-sampling path contains 3 × 3 double
convolutions with filter sizes of 64, 128, 256, 512 and
1024, each followed by a 2 × 2 max pooling layer.
Width and height of the feature map are then progres-
sively increased back to the original 128 ×128 size in
the up-sampling path via transpose convolution which
halves the filter dimension. Feature map from the cor-
responding down-sampling level is concatenated to
the result and this is followed by a double convolu-
tion whose filter size decreases from the bottom level
towards the top (1024, 512, 256, 128 and 64). The
final double convolution uses 19 filters to produce the
prediction heatmaps.
For the model based on Monte Carlo dropout (see
Section 2.4.3), dropout layers are added just before
each max pooling layer and right after the transposed
convolution in the up-sampling path.
2.4 Uncertainty Measures
We train three models, all based on the same CNN
architecture. Baseline model uses the activation
heatmap produced by the CNN when estimating un-
certainty while the Ensemble and MC-Dropout mod-
els both use prediction variance of the ensemble mem-
bers and MC samples respectively.
2.4.1 Maximum Heatmap Activation (MHA)
Baseline is a single CNN without dropout layers. Re-
call from Section 2.2 that the heatmap predicted by
the CNN is convolved with a Gaussian filter as a post-
processing step. The position of the maximum value
in the activation map produced this way is chosen as
the predicted landmark position. The Baseline model
additionally uses the maximum activation value (not
just the position) as a measure of uncertainty associ-
ated with the prediction. We hypothesized that there
is an inverse correlation between the maximum acti-
vation and the uncertainty of the model. The CNN is
trained to output a heatmap which has a strong maxi-
mum at the correct position. Consequently, when the
predicted maximum is low, it might be a good indi-
cator that the network is not sure about the predic-
tion. Note that maximum heatmap activation (MHA)
is technically a measure of model certainty since it
should increase proportional to model’s confidence in
its predictions.
For the purpose of experiment analysis in Sec-
tion 3, this quantity was normalized to a unit range.
The upper bound of one for normalization was cho-
sen based on the maximum value of this uncertainty
measure observed for all of the landmarks in the test
set. Note that the other two models described in this
section ignore the value of the MHA (and only use its
position) and do not use it for uncertainty estimation.
2.4.2 Ensemble Prediction Variance
Ensemble is an ensemble model consisting of 15
CNNs trained independently using the same CNN ar-
chitecture as the Baseline model. To predict landmark
positions for an input image, each CNN in the ensem-
ble is first evaluated as described in Section 2.2 and
produces its individual predictions of the landmark
positions. Predictions of all networks are then aver-
aged to produce the final position (see Equation 1).
While it is well-known that forming an ensemble of
Evaluating Deep Learning Uncertainty Measures in Cephalometric Landmark Localization
215

machine learning models improves prediction accu-
racy, (Lakshminarayanan et al., 2017) suggested treat-
ing the variance of the ensemble members’ predic-
tions (see Equation 2) as a measure of uncertainty.
Greater variance indicates discord in the ensemble
predictions. The member models were trained using
random initialization so they all ended up with dif-
ferent parameter values at the end of training. Since
they were trained using the same data, it is reasonable
to assume that there will not be a large difference be-
tween their predictions on data coming from a similar
distribution like the one they observed during train-
ing. On the other hand, when being evaluated on out-
of-distribution data (such as a misaligned X-ray, or
an X-ray from a different scanner) the difference be-
tween predictions will be larger since each model will
take a different guess on the unfamiliar data based on
its final parameters.
2.4.3 Monte Carlo Dropout Prediction Variance
The Monte Carlo (MC) Dropout technique is based
on the Bayesian assumption that neural network
weights W have probability distributions instead of
being point estimates as is common in deep learn-
ing. The goal of Bayesian modelling is to approxi-
mate the posterior distribution p(W|X, Y) given the
training data {X,Y}. While true Bayesian neural
networks are computationally expensive, (Gal and
Ghahramani, 2016) suggested approximating them
with dropout (Hinton et al., 2012). When applying a
dropout layer in a CNN, a randomly selected subset of
neurons in the previous layer is dropped at each itera-
tion. Since the number of CNN parameters is usually
in the millions, this essentially leads to a different net-
work being sampled at each iteration. The resulting
stochasticity of the network can be used to approxi-
mate a Bayesian neural network. In practice, evalu-
ating the prediction of a an MC Dropout based net-
work amounts to computing the mean of T stochas-
tic forward passes through the network, which sam-
ple from T network architectures (different neurons
are dropped for each one). The predictive uncertainty
over a prediction is obtained by computing the sample
variance of the T forward passes.
2.4.4 Prediction Mean and Prediction Variance
The Ensemble and MC-Dropout models both use pre-
diction variance as a measure of their uncertainty. For
the task of landmark localization, we compute the pre-
diction variance of a vector~y containing T prediction
samples as the mean Euclidean distance between the
prediction samples y
i
and the prediction mean ˆy:
ˆy =
1
T
T
∑
i=1
y
i
(1)
Var(~y) =
1
T
T
∑
i=1
ky
i
− ˆyk (2)
Note that the prediction mean ˆy is also used as
the landmark location predicted by the Ensemble and
MC-Dropout models.
2.5 Implementation Details
All training images were resized to 128 × 128 size to
speed up training and allow for faster experimenta-
tion. The predictions and prediction variance of the
Ensemble and MC-Dropout models was computed
using 15 ensemble CNNs and MC samples respec-
tively. The probability of a unit being dropped in the
MC-Dropout model was set uniformly to p = 0.4. All
models along with the training process were imple-
mented using the PyTorch (Paszke et al., 2017) li-
brary.
3 EXPERIMENTS AND RESULTS
We first shortly evaluate the landmark localization ac-
curacy of the trained models. We then describe two
experiments which aimed to assess whether the eval-
uated uncertainty measures are able to reliably detect
out-of-distribution data on the cephalometric land-
mark localization task.
3.1 Landmark Localization Accuracy
We first verified that the performance of our models
was comparable to that of the best previous solutions
on the dataset we used (see Table 1). Due to compu-
tational reasons, we trained on images resized to the
128 × 128 size from the original 1935 × 2400. While
it was sufficient for the purpose of our study, image
sub-sampling reduced the accuracy of the models and
direct clinical application would require it to be less
aggressive.
3.2 Elastically Distorted
Out-of-Distribution Data Detection
Elastic distortion was applied to the entire test set to
evaluate the ability of the uncertainty measures to de-
tect out-of-distribution data examples. Forty versions
of the test set were created in total, and each copy had
an elastic distortion of progressively stronger mag-
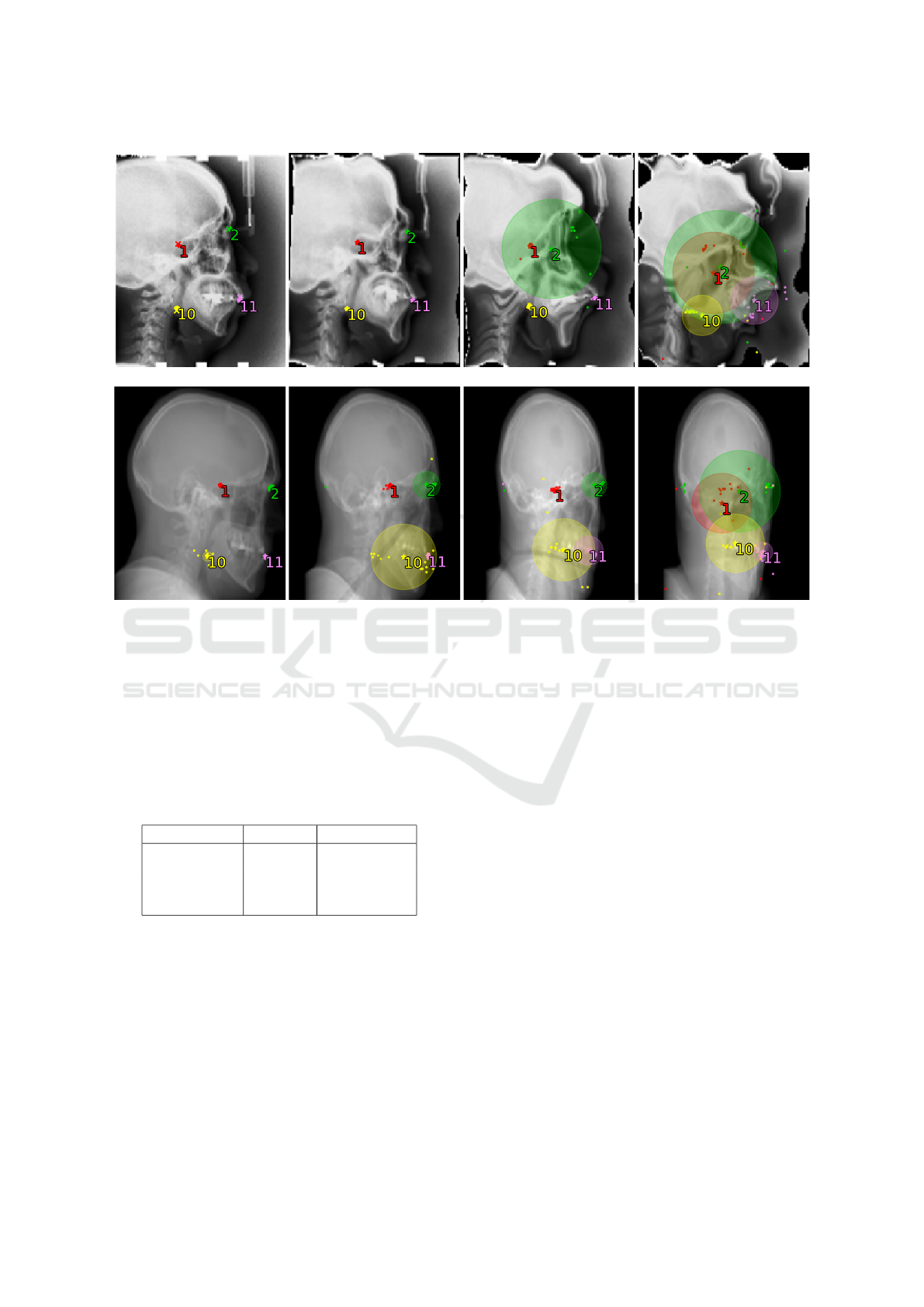
nitude applied to it. First row in Figure 2 shows a
BIOIMAGING 2020 - 7th International Conference on Bioimaging
216
λ=0
λ=70
λ=140
λ=200
θ=0°
θ=15°
θ=30°
θ=45°
Figure 2: Visualization of the Ensemble model’s predictions and uncertainty values. Top row shows an image from the test
set transformed with elastic distortion of increasing magnitude λ. Bottom row shows a skull CT scan rotated in the horizontal
plane by angle θ and projected onto the sagittal plane. The individual ensemble members’ predictions (dots) are combined
into a final position prediction (star), and the ground truth is marked by a cross (only applicable to the top left undistorted
image with known ground truth). Only four landmarks are shown for clarity. As the magnitude of elastic distortion and
rotation increases, so does the model uncertainty (prediction variance).
Table 1: Accuracy of the proposed models on the test1 split
compared with the best solution from the 2015 IEEE ISBI
challenge (Wang et al., 2016). Mean Radial Error gives the
mean error in landmark detection. Success Detection Rate
gives the percentage of predictions within that radius of the
ground truth.
MRE SDR 2.5 mm
Lindner et al. 1.67 mm 80.2 %
Baseline 2.05 mm 74.4 %
Ensemble 1.79 mm 78.5 %
MC-Dropout 1.92 mm 74.7 %
test image transformed with an elastic distortion of
varying strength, along with the landmark predictions
of the Ensemble model for that image. Uncertainty
for each predicted landmark position (variance of the
prediction samples) is visualized by a circle superim-
posed upon the predicted location.
Each model’s predictions and uncertainty esti-
mates for every version of the distorted test set was
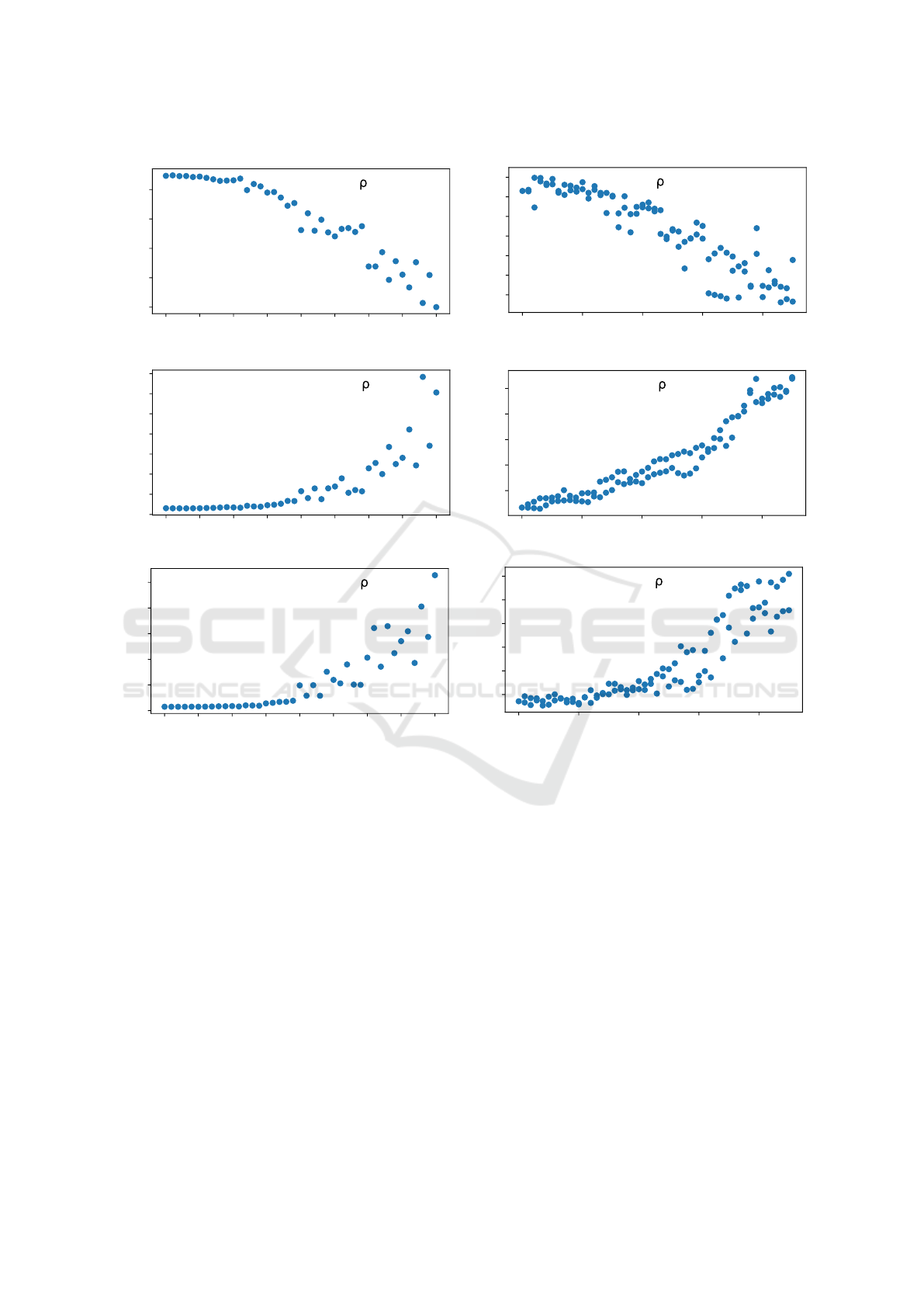
then computed. Left column in Figure 3 shows the
correlation between the mean uncertainty measure
value for all landmark position predictions for a given
version of the test set, and the elastic distortion mag-
nitude applied to that version of the test set. The anal-
ysis shows that a strong correlation exists between
the mean value of each uncertainty measure and the
strength of the elastic distortion being applied on the
data.
3.3 Rotated Out-of-Distribution Data
Detection
During the process of X-ray scanning for the purpose
of cephalometric analysis, patient’s head in the scan-
ner should be perfectly aligned with the sagittal plane.
However, patients sometimes rotate their head in the
horizontal plane which distorts the resulting image
and may even lead to some of the landmarks over-
lapping. A model should detect such data by being
uncertain about its predictions.
Since a dataset of cephalograms containing hori-
zontal head rotation is not publicly available, we used
a volumetric CT scan of a single skull to create one.
Evaluating Deep Learning Uncertainty Measures in Cephalometric Landmark Localization
217
0 25 50 75 100 125 150 175 200
Elastic Distortion Magnitude
0.3
0.4
0.5
0.6
0.7
Mean Heatmap Activation
= -0.95
Baseline
0 10 20 30 40
Skull Rotation (°)
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Mean Heatmap Activation
= -0.91
Baseline
0 25 50 75 100 125 150 175 200
Elastic Distortion Magnitude
0.0
2.5
5.0
7.5
10.0
12.5
15.0
17.5
Mean Prediction Variance (mm)
= 0.81
Ensemble
0 10 20 30 40
Skull Rotation (°)
5
10
15
20
25
Mean Prediction Variance (mm)
= 0.95
Ensemble
0 25 50 75 100 125 150 175 200
Elastic Distortion Magnitude
0
5
10
15
20
25
Mean Prediction Variance (mm)
= 0.85
MC-Dropout
0 10 20 30 40
Skull Rotation (°)
10
20
30
40
50
60
Mean Prediction Variance (mm)
= 0.88
MC-Dropout
Figure 3: Correlation of the three uncertainty measure values with elastic distortion magnitude (left) and skull rotation mag-
nitude (right). In the first experiment, each of the models along with its uncertainty measure was evaluated on forty versions
of the test set modified by elastic distortion of varying magnitude. In the second experiment, the models were evaluated on
91 images of a skull CT scan projected onto the sagittal plane. The skull was transformed before projection with different
magnitudes of rotation. As distortion and rotation magnitude increase, so does model uncertainty for all three measures. Note
that maximum heatmap activation (top row) is actually a measure of model certainty so the correlation is negative as expected.
The skull volume (originally aligned with the sagit-
tal plane) was first rotated by θ degrees in the hori-
zontal plane to simulate a patient’s undesirable move-
ment in the scanner. To simulate X-ray acquisition
process, the resulting volume was then projected onto
the sagittal plane by summing the intensity values of
overlapping voxels. Pixel values in the resulting 2D
image were then normalized by dividing them with
the maximum pixel intensity present in the image.
The resulting dataset contains 91 images with θ rang-
ing from −45° to 45° including a rotation of 0°.
We first verified that the model predictions for the
CT volume projection without any rotation were rea-
sonably accurate. The models provided acceptable
predictions but their mean uncertainty increased com-
pared with the predictions from the X-ray images in
the test set (compare the model uncertainty in the first
image in the top row with the first image in the bottom
row of Figure 2). This is not unexpected since even
a CT projection created from an unrotated skull vol-
ume is an out-of-distribution data point for a network
trained on X-ray images. However, the sensible pre-
dictions of the models indicate that it is plausible to
apply X-ray trained models on CT projections with-
out a substantial loss of performance. A more con-
fident conclusion would require further research us-
ing more CT scans. Also note that the viability of
an inverse knowledge transfer (i.e., applying models
BIOIMAGING 2020 - 7th International Conference on Bioimaging
218

trained on CT projections to X-ray data) was previ-
ously observed by (Bier et al., 2018).
The models’ prediction and uncertainty measure
values were then evaluated for each image in the cre-
ated dataset. Right column in Figure 3 shows the
correlation between the mean uncertainty value for
a given image (computed as the mean of uncertainty
estimates for all of the landmarks predicted for the
image) and the magnitude of rotation corresponding
to that image. For each evaluated uncertainty mea-
sure, there is a very strong correlation with the rota-
tion magnitude.
It is noteworthy that the ensemble uncertainty in-
creases more stably than MHA uncertainty as the ro-
tation applied to the image intensifies. For most steps
in rotation increase (an increase of 1°, e.g., from
10° to 11°), there is a corresponding increase in un-
certainty. Additionally, this increase has a consistent
magnitude between all rotation steps. On the other
hand, the MHA uncertainty values increase on the
whole, but the difference in the uncertainty values be-
tween successive rotation steps oscillates. Moreover,
for some consecutive rotation steps, the MHA uncer-
tainty actually decreases significantly for such a small
change in the input image. The MC Dropout method
suffers from a similar instability.
We hypothesize that the superior stability of the
ensemble prediction variance is due to the fact that the
Ensemble model consists of 15 unique CNNs while
the other two measures only have a single CNN avail-
able. A single network might have a weak spot in
its parameters for some inputs, which then also af-
fects the associated uncertainty estimate. Multiple
networks will possibly different weak spots and the
average of their predictions will be more reasonable
which will positively affect uncertainty estimate as
well.
A visualization of the Ensemble model’s predic-
tions and corresponding uncertainty values for a skull
projection rotated by different angle θ are in the bot-
tom row of Figure 2.
4 CONCLUSION
In this paper, we evaluated three measures for estimat-
ing deep learning model uncertainty on the cephalo-
metric landmark localization task. We compared un-
certainty estimation based on the maximum heatmap
activation (MHA) of a heatmap regression CNN with
an ensemble-based and a Bayesian-based approach.
Our experiments with out-of-distribution data
showed a strong correlation between the uncertainty
estimates accompanying model predictions and the
distance of the data from the training distribution for
all measures. This suggests their usability in detect-
ing images unsuitable for automatic evaluation. When
individually comparing the measures’ performance,
MHA showed the strongest correlation with image
distance from training distribution when both exper-
iments are taken into account. On the other hand,
both MHA and the MC Dropout uncertainty values
increased inconsistently in the rotation experiment
while the ensemble uncertainty was very stable in this
regard.
The usability of MHA is an interesting finding be-
cause this uncertainty measure is directly available
when using a CNN trained for heatmap regression.
Conversely, the other two measures require the model
to contain dropout layers or necessitate the training
of multiple networks. Additionally, while MHA re-
quires a single forward pass of the image, the other
examined methods both need multiple passes and are
more computationally expensive.
Although MHA could be used as a strong baseline
uncertainty estimation method on its own, due to its
observed instability it might be useful to combine it
(e.g., by a weighted average) with one of the ensem-
ble (preferrably) or MC Dropout methods when their
requirements and the increase in computation time are
not a problem.
To further verify that the uncertainty measures we
explored in this work are able to detect the failure
cases when a model is being applied on data distant
from its training distribution, it would be desirable
to train the CNN on cephalograms from one set of
scanners and then evaluate it on images from a dif-
ferent set of scanners. Another experiment could tar-
get a more confident result regarding the potential of
applying X-ray trained deep learning models on CT
projection images by using a larger dataset of CT vol-
umes. Since this issue is not necessarily restricted to
cephalometry or landmark localization, it would also
be preferable to expand the experiments to include
other machine learning tasks and other type of struc-
tures beside skulls.
ACKNOWLEDGEMENTS
This work was supported by the company
TESCAN 3DIM. We would also like to thank
the same company for providing us with the CT data
used in the experiments.
Evaluating Deep Learning Uncertainty Measures in Cephalometric Landmark Localization
219

REFERENCES
Arik, S., Ibragimov, B., and Xing, L. (2017). Fully
automated quantitative cephalometry using convolu-
tional neural networks. Journal of Medical Imaging,
4:014501.
Bier, B., Unberath, M., Zaech, J.-N., Fotouhi, J., Armand,
M., Osgood, G., Navab, N., and Maier, A. (2018).
X-ray-transform invariant anatomical landmark de-
tection for pelvic trauma surgery. In Frangi, A. F.,
Schnabel, J. A., Davatzikos, C., Alberola-López, C.,
and Fichtinger, G., editors, Medical Image Computing
and Computer Assisted Intervention – MICCAI 2018,
pages 55–63, Cham. Springer International Publish-
ing.
Cardillo, J. and Sid-Ahmed, M. A. (1994). An image pro-
cessing system for locating craniofacial landmarks.
IEEE Transactions on Medical Imaging, 13(2):275–
289.
Cootes, T., Edwards, G., and Taylor, C. (2006). Active ap-
pearance models, volume 23, pages 484–498.
Cootes, T., Taylor, C., Cooper, D., and Graham, J.
(1995). Active shape models-their training and appli-
cation. Computer Vision and Image Understanding,
61:38–59.
Davis, D. N. and Taylor, C. (1991). A blackboard architec-
ture for automating cephalometric analysis. Medical
informatics = Médecine et informatique, 16:137–49.
Eaton-Rosen, Z., Bragman, F., Bisdas, S., Ourselin, S., and
Cardoso, M. J. (2018). Towards Safe Deep Learn-
ing: Accurately Quantifying Biomarker Uncertainty
in Neural Network Predictions: 21st International
Conference, Granada, Spain, September 16–20, 2018,
Proceedings, Part I, pages 691–699.
Gal, Y. (2016). Uncertainty in Deep Learning. PhD thesis,
University of Cambridge.
Gal, Y. and Ghahramani, Z. (2016). Dropout as a bayesian
approximation: Representing model uncertainty in
deep learning. In Proceedings of the 33rd Inter-
national Conference on International Conference on
Machine Learning - Volume 48, ICML’16, pages
1050–1059. JMLR.org.
Grau, V., Alcañiz Raya, M., Juan, M.-C., Monserrat, C., and
Knoll, C. (2001). Automatic localization of cephalo-
metric landmarks. Journal of biomedical informatics,
34:146–56.
Guha Roy, A., Conjeti, S., Navab, N., and Wachinger, C.
(2018). Inherent Brain Segmentation Quality Con-
trol from Fully ConvNet Monte Carlo Sampling, pages
664–672.
Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever,
I., and Salakhutdinov, R. (2012). Improving neural
networks by preventing co-adaptation of feature de-
tectors. CoRR, abs/1207.0580.
Lakshminarayanan, B., Pritzel, A., and Blundell, C. (2017).
Simple and scalable predictive uncertainty estimation
using deep ensembles. In Guyon, I., Luxburg, U. V.,
Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S.,
and Garnett, R., editors, Advances in Neural Informa-
tion Processing Systems 30, pages 6402–6413. Curran
Associates, Inc.
Leibig, C., Allken, V., Ayhan, M. S., Berens, P., and Wahl,
S. (2017). Leveraging uncertainty information from
deep neural networks for disease detection. Scientific
Reports, 7.
Levy-Mandel, A. D., Tsotsos, J. K., and Venetsanopou-
los, A. N. (1985). Knowledge-based landmarking of
cephalograms. In Lemke, H., Rhodes, M. L., Jaffee,
C. C., and Felix, R., editors, Computer Assisted Ra-
diology / Computergestützte Radiologie, pages 473–
478, Berlin, Heidelberg. Springer Berlin Heidelberg.
Litjens, G. J. S., Kooi, T., Bejnordi, B. E., Setio, A. A. A.,
Ciompi, F., Ghafoorian, M., van der Laak, J., van Gin-
neken, B., and Sánchez, C. I. (2017). A survey on
deep learning in medical image analysis. Medical im-
age analysis, 42:60–88.
Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E.,
DeVito, Z., Lin, Z., Desmaison, A., Antiga, L., and
Lerer, A. (2017). Automatic differentiation in pytorch.
In NIPS-W.
Payer, C., Stern, D., Bischof, H., and Urschler, M. (2016).
Regressing Heatmaps for Multiple Landmark Local-
ization Using CNNs, volume 9901 of Lecture Notes in
Computer Science, pages 230–238. Springer Interna-
tional Publishing AG, Switzerland.
Pei, Y., Liu, B., Zha, H., Han, B., and Xu, T. (2006).
Anatomical structure sketcher for cephalograms by bi-
modal deep learning. Trans. Biomed. Eng., 53:1615–
1623.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-
net: Convolutional networks for biomedical image
segmentation. In Navab, N., Hornegger, J., Wells,
W. M., and Frangi, A. F., editors, Medical Image Com-
puting and Computer-Assisted Intervention – MICCAI
2015, pages 234–241, Cham. Springer International
Publishing.
Wang, C.-W., Huang, C.-T., Lee, J.-H., Li, C.-H., Chang,
S.-W., Siao, M.-J., Lai, T.-M., Ibragimov, B., Vrtovec,
T., Ronneberger, O., Fischer, P., Cootes, T. F., and
Lindner, C. (2016). A benchmark for comparison of
dental radiography analysis algorithms. Medical Im-
age Analysis, 31:63 – 76.
Widdowson, S. and Taylor, D. (2016). The management of
grading quality: good practice in the quality assurance
of grading. Tech Report.
BIOIMAGING 2020 - 7th International Conference on Bioimaging
220
