Researching the Efficiency of Configurations of a Collective

Decision-making System on the Basis of Fuzzy Logic

Anastasiya Polyakova

, Lipinskiy Leonid

and Eugene Semenkin

Reshetnev Siberian State University of Science and Technology,

Krasnoyarsky rabochy ave. 31, 660041, Krasnoyarsk, Russia

Keywords: Fuzzy Rule-based Systems, the Problem of Restoring the Cryolite Ratio, Regression Problem, Evolutionary

Algorithm, Parameter Optimization, Ensemble, Collective Decision-making System.

Abstract: Collective decision-making systems (or ensembles) based on fuzzy logic have proven their effectiveness in a

number of test and practical tasks. However, the problem of configuring the system and forming the main

operators remains unsolved. In this paper is a study of the effectiveness of different sequences of applying

optimization procedures for the formation of the main operators of a collective decision-making system based

on fuzzy logic. The effectiveness of tuning schemes for a collective decision-making system is investigated

using the problem of restoring the cryolite ratio and the content of calcium and magnesium fluorides. It is

shown in the research that an effective choice of the sequence of applying optimization procedures for tuning

and forming the main operators can significantly increase the overall efficiency of the system.

1 INTRODUCTION

Fuzzy rule-based systems (FRBS) are one of the most

important application areas of fuzzy sets and fuzzy

logic. These concepts were first proposed by the

American scientist Lotfi Zadeh in 1965 (Zadeh,

1965). As an extension of classical rule-based

systems, FRBS are successfully applied to a wide

range of problems in various fields of human activity

(Chi et al., 1996), (Pedrycz, 2012).

An FRBS allows us to implement a fuzzy

inference, which is an algorithm for obtaining fuzzy

conclusions based on fuzzy conditions or

assumptions using the concepts of fuzzy logic. This

process combines all the basic concepts of fuzzy set

theory: membership functions, linguistic variables

(LV), fuzzy logical operations, and methods of fuzzy

implication and fuzzy composition.

The work (Polyakova et al., 2019) first examined

the usage of FRBS as a collective decision-making

method (CDMM). We have also investigated the

performance of hybrid approaches, which combine

FRBS and final solution building using mean (mean)

and weighted mean (Wmean), titled “FRBS +

https://orcid.org/0000-0003-1035-4403

https://orcid.org/0000-0002-7833-8656

https://orcid.org/0000-0002-3776-5707

Wmean” (or “FLS + Wmean”). The proposed scheme

for forming the ensemble output based on fuzzy logic

systems (FLS) can significantly improve the quality

of decisions in classification and regression problems

(Polyakova et al., 2017).

A number of successful studies show that the

effective selection of individual parameters of a fuzzy

system can improve the efficiency in solving

classification and regression problems. Thus in

(Cord, 2001), (Lee, 1994), algorithms were proposed

for automating the stage of forming a knowledge

base. In (Delgado et al., 2001), (LóPez et al., 2013),

(Chien et al., 2002) and (Hoffmann et al., 2001)

effective learning algorithms, based on various

intelligent information technologies were proposed

for both the LV structure and the parameters of fuzzy

models.

The results of many experiments, for example

(Mazurowski et al., 2010) and (Grochowski et al.,

2004), show that the use of instance selection

algorithms allows us to obtain various compromises

between data compression and the accuracy of

problem solving, depending on the acceptability

threshold and characteristic relationship parameters.

Polyakova, A., Leonid, L. and Semenkin, E.

Researching the Efﬁciency of Conﬁgurations of a Collective Decision-making System on the Basis of Fuzzy Logic.

DOI: 10.5220/0009976602770285

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 277-285

ISBN: 978-989-758-475-6

277

In some cases, it is possible to achieve higher

compression and higher accuracy than the algorithm

for selecting an individual instance (Millán-Giraldo et

al., 2013).

Despite the high accuracy of “FRBS + Wmean”,

the practical implementation of the approach is

complicated by a large number of hyper-parameters

and ways for their tuning. When solving hard data

analysis problems, it is important not only to choose

effective parameter values, but also to use appropriate

order of their adjustment.

This paper provides a study of the influence of the

order of the application of the FRBS design stages on

the accuracy of solving a problem.

We have chosen the problem of identifying the

cryolite ratio (CR) as a benchmark data analysis

problem (Yurkov et al., 2002), (Jinhong et al., 2008).

This problem is real-world industrial and is associated

with a large number of uncontrolled and unmeasured

factors. Thus, it can be considered hard and suitable

for the purposes of our research.

The explanatory factors do not always fully

represent the resulting variable and are not always

measured accurately enough. At the same time, in

order to predict the cryolite ratio, metallurgical

industry experts have developed a specialized model

that takes into account technological and chemical

dependencies between explanatory factors and the

resulting variable.

The study shows that the appropriate choice of

system parameters and of the order of their formation

allow designing effective systems of an ensemble

inference and improving industrial models obtained

by industry specialists.

The following sections describe in detail the

proposed approach, experimental results, conclusions

and future plans.

2 PREDICTIVE MODELLING

2.1 Collective Decision-Making System

based on Fuzzy Logic “FRBS +

Wmean”

The general scheme of the fuzzy logic based system

for ensemble decision making “FRBS+Wmean” is

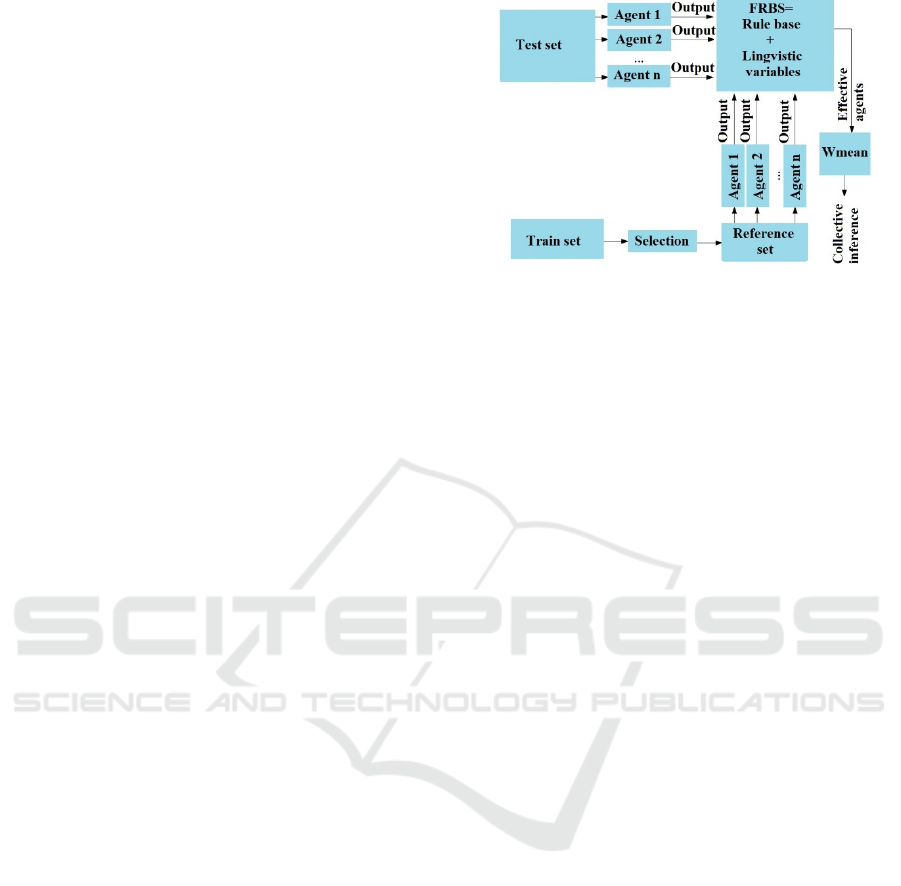
presented in Figure 1.

Figure 1: The general scheme for ensemble inference using

“FRBS+Wmean”.

“FRBS + Wmean” is formed in a way to

effectively combine algorithms (so called “agents”)

into an ensemble. The FRBS makes a decision on the

choice of a classifier or regression algorithm based on

the distance of the test object to the objects of the

training sample and on the success of the classifier at

the nearest object.

The original sample is divided into 3 parts:

training, test and validation. Agents are trained

independently using the training set. We use the test

set for estimating the effectiveness of agent training

and training the fuzzy rule base in FRBS. Finally, the

validation set is used for the assessment of the

efficiency of the whole system.

The FRBS uses the following three input and one

output linguistic variables:

1. Distance: the distance of the test sample object

to the nearest point from the training set.

2. Error: the difference between the output of the

model (agent) on the test sample and at the nearest

point of the training set (agent error on the sample

object).

3. Weight_agent: agent's weight that is calculated

based on agent errors on the training set.

4. Confidence: the degree of confidence in the

agent, which is calculated using a fuzzy inference

procedure, taking into account 3 inputs.

The output of the FRBS for each sample object

from the test set is the degree of confidence in the

agent. Fuzzy inference of the degree of confidence is

evaluated for each agent. One or more agents with the

highest confidence are selected.

The reference set is a subset of the training set

(nPoints of instances from the training set without

taking into account the value of their output)

(Polyakova et al., 2019). In an ensemble output using

a fuzzy logic system for a point from the test set, one

(in the case of nPoints = 1) or several nearest points

(in the case of nPoints> 1) is determined not from the

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

278

training set, but from the reference one. Depending on

how close this point is to an object from the test set

and how well the algorithm copes with it, the agent’s

confidence in this test point is determined.

One or more decision-making agents are selected

for each point of the test set using FRBS. If there are

several agents, then the final decision is made by

averaging.

2.2 About of Designing a “FRBS +

Wmean”

A distinctive feature of FLS is that the model is built

on the principle of a "white box". FLS allow you to

coordinate and combine the experience of experts,

and are also able to model nonlinear functional

dependencies of arbitrary complexity. Therefore, the

use of “FRBS+Wmean” as a method of collective

decision-making in this work will significantly

improve the quality of decisions made, as well as their

interpretability.

The effectiveness of the formation of a fuzzy

system for ensemble output depends not only on the

composition of the ensemble and the examples on the

basis of which each agent is trained, but also on the

type of intra-collective communication (collective

inference, selection of agents into the ensemble, and

distribution of resources between agents). Each of the

design stages of “FRBS + Wmean” requires tuning

and optimization of the corresponding parameters.

For effective options for forming ensembles, each

stage requires the use of powerful and universal

adaptive-type optimization procedures. For this, the

use of adaptive stochastic algorithms for solving

global optimization problems of algorithmically

defined functions of mixed variables, in particular,

evolutionary algorithms (EA), is proposed. An EA

allows you to automatically select a configuration and

configure the parameters of collective decision-

making models based on fuzzy logic.

In this work, rule base is formed via two stages

(Polyakova et al., 2019). At the first stage, a

population of different rule bases (RB1) is formed

using a genetic algorithm. The most effective rule

bases are selected and merged into a single RB1 base.

At the second stage, effective rules are selected from

RB1 in order to form the most accurate base with the

minimum number of rules using the two-criteria

Nondominated Sorting Genetic Algorithm NSGA-II.

The resulting base is RB2.

When selecting a final set of fuzzy rules, the

following criteria are used accuracy, expressed by the

mean squared error of the rules (MSE) for the

regression problem, and complexity, evaluated as the

number of selected rules.

An example of the resulting RB2 Rule Base is:

1) IF error - high THEN confidence – low;

2) IF error - medium AND distance – close

AND weight_agent - high THEN confidence – high;

3) IF error - medium AND distance – medium

THEN confidence – medium;

4) IF error - low AND distance – close AND

weight_agent - high THEN confidence – high;

5) IF error - low AND distance – close AND

weight_agent - low THEN confidence – medium;

6) IF error - low AND distance – medium

AND weight_agent - high THEN confidence – high;

7) IF distance – far THEN confidence – low.

For optimizing the parameters of the membership

functions LV (Distance, Error, Weigh_agent, nAgent,

nPoints) the differential evolution (DE) algorithm is

applied (Polyakova et al., 2019). The membership

function is triangular.

As an evolutionary procedure for the automated

selection of the training set samples to the reference

set (NP), a genetic algorithm of unconstrained single-

objective optimization with a special encoding

scheme is used.

For the automated formation of an ensample (Ag),

the NSGA-II algorithm is proposed. This algorithm is

able to automate the formation of the composition of

the ensemble, thereby saving computing resources

(by minimizing the number of agents), and to solve

the assigned problems efficiently (by increasing the

ability to generalize the result).

In this paper, we consider the dependence of the

quality of the problem solution on the sequence of the

following design and optimization stages of “FRBS +

Wmean”: formation of the ensemble formation (Ag),

selection of the reference set (NP), formation of the

rule base (generation (RB1) and selection of rules

(RB2)), the formation of linguistic variables (LV)

(Polyakova et al., 2019).

2.3 Forming of the Ensemble

Composition for “FRBS+Wmean”

Generally, most problems of technological

production have their own specifics. When solving

them, specialized mathematical models are often

used. However, each such model is intended only for

solving a specific type of problem and is not

applicable (or “not replicated”) to others. The use of

such models often does not provide the desired

efficiency, but they can carry some additional and

important information.

Researching the Efﬁciency of Conﬁgurations of a Collective Decision-making System on the Basis of Fuzzy Logic

279

When using a CDMM, the effectiveness depends

on the set of relevant agents and their diversity. From

the substantive point of view, in the CDMM each

agent should improve or at least not worsen the value

of its utility function, or the system as a whole should

improve the quality of solving the general problem.

In accordance with this, it is necessary to include such

mathematical models as an agent in the ensemble.

In this paper, to solve the problem of modelling

the technological process of metallurgical production

(restoration of the cryolite ratio), it is proposed to

study the following two schemes:

1) Agent training is based on the available data set

for solving the CR recovery problem. A comparative

analysis of the effectiveness of an ensemble based on

fuzzy logic FRBS + Wmean and a model available in

aluminium production is performed.

2) The training of agents is performed using the

same inputs as in Scheme 1, but the model from

production is included in the ensemble.

Accordingly, it is additionally proposed to

investigate the situation (Scheme 3) when agents are

trained on the basis of the available data set for

solving the problem of restoring the cryolite ratio and

on the basis of the model’s output from production,

i.e. the model output is also the agent input. The

model from production is also part of the ensemble as

a separate agent.

3 DATABASE DESCRIPTION

The electrolyte composition is determined by the

values of three parameters - the cryolite ratio and the

content of calcium and magnesium fluorides.

The electrolyte composition is adjusted based on

the selection of the optimal CR: the ratio of

aluminium fluoride to sodium fluoride (NaF / AlF

The complexity of the problem facing analysts is that

the CR is not a measurable quantity, but is calculated

from the measured amounts of fluorides of sodium,

aluminium, calcium, magnesium and lithium. The

analysis of crystallized samples taken from the baths

is performed by chemical or X-ray diffractometric

methods in laboratory conditions after sampling

(Zaloga et al., 2016), (Chen et al., 2017).

The disadvantage of diffractometric method for

determining the CR is that the selection of samples of

the electrolyte for analysis of its chemical

composition is usually carried out once every three

days, which is insufficient from the point of view of

the efficiency of control, since the value of the

cryolite ratio can vary significantly over several

hours. In this regard, the electrolyzer for a long time

works with the deviation of the parameters from the

set values, which entails a decrease in the

performance indicators of his work (Wade et al.,

2016).

In this paper, the problem was set to simulate the

process of determining the cryolite ratio to forecast

the values of the indicator at the moments when it is

impossible to take readings from the equipment

directly (true values).

Data was provided by an aluminium smelter. In

the problem of predicting the cryolite ratio, we used a

feature space with nine features and 2193

measurements.

The accuracy of each agent in the training sample

is calculated on the basis of the efficiency criterion -

Concordance Correlation Coefficient (CCC)



(1):

)(

yxyx











(1)

where



and



are average values of two

variables,



and



are dispersions. 𝜌 is the

correlation coefficient between two variables.

The CCC shows the degree of agreement between

the studied variables. The concordance coefficient

takes a value in the range from 0 to 1:

- if there is no correlation between the studied

variables, it is equal to 0;

- a coefficient equal to 1 denotes full agreement of

the studied variables.

This coefficient was chosen as a criterion of

efficiency in order to conduct a comparative analysis

of efficiency with other scientific papers in which the

task of predicting indicators of technological

production for aluminium was solved.

4 EXPERIMENTS AND RESULTS

To solve the CR recovery problem, a comparative

analysis of the effectiveness of the three proposed

schemes for an ensemble based on FRBS with a

model available in aluminium production is

performed:

- agents are trained based on the available data set

to solve the problem of CR recovery;

- agents are trained using the same inputs as in

scheme 1, but the model from production is included

in the ensemble;

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

280

- the model from production is also part of the

ensemble as a separate agent. However, additional

training for agents is based on the model’s exit from

production.

To configure the FRBS, it is necessary to solve the

problem of setting parameters for each design phase

of “

FRBS + Wmean” separately. Accordingly, the

problem arises of choosing effective options for the

ensemble. These require the use of powerful and

universal adaptive-type optimization procedures.

For each stage of “

FRBS + Wmean”, the

corresponding optimization procedures were

launched with the following resources:

- 100 individuals, 100 generations;

- FRBS parameters: nPoints = 1, nAgent = varies

from 1 to 5.

The initial sample was divided into three parts:

learning comprises 60% of the total number of points,

validation - 25%, and testing - 15%.

The criterion of efficiency is the concordance

correlation coefficient (Pvalid is the accuracy on the

test sample, and Ptest is the control);

The following algorithms presented in the Scikit-

learn library (Python) were selected as methods in the

ensemble: the ensemble of decision trees using

gradient boosting (GBR); algorithm of k-nearest

neighbours for the regression problem (KNR); linear

regression, which is based on the metric L1 (LLasso);

linear regression, which is constructed by the method

of least squares (LR); ridge linear regression, which

is based on the L2 metric (LRidge); artificial neural

network (multilayer perceptron) (MLP), network

structure: 200x100x50x20 neurons on the

corresponding layers, sigmoidal activation function;

the ensemble of decision trees by the method of

"random forest" (RFR), the number of trees in the

ensemble: 10, 50, the depth of the tree: 18, the number

of signs used by one tree: 100; the Support Vector

Regression (SVR) method.

Table 1 presents a study of the effectiveness of

FRBS based on Scheme 1 depending on different

sequences of the following optimization stages:

formation of the ensemble formation (Ag), selection

of the reference set (NP), generation (RB1) and

selection of rules (RB2), formation of linguistic

variables (Linguistic variables, LV).

Table 1: A study of the effectiveness of different sequences of the design and formation stages of FRBS based on Scheme 1.

Optimization stage

Scheme №1

1 2 3 4 5

Pvalid Ptest Pvalid Ptest Pvalid Ptest Pvalid Ptest Pvalid Ptest

Stages of formation

and optimization of

FRBS

Best agent 0.533

0.508 0.533 0.508 0.533 0.508 0.533 0.508 0.533 0.508

Worst agent 0.348 0.339 0.348 0.339 0.348 0.339 0.348 0.339 0.348 0.339

Medium

ent

0.477 0.459 0.477 0.459 0.477 0.459 0.477 0.459 0.477 0.459

Mean 0.501 0.481 0.501 0.481 0.501 0.481 0.501 0.481 0.501 0.481

Wmean 0.500 0.482 0.500 0.482 0.500 0.482 0.500 0.482 0.500 0.482

RB1, RB2, LV, Ag, NP

+Wmean

0.531 0.441 0.531 0.441 0.549 0.434 0.528 0.481 0.548 0.483

Ag, RB1, RB2, LV, NP 0.528 0.481 0.546 0.490 0.546 0.490 0.547 0.490 0.546 0.481

Ag, NP, RB1, RB2, LV 0.528 0.481 0.547 0.484 0.528 0.481 0.528 0.481 0.528 0.481

RB1, RB2, LV, NP, Ag 0.542 0.465 0.542 0.465 0.549 0.472 0.549 0.472 0.528 0.481

NP, RB1, RB2, LV, Ag 0.554 0.499 0.555 0.497 0.555 0.497 0.559 0.491 0.528 0.481

NP, Ag, RB1, RB2, LV 0.540 0.471 0.528 0.481 0.541 0.485 0.541 0.485 0.541 0.485

LV, RB1, RB2, Ag, NP 0.541 0.464 0.541 0.464 0.541 0.464 0.528 0.481 0.545 0.489

Ag, LV, RB1, RB2, NP 0.528 0.481 0.541 0.487 0.544 0.483 0.544 0.483 0.550 0.483

Ag, NP, LV, RB1, RB2 0.528 0.481 0.546 0.491 0.548 0.491 0.548 0.491 0.548 0.491

LV, RB1, RB2, NP, Ag 0.521 0.505 0.540 0.521 0.540 0.521 0.540 0.521 0.540 0.521

NP, LV, RB1, RB2, Ag 0.556 0.489 0.556 0.489 0.556 0.489 0.556 0.489 0.556 0.489

NP, Ag, LV, RB1, RB2 0.559 0.480 0.528 0.481 0.544 0.497 0.545 0.481 0.545 0.481

Researching the Efﬁciency of Conﬁgurations of a Collective Decision-making System on the Basis of Fuzzy Logic

281

The combination of tuning procedures and the

automated formation of FRBS does not significantly

improve the results compared with the effectiveness

of the best agent. The maximum accuracy can be

achieved only with one sequence of tuning

procedures: “LV, RB1, RB2, NP, Ag”.

Using the sequence of steps “NP, LV, RB1, RB2,

Ag”, it can be seen that the application of each

subsequent stage of design and optimization of FRBS

does not improve efficiency, but at the same time

does not impair it. In all other cases, the use of various

such sequences can increase the efficiency in

comparison with when the optimization procedure is

applied only at the first stage. Table 2 presents the

results of a study of the effectiveness of the

application of Scheme 2 in the design of FRBS.

The greatest value of the performance criterion is

achieved with the sequence of stages: “RB1, RB2,

LV, Ag, NP”. However, as with the combination

“LV, RB1, RB2, NP, Ag” in Scheme 1, the efficiency

of solving the problem is higher in comparison with

the best agent. Other combinations give even better

results.

The efficiency of the model available in

production for solving the problem of modelling the

technological process of metallurgical production,

namely the recovery of CR is 54% in the control

sample and 50% in the test sample. The maximum

efficiency obtained on the basis of FRBS in Scheme

2 is 67.6% for the test sample and 59.8% for the

control one, which is a significant increase in the

accuracy of solving the problem.

Consistent application of the design and

optimization stages of FRBS also improves the

efficiency from stage to stage.

Research is also conducted in a situation (Scheme

3), whereby agents are trained on the basis of the

available data set for solving the problem of CR

recovery and on the basis of the model’s output from

production, i.e. the model output is also the agent

input. Additionally, the model from production is part

of the ensemble as a separate agent.

Table 2: A study of the effectiveness of different sequences of the design and formation stages of FRBS based on Scheme 2.

timization sta

Scheme №2

1 2 3 4 5

Pvalid Ptest Pvalid Ptest Pvalid Ptest Pvalid Ptest Pvalid Ptest

Stages of formation

and optimization of

FRBS

Best agent 0.546

0.509 0.546 0.509 0.546 0.509 0.546 0.509 0.546 0.509

Worst a

ent 0.348 0.339 0.348 0.339 0.348 0.339 0.348 0.339 0.348 0.339

Medium A

ent 0.485 0.464 0.485 0.464 0.485 0.464 0.485 0.464 0.485 0.464

Mean 0.552 0.525 0.552 0.525 0.552 0.525 0.552 0.525 0.552 0.525

Wmean 0.545 0.522 0.545 0.522 0.545 0.522 0.545 0.522 0.545 0.522

RB1, RB2, LV, Ag, NP

+Wmean

0.641 0.584 0.641 0.584 0.676 0.598 0.676 0.598 0.676 0.598

, RB1, RB2, LV, NP 0.587 0.560 0.587 0.560 0.587 0.560 0.587 0.560 0.587 0.560

, NP, RB1, RB2, LV 0.587 0.530 0.606 0.484 0.623 0.499 0.623 0.499 0.623 0.499

RB1, RB2, LV, NP, A

0.697 0.585 0.697 0.585 0.697 0.585 0.697 0.585 0.697 0.585

NP, RB1, RB2, LV, Ag 0.672 0.506 0.672 0.506 0.672 0.506 0.689 0.510 0.689 0.510

NP, Ag, RB1, RB2, LV 0.632 0.520 0.587 0.530 0.617 0.492 0.617 0.492 0.611 0.484

LV, RB1, RB2, Ag, NP 0.612 0.580 0.663 0.521 0.663 0.521 0.587 0.530 0.587 0.530

, LV, RB1, RB2, NP 0.587 0.530 0.587 0.530 0.587 0.530 0.587 0.530 0.587 0.530

, NP, LV, RB1, RB2 0.587 0.530 0.587 0.530 0.587 0.530 0.587 0.530 0.587 0.530

LV, RB1, RB2, NP, A

0.640 0.490 0.632 0.531 0.632 0.531 0.664 0.523 0.587 0.530

NP, LV, RB1, RB2, Ag 0.642 0.467 0.631 0.478 0.631 0.478 0.631 0.478 0.587 0.530

NP, Ag, LV, RB1, RB2 0.669 0.509 0.587 0.530 0.587 0.530 0.587 0.530 0.587 0.530

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

282

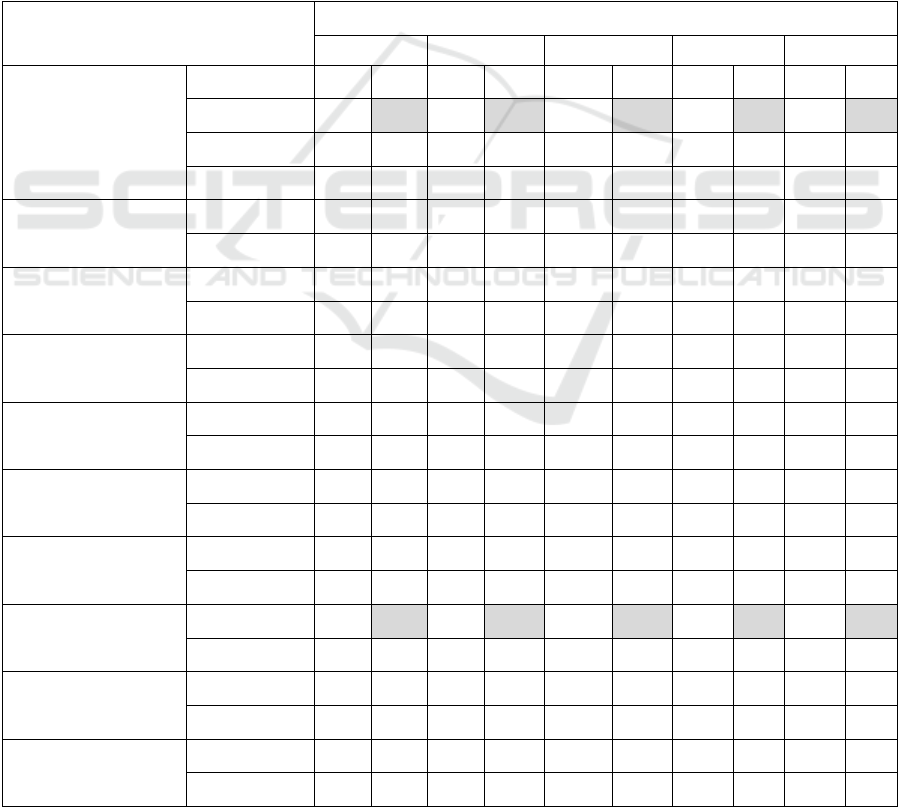
Table 3 presents a study of the effectiveness of

incorporating the recovery model of CR from

production into the ensemble and as an input to FRBS

(according to scheme No. 3) with a different sequence

of stages of design and optimization of FRBS.

Based on the results obtained, it can be concluded

that the sequence of stages of design and optimization

of FRBS is important, since it can significantly

increase the accuracy of the ensemble output as a

whole.

Furthermore, as in the previous two schemes, the

sequence of steps “LV, RB1, RB2, NP, Ag” allows

you to increase the efficiency of solving the problem

and get a better solution than the best of the agents.

It is also worth noting that in the sequence of steps

“LV, RB1, RB2, Ag, NP”, when designing FRBS

with a combination of mean output, each subsequent

step in designing FRBS does not improve the

solution. In addition, with a combination of the

sequences of steps "RB1, RB2, LV, Ag, NP" with

Wmean, each subsequent step increases the

effectiveness of FRBS.

The maximum value of the effectiveness of the

solution to the CR recovery problem obtained on the

basis of three schemes is 68.6% for the control sample

and 61.5% for the test sample.

In general, according to the results of the three

cases, it can be noted that schemes are more effective

than others if the fuzzy decision-making system is set

up before the remaining operators: the choice of

agents and the choice of the reference set.

Table 3: A study of the effectiveness of different sequences of the design and formation stages of FRBS based on Scheme 3.

Scheme №3

timization sta

1 2 3 4 5

Stages of formation

and optimization of

FRBS

Pvalid Ptest Pvalid Ptest Pvalid Ptest Pvalid Ptest Pvalid Ptest

Best a

ent 0.687 0.577 0.687 0.577 0.687 0.577 0.687 0.577 0.687 0.577

Worst a

ent 0.298 0.340 0.298 0.340 0.298 0.340 0.298 0.340 0.298 0.340

Medium A

ent 0.579 0.517 0.579 0.517 0.579 0.517 0.579 0.517 0.579 0.517

RB1, RB2, LV, Ag, NP

+mean 0.652 0.560 0.652 0.560 0.695 0.571 0.667 0.572 0.692 0.575

+Wmean 0.671 0.557 0.671 0.557 0.656 0.564 0.667 0.572 0.690 0.574

Ag, RB1, RB2, LV, NP

+mean 0.667 0.572 0.688 0.577 0.680 0.577 0.692 0.570 0.692 0.570

+Wmean 0.667 0.572 0.688 0.572 0.688 0.572 0.687 0.570 0.687 0.570

Ag, NP, RB1, RB2, LV

+mean 0.663 0.559 0.692 0.563 0.692 0.563 0.692 0.563 0.693 0.563

+Wmean 0.667 0.572 0.692 0.570 0.693 0.570 0.693 0.570 0.693 0.570

RB1, RB2, LV, NP, Ag

+mean 0.695 0.597 0.695 0.597 0.695 0.597 0.695 0.597 0.695 0.597

+Wmean 0.673 0.591 0.673 0.591 0.673 0.591 0.673 0.591 0.673 0.591

NP, RB1, RB2, LV, Ag

+mean 0.716 0.544 0.711 0.552 0.714 0.552 0.586 0.599 0.586 0.599

+Wmean 0.704 0.560 0.704 0.551 0.704 0.551 0.704 0.555 0.667 0.572

NP, Ag, RB1, RB2, LV

+mean 0.718 0.522 0.667 0.572 0.689 0.577 0.689 0.577 0.684 0.572

+Wmean 0.721 0.592 0.721 0.592 0.721 0.592 0.721 0.592 0.721 0.592

LV, RB1, RB2, Ag, NP

+mean 0.720

0.603 0.720 0.603 0.720 0.603 0.720 0.603 0.720 0.603

+Wmean 0.724 0.591 0.724 0.591 0.724 0.591 0.724 0.591 0.724 0.591

Ag, LV, RB1, RB2, NP

+mean 0.667 0.572 0.667 0.572 0.667 0.572 0.667 0.572 0.667 0.572

+Wmean 0.667 0.572 0.692 0.578 0.693 0.573 0.693 0.573 0.687 0.571

Ag, NP, LV, RB1, RB2

+mean 0.667 0.572 0.691 0.565 0.693 0.572 0.689 0.571 0.689 0.571

+Wmean 0.663 0.559 0.694 0.558 0.694 0.563 0.694 0.564 0.694 0.564

Researching the Efﬁciency of Conﬁgurations of a Collective Decision-making System on the Basis of Fuzzy Logic

283

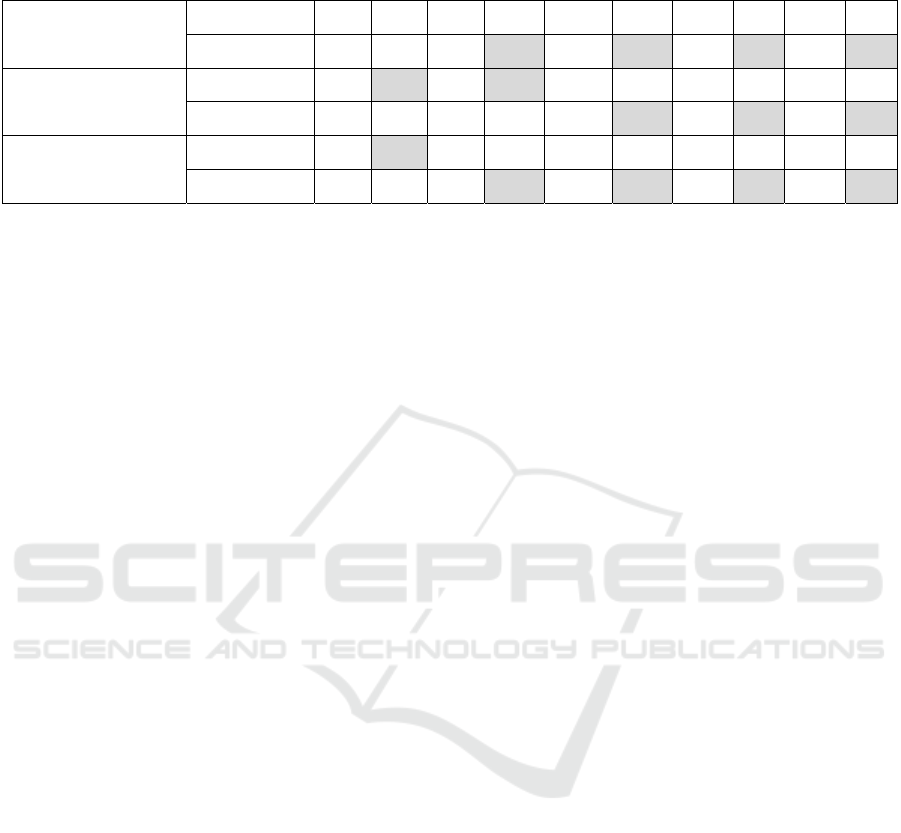
Table 3: A study of the effectiveness of different sequences of the design and formation stages of FRBS based on

Scheme 3 (cont.).

LV, RB1, RB2, NP, Ag

+mean

0.694 0.564 0.691 0.562 0.691 0.562 0.733 0.553 0.667 0.572

+Wmean 0.680 0.565 0.686 0.615 0.686 0.615 0.686 0.615 0.686 0.615

NP, LV, RB1, RB2, Ag

+mean 0.723

0.600 0.722 0.605 0.724 0.596 0.721 0.596 0.667 0.572

+Wmean 0.719 0.557 0.723 0.574 0.725 0.601 0.725 0.601 0.725 0.601

NP, Ag, LV, RB1, RB2

+mean 0.723

0.606 0.667 0.572 0.681 0.555 0.675 0.580 0.675 0.580

+Wmean 0.711 0.543 0.682 0.612 0.682 0.612 0.682 0.612 0.682 0.612

For example, in each of the three schemes, the

sequence of steps “LV, RB1, RB2, NP, Ag” allows

you to achieve a better efficiency than the best agent.

This effect can be explained by the fact that an

efficiently tuned fuzzy system reduces the influence

of “bad” agents and objects from the reference set by

extracting useful solutions even from these objects.

Also for configuring a fuzzy system, it is important to

maintain diversity of agents and points of the

reference set.

When using the reverse order of the stages, the

execution of Ag and NP is performed using the

starting rule base and linguistic variables that are not

optimal for the given problem. The diversity of agents

and reference points is reduced, which leads to

limitations in tuning the rule base and linguistic

variables.

5 CONCLUSION

Thus, an ensemble output based on general machine

learning methods allows you to achieve a result at the

level of a model developed by industry experts.

Moreover, the inclusion of such a model in the

ensemble makes it possible to significantly increase

the accuracy of the forecast. In addition, the inclusion

of model data for training general machine learning

models and the inclusion of the model in the ensemble

makes it possible to further increase the accuracy of

the forecast.

For the successful formation of a collective

decision-making system based on fuzzy logic, the

schemes where the system core is formed first — the

fuzzy decision-making procedure according to the

schemes “LV, RB1, RB2” or “RB1, RB2, LV” –

proved to be more effective, and then the reference

set and set of agents are configured. In some cases,

tuning the reference set and set of agents does not

improve the performance of FRBS.

However, tuning the system kernel from scratch

requires a lot of computing resources. The problem

can be solved by researching and developing a pre-

trained universal core of the system. Adaptation of the

kernel to a specific problem could reduce the amount

of computations required to configure the whole

system for a specific problem.

ACKNOWLEDGEMENTS

The reported study was funded by Russian

Foundation for Basic Research, Government of

Krasnoyarsk Territory, Krasnoyarsk Regional Fund

of Science, to the re-search project: 18-41-242011

«Multi-objective design of predictive models with

compact interpretable strictures in epidemiology».

REFERENCES

Chen, X., Yang, J., Li, Z., Weiping, W. U., 2017. U.S.

Patent No. 9,611,151. Washington, DC: U.S. Patent

and Trademark Office.

Chi, Z., Yan, H., & Pham, T., 1996. Fuzzy algorithms: with

applications to image processing and pattern

recognition, vol. 10, World Scientific.

Chien, B. C., Lin, J. Y., Hong, T. P., 2002. Learning

discriminant functions with fuzzy attributes for

classification using genetic programming. Expert

Systems with Applications, 23(1), pp. 31-37.

Cord, O., 2001. Genetic fuzzy systems: evolutionary tuning

and learning of fuzzy knowledge bases, vol. 19, World

Scientific.

Delgado, M. R., Von Zuben, F., Gomide, F., 2001.

Hierarchical genetic fuzzy systems. Information

Sciences, 136(1-4), pp. 29-52.

Grochowski, M., Jankowski, N., 2004. Comparison of

instance selection algorithms II. Results and comments.

In International Conference on Artificial Intelligence

and Soft Computing, pp. 580-585, Springer, Berlin,

Heidelberg.

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

284

Hoffmann, F., Nelles, O., 2001. Genetic programming for

model selection of TSK-fuzzy systems. Information

Sciences, 136(1-4), pp. 7-28.

Jinhong, L. 2008. Fuzzy predictive control system of

cryolite ratio for prebake aluminum production cells. In

2008 7th World Congress on Intelligent Control and

Automation, pp. 1229-1233, IEEE.

Lee, M. A., 1994. Automatic design and adaptation of fuzzy

systems and genetic algorithms using soft computing

techniques. PhD Thesis, University of California,

Davis.

LóPez, V., FernáNdez, A., Del Jesus, M. J., Herrera, F.,

2013. A hierarchical genetic fuzzy system based on

genetic programming for addressing classification with

highly imbalanced and borderline data-sets.

Knowledge-Based Systems, vol. 38, pp. 85-104.

Mazurowski, M. A., Malof, J. M., Tourassi, G. D., 2010.

Comparative analysis of instance selection algorithms

for instance-based classifiers in the context of medical

decision support. Physics in Medicine & Biology, 56(2),

pp. 473.

Millán-Giraldo, M., García, V., Sánchez, J. S., 2013.

Instance Selection Methods and Resampling

Techniques for Dissimilarity Representation with

Imbalanced Data Sets. In Pattern Recognition-

Applications and Methods, pp. 149-160, Springer,

Berlin, Heidelberg.

Pedrycz, W. (Ed.), 2012. Fuzzy modelling: paradigms and

practice, vol. 7, Springer Science & Business Media.

Polyakova, A., Lipinskiy, L., 2017. A study of fuzzy logic

ensemble system performance on face recognition

problem. In IOP Conference Series: Materials Science

and Engineering, vol. 173, no. 1, p. 012013. IOP

Publishing.

Polyakova, A. S., Lipinskiy, L. V., Semenkin, E. S., 2019.

Investigation of resource allocation efficiency in

optimization of fuzzy control system. In IOP

Conference Series: Materials Science and Engineering,

vol. 537, no. 5, p. 052036. IOP Publishing.

Polyakova, A., Lipinskiy, L., Semenkin, E., 2019.

Investigation of Reference Sample Reduction Methods

for Ensemble Output with Fuzzy Logic-Based Systems.

In 2019 8th International Congress on Advanced

Applied Informatics (IIAI-AAI), pp. 583-586, IEEE.

Wade, K., Banister, A. J., 2016. The Chemistry of

Aluminium, Gallium, Indium and Thallium:

Comprehensive Inorganic Chemistry. Elsevier.

Yurkov, V., Mann, V., Piskazhova, T., Nikandrov, K.,

Trebukh, O. 2002. Dynamic control of the cryolite ratio

and the bath temperature of aluminium reduction cell.

In light metals-warrendale-proceedings, pp. 383-388.

Zadeh, L. A., 1965. Fuzzy sets. Information and control,

8(3), pp. 338-353.

Zaloga, A., Akhmedova, S., Yakimov, I., Burakov, S.,

Semenkin, E., Dubinin, P., ... & Andryushchenko, E.,

2016. Genetic Algorithm for Automated X-Ray

Diffraction Full-Profile Analysis of Electrolyte

Composition on Aluminium Smelters. In Informatics in

Control, Automation and Robotics 12th International

Conference, ICINCO 2015 Colmar, France, July 21-

23, pp. 79-93, Springer, Cham.

Researching the Efﬁciency of Conﬁgurations of a Collective Decision-making System on the Basis of Fuzzy Logic

285