
A Feature Space Transformation to Intrusion Detection Systems
Roberto Saia, Salvatore Carta, Diego Reforgiato Recupero and Gianni Fenu
Department of Mathematics and Computer Science,
University of Cagliari, Via Ospedale 72 - 09124 Cagliari, Italy
Keywords:
Intrusion Detection, Anomaly Detection, Data Preprocessing, Machine Learning, Algorithms.
Abstract:
The anomaly-based Intrusion Detection Systems (IDSs) represent one of the most efficient methods in coun-
tering the intrusion attempts against the ever growing number of network-based services. Despite the central
role they play, their effectiveness is jeopardized by a series of problems that reduce the IDS effectiveness in a
real-world context, mainly due to the difficulty of correctly classifying attacks with characteristics very similar
to a normal network activity or, again, due to the difficulty of contrasting novel forms of attacks (zero-days).
Such problems have been faced in this paper by adopting a Twofold Feature Space Transformation (TFST)
approach aimed to gain a better characterization of the network events and a reduction of their potential pat-
terns. The idea behind such an approach is based on: (i) the addition of meta-information, improving the
event characterization; (ii) the discretization of the new feature space in order to join together patterns that
lead back to the same events, reducing the number of false alarms. The validation process performed by using
a real-world dataset indicates that the proposed approach is able to outperform the canonical state-of-the-art
solutions, improving their intrusion detection capability.
1 INTRODUCTION
A good definition of the intrusion concept is that made
in (Sundaram, 1996), where such a concept is summa-
rized as the attempt to compromise or bypass the se-
curity of a given target environment. In a general and
shared way, the most authoritative literature in this
area indicates confidentiality, integrity, and availabil-
ity as the three requirements to be met to obtain the se-
curity of a system/environment (Pfleeger and Pfleeger,
2012).
The Intrusion Detection Systems (IDSs) (McHugh
et al., 2000) cover a central role in the context of the
security of the network services. It is given by the
fact that, nowadays, an enormous number of private
and public services are provided through the network,
important services such as those related to the educa-
tion, medicine, finance, and so on. Nowadays, an in-
creasing number of devices uses network services, re-
lated to a series of new technologies/paradigms such
as Internet of Things (IoT), smart grids, and the 5G
technology.
The dramatic increase in the number of network
services has led toward an increasing in the IDS us-
age in order to improve the protection provided by
other systems, such as the firewalls. This because the
canonical approaches based on, for instance, authen-
tication, data encryption, or defined rules, are not able
to face this kind of problem, effectively.
An IDS operates on the basis of several ap-
proaches, with the goal of classifying the intrusion
network activities, correctly. Its operative range could
be a single machine or an entire network, but regard-
less of the technique and strategy used in order to
classify the network events, there are a series of prob-
lems that affect its effectiveness. It is mainly given by
the high level of heterogeneity of the involved oper-
ative scenarios and services. Also the event patterns
present an high level of heterogeneity and such a data
dynamism is further worsened by the similarity that,
in many cases, exists between intrusion and normal
events. Another important problem is the difficulty of
correctly detecting attacks that have never been car-
ried out previously (zero-days).
Based on our previous experience (Saia et al.,
2019b; Saia et al., 2019a), where we have experi-
mented the positive effects resulting from the trans-
formation of the original data feature space, here we
propose a revised and improved approach, named
Twofold Feature Space Transformation (TFST). It is
aimed to get a better characterization of the network
events by a twofold process: (i) addition of meta-
information in order to get a better characterization
of the network events aimed to discriminate the nor-
Saia, R., Carta, S., Recupero, D. and Fenu, G.
A Feature Space Transformation to Intrusion Detection Systems.
DOI: 10.5220/0009982901370144
In Proceedings of the 12th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2020) - Volume 1: KDIR, pages 137-144
ISBN: 978-989-758-474-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
137

mal activities from the intrusion ones; (ii) discretiza-
tion of the new extended feature space aimed to re-
duce the number of potential event patterns, decreas-
ing the false alarm rate and improving the IDS per-
formance. It should be observed that, in spite the
fact that the data discretization is a preprocessing
strategy largely used in literature, the combination of
it with the addition of meta-information overcomes
some well-known side effects (e.g., the related loss of
information). The scientific contributions related to
the research performed in this paper are therefore the
following:
- formalization of the Twofold Feature Space Trans-
formation (TFST) approach in the IDS domain;
- definition of an algorithm able to classify the new
network events by using the TFST approach;
- evaluation of the TFST approach performance, with
regards to a series of state-of-the-art competitors.
2 BACKGROUND AND RELATED
WORK
The concept of intrusion detection has been formal-
ized for the first time in 1980 by Anderson (Ander-
son, 1980), subsequently it has been later refined by
Denning (Denning, 1987). Both of them have also
formalized the different type of Intrusion Detection
Systems.
Intrusion Detection Systems: The Intrusion Detec-
tion Systems (IDSs) are placed within a network in
order to allow them to capture and analyze the re-
lated traffic of either a single or all the machines in
the network. Their objective is the correct classifi-
cation of the intrusion network activity, which can be
generated by a software (Campbell, 2016) (e.g., virus,
worm, trojan-horse, root-kits, spy-ware, etc.) or it can
depend on a human activity (e.g., attempt to exploit a
network service or resource).
Similarly to other domains such as, for instance,
those related to the Fraud Detection (Carta et al.,
2019; Saia and Carta, 2017) or Credit Scoring (Saia
and Carta, 2016; Saia et al., 2018), also the Intru-
sion Detection Systems area is characterized by un-
balanced data, an aspect to take into account both in
the context of the strategies/approaches and evalua-
tion metrics (Rodda and Erothi, 2016).
There are different ways to classify the IDSs. One
largely adopted approach classifies them into two
types, anomaly detection and signature-based detec-
tion (Wang et al., 2014a). The first type of IDSs
(anomaly detection) operates by classifying the net-
work traffic in a binary way, normal or intrusion,
whereas the second type of IDSs (signature-based de-
tection) relies on a database which contains the pat-
tern related to the known intrusion network activi-
ties (Liao et al., 2013). The literature presents also
some hybrid solutions named Specification-based De-
tection, where the anomaly and signature-based de-
tection strategies have been combined in order to im-
prove the IDS performance (Gilmore and Haydaman,
2016).
Another way largely used in order to classify the
IDSs divides them into four categories, on the basis
of their operative approach: Host-based (Jose et al.,
2018), Network-based (Mazini et al., 2019), Network-
node-based (Potluri and Diedrich, 2016), and Hybrid-
based (Amrita, 2018).
A Host-based Intrusion Detection System (HIDS)
works by using several machines that operate as
agents in order to intercept the network activity. The
behavior of these machines (i.e., in term of processes,
logs, etc.) is compared with the information about
the known intrusion events, stored in a database, and
when an intrusion activity is detected, the configured
countermeasures will be activated. The advantages
related to this approach are the opportunity to em-
ploy many machines to improve the network security,
whereas the disadvantages are given by the excessive
latency (from the intrusion event occurrence to its de-
tection) and the high number of false alarms (false
positives and false negatives rate).
A Network-based Intrusion Detection System
(NIDS) operates by following a twofold approach
aimed to intercept and analyze all the network traffic.
As first step, each event is analyzed on the basis of
a series of known patterns stored in a database (sig-
natures), and when there is no matching, a network
analysis is performed. The advantages of such an
approach are the capability to detect both the known
and unknown intrusion activities, activating automatic
(e.g., IP address block) or manual (e.g., network ad-
ministrator alerts) countermeasures. The disadvan-
tages are in this case given by the inability to well op-
erate in scenarios characterized by a high level of net-
work traffic, along with the inability to operate with
encrypted data and in a proactive way.
A Network-Node-based Intrusion Detection Sys-
tem (NNIDS) operates by listening the network traffic
at a specific network node, with the aim to operate in
a strategic position of the network. On the basis of its
function, it is possible to consider its operative strat-
egy as a combination of the HIDS and NIDS ones.
Other types of Intrusion Detection Systems are the
hybrid ones, where the operative approaches men-
tioned above have been combined in some way.
They are commonly classified as Hybrid-based or as
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
138

Distributed-based.
Evaluation Metrics: Premising that the IDS effec-
tiveness is related to its capability to detect anomalous
network events that could be related to an attacker ac-
tivity, the literature offers several metrics able to eval-
uate this aspect (Kumar, 2014). The classification of
a network event, performed by an IDS, is usually a
binary response (i.e., normal or intrusion). For this
reason, most of the used metrics are based on the con-
fusion matrix
1
, metrics such as, for instance, the True
Negative Rate (also called Specificity), the True Posi-
tive Rate (also called Sensitivity), the F-measure (also
called F-score), and the Matthews Correlation Coef-
ficient. These metrics are usually flanked by other
ones (Munaiah et al., 2016) able to operate even in
the case of unbalanced data, effectively, such as those
based on the ROC (Receiver Operating Characteris-
tic) curve, especially the AUC (Area Under the Re-
ceiver Operating Characteristic).
Open Issues: The main source of problems, which
makes the correct classification of network events a
very difficult task, is the similarity between normal
and intrusion events. We can say that the limit of the
Anomaly Detection approaches is given by the impos-
sibility of having a dataset that contains all the pos-
sible intrusion activities patterns, especially when we
do not have very discriminant features able to differ-
entiate these activities from the legitimate ones. In
such a context the Unsupervised Anomaly Detection
approaches (Falc
˜
ao et al., 2019) are aimed to identify
unknown network activities, but they rely on the as-
sumption that almost all the previous collected cases
are related to legitimate network activities, and this
may not always be true. In the context of the Misuse
Detection strategy, instead, the limit is related to the
inability for such an IDS to detect unknown intrusion
activities (i.e., pattern never detected before). The
Specification-based strategy, which is based on the
two aforementioned ones, is obviously jeopardized by
the same limits.
3 APPROACH DEFINITION
Before continuing, we premise the formal notation
used in this paper: given the set E = {e
1
, e
2
, . . . , e
X
}
of classified events, which is composed by the sub-
set E
+
= {e
+
1
, e
+
2
, . . . , e
+
Y
} (with E
+
⊆ E) of nor-
mal events, and the subset E
−
= {e
−
1
, e
−
2
, . . . , e
−
W
}
of intrusion events (with E
−
⊆ E), we denote as
ˆ
E = {ˆe
1
, ˆe
2
, . . . , ˆe
Z
} the set of unclassified events.
1
A matrix 2x2 that reports the number of True Negatives
(TN), False Negatives (FN), True Positives (TP), and False
Positives (FP).
1 2 3 4
5 6
7 8 9 10
0.0
20.0
40.0
60.0
80.0
100.0
5
19
41
71
Range o f discretization
Continuous values
Figure 1: Data Discretization.
Each event is composed by a set of features F =
{f
1
, f
2
, . . . , f
N
}, and it can belong to only one of the
classes of the set C = {normal, intrusion}.
Approach Introduction: The Twofold Feature Space
Transformation (TFST) approach proposed in this pa-
per is aimed to well characterize the class of informa-
tion taken into account by an IDS (i.e., normal and
intrusion events). This has been performed by operat-
ing an extension of the original feature space through
the addition of several meta-information, which is fol-
lowed by a data discretization. The data extension
represents an approach that the literature classifies
as a way that in some cases is able to improve the
performance of a machine learning classifier, which
can be performed on the basis of the single data
vector information (dataset row) or/and on the ba-
sis of the entire dataset information (Castiello et al.,
2005). By way of example, Equation 1 formalizes
such an extended feature space, where {f
1
, f
2
, . . . , f
N
}
denotes the set of original features that characterize
each event, and {m
1
, m
2
, . . . , m
O
} denotes the added
meta-information.
f
1
, f
2
, . . . , f
N
, m
N+1
, m
N+2
, . . . , m
N+O
(1)
The data discretization (Liu et al., 2002) repre-
sents our second step, a process largely used in the
literature in order to transform continuous values into
a categorical form, in order to use some classifier
that are not able to operate with continuous values.
Such a process is performed by dividing each fea-
ture value that characterizes an event into a discrete
number of non overlapped intervals, then by mapping
each numerical value (continuous or discrete) into one
of these intervals. In addition to the advantage of al-
lowing us the use of algorithms unable to operate on
continuous data, this preprocessing approach allows
us also a reduction of the data size and a better data
understandability. Figure 1 exemplifies this process
in the context of four feature values, which are con-
verted from their original continuous form (range of
values [0, 100]) to a new discrete form (range of val-
ues {0,1, . . . , 10}). The result of the process produces
the values {3, 5, 7, 9} that represent the discretization
of the original continuous values [5, 19, 41, 71].
By following this twofold approach we want to
A Feature Space Transformation to Intrusion Detection Systems
139

obtain two results: (i) an improvement of the event
characterization through the addition of several meta-
information; (ii) the reduction of the number of pat-
terns for each class of information (normal and intru-
sion) through the data discretization.
Approach Description: The proposed TFST ap-
proach has been defined by following the three steps
below:
1. Extension: the original feature space is extended
by adding several meta-information calculated on
the basis of the values they extend, for each in-
stance e ∈ E and ˆe ∈
ˆ
E, both characterized by
the set of features F. In more detail, each event
vector in the sets E and
ˆ
E is here extended by
introducing four meta-information calculated in
the vector context, which we denoted as Ξ =
{m
1
, m
2
, m
3
, m
4
}. Such meta-information are the
Minimum (m
1
), Maximum (m
2
), Average (m
3
),
and Standard Deviation (m
4
), as formalized in
Equation 2.
Ξ =
m
1
= min( f
1
, f
2
, . . . , f
N
)
m
2
= max( f
1
, f
2
, . . . , f
N
)
m
3
=
1
N
∑
N
n=1
( f
n
)
m
4
=
q
1
N−1
∑
N
n=1
( f
n
−
¯
f )
2
(2)
2. Discretization: the extended feature space is then
discretized according to an optimal discretization
range experimentally defined. In more detail, the
extended features related to the events in the sets
E and
ˆ
E (i.e., {f
1
, f
2
, . . . , f
N
, m
1
, m
2
, m
3
, m
4
}) are
discretized by transforming each value from the
original continuous or discrete range to a dis-
crete range of values {0, 1, . . . , δ} ∈ Z according
to a discretization value experimentally defined,
as detailed in Section 4.3. More formally, de-
noting as f
δ
−→ d the discretization function, we
transform each feature f ∈ F from its continuous
or discrete value to one of the discrete values in
the range {d
1
, d
2
, . . . , d
δ
}, as shown in Equation 3
(∀ e ∈ E ∧ ˆe ∈
ˆ
E).
{f
1
, f
2
, . . . , f
N
, f
N+1
, f
N+2
, f
N+3
, f
N+4
}
↓ δ
{d
1
, d
2
, . . . , d
N
, d
N+1
, d
N+2
, d
N+3
, d
N+4
}
(3)
3. Classification: the new feature space obtained
through the TFST approach is finally exploited in
the context of a classifier of the network events.
In more detail, the new feature space is here used
in the context of the classifier formalized in Algo-
rithm 1: at step 1, it takes as input parameters the
core algorithm alg, the classified events in the set
E, and the unclassified ones in the set
ˆ
E; the TFST
approach is applied at steps 2 and 3, and the new
feature space related to the set E is exploited in or-
der to train the evaluation model of the algorithm
alg at step 4; the events in the set
ˆ
E are classified
at steps from 5 to 8 and the result is saved in out
and returned at step 9.
Algorithm 1: Events classification.
Require: alg=Classifier, E=Classified events,
ˆ
E=Unclassified events
Ensure: out=Classification of
ˆ
E events
1: procedure INSTANCECLASSIFICATION(alg, E,
ˆ
E)
2: E
00
← getNewFeatureSpace(E)
3:
ˆ
E
00
← getNewFeatureSpace(
ˆ
E)
4: model ←Classi f ierTraining(alg, E
00
)
5: for each ˆe
00
∈
ˆ
E
00
do
6: c ←getEventClass(model, ˆe
00
)
7: out.add(c)
8: end for
9: return out
10: end procedure
4 EXPERIMENTS
The code related to the proposed approach has been
developed in Python language, exploiting the scikit-
learn
2
library. In the scikit-learn context, the exper-
iments reproducibility has been granted by fixing the
pseudo-random number generator seed to 1 (i.e., ran-
dom state=1).
4.1 Dataset
Overview: In order to validate the proposed ap-
proach we used the real-world dataset NSL-KDD
3
,
and updated an improved version of the KDD-
CUP99 dataset, which was suffering from some prob-
lems (Wang et al., 2014b), e.g., the data redundancy.
Its characteristics are reported in Table 1, which
shows the events distribution in terms of normal (i.e.,
|E
+
|) and intrusion (i.e., |E
−
|) ones. It should be
noted that the number of distinct events is not the
same in the training and test parts of the dataset, be-
cause some events exist in a dataset and not in the
other one, and vice versa.
Table 1: NSL-KDD Characteristics.
Dataset Total events Normal Intrusion Features Distinct
|E| |E
+
| |E
−
| |F| events
Training 125, 973 67, 343 58, 630 41 23
Test 22, 543 9, 710 12,833 41 38
Total 148, 516 77,053 71, 463
Events Distribution: Detailed information about the
events distribution are provided through Table 2 and
2
http://scikit-learn.org
3
https://github.com/defcom17/NSL KDD
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
140

Table 3, according to the following classification:
- Privilege Escalation Attack (PEA): attacks aimed to
gain a privileged access, operating as unprivileged
user (e.g., buffer overflow);
- Denial of Service Attack (DSA): attacks aimed to
make ineffective a service/system through a huge
number of normal iterations with it (e.g., syn flood-
ing);
- Remote Scanning Attack (RSA): attacks aimed to
get information about services/systems, through the
exploitation of invasive techniques (e.g., port scan-
ning);
- Remote Access Attack (RAA): attacks aimed to ob-
tain a remote system access by using raw techniques
(e.g., brute-force);
- Normal Network Activity (NNA): it has been used to
classify the normal network activities.
Table 2: NSL-KDD Events Distribution.
Event Training Test Type Event Training Test Type
01 apache2 0 737 DSA 21 processtable 0 685 DSA
02 back 956 359 DSA 22 ps 0 15 PEA
03 buffer overflow 30 20 PEA 23 rootkit 10 13 PEA
04 ftp write 8 3 RAA 24 saint 0 319 RSA
05 guess passwd 52 1231 RAA 25 satan 3633 735 RSA
06 httptunnel 0 133 RAA 26 sendmail 0 14 RAA
07 imap 11 1 RAA 27 smurf 2646 665 DSA
08 ipsweep 3599 141 RSA 28 snmpgetattack 0 178 RAA
09 land 18 7 DSA 29 snmpguess 0 331 RAA
10 loadmodule 9 2 PEA 30 sqlattack 0 2 PEA
11 mailbomb 0 293 DSA 31 spy 2 0 RAA
12 mscan 0 996 RSA 32 teardrop 892 12 DSA
13 multihop 7 18 RAA 33 udpstorm 0 2 DSA
14 named 0 17 RAA 34 warezclient 890 0 RAA
15 neptune 41214 4657 DSA 35 warezmaster 20 944 RAA
16 nmap 1493 73 RSA 36 worm 0 2 DSA
17 perl 3 2 PEA 37 xlock 0 9 RAA
18 phf 4 2 RAA 38 xsnoop 0 4 RAA
19 pod 201 41 DSA 39 xterm 0 13 PEA
20 portsweep 2931 157 RSA 40 normal 67343 9710 NNA
Table 3: NSL-KDD Events Overview.
Dataset PEA DSA RSA RAA NNA
Training 52 45,927 11, 656 994 67,343
Test 67 7,460 2, 421 2, 885 9, 710
Total 119 53, 387 14, 077 3, 879 77, 053
% 0.08 35.95 9.48 2.61 51.88
Some examples of the four categories of attacks
reported in Table 2 are provided in the following:
• PEA: Buffer overflow, Loadmodule, Rootkit,
Perl, Sqlattack, Xterm, and Ps;
• DSA: Back, Land, Neptune, Pod, Smurf,
Teardrop, Mailbomb, Processtable, Udpstorm,
Apache2, and Worm;
• RSA: Satan, IPsweep, Nmap, Portsweep, Mscan,
and Saint;
• RAA: Guess password, Ftp write, Imap, Phf,
Multihop, Warezmaster, Xlock, Xsnoop, Sn-
mpguess, Snmpgetattack, Httptunnel, Sendmail,
and Named.
4.2 Metrics
Specificity: The Specificity metric is formalized in
Equation 4, where
ˆ
E denotes the set of unclassified
instances, the TN denotes the number of events cor-
rectly classified as intrusion, and FP denotes the num-
ber of intrusion events wrongly classified as normal.
It gives us the true negative rate of an IDS, focusing
on its capability to detect the intrusion events.
Speci f icity(
ˆ
E) =
T N
(T N + FP)
(4)
Matthews Correlation Coefficient: The Matthews
Correlation Coefficient (MCC), whose formalization
is shown in Equation 5, is able to operate with datasets
characterized by unbalanced data (Luque et al., 2019),
providing an evaluation in the range [−1, +1], where
+1 indicates the correctness of all classifications, −1
indicates that all classifications are wrong, and 0 indi-
cates the effectiveness of a random classifier.
MCC =
(T P·T N)−(FP·FN)
√
(T P+FP)·(T P+F N)·(T N+FP)·(T N+FN)
(5)
AUC: The Area Under the Receiver Operating Char-
acteristic curve (AUC) is a metric based on the ROC
curve (Fawcett, 2004) that allows us a reliable evalu-
ation of an IDS effectiveness in terms of its capability
to discriminate the normal events from the intrusion
ones, since it is not biased by the data unbalance. As
shown in Equation 7, given the normal (E
+
) and in-
trusion (E
−
) events that compose the set E, we denote
as κ all the possible comparisons of the scores of each
event e, and the result is the average of them, which is
a value in the range [0, 1], where 1 indicates the best
performance, as formalized in Equation 7.
κ(i
+
, i
−
) =
1, i f i
+
> i
−
0.5, i f i
+
= i
−
0, i f i
+
< i
−
(6)
AUC =
1
I
+
·I
−
|I
+
|
∑
1
|I
−
|
∑
1
κ(i
+
, i
−
) (7)
4.3 Strategy
Baseline Algorithms: The assessment of the pro-
posed TFST approach has been performed by com-
paring its performances to those related to a state-
of-the-art competitor that we selected on the basis of
its effectiveness, taken from one of the algorithms re-
ported in Table 4, among those most used in the liter-
ature. In more detail, we compared the performance
of the best of these classification algorithms, with and
without the application of the TFST approach on the
A Feature Space Transformation to Intrusion Detection Systems
141
Table 4: Competitor Algorithms.
Algorithm Used acronym Literature reference
Gradient Boosting GB (Chopra and Bhilare, 2018)
Adaptive Boosting AB (Xia et al., 2017)
Random Forests RF (Malekipirbazari and Aksakalli, 2015)
Multilayer Perceptron MP (Luo et al., 2017)
Decision Tree DT (Damrongsakmethee and Neagoe, 2019)
data feature space. It should be observed that each al-
gorithm has been optimized by cross-validated grid-
search over a parameter grid.
Validation Process: The performance of the pro-
posed TFST approach have been evaluated by follow-
ing a k-fold cross-validation criterion (k=5) in order
to reduce the impact of the data dependency.
Data Preprocessing: As a preliminary operation, we
transformed the categorical features in the dataset into
a numerical features and, with the aim to perform a
binary classification of each event (i.e., 0 = normal
and 1 = intrusion), we introduced a new class feature.
Discretization Range Definition: A new series of
experiments, whose results are shown in Table 5, have
been performed in order to detect the optimal δ value
to use in the discretization process, i.e., the value that
leads to the best algorithm performance.
Table 5: Optimal Discretization Value.
Dataset Algorithm δ
AB 12
DT 120
DSA GB 27
MP 7
RF 6
AB 125
DT 158
NNA GB 135
MP 112
RF 77
AB 171
DT 157
PEA GB 47
MP 70
RF 123
Dataset Algorithm δ
AB 71
DT 73
RAA GB 250
MP 247
RF 89
AB 148
DT 187
RSA GB 221
MP 138
RF 118
4.4 Validation
Table 6 shows the results obtained by comparing the
proposed approach to all of its competitor algorithms,
for of all the datasets. The Performances have been
expressed in terms of average value between Speci-
ficity, MCC, and AUC and the Comparison indicates
when the proposed approach performs better than its
competitor (i.e., +).
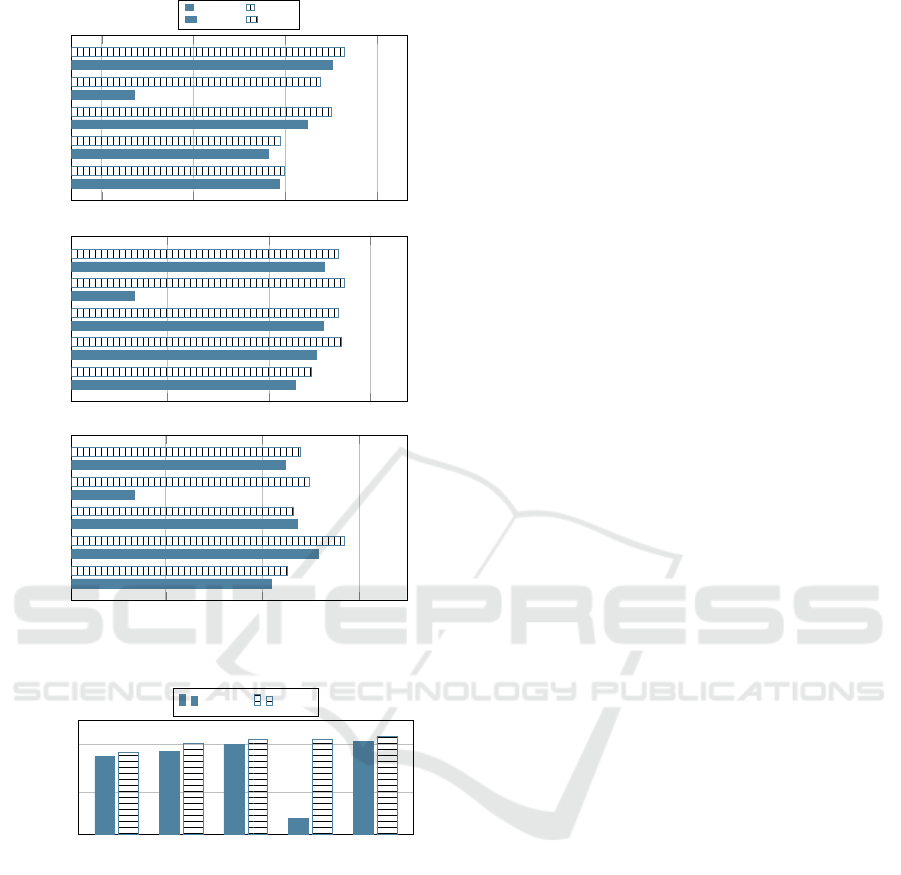
In more detail, Figure 2 shows the mean Speci-
ficity, MCC, and AUC measured in the context of all
the algorithms, with (TFST) and without (Baseline)
the adoption of the proposed approach. It means that
it represents the average value of these metrics for
each algorithm in all the datasets.
Figure 3 gives us an overview about the perfor-
mances (average value of all metrics) with respect to
each single algorithm, in the context of all the events
Table 6: Performance Comparison.
TFST Baseline
Dataset Algorithm Performance Performance Comparison
AB 0.9827 0.9875 -
DT 0.9859 0.9865 -
DSA GB 0.9884 0.9863 +
MP 0.9869 0.9697 +
RF 0.9851 0.9853 -
AB 0.9443 0.9445 -
DT 0.9691 0.9627 +
NNA GB 0.9614 0.9620 -
MP 0.9697 0.8762 +
RF 0.9650 0.9645 +
AB 0.7634 0.7427 +
DT 0.7107 0.6480 +
PEA GB 0.7512 0.7139 +
MP 0.7489 0.3158 +
RF 0.7839 0.7405 +
AB 0.7757 0.7321 +
DT 0.8700 0.8611 +
RAA GB 0.8859 0.8640 +
MP 0.8825 0.6814 +
RF 0.8798 0.8722 +
AB 0.9564 0.9663 -
DT 0.9760 0.9704 +
RSA GB 0.9706 0.9661 +
MP 0.9708 0.8842 +
RF 0.9729 0.9680 +
in the datasets.
On the basis of the experimental results, the fol-
lowing considerations can be made:
- in terms of average performance between the Speci-
ficity, MCC, and AUC metrics, the proposed TFST
approach outperforms its competitor in almost all
the cases, 19 cases out of 25, as reported in Table 6;
- also by analyzing the mean value in terms of Speci-
ficity, MCC, and AUC, individually, we can observe
how the TFST approach outperforms its competi-
tors, as reported in Figure 2;
- it outperforms the competitor algorithms in the con-
text of both the single algorithm performance and
the different data scenarios, focusing the perfor-
mance on its capability to correctly identify the in-
trusion events, since they are expressed as the aver-
age value between Specificity, MCC, and AUC;
- considering that the competitor and the proposed
approach operate both with the same parameter
configuration of each algorithm, it means that it is
able to improve the performance of state-of-the-art
classifiers, regardless of the used algorithm;
- although in some cases the TFST performance im-
provement is slight, it still represents an impor-
tant achievement, considering the huge number of
events processed by an IDS;
- it outperforms the competitor algorithms in datasets
characterized by different number of events, type of
events, and level of class balance, showing its capa-
bility to operate in different real-world scenarios;
- the performance measurement, made in terms of
Specificity, MCC, and AUC metrics according to
a 5-folds cross-validation criterion, underlines the
capabilities of the proposed approach in terms of
effectiveness to detect the intrusion events (Speci-
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
142
0.70 0.80 0.90 1.00
RF
MP
GB
DT
AB
0.9515
0.7354
0.9236
0.8817
0.8935
0.9637
0.9375
0.9500
0.8940
0.8990
Mean Specificity
Algorithms
Baseline TFST
0.70 0.80 0.90
RF
MP
GB
DT
AB
0.8548
0.6672
0.8538
0.8469
0.8258
0.8686
0.8738
0.8686
0.8711
0.8417
Mean MCC
Algorithms
0.85
0.90
0.95
RF
MP
GB
DT
AB
0.9119
0.8338
0.9180
0.9286
0.9046
0.9197
0.9239
0.9160
0.9420
0.9129
Mean AUC
Algorithms
Figure 2: Classification Performance.
RFMP
GB
DTAB
0.80
0.90
Algorithms
Performance
Baseline TFST
Figure 3: Overall Performance.
ficity), along to its ability to discriminate the nor-
mal ones (MCC and AUC), regardless of the level of
data balance, reducing the number of false alarms;
- the performance of each single algorithm in the
context of all events in the dataset, shown in Fig-
ure 3, indicates that the proposed approach is able
to improve the average performance of each of the
algorithms, showing in some cases a really signifi-
cant improvement (e.g., MP);
- on the basis of the preceding considerations, it is
possible to deduce that the proposed approach is
able to improve the performance of the state-of-the-
art solutions, regardless both the involved classifi-
cation algorithms and the data scenarios, also by
considering that such an improvement can be ex-
ploited in the context of the single-algorithm and
multi-algorithms solutions (e.g., hybrid-based or
ensemble-based approaches).
5 CONCLUSIONS
In our age increasingly dominated by network-based
technologies, ensuring the security of the transmit-
ted information becomes a crucial aspect. For this
reason, in recent decades we have seen an impres-
sive growth in efforts aimed at identifying approaches
and strategies that can efficiently manage this prob-
lem. However, solutions such as the IDS have to face
hard challenges, mainly due to the huge number of
involved events to process and classify, activity made
more difficult by the data heterogeneity and imbal-
ance between normal and intrusion events.
The Twofold Feature Space Transformation
(TFST) approach we proposed in this paper is aimed
to improve the performance of the state-of-the-art
classification algorithms through a twofold transfor-
mation of the events data before its classification, on
the basis of the idea that a better characterization of
the events, combined with a reduction of their poten-
tial patterns, lead to better performances. This idea
has been validated by a series of experiments con-
ducted using different algorithms and different types
of events, by adopting metrics able to assess both the
ability to identify intrusion events, and the ability to
correctly discriminate the two classes of information
(normal and intrusion), reducing the number of incor-
rect classifications.
ACKNOWLEDGEMENTS
This research is partially funded by Italian Ministry
of Education, University and Research - Program
Smart Cities and Communities and Social Innovation
project ILEARNTV (D.D. n.1937 del 05.06.2014,
CUP F74G14000200008 F19G14000910008).
REFERENCES
Amrita, K. K. R. (2018). A hybrid intrusion detection
system: Integrating hybrid feature selection approach
with heterogeneous ensemble of intelligent classifiers.
International Journal of Network Security (IJNS’18),
20(1):41–55.
A Feature Space Transformation to Intrusion Detection Systems
143

Anderson, J. P. (1980). Computer security threat monitoring
and surveillance.
Campbell, T. (2016). Protection of systems. In Prac-
tical Information Security Management, pages 155–
177. Springer.
Carta, S., Fenu, G., Recupero, D. R., and Saia, R. (2019).
Fraud detection for e-commerce transactions by em-
ploying a prudential multiple consensus model. J. Inf.
Secur. Appl., 46:13–22.
Castiello, C., Castellano, G., and Fanelli, A. M. (2005).
Meta-data: Characterization of input features for
meta-learning. In International Conference on Mod-
eling Decisions for Artificial Intelligence, pages 457–
468. Springer.
Chopra, A. and Bhilare, P. (2018). Application of ensemble
models in credit scoring models. Business Perspec-
tives and Research, 6(2):129–141.
Damrongsakmethee, T. and Neagoe, V.-E. (2019). Principal
component analysis and relieff cascaded with decision
tree for credit scoring. In Computer Science On-line
Conference, pages 85–95. Springer.
Denning, D. E. (1987). An intrusion-detection model. IEEE
Transactions on software engineering, (2):222–232.
Falc
˜
ao, F., Zoppi, T., Silva, C. B. V., Santos, A., Fonseca,
B., Ceccarelli, A., and Bondavalli, A. (2019). Quanti-
tative comparison of unsupervised anomaly detection
algorithms for intrusion detection. In Proceedings of
the 34th ACM/SIGAPP Symposium on Applied Com-
puting, pages 318–327.
Fawcett, T. (2004). Roc graphs: Notes and practical consid-
erations for researchers. Machine learning, 31(1):1–
38.
Gilmore, C. and Haydaman, J. (2016). Anomaly detection
and machine learning methods for network intrusion
detection: An industrially focused literature review. In
Proceedings of the International Conference on Secu-
rity and Management (SAM), page 292. The Steering
Committee of The World Congress in Computer Sci-
ence, Computer . . . .
Jose, S., Malathi, D., Reddy, B., and Jayaseeli, D. (2018). A
survey on anomaly based host intrusion detection sys-
tem. In Journal of Physics: Conference Series, vol-
ume 1000, page 012049. IOP Publishing.
Kumar, G. (2014). Evaluation metrics for intrusion detec-
tion systems-a study. Evaluation, 2(11):11–7.
Liao, H.-J., Lin, C.-H. R., Lin, Y.-C., and Tung, K.-Y.
(2013). Intrusion detection system: A comprehensive
review. Journal of Network and Computer Applica-
tions, 36(1):16–24.
Liu, H., Hussain, F., Tan, C. L., and Dash, M. (2002). Dis-
cretization: An enabling technique. Data mining and
knowledge discovery, 6(4):393–423.
Luo, C., Wu, D., and Wu, D. (2017). A deep learn-
ing approach for credit scoring using credit default
swaps. Engineering Applications of Artificial Intel-
ligence, 65:465–470.
Luque, A., Carrasco, A., Mart
´
ın, A., and de las Heras, A.
(2019). The impact of class imbalance in classifica-
tion performance metrics based on the binary confu-
sion matrix. Pattern Recognition, 91:216–231.
Malekipirbazari, M. and Aksakalli, V. (2015). Risk assess-
ment in social lending via random forests. Expert Sys-
tems with Applications, 42(10):4621–4631.
Mazini, M., Shirazi, B., and Mahdavi, I. (2019). Anomaly
network-based intrusion detection system using a re-
liable hybrid artificial bee colony and adaboost algo-
rithms. Journal of King Saud University-Computer
and Information Sciences, 31(4):541–553.
McHugh, J., Christie, A., and Allen, J. (2000). Defend-
ing yourself: The role of intrusion detection systems.
IEEE software, 17(5):42–51.
Munaiah, N., Meneely, A., Wilson, R., and Short, B. (2016).
Are intrusion detection studies evaluated consistently?
a systematic literature review.
Pfleeger, C. P. and Pfleeger, S. L. (2012). Security in Com-
puting, 4th Edition. Prentice Hall.
Potluri, S. and Diedrich, C. (2016). High performance in-
trusion detection and prevention systems: A survey. In
ECCWS2016-Proceedings fo the 15th European Con-
ference on Cyber Warfare and Security, page 260.
Academic Conferences and publishing limited.
Rodda, S. and Erothi, U. S. R. (2016). Class imbal-
ance problem in the network intrusion detection sys-
tems. In 2016 International Conference on Electrical,
Electronics, and Optimization Techniques (ICEEOT),
pages 2685–2688. IEEE.
Saia, R. and Carta, S. (2016). A linear-dependence-based
approach to design proactive credit scoring models. In
KDIR, pages 111–120. SciTePress.
Saia, R. and Carta, S. (2017). Evaluating credit card trans-
actions in the frequency domain for a proactive fraud
detection approach. In SECRYPT, pages 335–342.
SciTePress.
Saia, R., Carta, S., and Fenu, G. (2018). A wavelet-based
data analysis to credit scoring. In ICDSP, pages 176–
180. ACM.
Saia, R., Carta, S., Recupero, D. R., Fenu, G., and Saia, M.
(2019a). A discretized enriched technique to enhance
machine learning performance in credit scoring. In
KDIR, pages 202–213. ScitePress.
Saia, R., Carta, S., Recupero, D. R., Fenu, G., and Stan-
ciu, M. (2019b). A discretized extended feature space
(DEFS) model to improve the anomaly detection per-
formance in network intrusion detection systems. In
KDIR, pages 322–329. ScitePress.
Sundaram, A. (1996). An introduction to intrusion detec-
tion. Crossroads, 2(4):3–7.
Wang, W., Guyet, T., Quiniou, R., Cordier, M.-O.,
Masseglia, F., and Zhang, X. (2014a). Autonomic
intrusion detection: Adaptively detecting anomalies
over unlabeled audit data streams in computer net-
works. Knowledge-Based Systems, 70:103–117.
Wang, Y., Yang, K., Jing, X., and Jin, H. L. (2014b). Prob-
lems of kdd cup 99 dataset existed and data prepro-
cessing. In Applied Mechanics and Materials, volume
667, pages 218–225. Trans Tech Publ.
Xia, Y., Liu, C., Li, Y., and Liu, N. (2017). A boosted de-
cision tree approach using bayesian hyper-parameter
optimization for credit scoring. Expert Systems with
Applications, 78:225–241.
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
144
