Self-supervised Dimensionality Reduction with Neural Networks and

Pseudo-labeling

Mateus Espadoto

1,3 a

, Nina S. T. Hirata

1 b

and Alexandru C. Telea

2 c

Institute of Mathematics and Statistics, University of S

ao Paulo, Brazil

Department of Information and Computing Sciences, University of Utrecht, The Netherlands

Johann Bernoulli Institute, University of Groningen, The Netherlands

Keywords:

Dimensionality Reduction, Machine Learning, Neural Networks, Autoencoders.

Abstract:

Dimensionality reduction (DR) is used to explore high-dimensional data in many applications. Deep learning

techniques such as autoencoders have been used to provide fast, simple to use, and high-quality DR. How-

ever, such methods yield worse visual cluster separation than popular methods such as t-SNE and UMAP.

We propose a deep learning DR method called Self-Supervised Network Projection (SSNP) which does DR

based on pseudo-labels obtained from clustering. We show that SSNP produces better cluster separation than

autoencoders, has out-of-sample, inverse mapping, and clustering capabilities, and is very fast and easy to use.

1 INTRODUCTION

Analyzing high-dimensional data, a central task in

data science and machine learning, is challenging due

to the large size of the data both in the number of

observations and measurements recorded per obser-

vation (also known as dimensions, features, or vari-

ables). As such, visualization of high-dimensional

data has become an important, and active, ﬁeld of

information visualization (Kehrer and Hauser, 2013;

Liu et al., 2015; Nonato and Aupetit, 2018; Espadoto

et al., 2019a).

Dimensionality reduction (DR) methods, also

called projections, have gained a particular place

in the set of visualization methods for high-

dimensional data. Compared to other techniques

such as glyphs (Yates et al., 2014), parallel coor-

dinate plots (Inselberg and Dimsdale, 1990), table

lenses (Rao and Card, 1994; Telea, 2006), and scat-

ter plot matrices (Becker et al., 1996), DR meth-

ods scale visually far better both on the number

of observations and dimensions, allowing the vi-

sual exploration of datasets having thousands of di-

mensions and hundreds of thousands of samples.

Many DR techniques have been proposed (Nonato

and Aupetit, 2018; Espadoto et al., 2019a), with

https://orcid.org/0000-0002-1922-4309

https://orcid.org/0000-0001-9722-5764

https://orcid.org/0000-0003-0750-0502

PCA (Jolliffe, 1986), t-SNE (Maaten and Hinton,

2008), and UMAP (McInnes and Healy, 2018) hav-

ing become particularly popular.

Neural networks, while very popular in machine

learning, are less commonly used for DR, with

self-organizing maps (Kohonen, 1997) and autoen-

coders (Hinton and Salakhutdinov, 2006) being no-

table examples. While having useful properties such

as ease of use, speed, and out-of-sample capability,

they lag behind t-SNE and UMAP in terms of good

visual cluster separation, which is essential for the in-

terpretation of the created visualizations. More recent

deep-learning DR methods include NNP (Espadoto

et al., 2020), which learns how to mimic existing DR

techniques, and ReNDA (Becker et al., 2020), which

uses two neural networks to accomplish DR.

DR methods aim to satisfy multiple functional

requirements (quality, cluster separation, out-of-

sample support, stability, inverse mapping) and non-

functional ones (speed, ease of use, genericity). How-

ever, to our knowledge, none of the existing meth-

ods scores well on all such criteria (Espadoto et al.,

2019a). In this paper, we propose to address this

by a new DR method based on a single neural net-

work trained with a dual objective, one of reconstruct-

ing the input data, as in a typical autoencoder, and

the other of data classiﬁcation using pseudo-labels

cheaply computed by a clustering algorithm to in-

troduce neighborhood information, since intuitively,

Espadoto, M., Hirata, N. and Telea, A.

Self-supervised Dimensionality Reduction with Neural Networks and Pseudo-labeling.

DOI: 10.5220/0010184800270037

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 3: IVAPP, pages 27-37

ISBN: 978-989-758-488-6

clustering gathers and aggregates ﬁne-grained dis-

tance information at a higher level, telling how groups

of samples are similar to each other (at cluster level),

and this aggregated information helps us next in pro-

ducing projections which reﬂect this higher-level sim-

ilarity.

Our method aims to jointly cover all the following

characteristics, which, to our knowledge, is not yet

achieved by existing DR methods:

Quality (C1). We provide better cluster separation

than standard autoencoders, and close to state-of-the-

art DR methods, as measured by well-known metrics

in DR literature;

Scalability (C2). Our method can do inference in lin-

ear time in the number of dimensions and observa-

tions, allowing us to project datasets of up to a mil-

lion observations and hundreds of dimensions in a few

seconds using commodity GPU hardware;

Ease of Use (C3). Our method produces good results

with minimal or no parameter tuning;

Genericity (C4). We can handle any kind of high-

dimensional data that can be represented as real-

valued vectors;

Stability and Out-of-Sample Support (C5). We

can project new observations for a learned projection

without recomputing it, in contrast to standard t-SNE

and any other non-parametric methods;

Inverse Mapping (C6). We provide, out-of-the-

box, an inverse mapping from the low- to the high-

dimensional space;

Clustering (C7). We provide, out-of-the-box, the

ability to learn how to mimic clustering algorithms,

by assigning labels to unseen data.

We structure our paper as follows: Section 2

presents the notation used and discusses related work

on dimensionality reduction, Section 3 details our

method, Section 4 presents the results that support our

contributions outlined above, Section 5 discusses our

proposal, and Section 6 concludes the paper.

2 BACKGROUND

We start with a few notations. Let x = (x

, . . . , x

∈ R, 1 ≤ i ≤ n be a n-dimensional (nD) real-valued

sample, and let D = {x

}, 1 ≤ i ≤ N be a dataset of N

samples. D can be seen as a table with N rows (sam-

ples) and n columns (dimensions). A DR, or projec-

tion, technique is a function

P : R

→ R

, (1)

where q  n, and typically q = 2. The projection

P(x) of a sample x ∈ D is a qD point p ∈ R

Projecting a set D yields thus a qD scatter plot, which

we denote next as P(D). The inverse of P, denoted

−1

(p), maps a qD point to the high-dimensional

space R

Dimensionality Reduction. Tens of DR methods

have been proposed in the last decades, as extensively

described and reviewed in various surveys (Hoffman

and Grinstein, 2002; Maaten and Postma, 2009; En-

gel et al., 2012; Sorzano et al., 2014; Liu et al., 2015;

Cunningham and Ghahramani, 2015; Xie et al., 2017;

Nonato and Aupetit, 2018; Espadoto et al., 2019a).

Below we only highlight a few representative ones,

referring for the others to the aforementioned surveys.

Principal Component Analysis (Jolliffe, 1986)

(PCA) has been widely used for many decades due

to its simplicity, speed, and ease of use and interpreta-

tion. PCA is also used as pre-processing step for other

DR techniques that require the data dimensionality to

be not too high (Nonato and Aupetit, 2018). PCA is

highly scalable, easy to use, predictable, and has out-

of-sample capability. Yet, due to its linear and global

nature, PCA lacks on quality, especially for data of

high intrinsic dimensionality, and is thus worse for

data visualization tasks related to cluster analysis.

The methods of the Manifold Learning family,

such as MDS (Torgerson, 1958), Isomap (Tenenbaum

et al., 2000) and LLE (Roweis and Saul, 2000) with

its variations (Donoho and Grimes, 2003; Zhang and

Zha, 2004; Zhang and Wang, 2007) try to map to

2D the high-dimensional manifold on which data is

embedded, and can capture nonlinear data structure.

These methods are commonly used in visualization

and they generally yield higher quality results than

PCA. However, these methods can be hard to tune, do

not have out-of-sample capability, do not work well

for data that is not restricted to a 2D manifold, and

generally scale poorly with dataset size.

Force-directed methods such as LAMP (Joia et al.,

2011) and LSP (Paulovich et al., 2008) are popular in

visualization and have also been used for graph draw-

ing. They can yield reasonably high visual quality,

good scalability, and are simple to use. However, they

generally lack out-of-sample capability. In the case of

LAMP, there exists a related inverse projection tech-

nique, iLAMP (Amorim et al., 2012), however, the

two techniques are actually independent and not part

of a single algorithm. Clustering-based methods, such

as PBC (Paulovich and Minghim, 2006), share many

of the characteristics of force-directed methods, such

as reasonably good quality and lack of out-of-sample

capability.

The SNE (Stochastic Neighborhood Embedding)

family of methods, of which t-SNE (Maaten and Hin-

ton, 2008) is arguably the most popular, have the key

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

Table 1: Summary of DR techniques and their characteristics.

Characteristic

Technique Quality Scalability Ease of use Genericity Out-of-sample Inverse mapping Clustering

PCA low high high high yes yes no

MDS mid low low low no no no

Isomap mid low low low no no no

LLE mid low low low no no no

LAMP mid mid mid high no no no

LSP mid mid mid high no no no

t-SNE high low low high no no no

UMAP high high low high yes no no

Autoencoder low high high low yes yes no

ReNDA mid low low mid yes no no

NNP high high high high yes no no

SSNP high high high high yes yes yes

ability to visually segregate similar samples, thus be-

ing very good for cluster analysis. While praised

for high visual quality, t-SNE has a (high) complex-

ity of O(N

) in sample count, is very sensitive to

small data changes, can be hard to tune (Wattenberg,

2016), and has no out-of-sample capability. Sev-

eral reﬁnements of t-SNE improve speed, such as

tree-accelerated t-SNE (Maaten, 2014), hierarchical

SNE (Pezzotti et al., 2016), and approximated t-

SNE (Pezzotti et al., 2017), and various GPU accel-

erations of t-SNE (Pezzotti et al., 2020; Chan et al.,

2018). Yet, these methods require quite complex

algorithms, and still largely suffer from the afore-

mentioned sensitivity, tuning, and out-of-sample is-

sues. Uniform Manifold Approximation and Pro-

jection (UMAP) (McInnes and Healy, 2018) gener-

ates projections with comparable quality to t-SNE but

much faster, and with out-of-sample capability. How-

ever, UMAP shares some disadvantages with t-SNE,

namely the sensitivity to small data changes and pa-

rameter tuning difﬁculty.

Deep Learning. Autoencoders (AE) (Hinton and

Salakhutdinov, 2006; Kingma and Welling, 2013) aim

to generate a compressed, low-dimensional represen-

tation on their bottleneck layers by training the net-

work to reproduce its high-dimensional inputs on its

outputs. Autoencoders produce results comparable to

PCA on the quality criterion. However, they are easy

to set up, train, and use, are easily parallelizable, and

have out-of-sample and inverse mapping capabilities.

The ReNDA method (Becker et al., 2020) is a

deep learning approach that uses two networks, im-

proving on earlier work from the same authors. One

network implements a nonlinear generalization of

Fisher’s Linear Discriminant Analysis (Fisher, 1936);

the other network is an autoencoder used as a regular-

izer. ReNDA scores well on predictability and has

out-of-sample capability. However, it requires pre-

training of each individual network and scalability is

quite low.

Recently, Espadoto et al. (Espadoto et al., 2020)

proposed Neural Network Projections (NNP), where

a training subset D

⊂ D is selected and projected by

any DR method to yield a so-called training projec-

tion P(D

) ⊂ R

. D

is fed into a regression neural

network which is trained to output a 2D scatter plot

) ⊂ R

by minimizing the error between P(D

)

and P

). The trained network then projects un-

seen data by means of 2-dimensional, non-linear re-

gression. NNP is very fast, simple to use, generic,

and stable. However, the results show fuzzier clus-

ter separation (lower quality) than the training projec-

tions, and cannot do inverse projections. The NNInv

technique (Espadoto et al., 2019b), proposed by the

same authors, provides inverse projection capability,

but this requires setting up, training, and using a sep-

arate network.

Table 1 shows a summary of the aforementioned

DR techniques and how they fare with respect to each

characteristic. The last row highlights SSNP, our

technique, which we describe next.

Step 1: Label assignment

In: Clustering algo, D

Out: Y

Clustering (K-means, Affinity Propagation, DBSCAN, etc)

Ground Truth labels

Step 2: Training

In: D

, Y

Out: Trained network

Stochastic Gradient Descent

Joint optimization of classifier and reconstruction targets

Step 3: Assembly of final networks

In: Trained network

Out: N

, N

Dismantle trained network

Construct final networks based on trained layers

Step 4: Inference

In: D→N

P(D)→N

D→N

Out: N

→P(D) N

→D N

→ Y

Networks trained and ready to use for

Direct projection, inverse projection and clustering

Figure 1: SSNP training-and-inference pipeline.

Self-supervised Dimensionality Reduction with Neural Networks and Pseudo-labeling

Encoder layers

Activation: ReLU

Init: Glorot Uniform

Bias: constant 0.0001

Embedding layer

Activation: Linear

Init: Glorot Uniform

Bias: constant 0.0001

L2: 0.5

Decoder layers

Activation: ReLU

Init: Glorot Uniform

Bias: constant 0.0001

Dense layer: 512 units

Input: n-dimensional

Dense layer: 128 units

Dense layer: 32 units

Dense layer: 2 units

Dense layer: 512 units

Dense layer: 128 units

Dense layer: 32 units

Classifier output:

k classes

Softmax activation

Categorical cross entropy loss

Reconstruction output:

n-dimensional

Sigmoid activation

Binary cross entropy loss

Direct

Projection

Inverse

Projection

Clustering

Figure 2: SSNP network architecture used for training.

Dense layer: 512 units

Input: n-dimensional

Dense layer: 128 units

Dense layer: 32 units

Output: 2-dimensional

Projection

Network

Input: 2-dimensional

Dense layer: 512 units

Dense layer: 128 units

Dense layer: 32 units

Inverse

Mapping

Network

Output: n-dimensional

Dense layer: 512 units

Input: n-dimensional

Dense layer: 128 units

Dense layer: 32 units

Dense layer: 2 units

Dense layer: 512 units

Dense layer: 128 units

Dense layer: 32 units

Clustering

Network

Output: k classes

Figure 3: Three SSNP networks used during inference.

3 METHOD

As stated in Section 2, autoencoders have desirable

DR properties (simplicity, speed, out-of-sample and

inverse mapping capabilities), but create projections

of lower quality than, e.g., t-SNE and UMAP. We

believe that the key difference is that autoencoders

do not use neighborhood information during training,

while t-SNE and UMAP (obviously) do that. This

raises the following questions: Could autoencoders

produce better projections if using neighborhood in-

formation? and, if so, How to inject neighborhood

information during autoencoder training? Our tech-

nique answers both questions by using a network ar-

chitecture with a dual optimization target. First, we

have a reconstruction target, exactly as in standard au-

toencoders; next, we use a classiﬁcation target based

on pseudo-labels assigned by some clustering algo-

rithm e.g. K-means (Lloyd, 1982), Agglomerative

Clustering (Kaufman and Rousseeuw, 2005), or any

other way of assigning labels, including using “true”

ground-truth labels if available.

Our key idea is that labels –ground-truth or given

by clustering – are a high-level similarity measure

between data samples which can be used to infer

neighborhood information, i.e., same-label data are

more similar than different-label data. Since classi-

ﬁers seek to learn a representation that separates input

data based on labels, by adding an extra classiﬁer tar-

get to an autoencoder, we learn how to project data

with better cluster separation than standard autoen-

coders. We call our technique Self-Supervised Neural

Projection (SSNP).

SSNP ﬁrst takes a training set D

⊂ D and assigns

to it pseudo-labels Y

∈ Z by using some clustering

technique. We then take samples (x ∈ D

, y ∈ Y

) to

train a neural network with two target functions, one

for reconstruction, other for classiﬁcation, which are

then added together to form a joint loss. The errors

from this joint loss are then back-propagated to the

entire network, during training. This network (Fig-

ure 2) contains a two-unit bottleneck layer, same as

an autoencoder, used to generate the 2D projection

when in inference mode. After training, we ‘split’

the trained layers of the network to create three new

networks for inference: a projector N

(x), an in-

verse projector N

(p) and, as a by-product, a classi-

ﬁer N

(x), which mimics clustering algorithm used

to create Y

(see Figure 3). The entire training-and-

inference operation of SSNP is summarized in Fig-

ure 1.

4 RESULTS

To evaluate SSNP’s performance we propose several

experiments to compare it with other DR techniques

using different datasets. We select the following

evaluation metrics, which are widely used in the

projection literature:

Trustworthiness (T ) (Venna and Kaski, 2006).

Measures the fraction of close points in D that are

also close in P(D). T tells how much one can trust

that local patterns in a projection, e.g. clusters,

represent actual patterns in the data. In the deﬁnition

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

Table 2: Projection quality metrics. Right column gives the metric ranges, with optimal values marked in bold.

Metric Deﬁnition Range

Trustworthiness (T ) 1 −

NK(2n−3K−1)

∑

i=1

∑

j∈U

(K)

(r(i, j) − K) [0, 1]

Continuity (C) 1 −

NK(2n−3K−1)

∑

i=1

∑

j∈V

(K)

(ˆr(i, j) − K) [0, 1]

Neighborhood hit (NH)

∑

y∈P(D)

[0, 1]

Shepard diagram correlation (R) Spearman’s ρ of (kx

− x

k, kP(x

) − P(x

)k), 1 ≤ i ≤ N, i 6= j [0, 1]

(Table 2), U

(K)

is the set of points that are among the

K nearest neighbors of point i in the 2D space but not

among the K nearest neighbors of point i in R

; and

r(i, j) is the rank of the 2D point j in the ordered-set

of nearest neighbors of i in 2D. We choose K = 7, in

line with (Maaten and Postma, 2009; Martins et al.,

2015);

Continuity (C) (Venna and Kaski, 2006). Measures

the fraction of close points in P(D) that are also close

in D. In the deﬁnition (Table 2), V

(K)

is the set of

points that are among the K nearest neighbors of

point i in R

but not among the K nearest neighbors

in 2D; and ˆr(i, j) is the rank of the R

point j in the

ordered set of nearest neighbors of i in R

. As with

T , we choose K = 7;

Neighborhood Hit (NH) (Paulovich et al., 2008).

Measures how well-separable labeled data is in a

projection P(D), in a rotation-invariant fashion,

from perfect separation (NH = 1) to no separation

(NH = 0). NH is the number y

of the k nearest

neighbors of a point y ∈ P(D), denoted by y

, that

have the same label as y, averaged over P(D). In this

paper, we used k = 3;

Shepard Diagram Correlation (R) (Joia et al.,

2011). The Shepard diagram is a scatter plot of the

pairwise distances between all points in P(D) vs the

corresponding distances in D. The closer the plot

is to the main diagonal, the better overall distance

preservation is. Plot areas below, respectively above,

the diagonal show distance ranges for which false

neighbors, respectively missing neighbors, occur. We

measure how close a Shepard diagram is to the ideal

main diagonal line by computing its Spearman rank

correlation R. A value of R = 1 indicates a perfect

(positive) correlation of distances;

We next show how SSNP performs on differ-

ent datasets when compared to t-SNE, UMAP, au-

toencoders, and NNP. We use different algorithms to

generate pseudo-labels, and also use ground-truth la-

bels. For conciseness, we name SSNP variants using

K-means, agglomerative clustering and ground-truth

labels as SSNP(Km), SSNP(Agg) and SSNP(GT),

respectively. We use two types of datasets: syn-

thetic blobs and real-world data. The synthetic blobs

datasets are sampled from a Gaussian distribution

where we vary the number of dimensions (100 and

700), the number of cluster centers (5 and 10), and use

increasing values of the standard deviation σ. This

yields datasets with cluster separation varying from

very sharp to fuzzy clusters. All synthetic datasets

have 5K samples.

Real-world datasets are selected from publicly

available sources, matching the criteria of being

high-dimensional, reasonably large (thousands of

samples), and having a non-trivial data structure:

MNIST (LeCun and Cortes, 2010). 70K samples of

handwritten digits from 0 to 9, rendered as 28x28-

pixel gray scale images, ﬂattened to 784-element

vectors;

Fashion MNIST (Xiao et al., 2017). 70K samples

of 10 types of pieces of clothing, rendered as 28x28-

pixel gray scale images, ﬂattened to 784-element

vectors;

Human Activity Recognition (HAR) (Anguita et al.,

2012). 10299 samples from 30 subjects performing

activities of daily living used for human activity

recognition, described with 561 dimensions.

Reuters Newswire Dataset (Thoma, 2017). 8432

observations of news report documents, from which

5000 attributes were extracted using TF-IDF (Salton

and McGill, 1986), a standard method in text pro-

cessing. This is a subset of the full dataset which

contains data for the six most frequent classes only.

All datasets had their attributes rescaled to the in-

terval [0, 1], to conform with the sigmoid activation

function used at the reconstruction layer (see Fig-

ure 2).

4.1 Quality: Synthetic Datasets

Figure 4 shows the projection of the synthetic blob

datasets with SSNP(Km) using the correct number of

clusters, alongside Autoencoders, t-SNE and UMAP.

We see that in most cases SSNP-Km shows better

visual cluster separation than Autoencoders. Also,

SSNP-Km preserves the spread of the data better than

t-SNE and UMAP, which can be seen by the fact that

the projections using these look almost the same re-

gardless of the standard deviation in the data. We omit

the plots and measurements for NNP, since these are

Self-supervised Dimensionality Reduction with Neural Networks and Pseudo-labeling

Table 3: Quality measurements for the synthetic blobs experiment with 100 and 700 dimensions, 5 and 10 cluster centers.

100 dimensions 700 dimensions

5 clusters 10 clusters 5 clusters 10 clusters

Algorithm σ T C R N T C R N σ T C R N T C R N

1.3

0.923 0.938 0.547 1.000 0.958 0.963 0.692 1.000

1.6

0.909 0.914 0.739 1.000 0.953 0.955 0.254 1.000

t-SNE 0.937 0.955 0.818 1.000 0.967 0.977 0.192 1.000 0.917 0.951 0.362 1.000 0.960 0.976 0.346 1.000

UMAP 0.921 0.949 0.868 1.000 0.957 0.970 0.721 1.000 0.906 0.933 0.878 1.000 0.954 0.965 0.471 1.000

SSNP-KM 0.910 0.919 0.687 1.000 0.956 0.959 0.602 1.000 0.904 0.908 0.568 1.000 0.953 0.955 0.399 1.000

3.9

0.919 0.926 0.750 1.000 0.959 0.963 0.484 1.000

4.8

0.910 0.914 0.615 1.000 0.953 0.954 0.354 1.000

t-SNE 0.931 0.953 0.707 1.000 0.966 0.978 0.227 1.000 0.914 0.950 0.608 1.000 0.960 0.977 0.331 1.000

UMAP 0.911 0.940 0.741 1.000 0.956 0.969 0.537 1.000 0.906 0.931 0.697 1.000 0.954 0.965 0.390 1.000

SSNP-KM 0.910 0.918 0.622 1.000 0.955 0.958 0.549 1.000 0.905 0.907 0.612 1.000 0.953 0.954 0.296 1.000

9.1

0.905 0.901 0.569 1.000 0.938 0.945 0.328 0.999

11.2

0.911 0.906 0.600 1.000 0.955 0.954 0.382 1.000

t-SNE 0.913 0.951 0.533 1.000 0.948 0.974 0.254 1.000 0.914 0.950 0.492 1.000 0.959 0.977 0.296 1.000

UMAP 0.888 0.939 0.535 1.000 0.929 0.966 0.342 1.000 0.905 0.931 0.557 1.000 0.953 0.965 0.336 1.000

SSNP-KM 0.888 0.917 0.595 0.998 0.927 0.952 0.437 0.995 0.904 0.906 0.557 1.000 0.950 0.945 0.314 0.998

700 dimensions, 5 clusters

=11.2 =4.8 =1.6

SSNP (Km) Autoencoder t-SNE UMAP

700 dimensions, 10 clusters

SSNP (Km) Autoencoder t-SNE UMAP

100 dimensions, 5 clusters

=9.1 =3.9 =1.3

SSNP (Km) Autoencoder t-SNE UMAP

100 dimensions, 10 clusters

SSNP (Km) Autoencoder t-SNE UMAP

=9.1 =3.9 =1.3

=11.2 =4.8 =1.6

Figure 4: Projection of synthetic blobs datasets with SSNP(Km) and other techniques, with different number of dimensions

and clusters. In each quadrant, rows show datasets having increasing standard deviation σ.

very close to the ones created by the technique it is

trying to mimic, typically t-SNE– see e.g. (Espadoto

et al., 2020).

Table 3 shows the quality measurements for this

experiment for the datasets using 5 and 10 cluster

centers. We see that SSNP performs very similarly

quality-wise to AE, t-SNE, and UMAP. We will bring

more insight to this comparison in Section 4.2, which

studies more challenging, real-world, datasets.

4.2 Quality: Real-world Datasets

Figure 5 shows in the ﬁrst three columns the projec-

tion of real-world datasets by SSNP using pseudo-

labels assigned by K-means and Agglomerative Clus-

tering, alongside the projection created by an autoen-

coder. The next three columns show the same datasets

projected by t-SNE, UMAP, and SSNP using ground-

truth labels. Again, we omit the plots and measure-

ments for NNP, since they are very close to the ones

created by t-SNE and UMAP.

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

SSNP (Km) SSNP (Agg) Autoencoder t-SNE UMAP SSNP (GT)

Reuters HAR FashionMNIST MNIST

Figure 5: Projection of real-world datasets with SSNP and other techniques. Left to right: SSNP using K-means, SSNP using

Agglomerative clustering, Autoencoder, t-SNE, UMAP, and SSNP using ground truth labels.

Table 4: Quality measurements for the real-world datasets.

Dataset Method T C R NH

MNIST

SSNP(Km) 0.882 0.903 0.264 0.767

SSNP(Agg) 0.859 0.925 0.262 0.800

AE 0.887 0.920 0.009 0.726

SSNP(GT) 0.774 0.920 0.398 0.986

NNP 0.948 0.969 0.397 0.891

t-SNE 0.985 0.972 0.412 0.944

UMAP 0.958 0.974 0.389 0.913

FashionMNIST

SSNP(Km) 0.958 0.982 0.757 0.739

SSNP(Agg) 0.950 0.978 0.707 0.753

AE 0.961 0.977 0.538 0.725

SSNP(GT) 0.863 0.944 0.466 0.884

NNP 0.963 0.986 0.679 0.765

t-SNE 0.990 0.987 0.664 0.843

UMAP 0.982 0.988 0.633 0.805

HAR

SSNP(Km) 0.932 0.969 0.761 0.811

SSNP(Agg) 0.926 0.964 0.724 0.846

AE 0.937 0.970 0.805 0.786

SSNP(GT) 0.876 0.946 0.746 0.985

NNP 0.961 0.984 0.592 0.903

t-SNE 0.992 0.985 0.578 0.969

UMAP 0.980 0.989 0.737 0.933

Reuters

SSNP(Km) 0.794 0.859 0.605 0.738

SSNP(Agg) 0.771 0.824 0.507 0.736

AE 0.747 0.731 0.420 0.685

SSNP(GT) 0.720 0.810 0.426 0.977

NNP 0.904 0.957 0.594 0.860

t-SNE 0.955 0.959 0.588 0.887

UMAP 0.930 0.963 0.674 0.884

Figure 5 shows that SSNP with pseudo-labels

shows better cluster separation than Autoencoders,

and, for more challenging datasets, such as HAR and

Reuters, SSNP with ground-truth labels looks better

than t-SNE and UMAP. SSNP and Autoencoder were

trained for 10 epochs in all cases. SSNP used twice

the number of classes as the target number of clus-

ters for the clustering algorithms used for pseudo-

labeling. We see also that SSNP creates elongated

clusters, in a star-like pattern. We believe this is due to

the fact that one of the targets of the network is a clas-

siﬁer, which is trained to partition the space based on

the data. This results in placing samples that are near

a decision boundary between classes closer to the cen-

ter of the star pattern; samples that are far away from a

decision boundary are placed near the tips of the star,

according to its class.

Table 4 shows the quality measurement for this ex-

periment. We see that SSNP with pseudo-labels con-

sistently shows better cluster separation than Autoen-

coders, as measured by the NH, as well as better dis-

tance correlation, as measured by R. For the harder

HAR and Reuters datasets, SSNP with ground-truth

labels shows NH results that are competitive and even

better than the ones for t-SNE and UMAP. For the

T and C metrics, SSNP outperforms again Autoen-

coders in most cases; for FashionMNIST and HAR,

SSNP yields T and C values close to the ones for

NNP, t-SNE, and UMAP.

Self-supervised Dimensionality Reduction with Neural Networks and Pseudo-labeling

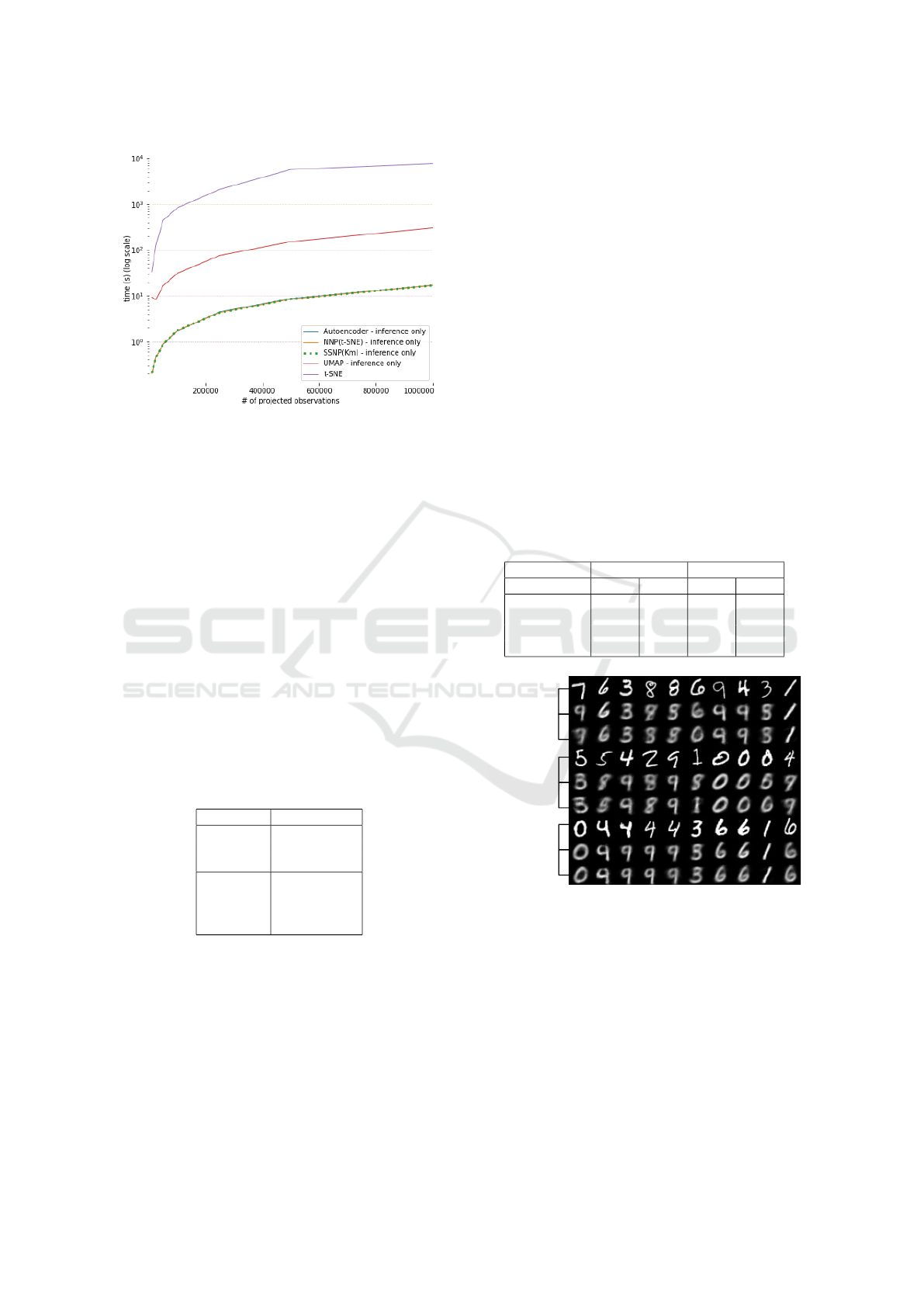
Figure 6: Inference time for SSNP and other techniques.

All techniques trained with 10K samples from the MNIST

dataset. Inference done on MNIST upsampled up to 1M

samples.

4.3 Computational Scalability

Table 5 shows the time required to set up SSNP and

other projection techniques. For SSNP, this means

training the network. For t-SNE, this means actual

projection of the data, since this technique is non-

parametric. All SSNP variants take far under a minute

to set up, with SSNP(GT) being the fastest, as it does

not need the clustering step. Of the pseudo-labeling

varieties, SSNP(Km) is the fastest. We used 10K

training samples, which is on the conservative side.

In practice, we get good results (quality-wise) with as

few as 1K samples.

Table 5: Set-Up time for different methods, using 10K train-

ing samples, MNIST dataset. All SSNP variants and Au-

toencoders were trained for 10 epochs. t-SNE is here for

reference only, since it is a non-parametric technique.

Method Training time (s)

SSNP(GT) 6.029

SSNP(Km) 20.478

SSNP(Agg) 31.954

Autoencoder 3.734

UMAP 25.143

t-SNE 33.620

NNP(t-SNE) 51.181

Figure 6 shows the time needed to project up to

1M samples using SSNP and the other techniques.

Being GPU-accelerated neural networks, SSNP, Au-

toencoders and NNP perform very fast, all being able

to project up to 1M samples in a few seconds – an

order of magnitude faster than UMAP, and over three

orders of magnitude faster than t-SNE.

4.4 Inverse Projection

Figure 7 shows a set of digits from the MNIST

dataset – both the actual images x and the ones ob-

tained by inverse projection P

−1

(P(x)). We see that

SSNP(Km) yields results very similar to Autoen-

coders, so SSNP’s dual-optimization target succeeds

in learning a good inverse mapping based on the di-

rect mapping given by the pseudo-labels (Section 3).

Table 6 strengthens this insight by showing the val-

ues for Mean Squared Error between original and

inversely-projected data for SSNP(Km) and Autoen-

coder, which, again, are very similar. Furthermore,

the SSNP MSE errors are of the same order of mag-

nitude – that is, small – as those obtained by the re-

cent NNInv technique and the older iLAMP (Amorim

et al., 2012) one – compare Table 6 with Figure

2 in (Espadoto et al., 2019b), not included here for

space reasons.

Table 6: Inverse projection Mean Square Error (MSE) for

SSNP(Km) and Autoencoder, trained with 5K samples,

tested with 1K samples.

SSNP(Km) Autoencoder

Dataset Train Test Train Test

MNIST 0.0474 0.0480 0.0424 0.0440

FashionMNIST 0.0309 0.0326 0.0291 0.0305

HAR 0.0072 0.0074 0.0066 0.0067

Reuters 0.0002 0.0002 0.0002 0.0002

Original

Autoencoder

SSNP(Km)

Original

Autoencoder

SSNP(Km)

Original

Autoencoder

SSNP(Km)

Figure 7: Sample images from MNIST inversely projected

by SSNP and Autoencoder, both trained with 10 epochs and

5K samples. Bright images show the original data.

4.5 Data Clustering

Table 7 shows how SSNP performs when doing clas-

siﬁcation or clustering, which corresponds respec-

tively to its usage of pseudo-labels or ground-truth

labels. We see that SSNP generates good results in

both cases when compared to the ground-truth labels

and, respectively, the underlying clustering algorithm.

We stress that this is a side result of SSNP. While one

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

gets this for free, SSNP only mimics the underlying

clustering algorithm that it learns, rather than doing

clustering from scratch.

Table 7: Classiﬁcation/clustering accuracy of SSNP when

compared to ground truth (GT) and clustering labels (Km),

trained with 5K observations, test with 1K observations.

SSNP(GT) SSNP(Km)

Dataset Train Test Train Test

MNIST 0.984 0.942 0.947 0.817

FashionMNIST 0.866 0.815 0.902 0.831

HAR 0.974 0.974 0.931 0.919

Reuters 0.974 0.837 0.998 0.948

4.6 Implementation Details

All experiments discussed above were run on a 4-

core Intel Xeon E3-1240 v6 at 3.7 GHz with 64 GB

RAM and an NVidia GeForce GTX 1070 GPU with

8 GB VRAM. Table 8 lists all open-source software

libraries used to build SSNP and the other tested tech-

niques. Our neural network implementation lever-

ages the GPU power by using the Keras framework.

The t-SNE implementation used is a parallel version

of Barnes-Hut t-SNE (Ulyanov, 2016; Maaten, 2013),

run on all four available CPU cores for all tests. The

UMAP reference implementation is not parallel, but

is quite fast (compared to t-SNE) and well-optimized.

Our implementation, plus all code used in this ex-

periment, are publicly available at https://github.com/

mespadoto/ssnp.

Table 8: Software used for the evaluation.

Technique Software used publicly available at

SSNP (our technique) keras.io (TensorFlow backend)

Autoencoder

t-SNE github.com/DmitryUlyanov/Multicore-t-SNE

UMAP github.com/lmcinnes/umap

K-means scikit-learn.org

Agglomerative Clustering

5 DISCUSSION

We discuss next how SSNP performs with respect to

the seven criteria laid out in Section 1.

Quality (C1). As shown in Figures 4 and 5, SSNP

provides better cluster separation than Autoencoders,

as measured by the selected metrics (Tables 3 and

4). The choice of clustering algorithm does not seem

to be a key factor, with K-means and Agglomer-

ative clustering yielding similar results for all metrics;

Scalability (C2). SSNP, while not as fast to train as

standard Autoencoders, is still very fast, with most of

the training time being used by clustering – visible

by the fact that SSNP(GT)’s training time is close

to Autoencoder’s one. In our experiments, K-means

seems to be faster than Agglomerative clustering,

being thus more suitable when training SSNP with

very large datasets. Inference time for SSNP is

very close to Autoencoders and NNP, and much

faster than UMAP (let alone t-SNE), which shows

SSNP’s suitability to cases where one needs to project

large amounts of data, such as streaming applications;

Ease of Use (C3). SSNP yielded good projection

results with little training (10 epochs), little training

data (5K samples) and a simple heuristic of setting

the number of clusters for the clustering step to

twice the number of expected clusters in the data.

Other clustering techniques which do not require

setting the number of clusters can be used, such as

DBSCAN (Ester et al., 1996) and Afﬁnity Propaga-

tion (Frey and Dueck, 2007), making SSNP usage

even simpler. We see this experiments as part of

future work;

Genericity (C4). We show results for SSNP with dif-

ferent types of high-dimensional data, namely tabular

(HAR), images (MNIST, FashionMNIST), and text

(Reuters). We believe this shows the versatility of the

method;

Stability and Out-of-Sample Support (C5). All

measurements we show for SSNP are based on

inference, i.e., we pass the data through the trained

network to compute them. This is evidence of the

out-of-sample capability, which allows one to project

new data without recomputing the projection, as is

the case for t-SNE and other non-parametric methods;

Inverse Mapping (C6). SSNP shows inverse map-

ping results which are, quality-wise, very similar

to results from Autoencoders, NNInv and iLAMP,

which is evidence of SSNP’s inverse mapping abili-

ties;

Clustering (C7). SSNP is able to mimic the behav-

ior of the clustering algorithm used as its input, as

a byproduct of the training with labels. We show that

SSNP produces competitive results when compared to

pseudo- or ground truth labels. Although SSNP is not

a clustering algorithm, it provides this for free (with

no additional execution cost), which can be useful in

cases where one wants to do both clustering and DR.

In addition to the good performance shown for the

aforementioned criteria, a key strength of SSNP is its

ability of performing all the operations described in

Section 4 after a single training phase, which saves

effort and time in cases where all or a subset of

Self-supervised Dimensionality Reduction with Neural Networks and Pseudo-labeling

those results (e.g., direct projection, inverse projec-

tion, clustering) are needed.

6 CONCLUSION

We presented a new dimensionality reduction tech-

nique called SSNP. Through several experiments,

we showed that SSNP creates projections of high-

dimensional data that obtain a better visual clus-

ter separation than autoencoders, the technique that

SSNP is closest to, and have similar (albeit slightly

lower) quality to those obtained by state-of-the-art

methods. SSNP is, to our knowledge, the only tech-

nique that jointly addresses all characteristics listed

in Section 1 of this paper, namely producing projec-

tions that exhibit a good visual separation of simi-

lar samples, handling datasets of millions of elements

in seconds, being easy to use (no complex parame-

ters to set), handling generically any type of high-

dimensional data, providing out-of-sample support,

and providing an inverse projection function.

One low-hanging fruit is to study SSNP in con-

junction with more advanced clustering algorithms

than the K-means and agglomerative clustering used

in this paper, yielding potentially even better visual

cluster separation. A more ambitious, but realizable,

goal is to have SSNP learn its pseudo-labeling dur-

ing training and therefore remove the need for using a

separate clustering algorithm. We plan to explore this

directions in future work.

ACKNOWLEDGMENTS

This study was ﬁnanced in part by FAPESP

(2015/22308-2 and 2017/25835-9) and the

Coordenac¸

ao de Aperfeic¸oamento de Pessoal de

ıvel Superior - Brasil (CAPES) - Finance Code 001.

REFERENCES

Amorim, E., Brazil, E. V., Daniels, J., Joia, P., Nonato,

L. G., and Sousa, M. C. (2012). iLAMP: Exploring

high-dimensional spacing through backward multidi-

mensional projection. In Proc. IEEE VAST, pages 53–

62.

Anguita, D., Ghio, A., Oneto, L., Parra, X., and Reyes-

Ortiz, J. L. (2012). Human activity recognition

on smartphones using a multiclass hardware-friendly

support vector machine. In Proc. Intl. Workshop on

Ambient Assisted Living, pages 216–223. Springer.

Becker, M., Lippel, J., Stuhlsatz, A., and Zielke, T. (2020).

Robust dimensionality reduction for data visualiza-

tion with deep neural networks. Graphical Models,

108:101060.

Becker, R., Cleveland, W., and Shyu, M. (1996). The visual

design and control of trellis display. Journal of Com-

putational and Graphical Statistics, 5(2):123–155.

Chan, D., Rao, R., Huang, F., and Canny, J. (2018). T-SNE-

CUDA: GPU-accelerated t-SNE and its applications

to modern data. In Proc. SBAC-PAD, pages 330–338.

Cunningham, J. and Ghahramani, Z. (2015). Linear dimen-

sionality reduction: Survey, insights, and generaliza-

tions. JMLR, 16:2859–2900.

Donoho, D. L. and Grimes, C. (2003). Hessian eigen-

maps: Locally linear embedding techniques for high-

dimensional data. Proc Natl Acad Sci, 100(10):5591–

5596.

Engel, D., Hattenberger, L., and Hamann, B. (2012). A

survey of dimension reduction methods for high-

dimensional data analysis and visualization. In Proc.

IRTG Workshop, volume 27, pages 135–149. Schloss

Dagstuhl.

Espadoto, M., Hirata, N., and Telea, A. (2020). Deep learn-

ing multidimensional projections. J. Information Vi-

sualization. doi.org/10.1177/1473871620909485.

Espadoto, M., Martins, R. M., Kerren, A., Hirata, N. S., and

Telea, A. C. (2019a). Towards a quantitative survey of

dimension reduction techniques. IEEE TVCG. Pub-

lisher: IEEE.

Espadoto, M., Rodrigues, F. C. M., Hirata, N. S. T., Hi-

rata Jr., R., and Telea, A. C. (2019b). Deep learning in-

verse multidimensional projections. In Proc. EuroVA.

Eurographics.

Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In Proc. KDD,

pages 226–231.

Fisher, R. A. (1936). The use of multiple measurements in

taxonomic problems. Annals of eugenics, 7(2):179–

188.

Frey, B. J. and Dueck, D. (2007). Clustering by

passing messages between data points. Science,

315(5814):972–976. Publisher: AAAS.

Hinton, G. E. and Salakhutdinov, R. R. (2006). Reducing

the dimensionality of data with neural networks. Sci-

ence, 313(5786):504–507. Publisher: AAAS.

Hoffman, P. and Grinstein, G. (2002). A survey of visualiza-

tions for high-dimensional data mining. Information

Visualization in Data Mining and Knowledge Discov-

ery, 104:47–82. Publisher: Morgan Kaufmann.

Inselberg, A. and Dimsdale, B. (1990). Parallel coordinates:

A tool for visualizing multi-dimensional geometry. In

Proc. IEEE Visualization, pages 361–378.

Joia, P., Coimbra, D., Cuminato, J. A., Paulovich, F. V., and

Nonato, L. G. (2011). Local afﬁne multidimensional

projection. IEEE TVCG, 17(12):2563–2571.

Jolliffe, I. T. (1986). Principal component analysis and fac-

tor analysis. In Principal Component Analysis, pages

115–128. Springer.

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

Kaufman, L. and Rousseeuw, P. (2005). Finding Groups in

Data: An Introduction to Cluster Analysis. Wiley.

Kehrer, J. and Hauser, H. (2013). Visualization and vi-

sual analysis of multifaceted scientiﬁc data: A survey.

IEEE TVCG, 19(3):495–513.

Kingma, D. P. and Welling, M. (2013). Auto-encoding

variational bayes. CoRR, abs/1312.6114. eprint:

1312.6114.

Kohonen, T. (1997). Self-organizing Maps. Springer.

LeCun, Y. and Cortes, C. (2010). MNIST handwritten digits

dataset. http://yann.lecun.com/exdb/mnist.

Liu, S., Maljovec, D., Wang, B., Bremer, P.-T., and

Pascucci, V. (2015). Visualizing high-dimensional

data: Advances in the past decade. IEEE TVCG,

23(3):1249–1268.

Lloyd, S. (1982). Least squares quantization in PCM. IEEE

Trans Inf Theor, 28(2):129–137.

Maaten, L. v. d. (2013). Barnes-hut-SNE. arXiv preprint

arXiv:1301.3342.

Maaten, L. v. d. (2014). Accelerating t-SNE using tree-

based algorithms. JMLR, 15:3221–3245.

Maaten, L. v. d. and Hinton, G. (2008). Visualizing data

using t-SNE. JMLR, 9:2579–2605.

Maaten, L. v. d. and Postma, E. (2009). Dimensionality

reduction: A comparative review. Technical report,

Tilburg University, Netherlands.

Martins, R. M., Minghim, R., Telea, A. C., and others

(2015). Explaining neighborhood preservation for

multidimensional projections. In CGVC, pages 7–14.

McInnes, L. and Healy, J. (2018). UMAP: Uniform man-

ifold approximation and projection for dimension re-

duction. arXiv:1802.03426v1 [stat.ML].

Nonato, L. and Aupetit, M. (2018). Multidimensional

projection for visual analytics: Linking techniques

with distortions, tasks, and layout enrichment. IEEE

TVCG.

Paulovich, F. V. and Minghim, R. (2006). Text map ex-

plorer: a tool to create and explore document maps.

In Proc. Intl. Conference on Information Visualisation

(IV), pages 245–251. IEEE.

Paulovich, F. V., Nonato, L. G., Minghim, R., and Lev-

kowitz, H. (2008). Least square projection: A fast

high-precision multidimensional projection technique

and its application to document mapping. IEEE

TVCG, 14(3):564–575.

Pezzotti, N., H

ollt, T., Lelieveldt, B., Eisemann, E., and

Vilanova, A. (2016). Hierarchical stochastic neighbor

embedding. Computer Graphics Forum, 35(3):21–30.

Pezzotti, N., Lelieveldt, B., Maaten, L. v. d., H

ollt, T., Eise-

mann, E., and Vilanova, A. (2017). Approximated and

user steerable t-SNE for progressive visual analytics.

IEEE TVCG, 23:1739–1752.

Pezzotti, N., Thijssen, J., Mordvintsev, A., Hollt, T., Lew,

B. v., Lelieveldt, B., Eisemann, E., and Vilanova, A.

(2020). GPGPU linear complexity t-SNE optimiza-

tion. IEEE TVCG, 26(1):1172–1181.

Rao, R. and Card, S. K. (1994). The table lens: Merging

graphical and symbolic representations in an interac-

tive focus+context visualization for tabular informa-

tion. In Proc. ACM SIGCHI, pages 318–322.

Roweis, S. T. and Saul, L. L. K. (2000). Nonlinear di-

mensionality reduction by locally linear embedding.

Science, 290(5500):2323–2326. Publisher: American

Association for the Advancement of Science.

Salton, G. and McGill, M. J. (1986). Introduction to modern

information retrieval. McGraw-Hill.

Sorzano, C., Vargas, J., and Pascual-Montano, A. (2014).

A survey of dimensionality reduction techniques.

arXiv:1403.2877 [stat.ML].

Telea, A. C. (2006). Combining extended table lens and

treemap techniques for visualizing tabular data. In

Proc. EuroVis, pages 120–127.

Tenenbaum, J. B., Silva, V. D., and Langford, J. C. (2000).

A global geometric framework for nonlinear dimen-

sionality reduction. Science, 290(5500):2319–2323.

Thoma, M. (2017). The Reuters dataset.

Torgerson, W. S. (1958). Theory and Methods of Scaling.

Wiley.

Ulyanov, D. (2016). Multicore-TSNE.

Venna, J. and Kaski, S. (2006). Visualizing gene interaction

graphs with local multidimensional scaling. In Proc.

ESANN, pages 557–562.

Wattenberg, M. (2016). How to use t-SNE effectively. https:

//distill.pub/2016/misread-tsne.

Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-

MNIST: A novel image dataset for benchmarking ma-

chine learning algorithms. arXiv:1708.07747.

Xie, H., Li, J., and Xue, H. (2017). A survey of dimen-

sionality reduction techniques based on random pro-

jection. arXiv:1706.04371 [cs.LG].

Yates, A., Webb, A., Sharpnack, M., Chamberlin, H.,

Huang, K., and Machiraju, R. (2014). Visualizing

multidimensional data with glyph SPLOMs. Com-

puter Graphics Forum, 33(3):301–310.

Zhang, Z. and Wang, J. (2007). MLLE: Modiﬁed lo-

cally linear embedding using multiple weights. In

Advances in Neural Information Processing Systems

(NIPS), pages 1593–1600.

Zhang, Z. and Zha, H. (2004). Principal manifolds and

nonlinear dimensionality reduction via tangent space

alignment. SIAM Journal on Scientiﬁc Computing,

26(1):313–338.

Self-supervised Dimensionality Reduction with Neural Networks and Pseudo-labeling