
PRAQA: Protein Relative Abundance Quantification Algorithm
for 3D Fluorescent Images
Corrado Ameli
1,4 a
, Sonja Fixemer
1,2 b
, David S. Bouvier
1,2,3 c
and Alexander Skupin
1,5 d
1
Luxembourg Centre for Systems Biomedicine, University of Luxembourg, Luxembourg
2
Luxembourg Centre for Neuropathology, Laboratoire National de Sant
´
e, Dudelange, Luxembourg
3
National Center of Pathology, Laboratoire National de Sant
´
e, Dudelange, Luxembourg
4
Universit
`
a degli Studi di Milano, Milan, Italy
5
University California San Diego, La Jolla, U.S.A.
Keywords:
Confocal Fluorescent Microscopy, Image Processing, Protein Quantification, Alzheimer’s Disease, Lewy
Body Dementia.
Abstract:
In confocal fluorescent microscopy, the quality of the acquisition strongly depends on diverse factors including
the microscope parameterization, the light exposure time, the type and concentration of the antibodies used,
the thickness of the sample and the degradation of the biological tissue itself. All these factors critically
influence the final result and render tissue protein quantification challenging due to intra- and inter-sample
variability. Therefore, image processing techniques need to address the acquisitions variability to minimize the
risk of bias coming from changes in signal intensity, noise and parameterization. Here, we introduce Protein
Relative Abundance Quantification Algorithm (PRAQA), a 1-parameter based, fast and adaptive approach for
quantifying protein abundance in 3D fluorescent-immunohistochemistry stained tissues that requires no image
preprocessing. Our method is based on the assessment of the global pixel intensity neighborhood dispersion
that allows to statistically infer whether each small region of an image can be considered as positive signal
or background noise. We benchmark our method with alternative approaches from literature and validate its
applicability and efficiency based on synthetic scenarios and a real-world application to post-mortem human
brain samples of Alzheimer’s Disease and Lewy Body Dementia patients. PRAQA is implemented in Matlab
and freely available at https://doi.org/10.17881/j20h-pa27.
1 INTRODUCTION
Life relies on the proper function of its essential build-
ing blocks, the cells (Alberts, 2017). The functional-
ity of cells is ensured by the orchestrated action of
a plethora of molecules where in particular proteins
encoded by genes are essential for structure, func-
tion and regulation. Impairment in protein functions
caused by mutations in the encoding genes or by ex-
ternal perturbations often result in perturbed regula-
tory mechanisms and subsequent changes in protein
abundance which in turn may trigger different dis-
eases including cancer, diabetes and neurodegener-
ation. To investigate underlying regulatory disease
a
https://orcid.org/0000-0002-9101-0890
b
https://orcid.org/0000-0002-2312-6947
c
https://orcid.org/0000-0002-8630-1044
d
https://orcid.org/0000-0002-8955-8304
mechanisms, it is therefore essential to characterize
protein abundance and localization also in the context
of cellular heterogeneity (Komin and Skupin, 2017).
Immunostaining methods, including immunoflu-
orescence, revolutionized the scientific world by ex-
ploiting antibody specificities to target and visual-
ize antigens of interest in biological tissues by mi-
croscopy (Im et al., 2019). This technique allows
for estimating the distribution and the quantification
of targeted proteins at the microscopic scales, which
are essential for assessing the roles of proteins or cel-
lular and subcellular alterations in pathological con-
ditions. A general challenge is thereby the post-
acquisition analysis of microscopy images for which
different methods have been developed as compre-
hensively discussed in (Varghese et al., 2014).
In fluorescent microscopy, a common drawback of
these methods is the typical need of a preprocessing
step to transform the image into an appropriate in-
Ameli, C., Fixemer, S., Bouvier, D. and Skupin, A.
PRAQA: Protein Relative Abundance Quantification Algorithm for 3D Fluorescent Images.
DOI: 10.5220/0010187400210030
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 2: BIOIMAGING, pages 21-30
ISBN: 978-989-758-490-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
21

put format fulfilling requirements such as background
uniformity or noise reduction, or the dependence of
more than one tuning parameter in order to achieve
the quantification. The wide range of options for
parameterizing has the advantage that the quantifi-
cation procedure can be adapted to different imag-
ing conditions but irremediably increases the proce-
dure complexity and subsequently leads to potential
biases originated by an inaccurate choice of methods
or parameters. While deep-learning methods are able
to provide parameter-free analysis, the adaptability
to a plethora of acquisition conditions requires huge
amount of data to train the network (Belthangady and
Royer, 2018). This requirement cannot always be sat-
isfied, particularly for limited sample availability such
as for human brain samples.
Furthermore, advances in high-resolution fluores-
cent microscopy now allow for processing of thicker
samples in the range of 50 to several hundreds of mi-
crometers. Larger 3D acquisitions have higher infor-
mation content but, on the other hand, they are af-
fected by larger signal intensity variability caused by
the thickness of the section (Chung et al., 2013; Bou-
vier et al., 2016) that makes reliable and robust quan-
tification challenging.
To address these challenges, we here introduce
PRAQA (Protein Relative Abundance Quantifi-
cation Algorithm), that is optimized for protein
quantification in 3D fluorescent confocal tile scan
microscope acquisitions. With only one parameter
and no preprocessing required, PRAQA is easy to
use, fast and extremely resilient to intensity changes
as well as robust for noise compromised images. We
benchmark PRAQA against alternative approaches
in synthetic scenarios and test its efficiency by
an application to paraformaldehyde fixed human
brain samples in the context of neurodegeneration
representing a challenging scenario due to extreme
inter- and intra-sample variability.
The manuscript is organised as follows:
• Section 2 describes the algorithm and its imple-
mentation.
• Section 3 presents two synthetic scenarios and
benchmarks PRAQA with alternative algorithms
from literature.
• Section 4 presents an application on a real sce-
nario.
• Section 5 discusses advantages and drawbacks of
PRAQA and points to future work.
2 METHODOLOGY
The different sources of variability mentioned above
render a robust correction challenging and practically
impossible. Hence, image processing aims at solving
the parallel problem of an image binarization obeying
invariance with respect to the overall signal power.
PRAQA is approaching this challenge by a statisti-
cal test based on Median Absolute Deviation (MAD)
to reliably distinguish background noise from fluores-
cent signal among images with different contrast.
The advantage of MAD compared to other dis-
persion or outlier detection methods is its robustness
with respect to extreme values (Leys et al., 2013) and
is therefore an appropriate choice for binarization.
PRAQA classifies pixels as positive when the neigh-
borhood average intensity exceeds θ scaled MAD
where the scaled MAD of a vector x is determined
by
MAD
S
(x) =
|
x
i
− med(x)
|
med(
|
x
i
− med(x)
|
)
(1)
with med(x) being the median of the vector x.
In Section 3.3, we empirically evaluate the robust-
ness of θ with respect to different signal strengths.
2.1 PRAQA Pseudocode
The implementation of PRAQA is described in the
following by pseudocode and corresponding expla-
nations. For a given 3D image I and a threshold θ,
PRAQA calls the binarizeMAD function:
1 function binarizeMAD(I,theta)
2 I = I./max(I);
3 SE_List = getSE();
4 for z = 1 : numberOfSlices(I)
5 for i = 1 to numberOfSE
6 Feats(:,i) = getFeat(I(z),SE_List(i));
7 I_MAD(:,i) = MADS(Feats(:,i));
8 Positive_P(:,i) = I_MAD(:,i) > theta;
9 end
10 end
11 for i = 1 to numberOfSE
12 I_Positive = sum(Positive_P(:,i)) > 1;
13 end
14 return I_Positive;
15 end
In line 2, the image I is first normalized to a [0, 1]
range. In line 3, a predefined list of Structuring Ele-
ments (SE) is loaded into the memory which are used
to define the local neighborhood. These structuring
elements can be considered as an additional parame-
ter of the algorithm but here we kept specifically 3 cir-
cle SEs with radius 4, 6, and 8 throughout the whole
study.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
22

From line 4 to line 10, we start iterating through
each slice of the 3D image by moving in the z direc-
tion. The nested loop (line 5 to 9) iterates through all
the SEs and retrieves the pixel features by the function
getFeat (line 6). This function returns a vector which
contains the value of the average neighborhood inten-
sity defined by the SEs for each pixel (see below).
Next, the scaled MAD (Eq. 1) is calculated for each
feature (line 7) and all pixels for which the thresh-
old θ is exceeded are marked as positive and stored
together with the the scaled MADs of each SE in the
variable PositiveP (line 8).
Hence, this loop (line 4 to 10) generates PositiveP
as a 3D matrix of size NxM where N is number of pix-
els and M is the number of SEs. For final pixel clas-
sification, we next loop through the matrix PositiveP
and check whether a pixel has been labeled as an out-
lier in more than one SE-based MAD (line 11 to 13).
If this is the case, the corresponding pixel is classified
as a positive signal pixel (line 12). The imposed re-
quirement of at least two outlier classifications in the
same pixel reduces the probability of false positive or
false negative detection. Finally, the function returns
the binarized image (line 14).
The aforementioned pixel features are calculated
by the routine getFeat as
1 function getFeat(I,SE)
2 SE = SE./sum(SE);
3 feat = convolute(I,SE);
4 return feat;
5 end.
The feature is evaluated by convolving a moving aver-
age filter with the SE neighborhood (obtained in line
2) with the image. The returned variable feat is a 1xN
vector containing the average neighborhood intensity
for all N pixels.
2.2 Comment on Implementation
PRAQA is splitting the 3D images into 2D stacks and
is iterating through these in a 2D-wise manner. The
reasoning behind this is twofold. First, due to im-
age acquisition and corresponding optical constraints,
the z resolution is typically lower compared to x and
y directions making the use of 3D SEs not suitable.
The second reason is that signals from different slices
will vary in intensity caused by different penetration
of antibody staining and optical constraints. This ef-
fect is proportional to the sample thickness. Hence,
the definition of one global threshold for the standard
intensity-value is not a suitable approach. However,
since our algorithm is invariant with respect to the sig-
nal intensity, we can still adopt a one-threshold policy
for the whole image with no prior slice-wise normal-
ization required.
Furthermore, we chose here circular shaped SEs
since most of the protein localization do not occur in
sharp edgy shapes but rather as smooth edgeless ob-
jects. However, this choice may not be optimal when
dealing in a poor 2D resolution scenario with proteins
that come in a filamentous or ramified arrangement.
3 BENCHMARKING WITH
SYNTHETIC SCENARIOS
To evaluate the performance of PRAQA, we bench-
mark and compare our method with alternative image
processing pipelines in terms of accuracy, robustness
and runtime. For this purpose, we synthetically gener-
ated 3D images that can resemble an ideal acquisition
without noise or intensity changes, and keep those
images as ground truth to benchmark the algorithms
efficiency on the identical images with added noise
and intensity changes. We generated these images by
randomly placing two kinds of shapes, either spheres
or spirals, of different sizes throughout the whole 3D
image. The two different object shapes were chosen
to have a simpler scenario with well defined contours
(spheres) and a harder scenario that contains irregular
thinner shapes (spirals). Small binary spheres are ap-
proximated and do not look perfectly round.
In analogy to real image data, the synthetic image
dimension was set to 2048 by 2048 by 30 pixels. Ta-
ble 1 summarizes the object sizes and quantities used
to fill the images.
Table 1: Description of objects used in the synthetic images.
Sphere Spiral
Radius Quantity Size (x y z) Quantity
10 100 25 25 6 100
15 50 45 45 8 50
20 30 70 70 10 15
Additional 3 slices were added at the top and the
bottom of the image stack before randomly placing
the objects to avoid having less positive pixels on
the boundaries. Those additional slices were subse-
quently removed leading to some partly cut objects in
analogy to experimental image acquisition.
Noise and intensity alteration were introduced at
different strength to evaluate the resilience of the
pipelines tested. We used Gaussian white noise (µ =
0, σ = 1) multiplied by a scaling factor η and added
to each pixel. Figure 1 and 2 show a zoom in of 110
by 110 pixels on the two scenarios for different val-
ues of η. We also simulated the luminescence loss
PRAQA: Protein Relative Abundance Quantification Algorithm for 3D Fluorescent Images
23

Figure 1: Zoom in for the sphere noise scenario with noise intensities η = [0, 1, 2, 3] from left to right, respectively.
Figure 2: Zoom in for the spiral noise scenario with noise intensities η = [0, 0.5, 0.75, 1] from left to right, respectively.
(LL) and luminescence variability (LV) throughout
the z dimension by additionally reducing the intensity
of each slice away from the middle of a factor ι. In de-
pendence to the experimental setting this is one likely
scenario but in different settings the LV can have also
an inverse character where the middle average inten-
sity is lower than at the borders. Since PRAQA works
in a 2D slice-specific mode, the direction of LL and
LV does not affect the results.
We compare our algorithm with BM3D (Dabov
et al., 2007), median filtering (Lim, 1990), non-local
means filtering (Buades et al., 2005) and wavelet de-
noising (Donoho, 1995). We parameterized BM3D
with σ = 60 without reporting benchmarks with lower
values since this configuration always performed bet-
ter than others. By contrast, we parameterized me-
dian filtering with different neighborhoods (5, 10 and
15 pixels) because in dependence on the input the
different parameterization exhibited different perfor-
mances. Since our algorithm directly outputs a bi-
nary image, we then used either a global thresh-
old, Otsu method (Otsu, 1979) or Niblack threshold-
ing (Niblack, 1985), for binarizing the results of the
benchmark algorithms. All algorithms implementa-
tions are based on MATLAB and we used the native
MATLAB implementations for all the competing al-
gorithms except for BM3D for which the implemen-
tation of the original paper was used (Dabov et al.,
2007).
In the following sections, we will refer to BM3D
(σ = 60) as B60, to median filtering with the different
neighborhood settings as M5, M10 and M15, to non-
local means filtering as NLF, to wavelet denoising as
WAV and to our algorithm as PRA.
3.1 Accuracy Benchmark
In this section we evaluate the algorithms perfor-
mance by means of Receiver Operating Char-
acteristic (ROC) curve and Precision-Recall (PR)
curve (Saito and Rehmsmeier, 2015). In these first
tests, we did not apply intensity changes (ι = 0) and
evaluated the average performance on slices in differ-
ent noise conditions with η = (1, 2, 3) for the sphere
scenario and η = (0.5, 0.75, 1) for the spiral scenario,
respectively.
For the alternative approaches, the performance
curves were obtained by changing the global inten-
sity threshold after filtering. Since PRAQA directly
returns a binarized image, the performance curve was
obtained by changing θ. To avoid the use of a trained
classifier which could unevenly bias the result, we
kept only one feature of the 3 features obtained by cir-
cular SEs. In particular, we chose the largest SE for
the sphere scenario and the smallest SE for the spiral
scenario, respectively.
Table 3 and 2 report the Area Under Curve
(AUC) for both the sphere and spherical scenario, re-
spectively. Without intensity changes along the z di-
mension, BM3D performs best and in particular better
than PRAQA. Still, PRAQA performs typically bet-
ter than all the other algorithms and yields acceptable
results in all cases except in the noisiest spiral sce-
nario. The great performance of BM3D is based on
BIOIMAGING 2021 - 8th International Conference on Bioimaging
24

Table 2: Spiral scenario accuracy benchmark.
η = 1 η = 2 η = 3
ROC PR ROC PR ROC PR
PRA .99 .99 .99 .94 .98 .77
B60 .99 .99 .99 .96 .99 .88
M5 .99 .88 .90 .28 .80 .10
M10 .99 .98 .98 .79 .93 .45
M15 .99 .98 .99 .90 .97 .71
NLF .99 .98 .98 .78 .94 .44
WAV .99 .97 .99 .84 .97 .61
Table 3: Sphere scenario accuracy benchmark.
η = 0.5 η = 0.75 η = 1
ROC PR ROC PR ROC PR
PRA .99 .87 .99 .70 .97 .45
B60 .99 .91 .99 .80 .99 .68
M5 .99 .81 .97 .53 .94 .24
M10 .98 .55 .97 .43 .95 .28
M15 .98 .35 .97 .29 .94 .20
NLF .99 .91 .98 .60 .95 .25
WAV .97 .63 .93 .33 .88 .14
its specific focus on white Gaussian noise and its per-
formance still remains a gold standard nowadays.
3.2 Performance with LV Benchmark
Next, we investigated the performance of the algo-
rithms in a scenario with both noise and intensity
changes. We fixed ι = 0.03 and η = 0.75 in the spiral
scenario and measured the performance with respect
to true positive rate (TPR) and true negative rate
(TNR). The MAD
S
threshold parameter θ was set to 3.
Since using just one global threshold for the binariza-
tion for the competing algorithms would be unfair, we
picked automatically a threshold for each slice by the
Otsu method and Niblack thresholding. In Figure 3,
the variability of TPR among slices for the different
algorithms is shown. We empirically assess the ro-
bustness of PRAQA with respect to intensity changes
among slices emphasized by the small TPR variance
compared to the other methods. This result further
demonstrates the great potential of PRAQA for im-
ages with high LV that is typically observed in tissue
staining.
In Figures 4 and 5, we next investigated the perfor-
mance of the algorithms by averaging TPR and TNR
slice-wise for the different threshold approaches, re-
spectively. These plots indicate that PRAQA robustly
binarizes images with high accuracy since it exhibits
high TPR and TNR while the alternative algorithms
typically are more targeted for one criterion. Thus,
PRA B60 M5 M10 M15 WAV NLM
0
0.2
0.4
0.6
0.8
1
TPR
Figure 3: TPR Boxplot slicewise.
WAV and B60 exhibited a slightly higher TNR com-
pared to PRAQA but performed significantly worse
with respect to TPR using Otsu thresholding (Fig. 4).
For Niblack thresholding, WAV resulted in a higher
TPR than PRAQA but had the worst TNR perfor-
mance of all algorithms (Fig. 5). Hence, the tar-
geted approach of PRAQA represents a good compro-
mise for binarization that significantly outperforms
the other algorithms.
Figure 4: Performance Scatter Plot with Otsu thresholding.
3.3 Robustness against Positive Pixel
Content
To investigate the performance of PRAQA in depen-
dence on signal (i.e. object) density, we fixed the
threshold parameter θ in the binarizedMAD routine
(Section 2.1) and considered the spiral scenario with
η = [0.5,0.75] and ι = 0.03. We first investigated the
dependency of MAD (Eq. 1) with respect to the num-
ber of objects and subsequently confirmed the results
in the synthetic scenario. For this purpose, we in-
creased the number of objects by adding a multiplying
constant to the number of objects listed in Table 1.
PRAQA: Protein Relative Abundance Quantification Algorithm for 3D Fluorescent Images
25

Figure 5: Performance Scatter Plot with Niblack threshold-
ing.
1 3 5 7 9 11 13 15 17 19
Object Density
1.35
1.351
1.352
1.353
1.354
MAD
Figure 6: Variation of MAD with respect to object density.
In Figure 6, we observe a linear dependency be-
tween the amount of positive signal given by the ob-
ject density and resulting MAD values. Thus, the
MAD scaling factor used to obtain MAD
S
as defined
by Eq. 1 leads to changes in the algorithm positive
pixels detection. Figure 7 depicts the change of TPR
in a spiral scenario with a fixed θ = 3 for an increase
of objects increases by 10 and 20 times and two differ-
ent noise intensities. Interestingly, we observed only a
minor loss in TPR of 0.008 for a 10 fold change in the
amount of positive signal when noise is low (η = 0.5)
and 0.025 for larger noise (η = 0.75). Even for the
higher density with a scaling factor of 20, the reduc-
tion in TPR is relatively low following the linear de-
pendency and further demonstrates the robustness of
PRAQA.
3.4 Runtime Benchmark
To investigate the applicability of the different algo-
rithms also with respect to real-world applications, we
benchmarked the time required to process 30 slices
0.97
0.98
0.99
TPR ( = 0.5)
1 10 20
0.8
0.85
0.9
TPR ( = 0.75)
Figure 7: Boxplots of TPR performance with respect to ob-
ject density (top: η = 0.5, bottom: η = 0.75).
51.9
2132.7
7.1
46.3
46.9
437.7
596.5
PRA B60 M5 M10 M15 NLF WAV
0
500
1000
1500
2000
2500
Runtime (s)
Figure 8: Runtime in seconds for each algorithm.
of size 2048 by 2048 pixels. The machine used
for benchmarking was equipped with two Intel Xeon
E5645 @2.40 Ghz and 96 GB RAM. Figure 8 depicts
a bar plot for each tested algorithm demonstrating
that PRAQA exhibits a great runtime performance. In
particular, PRAQA performs significantly better com-
pared with the second accurate algorithms WAV and
BM3D (B60) with a 40 times faster performance than
BM3D. The PRAQA algorithm execution time is in-
dependent with respect to the choice of θ but directly
proportional to the number of SEs.
A GPU parallelized version of the algorithm has
also been developed. However, most of the time
needed for the processing is taken by the MAD eval-
uation, which is not a parallelizable operation when
the exact MAD values are computed. A faster solu-
tion can be obtained by losing accuracy in the mea-
surement via pixel intensity binning, which may make
PRAQA be even suitable for real time applications.
Overall, the extensive benchmarking of PRAQA has
shown that its targeted approach for 3D fluoresecent
images with LV and LL outperforms alternative algo-
rithms in terms of accuracy and runtime.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
26
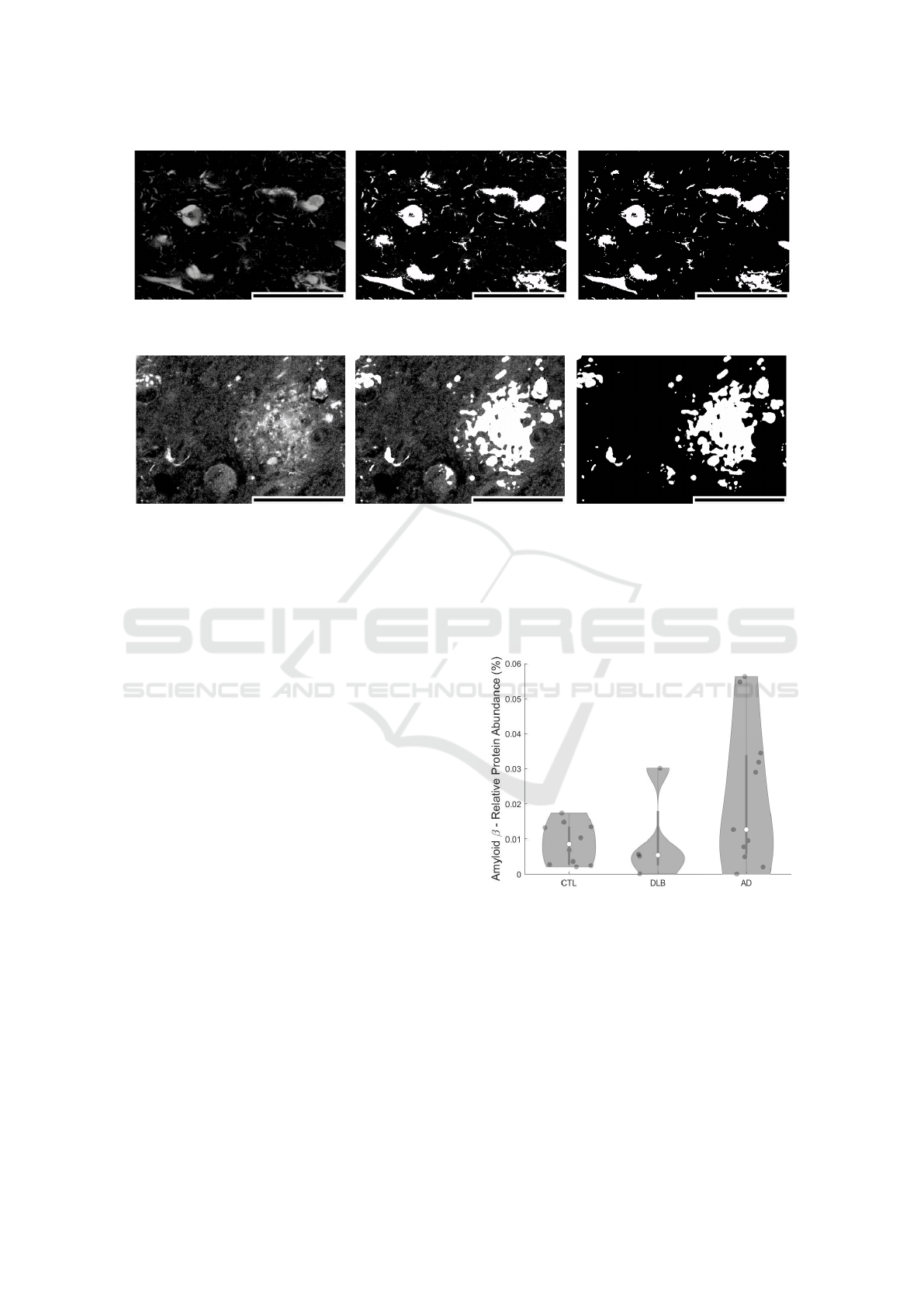
Figure 9: Hyperphosphorylated tau aggregation by AT8-staining acquisition in a region of interest. From left to right: original
acquisition, original + PRAQA overlay, PRAQA. Scale bar: 60 µm.
Figure 10: Amyloid-beta aggregation by 4G8-staining acquisition in a region of interest. From left to right: original acquisi-
tion, original + PRAQA overlay, PRAQA. Scale bar: 60 µm.
4 REAL SCENARIO
Based on the successful benchmarking of PRAQA
with the synthetic scenarios in Section 3, we next
applied PRAQA to a real world application of neu-
rodegeneration (Salamanca et al., 2019). A common
feature of different neurodegenerative diseases such
as Alzheimer’s or Parkinson’s disease is the accumu-
lation of proteins either intracellular or extracellular
(Ross and Poirier, 2004). While the function and im-
pact of these aggregates is still not fully understood,
they are essential for the diagnosis. Current biomedi-
cal research is focusing on the characteristics of these
protein aggregates and their relation to different dis-
ease stages (Dugger and Dickson, 2017). For this pur-
pose, a reliable quantification approach of protein ag-
gregation in tissue is essential and PRAQA is exactly
targeting this need.
Here, we demonstrate the potential of PRAQA in
the context of Alzheimer’s Disease (AD) and De-
mentia with Lewy Bodies (DLB). Both conditions
share the accumulation of extracellular aggregation
of amyloid-beta 1-42 and intracellular aggregation
of hyperphosphorylated tau in the parenchyma but
with an higher burden expected in AD samples. To
characterize amyloid and tau aggregation in a cohort
of human post-mortem brain samples (Tab. 4), we
have stained our collection of samples with antibod-
ies commonly used in neuropathology to vizualize re-
spective protein/peptide aggregation (Figs. 9 and 10),
acquired 3D stacks with a confocal microscope and
performed relative protein abundance quantification
with PRAQA (Figs. 11 and 12).
Figure 11: Amyloid peptide abundance per sample condi-
tion stained by 4G8.
4.1 Human Brain Sections Preparation
and Data Acquisition
Anonymized human brain samples were provided
by the Douglas-Bell Brain Bank (Douglas Mental
Health University Institute, Montr
´
eal, QC, Canada)
and all experiments were conducted in accordance
with the guidelines approved by the Ethics Board of
the Douglas-Bell Brain Bank and the Ethics Panel of
PRAQA: Protein Relative Abundance Quantification Algorithm for 3D Fluorescent Images
27
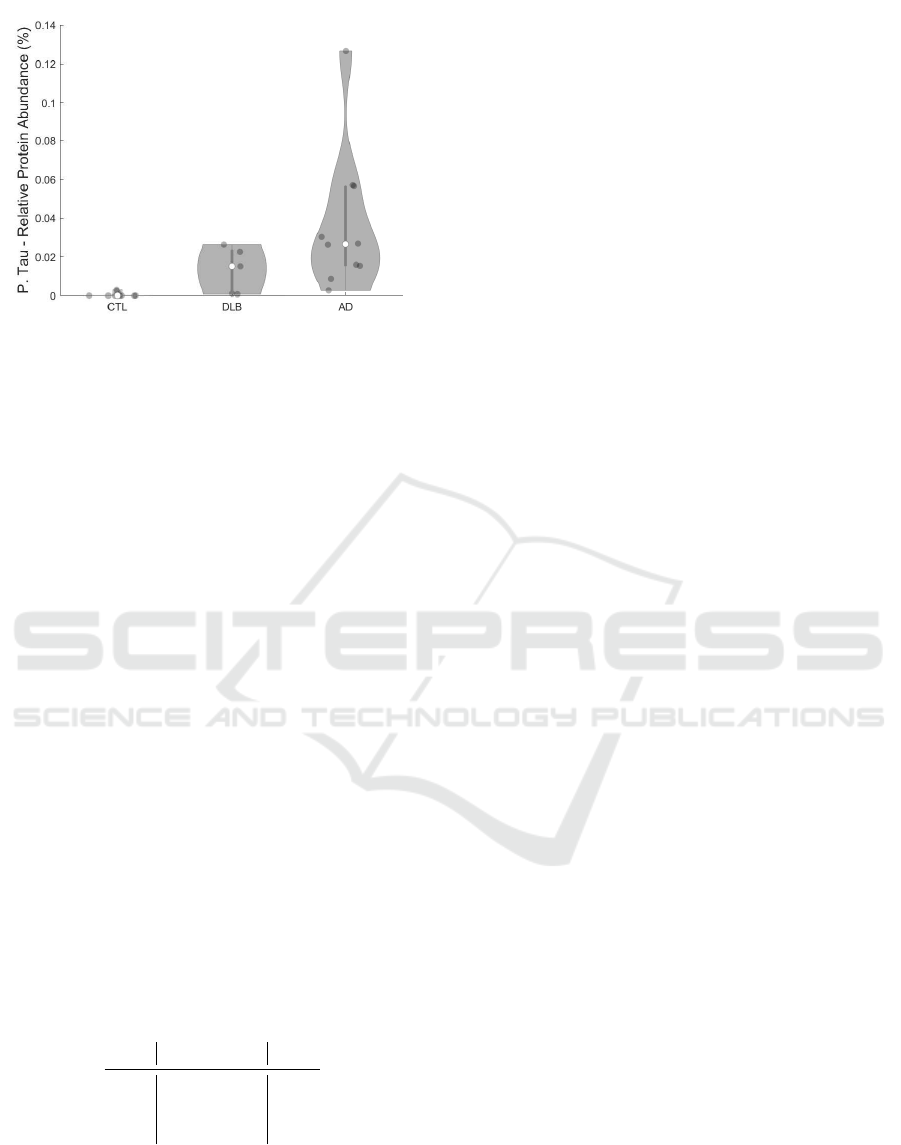
Figure 12: P-tau protein abundance per sample condition
stained by AT8.
University of Luxembourg. For this study, cases of
neuropathologically confirmed AD and DLB, as well
as from age-matched controls (CTLs) were selected.
Immunohistochemistry protocol was performed as
previously described (Bouvier et al., 2016) (Ques-
seveur et al., 2019). Briefly, sections were im-
munostained with the primary antibody Mouse anti-
4G8 (amyloid-beta) (Biolegend [800712]) or Mouse
anti-AT8 (hyperphosphorylated tau) (Thermofisher
[MN1020]). Afterwards, sections were incubated
with secondary antibodies Donkey anti-Mouse Alexa
Fluor 488 (4G8) or 647 (AT8) (Jackson ImmunoRe-
search Laboratories, West Grove, PA and Invitrogen,
Molecular Probes, Eugene, OR) and mounted. Flu-
orescent 3D confocal tile scans were captured and
stitched on a confocal Zeiss Laser Scanning Micro-
scope710 with a 20x air objective. Tile scans were
acquired to cover a larger area of the CA1 subfield of
the hippocampus. Identical image acquisition param-
eters were respectively used for each of the staining
on all samples.
4.2 Dataset and Processing
Table 4 reports the number of acquisitions processed
in this study grouped by condition.
Table 4: Number of samples per condition and marker.
Amyloid β Tau
CTL 11 12
AD 13 12
DLB 4 5
To compute the positive pixel sum coming from
the binarized image processed by PRAQA, we used
a parameterization of θ = 5 for all images except for
three CTL samples with 4G8 staining for which we
used θ = (8, 8, 10) to counteract a higher presence of
noise. Each sample had on average 25 slices separated
by 1 µm in the third dimension. For some samples, be-
ginning and/or ending slices had to be removed due to
tile-related artifacts occurred during the microscope
acquisition. For final analysis, the positive pixel sum
was normalized to the 3D image size.
4.3 Results
Figures 9 and 10 show a region of interest (ROI) of
AT8 and 4G8 stained structures in post-mortem AD
brains. The ROI is the CA1 subfield of the hip-
pocampus, a brain region involved in memory con-
solidation and retrieval and known to be severely af-
fected by AD. AT8 staining reveals intraneuronal fib-
rillar structures called neurofibrillary tangles(Goedert
et al., 1995) and 4G8 staining shows accumulations
of the amyloid-beta peptide in intracellular inclusions
and extracellular plaques (Hunter and Brayne, 2017).
These protein accumulations are considered typical
neuropathological hallmarks of Alzheimer’s Disease
and are clinically used to assess disease staging. All
structural details of both stainings are preserved af-
ter PRAQA processing (Figure 9) and the presence
of noise is counteracted in the example of the 4G8
stained sample (Figure 10).
The comparison between the original acquisitions
and the by PRAQA binarized images demonstrates
that PRAQA is capable to segment the qualitatively
different protein aggregations successfully as vali-
dated by visually inspection of the overlay of the
original images and the PRAQA output by a neu-
ropathology expert. For the hyperphosphorylated tau
staining, the original image does not exhibit strong
background signal and PRAQA resolved also subtle
structures (Fig. 9). The original amyloid-beta stain-
ing has a stronger background signal and less well-
defined structures. In this scenario, PRAQA did not
resolve all potential substructures but successfully
classified positive pixels that represent the amyloid-
beta plaques (Fig. 10).
As a demonstration how PRAQA can be used for
disease classification, Figures 11 and 12 show the rel-
ative protein abundance in dependence on the sam-
ple condition. The analysis of amyloid-beta pep-
tide abundance within the CA1 hippocampal sub-
field shows in agreement with literature an enriche-
ment overall of amyloid-beta level in AD samples
(Marti Colom-Cadena, 2013). Interestingly, a lower
and residual amyloid-beta presence is also revealed
in age-matched controls as well as in samples from
patients with DLB. The relative abundance is here
comparable to AD samples with low Amyloid bur-
den (Marti Colom-Cadena, 2013). This finding may
indicate a general age-dependent increase of amyloid-
BIOIMAGING 2021 - 8th International Conference on Bioimaging
28

beta aggregation even in cognitively healthy controls
which is also coherent with previous findings (Ro-
drigue, 2012).
The comparison of hyperphosphorylated tau ag-
gregation among samples exhibits an even stronger
disease dependence (Fig. 12). While CTL samples
were consistently negative for tau aggregation, AD
samples exhibited a very strong enrichment to up of
0.13%. Strikingly, some DLB samples also showed
considerable amounts of phospho-tau proteins com-
pared to the age-matched control samples with lev-
els similar to AD condition (Marti Colom-Cadena,
2013).
Overall, this first application of PRAQA to hu-
man brain samples demonstrated that the targeted
approach allows for quantification of protein aggre-
gation within heterogeneous tissue. Furthermore,
PRAQA analysis of amyloid-beta and hyperphospho-
rylated tau distribution in CA1 subregions of AD and
DLB cases confirms that the two conditions share
common mechanisms of protein aggregation and may
represent a more continuous spectrum of cellular
pathologies than typically anticipated.
5 CONCLUSIONS
Protein function is essential for cellular and tissue
homeostasis and impairments are linked to diverse
diseases. Here, we introduced PRAQA as an effi-
cient tool to quantify relative protein abundance and
localization in complex tissues from 3D fluorescent
images. For this purpose, PRAQA specifically targets
luminescence variability caused by optical constraints
along the z dimension and by inter-sample variability
by applying an Median Absolute Deviation approach
for each 2D (x-y) plane of the image (Section 2).
Extensive benchmarking of PRAQA against alter-
native algorithms for synthetic scenarios has demon-
strated that the targeted approach allows for accu-
rate, robust and efficient quantifcation of relative
protein abundance in cases where noise and inten-
sity changes play an important role in the measure-
ment (Section 3). In particular, we have shown
that PRAQA performs well when dealing with im-
ages compromised by intensity changes (either intra-
acquisition or inter-acquisition) and is also resilient
up to a considerable amount of noise. The key ad-
vantages of this algorithm are its simple parameteri-
zation (1-parameter), computational efficiency and di-
rect applicability that does not require any preprocess-
ing. These features prevent typical biases of alterna-
tive approaches based on versatile parameters which
may compromise measurements and thus the results.
However, in cases of extreme noise, dedicated multi-
parametric pipelines might be used to deal with these
peculiar situations but care has to be taken for sample
comparison.
Finally, we have used PRAQA for a real applica-
tion in neurodegeneration and quantified protein ag-
gregation in human brain samples (Section 4). In this
application, we quantified amyloid-beta and hyper-
phosphorylated tau protein aggregation in immunos-
tained brain samples of AD, DLB and control sub-
jects where PRAQA was able to segment reliably the
qualitatively different structures. The first compari-
son of protein aggregation between the disease condi-
tions substantiates the essential role of amyloid-beta
plaques in AD but also indicates some shared proper-
ties of protein aggregation in neurodegenerative dis-
eases.
Overall, the targeted approach of PRAQA repre-
sents an efficient and easy-to-use tool to investigate
spatially resolved protein abundance in health and
disease conditions.
5.1 Future Work
We plan to extend the algorithm by an additional mod-
ule to estimate an optimal range for the threshold pa-
rameter θ. This automation may be achieved by sta-
tistically inferring when false positive pixels start to
appear in a salt and pepper manner throughout the
acquisition by progressively lowering θ. Furthermore,
we will test PRAQA with other staining markers lead-
ing to different structures and potentially adapted SEs
for ad-hoc situations (e.g. filaments or branches) also
in the context of the neurodegenerative samples. In
this respect, PRAQA will be also a valuable extension
to combine morphological characterizations (Sala-
manca et al., 2019) with protein abundances for in-
vestigations of multicellular mechanisms in neurode-
generation.
CONFLICT OF INTEREST
The authors declare no competing financial interests.
ACKNOWLEDGEMENTS
The authors thank the Douglas-Bell Brain Bank
for providing human brain samples, the Bioimag-
ing Facility of the Luxembourg Centre for Sys-
tems Biomedicine (LCSB) for support of microscopy,
the Reproducible Research Results (R3) team of
the LCSB for promoting reproducible research, R.
PRAQA: Protein Relative Abundance Quantification Algorithm for 3D Fluorescent Images
29

Sassi and E. Casiraghi for fruitful discussions.
C.A. and S.F. were supported by the PRIDE pro-
gram of the Luxembourg National Research Found
through the grants PRIDE17/12252781/DRIVEN and
PRIDE17/12244779/PARK-QC, respectively. This
work was further supported by the Luxembourgish
Espoir-en-T
ˆ
ete Rotary Club award, the Auguste et Si-
mone Pr
´
evot foundation, and the Agaajani family do-
nation for Alzheimer’s Disease research.
REFERENCES
Alberts, B. (2017). Molecular Biology of the Cell. W.W.
Norton.
Belthangady, C. and Royer, L. (2018). Applications,
promises, and pitfalls of deep learning for fluores-
cence image reconstruction.
Bouvier, D. S., Jones, E. V., Quesseveur, G., Davoli, M. A.,
A Ferreira, T., Quirion, R., Mechawar, N., and Murai,
K. K. (2016). High Resolution Dissection of Reactive
Glial Nets in Alzheimer’s Disease. Sci Rep, 6:24544.
Buades, A., Coll, B., and Morel, J. . (2005). A non-local al-
gorithm for image denoising. In 2005 IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition (CVPR’05), volume 2, pages 60–65 vol.
2.
Chung, K., Wallace, J., Kim, S.-Y., Kalyanasundaram, S.,
Andalman, A., Davidson, T., Mirzabekov, J., Zalo-
cusky, K., Mattis, J., Denisin, A., Pak, S., Bernstein,
H., Ramakrishnan, C., Grosenick, L., Gradinaru, V.,
and Deisseroth, K. (2013). Structural and molecu-
lar interrogation of intact biological systems. Nature,
497.
Dabov, K. ., Foi, A. ., Katkovnik, V. ., and Egiazarian, K. .
(2007). Image Denoising by Sparse 3-D Transform-
Domain Collaborative Filtering. IEEE Transactions
on Image Processing, 16(8):2080–2095.
Donoho, D. L. (1995). De-noising by soft-thresholding.
IEEE Transactions on Information Theory,
41(3):613–627.
Dugger, B. N. and Dickson, D. W. (2017). Pathology of
neurodegenerative diseases. Cold Spring Harbor per-
spectives in biology, 9(7):a028035. 28062563[pmid].
Goedert, M., Jakes, R., and Vanmechelen, E. (1995). Mon-
oclonal antibody at8 recognises tau protein phospho-
rylated at both serine 202 and threonine 205. Neuro-
science Letters, 189(3):167 – 170.
Hunter, S. and Brayne, C. (2017). Do anti-amyloid beta
protein antibody cross reactivities confound alzheimer
disease research? Journal of negative results in
biomedicine, 16(1):1–1. 28126004[pmid].
Im, K., Mareninov, S., Diaz, M. F. P., and Yong, W. H.
(2019). An Introduction to Performing Immunofluo-
rescence Staining. Methods Mol Biol, 1897:299–311.
Komin, N. and Skupin, A. (2017). How to address cellular
heterogeneity by distribution biology. Current Opin-
ion in Systems Biology, 3:154–160.
Leys, C., Ley, C., Klein, O., Bernard, P., and Licata, L.
(2013). Detecting outliers: Do not use standard devi-
ation around the mean, use absolute deviation around
the median. Journal of Experimental Social Psychol-
ogy, 49(4):764 – 766.
Lim, J. S. (1990). Two-Dimensional Signal and Image Pro-
cessing. Prentice-Hall, Inc., USA.
Marti Colom-Cadena, E. G. (2013). Confluence of a-
synuclein, tau, and b-amyloid pathologies in demen-
tia with Lewy bodies. J. Neuropathol. Exp. Neurol.,
72(12):1203–1212.
Niblack, W. (1985). An Introduction to Digital Image Pro-
cessing. Strandberg Publishing Company, DNK.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE Transactions on Systems,
Man, and Cybernetics, 9(1):62–66.
Quesseveur, G., Fouquier d’Herouel, A., Murai, K. K., and
Bouvier, D. S. (2019). A Specialized Method to Re-
solve Fine 3D Features of Astrocytes in Nonhuman
Primate (Marmoset, Callithrix jacchus) and Human
Fixed Brain Samples. Methods Mol. Biol., 1938:85–
95.
Rodrigue, K. M. (2012). β-amyloid burden in healthy ag-
ing: regional distribution and cognitive consequences.
Neurology, 78(6):387–395. 22302550[pmid].
Ross, C. A. and Poirier, M. A. (2004). Protein aggrega-
tion and neurodegenerative disease. Nature Medicine,
10(7):S10–S17.
Saito, T. and Rehmsmeier, M. (2015). The precision-recall
plot is more informative than the roc plot when evalu-
ating binary classifiers on imbalanced datasets. PLOS
ONE, 10(3):1–21.
Salamanca, L., Mechawar, N., Murai, K. K., Balling, R.,
Bouvier, D. S., and Skupin, A. (2019). Mic-mac: An
automated pipeline for high-throughput characteriza-
tion and classification of three-dimensional microglia
morphologies in mouse and human postmortem brain
samples. Glia.
Varghese, F., Bukhari, A. B., Malhotra, R., and De, A.
(2014). Ihc profiler: An open source plugin for the
quantitative evaluation and automated scoring of im-
munohistochemistry images of human tissue samples.
PLOS ONE, 9(5):1–11.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
30
