A Raster-based Approach for Waterbodies Mesh Generation

Roberto Nisxota Menegais, Flavio Paulus Franzin, Lorenzo Schwertner Kaufmann and

Cesar Tadeu Pozzer

Curso de Ci

encia da Computac¸

ao, Universidade Federal de Santa Maria, Santa Maria, Brazil

Keywords:

Mesh Generation, Large Scale, Rasterization, GIS.

Abstract:

Meshes representing the water plane for rivers and lakes are used in a broad range of graphics applications

(e.g., games and simulations) to enhance the visual appeal of 3D virtual scenarios. These meshes can be

generated manually by an artist or automatically from supplied vector data (e.g. GIS data - Geographic Infor-

mation System), where rivers and lakes are represented by polylines and polygons, respectively. In automated

solutions, the polylines and polygons are extruded and then merged, commonly using geometric approaches,

to compose a single polygonal mesh, which is used to apply the water shaders during the rendering process.

The geometric approaches usually fail to present scalability for large datasets with a high vertex and feature

count. Also, these approaches require speciﬁc algorithms for dealing with river-river and river-lake junctions

between the entities. In opposition to geometric approaches, in this paper, we propose a raster-based solution

for efﬁcient ofﬂine mesh generation for lakes and rivers, represented as polygons and polylines, respectively.

The solution uses a novel buffering algorithm for generating merged waterbodies from the vector data. A

modiﬁcation of the Douglas-Peucker simpliﬁcation algorithm is applied for reducing the vertex count and a

constrained Delaunay triangulation for obtaining the triangulated mesh. The algorithm is designed with a high

level of parallelism, which can be exploited to speed up the generation time with a multi-thread processor and

GPU computing. The results show that our solution is scalable and efﬁcient, generating seamless polygonal

meshes for lakes and rivers in arbitrary large scenarios.

1 INTRODUCTION

Waterbody meshes are used in a broad range of appli-

cations, including games and simulations, to enhance

the visual appeal of 3D virtual scenarios. The digi-

tal portrayal of environments usually combines lakes

and rivers to represent a determined region’s hydrog-

raphy, using GIS (Geographic Information System)

vector and raster data. In this context, waterbodies re-

fer to the combination of river and lake data, being a

unique element to be rendered in a real-time graphics

application.

Even though it is an important element in vir-

tual scenarios, few studies have explored real-world

data on water mesh generation or ways to efﬁciently

generate it for large scenarios with a high density of

features. With the growing use of real-world loca-

tions in simulations and games (e.g. ﬂight simula-

tors), the need for a solution to generate a polygonal

mesh based on previously generated data arises.

Usually, the river courses are represented by poly-

line datasets, and the lakes by polygons datasets,

causing a mismatch and overlap among them in the

input dataset, demanding additional data processing

to guarantee its correct mesh generation and, conse-

quently, correct rendering.

Considering this, the main aim of our solution is

to provide an ofﬂine approach to generate a polyg-

onal mesh representing the water plane of the junc-

tion between rivers and lakes represented by vector

data. The generation must guarantee a seamless junc-

tion between rivers and lakes, avoiding artifacts and

overlaps in the polygons, and be able to generate a

mesh for arbitrary large virtual scenarios.

Given a polyline dataset and a polygon dataset

representing a waterbody network, the problem can

be summarized as:

• How to efﬁciently generate a polygon dataset

from a polyline dataset;

• How to merge multiple datasets of rivers and lakes

into a single one;

• How to treat junctions between multiple rivers and

between lakes and rivers;

• How to achieve a minimal vertex count on the

generated polygons;

Menegais, R., Franzin, F., Kaufmann, L. and Pozzer, C.

A Raster-based Approach for Waterbodies Mesh Generation.

DOI: 10.5220/0010195501430152

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 1: GRAPP, pages

143-152

ISBN: 978-989-758-488-6

143

• How to efﬁciently triangulate the generated poly-

gons representing rivers and lakes;

• How to scale the algorithm to apply to arbitrary

large scale scenarios, considering a memory and

time constraints.

Usually, solutions to treat this problem are

geometric-based, as proposed by (Dong et al., 2003),

which treat polylines and polygons as different enti-

ties when applying the buffering algorithm, deﬁned

by (Bhatia et al., 2013) as a zone with speciﬁed dis-

tance surrounding a spatial data feature. At the end of

the buffering process, the generated entities will over-

lap with each other. Commonly, these problems are

solved by applying a dissolve algorithm in the gen-

erated polygons; this operation consists of taking the

intersections between the edges of the buffered poly-

gons and merging them, creating vertices on the inter-

section points, as seen in Fig. 1.

InputBueringDissolve

Figure 1: Example of the buffering and dissolve operation.

The geometric approaches result in optimal ver-

tex count for the generated polygons, although they

demand individual treatments between river-river and

river-lake junctions. In this case, river-river junctions

are considered the intersection between multiple river

entities at the same vertex. This individual treatment

can also lead to high computational cost depending

on the number of entities being processed, yielding a

fast-growing algorithm on time complexity.

We propose a raster-based approach for the wa-

terbodies mesh generation, employing a rasteriza-

tion algorithm for the buffer generation. The solu-

tion eliminates the complexity of dealing with line

extrusion and junctions between line-line and line-

polygon. Also, it avoids the need to apply a dissolve

algorithm afterward. Optimizations are also proposed

to enable the application of our solution to arbitrary

large virtual scenarios.

The main contributions of our work are:

• A raster-based solution for buffering and dissolv-

ing a set of polylines and polygons data;

• An efﬁcient approach for generating a 2D polyg-

onal mesh based on vector data;

• A scalable solution for waterbodies mesh genera-

tion that can be applied to arbitrary large scenar-

ios, with high parallelism levels.

The paper is organized as follows: Section 2 dis-

cuss related works on water mesh generation and ren-

dering. Section 3 presents an overview of the pro-

posed solution and sections 4, 5, 6, and 7 discuss each

step in-depth. Finally, in Section 8, the results are dis-

cussed and Section 9 presents the ﬁnal remarks and

future work.

2 RELATED WORK

Water surface-level representation for water rendering

is commonly used when a realistic ﬂuid simulation is

not needed, or a coarse approximation can be used.

Games and simulations apply a normal or bump map-

ping to the water surface for providing water move-

ment and the illusion of ripples and waves (Kryachko,

2005). The presence of a water plane mesh simpliﬁes

the illumination and shading for rendering the water.

(Engel and Pozzer, 2016) proposed a framework

to generate and render river networks based on vector

data. Although the rendering results obtained were

satisfactory, the generated mesh lacked a robust junc-

tion treatment between rivers. It did not support river-

lakes junctions.

(Yu et al., 2009) proposed a scalable real-time an-

imation for rivers based on vector data, ﬂow texture,

and a heightmap as input. The vector data used for

the application was in polygon form, meaning that

datasets representing rivers as polylines would need

a preprocessing step to convert them to polygons.

Concerning buffering algorithms, which aim is the

generation of eroded or dilated polygons, lines, and

the addition of area to points, geometric based solu-

tions were proposed (Bhatia et al., 2013), (Dong et al.,

2003). The problem with these solutions is that they

demand a dissolve algorithm after the buffering algo-

rithm to guarantee a seamless junction between fea-

tures, which adds greater complexity to the solution.

In contrast, our algorithm treats both buffering and

dissolve as a single process. Also, geometric solu-

tions may provide better results on small datasets, but

as the scale of the datasets grows, the solutions may

present a worse running time.

(Shen et al., 2018) proposes a parallel approach

for accelerated dissolved buffer generation, using In-

Memory cluster architecture. Although the solution is

highly efﬁcient for large data and surpasses previous

solutions on buffer generation, it’s fairly complex and

uses a distributed computing approach, whereas our

approach can also deal with large data in a far simpler

manner, still using parallelization.

Regarding rasterization approaches for dealing

with vector data, (Fan et al., 2018) proposes a par-

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

144

allel rasterization algorithm for vector polygon over-

lay analysis using OpenMP, they discuss in length the

beneﬁts and errors introduced by the discretization of

the vector features, but the implementation is done us-

ing CPU cores. A GPU implementation is discussed

only in the future works. Although the goal of the

paper differs from ours, the solution is interesting to

testify the eligibility of the rasterization approach.

(Ma et al., 2018) proposed a highly efﬁcient tech-

nique for real-time buffer analysis of large-scale spa-

tial data. Their solution uses raster-based buffering

with R-tree queries optimizations and a LOD algo-

rithm to manage rasterization quality. Although they

succeed in providing a visualization oriented paral-

lel model, their buffer generation algorithm does not

beneﬁt from the inherited parallel nature of rasteriza-

tion. In our work, we explore buffer generation with

per-pixel parallelization using acceleration structures

proposed in (Pozzer et al., 2014) and (Engel et al.,

2016).

3 PROPOSED SOLUTION

The proposed solution performs over shapeﬁles rep-

resenting polylines and polygons. The shapeﬁles are

primarily loaded and set up in the auxiliary data struc-

tures on the GPU memory (V-RAM), ensuring par-

allelizable optimized spatial queries of the data. In

this process, a spatial hash (Pozzer et al., 2014) is

used to structure the polylines and a quadtree (Engel

et al., 2016) for the polygons. Also, to reduce pro-

cessing and memory cost, the scenario is segmented

into blocks of ﬁxed size in the CPU. Fig. 2 presents a

visual overview of the process discussed below.

The process begins by selecting a block and invok-

ing a Buffering (Sec. 4) process. A texture is used,

in which each pixel covers a speciﬁc area within the

block. On the GPU, each pixel is processed indepen-

dently and ﬁlled according to its position relative to

the waterbodies, being classiﬁed as Inside, Outside or

Border pixel.

The texture generated in the previous step is re-

trieved to the CPU. It goes through a Vectorization

(Sec. 5) process to extract the previously ﬁlled pix-

els, where Border pixels form a circular path that is

traversed to generate the ﬁnal polygons representing

the waterbodies. This process works based on a graph

data structure with a backtracking-like algorithm. Af-

terward, these polygons are then Simpliﬁed (Sec. 6)

using a modiﬁed version of the Douglas-Peucker al-

gorithm (Douglas and Peucker, 1973), which is a so-

lution to simplify a curve composed of line segments

to a similar curve with fewer points.

The extracted polygons are Triangulated (Sec. 7)

using a constrained Delaunay triangulation algorithm

(Chew, 1989), generating the mesh for a block of the

scenario, which is saved in the disk.

4 TEXTURE GENERATION

A texture represents a discretization of a continuous

block of the scenario, where each pixel represents a

small portion of a block. A pixel size covering a spe-

ciﬁc area inside the block and a portion of the scenario

is selected. The texture size is then calculated by:

TextureSize = BlockSize/PixelSize (1)

An extra padding of 1 pixel is added on Eq. (1),

ensuring the correct connection between blocks.

The PixelSize value directly relates to the ﬁnal

mesh quality and the memory and time resources

spent on the texture generation. If a small pixel size

is used, the ﬁnal mesh is closer to a geometric so-

lution, resulting in a more accurate representation in

exchange of adding more vertices. Albeit the more

reﬁned result, the memory use increases due to the

large texture needed to cover the block area. A larger

pixel size will result in a coarser mesh, where small

details can be lost due to the pixel covering a large

scenario area, but the time and memory cost will be

much lower. Usually, the chosen PixelSize is kept be-

tween a range of 0.5 and 1 meter, to allow a good ge-

ometric result and to keep the memory cost in a good

range. Larger or smaller PixelSize will lead to a worse

mesh or a higher memory cost, respectively.

Using the information previously set, the genera-

tion consists on taking the distance of every pixel to

the closest river or lake edge, using the acceleration

structures on the GPU. The used accelerated struc-

tures are composed of a linear spatial hash (Pozzer

et al., 2014) for subdividing the terrain and allowing

fast access to the polyline data, and a quadtree struc-

ture (Engel et al., 2016) representing the polygons,

allowing fast point-in-polygon queries. According to

the distance, pixels are classiﬁed in three different

types (Fig. 2):

• Outside, pixels outside a river ∧ lake;

• Inside, pixels fully contained in the river ∨ lake;

• Border, pixels as border to a river ⊕ lake.

where ∧ denotes AND operation; ∨ inclusive OR;

and, ⊕ exclusive OR.

Pixels belonging to the texture border, classiﬁed

as Inside, are overwritten as Border pixels. This spe-

cial case is necessary to guarantee a correct junction

A Raster-based Approach for Waterbodies Mesh Generation

145

Block

Inside

Outside

Border

Buffering

Vectorization

Simplification

Triangulation

Scenario

Figure 2: Overview of the algorithm execution.

between blocks, without T-vertex, as well to ensure a

circular path through the Border pixels, to traverse the

texture and extract the polygons.

(A’ B)

Outside

Border

Inside

Foreground

Background

Eroded Border

A’

A’ B

A’

V =

Input Block

Figure 3: A visual description of the erosion process. B

represents the structuring element, A the generated texture.

A’ is the A texture without its borders. The subsequent ﬁg-

ures indicated by the arrows are a visual representation of

the process. In the last ﬁgure, the grey pixels indicate the

eroded border obtained.

Due to the high computational cost of the Vector-

ization step, since the execution time of the algorithm

used to guarantee the correct polygon is directly re-

lated to the number of neighbors to a pixel, an erosion

process, described in Eq. (2) and illustrated on Fig. 3,

is applied to mitigate the number of neighbors.

This process works as follows: Let A represent

the pixel set deﬁned by the generated texture, where

Inside pixels are foreground pixels, and every other

pixel type are background pixels, considering A

the A pixels set without its borders, represented on

Fig. 3. Let B represent the structuring element of a

3x3 matrix in a cross structure. The resulting texture

is given by:

T = (A

 B) ⊕ A

(2)

where  denotes erosion and ⊕ denotes an exclusive

OR operation applied pixel-wise.

The texture T obtained is again padded with the

original borders present in A, generating a polygon

representing an eroded version of the polygon gener-

ated in the previous step.

Due to the erosion process, an offset is applied to

the vertex positions in relation to the initial computed

position. For the rivers, the vertices after the erosion

will have a position of

RiverWidth

− PixelSize in rela-

tion to the river polyline. For the polygons, there is an

offset of PixelSize in relation to the original border.

To guarantee that the ﬁnal vertices will have the

desired position, the RiverWidth is considered as

RiverWidth + (2 ∗ PixelSize). For lakes, instead of

setting pixels that intersect the polygon edges as Bor-

der, pixels at a distance of PixelSize from the edge are

considered.

Fig. 4 presents the difference between the ex-

tracted polygon before and after erosion. It’s possi-

ble to notice that the original borders of the polygon

have more neighbors than needed, leading to errors or

stair-like behavior on the border of the polygon being

extracted.

5 POLYGON EXTRACTION

With the generated texture a vectorization algorithm,

as seen in Fig. 2, is applied, in CPU, to extract the

generated polygons border from the texture. The pro-

cess starts by selecting any Border pixel from the tex-

ture. From this pixel, its neighbors are evaluated, and

the chosen neighbor is selected as the next pixel. This

process occurs until the ﬁrst selected pixel is reached

again. When a pixel is evaluated, it is set as visited. If

it gets revisited, it is marked to not be chosen again,

avoiding self-intersections in the extracted polygon.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

146

Border

Eroded Border

Figure 4: Representation of the difference between the ex-

tracted path on a polygon before and after applying the ero-

sion process. The red arrows represents the ordered pixels

list being extracted as the polygon border, before applying

the erosion, while the yellow arrows represents the path col-

lected after the erosion.

In some cases, as described in Fig. 5, a pixel has

more than one neighbor; this can lead to ambiguity

when extracting the polygon. In such cases, a set of

possible heuristics to select the next pixel from the

neighbor’s list can be deﬁned:

• Closest Distance: The closest pixel to the current

pixel is selected;

• Directional: The most clockwise or counter-

clockwise pixel in relation to the last formed seg-

ment is selected;

• Least Angle: The pixel forming the least angle in

relation to the last formed segment is selected.

Closest Distance Directional Least Angle (Clockwise )

Figure 5: Representation of how the different heuristics deal

with branches in the polygon extraction step. The red line

represents what polygon would be extracted in each heuris-

tic.

An extracted polygon is one that the last extracted

pixel has no more valid neighbors and is inside a de-

ﬁned distance threshold to the ﬁrst extracted pixel.

The previously deﬁned heuristics present a problem.

If it chooses a wrong pixel, it can lead to the polygon

not being extracted, as seen in Fig. 6. To avoid this, as

it would lead to inconsistencies between the original

river network and the generated mesh, a graph data

structure with a backtracking-like algorithm is intro-

duced to solve this inconsistency. The algorithm runs

as follows:

Path

Possible Path B

Possible Path A

Border

Eroded Border

Figure 6: Representation of a wrong path when extracting

the polygon. The black path represents the extraction until

a branch is found, then the red path represents a wrong path,

while the yellow path is the correct one.

WHILE(!extracted(threshold, current, initial))

neighbours = getNeighbours(current)

IF (neighbours = 0)

IF (extracted(threshold, current, initial))

RETURN generatePolygon(current)

ELSE

neighbours = getVisited(current)

IF (neighbours = 0)

current = backtrack(current)

ENDIF

ELSE

current.neighbours = neighbours

current = getNextNode(current)

ENDIF

ENDWHILE

Given an initial pixel chosen at random, a node

denoted as current is created representing it. Then, all

adjacent pixels are searched to verify if any of them

is valid. If no neighbors are found, a veriﬁcation is

made to check if the polygon is already extracted. If

not, the algorithm backtracks to the last node that had

more than one neighbor and removes the pixel leading

to the dead-end path from the neighbor’s list. If there

are valid neighbors around the current node, they are

added to the neighbor’s list, and one of the aforemen-

tioned heuristics is applied to ﬁnd the next node to

be processed. When the initial pixel is reached, the

polygon is saved for the next steps, and the process

starts again since more polygons can be encoded in

the texture.

Contrary to the texture generation, which presents

a high level of parallelism, the polygon collection step

is not trivially parallelizable, since the vertex order

must be kept. Considering this, the process is done

sequentially, and the feature density is a factor that

increases the execution time.

A Raster-based Approach for Waterbodies Mesh Generation

147

6 POLYGON SIMPLIFICATION

Geometric buffering solutions guarantee a minimal

vertex count of the generated polygons. Opposed to

this, our solution produces more vertices than neces-

sary, requiring a simpliﬁcation to ensure a lower num-

ber of vertices that composes the ﬁnal polygon geom-

etry, which, in turn, will speed up the rendering. Also,

the fact that any vertex can be removed from the ﬁnal

simpliﬁed polygon presents a problem when dealing

with vertices in the borders of blocks, as removing

these vertices can lead to t-junctions in the generated

mesh between distinct blocks.

As such, an adaptation of the Douglas-Peucker

simpliﬁcation algorithm is proposed.

The Douglas-Peucker algorithm takes as input an

ordered set of points and a parameter T as a distance

for deﬁning whether a vertex shall belong to the sim-

pliﬁed curve or not. The algorithm maintains the ﬁrst

and last points to be kept and ﬁnd the farthest point to

the formed line. If the distance from the point to the

line is greater than the distance T , it is added to the

list and the algorithm splits the curve into two sepa-

rate pieces to be processed: The initial point and the

collected point P; and the point P and the ﬁnal point.

This process occurs until there are no more points at

a distance greater than T .

The modiﬁcation consists of adding the necessary

vertices in the list of vertices to be kept, together with

the initial and ﬁnal vertex, at the start of the algo-

rithm execution. There is a need to remove duplicated

points in the algorithm output since the border ver-

tices are not removed from the algorithm input and

are added to the output list at the beginning of the ex-

ecution.

For measuring the simpliﬁcation amount, Eq. (3)

describes an approximation for the minimal vertex

count that should be achieved.

V =

VertexCount

2 ∗ River

Vertices

+ Lake

Vertices

(3)

The river segments vertex count is duplicated in

the equation since the input polyline is extruded in

both sides to compose the river’s border. As a result,

if V = 1, the minimum number of vertices has been

achieved, values greater than one characterize a ge-

ometry with an excess of vertices.

It is essential to keep a small simpliﬁcation factor,

as the Douglas-Peucker algorithm is known to gen-

erate polygon self-intersections when using a large

parameter T . A non-self-intersecting algorithm was

proposed by (Wu and Marquez, 2003).

7 TRIANGULATION

The triangulation is the last step. It’s applied after the

polygon simpliﬁcation step. First, a hole detection al-

gorithm is employed. The bounding box of a polygon

is checked to assert that it is fully contained inside

another polygon bounding box. If the bounding box

is contained, a point in polygon test is done to every

polygon point. If all points are contained inside an-

other polygon, it is set as a hole. This test is executed

to all polygons in the block.

Each polygon and its respective holes, if existent,

are input into a Constrained Delaunay Triangulation

algorithm (Chew, 1989). The triangulation result is a

polygonal mesh corresponding to the borders of the

extruded river and lake data initially fed to the algo-

rithm.

The generated mesh undergoes a mesh simpliﬁca-

tion algorithm (Schroeder et al., 1992),(Heckbert and

Garland, 1999) with vertex-vertex distance criteria.

This process reduces the vertex count even more on

the ﬁnal mesh, as well as creating seamless junctions

between block borders, which is possible through the

addition of padding to the texture, discussed in sec-

tion 4. The resulting mesh is then saved to disk in the

desired format.

8 RESULTS

The experiments were performed on an AMD

Ryzen 5 3.6 GHz processor, with 16 GB of RAM and

an NVIDIA GeForce GTX 1070 graphics card, with

8 GB VRAM. The proposed architecture was imple-

mented in C# and HLSL languages using the Unity

engine. However, it is a generic solution and can be

implemented in any language.

We run experiments on ﬁve real-world datasets

comprised of vector data. The datasets were cho-

sen based on feature density, covered area, and vertex

count. The experiments explore time, memory, and

visual ﬁdelity results; also, total triangle and vertex

count for the resulting polygonal mesh are analyzed.

All results were based on an average time of ﬁve ex-

ecutions. The individual information for each dataset

can be seen in Table 1.

8.1 Memory Analysis

First, a static memory consumption analysis of the so-

lution is made. Due to the block approach, the analy-

sis is done considering a single block of the scenario.

For implementation purposes, we use an integer

texture for storing an index pointing to a position in-

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

148

Table 1: Test Datasets.

Dataset

River

Vertices

River

Features

Lake

Vertices

Lake

Features Area

L1 34923 1059 8122 130 1980

L2 90741 2939 3376 14 729

L3 279354 24922 41520 731 1485

L4 281743 5208 2266 9 1485

L5 641022 44825 83867 1519 36852

Area is represented in KM².

side a buffer containing the vertex data. This buffer

contains two ﬂoat values for storing the vertex posi-

tion, an integer storing a pointer to the texture pixel

representing this vertex, and 1 byte for storing addi-

tional info. As such, the V-RAM cost can be calcu-

lated as deﬁned in Eq. (4).

V RAM

Usage

= (TextureSize

× 4) + (α ∗Vertex

Cost

)

(4)

where α denotes the variable buffer size, Vertex

Cost

is the individual memory cost for each vertex and

TextureSize is calculated as deﬁned in Eq. (1).

In CPU, the memory cost is calculated as the pre-

viously estimated V-RAM usage plus the individual

graph node memory cost times the vertex buffer size.

The memory cost is relevant because it deﬁnes

how large a block can be and what resolution can be

used to represent a portion of the virtual scenario. For

example, a 100x100 kilometers scenario, with 4096

meters per block and a pixel size of 0.5 meters, will

have a total of 625 blocks, considering α as 65000

vertices, where each block requires 256 MB of mem-

ory.

Since each block is individually processed, an op-

timization based on CPU parallelization can be em-

ployed to process more than one block in parallel.

As such, the parallelization amount is deﬁned by how

many blocks can be ﬁt into the memory and the num-

ber of cores available.

8.2 Time Performance Analysis

Table 2 presents the performance of the solution. The

test suite settings were: Block size of 4096 meters,

pixel size of 0.5 meters, Closest Distance heuristics,

and simpliﬁcation using T = 0.25 meters.

It’s possible to notice that the Texture Genera-

tion process time is linear, highly dependent on the

scenario area. For example, the datasets L3 and L4

present the same size, with similar texture genera-

tion times; or, between L2 and L3, where L3 area is

roughly double the size of L2 and presents a propor-

tional time cost. Finally, L5 presents a larger texture

generation time than others due to its larger area.

Since this step happens in a highly parallel fash-

ion, the acceleration structures avoid that the fea-

ture density increase drastically the texture generation

time, as well as the fact that each pixel is processed

independently.

The polygon extraction step is executed on the

CPU and is more dependent on feature density than

the block size. L3, having the same area as L4, takes

3.11 more time on the polygon extraction than L4.

We can make a relation between the time growth

and the feature density difference between datasets.

While L3 has 1.13 more vertices than L4, which

would not justify the difference in time, the more sig-

niﬁcant difference is in the number of river and lake

features. This means that L3 has a higher density of

features per block, leading to a higher number of in-

tersections between different rivers and lakes, and a

greater number of cases where the backtracking algo-

rithm may execute.

L5 has the expected execution time, being the

largest dataset, indicating a growth based on the num-

ber of blocks and area size. At the same time, it is less

affected by the increase in execution time due to the

feature density.

The Polygon Simpliﬁcation, Hole Detection and

Triangulation steps present execution times directly

related to the polygons amount extracted on the

Polygon Extraction step and the total vertex count.

Datasets with high vertices count perform worse than

others with fewer vertices, as seen in L5 and L3 com-

pared to the other datasets. L3 fares even worse than

L5 due to the smaller area and the high vertex count,

leading to a bigger vertices/block count. The high

number of lake vertices also contributes to the slow

execution, as usually only lakes contain holes.

In L4 and L3, there is a signiﬁcant difference in

execution time besides both datasets having a small

difference in vertex count. The lake vertices count in

L3 is 18.32 times bigger compared to L4, justifying

the difference in time.

8.3 Simpliﬁcation Impact Analysis

Table 3 presents ﬁve results of vertices count on L3

and L2, using different simpliﬁcation factors. It’s pos-

sible to conclude that a suitable simpliﬁcation param-

eter is achieved when T equals the pixel size value,

as larger simpliﬁcation values do not reduce much

the total vertex count and can lead to polygon self-

intersection, as discussed in Sec. 6. Small simpliﬁca-

tions should be avoided; the results indicate that the

time is exponentially larger as the simpliﬁcation fac-

tor is low or nonexistent. Also, high vertices lead to

low performance when rendering the mesh.

The simpliﬁcation factor is directly related to the

Hole Detection and Triangulation steps. The time

A Raster-based Approach for Waterbodies Mesh Generation

149

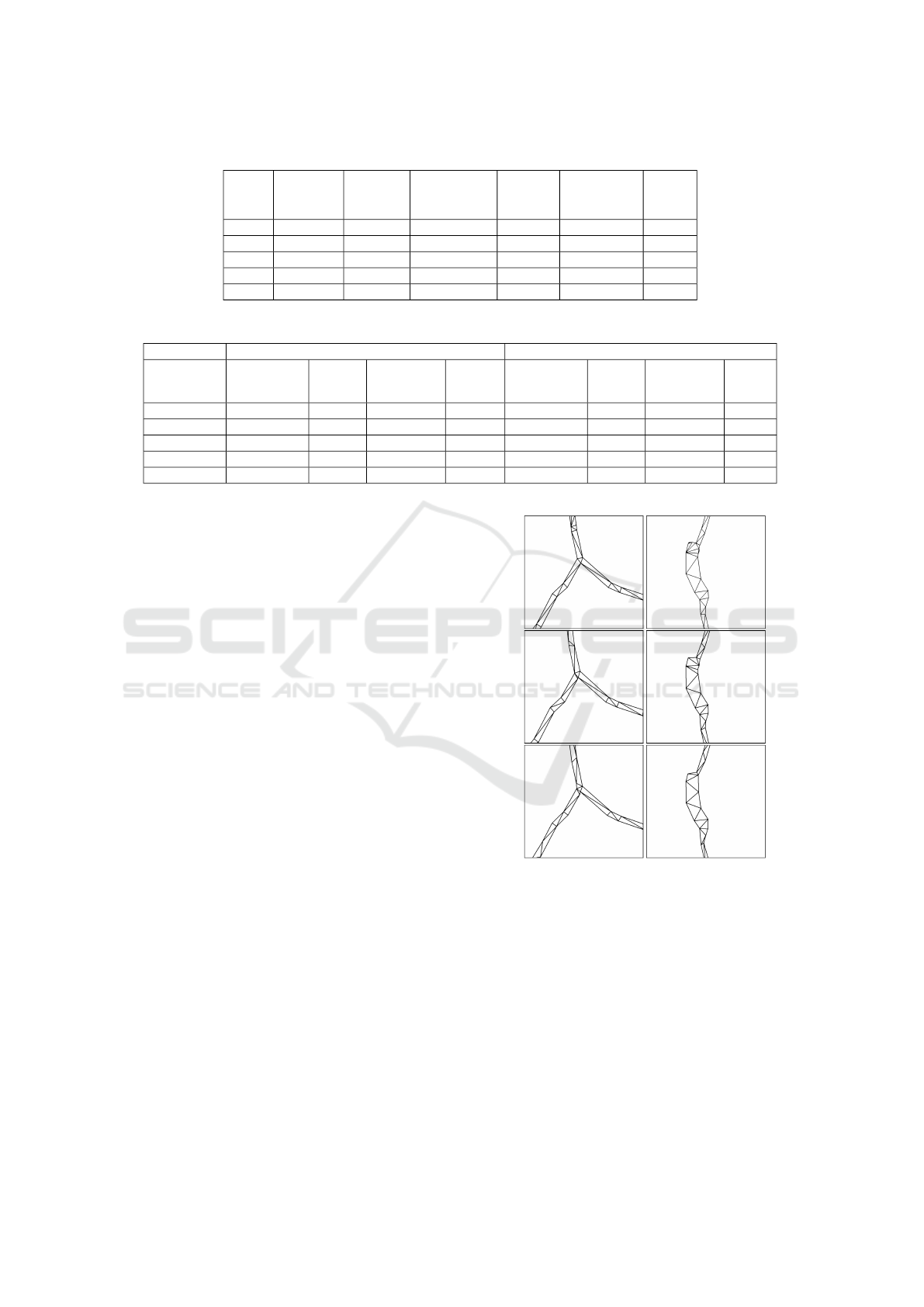
Table 2: Datasets Performance.

Dataset

Texture

Generation

Time

Polygon

Collection

Time

Polygon

Simpliﬁcation

Time

Hole

Detection

Time

Triangulation

Time

Total

Time

L1 16.95 6.41 22.76 17.37 13.73 77.24

L2 5.66 9.06 32.69 134.65 22.64 204.72

L3 11.83 54.35 146.57 3344.83 111.80 3669.39

L4 10.25 17.46 59.49 125.42 41.48 254.12

L5 244.73 229.71 945.62 1828.28 564.40 3812.75

All times presented are in seconds.

Table 3: Simpliﬁcation Results.

Datasets L1 L2

Simpliﬁcation

Amount

Simpliﬁcation

Time

Hole

Detection

Time

Triangulation

Time

Vertex

Count

Simpliﬁcation

Time

Hole

Detection

Time

Triangulation

Time

Vertex

Count

0 0 48917.26 617.16 26012450 0 2379.94 134.24 6189517

0.25 147.07 3137.94 113.04 6537075 32.65 137.86 22.87 1486307

0.5 94.19 55.25 9.37 882699 22.1 2.61 1.72 185680

0.75 91.71 46.24 8.22 809815 21.53 1.89 1.41 159763

1 90.78 48.57 7.88 775492 21.02 1.49 1.19 140686

All times presented are in seconds.

with a simpliﬁcation equal to the pixel’s size pre-

sented a reduction of almost a thousand times in the

execution time for L3 and L2 Hole Detection step, in-

dicating the importance of applying a simpliﬁcation

algorithm.

The simpliﬁcation amount, considering the 0.5

simpliﬁcation parameter, as calculated in Eq. (3), for

L3 was V = 1.47, which is a good result considering

the raster-based generation. For L2, it was V = 1.00,

indicating an optimal simpliﬁcation.

8.4 Visual Results

Concerning the visual results, Fig. 7 presents a wire-

frame representation of the generated meshes using a

pixel size of 0.5, 1, and 2 meters. The visual differ-

ence is perceptible when larger pixel sizes are used,

mainly in the junctions, where they tend to be rougher.

The lake part of the mesh also suffered a loss of detail

with larger pixel sizes.

Fig. 8 shows the mesh laid on top of the terrain,

allowing the analysis of the obtained triangulation,

which presented satisfactory results.

Fig. 9 presents the generated mesh rendered onto

the terrain. Two different water shaders are being ap-

plied in Fig. 9, showing that our resulting mesh can

be used for an accurate representation of the water-

bodies.

Figure 7: Representation of the generated mesh. In this

case, a river-river (left) and river-lake (right) junctions are

presented. From top to bottom, the pixel size used was: 0.5,

1.0, 2.0 meters.

9 CONCLUSION

We presented a solution for generating waterbody

meshes for arbitrarily sized scenarios with a straight-

forward approach based on buffering and dissolve

techniques, using a raster-based approach to simplify

the process and allow a simple treatment of junctions

between the input data.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

150

Figure 8: Depiction of a river-river (bottom) and a river-lake

(top) junction, laid onto the terrain. In the left images, for

a better viewing of the wireframe, the water plane has been

lift above the terrain.

Figure 9: Representation of the generated mesh laid onto

the terrain with a water shader applied.

Our results show that the proposed solution is

scalable and allows the mesh generation for large sce-

narios, having an execution time directly related to the

scenario size and feature density. The solution’s bot-

tleneck is the Hole Detection algorithm used, which

is not the primary concern of this work.

The Polygon Extraction and Texture Generation

steps, which were the main concerns of this work,

together with the Triangulation step, presented satis-

factory results in relation to time and output results.

Utilizing a texture to create the buffered lines dis-

solved with the polygons allowed the treatment of

both rivers and lakes interchangeably, eliminating the

need to create different algorithms for each type of

junctions, simplifying the polygon generation. The

quality of the exported mesh and its vertex count is

also satisfactory when small pixel sizes are used to-

gether with a good simpliﬁcation factor, as shown in

Fig. 7 and Fig. 9. The block approach allows the

solution to work with large scenarios and enables the

use of a parallelization algorithm where each block is

independently processed, leading to further optimiza-

tions on the solution.

For future work, we propose:

• Study better and more stable methods of triangu-

lation, and discuss the relation between quality

and performance of the triangulation in the con-

text of the proposed solution;

• Use other type of georeferenced data, like eleva-

tion maps, to generate a more accurate and de-

tailed mesh;

• Parallelize each block processing, in a pipeline

fashion;

• Implement a faster and more robust Hole Detec-

tion algorithm;

• Implement a non-self-intersecting Douglas-

Peucker algorithm, allowing greater levels of

simpliﬁcation;

• Analyse and attempt to extend the solution to

other similar problems, such as mesh genera-

tion for roads, which present the same geometry

generation issue, allowing to generate highway

meshes with seamless junctions between roads

and bridges.

ACKNOWLEDGEMENTS

We thank the Brazilian Army and its Prg EE AS-

TROS 2020 for the ﬁnancial support through the SIS-

ASTROS project.

REFERENCES

Bhatia, S., Vira, V., Choksi, D., and Venkatachalam, P.

(2013). An algorithm for generating geometric buffers

for vector feature layers. Geo-Spatial Information Sci-

ence, 16(2):130–138.

A Raster-based Approach for Waterbodies Mesh Generation

151

Chew, L. P. (1989). Constrained delaunay triangulations.

Algorithmica, 4(1-4):97–108.

Dong, P., Yang, C., Rui, X., Zhang, L., and Cheng, Q.

(2003). An effective buffer generation method in

gis. In IGARSS 2003. 2003 IEEE International Geo-

science and Remote Sensing Symposium. Proceedings

(IEEE Cat. No. 03CH37477), volume 6, pages 3706–

3708. Ieee.

Douglas, D. H. and Peucker, T. K. (1973). Algorithms for

the reduction of the number of points required to rep-

resent a digitized line or its caricature. Cartographica:

the international journal for geographic information

and geovisualization, 10(2):112–122.

Engel, T. A., Frasson, A., and Pozzer, C. T. (2016). Op-

timizing tree distribution in virtual scenarios from

vector data. Proceedings of Brazilian Sympo-

sium on Computer Games and Digital Entertainment

(SBGames).

Engel, T. A. and Pozzer, C. T. (2016). Shape2river: a tool

to generate river networks from vector data. Proceed-

ings of Brazilian Symposium on Computer Games and

Digital Entertainment (SBGames).

Fan, J., He, H., Hu, T., Li, G., Qin, L., and Zhou, Y.

(2018). Rasterization computing-based parallel vec-

tor polygon overlay analysis algorithms using openmp

and mpi. IEEE Access, 6:21427–21441.

Heckbert, P. S. and Garland, M. (1999). Optimal triangu-

lation and quadric-based surface simpliﬁcation. Com-

putational Geometry, 14(1-3):49–65.

Kryachko, Y. (2005). Using vertex texture displacement for

realistic water rendering. GPU gems, 2:283–294.

Ma, M., Wu, Y., Luo, W., Chen, L., Li, J., and Jing, N.

(2018). Hibuffer: buffer analysis of 10-million-scale

spatial data in real time. ISPRS International Journal

of Geo-Information, 7(12):467.

Pozzer, C. T., Pahins, C., Heldal, I., Mellin, J., and Gustavs-

son, P. (2014). A hash table construction algorithm for

spatial hashing based on linear memory. In Proceed-

ings of the 11th Conference on Advances in Computer

Entertainment Technology, pages 1–4.

Schroeder, W. J., Zarge, J. A., and Lorensen, W. E. (1992).

Decimation of triangle meshes. In Proceedings of the

19th annual conference on Computer graphics and in-

teractive techniques, pages 65–70.

Shen, J., Chen, L., Wu, Y., and Jing, N. (2018). Approach

to accelerating dissolved vector buffer generation in

distributed in-memory cluster architecture. ISPRS In-

ternational Journal of Geo-Information, 7(1):26.

Wu, S.-T. and Marquez, M. R. G. (2003). A non-

self-intersection douglas-peucker algorithm. In 16th

Brazilian symposium on computer graphics and Im-

age Processing (SIBGRAPI 2003), pages 60–66.

IEEE.

Yu, Q., Neyret, F., Bruneton, E., and Holzschuch, N. (2009).

Scalable real-time animation of rivers. Computer

Graphics Forum (Proceedings of Eurographics 2009),

28(2). to appear.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

152