An Embedded Polygon Strategy for Quality Improvement of 2D

Quadrilateral Meshes with Boundaries

Muhammad Naeem Akram, Lei Si and Guoning Chen

University of Houston, Houston, U.S.A.

Keywords:

Quadrilateral Meshes, Quality Improvement, Embedded Polygon.

Abstract:

Quadrilateral (or quad) meshes generated by various remeshing and simpliﬁcation methods for input models

with complex structure and boundary conﬁgurations often possess elements with minimal quality, which calls

for an optimization approach to improve their individual elements’ quality while preserving the boundary

features. Many existing methods either ﬁx boundary vertices during optimization or assume a simple boundary

conﬁguration. In this paper, we introduce a new quality improvement framework for 2D quad meshes with

open boundaries. Our framework aims to optimize the conﬁguration of an embedded polygon constructed

based on the one-ring neighbors of each interior vertex. A feature-preserved boundary optimization is also

introduced based on the angle conﬁguration of the individual boundary vertices to further improve the quality

of the boundary elements. Our framework has been applied to a number of 2D quad meshes with various

boundary conﬁgurations and compared with other representative methods to demonstrate its advantages.

1 INTRODUCTION

Quadrilateral (or quad) meshes are preferred by many

mechanical engineering applications due to their de-

sired properties for numerical simulations (Gao et al.,

2017). Numerous efforts have been made to ad-

dress the generation of high-quality quad meshes

(Bommes et al., 2009; Bommes et al., 2013; Campen,

2017; Fang et al., 2018; Viertel and Osting, 2019;

Docampo-Sanchez and Haimes, 2019). Nonethe-

less, robustly generating high-quality quad meshes

for input with arbitrary geometry and topology re-

mains a challenge. Most methods produce initial

quad meshes with sub-optimal quality which require

a post-processing to improve the element quality by

re-positioning the vertices. This post-processing is

called mesh quality improvement. If done properly,

mesh quality improvement can signiﬁcantly improve

the quality of a mesh (see Figure 5).

Existing quad mesh quality improvement tech-

niques either apply a local tangential space smoothing

(Sorkine, 2005; Daniels et al., 2009; Xu et al., 2018)

after mesh generation or perform re-parameterization,

re-sampling, or edge ﬂipping (Ben-Chen et al., 2008;

Tarini et al., 2011; Pietroni et al., 2009; Prasad,

2018; Gao et al., 2015) during mesh processing. The

smoothing approach preserves the mesh connectivity

https://orcid.org/0000-0003-0581-6415

which is required for structured mesh improvement.

However, this constraint may limit its capability of

improving meshes with challenging connectivity con-

ﬁgurations. In contrast, the re-parameterization, re-

sampling, or edge-ﬂipping methods optimize the lo-

cal mesh connectivity to achieve better element qual-

ity, while sacriﬁcing the preservation of the structure

of the mesh (i.e., introducing additional irregular ver-

tices). In this work, we focus on the former approach.

Most times, the quality of a quad mesh can be

measured by the scaled Jacobian measures (P

ebay

et al., 2007). By deﬁnition, the scaled Jacobian mea-

sure of each quad is determined by it’s four interior

angles. A perfect scaled Jacobian (i.e., 1) can be

achieved if all four interior angles are 90

◦

. If one

angle is larger than 180

◦

, the scaled Jacobian be-

comes negative, and the element with negative Jaco-

bian is referred to as an inverted element. An effec-

tive quality improvement technique should remove in-

verted elements in the mesh as much as possible. For

simple quad meshes with non complex structure and

boundaries, smoothing methods like Laplacian mesh

smoothing work well and generate high-quality ele-

ments, but for quad meshes with complex boundaries

(e.g., with many small and sharp features), further

optimization and element reﬁnement is vital in tack-

ling the inverted elements, preserving features, and

smoothing the mesh.

This paper introduces a new quality improvement

Akram, M., Si, L. and Chen, G.

An Embedded Polygon Strategy for Quality Improvement of 2D Quadrilateral Meshes with Boundaries.

DOI: 10.5220/0010209101770184

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 1: GRAPP, pages

177-184

ISBN: 978-989-758-488-6

177

technique, aiming to improve the Jacobian measures

of the mesh. Our method is inspired by Xu and New-

man’s approach (Xu and Newman, 2005) that opti-

mizes the position of a vertex of each quad to be

closer to the bi-sector line of its opposite corner. Dif-

ferent from their method, we optimize the conﬁgu-

ration of an embedded polygon surrounding an in-

terior vertex based on its direct one-ring neighbors

(see Figure 1). Furthermore, a boundary optimiza-

tion strategy is introduced to optimize the positions of

boundary vertices based on their angle conﬁguration,

while still preserving boundary features. This enables

further improvement of the quality of the quad ele-

ments at the boundary. We have applied our method

to a number of quad meshes produced by some quad

mesh generation and simpliﬁcation processes. We

compared the quality of the optimized meshes ob-

tained using our method with those obtained with

Xu and Newman’s method (Xu and Newman, 2005),

Laplacian smoothing (Sorkine, 2005), and Mesquite

(Brewer et al., 2003). The comparison shows that

the optimized meshes with our method usually have

higher minimum and average scaled Jacobians than

those produced by other methods.

2 RELATED WORK

Two different groups of methods have been proposed

for mesh quality improvement, i.e., smoothing and

optimization with ﬁxed mesh connectivity (Vartziotis

and Himpel, 2014; Xu et al., 2018) and local connec-

tivity modiﬁcation (Prasad, 2018; Tarini et al., 2010;

Gao et al., 2017). The present work belongs to the

former group; thus, we review some representative

methods in this group.

Among all smoothing techniques, Laplacian

smoothing is the most popular technique that aims

to move the individual interior vertices of a mesh to-

ward the average of their direct neighbors. A recent

work shows that Laplacian smoothing is essentially

optimizing the mean ratio quality measure (Vartziotis

and Himpel, 2014). Both explicit (iterative) method

and implicit (direct solving) method (Ji et al., 2005)

of Laplacian smoothing have been proposed. Inter-

ested readers should refer to (Sorkine, 2005; Vartzio-

tis and Himpel, 2014) for a thorough review of Lapla-

cian smoothing and its many variations. Despite its

simplicity and popularity, Laplacian smoothing of-

ten fails for meshes that have undesired connectiv-

ity (especially near the concave area of the bound-

ary) (Canann et al., 1998). Later, optimization-based,

physics-based, or local (Kim et al., 2015) approaches

were introduced to address the limitations of Lapla-

cian smoothing with various levels of success.

Many quad mesh quality improvement methods

are adapted from the techniques for triangle meshes

(Canann et al., 1998), including Laplacian smooth-

ing and its variations. Zhang et al. (Zhang et al.,

2005) proposed a surface mesh smoothing technique

by moving vertices along normal direction based on

a surface diffusion ﬂow. Xu and Newman (Xu and

Newman, 2005) introduced an angle-based optimiza-

tion to optimize the position of each vertex of a quad

to be closer to the bi-sector line of its opposite cor-

ner and neighboring quads. An angle-based smooth-

ing strategy was introduced by Zhou and Shimada

(Zhou and Shimada, 2000) for 2D triangle meshes,

which was later extended by Xu et al. (Xu et al.,

2018) for the hexahedral mesh quality improvement.

Most recently, machine learning technique has been

applied to help address the untangling and smoothing

of meshes (Kim et al., 2020). Our smoothing strat-

egy is most similar to Xu and Newman’s approach

(Xu and Newman, 2005) but with an important dif-

ference, that is, we consider the bisectors of an em-

bedded polygon of each interior vertex (see Figure

1), which reduces the number of angles for consider-

ation by half. In addition, we include weighting strat-

egy and boundary optimization to further improve the

mesh quality.

3 OUR METHOD

We propose a smoothing method that makes use of

circumjacent angles of a vertex to achieve regular-

ization of an embedded polygon formed by one-ring

neighbors. This approach is inspired by a former for-

mulation of an energy function deﬁned by a torsion

springs system. Essentially, the energy based on a

system of torsion spring for a vertex in a mesh can

be deﬁned as (Zhou and Shimada, 2000):

E =

2(n−1)

∑

i=0

Kθ

(1)

where, n is the number of polygons incident to the

vertex, θ

is the angle between a side of the polygon

and the edge connecting the vertex to the polygon,

and K is a constant. It is not too difﬁcult to see E is

minimum when all θ

are identical.

Consider a vertex with n neighbors directly con-

nected to it as shown in Figure 1(a). In this example,

vertex v has four neighbors: v

, v

and v

. A poly-

gon can be constructed by connecting the neighbor-

ing vertices of v successively. We call such a poly-

gon an embedded polygon of v as shown with dashed

edges in the example of Figure 1 (a). The shape of

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

178

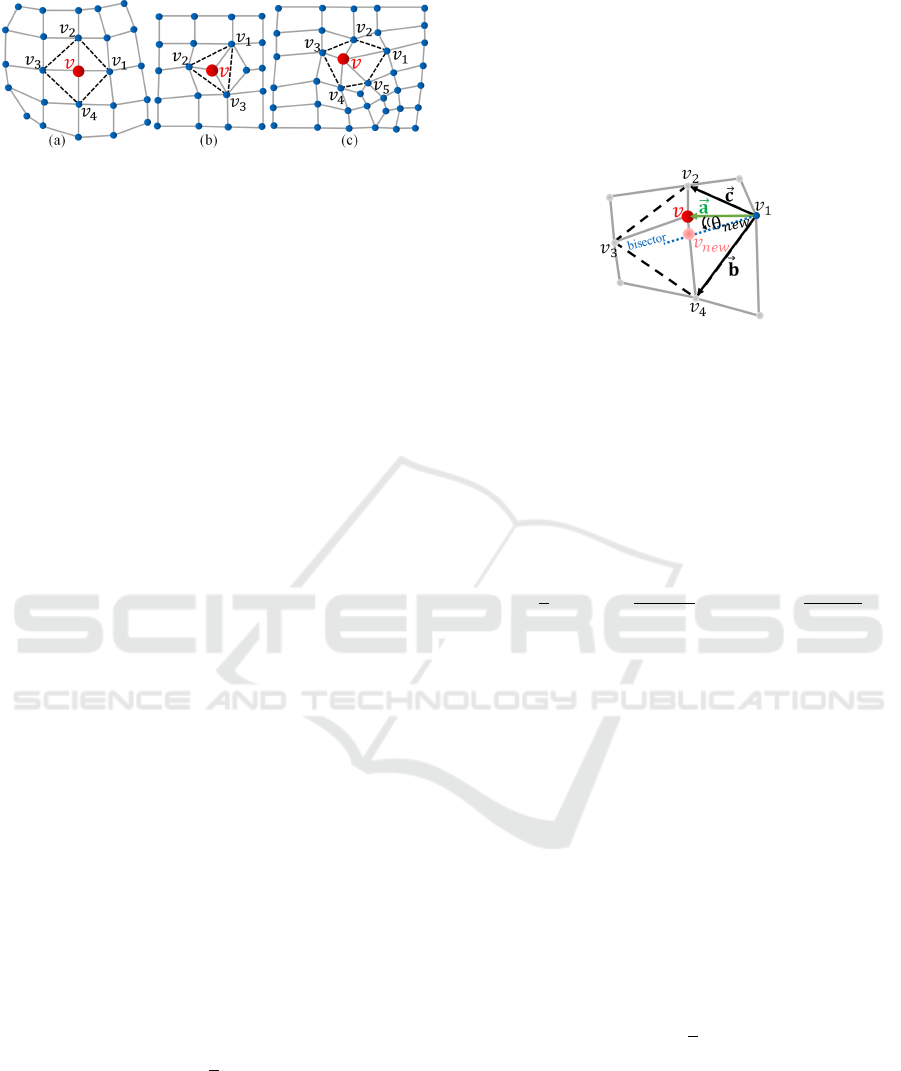
Figure 1: Examples embedded polygons for a valence-4

regular vertex (a), a valence-3 interior vertex (b), and a

valence-5 vertex (c), respectively.

the embedded polygon depends on the number of the

one-ring neighbors adjacent to source vertex (or the

valence of the vertex) (Figure 1(a-c)). The circumja-

cent angles to a vertex are inherently the interior an-

gles of the embedded polygon. A regular embedded

polygon implies that all the interior angles are equal

in magnitude and the source vertex is the centroid of

the embedded polygon being equidistant from all the

adjacent neighbors. In this ideal conﬁguration, the an-

gle bisectors of all the interior angles meet at a single

point. For irregular polygons, however, the interior

angles differ in magnitude and the angle bisectors of

all the interior angles are not equivalent. Thus, the

goal of optimizing the embedded polygon is to make

it as regular as possible, so that the intersections of the

individual bisectors converge to a point, which corre-

sponds to the ideal position of the center vertex.

3.1 Embedded Polygon Optimization

Given a source vertex and its embedded polygon as

illustrated in Figure 2, the position of the vertex can

be updated based on angle bisectors of the interior an-

gles. In an ideal regular polygon, the centroid bisects

all the interior angles of the polygon and the following

relation holds true:

∑

i=1

− X) = 0 (2)

where, n is the number of one-ring neighbors of a ver-

tex v or sides of the embedded polygon of v, x

is the

angle bisector, and X is the centroid of the em-

bedded polygon. For irregular polygons, solving the

above equation yields:

X =

∑

i=1

(3)

Therefore, the optimal position of a source vertex v in

its embedded irregular polygon can be achieved in the

following two steps:

1. By updating the interior angles of the embedded

polygon to be identical thus minimizing the en-

ergy function given by Eq.(1).

2. By updating the position of the source vertex to

its optimal value as evidenced by Eq. (3).

In (Xu and Newman, 2005), angles formed by

all the edges between successive neighboring vertices

(adjacent and non-adjacent) are considered while up-

dating the position of the source vertex.

Figure 2: Vertex rotation to bisect interior angle of the em-

bedded polygon.

In contrast, our approach considers the interior an-

gles of the embedded polygon. Therefore, the number

of angles under consideration is reduced in half. From

Figure 2, the interior angles can be bisected by ro-

tating the vectors formed by an edge between source

vertex and the corners of the embedded polygon. For

an interior angle θ, the extent of rotation for the vector

a to bisect the interior angle can be found as:

new



cos

−1



a · b

kakkbk



− cos

−1



a · c

kakkck



(4)

new

= b + Ra (5)

where, R =



cosθ

new

−sinθ

new

sinθ

new

cosθ

new



3.2 Interior Vertex Optimization

The rotation of the vertex v to bisect the n interior

angles of the embedded polygon produces a set of n

new coordinates. Consider a set A = {a

, a

} of

new coordinates for vertex v generated by its rotation

set B = {θ

, θ

} to bisect the interior angles of

the embedded polygon. Each of the new coordinates

is a candidate for moving the source vertex towards

the optimal position. The ﬁnal position of the source

vertex can be calculated by:

new

∑

i=1

(6)

This process is analogous to ﬁnding an optimal posi-

tion of the source vertex through Laplacian smooth-

ing. However, assigning equal weights to all of the

candidate coordinates can have undesirable effects

during smoothing and the process can sometimes get

stuck between local minimums. To avoid such situ-

ations, weights can be assigned to each item of the

candidate coordinates set A such that the movement

An Embedded Polygon Strategy for Quality Improvement of 2D Quadrilateral Meshes with Boundaries

179

of the source vertex is closest to the optimal position.

For a candidate a in the coordinate set A generated by

its corresponding θ in B, the weight can be assigned

according to the following criteria:

w = 1 −

|θ|

∑

i=1

|θ

(7)

where,

∑

i=1

|θ

| represents the sum of all rotation an-

gles for vertex v in B. The weights are assigned to

each candidate such that rotation of vertex v for the

worst interior angles bisection of the embedded poly-

gon of v is favored. In this way, the regularity of the

embedded polygon as well as approximation of the

optimal position for vertex v is achieved at a faster

speed since in later iterations of the smoothing pro-

cess, the already bisected angle will have a smaller

weight. The new coordinates v

new

for the source ver-

tex v can be calculated using weights as:

new

= λ(

∑

i=1

− v) (8)

λ is a parameter to control the speed of optimization.

For Laplacian smoothing different λ may affect the

quality of the output. However, in our experiment,

when varying λ between 0.1 and 1, no obvious im-

pact is observed, but larger λ usually results in faster

optimization process. Thus, we set λ = 1. The above

method is similar to Laplacian smoothing (Sorkine,

2005) where the weights are used to determine the

optimal position of a vertex. Hence, the regularity of

the embedded polygon is achieved by making its in-

terior angles close to the ideal angles through the ﬁrst

part of our approach (Section 3.1) while the optimal

position of the source vertex v in its embedded poly-

gon is achieved through the second part (Section 3.2)

of our approach.

We incorporate collective energy minimization

for the termination decision. The collective energy

total

∑

, where E

is given by Eq.(1), can be

computed by calculating and aggregating the ener-

gies of individual embedded polygons associated with

each vertex being optimized. As the optimization ad-

vances, collective mesh energy is calculated before

and after each optimization step and the optimization

is terminated if |E

new

− E

old

| < τ, where τ is a thresh-

old used to determine termination decision.

3.3 Boundary Optimization

Feature preservation is usually required during mesh

optimization where certain areas of the mesh are

deemed important in terms of sharp features and cor-

ners and such areas must be preserved during the

mesh optimization to keep the output mesh as close

to the input mesh as possible. In our proposed ap-

proach, we extract the boundary of the input mesh and

regard it as the reference for boundary optimization

and feature preservation. The corners in the bound-

ary are set as immobile (i.e., ﬁxed during boundary

optimization). A corner is a boundary vertex whose

valence is not regular (i.e., the number of quads adja-

cent to this vertex is not 2). To preserve the portion of

the boundary with large curvature and sharp features,

we also mark boundary vertices whose two boundary

edges form an angle θ

such that |θ

−180

◦

| > c (e.g.,

c = 45

◦

in our experiments). Most of the times, the

sharp features are also singularities as in the case of

Figure 3.

Figure 3: An example illustrating boundary optimization.

A boundary vertex with regular valence (or not

marked as a corner) has a half embedded polygon

with only one full interior angle as shown in Figure

Since only one interior angle is optimized, the sec-

ond part of our method is omitted for boundary opti-

mization. The boundary vertices can be optimized in

two ways:

• Approach 1: Similar to the interior vertices,

boundary vertices can be rotated to bisect the inte-

rior angle of the embedded polygon. The bound-

ary vertex in this case deviates from the boundary

and remapping is required to snap the drifted ver-

tex back to the original boundary. However, some

of the input examples might have complex bound-

ary conﬁguration as shown in Figure 4 (middle)

where the two regions of boundary are very close

to each other and can lead to boundary vertex be-

ing snapped to wrong position.

• Approach 2: The boundary vertices can be re-

stricted to move along the boundary only. From

Figure 3, the new position of vertex v to bisect

the interior angle of the embedded polygon can

be calculated as follows:

new

= v + (

kak) ˆa (9)

Although Approach 2 is more robust than Ap-

proach 1 in handling complicated boundary conﬁgu-

rations, as evidenced by Figure 4, in our experiments,

we have observed that the ﬁrst approach sometimes

produces meshes with better quality for meshes with

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

180

Figure 4: A boundary vertex is incorrectly mapped to a dif-

ferent part of the boundary after the boundary optimization

using the ﬁrst approach (middle). In contrast, the second

approach preserves the boundary better (right).

simpler boundary conﬁguration (e.g., no or little sharp

features/corners). Therefore, the user can choose ei-

ther of these two approaches to achieve a trade off

between better quality and better boundary preserva-

tion. For both approaches, the boundary optimization

is performed iteratively. We use a similar strategy

for termination of boundary optimization as described

in Section 3.2 with the same threshold τ. Our com-

plete optimization framework incorporates the above

boundary optimization and the interior vertex opti-

mization.

4 RESULTS

We have applied the proposed quality improvement

framework to a number of 2D quad meshes with vary-

ing boundary conﬁgurations and mesh connectivity.

Table 1 provides the statistics of the meshes, their

quality before and after optimization, and the run

times. Figure 5 visualizes some representative meshes

before and after optimization with our method. We

use a saturation color coding to show the individual

element quality measured by their scaled Jacobian.

Red indicates low quality elements (i.e., small scaled

Jacobian values) and white indicates elements with

high scaled Jacobian values. From these results, we

can see that the proposed optimization framework sig-

niﬁcantly improves the quality of all these meshes in

terms of their minimum and average scaled Jacobian.

The maximum scaled Jacobian of some meshes does

drop slightly, as it gives more room for more elements

to improve. In practice, the quality of the simulations

(or other scientiﬁc computation) run on those meshes

depends on the minimum and average scaled Jacobian

measures as shown by Gao et al. (Gao et al., 2017).

Comparison with Xu and Newman’s Approach.

Figure 6 shows the comparison of our method with

Xu and Newman’s approach. Since their approach as-

sumes ﬁxed boundary vertices during optimization, to

ensure a fair comparison we disable our boundary op-

timization for this comparison. Table 2 provides the

quality statistics of the meshes produced with the two

approaches. Our method without boundary optimiza-

tion generates meshes with better minimum scaled

Jacobian for almost all meshes. More importantly,

our method without boundary optimization produces

meshes with better average scaled Jacobian than Xu

and Newman’s method for all meshes.

Comparison with Laplacian Smoothing and

Mesquite. Here, we compare with two different

variants of Laplacian smoothing, i.e., the Laplacian

with cotangent weights (which we will simply refer

to as Laplacian), and a Laplacian smoothing imple-

mented in a popular mesh quality improvement tool,

Mesquite. Similar to the previous comparison, since

both Laplacian smoothing methods assume ﬁxed

boundaries (otherwise, the mesh will shrink), we

compare our method without boundary optimization

with these two Laplacian smoothing. Figure 7 shows

the meshes produced with the two Laplacian smooth-

ing and our method without boundary optimization.

Table 2 provides the quality statistics of the meshes

produced with the two Laplacian smoothing methods,

labeled as Laplacian and Mesquite, respectively.

From this comparison, we see our method without

boundary optimization outperforms the classic

Laplacian (with cotangent weight) in almost all

meshes except for the minimum scaled Jacobian for

the 1 hole mesh. This matches previous results that

Laplacian smoothing can work well for meshes with

simple boundary conﬁgurations. When compared

with the Mesquite results, our method without

boundary optimization produces meshes with better

average scaled Jacobian in almost all cases except

for the 1 hole and 3 hole 1 square. In terms of the

minimum scaled Jacobian, Mesquite produces better

minimum scaled Jacobian measure for ﬁve meshes,

i.e., 1 hole, 3 hole, 10 holes, 3 hole 1 square, and

mazewheel. It is worth noting that for patch 7, none

of the existing methods can successfully untangle its

inverted elements (that are highlighted by the black

arrow). In contrast, our method without boundary

optimization can already produce an inversion free

mesh. Nevertheless, by incorporating the boundary

optimization, we can produce the best quality meshes

for all meshes.

Impact of the Threshold Value τ. As described

earlier, a threshold value τ is used to determine when

our optimization should be terminated. In our exper-

iments, we have used different threshold values rang-

ing from 1e

−1

to 1e

−5

. For larger values of τ, the op-

timization algorithm terminates quicker as compared

to smaller values of τ but the extent of optimization

An Embedded Polygon Strategy for Quality Improvement of 2D Quadrilateral Meshes with Boundaries

181

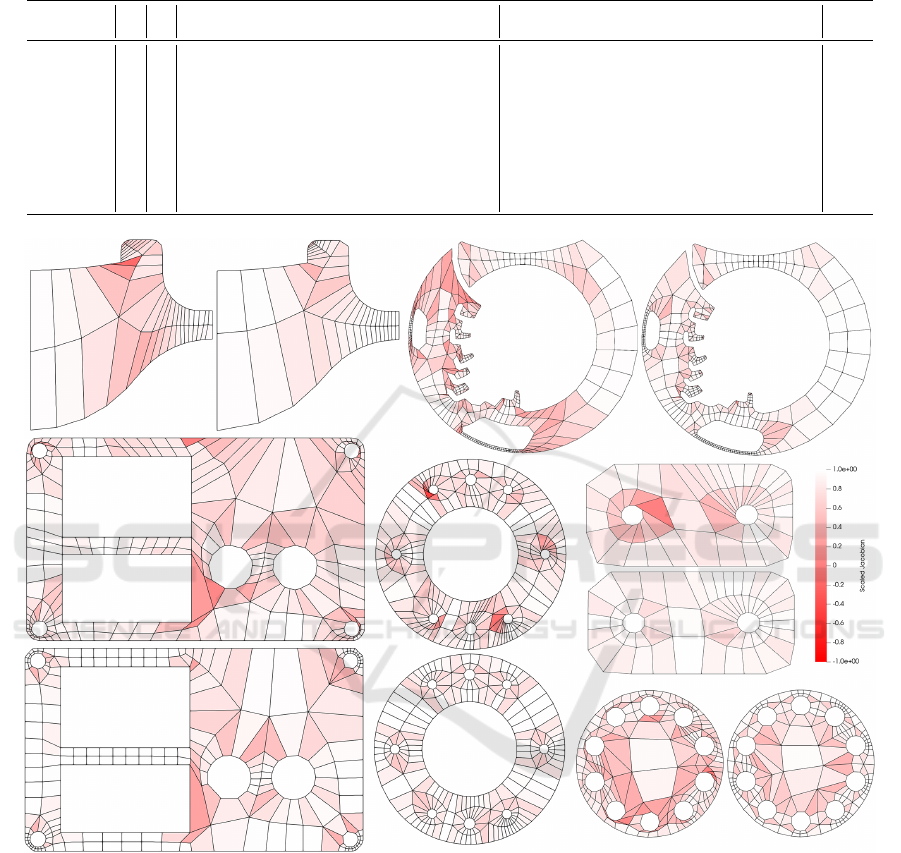
Table 1: Statistics for Scaled Jacobian measure of various meshes before smoothing and after smoothing using our

approach. The best quality measures are highlighted in bold. All results are obtained with the second boundary opti-

mization approach.

Input Output

Model #V #F Min. Scaled Jacobian Avg. Scaled Jacobian Max. Scaled Jacobian Min. Scaled Jacobian Avg. Scaled Jacobian Max. Scaled Jacobian Time (s)

1 hole 69 46 0.558289 0.896226 0.997788 0.742937 0.987127 0.991549 0.29

2 holes 90 61 0.0146683 0.77561 0.981719 0.701665 0.926261 0.993901 0.526

2 holes 2 squares 140 97 -0.556381 0.735316 0.993744 0.197108 0.84893 0.997823 0.112

3 holes 1 square 144 96 0.553854 0.832912 0.997128 0.724021 0.92366 0.998528 0.111

6 holes 2 squares 352 242 -0.164996 0.750487 0.996743 0.296134 0.880297 0.99996 0.547

8 holes 335 229 -0.513426 0.770411 0.999775 0.5811 0.892645 0.999414 0.304

10 holes 288 199 -0.0984454 0.680388 0.995199 0.411444 0.841136 0.995901 0.407

patch 5 87 55 -0.156262 0.756085 0.998083 0.360867 0.838986 0.999841 0.034

patch 7 126 90 -0.528536 0.717805 0.998884 0.312207 0.79753 0.993506 0.06

mazewheel 3 601 392 -0.327252 0.741232 0.999852 0.0558543 0.888563 0.999978 0.81

Figure 5: The representative results of the proposed method. For all meshes, the left (or top) image shows the input mesh

while the right (or bottom) image is the optimized mesh with our method.

is limited. Table 3 summarizes optimization results

for various meshes optimized using different values

of τ. The best quality measures are highlighted in

bold. As can be seen in Table 3, there is not a uni-

versally good τ value for different meshes. Thus, we

leave this threshold value for the user to decide.

5 CONCLUSION

This paper presents a new quality improvement

method for 2D quad meshes with open boundaries.

Our method is based on the optimization of the con-

ﬁguration of an embedded polygon constructed for

each interior vertex. A feature preserving boundary

optimization is also introduced. We have applied our

framework to a number of 2D quad meshes to eval-

uate its effectiveness. We also compare our method

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

182

Table 2: Statistics of Scaled Jacobian measures of various meshes optimized with different methods. The best quality

measures of all results are highlighted in bold. The best quality measures of the results produced by methods with ﬁxed

boundaries are highlighted in blue.

Xu and Newman Laplacian Mesquite Ours w/o bound Ours w bound

Model Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled

1 hole 0.558289 0.899476 0.640883 0.899255 0.643728 0.902054 0.614279 0.8973 0.97646 0.987127

2 holes 0.166075 0.79649 -0.0158924 0.773395 0.0205342 0.774537 0.0811026 0.777924 0.742937 0.926261

2 holes 2 squares -0.556381 0.752143 -0.453973 0.735066 -0.487485 0.738351 -0.15848 0.782632 0.197108 0.84893

3 holes 1 square 0.559189 0.842663 0.538608 0.833651 0.57367 0.838737 0.563918 0.83856 0.724021 0.92366

6 holes 2 squares -0.164996 0.761158 -0.36941 0.749143 -0.28024 0.760459 -0.117874 0.785367 0.296134 0.880297

8 holes -0.513426 0.767459 -0.544005 0.765766 -0.47977 0.772616 -0.147611 0.788872 0.5811 0.892645

10 holes -0.0984454 0.783175 -0.246311 0.675738 -0.188317 0.686278 -0.201791 0.708256 0.411444 0.841136

patch 5 -0.0247695 0.776693 -0.176222 0.750139 -0.15496 0.759693 -0.0813105 0.818403 0.360867 0.838986

patch 7 -0.528536 0.724826 -0.147158 0.727404 -0.556283 0.728614 0.276863 0.789242 0.312207 0.79753

mazewheel 3 -0.458242 0.745167 -0.699953 0.735654 -0.653876 0.742469 -0.65144 0.761198 0.0558543 0.888563

Table 3: Effect of different threshold (τ) values on mesh optimization using our method on a number of representative

meshes. The best quality measures are highlighted in bold.

τ = 0.1 τ = 0.01 τ = 0.001 τ = 0.0001 τ = 0.00001

Model Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled Min. Scaled Avg. Scaled

2 holes 2 squares 0.197108 0.847687 0.197108 0.849726 0.197108 0.849073 0.197108 0.84893 0.197108 0.84893

3 holes 1 square 0.720105 0.920828 0.721011 0.923883 0.723246 0.923717 0.724021 0.92366 0.724161 0.923631

6 holes 2 squares 0.318459 0.882613 0.320006 0.880864 0.298935 0.880412 0.296134 0.880297 0.29614 0.880295

8 holes 0.58685 0.891942 0.582073 0.892883 0.580989 0.89271 0.5811 0.892645 0.581242 0.892652

10 holes 0.413944 0.843625 0.411547 0.841411 0.411444 0.841136 0.411444 0.841136 0.449502 0.841136

patch 7 0.251875 0.794919 0.303568 0.797214 0.303568 0.797214 0.312207 0.79753 0.312207 0.79753

mazewheel 3 0.0066067 0.88877 0.0411956 0.88851 0.0518666 0.888541 0.0558543 0.888563 0.0566735 0.888568

Figure 6: Comparison of our method (right) with Xu and

Newman’s approach (left). The arrows indicate places that

the mesh quality in the results of Xu and Newman’s ap-

proach is less desired. The 2 holes with 2 square mesh is

shown. Red color indicate quad elements with low Jaco-

bian measures.

Figure 7: Comparison with conventional Laplacian smooth-

ing with cotangent weights and the Laplacian smoothing

implemented in Mesquite. The patch 7 mesh is shown. Red

color indicate quad elements with low Jacobian measures.

The arrows highlight area with elements that other methods

fail to improve, while our method can.

with a number of the state-of-the-art quad mesh opti-

mization methods. The comparison shows that our

method outperforms the existing methods in most

cases, especially for meshes with many complicated

boundary features.

Limitation and Future Work. Even though our

method is simple and easy to implement and has

shown outperforming many state-of-the-art methods

in most cases, our method cannot guarantee to always

produce inversion-free mesh. As shown in the inset,

our method fails to untangle an inverted element in

the mazewheel mesh. A closer look shows that three

vertices of this inverted element are on the boundary,

and two of them are corners, thus, ﬁxed. These three

vertices form a concave conﬁguration with an inner

angle larger than 180

◦

In fact, no smoothing method can ﬁx this unless

this boundary is modiﬁed to make the angle smaller

than 180

◦

. Alternatively, a local connectivity modiﬁ-

cation may help mitigate this situation, which is be-

yond the scope of this work.

An Embedded Polygon Strategy for Quality Improvement of 2D Quadrilateral Meshes with Boundaries

183

Our current framework provides two different

ways for boundary optimization. In the future, it will

be more ideal to have an automatic way to decide

the proper boundary optimization based on the input

mesh conﬁguration without user intervention.

ACKNOWLEDGEMENTS

We thank the anonymous reviewers for their valuable

feedback. This research was partially supported by

NSF IIS 1553329.

REFERENCES

Ben-Chen, M., Gotsman, C., and Bunin, G. (2008). Con-

formal ﬂattening by curvature prescription and metric

scaling. In Computer Graphics Forum, volume 27,

pages 449–458. Wiley Online Library.

Bommes, D., L

evy, B., Pietroni, N., Puppo, E., Silva, C.,

Tarini, M., and Zorin, D. (2013). Quad-mesh gener-

ation and processing: A survey. In Computer Graph-

ics Forum, volume 32, pages 51–76. Wiley Online Li-

brary.

Bommes, D., Zimmer, H., and Kobbelt, L. (2009). Mixed-

integer quadrangulation. ACM Trans. Graph., 28(3).

Brewer, M. L., Diachin, L. F., Knupp, P. M., Leurent, T.,

and Melander, D. J. (2003). The Mesquite Mesh Qual-

ity Improvement Toolkit. In Shepherd, J., editor, IMR.

Campen, M. (2017). Partitioning surfaces into quadrilat-

eral patches: a survey. In Computer Graphics Forum,

volume 36, pages 567–588. Wiley Online Library.

Canann, S. A., Tristano, J. R., Staten, M. L., et al. (1998).

An approach to combined laplacian and optimization-

based smoothing for triangular, quadrilateral, and

quad-dominant meshes. In IMR, pages 479–494. Cite-

seer.

Daniels, J., Silva, C. T., and Cohen, E. (2009). Localized

quadrilateral coarsening. In Computer Graphics Fo-

rum, volume 28, pages 1437–1444. Wiley Online Li-

brary.

Docampo-Sanchez, J. and Haimes, R. (2019). Towards fully

regular quad mesh generation. In AIAA Scitech 2019

Forum, page 1988.

Fang, X., Bao, H., Tong, Y., Desbrun, M., and

Huang, J. (2018). Quadrangulation through morse-

parameterization hybridization. ACM Transactions on

Graphics (TOG), 37(4):92.

Gao, X., Deng, Z., and Chen, G. (2015). Hexahedral mesh

re-parameterization from aligned base-complex. ACM

Transactions on Graphics (TOG), 34(4):1–10.

Gao, X., Huang, J., Xu, K., Pan, Z., Deng, Z., and Chen,

G. (2017). Evaluating hex-mesh quality metrics via

correlation analysis. In Computer Graphics Forum,

volume 36, pages 105–116. Wiley Online Library.

Ji, Z., Liu, L., and Wang, G. (2005). A global lapla-

cian smoothing approach with feature preservation. In

Ninth International Conference on Computer Aided

Design and Computer Graphics (CAD-CG’05), pages

6–pp. IEEE.

Kim, J., Choi, J., and Kang, W. (2020). A data-driven ap-

proach for simultaneous mesh untangling and smooth-

ing using pointer networks. IEEE Access, 8:70329–

70342.

Kim, J., Shin, M., and Kang, W. (2015). A derivative-

free mesh optimization algorithm for mesh quality im-

provement and untangling. Mathematical Problems in

Engineering, 2015.

ebay, P. P., Thompson, D. C., Shepherd, J., Knupp, P. M.,

Lisle, C., Magnotta, V., and Grosland, N. M. (2007).

New Applications of the Verdict Library for Standard-

ized Mesh Veriﬁcation Pre, Post, and End-to-End Pro-

cessing. In Brewer, M. L. and Marcum, D. L., editors,

IMR, pages 535–552. Springer.

Pietroni, N., Tarini, M., and Cignoni, P. (2009). Almost

isometric mesh parameterization through abstract do-

mains. IEEE Transactions on Visualization and Com-

puter Graphics, 16(4):621–635.

Prasad, T. (2018). A comparative study of mesh smooth-

ing methods with ﬂipping in 2D and 3D. PhD thesis,

Rutgers University-Camden Graduate School.

Sorkine, O. (2005). Laplacian Mesh Processing. In

Chrysanthou, Y. and Magnor, M., editors, Eurograph-

ics 2005 - State of the Art Reports. The Eurographics

Association.

Tarini, M., Pietroni, N., Cignoni, P., Panozzo, D., and

Puppo, E. (2010). Practical quad mesh simpliﬁcation.

In Computer Graphics Forum, volume 29, pages 407–

418. Wiley Online Library.

Tarini, M., Puppo, E., Panozzo, D., Pietroni, N., and

Cignoni, P. (2011). Simple quad domains for ﬁeld

aligned mesh parametrization. In Proceedings of the

2011 SIGGRAPH Asia Conference, pages 1–12.

Vartziotis, D. and Himpel, B. (2014). Laplacian smoothing

revisited. arXiv preprint arXiv:1406.4333.

Viertel, R. and Osting, B. (2019). An approach to quad

meshing based on harmonic cross-valued maps and

the ginzburg–landau theory. SIAM Journal on Scien-

tiﬁc Computing, 41(1):A452–A479.

Xu, H. and Newman, T. S. (2005). 2d fe quad mesh smooth-

ing via angle-based optimization. In International

Conference on Computational Science, pages 9–16.

Springer.

Xu, K., Gao, X., and Chen, G. (2018). Hexahedral

mesh quality improvement via edge-angle optimiza-

tion. Computers & Graphics, 70:17–27.

Zhang, Y., Bajaj, C. L., and Xu, G. (2005). Surface

Smoothing and Quality Improvement of Quadrilat-

eral/Hexahedral Meshes with Geometric Flow. In

Hanks, B. W., editor, IMR, pages 449–468. Springer.

Zhou, T. and Shimada, K. (2000). An angle-based approach

to two-dimensional mesh smoothing. IMR, 2000:373–

384.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

184