BASH: Biomechanical Animated Skinned Human for Visualization of

Kinematics and Muscle Activity

R. Schleicher

, M. Nitschke

, J. Martschinke

, M. Stamminger

, B. M. Eskoﬁer

, J. Klucken

and

A. D. Koelewijn

Machine Learning and Data Analytics Lab, Department Artiﬁcial Intelligence in Biomedical Engineering (AIBE),

Friedrich-Alexander-Universit

at Erlangen-N

urnberg (FAU), Germany

Chair of Visual Computing, Department of Computer Science, Friedrich-Alexander-Universit

at Erlangen-N

urnberg

(FAU), Germany

Department of Molecular Neurology, University Hospital Erlangen, Friedrich-Alexander-Universit

at Erlangen-N

urnberg

(FAU), Germany

Keywords:

Biomechanics, Surface Visualization, Animation, Statistical Human Model, Kinematics, Muscle Activity.

Abstract:

Biomechanical analysis of human motion is applied in medicine, sports and product design. However, visual-

izations of biomechanical variables are still highly abstract and technical since the body is visualized with a

skeleton and muscles are represented as lines. We propose a more intuitive and realistic visualization of kine-

matics and muscle activity to increase accessibility for non-experts like patients, athletes, or designers. To this

end, the Biomechanical Animated Skinned Human (BASH) model is created and scaled to match the anthro-

pometry deﬁned by a musculoskeletal model in OpenSim ﬁle format. Motion is visualized with an accurate

pose transformation of the BASH model using kinematic data as input. A statistical model contributes to a

natural human appearance and realistic soft tissue deformations during the animation. Finally, muscle activity

is highlighted on the model surface. The visualization pipeline is easily applicable since it requires only the

musculoskeletal model, kinematics and muscle activation patterns as input. We demonstrate the capabilities

for straight and curved running simulated with a full-body musculoskeletal model. We conclude that our visu-

alization could be perceived as intuitive and better accessible for non-experts than conventional skeleton and

line representations. However, this has to be conﬁrmed in future usability and perception studies.

1 INTRODUCTION

The progress in biomechanics has brought vast op-

portunities to analyse human movement (Ezati et al.,

2019). Biomechanical simulations enable a recon-

struction of recorded motion or prediction of a novel

movement (Ezati et al., 2019; Falisse et al., 2019; Lin

and Pandy, 2017; Nitschke et al., 2020). Humans

are represented with physics-based musculoskeletal

models to calculate biomechanical variables such as

joint angles, joint moments and muscle activation. As

the methodology continues to develop, applications

in medicine, sports and product design are emerg-

ing. Hence, multiple user groups besides biomechan-

ical engineers will inspect and interpret biomechan-

ical variables in future. For example, a visualiza-

tion of Parkinson-speciﬁc motion might be exploited

for modern patient education (Udow et al., 2018)

or for visual feedback for gait retraining (Richards

et al., 2018; Van den Noort et al., 2015). As alter-

native to video analysis in sports which is restricted

to a capture volume and might not always be avail-

able, motion could be reconstructed from inertial sen-

sor data using musculoskeletal simulation (Dorschky

et al., 2019b) and later be visualized for analysis

with a human model. This reconstruction has the

additional advantages that internal variables, such as

movement-related forces, could be analysed for in-

jury prevention (Bencke et al., 2018; Vannatta and

Kernozek, 2015). Although musculoskeletal simu-

lations can support product design of, for example,

prostheses (Fey et al., 2012; Koelewijn and van den

Bogert, 2016) or shoes (Dorschky et al., 2019a), they

lack a proper tool to communicate design decisions

with non-experts. In order to inspect and interpret

the simulated biomechanical variables, a visualization

has to be intuitive and accessible for non-experts like

patients, athletes, or designers.

1.1 Related Work

A wide variety of biomechanical simulation frame-

works exists for modelling and analysis of mus-

culoskeletal models. AnyBody (Damsgaard et al.,

Schleicher, R., Nitschke, M., Martschinke, J., Stamminger, M., Eskoﬁer, B., Klucken, J. and Koelewijn, A.

BASH: Biomechanical Animated Skinned Human for Visualization of Kinematics and Muscle Activity.

DOI: 10.5220/0010210600250036

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 1: GRAPP, pages

25-36

ISBN: 978-989-758-488-6

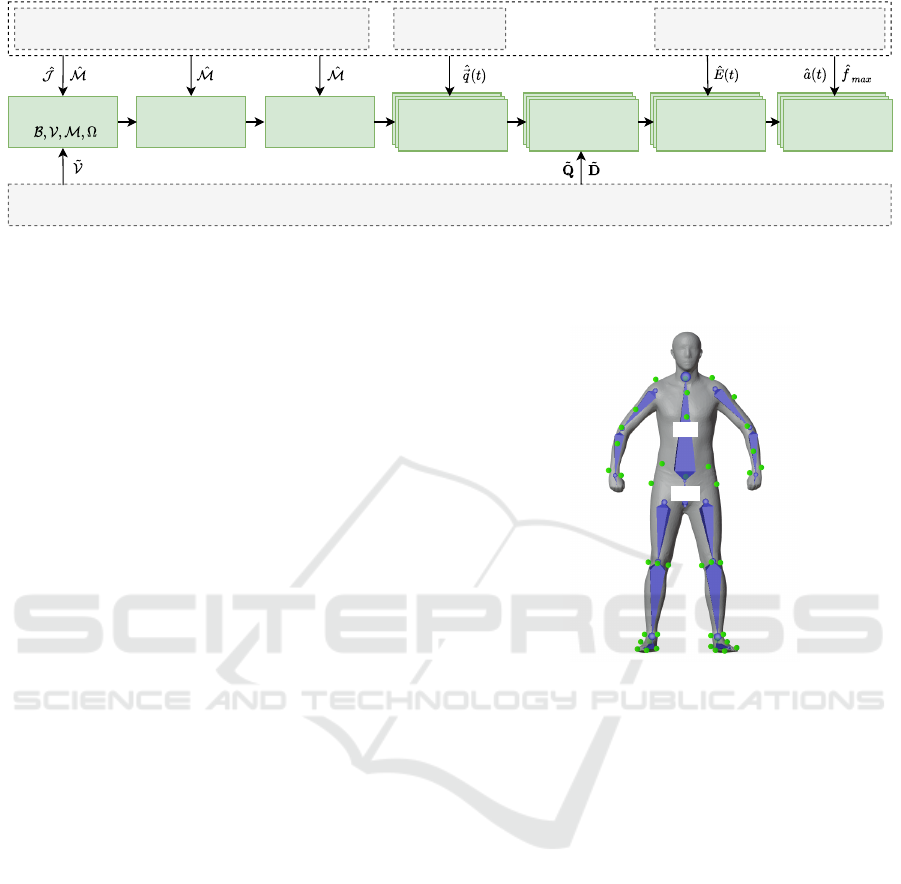
Figure 1: Proposed processing pipeline to visualize kinematics and muscle activity of biomechanical simulations using a

skinned human model. From left to right it shows the musculoskeletal model visualized with OpenSim (Seth et al., 2018)

and the proposed processing steps: creation of the BASH baseline model, scaling, initial pose matching, pose transformation,

statistical deformation, and visualization of muscle activity.

2006), D-Flow (Geijtenbeek et al., 2011; Van den

Bogert et al., 2013) and LifeModeler (McGuan,

2001) are commercial software packages and Open-

Sim (Delp et al., 2007; Seth et al., 2018) is an open-

source software package. OpenSim is reaching a

worldwide and rapidly growing community due to its

accessibility (Seth et al., 2018) and its support for for-

ward dynamics to predict novel movements. Abella

and Demircan (2019) incorporated musculoskeletal

models derived from OpenSim into the Unity envi-

ronment to simultaneously track and analyse motion.

These software solutions focus on the simulation

functionality and on an accurate representation of the

modelled body segments and muscle tendon units

(MTUs). Hence, they provide an interactive interface

displaying bones only as simple geometric shapes and

muscles as two-dimensional (2D) line representations

(see for example the OpenSim visualization in Fig-

ure 1, left). Muscle activity is shown by color coding

of the muscle pathways. Although these abstract and

technical visualizations are well suited for users with

biomechanical background, they are not appropriate

for non-experts. The visualization of musculoskele-

tal simulations was integrated into a computer-aided

design environment to facilitate user-centered design,

but the model was still visualized with a skeleton and

muscle pathways (Kr

uger and Wartzack, 2015).

Instead of using muscle pathways, muscles can be

modelled with volumetric geometries to increase ac-

curacy of the simulations or to study muscle deforma-

tion (Blemker and Delp, 2005; Maurice et al., 2009;

Peeters and Pronost, 2014; Teran et al., 2003; Teran

et al., 2005). However, volumetric muscle models are

rarely used in biomechanical simulations since com-

plexity of model creation and simulation increases

considerably. Others include volumetric muscle mod-

els only for visualization of computed muscle activ-

ity to increase interpretability without using them for

simulation (Pronost et al., 2011; Van den Bogert et al.,

2013). Pronost et al. (2011) provided an OpenSim

plugin with predeﬁned muscle geometries that can be

assigned to the MTUs of the musculoskeletal model.

However, none of these visualizations for biomechan-

ical analysis uses three-dimensional (3D) skinned hu-

man models. An overlay of volumetric muscle shapes

on a video stream for color coding of muscle activ-

ity (Murai et al., 2010) might be closer to reality

than the existing skeletal representations. This ap-

proach operates in real-time based on electromyog-

raphy measurements. Nevertheless, it is not appli-

cable if no video recording is available, which is the

case when motion is reconstructed from inertial sen-

sor data or when novel motions are predicted. Hence,

3D skinned human models might be the most intuitive

visualization of reconstructed and predicted biome-

chanical movements especially for non-specialists.

In computer graphics, biomechanical and physi-

cal knowledge is also used to increase realism of hu-

man animations. Muscle and soft tissue deforma-

tion are modelled with mass-spring systems, ﬁnite el-

ement method, or ﬁnite volume method (Aubel and

Thalmann, 2001; Lee et al., 2009; Lee et al., 2012;

Murai et al., 2017; Sueda et al., 2008). Geometries

have to be modelled by hand or based on medical

image data and simulations often have high compu-

tational demands. Hence, these methods are usually

only applied for single muscles or body parts. Alter-

natively, human surface models can be directly an-

imated with data-driven methods without explicitly

taking the deformation of underlying structures into

account (Lee et al., 2012). An elegant way to cre-

ate a virtual skin envelope is to use statistical para-

metric shape models, which are often used for ani-

mation of human subjects in motion (Cheng et al.,

2018). Anguelov et al. (2005) ﬁrst implemented a

parametric model for pose-induced soft tissue defor-

mation and body shape variation to perform Shape

Completion and Animation of PEople (SCAPE). Pa-

rameters are learned from 3D full-body scans of var-

ious poses and people. They separate rigid (skele-

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

tal) and non-rigid deformations to simplify mathemat-

ically formulation and to accelerate the learning al-

gorithm. However, the SCAPE model determines the

soft tissue deformation based on only a static pose and

does not take muscle activation or dynamics into ac-

count. The Dyna (Pons-Moll et al., 2015) model also

reﬂects dynamic soft tissue deformations caused by

motion. Nevertheless, the statistical surface models

used in computer graphics lack the connection to tra-

ditional biomechanical simulations of musculoskele-

tal models. Torque-driven animation is intensively in-

vestigated to obtain authentic human motion instead

of prescribing the motion (Geijtenbeek and Pronost,

2012; Jiang et al., 2019). But, in contrast to mus-

cle control, torque control does not generate biologi-

cally reasonable motion since human torques are not

limited to a constant range and the energy function

minimizing torques does not reﬂect the human mus-

culoskeletal system (Jiang et al., 2019).

1.2 Purpose

In this work, we aim to develop a method to ani-

mate 3D human surface models for biomechanical

analysis. We propose the Biomechanical Animated

Skinned Human (BASH) model which provides an

animated skinned visualization of a musculoskeletal

model deﬁned in the commonly used OpenSim for-

mat (Seth et al., 2018) without requiring any addi-

tional data. The body proportions of the virtual hu-

man are automatically adapted to match the subject-

speciﬁc dimensions of the musculoskeletal model.

Kinematic coordinates are processed to apply pose

transformation and thus to animate the skin envelope

in order to reﬂect a movement. The statistical model

SCAPE (Anguelov et al., 2005) should yield natu-

ral human appearance and realistic soft tissue defor-

mations. Furthermore, muscle activity of underlying

MTUs is highlighted on the surface which enables a

kinetic analysis. We evaluate the pipeline with ten

full-body musculoskeletal models scaled to each sub-

ject and simulated data of straight and curved running.

Though this assumption has to be proven in further

studies, we assume that our representation is more in-

tuitive than conventional visualizations and therefore

more accessible, especially for users without biome-

chanical background.

1.3 Outline

The processing pipeline is summarized in Figure 2.

In Section 2, the biomechanical data and the SCAPE

model are introduced. In Section 3, the generation of

the baseline version of the proposed BASH model is

described. Section 4 explains how the BASH model

was matched to a subject-speciﬁc musculoskeletal

model. Section 5 covers the animation and statisti-

cal deformation of the surface model. The visual-

ization of muscle activity is presented in Section 6.

The results of the experiments and analyses from

Section 7 are evaluated and discussed in Section 8.

The paper concludes with a short summary and out-

look in Section 9. The code is publicly available at

https://github.com/mad-lab-fau/BASH-Model.

2 VISUALIZATION INPUT

A musculoskeletal model, kinematics and muscle ac-

tivity serve as biomechanical input for the visualiza-

tion (see Figure 2). Since OpenSim (Seth et al., 2018)

is a widely used open-source software for muscu-

loskeletal simulations, its data format and framework

is used. All variables belonging to the biomechani-

cal data are denoted in this paper with a hat ˆ·. The

musculoskeletal model consists of a skeletal struc-

ture where bone segments are connected via moving

joints

J = {

,...,

−1

}. Joints can be manipulated

using generalized coordinates

~q(t), thus deﬁning the

kinematics of the model over time t. Virtual mark-

ers

M = {

,...,

−1

} are commonly attached to

the musculoskeletal model for subject-speciﬁc model

scaling and inverse kinematics. Muscles are described

by MTUs with 2D pathways

E(t) and maximum iso-

metric forces

max

, among other parameters. Forces

acting during a movement are encoded as muscle ac-

tivation ˆa(t) of a speciﬁc MTU.

To obtain a realistic surface representation of

the musculoskeletal model, the human statistical

SCAPE (Anguelov et al., 2005) model is used as ba-

sis. SCAPE, the ﬁrst established method of its kind,

provides a sophisticated framework for our approach.

All variables belonging to the SCAPE model are de-

noted in this paper with a tilde ˜·. Training of pose

parameters

Q and shape parameters

D was performed

on full-body 3D scans from a large data set (Yang

et al., 2014). Additionally, training of the shape co-

efﬁcients was reﬁned using further 3D scans (Hasler

et al., 2009b; Hasler et al., 2009a; Hasler et al., 2010).

In order to eliminate any pose deviations for the shape

learning, a volume aware non-rigid mesh registration

was performed (Colaianni et al., 2014). Training gen-

erates a template mesh

V which corresponds to the

envelope of a virtual person in static pose with aver-

age shape parameters.

BASH: Biomechanical Animated Skinned Human for Visualization of Kinematics and Muscle Activity

Musculoskeletal Model Muscle DataKinematics Biomechanical Data

SCAPE Model

Scaling of Body

Proportions

Initial Pose

Matching

Pose

Transformations

into SCAPE Space

Area of

Influence

Intensity

Visualization

Baseline Model

Pose

Transformations

Pose

Transformations

into SCAPE Space

Transformations

into SCAPE Space

Area of

Influence

Area of

Influence

Intensity

Visualization

Intensity

Visualization

Figure 2: Processing pipeline to visualize kinematics and muscle activity using a skinned human surface model. The input of

the pipeline (grey rectangles) and the processing steps (green rectangles) are explained in the following sections.

3 BASELINE MODEL

The simulated generalized coordinates of the mus-

culoskeletal model cannot directly be applied to the

SCAPE model due to differences in skeletal struc-

tures, body proportions and initial poses which would

lead to an incorrect visualization. In particular, the

disparate deﬁnition of the skeletal structure of both

models is a challenge. The BASH model is developed

to overcome the differences and to generate an accu-

rate yet realistic 3D surface representation of the sim-

ulated musculoskeletal motion. Figure 3 illustrates

the three components which deﬁne the BASH model:

• Mesh geometry to represent the model’s surface

and virtual appearance of the skinned human

• Articulated skeleton to enable surface deforma-

tions using the interconnected bones

• Marker attachments to create a clear relation-

ship to the musculoskeletal model for scaling of

body proportions and initial pose matching

The SCAPE template mesh

V is used as the

BASH geometry V with vertices ~v. A skeletal ar-

mature with the same hierarchical composition as the

musculoskeletal model is placed into the mesh by rig-

ging the bones B = {B

,...,B

−1

} as deﬁned by

the joints

J of the musculoskeletal model. Devia-

tions in position and dimensions can be neglected

since body proportions will be scaled in a separate

step. Automatic computed skinning weights Ω

{ω

,...,ω

Ω

−1

} connect the skeleton and the mesh

geometry (Kavan et al., 2009). The weight ω

deter-

mines by how much the transformation of a bone B

is transferred to its assigned vertices. The maximum

number of inﬂuencing bones for one vertex is set to

Ω

= 4 which is common in character animation due

to efﬁciency in hardware (McLaughlin et al., 2011).

Improperly assigned weights are corrected manually.

Finally, virtual markers M = {~m

,...,~m

−1

} cor-

humerus_l

ulna_l

hand_l

radius_l

torso

pelvis

humerus_r

ulna_r

hand_r

radius_r

tibia_l

femur_lfemur_r

tibia_r

talus_l

calcn_l

toes_l

talus_r

calcn_r

toes_r

Figure 3: The conceptual design of the generic BASH

model on the basis of SCAPE (Anguelov et al., 2005). It in-

corporates a surface mesh, an underlying articulated skele-

ton and attached marker points.

responding to the markers

M of the musculoskeletal

model are attached to the BASH model at landmark

points near the surface to establish a relationship be-

tween the models. The markers are used to determine

body proportions and to match the initial poses. The

resulting generic version of the BASH model reﬂects

a non-scaled musculoskeletal model with a speciﬁc

anatomical structure.

4 MODEL MATCHING

The baseline model has to be matched to a scaled ver-

sion of the musculoskeletal model in its initial pose.

This preprocessing step is performed once for a sub-

ject before animation.

4.1 Scaling of Body Proportions

In musculoskeletal modelling, individual variations in

body proportions are taken into account by adjust-

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

ing the body segments using recorded marker posi-

tions (Delp et al., 2007). Using the same principle,

we match the subject’s anthropometry and ensure a

realistic visualization by scaling segment sizes based

on the deﬁned virtual marker positions (see Figure 4).

For each bone B, an uniform scaling transformation

is determined as average ratio between marker

distances of the musculoskeletal model and of the

generic BASH model.

Figure 4: 3D positions of attached markers

~m and ~m are

used to scale body segments.

However, the scaling with matrix S

is not ap-

plied directly in bone space since a change of bone

size should only be applied to a particular bone B and

not inherited through the skeletal hierarchy. There-

fore, the new position N

of a bone B is computed by

propagation through the skeleton starting at the root

node:

= N

parent

· N

· S

−1

parent

, (1)

where N

is the 3D state of the bone before scal-

ing. Scaling of the parent bone B

parent

is reversed

by multiplying the inverse scaling matrix S

−1

parent

avoid inheritance. For the root node, N

parent

and

−1

parent

are the identity matrix. To scale the generic

mesh, the new position N

is multiplied by the in-

verse offset matrix O

−1

which denotes the projec-

tion from bone space B to world space W . The result-

ing transformation matrices are applied to the markers

and vertices of the generic mesh. Consequently, lin-

ear blend skinning shifts all vertices ~v by the extent

of the deﬁned skinning weights Ω

which simultane-

ously prevents hard borders and noticeable gaps be-

tween limbs (Magnenat-Thalmann et al., 1988).

4.2 Initial Pose Matching

Within OpenSim, pose transformations are speciﬁed

by generalized coordinates. However, the relation be-

tween the initial pose of the musculoskeletal model

and the scaled BASH model is unknown and has to be

established before deploying any pose transformation.

This relation is described by a change of basis, i.e. by

a projection P

from the coordinate system of joint

of the musculoskeletal model to the corresponding co-

ordinate system of bone B of the scaled BASH model.

The generalized coordinates

~q deﬁne the pose of the

musculoskeletal model which matches the initial pose

of the scaled BASH model. They are obtained by in-

verse kinematics using the OpenSim application pro-

gramming interface (API) (version 4.0) (Seth et al.,

2018). In inverse kinematics, the sum of squared dis-

tances between corresponding marker pairs of the two

models is minimized. For the resulting pose, the pro-

jection matrix P

is received from the OpenSim API

as global transformation of the bones with respect to

the ground. Applying the inverse transformations to

the scaled BASH model causes a deformation of the

mesh via skinning weights to match the pose of the

musculoskeletal model.

5 ANIMATION AND

STATISTICAL DEFORMATION

In order to create an animation of the simulated mus-

culoskeletal model, a series of transformations is ap-

plied to the scaled BASH model for each time frame

t of the motion sequence.

5.1 Pose Transformations

Traditional character animation techniques are used to

obtain an animated surface representation of the input

kinematics. The afﬁne transformation

(t) contains

the translation and the rotation deﬁned by the gen-

eralized coordinates ~q(t) given in the OpenSim mo-

tion ﬁle. For each frame, the input transformation

(t) can be directly applied to the bones of the scaled

BASH model in the global coordinate system due to

prior scaling and initial pose matching. The surface

deformation was achieved by linear blend skinning

with previously computed skinning weights. As a re-

sult, the pose transformed BASH model contained the

aggregated animation based on the given movement

of the musculoskeletal model.

5.2 Transformations into SCAPE Space

Statistical transformations introduced in the SCAPE

model (Anguelov et al., 2005) are performed for each

time frame t after the pose transformation to achieve

realistic soft tissue deformations and therefore en-

hance the natural appearance. Before applying the

statistical transformations, the rigid part rotations R

BASH: Biomechanical Animated Skinned Human for Visualization of Kinematics and Muscle Activity

of all body parts

B have to be determined in order

to deﬁne the current pose in the SCAPE space. The

original method proposed by Anguelov et al. (2005)

is adapted to operate without a full body scan of the

target person by using the pose transformed BASH

model from the previous processing step as reference

instead. All vertices of the mesh V serve as refer-

ence points to determine the current pose in corre-

spondence to the template mesh

V which requires

an identical geometric topology of all meshes in the

SCAPE space. The rigid registration of two corre-

sponding body parts

B with N

vertices is described as

minimization of the root mean square error (RMSE):

min

−1

∑

i=0

−~v

, (2)

where

~v and~v are the vertices of the SCAPE template

mesh and the pose transformed BASH model, respec-

tively. This optimization is solved as constrained Pro-

crustes problem (Sch

onemann, 1966) using the Kab-

sch algorithm (Kabsch, 1976) and performing singu-

lar value decomposition (Golub and Reinsch, 1970).

The obtained optimal rotations, i.e. the nearest or-

thogonal matrices, describe the rigid part transforma-

tions R

of the SCAPE model.

The main feature of SCAPE is a realistic soft tis-

sue deformation which is achieved by pose-induced

transformations

affecting the shape of each face

f on the mesh based on training data and the cur-

rent pose deﬁned by R

. The rotations of adja-

cent joints

and the learned regression vector

f ,i, j

= ( ˜a

, ˜a

)

from the SCAPE

framework are used to build the matrix:

[i, j] =



∆



i, j, f

, (3)

where i and j are the row and column indices, re-

spectively.

∆

= (∆

,∆

)

denotes the twist vec-

tor in angle-axis representation (Ma et al., 2004) of

a joint rotation R

= R

· R

composed of adjacent

rigid body parts

and

. The body shape is omit-

ted within this paper. Hence, the average shape of

the trained SCAPE template mesh is used by setting

shape deformation matrix

to the identity matrix

for all faces.

The geometry of the new mesh is retrieved by

minimizing the following non-linear optimization

problem to avoid inconsistencies within the mesh in-

stead of applying the rigid part rotations R

, pose

dependent deformations

, and shape dependent de-

formations

directly to the vertices~v:

min

−1

∑

f =0

∑

i=1,2

f ,i

− (~v

f ,0

−~v

f ,i

(4)

The two edges~v

f ,0

−~v

f ,i

with i = 1, 2 span the face f

built of the three vertices ~v

f ,0

, ~v

f ,1

, and ~v

f ,2

Since the SCAPE framework omits the global po-

sition and orientation of the model in space for com-

putational reasons, it has to be restored. A constrained

orthogonal Procrustes problem is solved globally to

transformed mesh.

6 VISUALIZATION OF MUSCLE

ACTIVITY

In addition to the animation of the model, muscle ac-

tivation is visualized on the model’s surface. The area

of inﬂuence and the intensity are computed dynami-

cally during run-time for the current time frame t.

6.1 Area of Inﬂuence

In the musculoskeletal model, a muscle

F is charac-

terized by a MTU with the 2D pathway

(t). The 3D

locations of the connected line segments are deﬁned

by multiple points

~p ﬁxed to the articulated skele-

ton. Before visualizing the muscle activity, a map-

ping from the 2D muscle pathways to the surface of

the animated BASH model is established by ﬁnding

the smallest distance from an underlying MTU to the

model’s surface. The perpendicular distance d is the

shortest way from the line segment deﬁned by

and

i+1

to a vertex. Vertices with a distance d smaller

than a threshold C

maxDist

are included into the area of

inﬂuence of the particular muscle.

6.2 Intensity Visualization

The identiﬁed areas of inﬂuence are used to highlight

the muscle activation ˆa

(t) on the surface via color

coding. The force of the muscle contraction scales

linearly with the muscle activation and the maximum

isometric force

max

(Thelen, 2003). Hence, the

measure i

(t) is composed as follows:

(t) =

maxMeasure

· ˆa

(t) ·

max

. (5)

The constant C

maxMeasure

is introduced to normalize

by the maximum possible value that concentrates on a

point. This enables an objective comparison of move-

ment visualizations of distinct subjects with different

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

muscular constitutions. For each vertex, the measures

(t) of all inﬂuencing muscles are accumulated and

added to the red color channel of the mesh. Due to the

implementation in the fragment shader, color values

are interpolated across the faces resulting in smooth

transitions at the boundaries and overlapping areas of

the inﬂuencing muscle regions.

7 EXPERIMENTS AND

ANALYSES

We conducted experiments and analyses to conﬁrm

the functionality of the visualization approach using

a full-body musculoskeletal model (Nitschke et al.,

2020). The comprehensive musculoskeletal structure

included 20 joints, 92 MTUs in the lower body and

46 markers.

The scaling functionality and the initial pose

matching were evaluated with ten male test sub-

jects. The generic musculoskeletal model (Nitschke

et al., 2020) was scaled using the OpenSim scaling

tool (Delp et al., 2007) to match the marker data of

static trials of nine subjects (Dorschky et al., 2019b)

(subject A to I). Additionally, an already scaled mus-

culoskeletal model was used as subject J (Nitschke

et al., 2020). To evaluate the scaling, the height H of

the scaled BASH model was determined as the dis-

tance between the smallest and greatest y-coordinate

of the mesh in the initial pose. The height should cor-

relate with the body height of the subject.

The pose transformation and animation of the

BASH model was analysed for subject J with simu-

lated kinematics of straight running and curved run-

ning with 50 time samples available in the OpenSim

ﬁle format (Nitschke et al., 2020). The proposed sur-

face visualization of the muscle activity was tested

with corresponding simulated muscle activation pat-

terns of the motions and compared to the line repre-

sentation in the OpenSim environment.

8 RESULTS AND DISCUSSION

Figure 5 presents the ﬁnal surface visualization in

comparison to the visualization from OpenSim (Seth

et al., 2018). In the following, the individual process-

ing and transformation steps are discussed separately.

8.1 Scaling of Body Proportions

The scaling of body proportions is an essential step

for a representative visualization. An incorrect model

(a) (b) (c)

Figure 5: Final visualization of the kinematics including

the muscle activation on the surface compared to the Open-

Sim (Seth et al., 2018) representation as reference. (a) and

(b) show frontal and sagittal view of simulated straight run-

ning, respectively. (c) shows superimposed frames of simu-

lated curved running.

size would lead to incorrect postures and would in-

ﬂuence the analysis. For example, the ground contact

time (Mooses et al., 2018) or foot clearance (Begg

et al., 2007) are of interest for biomechanical analy-

ses of gait, but would be erroneous.

Figure 6 shows the outcomes of the body part

scaling for the ten subjects. The height H of the

BASH model is greater than the actual body height

for all subjects except for subject D and J. The mean

and standard deviation of the absolute error is 6.7 ±

4.8cm. Nevertheless, the proposed scaling is bene-

ﬁcial since the height of the scaled model is always

closer to the body height than the generic model. We

propose uniform scaling to produce robust result even

when few markers are present. However, non-uniform

scaling with individual scale factors for each dimen-

sion might be beneﬁcial.

Nevertheless, the comparison of heights has to be

interpreted with caution since marker placement or

scaling of the musculoskeletal model can introduce

errors as well. Furthermore, the estimated height H

of the BASH model depends on the initial pose and

might change when the model is transformed into

SCAPE space. Also the skinning weights inﬂuence

the shape and thus the scaling and height.

8.2 Initial Pose Matching

The quality of the mapping P

between the initial

pose of the musculoskeletal model and the scaled

BASH model inﬂuences the accuracy of the following

pose transformations. Visual inspection shows that

the BASH model is brought into a pose very similar to

the pose of the musculoskeletal model (see Figure 7).

However, the surface geometry does not completely

envelope the musculoskeletal skeleton especially at

the extremities due to missing marker data and miss-

ing mobility of hands and feet.

In inverse kinematics, the objective is to mini-

BASH: Biomechanical Animated Skinned Human for Visualization of Kinematics and Muscle Activity

178 cm

(a) Sub. A

187 cm

(b) Sub. B

180 cm

178 cm

(d) Sub. D

186 cm

(e) Sub. E

185 cm

(f) Sub. F

176 cm

(g) Sub. G

189 cm

(h) Sub. H

180 cm

(i) Sub. I

195 cm

(j) Sub. J (k) Gen.

Figure 6: Frontal view of the scaled models before pose transformation and transformation into SCAPE space. Body heights

reported by the subjects are displayed in the upper right corners. As reference, the generic model with a height H of 185 cm

is displayed.

(a) (b) (c)

Figure 7: Visualization after the initial pose matching. (a),

(b), and (c) show the skeletal representation of subject J in

OpenSim (Seth et al., 2018), the proposed surface represen-

tation, and an overlay of both for comparison, respectively.

mize the marker tracking error. For the ten test sub-

jects, the mean and standard deviation of the RMSE

and of the maximum marker error is 2.1 ± 1.5 cm

and 5.0 ± 3.0cm, respectively. The error is therefore

mainly within the range of the OpenSim recommen-

dation (OpenSim, 2020). Similar to optical motion

capture, the quality of the pose estimation highly de-

pends on the marker placement.

8.3 Pose Transformation

The pose transformation is the main step of to ani-

mate the BASH model according to an input motion

sequence. Due to the initial pose matching, kinemat-

ics are directly applied to the mesh using linear blend

skinning which is commonly used in traditional com-

puter animation. Although it produces accurate vi-

sualizations, some regions like elbow and hip are af-

fected by strong deformations (see Figure 1).

8.4 Transformation into SCAPE Space

The transformation into SCAPE space makes use of

a large training data set of full-body scans and thus

can enrich the natural appearance of the animated hu-

man envelope. The SCAPE algorithm includes pose-

induced deformations

for realistic soft tissue de-

formation, e.g. muscle contractions, and shape de-

pendent deformations

for realistic representation

of the body structure.

The undesired strong deformations of the mesh at

elbow and hip are reduced by the transformation into

SCAPE space (see Figure 8a and 8b). Although the

realism is enhanced, the accuracy of the surface rep-

resentation suffers (see Figure 8c). Especially slight

offsets at the feet might impact gait analysis where

ground contact is crucial (Begg et al., 2007; Mooses

et al., 2018).

(a)

(b) (c)

Figure 8: Views after transformation into SCAPE space for

straight running. In (c) the articulated skeleton is overlaid.

The global registration of position and orienta-

tion after transformation into SCAPE space produces

robust results due to the use of 12500 vertex corre-

spondences. Alternatively, the pose transformation of

the root bone could be used to apply the global po-

sition and orientation. Nevertheless, this would not

acknowledge the fact that the SCAPE transformed

model is ﬁxed to the global coordinate system with

a vertex at the right foot instead of the root bone.

We did not yet include shape dependent deforma-

tions by applying the shape coefﬁcients provided by

the SCAPE framework, which would enable a rep-

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

resentation of individual’s anthropometry. For real-

ism and identiﬁcation with a virtual self, authenticity

of a subject-related representation is key (Waltemate

et al., 2018). Other statistical human models (Cheng

et al., 2018) are more complex, but might also further

increase the realism of the representation. Blending

of strong deformations is improved (Hirshberg et al.,

2012; Jain et al., 2010) and the Skinned Multi Person

Linear Model (SMPL) (Loper et al., 2015) produced

the most accurate results. SMPL+H (Romero et al.,

2017), a recent extension of SMPL, allows posing and

animation of individual ﬁngers which would lead to

an overall more natural representation. A slightly dif-

ferent aspect is included in the Dyna (Pons-Moll et al.,

2015) model as it produces realistic dynamical soft

tissue deformations during movement.

However, increased realism might not beneﬁt the

visualization. Lungrin et al. (2015) found that a

nearly realistic human visualization evoke a strange

feeling for an observer referred as the uncanny val-

ley effect. Whether the visualization is perceived as

realistic and whether subjects can identify themselves

with the visualized model has to be conﬁrmed in stud-

ies, especially with respect to the application and user

group. In general, a balance between ﬁdelity and de-

gree of realism has to be found.

8.5 Visualization of Muscle Activity

MTUs are projected orthogonally onto the model sur-

face to visualize muscle activity since it does not

require additional data in contrast to other methods

and allows therefore for easy visualization of various

MTU sets. Furthermore, we hypothesize that a vi-

sualization on the surface is more accessible for non

experts than volumetric muscle visualizations (Murai

et al., 2010; Pronost et al., 2011; Van den Bogert et al.,

2013) or line representations of OpenSim (Seth et al.,

2018) or AnyBody (Damsgaard et al., 2006).

Depending on the application, the maximal dis-

tance C

maxDist

has to be chosen in order to represent

the underlying MTUs well. For all ﬁgures in this pa-

per, C

maxDist

is set to 8 cm as this produces appropriate

results (see Figure 9). Alternatively, the maximum

isometric force

max

of each muscle could be in-

cluded in the deﬁnition of the maximal distance since

it is related to muscle volume.

Although the area is determined well for most

muscles, it overﬂows into the other leg for the gracilis

(see Figure 9c) and covers the complete shank instead

of the rear part of the calf for the peroneus longus

(see Figure 9d). This could be avoided by consider-

ing the orientation of the muscles with respect to the

attached bones. Additionally, anatomical knowledge

(a) vas int r (b) psoas l (c) grac r (d) per long l

Figure 9: Areas of inﬂuence (blue) assigned to the corre-

sponding muscle pathways (red) using a maximal distance

maxDist

of 8cm.

could be included, though this would limit the usabil-

ity of the approach for other musculoskeletal models.

Constraining the curvature in tangent space (Dennis

et al., 1997) or using alternative algorithms like re-

gion growing (Adams and Bischof, 1994) could pre-

vent propagation across valleys. Further improve-

ments might be achieved by using barycentric coor-

dinates (Rustamov, 2010) to overcome the limitation

to vertex assignments.

For color coding of the determined area, the in-

tensity is normalized with a constant C

maxMeasure

14000N to ensure comparability of the visualization

across different motion sequences or subjects. In-

tensity normalization is for example important when

evaluating temporal progress of diseases, gait train-

ing, or running technique of athletes or when com-

paring body constitutions or designs of equipment.

The constant C

maxMeasure

should be chosen speciﬁc to

the musculoskeletal model and application. Since the

intensity measure i

is added to the red color chan-

nel, the value of the red color channel could exceed

its limits for inappropriate constants and would be

cropped.

The color coding of the muscle activation is vi-

sually compared to the line representation of Open-

Sim (Seth et al., 2018) (see Figure 1). The mus-

cle activation is highlighted plausibly on the surface

with smooth transitions at borders and overlapping re-

gions due to the color interpolation of the fragment

shader. In Figure 5, kinematics and muscle activation

of straight and curved running are visualized. Es-

pecially for people with little biomechanical knowl-

edge, the surface representation likely appears more

vivid and realistic. At the same time, it does not re-

quire additional data and can easily be applied to dif-

ferent musculoskeletal models. Hence, the proposed

visualization of the muscle activity might offer a use-

ful alternative compared to the 2D line (Damsgaard

et al., 2006; Seth et al., 2018) or volumetric represen-

tation (Murai et al., 2010; Pronost et al., 2011; Van

den Bogert et al., 2013).

BASH: Biomechanical Animated Skinned Human for Visualization of Kinematics and Muscle Activity

9 CONCLUSION

We have presented a visualization pipeline to animate

a skinned representation for biomechanical analysis

of kinematics and muscle activity. The goal was to

make biomechanical analysis more intuitive and re-

alistic and increase accessibility for non-experts. To

this end, we developed the BASH model to establish

a bridge between the musculoskeletal model and a

statistical surface model. Traditional animation char-

acter techniques and the SCAPE framework enabled

body part scaling, pose transformations and realistic

surface deformations for the input kinematics. Ad-

ditionally, muscle activity related to the motion se-

quence is highlighted on the model’s surface. Still,

our approach does not require more input data than a

traditional biomechanical approach: a musculoskele-

tal model, kinematic data and muscle activation. This

ensures high usability and makes it easily applicable

to other musculoskeletal models.

The proposed approach was evaluated us-

ing scaled musculoskeletal models of ten sub-

jects (Dorschky et al., 2019b; Nitschke et al., 2020)

and data of simulated straight and curved run-

ning (Nitschke et al., 2020). Our method achieved a

realistic person-speciﬁc representation of the biome-

chanical input. Beside minor discrepancies, body

part dimensions and the movement sequence was re-

ﬂected accurately compared to state-of-the-art repre-

sentations like OpenSim (Seth et al., 2018). The pro-

posed 3D skinned human surface model seemed more

accessible for non-experts, especially the visualiza-

tion of muscular activity on the surface might offer

an intuitive representation.

However, various topics could be investigated for

further improvements. For applications where real-

time feedback is required, such as gait retraining,

Realtime-SCAPE (Chen et al., 2016) could be inves-

tigated. Furthermore, it might be possible to learn

the pose regression parameters using the skeleton of

the musculoskeletal model directly to eliminate some

intermediate processing steps. The body shape pa-

rameters could be included to enhance person-speciﬁc

visual representation. Besides expensive full-body

scans or medical imaging, an extraction of shape co-

efﬁcients from a photo of the subject could provide

a practical solution (Bogo et al., 2016) to determine

the body shape parameters. Constraint curvatures

in tangent space (Dennis et al., 1997), region grow-

ing (Adams and Bischof, 1994), or barycentric coor-

dinates (Rustamov, 2010), should be considered for

the visualization of the muscle activity since they

could be beneﬁcial without requiring additional input

data.

In this paper, the proposed methodology was eval-

uated by visual inspection and comparison with state-

of-the-art tools. Since realism, intuitiveness and body

ownership of a novel visualization cannot be mea-

sured objectively, there is a need to perform usability

and perception studies for an application speciﬁc eval-

uation. Besides questionnaires and interviews about

the proposed representation, efﬁciency of task execu-

tion should be studied with an user group.

The proposed pipeline is the ﬁrst step to study us-

ability and perception of biomechanical data visual-

ization for non-experts. Our visualization method has

the potential to enable non-experts, like patients, ath-

letes and designers, to gain from biomechanical anal-

ysis for patient education, gait retraining, technique

training, or design of equipment.

REFERENCES

Adams, R. and Bischof, L. (1994). Seeded Region Growing.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 16(6):641–647.

Anguelov, D., Srinivasan, P., Koller, D., Thrun, S., Rodgers,

J., and Davis, J. (2005). SCAPE: Shape Completion

and Animation of People. In ACM Transactions on

Graphics, volume 24, pages 408–416.

Aubel, A. and Thalmann, D. (2001). Interactive modeling

of the human musculature. In Proceedings Computer

Animation 2001. Fourteenth Conference on Computer

Animation (Cat. No.01TH8596), pages 167–255.

Begg, R., Best, R., Dell’Oro, L., and Taylor, S. (2007). Min-

imum foot clearance during walking: Strategies for

the minimisation of trip-related falls. Gait and Pos-

ture, 25(2):191–198.

Bencke, J., Aagaard, P., and Zebis, M. K. (2018). Mus-

cle Activation During ACL Injury Risk Movements in

Young Female Athletes: A Narrative Review. Fron-

tiers in Physiology, 9(445):1–10.

Blemker, S. S. and Delp, S. L. (2005). Three-dimensional

representation of complex muscle architectures and

geometries. Annals of Biomedical Engineering,

33(5):661–673.

Bogo, F., Kanazawa, A., Lassner, C., Gehler, P., Romero,

J., and Black, M. J. (2016). Keep it SMPL: Automatic

estimation of 3D human pose and shape from a single

image. In European Conference on Computer Vision,

volume 9909 LNCS, pages 561–578. Springer.

Chen, Y., Cheng, Z. Q., Lai, C., Martin, R. R., and Dang,

G. (2016). Realtime Reconstruction of an Animat-

ing Human Body from a Single Depth Camera. IEEE

Transactions on Visualization and Computer Graph-

ics, 22(8):2000–2011.

Cheng, Z. Q., Chen, Y., Martin, R. R., Wu, T., and Song,

Z. (2018). Parametric modeling of 3D human body

shape - A survey. Computers and Graphics (Perga-

mon), 71:88–100.

Colaianni, M., Zollhoefer, M., S

ußmuth, J., Seider, B., and

Greiner, G. (2014). A Pose Invariant Statistical Shape

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

Model for Human Bodies. In Proceedings of the 5th

International Conference on 3D Body Scanning Tech-

nologies, pages 327–336.

Damsgaard, M., Rasmussen, J., Christensen, S. T., Surma,

E., and de Zee, M. (2006). Analysis of musculoskele-

tal systems in the AnyBody Modeling System. Sim-

ulation Modelling Practice and Theory, 14(8):1100–

1111.

Delp, S. L., Anderson, F. C., Arnold, A. S., Loan, P.,

Habib, A., John, C. T., Guendelman, E., and The-

len, D. G. (2007). OpenSim: Open-source software

to create and analyze dynamic simulations of move-

ment. IEEE Transactions on Biomedical Engineering,

54(11):1940–1950.

Dennis, J., Maciel, M., Dennis, J., and El-Alem, M. (1997).

A global convergence theory for general trust-region-

based algorithms for equality constrained optimiza-

tion. SIAM Journal on Optimization, 7(1):177–207.

Dorschky, E., Kr

uger, D., Kurfess, N., Schlarb, H.,

Wartzack, S., Eskoﬁer, B. M., and van den Bogert,

A. J. (2019a). Optimal control simulation predicts ef-

fects of midsole materials on energy cost of running.

Computer Methods in Biomechanics and Biomedical

Engineering, 22(8):869–879.

Dorschky, E., Nitschke, M., Seifer, A. K., van den Bogert,

A. J., and Eskoﬁer, B. M. (2019b). Estimation of gait

kinematics and kinetics from inertial sensor data using

optimal control of musculoskeletal models. Journal of

Biomechanics, 95.

Ezati, M., Ghannadi, B., and McPhee, J. (2019). A review

of simulation methods for human movement dynam-

ics with emphasis on gait. Multibody System Dynam-

ics, 47(3):265–292.

Falisse, A., Serrancol

ı, G., Dembia, C. L., Gillis, J.,

Jonkers, I., and De Groote, F. (2019). Rapid predictive

simulations with complex musculoskeletal models

suggest that diverse healthy and pathological human

gaits can emerge from similar control strategies. Jour-

nal of The Royal Society Interface, 16(157):20190402.

Fey, N. P., Klute, G. K., and Neptune, R. R. (2012).

Optimization of prosthetic foot stiffness to reduce

metabolic cost and intact knee loading during below-

knee amputee walking: A theoretical study. Journal

of Biomechanical Engineering, 134(11):1–10.

Geijtenbeek, T. and Pronost, N. (2012). Interactive charac-

ter animation using simulated physics: A state-of-the-

art review. Computer Graphics Forum, 31(8):2492–

2515.

Geijtenbeek, T., Steenbrink, F., Otten, B., and Even-Zohar,

O. (2011). D-ﬂow: immersive virtual reality and real-

time feedback for rehabilitation. In Proceedings of the

10th International Conference on Virtual Reality Con-

tinuum and Its Applications in Industry, pages 201–

208.

Golub, G. H. and Reinsch, C. (1970). Singular value

decomposition and least squares solutions. In Nu-

merische Mathematik, volume 14, pages 403–420.

Springer.

Hasler, N., Stoll, C., Rosenhahn, B., Thorm

ahlen, T., and

Seidel, H. P. (2009a). Estimating body shape of

dressed humans. Computers and Graphics (Perga-

mon), 33(3):211–216.

Hasler, N., Stoll, C., Sunkel, M., Rosenhahn, B., and Seidel,

H. P. (2009b). A statistical model of human pose and

body shape. Computer Graphics Forum, 28(2):337–

346.

Hasler, N., Thorm

ahlen, T., Rosenhahn, B., and Seidel, H.-

P. (2010). Learning skeletons for shape and pose.

Number 212, pages 23–30.

Hirshberg, D. A., Loper, M., Rachlin, E., and Black, M. J.

(2012). Coregistration: Simultaneous alignment and

modeling of articulated 3D shape. Lecture Notes in

Computer Science (including subseries Lecture Notes

in Artiﬁcial Intelligence and Lecture Notes in Bioin-

formatics), 7577 LNCS(PART 6):242–255.

Jain, A., Thorm

ahlen, T., Seidel, H. P., and Theobalt, C.

(2010). MovieReshape: Tracking and Reshaping of

Humans in Videos. ACM Transactions on Graphics,

29(6):1–10.

Jiang, Y., Van Wouwe, T., De Groote, F., and Liu, C. K.

(2019). Synthesis of biologically realistic human mo-

tion using joint torque actuation. ACM Transactions

on Graphics (TOG), 38(4):1–12.

Kabsch, W. (1976). A solution for the best rotation to relate

two sets of vectors. Acta Crystallographica Section A,

32(5):922–923.

Kavan, L., Collins, S., and O’Sullivan, C. (2009). Auto-

matic linearization of nonlinear skinning. Proceedings

of I3D 2009: The 2009 ACM SIGGRAPH Symposium

on Interactive 3D Graphics and Games, pages 49–56.

Koelewijn, A. D. and van den Bogert, A. J. (2016). Joint

contact forces can be reduced by improving joint mo-

ment symmetry in below-knee amputee gait simula-

tions. Gait and Posture, 49:219–225.

uger, D. B. and Wartzack, S. (2015). Visualisation of

biomechanical stress quantities within cad environ-

ments. In Proceedings of the International Conference

on Engineering Design, ICED, pages 1–10.

Lee, D., Glueck, M., Khan, A., Fiume, E., Jackson, K.,

et al. (2012). Modeling and simulation of skeletal

muscle for computer graphics: A survey. Founda-

tions and Trends

 in Computer Graphics and Vision,

7(4):229–276.

Lee, S. H., Sifakis, E., and Terzopoulos, D. (2009). Com-

prehensive biomechanical modeling and simulation

of the upper body. ACM Transactions on Graphics,

28(4):1–17.

Lin, Y.-C. and Pandy, M. G. (2017). Three-dimensional

data-tracking dynamic optimization simulations of

human locomotion generated by direct collocation.

Journal of Biomechanics, 59:1–8.

Loper, M., Mahmood, N., Romero, J., Pons-Moll, G., and

Black, M. J. (2015). SMPL: A skinned multi-person

linear model. ACM Transactions on Graphics, 34(6).

Ma, Y., Soatto, S., Ko

seck

a, J., and Sastry, S. (2004). An

Invitation to 3D Vision, volume 19.

Magnenat-Thalmann, N., Laperrire, R., and Thalmann, D.

(1988). Joint-dependent local deformations for hand

animation and object grasping. In In Proceedings on

Graphics interface’88. Citeseer.

BASH: Biomechanical Animated Skinned Human for Visualization of Kinematics and Muscle Activity

Maurice, X., Sandholm, A., Pronost, N., Boulic, R., and

Thalmann, D. (2009). A subject-speciﬁc software so-

lution for the modeling and the visualization of mus-

cles deformations. Visual Computer, 25(9):835–842.

McGuan, S. P. (2001). Human modeling–from bubblemen

to skeletons. Technical report, SAE Technical Paper.

McLaughlin, T., Cutler, L., and Coleman, D. (2011).

Character rigging, deformations, and simulations in

ﬁlm and game production. ACM SIGGRAPH 2011

Courses, SIGGRAPH’11.

Mooses, M., Haile, D. W., Ojiambo, R., Sang, M., Kerli,

M., Lane, A. R., and Hackney, A. C. (2018). Shorter

ground contact time and better running economy:

Evidence from female kenyan runners. Journal of

Strength and Conditioning Research.

Murai, A., Kurosaki, K., Yamane, K., and Nakamura, Y.

(2010). Musculoskeletal-see-through mirror : Com-

putational modeling and algorithm for whole-body

muscle activity visualization in real time. Progress

in Biophysics and Molecular Biology, 103(2-3):310–

317.

Murai, A., Youn Hong, Q., Yamane, K., and Hodgins, J. K.

(2017). Dynamic skin deformation simulation us-

ing musculoskeletal model and soft tissue dynamics.

Computational Visual Media, 3(1):49–60.

Nitschke, M., Dorschky, E., Heinrich, D., Schlarb, H., Es-

koﬁer, B. M., Koelewijn, A. D., and Van den Bogert,

A. J. (2020). Efﬁcient trajectory optimization for

curved running using a 3D musculoskeletal model

with implicit dynamics. Scientiﬁc Reports, 10(17655).

OpenSim (2020). Getting started with inverse kinematics.

Accessed on 03.05.2020.

Peeters, P. and Pronost, N. (2014). A practical framework

for generating volumetric meshes of subject-speciﬁc

soft tissue. Visual Computer, 30(2):127–137.

Pons-Moll, G., Romero, J., Mahmood, N., and Black, M. J.

(2015). Dyna: A model of dynamic human shape in

motion. ACM Transactions on Graphics, 34(4):1–14.

Pronost, N., Sandholm, A., and Thalmann, D. (2011). A

visualization framework for the analysis of neuromus-

cular simulations. Visual Computer, 27(2):109–119.

Richards, R., van der Esch, M., van den Noort, J. C., and

Harlaar, J. (2018). The learning process of gait re-

training using real-time feedback in patients with me-

dial knee osteoarthritis. Gait & Posture, 62:1–6.

Romero, J., Tzionas, D., and Black, M. J. (2017). Embod-

ied hands: Modeling and capturing hands and bodies

together. ACM Transactions on Graphics, 36(6).

Rustamov, R. M. (2010). Barycentric coordinates on sur-

faces. In Computer Graphics Forum, volume 29,

pages 1507–1516. Wiley Online Library.

Sch

onemann, P. H. (1966). A generalized solution of the

orthogonal procrustes problem.

Seth, A., Hicks, J. L., Uchida, T. K., Habib, A., Dembia,

C. L., Dunne, J. J., Ong, C. F., DeMers, M. S., Ra-

jagopal, A., Millard, M., et al. (2018). OpenSim: Sim-

ulating musculoskeletal dynamics and neuromuscular

control to study human and animal movement. PLoS

Computational Biology, 14(7):1–20.

Sueda, S., Kaufman, A., and Pai, D. K. (2008). Musculo-

tendon simulation for hand animation. ACM Transac-

tions on Graphics, 27(3).

Teran, J., Blemker, S., Hing, V., and Fedkiw, R. (2003).

Finite volume methods for the simulation of skeletal

muscle. pages 68–74. Eurographics Association.

Teran, J., Sifakis, E., Blemker, S. S., Ng-Thow-Hing, V.,

Lau, C., and Fedkiw, R. (2005). Creating and sim-

ulating skeletal muscle from the visible human data

set. IEEE Transactions on Visualization and Com-

puter Graphics, 11(3):317–328.

Thelen, D. G. (2003). Adjustment of muscle mechanics

model parameters to simulate dynamic contractions in

older adults. Journal of Biomechanical Engineering,

125(1):70–77.

Udow, S. J., Hobson, D. E., Kleiner, G., Masellis, M., Fox,

S. H., Lang, A. E., and Marras, C. (2018). Educational

needs and considerations for a visual educational tool

to discuss parkinson’s disease. Movement Disorders

Clinical Practice, 5(1):66–74.

Van den Bogert, A. J., Geijtenbeek, T., Even-Zohar, O.,

Steenbrink, F., and Hardin, E. C. (2013). A real-time

system for biomechanical analysis of human move-

ment and muscle function. Medical and Biological

Engineering and Computing, 51(10):1069–1077.

Van den Noort, J. C., Steenbrink, F., Roeles, S., and Harlaar,

J. (2015). Real-time visual feedback for gait retrain-

ing: toward application in knee osteoarthritis. Medical

& Biological Engineering & Computing, 53(3):275–

286.

Vannatta, C. N. and Kernozek, T. W. (2015). Patellofemoral

Joint Stress during Running with Alterations in Foot

Strike Pattern. Medicine & Science in Sports & Exer-

cise, 47(5):1001–1008.

Waltemate, T., Gall, D., Roth, D., Botsch, M., and

Latoschik, M. E. (2018). The impact of avatar per-

sonalization and immersion on virtual body own-

ership, presence, and emotional response. IEEE

Transactions on Visualization and Computer Graph-

ics, 24(4):1643–1652.

Yang, Y., Yu, Y., Zhou, Y., Du, S., Davis, J., and Yang,

R. (2014). Semantic parametric reshaping of human

body models. In 2014 2nd International Conference

on 3D Vision, volume 2, pages 41–48. IEEE.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications