Clustering Pathologic Voice with Kohonen SOM and Hierarchical

Clustering

Alessa Anjos de Oliveira

1,2

, Maria Eugênia Dajer

and João Paulo Teixeira

Research Centre in Digitalization and Intelligent Robotics (CEDRI), Instituto Politecnico de Braganca,

Campus Sta. Apolonia, 5301 857, Braganca, Portugal

Federal University of Technology of Paraná, Campus Cornélio Procópio, 86300 000, Cornélio Procópio, Brazil

Keywords: Acoustic Parameters, Clustering, Hierarchical Clustering, Kohonen's Self-Organizing Maps, Unsupervised

Artificial Neural Networks, Voice Pathologies.

Abstract: The main purpose of clustering voice pathologies is the attempt to form large groups of subjects with similar

pathologies to be used with Deep-Learning. This paper focuses on applying Kohonen's Self-Organizing Maps

and Hierarchical Clustering to investigate how these methods behave in the clustering procedure of voice

samples by means of the parameters absolute jitter, relative jitter, absolute shimmer, relative shimmer, HNR,

NHR and Autocorrelation. For this, a comparison is made between the speech samples of the Control group

of subjects, the Hyper-functional Dysphonia and Vocal Folds Paralysis pathologies groups of subjects. As a

result, the dataset was divided in two clusters, with no distinction between the pre-defined groups of

pathologies. The result is aligned with previous result using statistical analysis.

1 INTRODUCTION

Pathologies related with the human phonation

apparatus can affect the characteristics of the voice,

and can be very limitative for the patients, depending

on the pathology and its degree of evolution. Some

pathologies impose serious limitation on voice and

consequentially on daily living, in addition to causing

serious damage on patient’s health (Teixeira, Alves

and Fernandes, 2020). Some of the most common

pathologies are: Carcinoma, Chronic Laryngitis,

Cysts, Granuloma, Intubation Granuloma,

Hypopharyngeal Tumor, Laryngeal Tumor, Reinke’s

Edema, Vocal Fold Paralysis, Vocal Fold Polyps,

Functional Dysphonia, Hyper-functional Dysphonia,

Hypofunctional Dysphonia, Hypotonic Dysphonia

and Psychogenic Dysphonia (Teixeira J. P.,

Fernandes, Teixeira F., Fernandes, 2018).

The traditional diagnostic exams can be very

cumbersome and expensive for the patient.

Vocal acoustic analysis techniques can allow a

screening test or pre-diagnose that can avoid the

traditional exams to several patients. These

techniques may also be used as a valuable tool for the

otolaryngologist exam. In the area of rehabilitation,

well-designed tools can be useful for the evaluation

of the recover after the treatment.

Support decision system for voice pathologies

diagnose and identification based on acoustic analysis

have been under research recently as alternative to

invasive technics like endoscopy, laryngoscopy and

stroboscopic exams (Martínez, Lleida, Ortega,

Miguel and Villalba, 2012), (Teixeira J. P.,

Fernandes, and Alves, 2017).

With this different approach we are able to do the

classification between healthy or pathologic voices or

even the identification of the pathology. Anyhow, the

length of the available dataset for each voice

pathology has shown as the bottleneck to use more

sophisticated and powerful Deep Learning tools such

as LSTM recurrent Deep Neural Networks (DNN), 1-

D Convolutional DNN or transfer learning

techniques, because of the higher dimension of the

dataset required (Guedes, Junior, Teixeira F.,

Fernandes J. and Teixeira J. P, 2018), (Teixeira F.,

and Teixeira J. P., 2020). This paper intends to step

forward searching the solution for the scarcity of the

existent speech datasets to classify the pathology and

not simply classify between healthy or control. The

main idea is to cluster similar pathologies based on

the traditional acoustic parameters used for voice

158

de Oliveira, A., Dajer, M. and Teixeira, J.

Clustering Pathologic Voice with Kohonen SOM and Hierarchical Clustering.

DOI: 10.5220/0010210901580163

In Proceedings of the 14th International Joint Conference on Biomedical Engineer ing Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 158-163

ISBN: 978-989-758-490-9

pathologies in order to enlarge the dataset for some

clustered pathologies (Fernandes J. et al, 2019).

Assessment of voice pathologies can be done by

means of acoustic analysis of the voice signal,

through the analysis of a set of parameters. In the

literature review other speech parameters can be

found like Energy, different order of moment,

kurtosis and relations between energy bandwidths

(Panek, Skalski, Gajda and Tadeusiewicz, 2015) and

(Teixeira J. P., Fernandes, and Alves, 2017). Tsanas,

Little, McSharry & Ramig (2010) used several order

of Mel-Frequency Cepstrum Coefficients (MFCC),

delta MFCC, ratio of the log transformed means

(VFER-NSR), extend of turbulent noise (DFA) and

several measures of Fundamental Frequency (F0) for

Parkinson’s disease symptoms severity.

In this work parameters such absolute jitter,

relative jitter, absolute shimmer, relative shimmer,

harmonic-to-noise ratio, noise-to-harmonic ratio,

autocorrelation will be used as a reference (Felippe,

Grillo and Grechi, 2006), (Finger, Cielo and Schwarz,

2009), (Teixeira J. P., and Fernandes P. O., 2014) and

(Fernandes J. et al, 2019).

The aforementioned set of parameters, were used

to apply clustering techniques that will contribute to

the organization of data into groups by means of the

similarity among the analyzed elements. Thus,

samples that belong to the same set tend to be more

similar than the rest of the elements formed by other

sets (Jain, Murty and Flynn, 1999). To achieve

clustering using an ANN, unsupervised learning is

required. This means that the network receives no

guidance, i.e., only the set of inputs is provided, there

is no predefined output (Jain, Murty and Flynn,

1999), (Haykin, 1999), (Pavel, 2006).

In this work, clustering techniques will be applied

in order to verify whether the dataset of voice features

can be grouped based on the set of parameters

previously referred. Kohonen's Self-Organizing

Maps (SOM) and Hierarchical Clustering are the

methods used in this work.

The section 2 of this document presents the

materials used in the study, presenting the database,

acoustic parameters and the clustering methods: SOM

and hierarchical clustering. Sequentially, section 3

presents the results and discussions. Closing with the

conclusions, presented in section 4.

2 MATERIALS AND METHODS

In this section the dataset will be presented, followed

by the definition of the used parameters and the

clustering methods, namely the Kohonen’s Self

Organizing Maps and Hierarchical Clustering.

2.1 Database

The Saarbruecken Voice Database (SVD) was used

as the original speech dataset. It has a collection of

speech recordings of over 2000 subjects pronouncing

the sustained vowels /a/, /i/ and /u/ in low, normal,

high, and low to high tone, plus a small sentence in

German. The SVD is an open dataset of pathologic

and healthy speech records provided by the Institute

of Phonetics of the University of Saarland. All audios

have a sampling frequency of 50 kHz and 16-bit

resolution (Martínez, Lleida, Ortega, Miguel and

Villalba, 2012), (Fernandes J. et al, 2019).

In this study, only the sustained vowel /a/ in

normal tone was used because it presents a larger

opening of the vocal tract compared to the other

vowels. Besides, samples of the Control group, the

Hyper-functional Dysphonia and Vocal Fold

Paralysis pathologies were used. These two

pathologies contains the largest number of subjects in

the database. Table 1 displays the characterization of

the used subset with 486 subjects.

2.2 Acoustic Parameters

The Praat software (Boersma P, Weenink D, n.a.)

allowed the extraction of parameters used in acoustic

analysis. By selecting the file from the SVD, it is

possible to select the complete voice segment and

extract the parameters: absolute jitter and shimmer,

relative jitter and shimmer, HNR, NHR and

autocorrelation (Teixeira, J. P., Fernandes, P. O.

2015).

Jitter is a periodic disturbance; shimmer is the

magnitude disturbance. Both can be measured using

four different formulas (Teixeira J. P. and Gonçalves,

2016), but in this work only the absolute and relative

versions of each parameter will be worked on.

Absolute jitter is the average absolute difference

among successive periods whereas relative jitter is the

absolute jitter divided by the average period,

expressed in percentage (Teixeira J. P., Fernandes J.,

Teixeira F., Fernandes P. O., 2018).

Absolute shimmer, according to Teixeira J. P. et

al (2018) is the logarithm of base 10 of the absolute

mean of the magnitude ratio between consecutive

periods multiplied by 20, given in decibel, whilst

relative shimmer is the average absolute difference

between amplitudes of successive periods, divided by

the mean magnitude, expressed in percentage.

Clustering Pathologic Voice with Kohonen SOM and Hierarchical Clustering

159

Table 1: Subset of subject of the Saarbruecken Voice Database used.

Test Groups

Number of Voice Sam

les

Average Participants’

Age

Female Male Total

Control 123 71 194 36,74

Hype

-Functional Dysphonia 95 32 127 40,91

Vocal Fold Paralysis 100 65 165 57,52

Total 318 138 486 45,06

Autocorrelation is the correlation of a signal with

itself, being a method of detecting the periodicity of

the signal. According to Fernandes J. et al. (2019),

this parameter provides a measure of the similar

speech parts repeated along the signal.

The harmonic-to-noise ratio (HNR) gives the

relation between the periodic and aperiodic

components of a speech segment, whereas the noise-

to-harmonic ratio (NHR) is given by the relation

between the aperiodic component and the periodic

component (Fernandes J., Teixeira F., Guedes,

Junior, and Teixeira J. P., 2018).

2.3 Kohonen’s Self Organizing Maps

Kohonen's Self-Organizing Maps (SOM) are

structured through unsupervised competitive training,

which allows the detection of similarities between the

input data, grouping them (Haykin, 1999), (Kohonen,

1994). SOM are useful comparing to other neural

networks because they are able to represent a

multidimensional data set in a two-dimensional space

(Haykin, 1999), (Kohonen, 1994), (Affonso, 2011).

The competitive learning process used by SOM

works with the principle of competition between

neurons, in which the winner has its weights modified

to suit the next input vector. The definition of the

winning neuron is given by the proximity between the

input vector and the weight vector of the neuron

(Haykin, 1999), (Affonso, 2011). This proximity is

conceived by the Euclidian distance, expressed by

equation (1). Where 𝑥 is the input vector and 𝑤



is the

weights vector.

𝑖

(

𝑥

)

=arg𝑚𝑖𝑛𝑥−𝑤



 𝑗 = 1,2,…𝑛

(1)

When defined a winner, having already arranged

the neurons in the topological map, one must define a

neighborhood criterion between the neurons so that

when a neuron wins, there is an adjustment of both

the winner and the neighborhood (Kohonen, 1994),

(Affonso, 2011). The Gaussian function is applied in

the neighborhood, so that the more distant neighbors

have a smaller adjusted value compared to the winner

(Kohonen, 1994). Thus, equation (2) is applied to the

winner and equation (3) is used in the neighborhood.

The Gaussian operator is 𝛼

()

, given by the

expression (4). The 𝜎 symbol in equation (4) is the

standard deviation of the dataset.

𝒘



(



)

=𝒘



(



)

𝜂×



𝒙



+𝒘



()



(2)

𝒘



(



)

=𝒘



(



)

𝜂×𝛼

()



𝒙



+𝒘



()



(3)

𝛼

()

=𝑒





𝒘



(



)

𝒘



(



)









(4)

2.4 Hierarchical Clustering

The Hierarchical Clustering method is divided into:

agglomerative, in which each object is a cluster and

each iteration the union with other similar objects

occurs until forming a single group; and divisive,

which starts in a single large group containing all

samples and recursively divides into smaller sets

(Pavel, 2006).

This clustering method works with the

(dis)similarity of the database elements, which is

done through a linkage metric (Pavel, 2006). To find

the (dis)similarity between each pair of objects in the

database, the distance between these observations is

calculated, given by the Euclidean distance, already

expressed in Equation (1) (Gan, Ma, and Wu, 2007).

After this calculation, it is possible to determine how

the objects in the dataset should be grouped into

clusters using the linkage metric (Gan Ma, and Wu,

2007), (Jain, Murty and Flynn, 1999). This metric

characterizes the proximity of a pair of clusters,

which defines whether the observations should merge

or split, creating the hierarchy tree. This linkage can

be complete, single, average, centroid, median, ward

or weighted. The first uses the longest distance

between objects in the two clusters, the average uses

the mean distance between pairs of observations in

two distinct groups, the centroid linkage, uses the

Euclidean distance between the centers of two

clusters, the median uses the Euclidean distance

between the weighted centroids of the two groups.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

160

Ward's linkage makes the incremental sum within the

cluster as a result of joining two clusters and, finally,

the weighted measure uses a recursive definition for

the distance between two clusters (MathWorks, n.d.).

2.5 Pre-processing Data

The Neural Network toolbox of MATLAB® software

was used to implement the artificial neural network

algorithms. The raw data was pre-processed for

cluster analysis. A normalization ranging from 0 to 1

was applied for the parameters, in which the

maximum and minimum values of each parameter are

identified. For each parameter, the normalization

consists in the difference of each sample and its

minimum divided by the difference of the maximum

and minimum values. Equation (5) shows the

normalization, wherein

is the parameter to be

normalized and i the sample for each subject.

𝑋



𝑋



−𝑋

 

𝑋





−𝑋





𝑖 = 1,2,…,486

(5)

After normalization, the neural network

conditions must be adjusted. In this work, the

characteristics of SOM were selected empirically

based on data available in the literature, reaching a

dimension of 100 neurons, with an initial

neighborhood radius ranging from 1 to 10, in a

hexagonal topology that is iterated 18000 times.

3 RESULTS AND DISCUSSION

Due to the sophisticated visualization of neurons in

SOM, it is possible to notice that there is a division

into two clusters. In Figure (1-a), the lower left corner

points out the yellow to light orange color, which

designates a proximity of the neurons forming a

cluster. The dark orange tending to the red in upper

right corner shows that the neurons are not so close to

the ones of the lower left, forming a second group.

For a more assertive result of the clusters, the

Hierarchical Clustering was also used. Like SOM,

this network uses the Euclidean equation in order to

determine the distance between each object in the

database. In sequence, the linkage metric is used to

create the clusters. To check if the linkage metric was

chosen correctly, just compare the cophenetic

distance. For a consistent result, this correlation must

present a value close to 1, proving that the solution of

this cluster represents the original data (MathWorks,

n.d.). In terms of proximity between clusters, the

average linkage is used, as it presents a better

similarity in relation to other connection metrics,

presenting a cophenetic correlation of 0.9297. Figure

(1-b) shows the dendrogram producing two final

clusters, which corroborates with the result presented

by the Kohonen network. When the subjects of each

group in the Hierarchical Clustering were analyzed, it

was found that the groups were divided into a large

group and a smaller one. All elements of the Control

group belong to the largest set. Hyper-functional

Dysphonia data also belong to this large set, with the

exception of 2 elements. The other data of the small

group are from the Vocal Fold Paralysis.

According to comparison of pathologies based on

same parameters presented in Oliveira, Dajer,

Fernandes, and Teixeira (2020) for the 3 groups under

study, using descriptive statistical analysis, it was

found that the Hyper-functional Dysphonia can be

grouped with Control group and with Vocal Fold

Paralysis group, but Vocal Fold Paralysis cannot be

grouped with Control group. Since Hyper-functional

Dysphonia, according to the descriptive statistical

analysis, can be grouped with the two other groups,

these subjects may become between the two (yellow

and red) ‘corners’ of the SOM. This can be explained

by the fact that the Hyper-functional Dysphonia in its

primary phase does not present irregular traces in the

laryngeal exam and the vocal symptoms are

inconstant, having fatigue and episodes of vocal

weakness as the main signs (Fawcus, 1991).

The (no) connection between the Vocal Fold

Paralysis and the other two groups, may be probably,

the reason for the distinction between their elements.

The reason is because the Vocal Fold Paralysis and

Hyper-functional Dysphonia pathologies are

distinguished both in etiology and physiology. The

Vocal Fold Paralysis is an injury to the recurrent

laryngeal nerve, incapacitating the muscular

contraction of the vocal folds (Chen, Jen, Wang, Lee,

and Lin, 2007), (Toutounchi, Eydi, Golzari, Ghaffari,

and Parvizian, 2014). Whereas the Hyper-functional

Dysphonia causes increased tension in the laryngeal

muscle, resulting in excessive stiffness of the vocal

cords, bringing them closer together (Holmberg,

Doyle, Perkell, Hammarberg, and Hillman, 2003),

(Kandoğan, Koç, and Aksoy, 2009). In the

comparison between the Control group and the

Paralysis group there might be a difference, as the

pathology inhibits the muscular contraction of the

vocal folds. Therefore, the voice is altered, even in a

minimal way.

Clustering Pathologic Voice with Kohonen SOM and Hierarchical Clustering

161

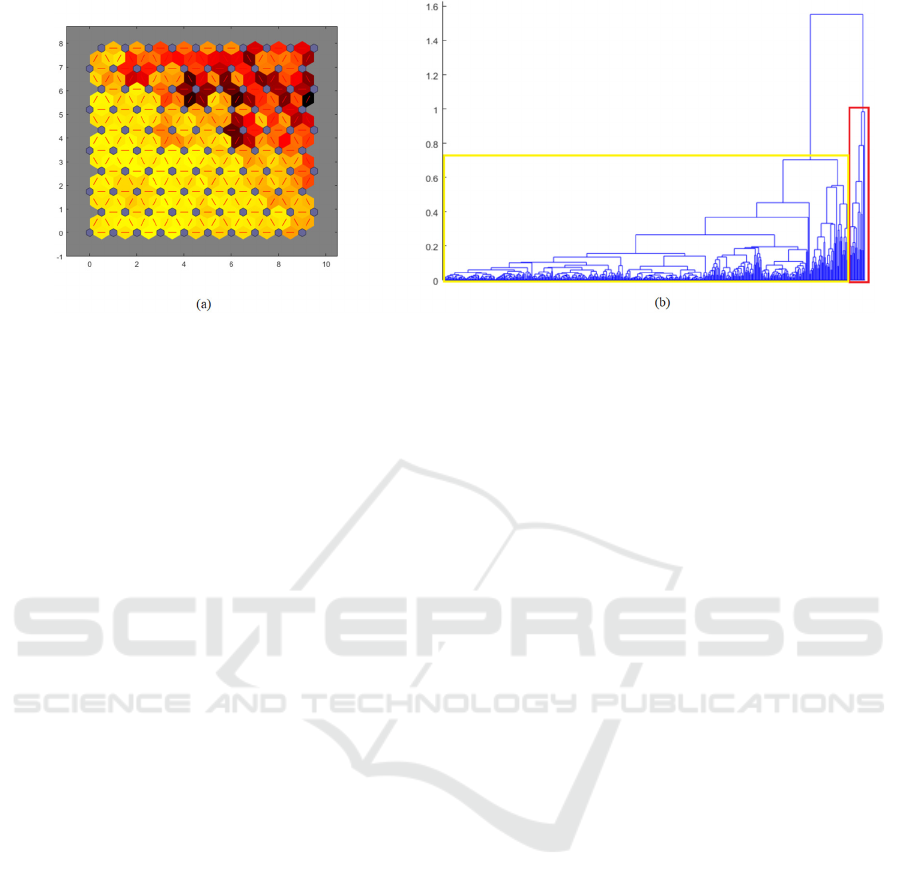
Figure 1: (a) Distance between the neighborhood of neurons in the Kohonen's Self-Organizing Maps; (b) Agglomerative

hierarchy tree resulting from the input vector.

4 CONCLUSIONS

The paper presents clustering analysis using

unsupervised ANNs, namely Kohonen's Self-

Organizing Maps, and Hierarchical Clustering to

gathering subjects of the Control group, Hyper-

functional Dysphonia, and Vocal Fold Paralysis,

using a set of speech parameters like jitter, shimmer,

HNR, NHR and autocorrelation.

The clustering techniques analyzed here in order

to group pathologies based on the acoustic parameters

were successful, evidencing the results presented in

previous research (Oliveira, Dajer, Fernandes, and

Teixeira, 2020), in which there was no statistical

distinction between Hyper-functional Dysphonia and

the Control group, but there is a significant statistical

difference between Vocal Fold Paralysis and Control

group. Hence, the SOM presented the expected

results considering that divided the dataset into two

‘corners’ with gradual scale between light yellow and

dark red, likewise the descriptive statistical analysis

method. This organization of subjects between the

two ‘corners’ can be interpreted as the Control

(Healthy) subjects in the light yellow, the Vocal Fold

Paralysis in the dark red and Hyper-functional

Dysphonia subjects between these two ‘corners’.

Even though it presented a good result, this work

is still in progress. Therefore, this comparison will be

extended to subjects with other pathologies in near

future, adding more audios for each subject in order

to obtain consistent results.

For future work, it is suggested to implement

SOM and Hierarchical Clustering to the remaining

pathologies and use other parameters extracted from

the voice signal, such as the mel-frequency cepstral

coefficient (MFCC), perceptual linear prediction

(PLP), linear prediction cepstral coefficient (LPCC),

among others.

ACKNOWLEDGEMENTS

This work has been supported by FCT – Fundação

para a Ciência e Tecnologia within the Project Scope:

UIDB/05757/2020.

REFERENCES

Affonso, G.S. 2011. Mapas Auto-Organizáveis de Kohonen

(SOM) Aplicados na Avaliação de Parâmetros da

Qualidade da Água. Dissertação de mestrado em

Ciências na Área de Técnologia Nuclear. Autarquia

associada à universidade de São Paulo.

Boersma P, Weenink D.: Praat: doing phonetics by

computer. Phonetic Sciences, University of

Amsterdam. http://www.fon.hum.uva.nl/praat/

Chen, H., Jen, Y., Wang, C., Lee, J., Lin, Y., 2007. Etiology

of Vocal Cord Paralysis. I n ORL, (3), pp.167-171.

Fawcus, M., 1991. Voice Disorders and Their

Management. 2 ed. Londres: Springer-

Science+Business Media, B.V., pp.1-392.

Felippe, A.C.N., Grillo, M.H.M.M., Grechi, T.H. 2006.

Normatização de medidas acústicas para vozes

normais. In Brazilian Journal of Otorhinolaryngology,

72 (5): 659-664.

Fernandes, J., Silva, L., Teixeira, F., Guedes, V., Santos, J.,

Teixeira, J. P. 2019. Parameters for Vocal Acoustic

Analysis - Cured Database. In Procedia Computer

Science, 164 (2019): 654-661.

Fernandes, J., Teixeira, F., Guedes, V. Junior, A. &

Teixeira, J. P., 2018. “Harmonic to Noise Ratio

Measurement - Selection of Window and Length”,

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

162

Procedia Computer Science - Elsevier. Volume 138,

Pages 280-285.

Finger, L.S., Cielo, C.A., Schwarz, K. 2009. Medidas

vocais acústicas de mulheres sem queixas de voz e com

laringe normal. In Brazilian Journal of

Otorhinolaryngology, 75 (3): 432-440.

Gan, G., Ma, C. & Wu, J., 2007. Data Clustering. 1 ed.

Philadelphia, Pa.: SIAM, Society for Industrial and

Applied Mathematics, pp.1-487.

Guedes, V., Junior, A., Teixeira, F., Fernandes, J., Teixeira,

J. P. 2018. Long Short-Term Memory on Chronic

Laryngitis Classification. In Procedia Computer

Science - Elsevier. 138 (2018): 250-257.

Haykin Simon. 1999. Neural Networks: A comprehensive

foundation. New Jersey, Prentice Hall.

Holmberg, E., Doyle, P., Perkell, J., Hammarberg, B.,

Hillman, R., 2003. Aerodynamic and acoustic voice

measurements of patients with vocal nodules: variation

in baseline and changes across voice therapy. In

Journal of Voice, 17(3), pp.269-282.

Jain, A.K., Murty, M.N., and Flynn P.J. 1999. Data

Clustering: A Review. In ACM Computing Surveys, 31

(3): 264-323.

Kandoğan, T., Koç, M., Aksoy, G., 2009. Effectiveness of

voice therapy in Hyper-functional dysphonia in adult

patients. In The Turkish Journal of Ear Nose and

Throat, 19(4), pp.198-202.

Kohonen, T. 1994. Self-Organizing-Maps. Filand: Sringer

Series. 3 ed, 1-520.

Martínez, D., Lleida, E., Ortega, A., Miguel, A., Villalba, J.

2012. Voice Pathology Detection on the Saarbruecken

Voice Database with Calibration and Fusion of Scores

Using MultiFocal Toolkit. In Comm. in Comp. and

Information Science, 328 (1): 99-109.

MathWorks. Hierarchical Clustering. Available on:

<https://www.mathworks.com/help/stats/hierarchical-

clustering.html>. Access in: 21 apr. 2020.

Oliveira, A., Dajer, M., Fernandes, P., Teixeira, J. P., 2020.

Clustering of Voice Pathologies based on Sustained

Voice Parameters. In Proceedings of the 13th

International Joint Conference on Biomedical

Engineering Systems and Technologies - Volume 4

BIOSIGNALS, pages 280-287. DOI:

10.5220/0009146202800287

Panek D., Skalski A., Gajda J. and Tadeusiewicz R., 2015.

Acoustic Analysis Assessment in Speech Pathology

Detection. Int. J. Appl. Math. Comput. Sci., Vol. 25,

No. 3, 631-643. DOI: 10.1515/amcs-2015-0046.

Pavel, B. 2006. A Survey of Clustering Data Mining

Techniques. In Kogan J., Nicholas C., Teboulle M.

(eds) Grouping Multidimensional Data. Springer,

Berlin, Heidelberg.

Teixeira, F., Fernandes, J., Guedes, V. Junior, A., Teixeira,

J. P. 2018. Classification of Control/Pathologic

Subjects with Support Vector Machines, In Procedia

Computer Science – Elsevier, 138 (2018): 272-279.

Teixeira, F., Teixeira, J. P. 2020. Deep-learning in

Identification of Vocal Pathologies. In Proceedings of

the 13th International Joint Conference on Biomedical

Engineering Systems and Technologies

- Volume 4

BIOSIGNALS, ISBN 978-989-758-398-8, ISSN 2184-

4305, pages 288-295. DOI:

10.5220/0009148802880295.

Teixeira, J. P., Fernandes, P. O. 2015 “Acoustic Analysis

of Vocal Dysphonia”. Procedia Computer Science -

Elsevier 64, pages 466 – 473.

Teixeira, J. P., Alves, N., Fernandes, P. O. 2020. Vocal

Acoustic Analysis: ANN Versos SVM in Classification

of Dysphonic Voices and Vocal Cords Paralysis. In

International Journal of E-Health and Medical

Communications (IJEHMC), 11 (1): 37-51.

Teixeira, J. P., Fernandes, J., Teixeira, F., Fernandes, P.

2018. Acoustic Analysis of Chronic Laryngitis -

Statistical Analysis of Sustained Speech Parameters. In

11th International Joint Conference on Biomedical

Engineering Systems and Technologies, 4 (2018): 168-

175. ISBN 978-989-758-279-0

Teixeira, J. P., Fernandes, P. O., 2014. “Jitter, Shimmer and

HNR classification within gender, tones and vowels in

healthy voices”. Procedia Technology - Elsevier,

Volume 16, Pages 1228-1237.

Teixeira, J. P., Fernandes, P. O., Alves, N. 2017. Vocal

Acoustic Analysis - Classification of Dysphonic Voices

with Artificial Neural Networks. In Procedia Computer

Science 121 (2017): 19–26.

Teixeira, J. P., Gonçalves, A., 2016. “Algorithm for jitter

and shimmer measurement in pathologic voices”,

Procedia Computer Science - Elsevier 100, 271 – 279.

Toutounchi, S., Eydi, M., Golzari, S., Ghaffari, M.,

Parvizian, N., 2014. Vocal Cord Paralysis and its

Etiologies: A Prospective Study. In Journal of

Cardiovascular and Thoracic Research, 6(1), pp.47-50.

Tsnas, A., Little, M., McSharry, P. & Ramig, L., 2010.

Nonlinear speech analysis algorithms mapped to a

standard metric achieve clinically useful quantification

of average Parkinson's disease symptom severity.

Journal of the Royal Society Interface, 17 Nov., pp.

842-855.

Clustering Pathologic Voice with Kohonen SOM and Hierarchical Clustering

163