Boosting Self-localization with Graph Convolutional Neural Networks

Takeda Koji and Tanaka Kanji

Department of Engineering, University of Fukui, 3-9-1, Bunkyo, Fukui, Japan

Keywords:

Visual Robot Self-localization, Graph Convolutional Neural Network, Map to DNN.

Abstract:

Scene graph representation has recently merited attention for being ﬂexible and descriptive where visual robot

self-localization is concerned. In a typical self-localization application, the objects, object features and object

relationships of the environment map are projected as nodes, node features and edges, respectively, on to

the scene graph and subsequently mapped to a query scene graph using a graph matching engine. However,

the computational, storage, and communication overhead costs of such a system are directly proportional

to the number of feature dimensionalities of the graph nodes, often signiﬁcant in large-scale applications.

In this study, we demonstrate the feasibility of a graph convolutional neural network (GCN) to train and

predict alongside a graph matching engine. However, visual features do not often translate well into graph

features in modern graph convolution models, thereby affecting their performance. Therefore, we developed a

novel knowledge transfer framework that introduces an arbitrary self-localization model as the teacher to train

the GCN-based self-localization system i.e., the student. The framework, additionally, facilitated lightweight

storage and communication by formulating the compact output signals from the teacher model as training data.

Results on the Oxford RobotCar datasets reveal that the proposed method outperforms existing comparative

methods and teacher self-localization systems.

1 INTRODUCTION

The graph-based scene model has recently received

signiﬁcant attention as being a ﬂexible and descrip-

tive scene model for visual robot self-localization.

In self-localization applications, the objects, object

features, and object relationships of the environment

map are generally transposed as nodes, node features,

and edges, respectively, in the scene graph, which

are then matched against a query scene graph by a

graph matching engine; such a scene graph model

can be used with various types of scene data. In

(Gawel et al., 2018), the input scene is segmented

semantically to procure the graph nodes, which are

linked to their neighbours via graph edges. Con-

versely, a view sequence-based localization can be

modelled as a scene graph wherein nodes become the

image frames and the edges connect successive image

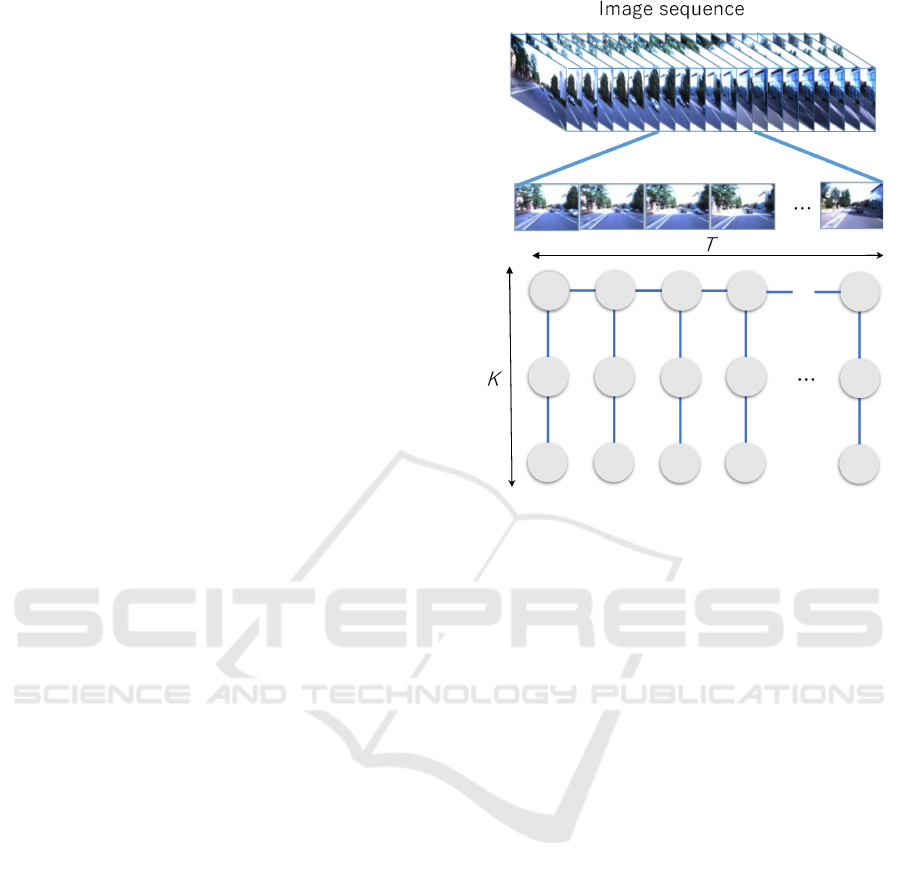
frames (Naseer et al., 2014). For this study, the view

sequence-based scene graph representation, as shown

in Fig. 1, is utilised.

Here, we attempt to analyse the scalability of

a graph-based representation for large-scale applica-

tions such as long-term map-learning (Milford and

Wyeth, 2012). The storage cost of a scene graph is

proportional to the number of dimensionalities of the

graph nodes, i.e., graphs, nodes per graph and dimen-

sionality of the node features, which escalates with

the size of the environment. Moreover, the computa-

tional cost of a graph matching engine is reliant on the

graph size and often requires approximations, such as

dimension-reduction, to achieve considerable compu-

tational speed. To address these issues, we propose a

novel framework to improve the efﬁciency of a scene

graph-based self-localization system without compro-

mising the accuracy.

In this study, we demonstrate the viability of a

graph-convolutional neural network (GCN), a popu-

lar graph neural network (GNN), as an efﬁcient tool to

train and predict with a graph matching engine (Wang

et al., 2019). In GCN, a graph-convolutional layer

is initially harnessed to extract graph features, which

are then supplied to the graph-summarisation process

to enrich the features. GCN has been successfully ap-

plied to various types of graphical data applications,

including chemical reactivity and web-scale recom-

mender systems (Coley et al., 2019; Ying et al., 2018).

The GCN training and prediction process is computa-

Koji, T. and Kanji, T.

Boosting Self-localization with Graph Convolutional Neural Networks.

DOI: 10.5220/0010212908610868

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages

861-868

ISBN: 978-989-758-488-6

861

tionally efﬁcient and the complexity is in the order of

O(m + n), where m and n are the edges and nodes re-

spectively.

To assess the performance of a visual robot self-

localization system, it is important to determine how

intuitively the robot converts a given visual feature to

a graph feature. As visual features typically aid in

visual self-localization tasks, such direct conversion

can adversely affect the quality of the resultant graph

features. To this effect, we propose a novel knowl-

edge transfer (KT) framework, which introduces an

arbitrary self-localization model as a teacher to train

the GCN-based self-localization system as the stu-

dent. The proposed framework adopts the standard

KT framework for knowledge distillation, and our

feature learning strategy is inspired by the multimedia

information retrieval (MMIR) domain (Hinton et al.,

2015; Imhof and Braschler, 2018).

The contributions of this study can be summarised

as follows: a) to evaluate the beneﬁts of GCN in not

only augmenting the self-localization performance

but also economising the computational, storage and

communication costs; and b) to conceive a versa-

tile framework for feature learning based on a novel

teacher-to-student KT model. Results on the Ox-

ford RobotCar datasets highlighted the superior per-

formance of the proposed method when compared to

other existing methods and teacher self-localization

systems.

2 RELATED WORK

Robot self-localization using vision is one of the

most important subdomains of mobile robotics and

has been studied in various contexts, including multi-

hypothesis pose tracking, map matching, image re-

trieval and view sequence matching (Himstedt and

Maehle, 2017; Neira et al., 2003; Cummins and New-

man, 2008; Milford and Wyeth, 2012). Our study bor-

rows from view sequence matching, wherein a real-

time short-term view sequence is supplied as a query

to obtain the corresponding component on the map

view sequence.

Unlike previous studies, the proposed approach

models self-localization as a classiﬁcation problem.

The problem consists of a) partitioning the robot

workspace into different place classes; b) training a

visual place classiﬁer using a class-speciﬁc training

set; c) predicting the place class for a given query

image using the pre-trained classiﬁer. For mobile

robotics, training a deep convolutional neural net-

work (DCN) as a visual place classiﬁer is relatively

straightforward. Recently, in (Kim et al., 2019), it

Figure 1: Overview of GCN-based self-localization frame-

work used in conjunction with view-sequence-based scene

graphs; the bottom panel illustrates nodes (circles) and

time/attribute (horizontal/vertical line-segments) edges of a

scene graph.

is successfully implemented for a 3-D point cloud-

based self-localization using scan context image rep-

resentation. However, the current study differs in two

aspects viz. it focuses on the graph-based view se-

quence representation that can accommodate interac-

tions between image frames, and it further addresses

KT from a teacher self-localization model to a student

GCN-based self-localization system.

GNNs have merited interest among the pattern

recognition community as being ﬂexible and efﬁcient

for pattern recognition and machine learning, and

GCN is the most widely used GNN that generalizes

the traditional convolution to data of graph structures.

In the past, GCN has been successfully harnessed in

applications where the traditional DCN proved to be

either inefﬁcient or unsuitable (Coley et al., 2019;

Ying et al., 2018; Zhang and Zhu, 2019). However,

in this study, we revisit a conventional visual robot

self-localization application with the aim to improve

existing solutions.

3 VISUAL SELF-LOCALIZATION

PROBLEM

Here, the self-localization process is modelled as

a classiﬁcation problem constituting three distinct

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

862

Figure 2: Pipeline of graph matching engine. (a) Scene graph descriptor; (b) KT from teacher self-localization model; and (c)

Supervised learning of the GCN model.

stages: (1) Place partitioning that partitions the robot

workspace into a collection of place classes; (2) Map-

ping (i.e., training) that takes a visual experience with

ground-truth viewpoint information collected in the

workspace as training data and trains a visual place

classiﬁer; (3) Self-localization (i.e., testing) that takes

a query graph representing a short-term live view-

sequence with length T , and predicts the place class.

To reduce storage costs, the trained visual place

classiﬁer is utilised instead of the original train-

ing data during testing. Additionally, the post-

veriﬁcation techniques like random sample consen-

sus (RANSAC) are omitted to alleviate the overall

computational burden (Raguram et al., 2012). Experi-

mental results nevertheless revealed the robustness of

the proposed framework toward outliers in measure-

ments.

A standard grid-based place partitioning method

is employed to deﬁne the place classes. First, a reg-

ular 2-D grid is imposed on the robot workspace i.e.,

a moving plane, and each grid cell is subsequently

viewed as a place class. It should be noted that place

partitioning can be enhanced by adopting pertinent

state-of-the-art techniques.

4 GCN-BASED

SELF-LOCALIZATION

Figure 2 depicts the pipeline of the graph-matching

engine. It consists of three modules, which are de-

tailed in the following.

1. A scene graph descriptor to translate an input view

sequence of length T to a scene graph.

2. A KT module to facilitate communication be-

tween the teacher (arbitrary self-localization

model) and student (GCN-based self-localization

system).

3. A supervised learning module that utilises the

view sequences to train the classiﬁer, which is

used to predict the place class for a given query

sample.

A supervised learning procedure is applied to train

the scene graph classiﬁer. In the mapping stage, a

collection of overlapping sub-sequences of length T

are sampled from the visual experience and divided

into place class-speciﬁc training sets according to the

available viewpoint information as well as the pre-

deﬁned place partitioning labels.

Boosting Self-localization with Graph Convolutional Neural Networks

863

We emphasize that all the training set can be

thrown away once the GCN classiﬁer is trained. Con-

sidering the proposed framework employs overlap-

ping sub-sequences as training data, the ﬁnal dataset

size as well as the number of graph nodes are expected

to be signiﬁcantly larger than that estimated originally

with the view sequences. Nevertheless, the training

data has no impact on the storage overhead after com-

pressing the training data into a GCN classiﬁer.

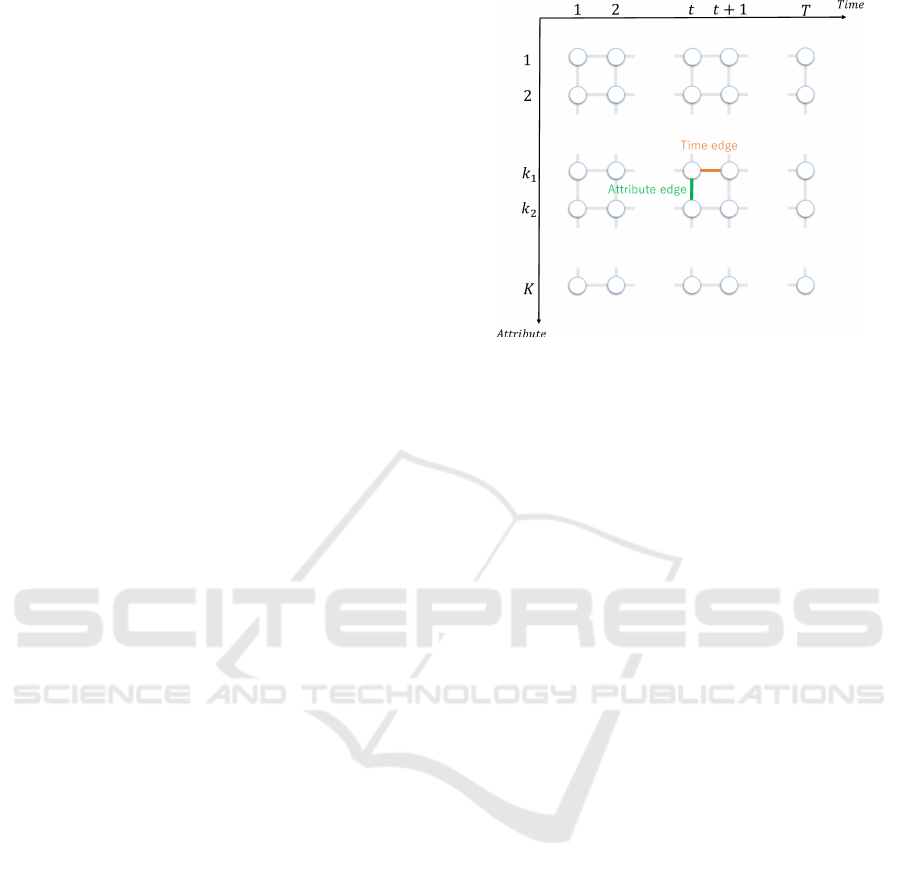
The domain invariance is elicited by modifying the

length and intervals of the map/query (for train-

ing/testing respectively) view sequences, as high-

lighted in Fig. 3.

A uniform length T is initially assumed for all

map/query view sequences to develop the invariance

across different domains. Moreover, these T frames

are selected such that the travel distance between

successive frames approximately matches a predeter-

mined value to obtain invariance against the vehi-

cle’s ego-motion speed. This setup is also empiri-

cally corroborated to highlight the efﬁciency of the

methodology for visual self-localization. It should be

noted that the GCN theory is not limited to homoge-

neous graphs, and extending the proposed approach

to tackle heterogeneous graphs is envisaged in future.

First, a collection of K different image feature ex-

tractors i.e., F

, · ··, F

, are collated using several

image processing techniques like NetVLAD, Canny

operation, depth regression and semantic segmenta-

tion, as shown in section 4 (Arandjelovi

c et al., 2016;

Canny, 1986; Alhashim and Wonka, 2018; Chen

et al., 2018b). Then, each graph node, n = (t, k, f

[t]),

represents an attribute feature vector f

[t] of the k-th

extractor from the tth image frame. Conversely, two

types of graph edges viz. time and attribute, are ap-

plied such that the time edge, e = (t, t + 1, k), con-

nects two graph nodes with successive time indices as

(t, t + 1) with the attribute index k and the attribute

edge, e = (t, k1, k2), connects two graph nodes with

different attribute indices as k

and k

having the same

time index t.

We now elucidate how a robot can translate input

view images to graph features required for training

and, subsequently, validating the model. A straight-

forward way to achieve this is by directly translat-

ing the visual features, originally designed for visual

self-localization tasks, to graph node features. De-

signing visual features has been a topic of interest in

recent self-localization literature, with past studies al-

ternatively proposing to apply compact, yet discrim-

inative, visual features like autoencoder-based meth-

ods, GAN-based methods, and CNN-based methods

(Merrill and Huang, 2019; Hu et al., 2019; Arand-

jelovi

c et al., 2016). In particular, NetVLAD is an

Figure 3: Time and attribute edges.

emerging visual feature extractor in computer vision

and robotics, and hence has been used against the

proposed methodology for comparison (Arandjelovi

et al., 2016).

One of the main concerns with incorporating

GNNs in this study is that visual features are not op-

timised for graph convolutions. In theory, their su-

perior performances of the past may not necessarily

be replicated in GCN-based self-localization tasks.

Results of our experiments, in fact, showed that the

self-localization performance deteriorated when vi-

sual features were directly used as node features in

the GCN model.

To address this issue, we engage a class-speciﬁc

probability distribution vector (PDV) output along

with a teacher self-localization model as the train-

ing data, which is derived from the standard KT

approach for knowledge distillation (Hinton et al.,

2015). The PDV representation facilitates applica-

bility to a broad range of teacher output signals, in-

cluding the tf-idf scores for the bag-of-words im-

age retrieval models, RANSAC scores in the post-

veriﬁcation stage and mean average intersection-

over-union in object matching systems (Sivic and

Zisserman, 2003; Garcia-Fidalgo and Ortiz, 2018;

underhauf et al., 2015).

A node image, I, is converted to a graph feature

vector using a teacher self-localization system, Y , and

an image-to-feature translator, M:

f = M(Y (I)). (1)

The conversion procedure is as follows: a) I is ﬁrst

supplied to Y to obtain the output PDV signal, o =

Y (I), from the teacher system; and b) o is then

mapped to a graph feature vector as f = M(o).

Four teacher systems, Y

, Y

and Y

, were de-

signed for this study, as shown in Fig. 4, by combin-

ing four different image ﬁlters, Z

(I) (i ∈ [1, 4]), with

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

864

a single nearest-neighbour (NN)-based VLAD match-

ing engine, Y

, given by:

= Y

(I)). (2)

An NN matching engine represents a place class

via a collection of VLAD descriptors that are ex-

tracted from images in the class-speciﬁc training set

(Chen et al., 2018a). Then, it computes the image-

to-class distance (i.e., dissimilarity) between a given

query VLAD vector and its nearest neighbour among

the class-speciﬁc VLAD vectors.

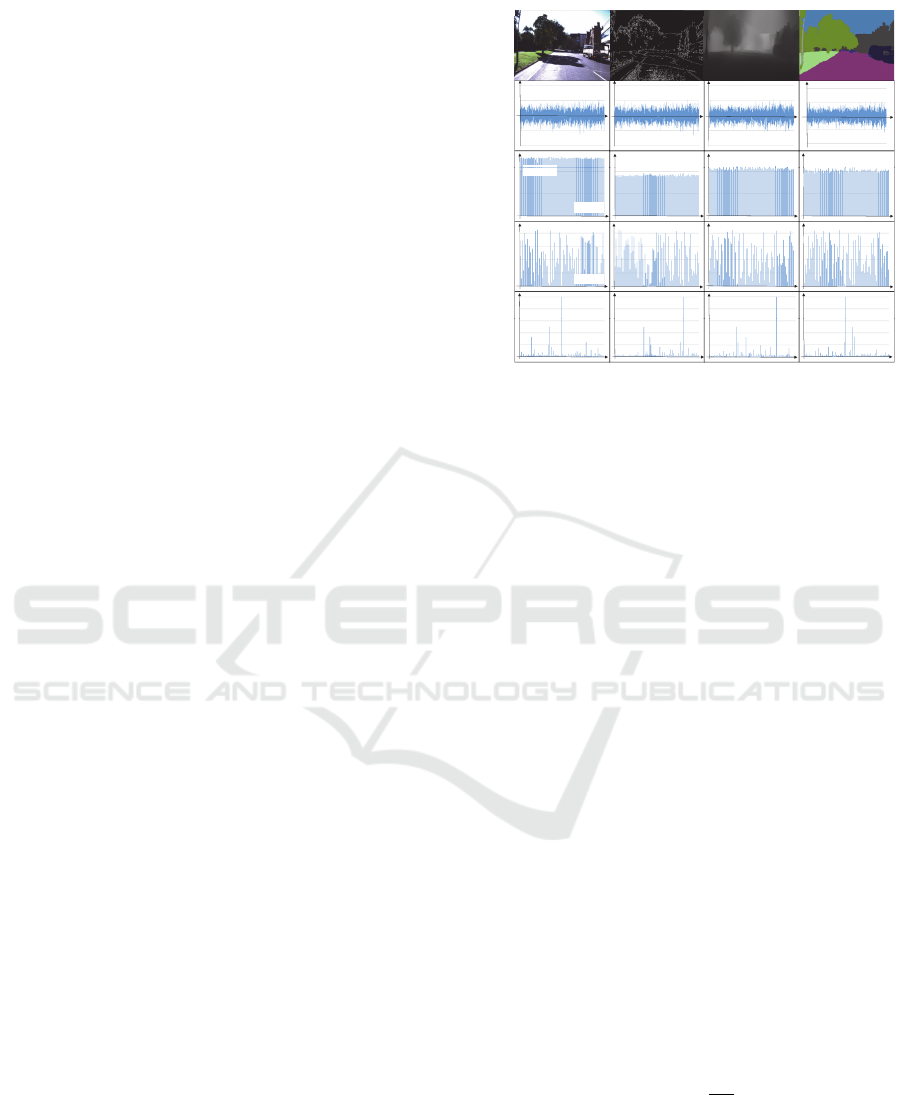
Four image ﬁlters were implemented as depicted

along the horizontal labels in Fig. 4. Z

is a basic

identity mapping function, Z

represents a Canny im-

age ﬁlter that emphasises the gradient of the input im-

age, Z

is a depth image regressor trained as an un-

supervised task that predicts a depth image from a

monocular image (Alhashim and Wonka, 2018), and

highlights a semantic segmentation ﬁlter that con-

verts an input image to a semantic label image whose

pixel colour is derived from the pixel-wise class la-

bels deﬁned in the original colour palette in (Chen

et al., 2018b). Furthermore, four different mapping

functions were applied to the image ﬁlters viz. M

(·),

(·), M

(·) and M

(·) as highlighted along the ver-

tical labels in Fig. 4. M

is an identity mapper used

solely with Z

. M

is a class-speciﬁc distance value

vector wherein each c-th place class is assigned the L2

norm of the distance between the query feature and its

nearest neighbour feature in the same class. M

em-

ploys a ranking function such that the c-th place class

in a given PDV is assigned a rank by sorting the PDV

elements in the ascending order of their probability

scores and the resultant vector of rank values is used

as the node feature vector; such rank-based represen-

tation was administered based on the recent success

it has found in MMIR applications where ranks are

used as features to fuse information across several do-

mains (for example, the domain of individuals using

MMIR systems) (Imhof and Braschler, 2018). M

different from M

in that the inverse rank values are

exploited instead, which was inspired by the rank fu-

sion approach in (Hsu and Taksa, 2005).

We adopt the standard training procedure for GCN, as

delineated in (Wang et al., 2019), to train the proposed

self-localization system. Initially, a graph is deﬁned

as G = (V, E), where V is the set of nodes and E is

the set of edges. All graphs are undirected i.e., a spe-

cial case of directed graphs where a pair of connected

nodes are indicated by a pair of edges with inverse di-

rections. Let v

in V denote a node and e

i j

= (v

, v

)

in E denote the edge pointing from v

to v

. Then,

the neighbourhood of node v can then be deﬁned as

N(v) = {u ∈ V | (u, v) ∈ E}. Each node has a corre-

sponding feature vector expressed as h ∈ R

. The rep-

Rawimage Canny Depth Semantic

Intensit

NetVLAD

Vector

ElementID

Match

Distance

ClassID

Distance

Rank

ClassID

Inverse

Rank

Inverse

Rank

ClassID

Figure 4: Image and feature vectors generated by individual

image ﬁlters and image-to-feature translators.

resentation of v is generated by aggregating its own

features h

and those in N(v) connected to v via edges,

(u ∈ N(v)), computed as follows: a) each node ini-

tially receives features from N(v); b) the features are

thereafter summarised in a summation operation; and

c) the summarised features are then supplied to a sin-

gle layer fully-connected neural network, followed by

a non-linear ReLU transformation expressed as:

new

= ReLU

(

∑

u∈N(v

)∪v

))

, (3)

where W is weight matrix W ∈ R

D×D

′

for applying

the linear transformation, and D and D

′

are the di-

mensions of the feature vector before and after the

operation. The operation at the l-th GCN layer is gen-

eralised as:

(l)

= ReLU

(

(l−1)

(

∑

u∈N(v

)∪v

(l−1)

))

. (4)

This operation is applied to all nodes to update the

node features and is repeated L times, corresponding

to the number of layers, which was conﬁgured as 2

for this study. Finally, the features of all nodes are

summarised as an average, and then passed to a fully-

connected (FC) and softmax operation given by:

p = Softmax

(

|V |

∑

u∈V

))

, (5)

where h

is the feature at the node u being the output

of the ﬁnal GCN layer. The system was implemented

using the deep graph library with a Pytorch backend,

as in (Wang et al., 2019).

Boosting Self-localization with Graph Convolutional Neural Networks

865

Table 1: Dataset characteristics.

dataset ID weather #images detour roadworks

15-08-28-09-50-22 (A) sun 31,855 × ×

15-10-30-13-52-14 (B) overcast 48,196 × ×

15-11-10-10-32-52 (C) overcast 29,350 × ◦

15-11-12-13-27-51 (D) clouds 41,472 ◦ ◦

15-11-13-10-28-08 (E) overcast 42,968 × ×

5 EXPERIMENTS

We evaluated the proposed methodology on the Ox-

ford RobotCar dataset (Maddern et al., 2017). Table 1

enumerates the characteristics of the dataset. For the

grid-based place partitioning process described in 3,

we used a 14×17 grid with a resolution of 0.1 degree

horizontally and vertically (approximately 110×70

m). Resultantly, the average number of place classes

was 81-86 and a place class was eliminated from the

training and test sets if the number of images belong-

ing to the class was less than or equal to 6. Every

image was cropped to 1080×800 pixels to eliminate

regions occluded by the vehicle itself (i.e., 100 pixels

from each side and 180 pixels from the bottom). The

length of the map and query view sequences was set to

T =10 and the intervals between successive frames in

the travel distance was approximately 2[m]. Finally,

the sequences spanning adjacent places were removed

altogether from both training and test sets. For sim-

plicity, we consider scene graphs with two image ﬁl-

ters (i.e., one attribute edges per image frame) and as

the default setting, the combination of the image ﬁl-

ters with Z

and Z

is used.

To compare the performance accuracy, we used

the implementation of an NN matching system with

the NetVLAD descriptor (Arandjelovi

c et al., 2016)

(adapting the implementation in (Cieslewski et al.,

2018)) which uses the ﬁrst image frame in each view-

sequence as the query. Conversely, the image-to-class

distance described in 4 was used to measure the class

dissimilarity.

Table 2: Top-1 accuracy.

A B C D E

A 92.3 88.5 80.8 88.4

B 92.4 97.3 87.3 97.6

C 91.5 94.8 90.9 95.7

D 88.2 88.0 93.2 91.6

E 92.7 97.4 99.2 94.4

The number of GCN layers was set to 2 and fea-

ture dimensionality of the GCN layers was conﬁgured

as C, 256, 256, and C for a size C class set. For

node summarisation, the SUM and ReLU operations

were administered. The number of epochs, batch

size and learning rate were set to 5, 32, and 0.001,

respectively. The training was conducted for 170 s

on 31,835 samples on a personal computer running

the Intel(R) Xeon(R) GOLC 6130 CPU at 2.10 GHz.

The self-localization performance was measured by

the top-1 accuracy, as highlighted in Table 4. The

horizontal and vertical indexes in the table are IDs

of query and map datasets, respectively. The predic-

tion turnaround time amounted to 15.5 ms per query

graph, rendering the proposed framework as compu-

tationally expeditious. This implies signiﬁcant reduc-

tion in computational complexity compared with pre-

vious approaches such as graph matching.

Table 4 shows results for the proposed method

with different choices of the image ﬁlter Z

as well

as the comparing method. From top to bottom, the

1st, 2nd and 3rd lines correspond to the combinations

of image ﬁlters (Z

, Z

), (Z

, Z

) and (Z

, Z

), while

the 4th line corresponds the result with the comparing

method. By comparing the different combinations of

image ﬁlters, the combination of Z

and Z

yielded

the best performance. It can be seen that the pro-

posed method outperforms the comparing method for

almost all settings considered here.

Table 4 enumerates the comparative results of ad-

ministering different combinations of image ﬁlters on

the proposed method against existing methods. From

top to bottom, each line corresponds to that image

ﬁlters Z

, Z

and Z

. Among the various com-

binations applied, that of Z

and Z

yielded the best

outcome. It can be seen that the proposed method

surpassed its competitors in most of the settings con-

sidered here.

Two experiments were performed as part of an ab-

lation study. In the ﬁrst instance, the scene graphs

were modiﬁed by removing the edges to train the

model and, in the second, the graph topology was

modiﬁed by removing one of the time and attribute

edges at random. Table Table 3 outlines the exper-

imental results. It is apparent that graphs with both

time and attribute edges worked signiﬁcantly better

in almost all cases. The use of attribute edges fa-

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

866

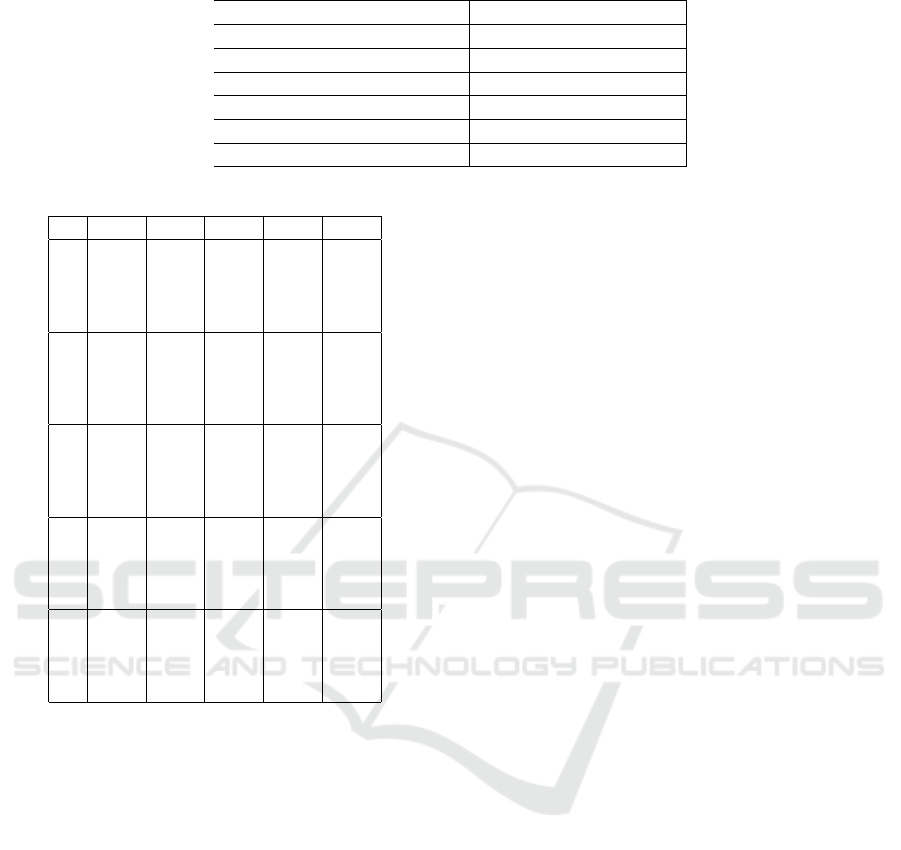
Table 3: Performance comparison.

Method Average Top-1 accuracy

Ours 92.3

NetVLAD 87.9

Ours w/o edge 89.0

Ours w/o attribute edge 91.5

Ours w/o time edge 88.7

Ours w/o attribute node/edge 91.7

Table 4: Results for different choices of image ﬁlters.

A B C D E

92.3

92.8

93.2

83.1

88.5

90.0

89.9

85.0

80.8

82.0

83.3

79.7

88.4

90.2

91.5

82.2

92.4

92.3

91.1

86.9

97.3

98.5

96.7

95.2

86.6

85.0

84.2

81.6

97.8

97.6

95.5

91.5

91.2

91.7

83.6

94.8

94.9

94.7

91.7

90.9

89.8

90.7

88.7

95.7

95.8

94.0

88.2

87.6

87.2

78.0

88.0

87.7

87.3

87.1

93.2

87.6

93.2

92.4

91.6

91.9

92.6

88.4

92.7

93.3

94.5

83.9

97.4

96.9

93.3

99.2

99.0

99.2

97.3

94.4

93.1

94.1

91.1

cilitated resistance against feature ambiguity by com-

pensating individual features’ drawbacks. The use of

time edges facilitated resistance against partial occlu-

sions incurred from changes in illumination between

the training and test domains. Consequently, the pro-

posed framework showed potential to solve a variety

of problems by integrating the available cues from

different image ﬁlters as well as the time and spatial

graphs.

6 CONCLUSIONS

We investigated the utility of a GCN model to aug-

ment the performance of visual robot self-localization

systems whilst alleviating the computational, stor-

age and communication costs. Furthermore, a novel

and versatile KT framework was conceived to fa-

cilitate information transfer from an arbitrary self-

localization model (teacher) that integrated the avail-

able cues from different image ﬁlters as well as the

time and spatial contextual information. Results on

the Oxford RobotCar datasets substantiated the ro-

bustness of the proposed framework when compared

to other existing methods and teacher self-localization

systems. Although we harnessed a view sequence-

based scene graph representation for this study, other

scene graph representations can also be employed, in-

cluding attribute grammar-based scene graphs (Stein-

lechner et al., 2019). We attempt to explore other

general heterogeneous scene graphs so as to tackle

map/query scene graphs of variable sizes and shapes

in future.

ACKNOWLEDGEMENTS

Our work has been supported in part by JSPS

KAKENHI Grant-in-Aid for Scientiﬁc Research (C)

17K00361, and (C) 20K12008.

REFERENCES

Alhashim, I. and Wonka, P. (2018). High quality monoc-

ular depth estimation via transfer learning. CoRR,

abs/1812.11941.

Arandjelovi

c, R., Gronat, P., Torii, A., Pajdla, T., and Sivic,

J. (2016). NetVLAD: CNN architecture for weakly

supervised place recognition. In IEEE Conference on

Computer Vision and Pattern Recognition.

Canny, J. (1986). A computational approach to edge de-

tection. IEEE Transactions on pattern analysis and

machine intelligence

, (6):679–698.

Chen, G. H., Shah, D., et al. (2018a). Explaining the suc-

cess of nearest neighbor methods in prediction. Now

Publishers.

Chen, L., Zhu, Y., Papandreou, G., Schroff, F., and Adam,

H. (2018b). Encoder-decoder with atrous separable

convolution for semantic image segmentation. In Fer-

rari, V., Hebert, M., Sminchisescu, C., and Weiss, Y.,

editors, Computer Vision - ECCV 2018 - 15th Euro-

pean Conference, Munich, Germany, September 8-14,

2018, Proceedings, Part VII, volume 11211 of Lecture

Notes in Computer Science, pages 833–851. Springer.

Cieslewski, T., Choudhary, S., and Scaramuzza, D. (2018).

Data-efﬁcient decentralized visual SLAM. In 2018

IEEE International Conference on Robotics and Au-

tomation, ICRA, pages 2466–2473.

Boosting Self-localization with Graph Convolutional Neural Networks

867

Coley, C. W., Jin, W., Rogers, L., Jamison, T. F., Jaakkola,

T. S., Green, W. H., Barzilay, R., and Jensen, K. F.

(2019). A graph-convolutional neural network model

for the prediction of chemical reactivity. Chemical

science, 10(2):370–377.

Cummins, M. and Newman, P. (2008). Fab-map: Proba-

bilistic localization and mapping in the space of ap-

pearance. Int. J. Robotics Research, 27(6):647–665.

Garcia-Fidalgo, E. and Ortiz, A. (2018). ibow-lcd: An

appearance-based loop-closure detection approach us-

ing incremental bags of binary words. IEEE Robotics

and Automation Letters, 3(4):3051–3057.

Gawel, A., Del Don, C., Siegwart, R., Nieto, J., and Cadena,

C. (2018). X-view: Graph-based semantic multi-view

localization. IEEE Robotics and Automation Letters,

3(3):1687–1694.

Himstedt, M. and Maehle, E. (2017). Semantic monte-

carlo localization in changing environments using rgb-

d cameras. In 2017 European Conference on Mobile

Robots (ECMR), pages 1–8. IEEE.

Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling

the knowledge in a neural network. arXiv preprint

arXiv:1503.02531.

Hsu, D. F. and Taksa, I. (2005). Comparing rank and score

combination methods for data fusion in information

retrieval. Information retrieval, 8(3):449–480.

Hu, H., Wang, H., Liu, Z., Yang, C., Chen, W., and

Xie, L. (2019). Retrieval-based localization based on

domain-invariant feature learning under changing en-

vironments. In IEEE/RSJ Int. Conf. Intelligent Robots

and Systems (IROS), pages 3684–3689.

Imhof, M. and Braschler, M. (2018). A study of untrained

models for multimodal information retrieval. Infor-

mation Retrieval Journal, 21(1):81–106.

Kim, G., Park, B., and Kim, A. (2019). 1-day learning, 1-

year localization: Long-term lidar localization using

scan context image. IEEE Robotics and Automation

Letters, 4(2):1948–1955.

Maddern, W., Pascoe, G., Linegar, C., and Newman, P.

(2017). 1 Year, 1000km: The Oxford RobotCar

Dataset. The International Journal of Robotics Re-

search (IJRR), 36(1):3–15.

Merrill, N. and Huang, G. (2019). CALC2.0: Com-

bining appearance, semantic and geometric informa-

tion for robust and efﬁcient visual loop closure. In

IEEE/RSJ Int. Conf. Intelligent Robots and Systems

(IROS), Macau, China.

Milford, M. J. and Wyeth, G. F. (2012). Seqslam: Vi-

sual route-based navigation for sunny summer days

and stormy winter nights. In 2012 IEEE Int. Conf.

Robotics and Automation, pages 1643–1649. IEEE.

Naseer, T., Spinello, L., Burgard, W., and Stachniss, C.

(2014). Robust visual robot localization across sea-

sons using network ﬂows. In AAAI, pages 2564–2570.

Neira, J., Tard

os, J. D., and Castellanos, J. A. (2003). Linear

time vehicle relocation in slam. In ICRA, pages 427–

433. Citeseer.

Raguram, R., Chum, O., Pollefeys, M., Matas, J., and

Frahm, J.-M. (2012). Usac: a universal framework for

random sample consensus. IEEE transactions on pat-

tern analysis and machine intelligence, 35(8):2022–

2038.

Sivic, J. and Zisserman, A. (2003). Video google: A text

retrieval approach to object matching in videos. In

null, page 1470.

Steinlechner, H., Haaser, G., Maierhofer, S., and Tobler,

R. F. (2019). Attribute grammars for incremental

scene graph rendering. In VISIGRAPP (1: GRAPP),

pages 77–88.

underhauf, N., Shirazi, S., Dayoub, F., Upcroft, B., and

Milford, M. (2015). On the performance of convnet

features for place recognition. In IEEE/RSJ Int. Conf.

Intelligent Robots and Systems (IROS), pages 4297–

4304.

Wang, M., Yu, L., Zheng, D., Gan, Q., Gai, Y., Ye, Z., Li,

M., Zhou, J., Huang, Q., Ma, C., Huang, Z., Guo, Q.,

Zhang, H., Lin, H., Zhao, J., Li, J., Smola, A. J., and

Zhang, Z. (2019). Deep graph library: Towards ef-

ﬁcient and scalable deep learning on graphs. ICLR

Workshop on Representation Learning on Graphs and

Manifolds.

Ying, R., He, R., Chen, K., Eksombatchai, P., Hamilton,

W. L., and Leskovec, J. (2018). Graph convolutional

neural networks for web-scale recommender systems.

In Proceedings of the 24th ACM SIGKDD Int. Conf.

Knowledge Discovery & Data Mining, pages 974–

983.

Zhang, L. and Zhu, Z. (2019). Unsupervised feature learn-

ing for point cloud understanding by contrasting and

clustering using graph convolutional neural networks.

In IEEE Int. Conf. 3D Vision, pages 395–404.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

868