A Multi-level Rank Correlation Measure for Image Retrieval

Nikolas Gomes de S

a, Lucas Pascotti Valem and Daniel Carlos Guimar

aes Pedronette

Department of Statistics, Applied Math. and Computing, S

ao Paulo State University (UNESP), Rio Claro, Brazil

Keywords:

Content-based Image Retrieval, Rank Correlation, Unsupervised Learning, Information Retrieval.

Abstract:

Accurately ranking the most relevant elements in a given scenario often represents a central challenge in many

applications, composing the core of retrieval systems. Once ranking structures encode relevant similarity

information, measuring how correlated are two rank results represents a fundamental task, with diversiﬁed

applications. In this work, we propose a new rank correlation measure called Multi-Level Rank Correlation

Measure (MLCM), which employs a novel approach based on a multi-level analysis for estimating the cor-

relation between ranked lists. While traditional weighted measures assign more relevance to top positions,

our proposed approach goes beyond by considering the position at different levels in the ranked lists. The

effectiveness of the proposed measure was assessed in unsupervised and weakly supervised learning tasks for

image retrieval. The experimental evaluation considered 6 correlation measures as baselines, 3 different image

datasets, and multiple features. The results are competitive or, in most of the cases, superior to the baselines,

achieving signiﬁcant effectiveness gains.

1 INTRODUCTION

Ranking tasks are ubiquitous in many aspects of

daily life: from arrangement of personal preferences

to modelling tool of priorities in enterprise environ-

ments (Webber et al., 2010). Many institutions keep

rankings of broad interest, aiming to guide decisions

in diversiﬁed domains, including books, universities,

artists, and many others. In fact, rankings represent

a powerful organization instrument in many scenar-

ios, allowing the deﬁnition of relationships among ob-

jects, according to a certain measure.

In artiﬁcial intelligence and information retrieval

applications, rankings have been widely used to rep-

resent the preferences of agents (humans or systems)

over a set of candidates (Xue et al., 2020). Due to

desired properties, as data reduction, independence

of scale and facilities for representation, rankings

and other ordinal data structures have been attract-

ing diverse applications (Farnoud Hassanzadeh and

Milenkovic, 2014).

As a result of the widely possibilities of applica-

tions, rankings are often needed to be compared. Such

comparisons often allow to infer the similarity of the

processes or systems which have generated the rank-

ings (Webber et al., 2010). Especially in information

retrieval, where information representation is often

supported by scores and ranked lists of items, the task

of performing comparison between two ranked lists

is of central importance (Yilmaz et al., 2008). This

relevance arises from distinct applications, includ-

ing comparison between rankings returned by dif-

ferent search engines, the lists of query recommen-

dation given by different algorithms (Vigna, 2015),

and complementarity between features in image re-

trieval (Valem and Pedronette, 2020).

In order to provide an objective and repeatable

comparison of ranked lists, it is needed to deﬁne a

rank correlation measure (Webber et al., 2010). In

fact, correlation coefﬁcients are well-known statis-

tical tools, widely exploited in statistical analysis,

pattern recognition, and image processing. One of

the more traditional measures is the Pearson corre-

lation coefﬁcient, which only measures linear depen-

dence relations (Couso et al., 2018). The rank cor-

relation measures or distances between permutations

have also a long and interdisciplinary history (Kumar

and Vassilvitskii, 2010; Fagin et al., 2004; Webber

et al., 2010).

The most popular rank correlation statistics are the

Kendall’s τ and Spearman correlation coefﬁcient (Ku-

mar and Vassilvitskii, 2010). While the Spear-

man correlation is equivalent to L1 distance between

ranks, the Kendall’s τ between two ranked lists is pro-

portional to the number of pairwise inversions needed

to convert one ranking into the other (Yilmaz et al.,

2008; Kumar and Vassilvitskii, 2010). Both are orig-

inally non-weighted measures in the sense that they

370

Gomes de Sá, N., Valem, L. and Pedronette, D.

A Multi-level Rank Correlation Measure for Image Retrieval.

DOI: 10.5220/0010220903700378

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages

370-378

ISBN: 978-989-758-488-6

do not assign different weights to elements at top po-

sitions of ranked lists. With applications predomi-

nantly in information retrieval, various efforts have

been made in extending traditional measures to gen-

eralized weighted models (Couso et al., 2018; Okada

et al., 2015; Vigna, 2015).

In addition to weighted approaches of traditional

measures, many other rank correlation measures have

been proposed (Fagin et al., 2004; Tan and Clarke,

2015; Xue et al., 2020; Vigna, 2015). In a representa-

tive work (Fagin et al., 2004), the challenge of deﬁn-

ing distance measures between top-k lists is addressed

considering different aspects. Various rank correla-

tion measures are presented under a uniﬁed frame-

work proposed to catalog them. The intersection met-

ric is ﬁrstly deﬁned in this work, based on the size of

intersection between ranked lists at different depths.

This information is also exploited by the Rank-Biased

Overlap (RBO) measure (Webber et al., 2010). RBO

analyzes the overlap of two rankings at incrementally

increasing depths, considering a parameter that mod-

els the user persistence in considering the overlap at

the next level. The weight of the overlap measured at

each depth is computed based on these probabilities.

Other rank correlation measures were proposed

by exploiting information retrieval measures formu-

lations. In (Yilmaz et al., 2008), a rank correlation

measure based on the average precision (AP) is pro-

posed. In (Tan and Clarke, 2015), a family of rank

measures based on effectiveness is proposed, con-

sidering some analogies with RBO. The interest of

the research community on rank correlation measures

keeps active and novel measures have been proposed.

Recently, a novel framework (Xue et al., 2020) was

proposed based on the analysis of the consensus of

rankings by considering common patterns embedded

in a ranking set.

Among the diversiﬁed scenarios of applications,

image retrieval systems have been successfully em-

ploying rank-based analysis and rank correlation

measures in the last years (Qin et al., 2011; Chen

et al., 2014; Valem et al., 2018; Pedronette et al.,

2019). The rank correlation measures have been

mostly exploited in contextual distance/similarity

learning tasks. In fact, ranked lists represent a relevant

source of contextual information in retrieval tasks.

Different from traditional distance/similarity mea-

sures, which perform only pairwise analysis, ranked

lists establish relationships among sets of images.

In these scenarios, unsupervised learning algorithms

have been proposed to compute more effective dis-

tance/similarity measures based on comparisons of

ranked lists (Chen et al., 2014). Diverse rank corre-

lation measures have been used for this purpose and

studies have shown that the measure drastically im-

pacts the results (Okada et al., 2015).

This paper proposes a novel Multi-Level Correla-

tion Measure (MLCM) for rank comparisons in im-

age retrieval tasks. While weighted measures assign

more relevance to top positions, our proposed ap-

proach goes beyond by considering the position at

different levels in the ranked lists. A broad experi-

mental evaluation was conducted in order to assess

the effectiveness of the measure in image retrieval

tasks. The experiments were performed on three pub-

lic datasets considering different features and effec-

tiveness evaluation. Comparisons with traditional and

recent rank correlation measures were also conducted

and the proposed approach achieved the higher results

on most of the experiments.

The remaining of this paper is organized as fol-

lows. Section 2 describes the rank model used along

the paper, and Section 3 presents the rank correlation

measures proposed. Section 4 describes the exper-

imental evaluation and Section 5 discusses conclu-

sions and future work.

2 RANK MODEL DEFINITION

This section presents a formal deﬁnition of the rank-

ing model considered along the paper. Let C ={img

img

, . . . , img

} be an image collection, where n de-

notes the size of the collection.

A distance between two images img

, img

is de-

ﬁned as ρ(i, j) and can be computed by different im-

age features. Based on the distance function ρ, a rank-

ing model can be derived. For a general image re-

trieval task, a ranked list τ

can be computed in re-

sponse to a query image img

, according to the dis-

tance function ρ. The top positions of ranked lists

are expected to contain the most relevant images with

regard to the query image, such that only the top-L

ranked images are considered, with L  n.

The ranked list τ

can be formally deﬁned as a

permutation (img

, img

, . . ., img

) of the subset

⊂ C , which contains the L most similar images

to a query image img

, such that |C

| = L. A per-

mutation τ

is a bijection from the set C

onto the

set [n

] = {1, 2, . . . , L}. The notation τ

(i) deﬁnes the

position (or rank) of image img

in the ranked list τ

Therefore, if img

is ranked before img

in the ranked

list of img

, i.e., τ

(i) < τ

( j), then ρ(q, i) ≤ ρ(q, j ).

Considering every image in the collection as a

query image, a set of ranked lists T = {τ

, τ

, . . . , τ

}

can be obtained. The ranked lists are used as input to

the rank correlation measures. The set T represents a

rich source of similarity information about the collec-

A Multi-level Rank Correlation Measure for Image Retrieval

371

tion, which can be exploited through rank correlation

measures in unsupervised learning tasks, as discussed

in the experimental evaluation.

3 MULTI-LEVEL CORRELATION

MEASURE

This section presents the proposed Multi-Level Cor-

relation Measure (MLCM). The key ideas and moti-

vations are introduced in Section 3.1. The formal def-

inition of MLCM is presented in Section 3.2, while

Section 3.3 discusses efﬁciency and complexity as-

pects.

3.1 Overview

In most of real-world information retrieval applica-

tions, both human and machines are interested in top-

k lists (Fagin et al., 2004). The size constraint allows

to handle the overhead of information and concentrate

on the essential. However, the deﬁnition of k often of-

fers a challenging trade-off. While small values can

ignore relevant information, large values can include

useless data or detrimental noise.

A natural way to reduce this problem is given by

weighted rank correlation measures (Vigna, 2015).

Assigning weights to top positions allows to consider

more information, once the low weights are assigned

to lower positions of ranked lists included in the anal-

ysis. Nevertheless, even for weighted measures, the

k continues to represent a binary boundary which

can exclude useful information right after the deﬁned

threshold.

With the objective of proposing a novel alternative

to this problem, we propose a multi-level approach.

Firstly, the elements at the top-k positions of a ranked

list are considered. The co-occurrence of such ele-

ments are veriﬁed in the other ranked list, but con-

sidering a relaxed level, until the top-ck positions. In

the following, the same analysis is reciprocally per-

formed by inverting the ranked lists and the thresh-

olds. In this way, relevant elements at top-k positions

of one ranked list and just after k in the other ranked

list can also contribute positively to the correlation

analysis.

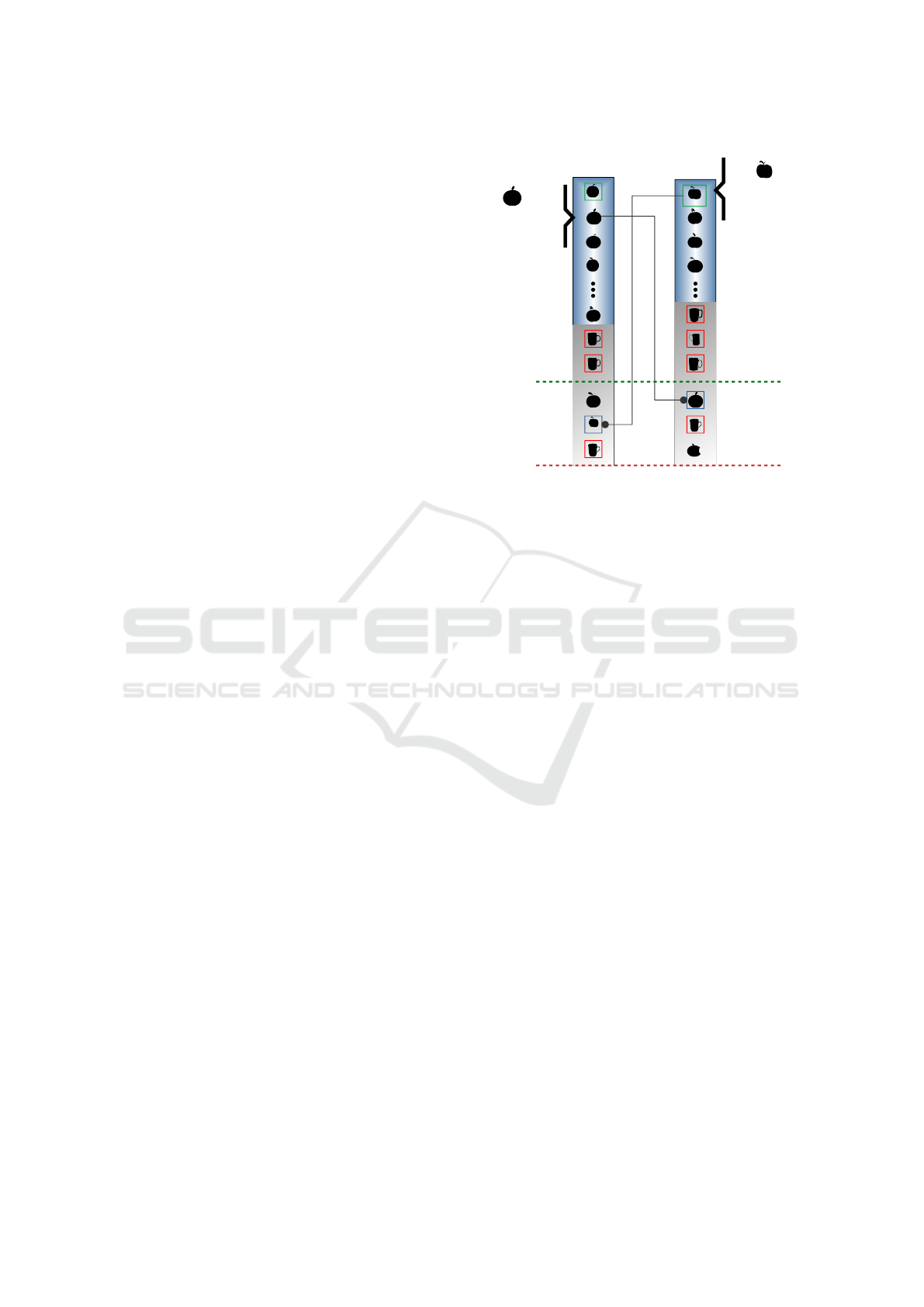
The proposed approach and its beneﬁts are illus-

trated in Figure 1, representing the comparison be-

tween two ranked lists τ

and τ

. Analogous to typical

real-world ranked lists, the top positions present high-

effective results (in blue). In the following, a mixed

zone contains both relevant and non-relevant elements

(in gray). Both elements x and y are at top-k positions

τ (y) = k+2ᵢ

τ (y)ⱼ = 1

τ (x) = 2ᵢ

τ (x)ⱼ = k+1

τj

τi

Figure 1: Multi-Level Correlation Measure (MLCM) ap-

plied to rank comparison between ranked lists τ

and τ

of one ranked list and at top-ck positions of the other

ranked list.

3.2 MLCM Formal Deﬁnition

This section formally deﬁnes the proposed MLCM

measure. The measure is computed considering the

top positions of ranked lists. Therefore, ﬁrstly we de-

ﬁned a k-neighborhood set N (τ

, k), which contains

the k most similar images to img

. The set can be for-

mally deﬁned according to our rank model as follows:

N (τ

, k) = {e : e ∈ S, S ⊆ C , |S| = k∧

∀x ∈ S, y ∈ (C − S ) : τ

(x) < τ

(y)}.

(1)

In order to characterize the multi-level behav-

ior of the measure, an extended intersection set

E(τ

, τ

, c, k) between ranked lists τ

and τ

is deﬁned.

The set takes the ranked list τ

at a level of top-k po-

sitions, while takes the τ

at a lower level, of top-ck.

Formally, the set is deﬁned as:

E(τ

, τ

, c, k) = N (τ

, k) ∩ N (τ

, c × k). (2)

The similarity between the ranked lists τ

and τ

is directly associated to the size of the extended in-

tersection set, once similar ranked lists are expected

to present co-occurrences at top positions. Beyond

that, the proposed MLCM measure assigns a weight

to each image in the set according to the position that

it appears in each ranked list.

An one-directional MLCM measure is deﬁned by

the sum of products of weights assigned to each ele-

ment in the extended intersection set. The function µ

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

372

is formally deﬁned as:

µ(τ

, τ

) =

∑

x∈E(τ

,τ

,c,k)

(x) × w

(x), (3)

where w

(x) denotes the weight of element img

in the

ranked list τ

. Higher weights are assigned to ﬁrst po-

sitions, with an exponential formulation according to

the position of img

in the ranked list τ

. The function

is formally deﬁned as:

(x) = p

(x)

, (4)

where p is a parameter deﬁned in the interval [0,1].

A low value of p reduces the weights of elements lo-

cated at lower positions of ranked lists.

The one-directional MLCM measure deﬁnition

given by the function µ(τ

, τ

, ) is not symmetric, due

to different levels deﬁned in the ranked lists. There-

fore, we can verify that µ(τ

, τ

) 6= µ(τ

, τ

). In order

to solve this problem, making the function symmetric,

a bi-directional MLCM measure is deﬁned as follows:

MLCM(τ

, τ

) = (1 − p) × µ(τ

, τ

) × µ(τ

, τ

). (5)

In addition to effectiveness, efﬁciency aspects are

crucial in real-world scenarios. The MLCM measure

can be also efﬁciently computed as discussed in the

next section.

3.3 Efﬁciency and Complexity Aspects

All the analysis computed by the MLCM measure are

constrained to the top-ck positions of ranked lists, and

therefore, independent of the collection size (n) or the

size of ranked lists (L). Such characteristic is crucial

to allow an efﬁcient computation of the measure.

We consider a hash table data structure, for repre-

senting each ranked list. The structure allows to insert

and ﬁnd elements in O(1) time complexity. Therefore

the construction of hash tables presents a complex-

ity of O(ck). In order to compute the extended in-

tersection set, for each element at top-k positions of

one ranked list, its presence in the other hash table

should be veriﬁed. Once each veriﬁcation requires

O(1) complexity, the whole set can be computed in

O(k).

The computation of function µ (Equation 3) re-

quires to retrieve the position of each element in the

intersection set in both ranked lists. Again, using

the hash structure, the position can be computed in

O(1) for each element, totaling O(ck) for the whole

set. In this way, the MLCM can be fully computed

in O(ck), i.e, in linear time according to the extended

ck-neighborhood.

4 EXPERIMENTAL EVALUATION

This section presents a broad experimental evaluation

conducted to assess the effectiveness of the proposed

measure. Section 4.1 discusses aspects of the experi-

mental protocol, describing the datasets, features, and

the effectiveness measures considered in the exper-

iments. Section 4.2 evaluates the proposed MLCM

measure in weakly supervised scenarios, on the task

of identifying similarity relationships among images

of the same class. Section 4.3 evaluates MLCM in

unsupervised re-ranking tasks for image retrieval, in

comparison with other rank correlation measures.

4.1 Experimental Protocol

This subsection describes the experimental protocol

adopted in this work, including information about the

datasets, features, effectiveness measures, and param-

eter settings.

The experimental evaluation considered three

public datasets, with different characteristics and

sizes ranging from 1,360 to 5,000 images. The

datasets used were MPEG-7 (Latecki et al., 2000),

Flowers (Nilsback and Zisserman, 2008) and

Corel5k (Liu and Yang, 2013).

Multiple features were considered

, including

global, local, and deep learning ones. In the ﬁrst set

of experiments, two features were used per dataset.

For the re-ranking evaluation, all the features were

considered. The employed Convolutional Neural

Networks (CNN) were all trained on the ImageNet

dataset. The implementations of these CNNs are pub-

licly available on the PyTorch framework

In the experimental evaluation, different well-

established effectiveness measures are considered,

such as Precision, Recall, F-Measure and Mean Av-

erage Precision (MAP).

4.1.1 Parameters Settings

The MLCM measure used the multi-level parameter

as c = 2 for all experiments. Regarding the similar-

ity relationships identiﬁcation tasks (Section 4.2), the

MLCM measure used the parameter value as p=0.93.

The size of neighborhood k was used as k=10 for

MPEG-7 and k=50 for Corel5k and Flowers datasets.

The baseline measures used k=20 for MPEG-7 and

k=50 for the Corel5k and Flowers datasets.

For the unsupervised re-ranking tasks (Sec-

tion 4.3), the parameter p=0.96 was used in all ex-

For the MPEG-7 dataset, we have used the distances to

other images as features.

https://github.com/Cadene/pretrained-models.pytorch

A Multi-level Rank Correlation Measure for Image Retrieval

373

periments

. The neighborhood size k was deﬁned as

k=20 for MPEG-7 and k=50 for Corel5k and Flow-

ers datasets. The re-ranking algorithm used T =2 for

MPEG7 and T =3 for Corel5k and Flowers datasets.

4.2 Similarity Relationships

Identiﬁcation

This section presents the experimental evaluation of

MLCM measure on weakly supervised scenarios,

with the objective of identifying similar elements.

Section 4.2.1 describes the task while Section 4.2.2

presents the baselines. Section 4.2.3 discusses the re-

sults.

4.2.1 Task Description

In a weakly supervised scenario, where only a small

set of labeled images are available, identifying sim-

ilar images is of crucial relevance. In this way, we

evaluate the capacity of MLCM measure on identify-

ing similar elements (of the same class) in the dataset.

If two images have their ranked lists very correlated,

i.e, with a rank correlation measure greater than a cer-

tain threshold, we assume that they belong to the same

class. This assumption may be more or less accurate

depending on the effectiveness of each measure.

With the objective of analyzing the behavior of the

proposed measure, an experiment was conducted by

varying the threshold to evaluate the impact in the ef-

fectiveness measures. High values of threshold lead

to small or insigniﬁcant expansions. On the other

hand, as the values decrease, the number of images

contained in the expanded set also increases. How-

ever, it tends to incorporate incorrect images in this

set as well, which can be especially harmful to the ac-

curacy results. This trade-off can be analyzed through

Precision and Recall measures.

4.2.2 Compared Rank Correlation Measures

Six correlation measures often used in the lit-

erature were considered as baselines and have

their results compared to MLCM measure. The

measures used were Intersection (Fagin et al.,

2003), Jaccard (Levandowsky and Winter, 1971),

Jaccard

(Okada et al., 2015), Kendallτ (Fagin et al.,

2003), Spearman (Fagin et al., 2003) and RBO (Web-

ber et al., 2010).

Except for AIR features on the MPEG-7 dataset, which

used p=0.81

4.2.3 Results and Discussion

Firstly, we evaluate the impact of threshold varia-

tion on Precision, Recall, and F-Measure. The curves

were reported in according to the threshold variation

in the interval [0, 1]. Figures 2 and 3 report the results

for the datasets MPEG-7, Flowers and Corel5K. The

features used were ASC for MPEG-7 and RESNET

for Flowers, and Corel5K. For comparison purposes,

we also report the results obtained by RBO measures

considering the same scenario. We can observe that

MLCM results are more stable to threshold variations

when considering F-Measure. RBO often achieves

higher precision scores, but with smaller recall scores.

In opposite, MLCM combine better both measures,

which leads to higher F-Measure scores.

The threshold that achieved the highest F-measure

for each measure/feature/dataset is reported in Ta-

ble 1. The results with the two best F-Measure values

are highlighted in bold for each feature and dataset

with the corresponding threshold. As we can observe,

the results obtained by MLCM are very signiﬁcant,

since F-Measure is practically always between the

two best results, which does not occur for any other

metric. The average F-measure is presented for each

measure and it is noticeable that MLCM presented

the highest mean as well. We can also observe that,

in comparison to the RBO measure, MLCM achieved

superior or comparable results in all the cases.

4.3 Unsupervised Re-ranking on Image

Retrieval Tasks

This section discusses the evaluation of MLCM mea-

sure on unsupervised re-ranking tasks of image re-

trieval. Section 4.3.1 provides more details about the

task. Section 4.3.2 discusses the results and 4.3.3

present some visual results.

4.3.1 Task Description

Despite the huge advances on image retrieval

achieved in last decades, mainly supported by deep

learning technologies, computing effective similar-

ity measures remains a challenging tasks. In this

scenario, various approaches have been proposed

for post-processing image similarities through more

global a contextual analysis. Such unsupervised re-

ranking approaches provides an attractive solution,

capable of signiﬁcantly improving the retrieval results

without the use of any labeled data.

The RL-Sim* (Okada et al., 2015) method is an

unsupervised re-ranking algorithm that relies on a

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

374

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Effectiveness Scores for Different Thresholds

Effectiveness Measure

Threshold

F Measure

Recall

Precision

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Effectiveness Scores for Different Thresholds

Effectiveness Measure

Threshold

F Measure

Recall

Precision

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Effectiveness Scores for Different Thresholds

Effectiveness Measure

Threshold

F Measure

Recall

Precision

(a) MPEG-7 (b) Flowers (c) Corel5k

Figure 2: Precision, Recall and F-Measure obtained for MLCM measure considering different thresholds. Results for MPEG-

7 - ASC, Flowers - RESNET, and Corel5k - RESNET, respectively.

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Effectiveness Measure

Effectiveness Scores for Different Thresholds

F Measure

Recall

Precision

Threshold

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Effectiveness Scores for Different Thresholds

Effectiveness Measure

Threshold

F Measure

Recall

Precision

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Effectiveness Scores for Different Thresholds

Effectiveness Measure

Threshold

F Measure

Recall

Precision

(a) MPEG-7 (b) Flowers (c) Corel5k

Figure 3: Precision, Recall and F-Measure obtained for RBO measure considering different thresholds. Results for MPEG-7

- ASC, Flowers - RESNET, and Corel5k - RESNET, respectively.

Table 1: F-Measure results: maximum F-Measure achieved by each rank correlation measure on different datasets.

MPEG-7 Flowers Corel5k

Mean

ASC CFD ACC RESNET ACC RESNET

MLCM

F-Measure 0.859 0.849 0.247 0.641 0.287 0.739 0.6037

Threshold 0.2 0.15 0.05 0.05 0.05 0.05 —

Intersection

F-Measure 0.850 0.838 0.226 0.633 0.286 0.759 0.5987

Threshold 0.3 0.25 0.05 0.05 0.15 0.15 —

Jaccard

F-Measure 0.825 0.810 0.243 0.616 0.281 0.756 0.5885

Threshold 0.3 0.25 0.1 0.15 0.1 0.1 —

Jaccard

F-Measure 0.853 0.842 0.248 0.626 0.289 0.759 0.6028

Threshold 0.15 0.1 0.05 0.05 0.05 0.05 —

Kendalτ

F-Measure 0.809 0.802 0.241 0.618 0.27 0.697 0.5728

Threshold 0.4 0.4 0.3 0.35 0.3 0.35 —

RBO

F-Measure 0.858 0.849 0.232 0.626 0.268 0.682 0.5858

Threshold 0.1 0.1 0.05 0.05 0.05 0.05 —

Spearman

F-Measure 0.851 0.838 0.245 0.633 0.286 0.759 0.6020

Threshold 0.3 0.25 0.15 0.15 0.15 0.15 —

correlation measure in order to compute a new sim-

ilarity score among images by comparing their kNN

sets. In this section, the proposed MLCM measure

is evaluated on re-ranking tasks through the RL-Sim*

algorithm. The evaluation is conducted considering

several recent deep learning features. We used the

RL-Sim* implementation available on the Unsuper-

vised Distance Learning Framework (UDLF) (Valem

and Pedronette, 2017). The RBO measure was also

considered as a baseline for this evaluation.

4.3.2 Results and Discussion

Tables 2, 3, and 4 present the results for re-

ranking tasks on MPEG-7, Corel5k and Flowers

datasets. Different effectiveness measures are

A Multi-level Rank Correlation Measure for Image Retrieval

375

Table 2: Effectiveness evaluation of MLCM compared to RBO, considering different measures on MPEG-7 dataset.

MPEG-7 Effectiveness

Descriptors Measures P@10 P@15 P@20 P@30 P@50 P@100 Recall@40 MAP

AIR MLCM 0.96 0.953 0.939 0.657 0.4 0.2 1.0 0.969

(Gopalan et al., 2010) RBO 0.951 0.949 0.939 0.656 0.4 0.2 0.999 0.961

ASC MLCM 0.927 0.904 0.874 0.619 0.382 0.194 0.946 0.908

(Ling et al., 2010) RBO 0.924 0.903 0.878 0.617 0.381 0.194 0.946 0.907

BAS MLCM 0.842 0.786 0.734 0.536 0.341 0.179 0.834 0.778

(Arica and Vural, 2003) RBO 0.831 0.781 0.735 0.534 0.34 0.178 0.834 0.774

CFD MLCM 0.934 0.907 0.878 0.621 0.384 0.195 0.949 0.912

(Pedronette and da S. Torres, 2010) RBO 0.929 0.906 0.879 0.617 0.382 0.194 0.944 0.909

IDSC MLCM 0.91 0.875 0.845 0.605 0.373 0.191 0.925 0.882

(Ling and Jacobs, 2007) RBO 0.907 0.875 0.851 0.603 0.373 0.191 0.925 0.882

SS MLCM 0.55 0.478 0.424 0.332 0.227 0.13 0.539 0.458

(da S. Torres and Falc

ao, 2007) RBO 0.538 0.465 0.417 0.328 0.224 0.128 0.531 0.451

Table 3: Effectiveness evaluation of MLCM compared to RBO, considering different measures on Corel5k dataset.

Corel5k Effectiveness

Descriptors Measure P@10 P@15 P@20 P@30 P@50 P@100 Recall@40 MAP

CNN-BnInception MLCM 0.895 0.882 0.872 0.855 0.823 0.716 0.336 0.739

(Ioffe and Szegedy, 2015) RBO 0.887 0.871 0.858 0.837 0.801 0.691 0.328 0.712

CNN-DPNet MLCM 0.905 0.893 0.885 0.87 0.846 0.776 0.343 0.807

(Chen et al., 2017) RBO 0.899 0.886 0.876 0.859 0.831 0.754 0.338 0.785

CNN-FBResNet MLCM 0.924 0.914 0.906 0.895 0.872 0.804 0.354 0.836

(He et al., 2016) RBO 0.913 0.9 0.891 0.878 0.855 0.776 0.347 0.809

CNN-ResNet MLCM 0.923 0.912 0.904 0.891 0.867 0.794 0.352 0.829

(He et al., 2016) RBO 0.919 0.905 0.895 0.879 0.854 0.771 0.347 0.808

CNN-ResNeXt MLCM 0.921 0.911 0.904 0.891 0.869 0.795 0.352 0.827

(Xie et al., 2017) RBO 0.915 0.903 0.894 0.878 0.852 0.771 0.346 0.804

CNN-VGGNet MLCM 0.874 0.858 0.846 0.824 0.788 0.678 0.322 0.705

(Liu and Deng, 2015) RBO 0.863 0.844 0.83 0.806 0.765 0.657 0.314 0.679

CNN-Xception MLCM 0.891 0.877 0.867 0.851 0.82 0.723 0.335 0.737

(Chollet, 2017) RBO 0.883 0.866 0.853 0.834 0.8 0.7 0.327 0.714

Table 4: Effectiveness evaluation of MLCM compared to RBO, considering different measures on Flowers dataset.

Flowers Effectiveness

Descriptors Measure P@10 P@15 P@20 P@30 P@50 P@100 Recall@40 MAP

CNN-BnInception MLCM 0.863 0.845 0.829 0.801 0.749 0.578 0.387 0.71

(Ioffe and Szegedy, 2015) RBO 0.853 0.834 0.817 0.791 0.748 0.58 0.386 0.704

CNN-DPNet MLCM 0.85 0.832 0.817 0.791 0.747 0.577 0.385 0.702

(Chen et al., 2017) RBO 0.842 0.818 0.805 0.779 0.735 0.58 0.379 0.69

CNN-FBResNet MLCM 0.871 0.854 0.841 0.819 0.774 0.591 0.398 0.734

(He et al., 2016) RBO 0.857 0.838 0.824 0.802 0.76 0.594 0.391 0.72

CNN-ResNet MLCM 0.857 0.838 0.825 0.802 0.759 0.587 0.391 0.723

(He et al., 2016) RBO 0.851 0.831 0.818 0.795 0.753 0.592 0.387 0.715

CNN-ResNeXt MLCM 0.852 0.839 0.825 0.804 0.766 0.593 0.392 0.727

(Xie et al., 2017) RBO 0.844 0.827 0.812 0.789 0.748 0.589 0.384 0.709

CNN-VGGNet MLCM 0.779 0.755 0.735 0.702 0.646 0.487 0.338 0.591

(Liu and Deng, 2015) RBO 0.775 0.749 0.728 0.695 0.639 0.487 0.333 0.583

CNN-Xception MLCM 0.826 0.803 0.788 0.761 0.713 0.559 0.368 0.677

(Chollet, 2017) RBO 0.819 0.796 0.777 0.748 0.7 0.555 0.361 0.665

considered: Precision, Recall and MAP. It can be

observed that MLCM achieved the best results in

most of the evaluated features and effectiveness mea-

sures. The MLCM measure also reaches the

highest MAP scores for the three datasets.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

376

(a) Re-Ranking by RBO measure.

(b) Re-Ranking by MLCM measure.

Figure 4: Visual results before and after RL-Sim* Re-Ranking computed by RBO and MLCM measures on MPEG-7 dataset.

4.3.3 Visual Results

Visual retrieval results for MPEG-7 dataset are illus-

trated on Figure 4. The ﬁgure shows the results before

and after the application RL-Sim* re-ranking algo-

rithm considering both the RBO and MLCM rank cor-

relation measures. The query image is illustrated in a

green board. The ranked lists obtained are presented

on the right, with incorrect images in red borders. Re-

markable effectiveness gains can be observed.

5 CONCLUSIONS

In this work, a novel rank correlation measure is pro-

posed, capable of exploiting multi-level information

of ranked lists. A diversiﬁed experimental evaluation

showed that the proposed MLCM measure achieves

results comparable or superior to other relevant mea-

sures. As future work, we intend to evaluate other re-

trieval scenarios (e.g. video, sound, and text retrieval

for example).

ACKNOWLEDGEMENTS

The authors are grateful to S

ao Paulo Research

Foundation - FAPESP (grants #2018/15597-6,

#2017/25908-6, #2019/11104-8, and #2020/11366-

0), Brazilian National Council for Scientiﬁc

and Technological Development - CNPq (grant

#308194/2017-9) and Microsoft Research.

REFERENCES

Arica, N. and Vural, F. T. Y. (2003). BAS: a perceptual

shape descriptor based on the beam angle statistics.

Pattern Recognition Letters, 24(9-10):1627–1639.

Chen, Y., Li, J., Xiao, H., Jin, X., Yan, S., and Feng, J.

(2017). Dual path networks. In Guyon, I., Luxburg,

U. V., Bengio, S., Wallach, H., Fergus, R., Vish-

wanathan, S., and Garnett, R., editors, Advances in

Neural Inf. Processing Systems, pages 4467–4475.

Chen, Y., Li, X., Dick, A., and Hill, R. (2014). Ranking

consistency for image matching and object retrieval.

Pattern Recognition, 47(3):1349 – 1360.

Chollet, F. (2017). Xception: Deep learning with depthwise

separable convolutions. In 2017 IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 1800–1807.

Couso, I., Strauss, O., and Saulnier, H. (2018). Kendall’s

rank correlation on quantized data: An interval-valued

approach. Fuzzy Sets and Systems, 343:50 – 64.

da S. Torres, R. and Falc

ao, A. X. (2007). Contour Salience

Descriptors for Effective Image Retrieval and Analy-

sis. Image and Vision Computing, 25(1):3–13.

Fagin, R., Kumar, R., Mahdian, M., Sivakumar, D., and

Vee, E. (2004). Comparing and aggregating rankings

with ties. In 23th ACM SIGMOD Symposium on Prin-

ciples of Database Systems (PODS’04), pages 47–58.

Fagin, R., Kumar, R., and Sivakumar, D. (2003). Compar-

ing top k lists. In SODA’03, pages 28–36.

Farnoud Hassanzadeh, F. and Milenkovic, O. (2014). An

axiomatic approach to constructing distances for rank

comparison and aggregation. IEEE Transactions on

Information Theory, 60(10):6417–6439.

Gopalan, R., Turaga, P., and Chellappa, R. (2010).

Articulation-invariant representation of non-planar

shapes. In ECCV’2010, volume 3, pages 286–299.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In IEEE CVPR

2016, pages 770–778.

Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-

celerating deep network training by reducing internal

covariate shift. In ICML’2015, pages 448–456.

Kumar, R. and Vassilvitskii, S. (2010). Generalized dis-

tances between rankings. In Proceedings of the 19th

International Conference on World Wide Web, WWW

’10, page 571–580.

Latecki, L. J., Lakmper, R., and Eckhardt, U. (2000). Shape

descriptors for non-rigid shapes with a single closed

contour. In CVPR, pages 424–429.

A Multi-level Rank Correlation Measure for Image Retrieval

377

Levandowsky, M. and Winter, D. (1971). Distance between

sets. Nature, 243:34 – 35.

Ling, H. and Jacobs, D. W. (2007). Shape classiﬁcation

using the inner-distance. PAMI, 29(2):286–299.

Ling, H., Yang, X., and Latecki, L. J. (2010). Balancing de-

formability and discriminability for shape matching.

In ECCV, volume 3, pages 411–424.

Liu, G.-H. and Yang, J.-Y. (2013). Content-based image

retrieval using color difference histogram. Pattern

Recognition, 46(1):188 – 198.

Liu, S. and Deng, W. (2015). Very deep convolutional

neural network based image classiﬁcation using small

training sample size. In ACPR 2015, pages 730–734.

Nilsback, M.-E. and Zisserman, A. (2008). Automated

ﬂower classiﬁcation over a large number of classes.

Computer Vision, Graphics and Image Processing,

pages 722–729.

Okada, C. Y., Pedronette, D. C. G., and da S. Torres,

R. (2015). Unsupervised distance learning by rank

correlation measures for image retrieval. In ACM

ICMR’2015, pages 331–338.

Pedronette, D. C. G. and da S. Torres, R. (2010). Shape

retrieval using contour features and distance optmiza-

tion. In VISAPP, volume 1, pages 197 – 202.

Pedronette, D. C. G., Valem, L. P., Almeida, J., and da S.

Torres, R. (2019). Multimedia retrieval through un-

supervised hypergraph-based manifold ranking. IEEE

Trans. on Image Processing, 28(12):5824–5838.

Qin, D., Gammeter, S., Bossard, L., Quack, T., and van

Gool, L. (2011). Hello neighbor: Accurate object re-

trieval with k-reciprocal nearest neighbors. In CVPR,

pages 777 –784.

Tan, L. and Clarke, C. L. A. (2015). A family of rank simi-

larity measures based on maximized effectiveness dif-

ference. IEEE Transactions on Knowledge and Data

Engineering, 27(11):2865–2877.

Valem, L. P., Oliveira, C. R. D., Pedronette, D. C. G. a., and

Almeida, J. (2018). Unsupervised similarity learning

through rank correlation and knn sets. ACM Trans.

Multimedia Comput. Commun. Appl., 14(4).

Valem, L. P. and Pedronette, D. C. G. (2020). Unsupervised

selective rank fusion for image retrieval tasks. Neuro-

computing, 377:182–199.

Valem, L. P. and Pedronette, D. C. G. a. (2017). An un-

supervised distance learning framework for multime-

dia retrieval. In ACM on International Conference on

Multimedia Retrieval, ICMR ’17, pages 107–111.

Vigna, S. (2015). A weighted correlation index for rankings

with ties. In International Conf. on World Wide Web,

WWW ’15, page 1166–1176.

Webber, W., Moffat, A., and Zobel, J. (2010). A similarity

measure for indeﬁnite rankings. ACM Transactions on

Information Systems, 28(4):20:1–20:38.

Xie, S., Girshick, R., Doll

ar, P., Tu, Z., and He, K. (2017).

Aggregated residual transformations for deep neural

networks. In IEEE CVPR 2017.

Xue, Z., Lin, Z., Wang, H., and McClean, S. (2020). Quan-

tifying consensus of rankings based on q-support pat-

terns. Information Sciences, 518:396 – 412.

Yilmaz, E., Aslam, J. A., and Robertson, S. (2008). A new

rank correlation coefﬁcient for information retrieval.

In ACM SIGIR 2008, page 587–594.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

378